Abstract
Cameras play a prominent role in the context of 3D data, as they can be designed to be very cheap and small and can therefore be used in many 3D reconstruction systems. Typical cameras capture video at 20 to 60 frames per second, resulting in a high number of frames to select from for 3D reconstruction. Many frames are unsuited for reconstruction as they suffer from motion blur or show too little variation compared to other frames. The camera used within this work has built-in inertial sensors. What if one could use the built-in inertial sensors to select a set of key frames well-suited for 3D reconstruction, free from motion blur and redundancy, in real time? A random forest classifier (RF) is trained by inertial data to determine frames without motion blur and to reduce redundancy. Frames are analyzed by the fast Fourier transformation and Lucas–Kanade method to detect motion blur and moving features in frames to label those correctly to train the RF. We achieve a classifier that omits successfully redundant frames and preserves frames with the required quality but exhibits an unsatisfied performance with respect to ideal frames. A 3D reconstruction by Meshroom shows a better result with selected key frames by the classifier. By extracting frames from video, one can comfortably scan objects and scenes without taking single pictures. Our proposed method automatically extracts the best frames in real time without using complex image-processing algorithms.
1. Introduction
A detailed description of the environment in the form of images or 3D data is of major importance for a whole range of applications. For example, such data are used for planning and developing our transport infrastructure [1], as well as geomonitoring [2] or medical practice [3]. The data are collected by a wide variety of sensors. In most cases, these are light detection and ranging (LiDAR), cameras, or radar. Cameras play a prominent role in this context, as they can be designed to be very cheap and small and can therefore be used in almost any detection system—either as a stand-alone acquisition system or in combination with the previously mentioned sensors.
When extracting or selecting images from videos at 30 frames per second, many images are created in a very short time. However, if one makes fast motions, translational, rotational, or even both, the frames can suffer from motion blur [4], as seen in Figure 1. Recordings of fast-moving objects can distort their shape and appear blurry. The problem can be simplified by ensuring that only static objects are in the recording. More simply, only the motion of the camera itself contributes to the distortion of the image. Moreover, during the video recording, one obtains many redundant images. At 30 frames per second, many of the images contain almost the same information, which is not necessary for further processes. Due to the high recording rate, the angular changes between two successive images are only marginal. With faster motions, this angle difference would increase, but the quality would suffer. If these images are used for further processes, such as 3D reconstruction, this would significantly increase the computation time. In addition, the detected features would lose accuracy when projected into three-dimensional space by less-accurate matching feature points if the images are distorted, due to faster motions during recording. If we could select images automatically, we would thereby reduce the computation time and expect a more accurate result. So how can one manage to extract key frames automatically and efficiently in real time to use the best-suited images for scene reconstruction, with respect to quality and redundancy?
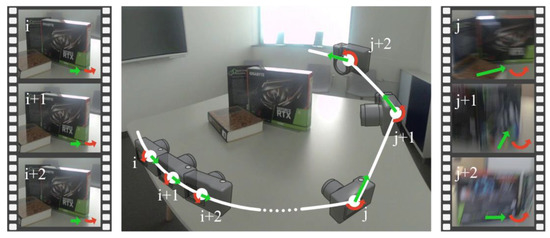
Figure 1.
Two sequences of consecutive images within a video stream shot along a trajectory (white) around a scene to be 3D reconstructed. The left sequence (i, i + 1, i + 2) contains image quality well-suited for reconstruction but no significant change in the image contents. The right sequence (j, j + 1, j + 2) contains variation in viewing angle and parallax but the images are motion blurred due to heavy camera motion. The camera’s IMU tracks translational acceleration (green) and angular velocity (red) for each frame. A set of images well-suited for reconstruction can be selected solely based on the IMU data without time-consuming image analysis.
2. Related Work
In the research, this problem is called “key frame extraction” and finds application in different fields. Most methods focus on finding images without motion blur and guaranteeing a certain coverage between the best images. Ahmed et al. [5] developed a method to extract key frames from video streams. First, a correspondence ratio determines if successive key frames share enough features with the preceding frame. Then, each key frame pair is investigated for degenerate motion or structure due to geometric robust information criteria (GRIC). Based on best-estimated epipolar geometry according to GRIC and a reprojection error from the point-to-epipolar line, key frames are selected. However, the proposed method rejects frames due to degenerate motion or structure that discards frames that can contain information of interest and assumes a recording strategy without camera rotation about its axis.
The method proposed by Zhang et al. [6] finds well-suited frames from recordings of a drone-mounted camera based on a blur metric and an overlap rate between adjacent frames. The overlap is calculated with additional flight control information, which is logging position and velocity of each frame. Frames satisfying the overlap ratio are further processed to determine if they also satisfy the blur metric due to intensity changes. In the last step, a geometric robust information criterion must be met, a strategy to compute the phenomenon of degradation using the fundamental matrix and the resulting reprojection errors between adjacent frames. Due to drift errors in the integration of acceleration and angular velocity, we cannot compute an overlap with inertial signals. The phenomenon of degradation would also limit the recording strategy and information of interest.
The work published by Ishijima et al. [7] describes an approach to find the best frame automatically from microendoscopy videos. The target key frames must be free of motion artifacts and exhibit sufficient intensity. The video is divided into a subset of frames that exhibit a calculated minimum frame-to-frame variation, which are depicted as motion artifacts. Secondly, they focus on the entropy of the intensity within each frame, which means that the frame’s image contents need to be analyzed. Lastly, by finding features in each frame, the method proposes to select frames with the most features. Besides the fact that the last step extracts the best frame, they focus on image content and minimizing the frame-to-frame variation. Thus, this method keeps redundant images and prevents large differences from consecutive images with respect to image content. The approach presented by Ren et al. [8] is designed to find the best key frame from a short video. By training a convolutional neural network with images, the proposed algorithm is supposed to select the best frame within a short video. This is a strong limitation on video duration and moreover not real-time capable. We aim to make real-time selection possible, minimizing the number of frames with motion blur and redundant scenes.
The camera used in this work, VuzeXR from Human Eyes Technologies Ltd., contains a built-in inertial measurement unit (IMU) with six degrees of freedom, tracking information about translational acceleration and angular velocity. More precisely, the inertial data are placed directly in the MP4 files. The MP4 files are encoded using the MPEG format and are structured in containers that either contain information or more containers. Recording videos with 30 frames per second produces many frames in a short time and motion blur due to camera motion. This led to the overall problem of redundant and low-quality frames. However, what if one could use the IMU to recognize suitable frames? By recording IMU data while recording, we can use the angular velocity and acceleration of the camera to make a statement about the quality of the images and determine if the camera has moved. If the camera does not move while recording, identical images are produced. If the camera moves too much, images suffer from motion blur. For this purpose, a calibration procedure firstly defines the requirements for which frames are suitable for further processing. The requirements are defined in terms of quality and motion in the frames itself. Quality is defined as the intensity change in a frame. By means of the 2D discrete Fourier transformation (2D-DFT), one can detect those intensity changes. Such intensity changes in a frame depend on the sharpness of edges. If the sharpness decreases, one can detect lower intensity changes, which leads to blurred areas. The second requirement refers to motion in frame-to-frame correspondences. The underlying assumption is that consecutive frames with little motion result in a high number of redundant frames. By calculating the optical flow via the Lucas–Kanade (LK) method [9], we provided a threshold that stated that the camera was not moving. We draw a direct connection between the current IMU state and the defined requirements of quality and motions in the frames. This leads to an automated way of labeling the inertial data that denotes a frame as good or bad. This paper aims to classify frames by a random forest classifier (RF) to identify suitable frames due to inertial data in real time. The result is an efficient and automated way to classify suitable frames. It is not necessary to perform complex and computationally demanding image-processing algorithms.
3. Materials and Methods
3.1. Quality Requirements
Image quality is a term widely used in the field of image processing. We used the term as a metric for motion blur, which reduces sharpness on edges and spatial details [10]. While recording a video, the user holds the camera by hand and is probably moving around an area and focusing objects. This could be walking, standing still, or motions and rotations by hand. However, such frames in videos can suffer from motion blur depending on the motion of the camera. The aim was to define a ground truth for image quality to detect unsuitable images for further processing. Therefore, we applied the 2D-DFT [11] to each image to detect image intensities in the frequency domain that exhibits sharp or smooth edges. Before applying any labeling to the corresponding inertial data, we calibrated the measurements to define a ground truth with respect to image content and lightning conditions. The DFT relates to mathematical fundamentals in the field of image processing and is an adaption of the continuous Fourier transformation, which is widely used in signal processing. However, the Fourier transformation in general decomposes a function into a sum of sines and cosines with different frequencies. According to image processing, the image is transformed into another coordinate system. However, we wanted to specify a threshold to label images either as bad since they are blurry or as good due to the opposite case.
Quality Threshold
Real digital images do not contain any imaginary part. However, due to the transformation, they are represented as complex numbers, consisting of a real and imaginary part, as z = x + jy, according to the image coordinates. Complex numbers have an angle in the complex plane, as well as a magnitude. We were interested in the magnitude of the decomposed discrete signals of the transformed images. The angle, corresponding to the phase, contains information about the image structure, whereas the magnitude denotes the periodic structure of cosines and sines and those intensities [12]. As proposed by Rekleitis [13], we used the magnitude of the Fourier spectrum to investigate the frame quality. The magnitude was defined as:
where R is the real part and I is the imaginary part of the Fourier transformation. First, we adapted the method proposed by Kalalembang et al. [14], which distinguishes between blurred and homogeneous areas in the image. This makes the analysis more robust and omits homogeneous parts as our calibration setting contains many homogeneous areas. Those have the same magnitude spectrum as blurred areas. Instead of calculating the magnitude for the whole frame, we only needed to perform the calculation of the magnitude on smaller chunks of the frame, divided into several equally sized boxes. We found a box size that fits properly to frame calibration objects that were seen in the captured frame. The experiments showed that if the boxes were too small, areas were restricted to mostly homogeneous areas, and if the boxes were too large, most of the area was dominated by homogeneous areas. To determine homogeneous and heterogeneous boxes, we first calculated the standard deviation of the magnitude spectrum in each box as:
where N denotes the number of samples, the mean magnitude of all samples, and the current samples magnitude. If the standard deviation was relatively low, it indicated a homogeneous area that was not part of the area of interest. Therefore, we needed to define a threshold that separates boxes from homogeneous areas. If the standard deviation of a box exceeded the threshold, it was considered for the quality measurement. The mean of the magnitude was calculated to measure the rate of intensity changes of relevant boxes.
3.2. Motion Requirements
In the last section, we introduced a quality threshold to neglect blurry frames and label the corresponding inertial data. Subsequently, we defined a metric to identify inertial data captured when no motion took place. The underlying assumption was that, while the user does not move during the recording, the camera produces redundant frames containing the same image information as the frames before. Thus, we aimed to reduce the number of redundant frames by means of the IMU. The optical flow determines pixel motion while holding the camera in hand with approximately no motion. Optical flow denotes the motion of pixels in a certain area between two consecutive frames. Motion occurs due to camera motion or moving objects. There are different approaches that measure the optical flow. A widely used algorithm to calculate the optical flow is the Lucas–Kanade (LK) algorithm [8], which exhibits a good performance and a low error rate and is easy to implement [15]. The LK algorithm applies to sparse scenes that define a window of n = mxm pixels around a point of interest, so-called feature points. A feature detection algorithm, such as the scale-invariant feature transform (SIFT) [16] or Harris corner detection [17], finds those points. The method assumes that the motion within such a patch is constant. However, if the motion is too fast, the direction of the intensity change is not trackable anymore because the feature point moves out of the window and violates the constant brightness assumption. Pixel motion is described by a 2D vector as between two consecutive frames. The main assumption is that the intensity of a pixel does not change between two consecutive frames, captured in a period Δt. Obviously, Δt must be small enough. The assumption provided by Horn and Schunk [18] with the first order Taylor series yields
where I(x,y,t) denotes the intensity of a pixel, Δx, Δy represent the change in image coordinates, and Δt represents the change in time.
I(x,y,t) = I(x + Δx,y + Δy,t + Δt)
Motion Threshold
The main purpose was to define the minimum amount of motion in terms of inertial data according to the optical flow. Therefore, we used the LK algorithm, which was implemented in the OpenCV open-source computer vision library [19], paired with the Shi-Tomasi corner detection [20] to detect the corresponding feature points. While recording, the camera was in a static position at approximately no motion to investigate the optical flow. The optical flow per frame was averaged. First, we extracted the Euclidean distance from each vector as:
and calculated the mean Euclidean distance of the vectors in each frame. Since our motion requirement is to distinguish between motion and no motion, we wanted to specify a threshold to label frames either as bad to filter redundant images, since they were not recorded during motion, or as good, due to the opposite case.
3.3. Feature Selection
After recording and analyzing the inertial data output of several videos, we determined the sample rate and that inertial data were referenced to video frames. As seen in Table 1, each frame was associated with 16 to 17 inertial data entries according to 3D acceleration and angular velocity. Let and represent a 3D signal of acceleration a or angular velocity ω addressed to a frame with i ≤ 17 inertial signals and n ≤ i. Then, the Euclidean norm of is defined as:

Table 1.
Feature importance resulted from the training of the RF classifier. Features based on angular velocity had more influence on splitting leaves.
Due to the norm, the signals become unbiased in case of negative numbers. Thereupon, we defined the following features.
- Signal Energy.
The signal energy [21] is the sum of the squared signal norm and was normalized by the number of signals per frame as:
where N denotes the number of signals per frame.
- 2.
- Mean Signal Norm.
The mean signal norm denotes the mean over all signals per frame of acceleration and angular velocity, respectively, as:
where N denotes the number of signals addressed to the frame.
- 3.
- Min Signal Norm.
The min signal norm denotes the min norm of all signals per frame of acceleration and angular velocity, respectively, as:
- 4.
- Max Signal Norm.
The max signal norm denotes the max norm of all signals per frame of acceleration and angular velocity, respectively, as:
- 5.
- Signal Variance.
The signal variance is the variance of the signal norms per frame of acceleration and angular velocity, respectively, as:
where N is the number of signals addressed to the frame. The signal variance detects the differences between the signals per frame.
4. Results and Discussion
4.1. Frame Quality Calibration
We investigated this measurement in more than 2500 frames, as seen in Figure 2 Finally, we set the mean of the standard deviation of all inspected frames as the threshold for regions of interest to omit homogeneous areas. Those computations were made on boxes of size 72 × 128 pixels per box, which relates to 15 × 15 boxes per frame, as seen in Figure 3a. Increasing the size of boxes would cover more homogeneous areas per box, which is not desirable. Decreasing the box size would produce insufficient robustness, recognizing homogeneous areas as heterogeneous, as one can see in Figure 3b.
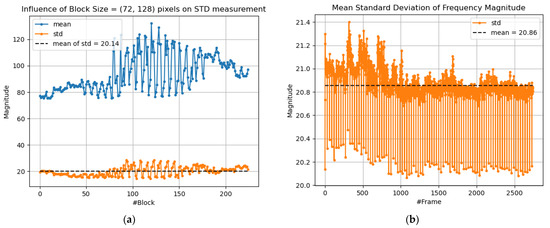
Figure 2.
Analysis of the mean standard deviation of frequency magnitude per image: (a) frequency magnitude and its standard deviation of an image, subdivided in boxes and (b) mean standard deviation of the frequency magnitude per image.
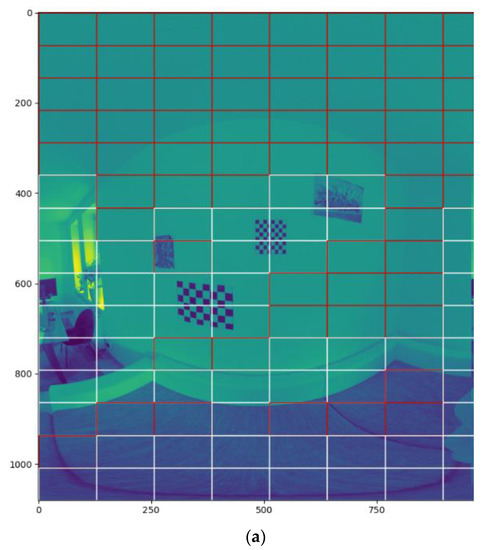
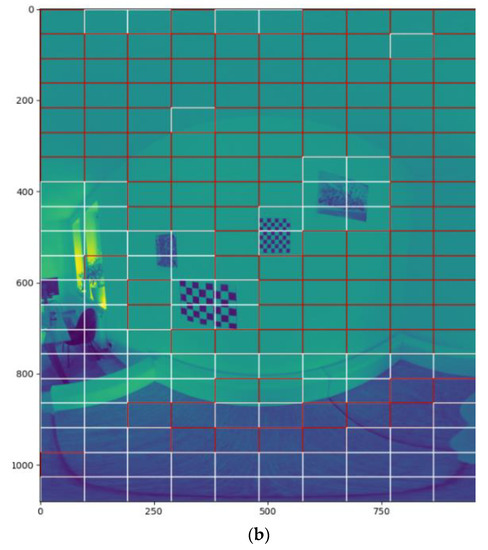
Figure 3.
Subdivision of image into boxes. Investigations showed that a box size of 72 × 128 pixel results in the best false-positive rate. White boxes represent recognized heterogeneous areas: (a) image with box size of 72 × 128 pixel; (b) image with box size of 54 × 96 pixel containing significantly more false-positives.
Then, we applied the 2D-DFT to each frame in the calibration recording while only taking heterogeneous boxes into account. The aim was to define a ground truth as a threshold to determine proper frames. The experiments showed that frames up to a mean magnitude of 98.4 exhibited blurry edges.
4.2. Frame Motion Calibraiton
The recording provided over 2500 frames, as seen in Figure 4. The mean Euclidean distance of the optical flow vectors between frames was 0.43 pixels. According to the deviations in the analysis, we applied the standard deviation to increase the threshold and neglect non-significant motion due to shaking. Thus, we increased the threshold to 0.83 pixels, an example is shown in Figure 5.
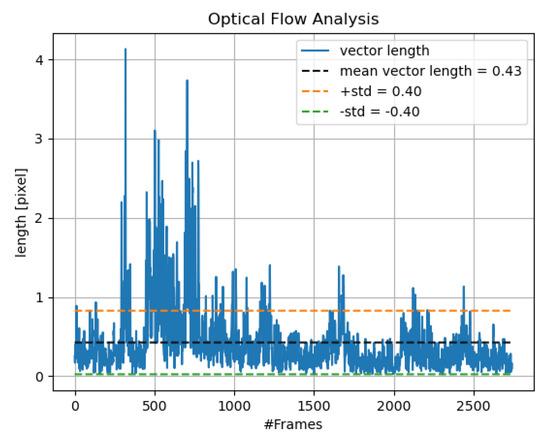
Figure 4.
Mean Euclidean distance of optical flow vectors in images. The video was recorded without motion, and the camera was held in hand.

Figure 5.
Image frequency magnitude threshold identification: (a) image satisfies the mean frequency magnitude threshold and (b) image does not satisfy the mean frequency magnitude threshold.
4.3. Feature Acquisition and Labeling
The labeled samples with respect to the features of acceleration were not clearly separable. While the acceleration sensor was only detecting gravity, measured values of both labels were superimposed. Thus, one cannot explicitly distinguish the difference between the good and bad class at the gravity’s magnitude. Motion was caused as far as the magnitude increased or decreased. Starting at about frame number 5000, there was significant motion as the magnitude decreased and increased; thus, the samples were labeled bad. However, samples were also placed at the gravity’s magnitude. Furthermore, the variance of the acceleration within a frame in Figure 5e was represented in stages. Unfortunately, the increase over motion according to the labels was weak and can be neglected. This behavior can be explained by the fact that an acceleration a of zero does not necessarily mean that there is no velocity v. Acceleration is described by , which states that acceleration is the change of velocity with respect to time, whereas the measurements of the angular velocity rather represented clear differences between samples. First, some samples of class good were recognized in the end where strong rotation was applied. On the other side, some samples were labeled as good while sharing the same magnitude as data that were labeled as bad. Nevertheless, the difference between the classes good and bad was clearly recognizable with the drawback of overlaps. Angular velocity and acceleration were independent of each other. Therefore, it was essential to rely on both inertial signals, independent of the feature, because motion can be described as translational, rotational, or both. If one only took translational motion into account, motion in terms of rotation would be neglected and omit further frames.
4.4. Classification
The first step was to determine the hyperparameters with the training set. We found the best hyperparameters by Grid Search [22]. By choosing the k = 3 for the k-fold cross validation, we increase the amount of test data. Although the dataset comprises more than 6000 frames, the dataset is separated in three sections, as one can see in Figure 6 and Figure 7. Each section contains about 2000 frames, and thus it is important to increase the test set to avoid a marginal amount of data with respect to a section. The three-fold cross-validation achieved a score of 87.51%. Furthermore, we trained the Random Forest with the training set and tested the predictions with the same data. The test resulted in a correct prediction rate of 94.52%. Finally, to evaluate the algorithm and to see if the classifier generalizes well, we tested the trained classifier with the test set, which was never seen during training. The Random Forest contains 20 decision trees with a maximum depth of 20, respectively. The test resulted in a correct prediction rate of 86.09%. Consequently, it seemed that the classifier does neither overfit nor underfit and is generalized with more than 85% of the correct prediction rate. In Figure 8, we can see that 92% of the class bad was positively predicted as bad, and therefore about 8% was negatively predicted as good. On the other hand, the performance of the class good was worse. Only 66% of the class good was positively labeled as good, which is slightly better than a random guess. Thus, 34% of the class good was negatively labeled as bad. Therefore, we took a closer look at the ratios of those predictions. In total, the number of frames in the test set was 1964. On the other hand, the precision of the class bad was nearly 91% with a recall of nearly 92%. The precision with respect to the class good on the test set was about 70%, providing a recall of 66%. Figure 9 represents a RF based on the training of (a), and obtained a test score of 86.1%. The red area denotes the class bad, and the blue area denotes the class good. The strong overlap was responsible for the relatively low precision of class good. Investigating more detailed representations of both classes, we saw that class bad generalized well on unseen data, but class good tended to overfit; neither revealed a good performance on training data or on test data. Table 1 represents the feature importance during training. The features regarding the angular velocity seem much more important, by factor ten, and had greater impact on the splitting of the leaves during training. However, the combination of acceleration and angular velocity was mandatory and achieved the highest performance.
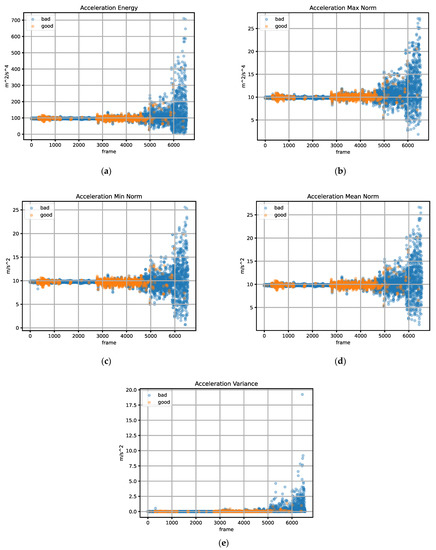
Figure 6.
Labeling result according to motion and quality requirements in accelerometer signal: (a) acceleration energy, (b) acceleration max norm, (c) acceleration min norm, (d) acceleration mean norm, and (e) acceleration variance.
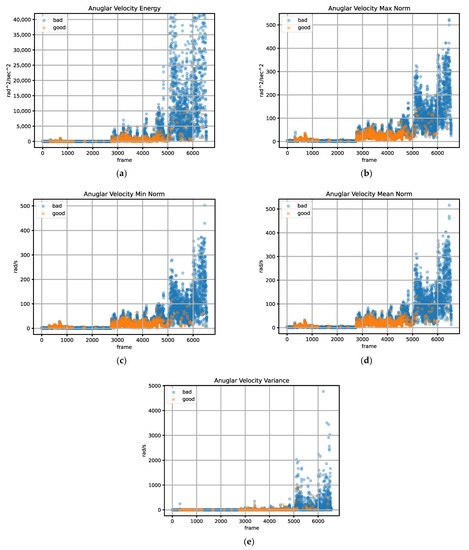
Figure 7.
Labeling result according to motion and quality requirements in gyroscope signals: (a) angular velocity energy, (b) angular velocity max norm, (c) angular velocity min norm, (d) angular velocity mean norm, and (e) angular velocity variance.
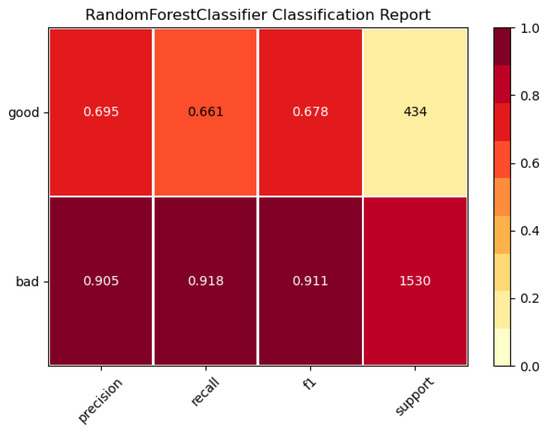
Figure 8.
Classification report with respect to the test set. Performance of class good underlies the performance of class bad.
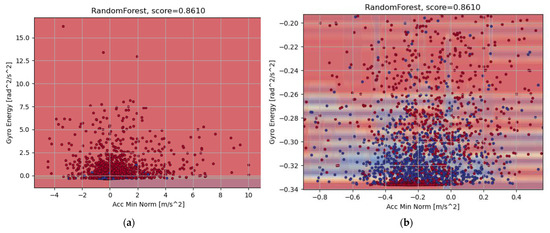
Figure 9.
Random forest classification representation on and . One can see a strong overlap between both classes, and the blue labels are significantly dominated by the red labels, (a) labeled representation of the training set, (b) more detailed representation focusing the blue labeled training data.
4.5. Reconstruction
For 3D reconstruction, we used the open-source photogrammetry software Meshroom [23] to show the results of the proposed method in a simple way. We started two experiments, as shown in Figure 10. First, we performed a reconstruction with all images, as well as with the selected key frames of a video recording. Meshroom is modular and therefore highly customizable. For a simple demonstration of the differences, we set the default settings. The reconstruction was performed on a system equipped with a NVIDIA RTX3090, 64GB RAM, and Intel Core i7. Table 2 below shows the result information of both reconstructions. The root-mean-square error (RMSE) relates to the StructureFromMotion node and describes the deviation of the projected feature points to 3D coordinates from 2D image coordinates, also called residuals. Due to an embedded outlier detection scheme during feature matching and camera pose estimation, the difference in RMSE between the two experiments was marginal. Thus, one could conclude that the low-quality images had little influence on the reconstruction. However, this is not true. In Figure 10a,c, one can see that the result by all frames led to less reconstruction of the observed model. Without such a feature and outlier detection scheme, the point cloud and its resulting mesh would be noisier and suffer even more from false camera pose estimation and thus 3D reprojection biased by features of blurred frames. By reducing the number of images by the presented algorithm, the computation time for the reconstruction was significantly reduced. Hereby, we can see that the presented method decreased the computation time due to the reduced number of frames. The filtering of low-quality and redundant images had also led to a more considerable reconstruction.

Figure 10.
Resulting mesh of a 3D reconstruction of images by the open-source software Meshroom. (a,c) represent the result of the reconstruction due to the whole set of captured frames. On the other side, (b,c) represent the result of the reconstruction based on selected key frames by the proposed method. (a) The front side of the resulting mesh due to non-filtered frames, (b) the front side of the resulting mesh due to selected key frames that were determined by the proposed method, (c) the back side of the resulting mesh due to non-filtered frames, and (d) the back side of the resulting mesh due to filtered frames that were determined by the proposed method.

Table 2.
Feature importance resulted from the training of the random forest classifier. Features based on angular velocity have more influence on splitting leaves.
5. Conclusions
We achieved a classifier that successfully omitted redundant frames and preserved frames with the required quality. However, it exhibited an unsatisfying performance with respect to ideal frames. Partly bad frames were unfortunately predicted as good ones. The main drawback was due to the acceleration values combined with slow motions, as one would record a video by preserving the quality of the individual frames. As we mentioned before, acceleration was unreliable as a metric during slow motion. Many frames of different labels refer to the same value of features, which made it ambiguous. Thus, we can say that when capturing high-quality frames, acceleration is not suitable to select them. Additionally, determining blurry frames was only possible by investigating a threshold. This depended strongly on the environment and brightness conditions seen in the frames. There was no ground truth indicating a proper bound, which made it impossible to evaluate new recordings based on the predefined threshold that was used for labeling. Due to the characteristics of acceleration, it was not reasonable to increase the threshold for optical flow. It would increase the necessary magnitude of acceleration, which exhibits frames during higher acceleration and thus a higher probability of blurry edges. On the other side, measured values of accelerated motions would fall below the threshold of constant motion. Research had already shown that certain motion patterns can be well-differentiated by IMU if the motions are very different from each other [20,21].
In this study, a method was presented that uses an individual calibration procedure and is based on the composition of the inertial data. This results in limitations to the interaction of camera frames and IMU, which in our case combines several inertial data per frame, as well as a complex calibration that is not based on a global optimum but must be determined individually.
The trained RF classifier was used to reduce the number of frames to a subset of frames with non-blurry edges. This can help to ease further processing and omit redundant frames as well as blurry frames simultaneously. Using 3D reconstruction with Meshroom, we were able to show that our method led to an improved result for frames that are characterized by redundancy and motion blur. The insight here was a significant improvement achieved by decreasing the runtime of the calculation as well as by increasing the quality of the reconstructed model.
For future work, one could determine the overlap between consecutive selected frames. Thus, the selection of the key frames is made by IMU and would be evaluated due to a certain overlap. One could define some threshold to require a minimum and maximum overlap. This would decrease the amount of similar successive frames despite motion. Such frames would differ significantly.
Author Contributions
Conceptualization, A.K. and C.M.; methodology, A.K. and C.M.; software, A.K.; validation, C.M.; formal analysis, A.K.; investigation, A.K.; resources, C.M. and A.R.; data curation, A.K.; writing—original draft preparation, A.K.; writing—review and editing, A.K., C.M. and A.R.; visualization, A.K. and C.M.; supervision, C.M. and A.R.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reiterer, A.; Wäschle, K.; Störk, D.; Leydecker, A.; Gitzen, N. Fully Automated Segmentation of 2D and 3D Mobile Mapping Data for Reliable Modeling of Surface Structures Using Deep Learning. Remote Sens. 2020, 12, 2530. [Google Scholar] [CrossRef]
- Paar, G.; Huber, N.B.; Bauer, A.; Avian, M.; Reiterer, A. Vision-Based Terrestrial Surface Monitoring. Terrigenous Mass Mov. 2012, 283–348. [Google Scholar] [CrossRef]
- Péntek, Q.; Hein, S.; Miernik, A.; Reiterer, A. Image-based 3D surface approximation of the bladder using structure-from-motion for enhanced cystoscopy based on phantom data. Biomed. Technol. 2017, 63, 461–466. [Google Scholar] [CrossRef] [PubMed]
- Seibold, C.; Hilsmann, A.; Eisert, P. Model-based motion blur estimation for the improvement of motion tracking. Comput. Vis. Image Underst. 2017, 160, 45–56. [Google Scholar] [CrossRef]
- Ahmed, M.T.; Dailey, M.; Landabaso, J.; Herrero, N. Robust key frame extraction for 3D reconstruction from video strams. In Proceedings of the Fifth International Conference on Computer Vision Theory and Applications, Angers, France, 17–21 May 2010; pp. 231–236. [Google Scholar]
- Zhang, C.; Wang, H.; Li, H.; Liu, J. A fast key frame extraction algorithm and an accurate feature matching method for 3D reconstruction from aerial video. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 6744–6749. [Google Scholar]
- Ishijima, A.; Schwarz, R.A.; Shin, D.; Mondrik, S.; Vigneswaran, N.; Gillenwater, A.M.; Anandasabapathy, S.; Richards-Kortum, R. Automated frame selection process for high-resolution microendoscopy. J. Biomed. Opt. 2015, 20, 46014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, J.; Shen, X.; Lin, Z.; Mech, R. Best frame selection in a short video. In Proceedings of the 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass Village, CO, USA, 1–5 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 3201–3210. [Google Scholar]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. Proceedings DARPA Image Understanding Workshop, Columnia, UK, 24–28 August 1981; pp. 121–130. [Google Scholar] [CrossRef]
- Yuen, M.; Wu, H. A survey of hybrid MC/DPCM/DCT video coding distortions. Signal Process. 1998, 70, 247–278. [Google Scholar] [CrossRef]
- Gonzales, R.C.; Woods, R.E. Digital Image Processing; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2008; Available online: http://sdeuoc.ac.in/sites/default/files/sde_videos/Digital%20Image%20Processing%203rd%20ed.%20-%20R.%20Gonzalez%2C%20R.%20Woods-ilovepdf-compressed.pdf (accessed on 28 January 2021).
- Jähne, B. Digitale Bildverarbeitung; Springer: Berlin/Heidelberg, Germany, 2005; pp. 29–79. [Google Scholar] [CrossRef]
- Rekleitis, J. Visual Motion Estimation Based on Motion Blur Interpretation. School of Computer Science, McGill University. 1996. Available online: https://www.researchgate.net/publication/2687203_Visual_Motion_Estimation_based_on_Motion_Blur_Interpretation (accessed on 23 February 2021).
- Kalalembang, E.; Usman, K.; Gunawan, I.P. DCT-based local motion blur detection. In Proceedings of the International Conference on Instrumentation, Communication, Information Technology, and Biomedical Engineering, Bandung, Indonesia, 23–25 November 2009; pp. 1–6. [Google Scholar]
- Barron, J.L.; Fleet, D.J.; Beauchemin, S.S. Performance of optical flow techniques. Int. J. Comput. Vis. 1994, 12, 43–77. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector. Alvey Vis. Conf. 1988, 15, 10–5244. [Google Scholar] [CrossRef]
- OpenCV. Open Source Computer Vision Library; Intel: Clara, CA, USA, 2015. [Google Scholar]
- Shi, J.; Tomasi, C. Good Features to Track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, DC, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
- Kasebzadeh, P.; Hendeby, G.; Fritsche, C.; Gunnarsson, F.; Gustafsson, F. IMU dataset for motion and device mode classification. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Susi, M.; Renaudin, V.; Lachapelle, G. Motion Mode Recognition and Step Detection Algorithms for Mobile Phone Users. Sensors 2013, 13, 1539–1562. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Macm. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Alice, V. Meshroom: A 3D Reconstruction Software. 2018. Available online: https://github.com/alicevision/meshroom (accessed on 23 February 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).