Numerically Efficient Fuzzy MPC Algorithm with Advanced Generation of Prediction—Application to a Chemical Reactor
Abstract
1. Introduction
2. Model Predictive Control Algorithms
2.1. MPC Algorithms Based on Nonlinear Models (NMPC)
2.2. MPC Algorithms Based on Linear Models (LMPC)
3. Fuzzy MPC Algorithm with Advanced Generation of Prediction
3.1. Generation of the Dynamic Matrix
3.2. Generation of the Free Response
- First, the nonlinear model (12) is used to obtain
- Next, the values are used when calculating the output values for the next sampling instant:
- For the ith iteration, using the values one obtains:
- After taking into account the estimation of unmeasured disturbances , containing also influence of modeling errors, the final form of the formula describing the elements of the free response is obtained:
3.3. Formulation of the Optimization Problem
3.4. Iterative Improvement of the Prediction
- First, the model is used to obtain values
- Next, the values are used to calculate the output values for the next sampling instant:
- For the ith iteration, using the values one obtains:
- After taking into account the estimation of unmeasured disturbances , containing also influence of modeling errors, like in (30), the final formula describing the elements of the free response is obtained:
3.5. Fast Generation of the Control Action—Analytical Approach
3.6. Disturbance Measurement Utilization
3.6.1. Employing Fuzzy Model
3.6.2. Employing Nonlinear Model
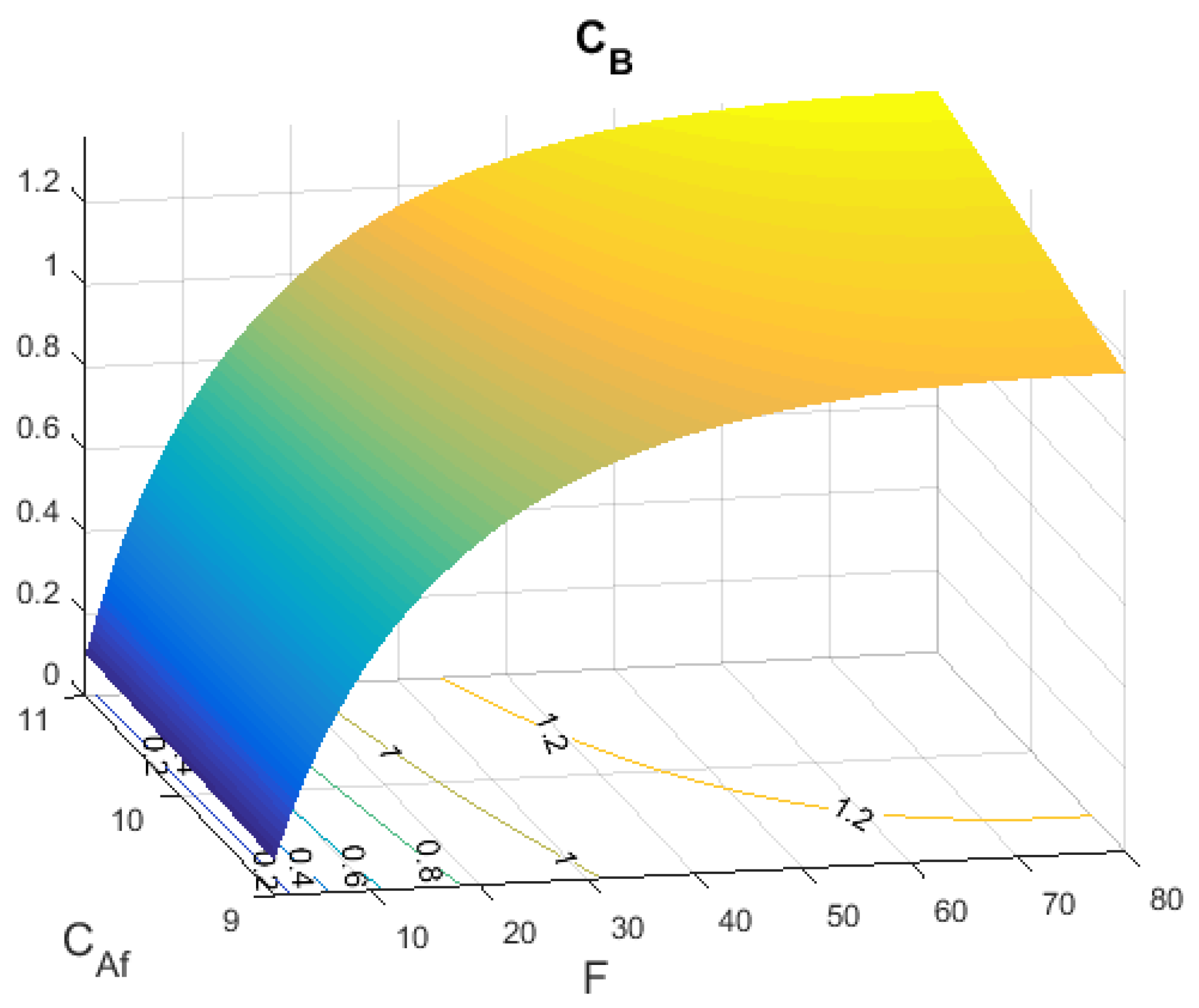
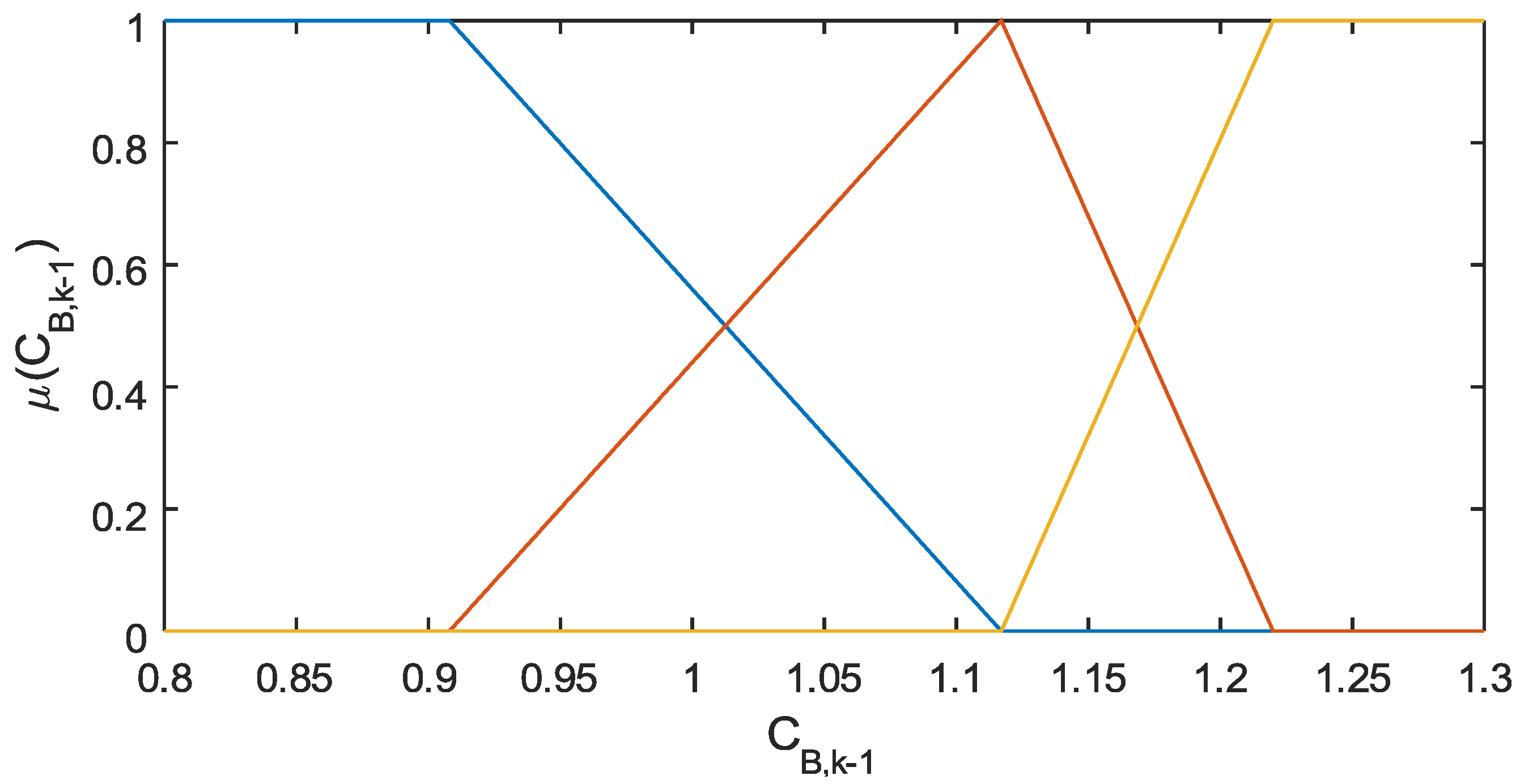
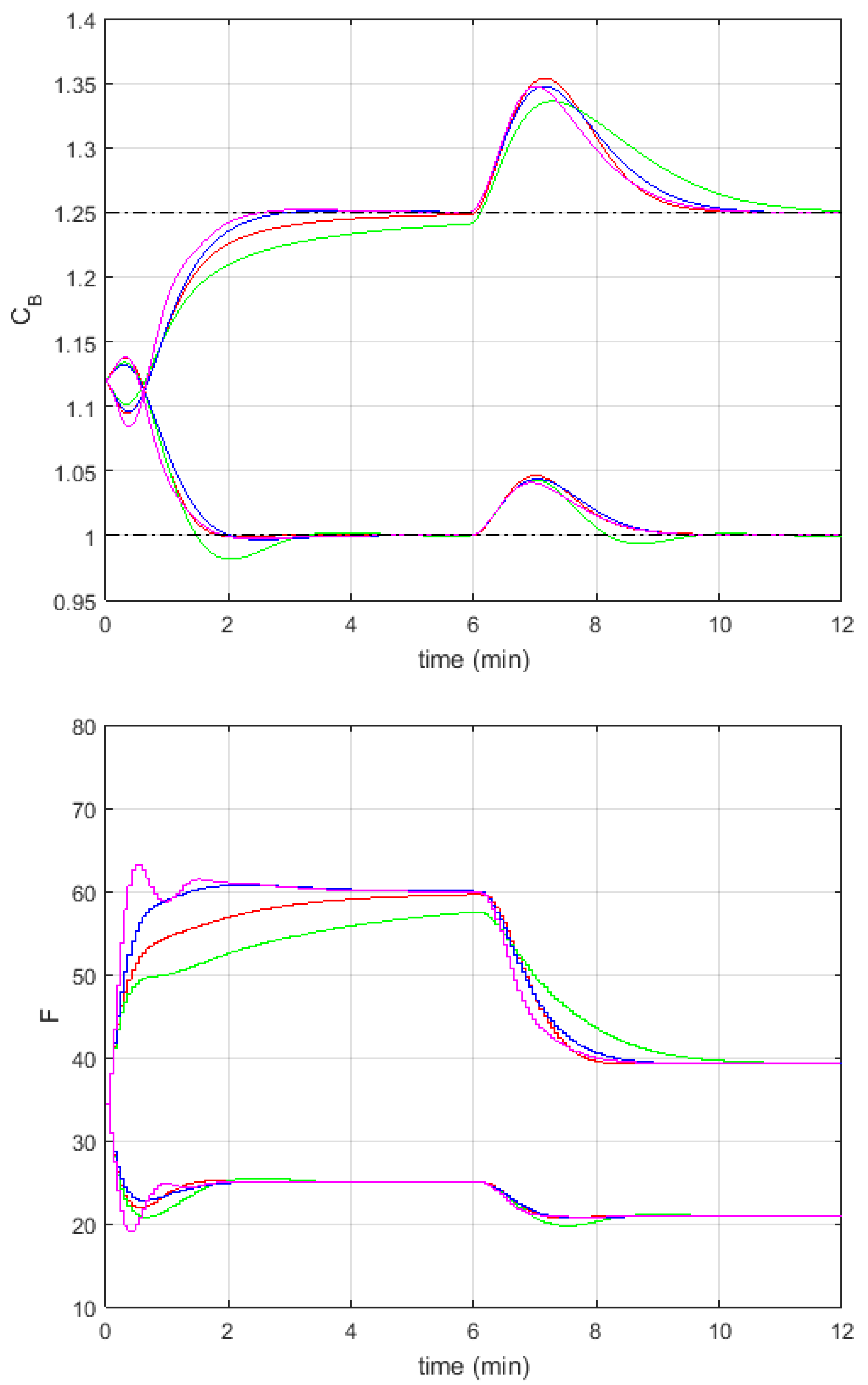
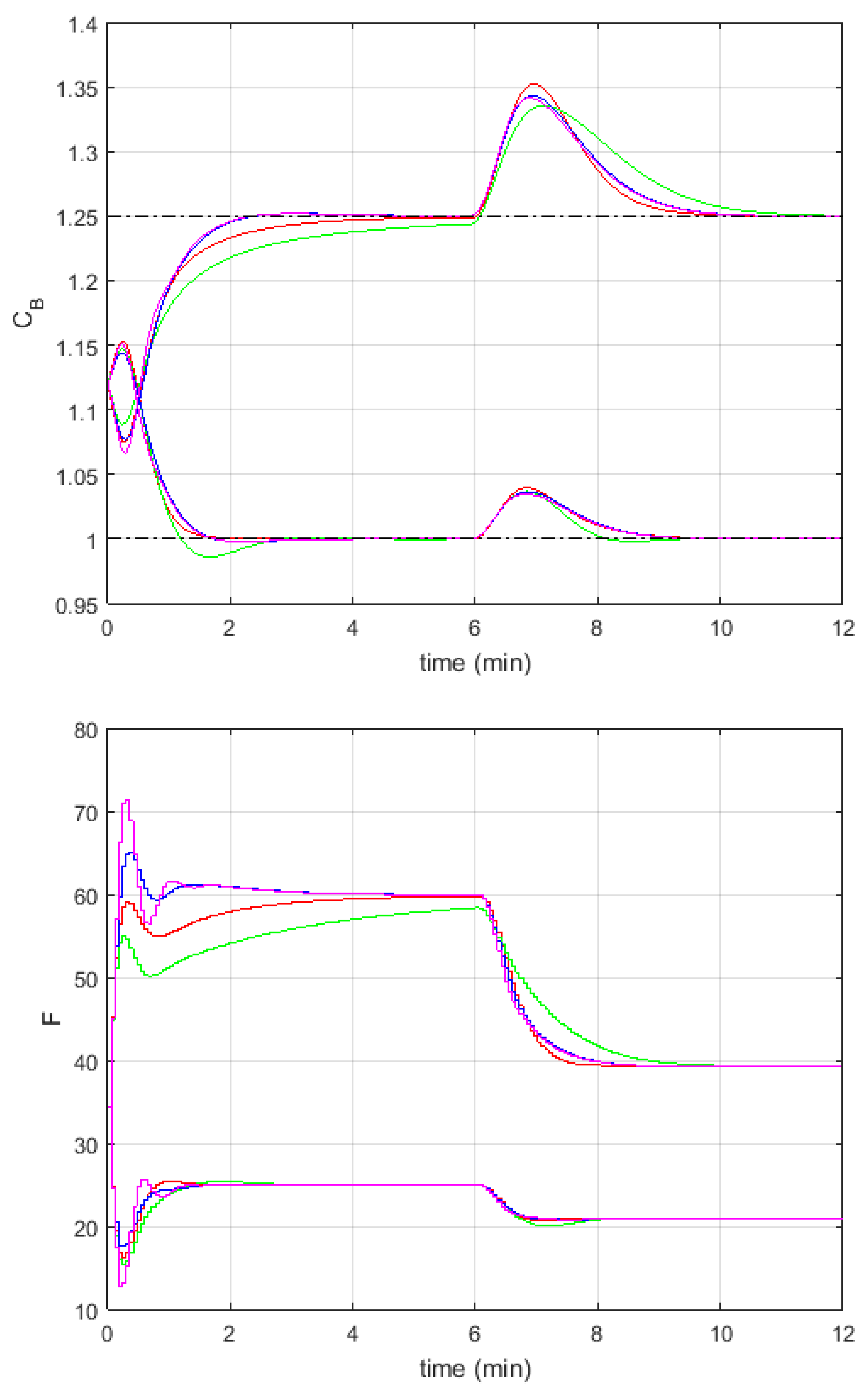
4. Example
Experiments
5. Conclusions
Funding
Conflicts of Interest
Abbreviations
| CSTR | Continuous Stirred–Tank Reactor |
| DMC | Dynamic Matrix Control |
| FMPC | Fuzzy Model Predictive Control |
| LMPC | Linear Model Predictive Control |
| LMIs | Linear Matrix Inequalities |
| MPC | Model Predictive Control |
| MIMO | Multiple–Input Multiple–Output |
| NMPC | Nonlinear Model Predictive Control |
References
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: London, UK, 1999. [Google Scholar]
- Domański, P.D. Performance Assessment of Predictive Control—A Survey. Algorithms 2020, 13, 97. [Google Scholar] [CrossRef]
- El Youssef, J.; Castle, J.; Ward, W.K. A Review of Closed–Loop Algorithms for Glycemic Control in the Treatment of Type 1 Diabetes. Algorithms 2009, 2, 518–532. [Google Scholar] [CrossRef]
- Rossiter, J.A. Model–Based Predictive Control: A Practical Approach; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Maciejowski, J.M. Predictive Control with Constraints; Prentice Hall: Harlow, UK, 2002. [Google Scholar]
- Sands, T. Comparison and Interpretation Methods for Predictive Control of Mechanics. Algorithms 2019, 12, 232. [Google Scholar] [CrossRef]
- Tatjewski, P. Advanced Control of Industrial Processes; Structures and Algorithms; Springer: London, UK, 2007. [Google Scholar]
- Tatjewski, P. Disturbance modeling and state estimation for offset–free predictive control with state–spaced process models. Int. J. Appl. Math. Comput. Sci. 2014, 24, 313–323. [Google Scholar] [CrossRef]
- Ławryńczuk, M.; Marusak, P.; Tatjewski, P. Cooperation of model predictive control with steady–state economic optimisation. Control. Cybern. 2008, 37, 133–158. [Google Scholar]
- Blevins, T.L.; McMillan, G.K.; Wojsznis, W.K.; Brown, M.W. Advanced Control Unleashed; ISA: Fort Belvoir, VA, USA, 2003. [Google Scholar]
- Abdelaal, M.; Schön, S. Predictive Path Following and Collision Avoidance of Autonomous Connected Vehicles. Algorithms 2020, 13, 52. [Google Scholar] [CrossRef]
- Chen, H.; Allgöwer, F. A Quasi-Infinite Horizon Nonlinear Model Predictive Control Scheme with Guaranteed Stability. Automatica 1998, 34, 1205–1217. [Google Scholar] [CrossRef]
- Tatjewski, P. Offset–free nonlinear model predictive control with state–space process models. Arch. Control. Sci. 2017, 27, 595–615. [Google Scholar] [CrossRef]
- Zavala, V.M.; Laird, C.D.; Biegler, L.T. A fast moving horizon estimation algorithm based on nonlinear programming sensitivity. J. Process Control 2008, 18, 876–884. [Google Scholar] [CrossRef]
- Diehl, M.; Bock, H.G.; Schlöder, J.P.; Findeisen, R.; Nagy, Z.; Allgöwer, F. Real–time optimization and nonlinear model predictive control of processes governed by differential–algebraic equations. J. Process Control 2002, 12, 577–585. [Google Scholar] [CrossRef]
- Schäfer, A.; Kühl, P.; Diehl, M.; Schlöder, J.; Bock, H.G. Fast reduced multiple shooting methods for nonlinear model predictive control. Chem. Eng. Process. 2007, 46, 1200–1214. [Google Scholar] [CrossRef]
- Johansen, T.A. On multi–parametric nonlinear programming and explicit nonlinear model predictive control. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 3, pp. 2768–2773. [Google Scholar]
- Johansen, T.A. Approximate explicit receding horizon control of constrained nonlinear systems. Automatica 2004, 40, 293–300. [Google Scholar] [CrossRef]
- Dominguez, L.F.; Pistikopoulos, E.N. A Novel mp-NLP Algorithm for Explicit/Multi-parametric NMPC. IFAC Proc. Vol. 2010, 43, 539–544. [Google Scholar] [CrossRef]
- Bemporad, A.; Borrelli, F.; Morari, M. Piecewise linear optimal controllers for hybrid systems. In Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No.00CH36334), Chicago, IL, USA, 28–30 June 2000; pp. 1190–1194. [Google Scholar]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Dua, V.; Bozinis, N.A.; Bemporad, A.; Morari, M. On–line optimization via off–line parametric optimization tools. Comput. Chem. Eng. 2002, 26, 175–185. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Fuzzy modeling and predictive control of superheater steam temperature for power plant. ISA Trans. 2015, 56, 241–251. [Google Scholar] [CrossRef]
- Khooban, M.H.; Vafam, N.; Niknam, T. Optimal partitioning of a boiler–turbine unit for Fuzzy model predictive control. ISA Trans. 2016, 64, 231–240. [Google Scholar] [CrossRef]
- Kong, L.; Yuan, J. Disturbance–observer–based fuzzy model predictive control for nonlinear processes with disturbances and input constraints. ISA Trans. 2019, 90, 74–88. [Google Scholar] [CrossRef]
- Kong, L.; Yuan, J. Generalized Discrete–time Nonlinear Disturbance Observer Based Fuzzy Model Predictive Control for Boiler–Turbine Systems. ISA Trans. 2019, 90, 89–106. [Google Scholar] [CrossRef]
- Shen, D.; Lim, C.-C.; Shi, P. Robust fuzzy model predictive control for energy management systems in fuel cell vehicles. Control. Eng. Pract. 2020, 98, 104364. [Google Scholar] [CrossRef]
- Killian, M.; Kozek, M. T–S fuzzy model predictive speed control of electrical vehicles. IFAC-Papers On Line 2017, 50, 2011–2016. [Google Scholar] [CrossRef]
- Marusak, P.; Tatjewski, P. Stability analysis of nonlinear control systems with unconstrained fuzzy predictive controllers. Arch. Control. Sci. 2002, 12, 267–288. [Google Scholar]
- Ławryńczuk, M. Nonlinear state–space predictive control with on–line linearisation and state estimation. Int. J. Appl. Math. Comput. Sci. 2015, 25, 833–847. [Google Scholar] [CrossRef]
- Boulkaibet, I.; Belarbi, K.; Bououden, S.; Marwala, T.; Chadli, M. A new T–S fuzzy model predictive control for nonlinear processes. Expert Syst. Appl. 2017, 88, 132–151. [Google Scholar] [CrossRef]
- Essien, E.; Ibrahim, H.; Mehrandezh, M.; Idem, R. Adaptive neuro-fuzzy inference system (ANFIS)—Based model predictive control (MPC) for carbon dioxide reforming of methane (CDRM) in a plug flow tubular reactor for hydrogen production. Therm. Sci. Eng. Prog. 2019, 9, 148–161. [Google Scholar] [CrossRef]
- Ławryńczuk, M. Computationally Efficient Model Predictive Control Algorithms: A Neural Network Approach; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Marusak, P. Advantages of an easy to design fuzzy predictive algorithm in control systems of nonlinear chemical reactors. Appl. Soft Comput. 2009, 9, 1111–1125. [Google Scholar] [CrossRef]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Marusak, P. Efficient model predictive control algorithm with fuzzy approximations of nonlinear models. LNCS 2009, 5495, 448–457. [Google Scholar]
- Lu, J.; Cao, Z.; Zhao, C.; Gao, F. Multipoint Iterative Learning Model Predictive Control. IEEE Trans. Ind. Electron. 2019, 66, 6230–6240. [Google Scholar] [CrossRef]
- Lu, J.; Cao, Z.; Zhang, R.; Gao, F. Nonlinear Monotonically Convergent Iterative Learning Control for Batch Processes. IEEE Trans. Ind. Electron. 2018, 65, 5826–5836. [Google Scholar] [CrossRef]
- Lu, J.; Cao, Z.; Gao, F. 110th Anniversary: An Overview on Learning–Based Model Predictive Control for Batch Processes. Ind. Eng. Chem. Res. 2019, 58, 17164–17173. [Google Scholar] [CrossRef]
- Fink, A.; Fischer, M.; Nelles, O.; Isermann, R. Supervision of nonlinear adaptive controllers based on fuzzy models. Control. Eng. Pract. 2000, 8, 1093–1105. [Google Scholar] [CrossRef]
- Foss, B.A.; Johansen, T.A.; Sorensen, A.V. Nonlinear predictive control using local models–applied to a batch fermentation process. Control. Eng. Pract. 1995, 3, 389–396. [Google Scholar] [CrossRef]
- Babuska, R.; Te Braake, H.A.; Van Can, H.J.; Krijgsman, A.J.; Verbruggen, H.B. Comparison of intelligent control schemes for real–time pressure control. Control. Eng. Pract. 1996, 4, 1585–1592. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its application to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Piegat, A. Fuzzy Modeling and Control; Physica–Verlag: Heidelberg, Germany, 2001. [Google Scholar]
- Marusak, P. Disturbance Measurement Utilization in the Efficient MPC Algorithm with Fuzzy Approximations of Nonlinear Models. LNCS 2013, 7824, 307–316. [Google Scholar]
- Ribeiro, L.M.; Secchi, A.R. A methodology to obtain analytical models that reduce the computational complexity faced in real time implementation of NMPC controllers. Braz. J. Chem. Eng. 2019, 36, 1255–1277. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Hoang , N.H.; Hussain, M.A. Tracking error plus damping injection control of non-minimum phase processes. IFAC-Pap. OnLine 2018, 51, 643–648. [Google Scholar] [CrossRef]
- Uçak, K. A Runge–Kutta neural network-based control method for nonlinear MIMO systems. Soft Comput. 2019, 23, 7769–7803. [Google Scholar] [CrossRef]
- Jain, A.; Taparia, R. Laguerre function based model predictive control for van–de–vusse reactor. In Proceedings of the 2018 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; Volume 3, pp. 1010–1015. [Google Scholar]
- Uçak, K. A Novel Model Predictive Runge–Kutta Neural Network Controller for Nonlinear MIMO Systems. Neural Process. Lett. 2020, 51, 1789–1833. [Google Scholar] [CrossRef]
- Mate, S.; Kodamana, H.; Bhartiya, S.; Nataraj, P.S.V. A Stabilizing Sub–Optimal Model Predictive Control for Quasi–Linear Parameter Varying Systems. IEEE Control. Syst. Lett. 2020, 4, 402–407. [Google Scholar] [CrossRef]
- Doyle, F.; Ogunnaike, B.A.; Pearson, R.K. Nonlinear model–based control using second–order Volterra models. Automatica 1995, 31, 697–714. [Google Scholar] [CrossRef]
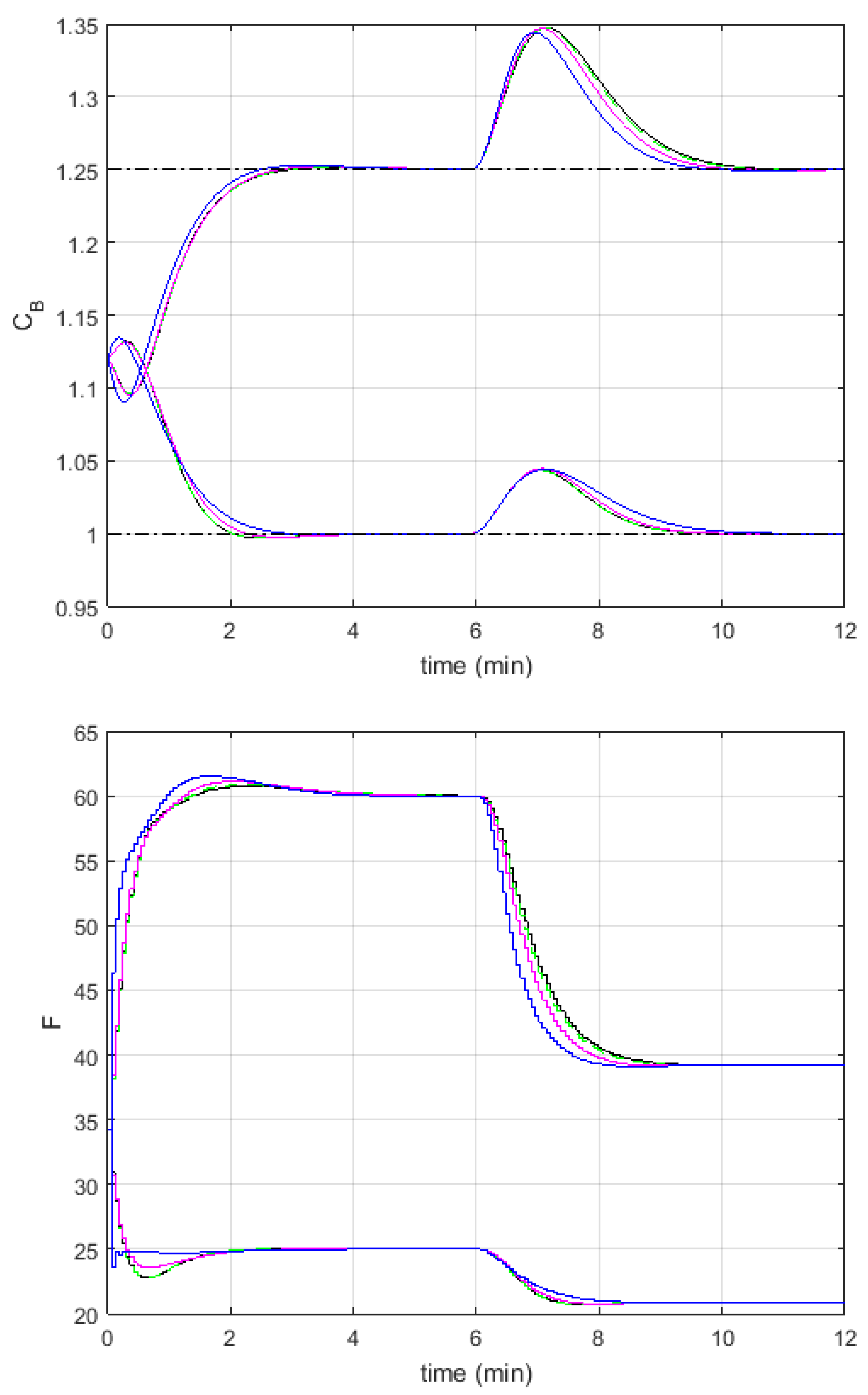
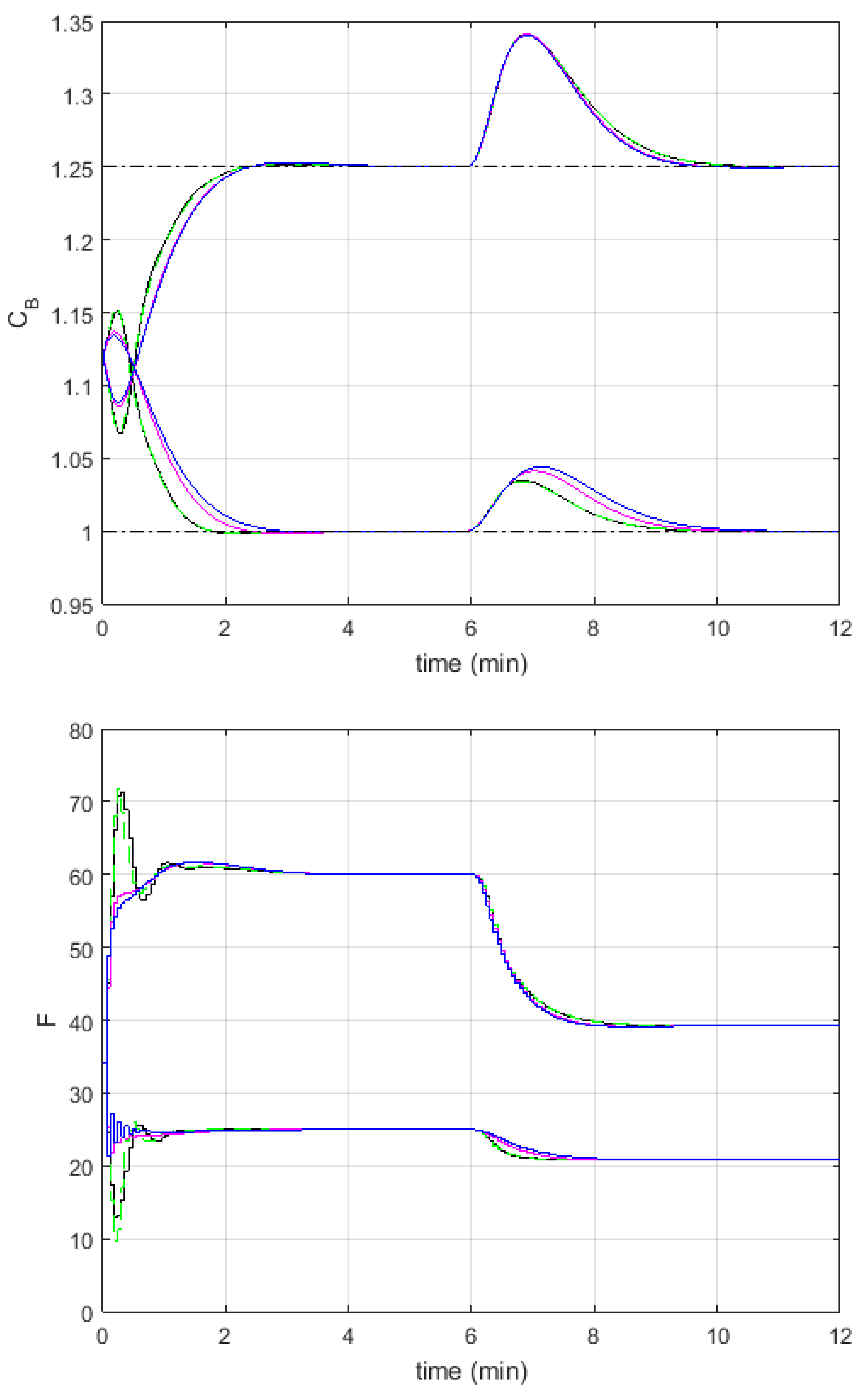

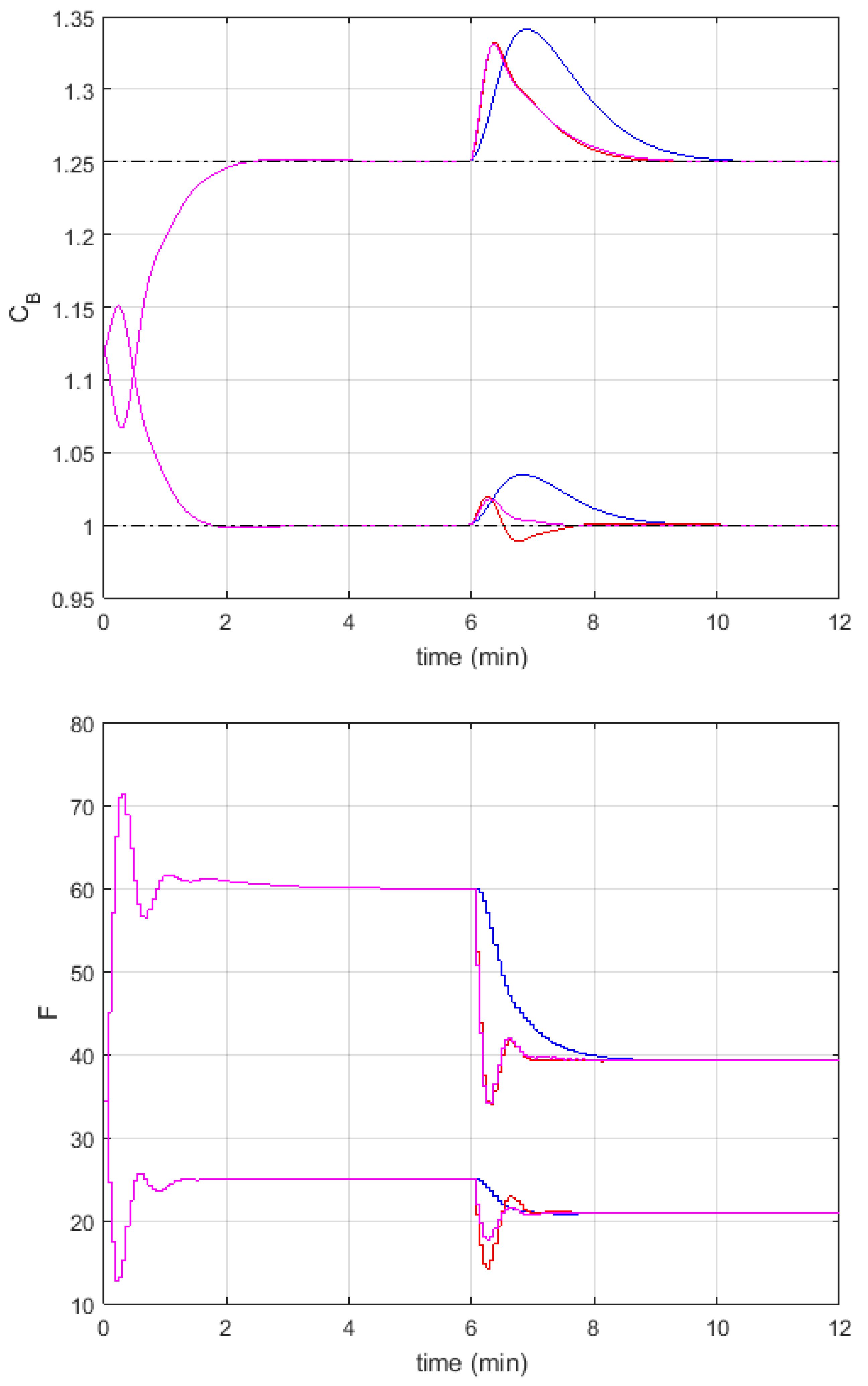
| NMPC | FMPC1 | FMPC2 | |
|---|---|---|---|
| mol/L | 29.1671 | 1.8175 | 1.8118 |
| mol/L | 47.0518 | 1.8116 | 1.8137 |
| sum | 76.2189 | 3.6291 | 3.6254 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marusak, P.M. Numerically Efficient Fuzzy MPC Algorithm with Advanced Generation of Prediction—Application to a Chemical Reactor. Algorithms 2020, 13, 143. https://doi.org/10.3390/a13060143
Marusak PM. Numerically Efficient Fuzzy MPC Algorithm with Advanced Generation of Prediction—Application to a Chemical Reactor. Algorithms. 2020; 13(6):143. https://doi.org/10.3390/a13060143
Chicago/Turabian StyleMarusak, Piotr M. 2020. "Numerically Efficient Fuzzy MPC Algorithm with Advanced Generation of Prediction—Application to a Chemical Reactor" Algorithms 13, no. 6: 143. https://doi.org/10.3390/a13060143
APA StyleMarusak, P. M. (2020). Numerically Efficient Fuzzy MPC Algorithm with Advanced Generation of Prediction—Application to a Chemical Reactor. Algorithms, 13(6), 143. https://doi.org/10.3390/a13060143





