Monitoring Blockchain Cryptocurrency Transactions to Improve the Trustworthiness of the Fourth Industrial Revolution (Industry 4.0)
Abstract
1. Introduction
2. Related Works
3. Statistical Modeling of Network and Parameter Estimation
3.1. Notations
3.2. Hidden Markov Multi Linear Tensor Model
4. Monitoring Scheme
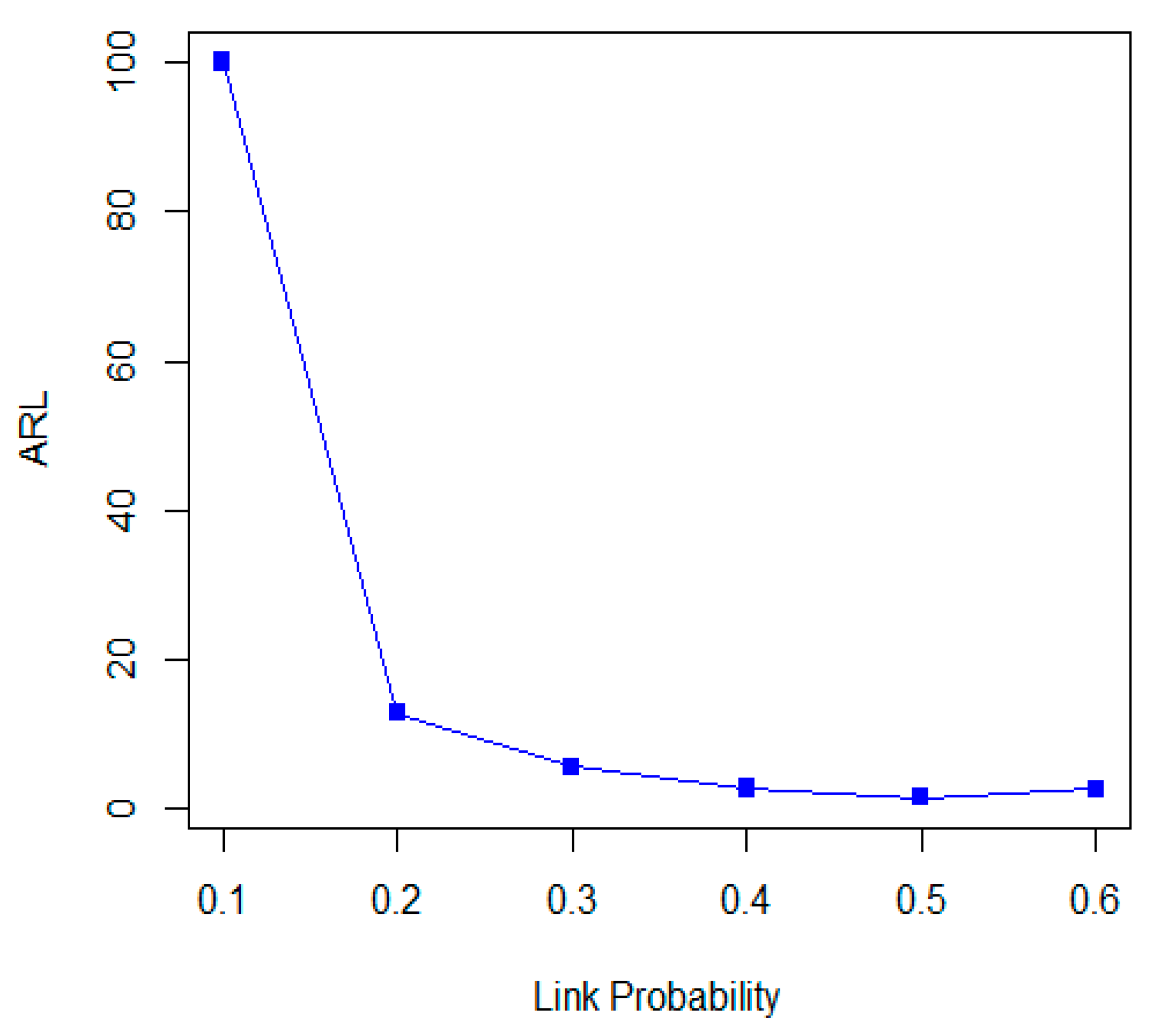
5. Performance Evaluation Using Simulation
- (1)
- For to ;
- For and based on the probability of edge creation between nodes i and j generate ;
- Use the MCMC algorithm to estimate vector for the generated network;
- (2)
- For to , calculate based on relation (6);
- (3)
- For to , evaluate the statistics based on relation (7);
- (4)
- For all statistics, find a UCL that the type I error meets.
- (1)
- For to 10000;
- (a)
- Set ;
- (b)
- While < UC;
- Generate a random network based on different probabilities;
- Estimate model parameters with the MCMC algorithm and obtain statistic from relation (7);
- Put ;
- (2)
- Evaluate .
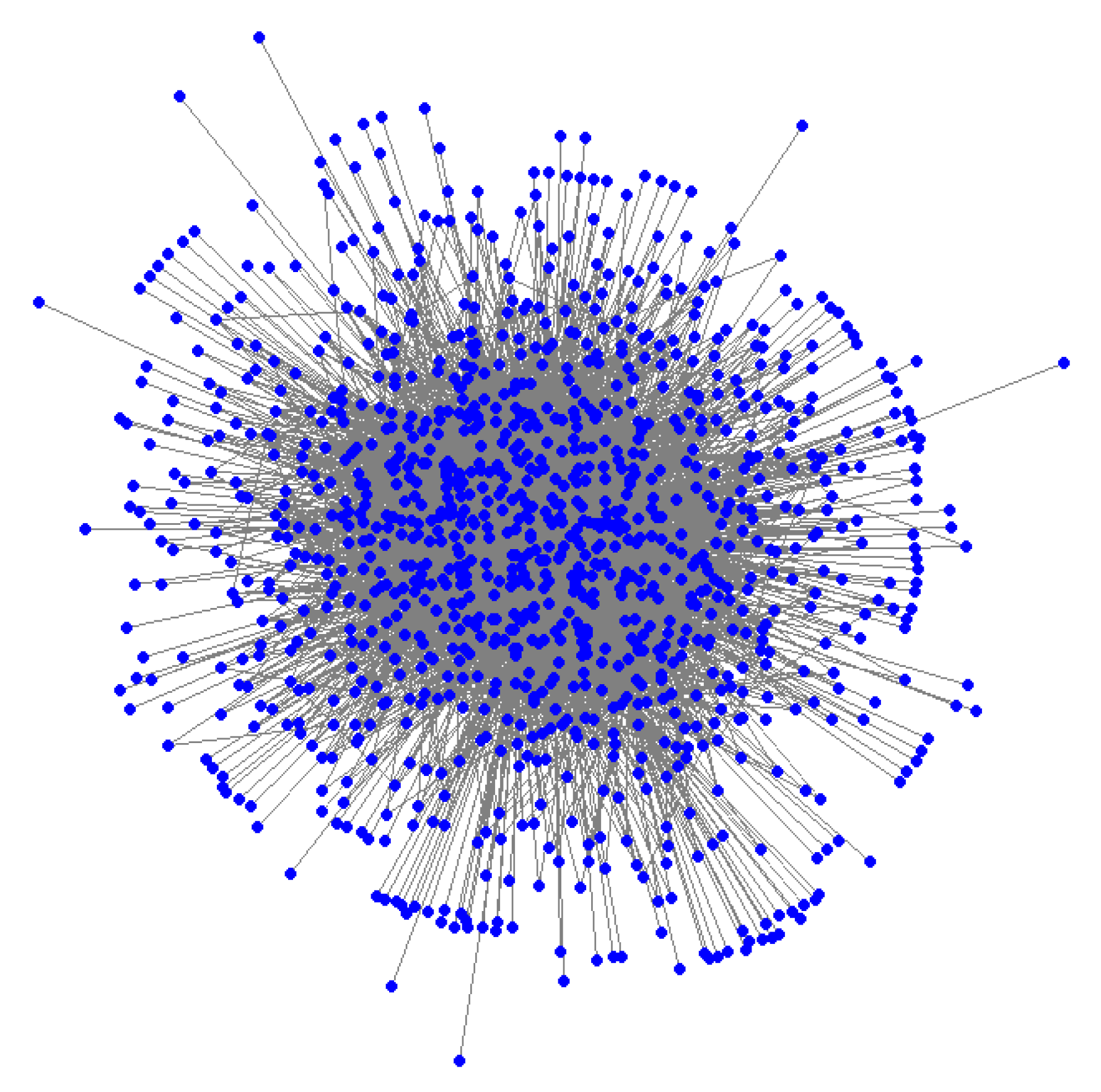
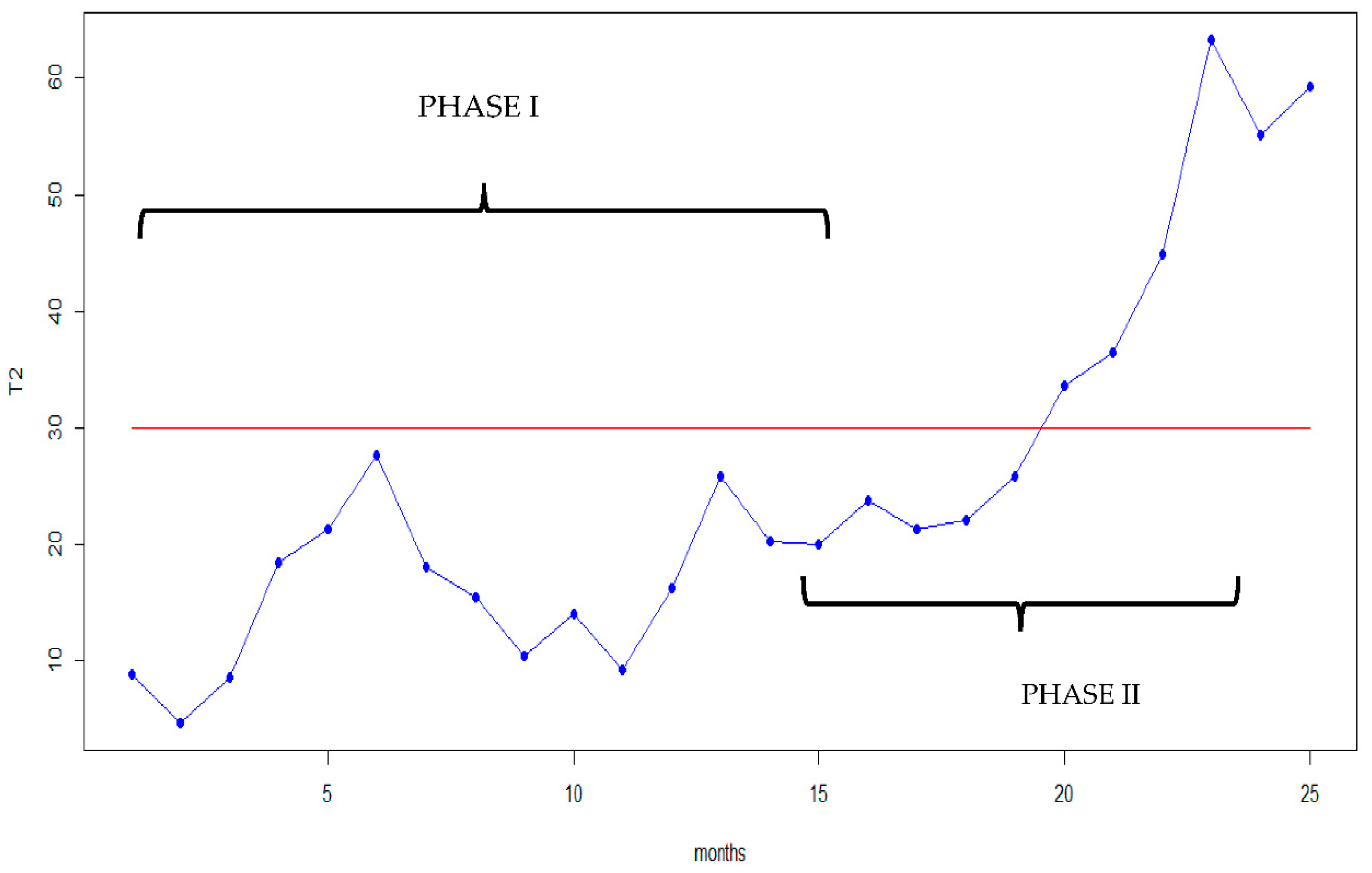
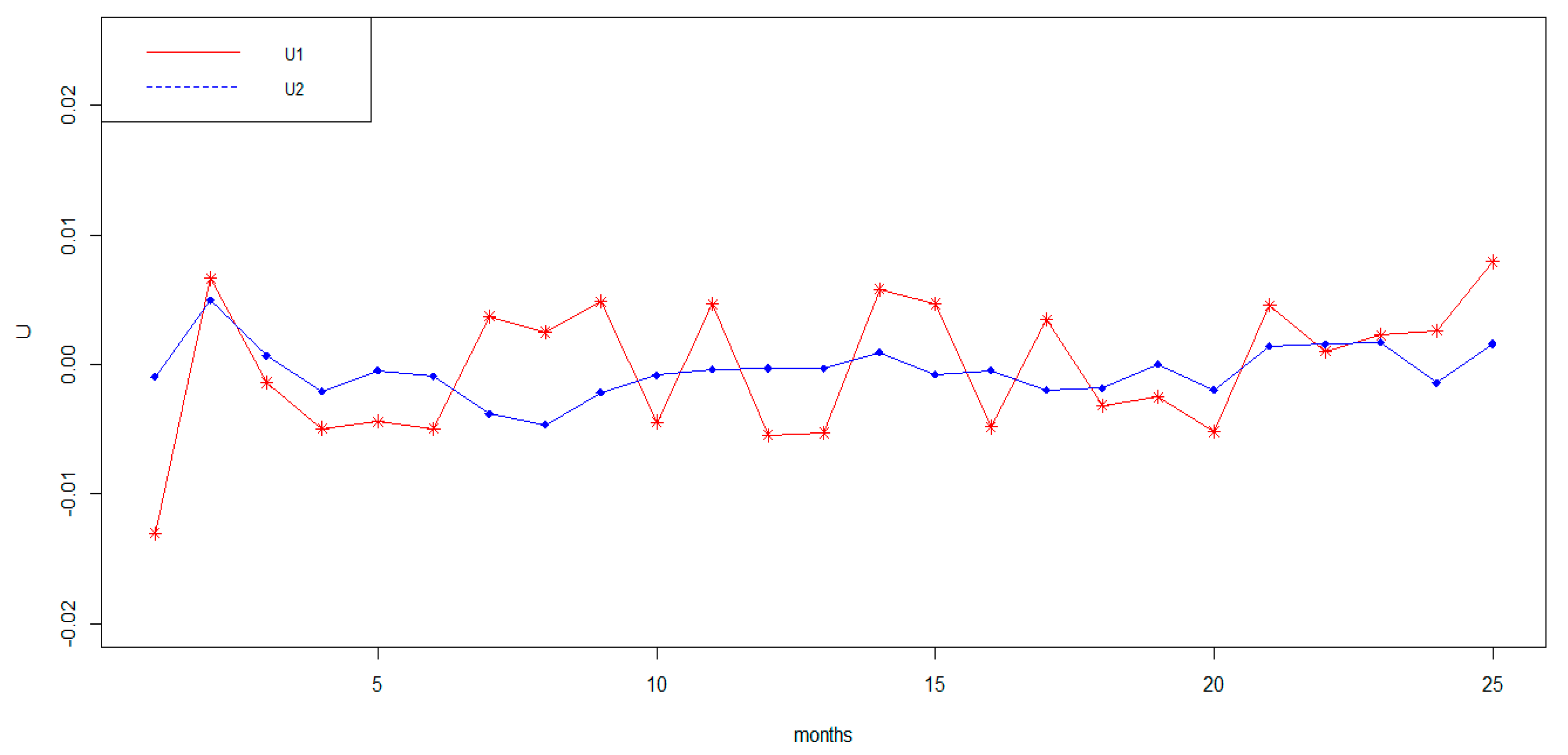
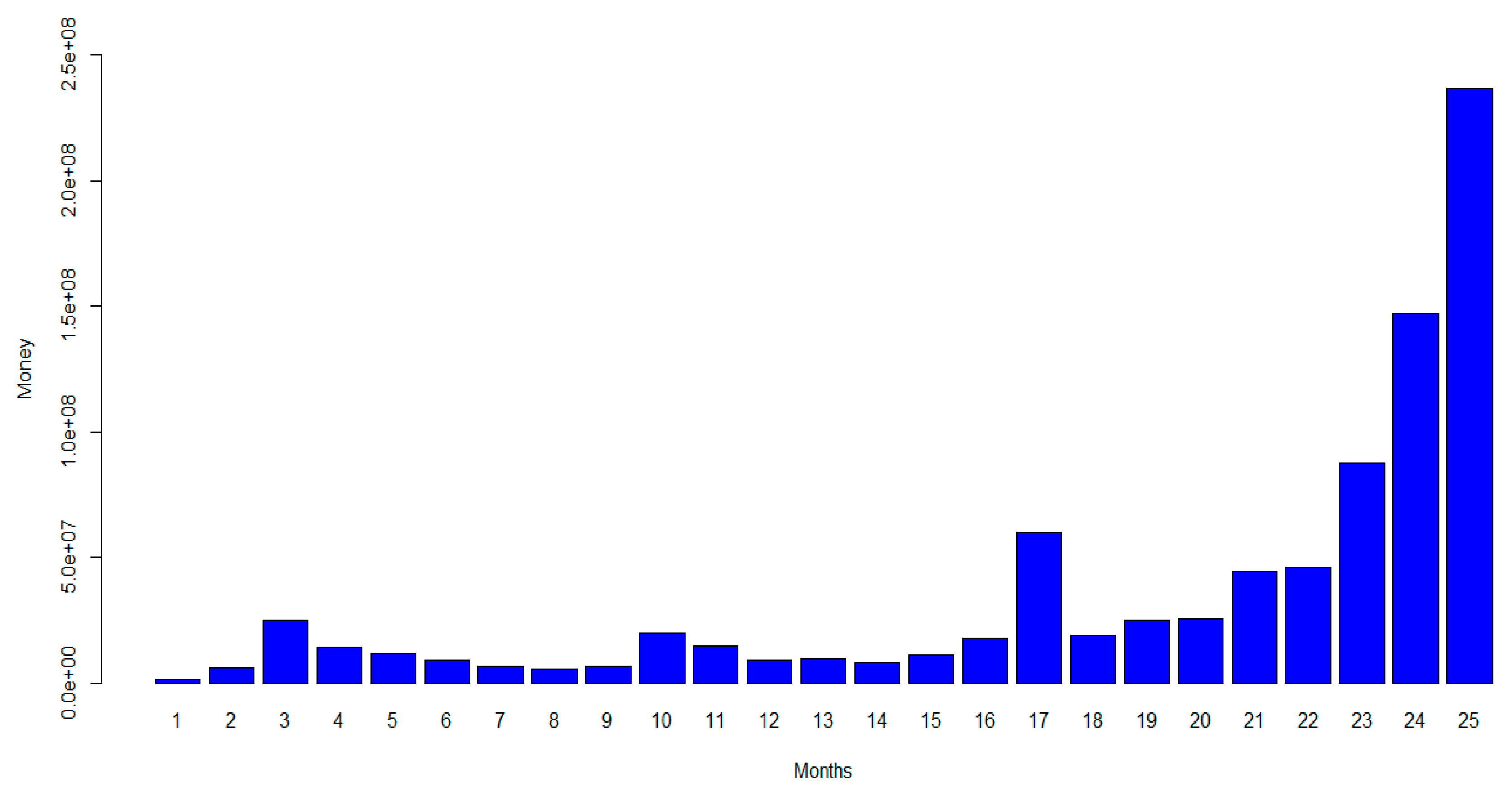
6. Real-World Example
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Akdoğan, D.A.; Kurular, G.Y.S.; Geyik, O. Cryptocurrencies and Blockchain in 4th Industrial Revolution Process: Some Public Policy Recommendations. Available online: https://www.researchgate.net/publication/337635983_Cryptocurrencies_and_Blockchain_In_4th_Industrial_Revolution_Process_Some_Public_Recommendations (accessed on 12 November 2020).
- Lasi, H.; Fettke, P.; Kemper, H.G.; Feld, T.; Hoffmann, M. Industry 4.0. Bus. Inf. Syst. Eng. 2013, 6, 239–242. [Google Scholar] [CrossRef]
- Bodkhe, U.; Tanwar, S.; Parekh, K.; Khanpara, P.; Tyagi, S.; Kumar, N.; Alazab, M. Blockchain for industry 4.0: A comprehensive review. IEEE Access 2020, 8, 79764–79800. [Google Scholar] [CrossRef]
- Mushtaq, A.; Haq, I.U. Implications of blockchain in industry 4. o. In Proceedings of the 2019 International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 21–22 February 2019. [Google Scholar]
- Lee, S.C. Magical capitalism, gambler subjects: South Korea’s bitcoin investment frenzy. Cult. Stud. 2020, 1–24. [Google Scholar] [CrossRef]
- Yli-Huumo, J.; Ko, D.; Choi, S.; Park, S.; Smolander, K. Where Is Current Research on Blockchain Technology?—A Systematic Review. PLoS ONE 2016, 11, e0163477. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, E.; Rüsch, M. Industry 4.0 and the current status as well as future prospects on logistics. Comput. Ind. 2017, 89, 23–34. [Google Scholar] [CrossRef]
- Aitzhan, N.Z.; Svetinovic, D. Security and Privacy in Decentralized Energy Trading Through Multi-Signatures, Blockchain and Anonymous Messaging Streams. IEEE Trans. Dependable Secur. Comput. 2016, 15, 840–852. [Google Scholar] [CrossRef]
- Chen, W.; Wu, J.; Zheng, Z.; Chen, C.; Zhou, Y. Market manipulation of bitcoin: Evidence from mining the Mt. Gox transaction network. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Manubot. 2019. Available online: https://git.dhimmel.com/bitcoin-whitepaper (accessed on 10 October 2020).
- Teichmann, F.M.J.; Falker, M.-C. Cryptocurrencies and Financial Crime: Solutions from Liechtenstein. Available online: https://www.emerald.com/insight/content/doi/10.1108/JMLC-05-2020-0060/full/html (accessed on 10 October 2020).
- Luqman, A.; Akram, M.; Smarandache, F. Complex Neutrosophic Hypergraphs: New Social Network Models. Algorithms 2019, 12, 234. [Google Scholar] [CrossRef]
- Behera, R.K.; Rath, S.K.; Misra, S.; Damaševičius, R.; Maskeliūnas, R. Distributed Centrality Analysis of Social Network Data Using MapReduce. Algorithms 2019, 12, 161. [Google Scholar] [CrossRef]
- Rizi, F.S.; Granitzer, M. Properties of Vector Embeddings in Social Networks. Algorithms 2017, 10, 109. [Google Scholar] [CrossRef]
- Swan, M. Blockchain: Blueprint for a New Economy; O’Reilly Media, Inc.: Newton, MA, USA, 2015. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Bitcoin. Org. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 24 February 2020).
- Wu, J.; Lin, D.; Zheng, Z.; Yuan, Q. T-EDGE: Temporal weighted multidigraph embedding for Ethereum transaction network analysis. arXiv 2019, arXiv:1905.08038. [Google Scholar]
- Nofer, M.; Gomber, P.; Hinz, O.; Schiereck, D. Blockchain. Bus. Inform. Syst. Eng. 2017, 59, 183–187. [Google Scholar] [CrossRef]
- Chan, S.; Chu, J.; Nadarajah, S.; Osterrieder, J. A statistical analysis of cryptocurrencies. J. Risk Financ. Manag. 2017, 10, 12. [Google Scholar] [CrossRef]
- Chu, J.; Nadarajah, S.; Chan, S. Statistical Analysis of the Exchange Rate of Bitcoin. PLoS ONE 2015, 10, e0133678. [Google Scholar] [CrossRef] [PubMed]
- Bakar, N.A.; Rosbi, S. High volatility detection method using statistical process control for cryptocurrency exchange rate: A case study of Bitcoin. Int. J. Eng. Sci. 2017, 6, 39–48. [Google Scholar]
- Szetela, B. The Use of Control Charts in the Study of Bitcoin’s Price Variability. In Quality Control and Assurance—An Ancient Greek Term Re-Mastered; IntechOpen: London, UK, 2017; p. 201. [Google Scholar]
- Li, Z.; Wang, Y.; Huang, Z. Risk Connectedness Heterogeneity in the Cryptocurrency Markets. Front. Phys. 2020, 8, 243. [Google Scholar] [CrossRef]
- Motamed, A.P.; Bahrak, B. Quantitative analysis of cryptocurrencies transaction graph. Appl. Netw. Sci. 2019, 4, 1–21. [Google Scholar] [CrossRef]
- Elliott, A.; Cucuringu, M.; Luaces, M.M.; Reidy, P.; Reinert, G. Anomaly detection in networks with application to financial transaction networks. arXiv 2019, arXiv:1901.00402. [Google Scholar]
- Lin, D.; Wu, J.; Yuan, Q.; Zheng, Z. Modeling and Understanding Ethereum Transaction Records via a Complex Network Approach. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2737–2741. [Google Scholar] [CrossRef]
- Ferretti, S.; D’Angelo, G. On the Ethereum blockchain structure: A complex networks theory perspective. Concurr. Comput. Pr. Exp. 2020, 32, 5493. [Google Scholar] [CrossRef]
- Javarone, M.A.; Wright, C.S. From Bitcoin to Bitcoin Cash: A network analysis. In Proceedings of the 1st Workshop on Cryptocurrencies and Blockchains for Distributed Systems, Munich Germany, 15 May–15 June 2018. [Google Scholar]
- Park, J.H.; Sohn, Y. Detecting Structural Changes in Longitudinal Network Data. Bayesian Anal. 2020, 15, 133–157. [Google Scholar] [CrossRef]
- Hoff, P.D. Hierarchical multilinear models for multiway data. Comput. Stat. Data Anal. 2011, 55, 530–543. [Google Scholar] [CrossRef][Green Version]
- Hoff, P. Multilinear tensor regression for longitudinal relational data. Ann. Appl. Stat. 2015, 9, 1169–1193. [Google Scholar] [CrossRef] [PubMed]
- Crowder, S.V.; Wiel, S.A. Exponentially Weighted Moving Average (EWMA) Control Chart; Wiley StatsRef: Statistics Reference Online; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lowry, C.A.; Woodall, W.H.; Champ, C.W.; Rigdon, S.E. A Multivariate Exponentially Weighted Moving Average Control Chart. Technometrics 1992, 34, 46–53. [Google Scholar] [CrossRef]
| Notation | Definition |
|---|---|
| Node index, for i = 1, 2, …, N | |
| Node index, j = 1, 2, …, N | |
| Number of nodes | |
| Time periods, for t = 1, 2, …, T | |
| Adjacency matrix | |
| Covariate vector for nodes i and j and time t | |
| Coefficient vector of covariates | |
| Probability distribution of network | |
| Number of latent variables | |
| Latent node position | |
| Node connection rule | |
| Error term for nodes i and j and time t | |
| matrix with all one elements | |
| Hidden state variable | |
| Vector of variables for monitoring | |
| MEWMA statistic | |
| Number of variables for monitoring | |
| Vector of smoothing parameters | |
| Error type-I |
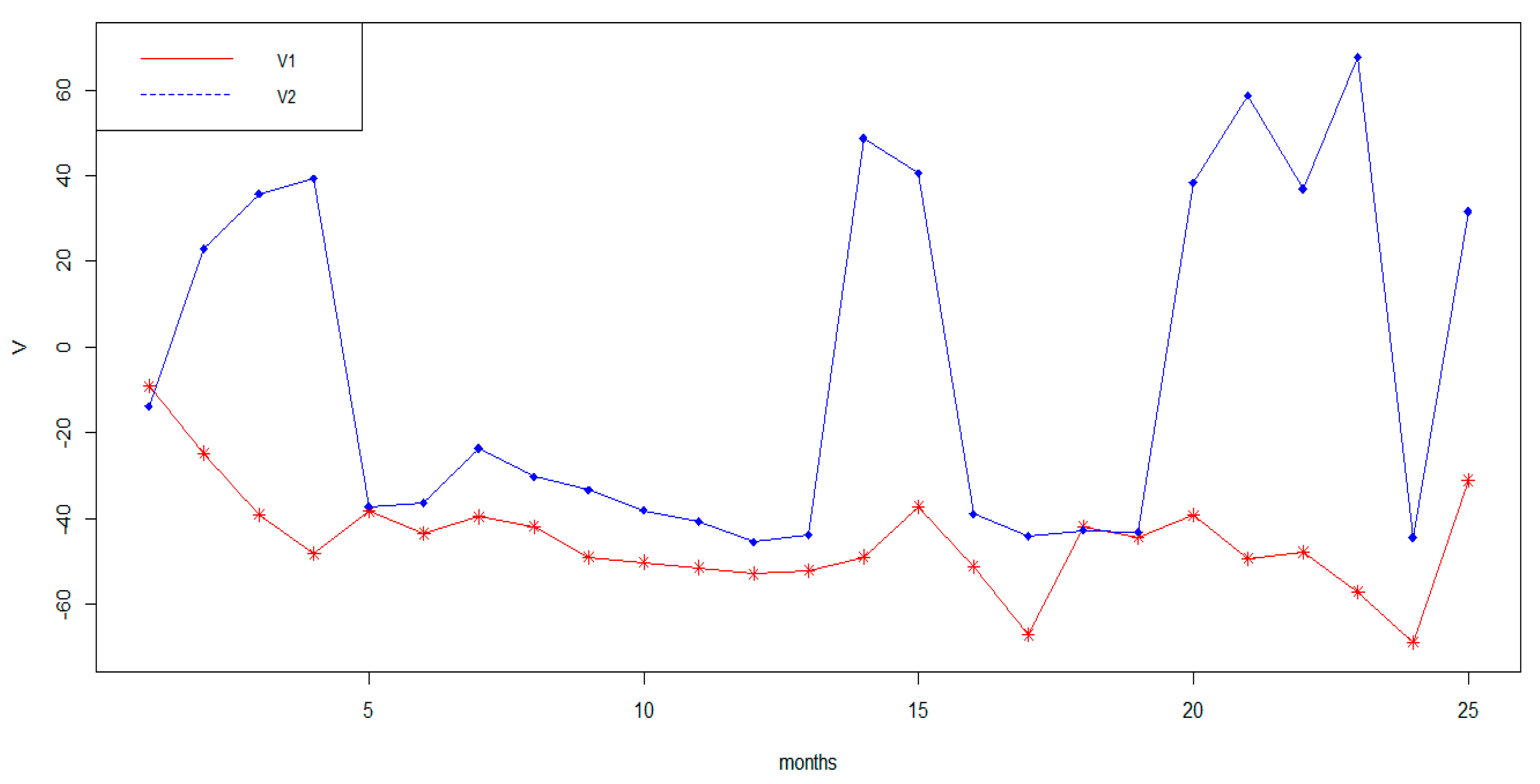
| months | ||||
|---|---|---|---|---|
| 1 | −0.01304 | −0.00098 | −9.13859 | −13.82489 |
| 2 | 0.00663 | 0.00494 | −24.7135 | 22.90376 |
| 3 | −0.00139 | 0.00067 | −38.9954 | 35.69328 |
| 4 | −0.00494 | −0.00208 | −48.2437 | 39.23815 |
| 5 | −0.00441 | −0.00048 | −38.2289 | −37.16167 |
| 6 | −0.00497 | −0.00092 | −43.4409 | −36.36019 |
| 7 | 0.00372 | −0.00384 | −39.5655 | −23.62889 |
| 8 | 0.00248 | −0.00466 | −41.8008 | −30.24743 |
| 9 | 0.00484 | −0.00215 | −48.9446 | −33.28495 |
| 10 | −0.00444 | −0.00082 | −50.1390 | −38.11684 |
| 11 | 0.00467 | −0.00036 | −51.3839 | −40.68477 |
| 12 | −0.00546 | −0.00031 | −52.8679 | −45.47404 |
| 13 | −0.00528 | −0.00035 | −52.0766 | −43.80679 |
| 14 | 0.00582 | 0.00094 | −48.9130 | 48.70567 |
| 15 | 0.00468 | −0.00077 | −37.2179 | 40.55287 |
| 16 | −0.00484 | −0.00048 | −51.1166 | −38.95125 |
| 17 | 0.00345 | −0.00197 | −67.0583 | −44.05735 |
| 18 | −0.00316 | −0.00181 | −41.8440 | −42.76087 |
| 19 | −2.5111 × 10−3 | 2.3869 × 10−5 | −44.2593 | −43.10673 |
| 20 | −0.00519 | −0.00197 | −39.2207 | 38.30627 |
| 21 | 0.00457 | 0.00142 | −49.32448 | 58.63748 |
| 22 | 0.00103 | 0.00155 | −47.7910 | 36.85834 |
| 23 | 0.00227 | 0.00172 | −57.01123 | 67.6237 |
| 24 | 0.00260 | −0.00143 | −68.80305 | −44.41586 |
| 25 | 0.00792 | 0.00158 | −31.07843 | 31.59579 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabri-Laghaie, K.; Jafarzadeh Ghoushchi, S.; Elhambakhsh, F.; Mardani, A. Monitoring Blockchain Cryptocurrency Transactions to Improve the Trustworthiness of the Fourth Industrial Revolution (Industry 4.0). Algorithms 2020, 13, 312. https://doi.org/10.3390/a13120312
Sabri-Laghaie K, Jafarzadeh Ghoushchi S, Elhambakhsh F, Mardani A. Monitoring Blockchain Cryptocurrency Transactions to Improve the Trustworthiness of the Fourth Industrial Revolution (Industry 4.0). Algorithms. 2020; 13(12):312. https://doi.org/10.3390/a13120312
Chicago/Turabian StyleSabri-Laghaie, Kamyar, Saeid Jafarzadeh Ghoushchi, Fatemeh Elhambakhsh, and Abbas Mardani. 2020. "Monitoring Blockchain Cryptocurrency Transactions to Improve the Trustworthiness of the Fourth Industrial Revolution (Industry 4.0)" Algorithms 13, no. 12: 312. https://doi.org/10.3390/a13120312
APA StyleSabri-Laghaie, K., Jafarzadeh Ghoushchi, S., Elhambakhsh, F., & Mardani, A. (2020). Monitoring Blockchain Cryptocurrency Transactions to Improve the Trustworthiness of the Fourth Industrial Revolution (Industry 4.0). Algorithms, 13(12), 312. https://doi.org/10.3390/a13120312







