A Novel Blind Restoration and Reconstruction Approach for CT Images Based on Sparse Representation and Hierarchical Bayesian-MAP
Abstract
:1. Introduction
2. Materials and Methods
2.1. CT Image Blind Restoration and Reconstruction
2.2. The Hierarchical Bayesian MAP
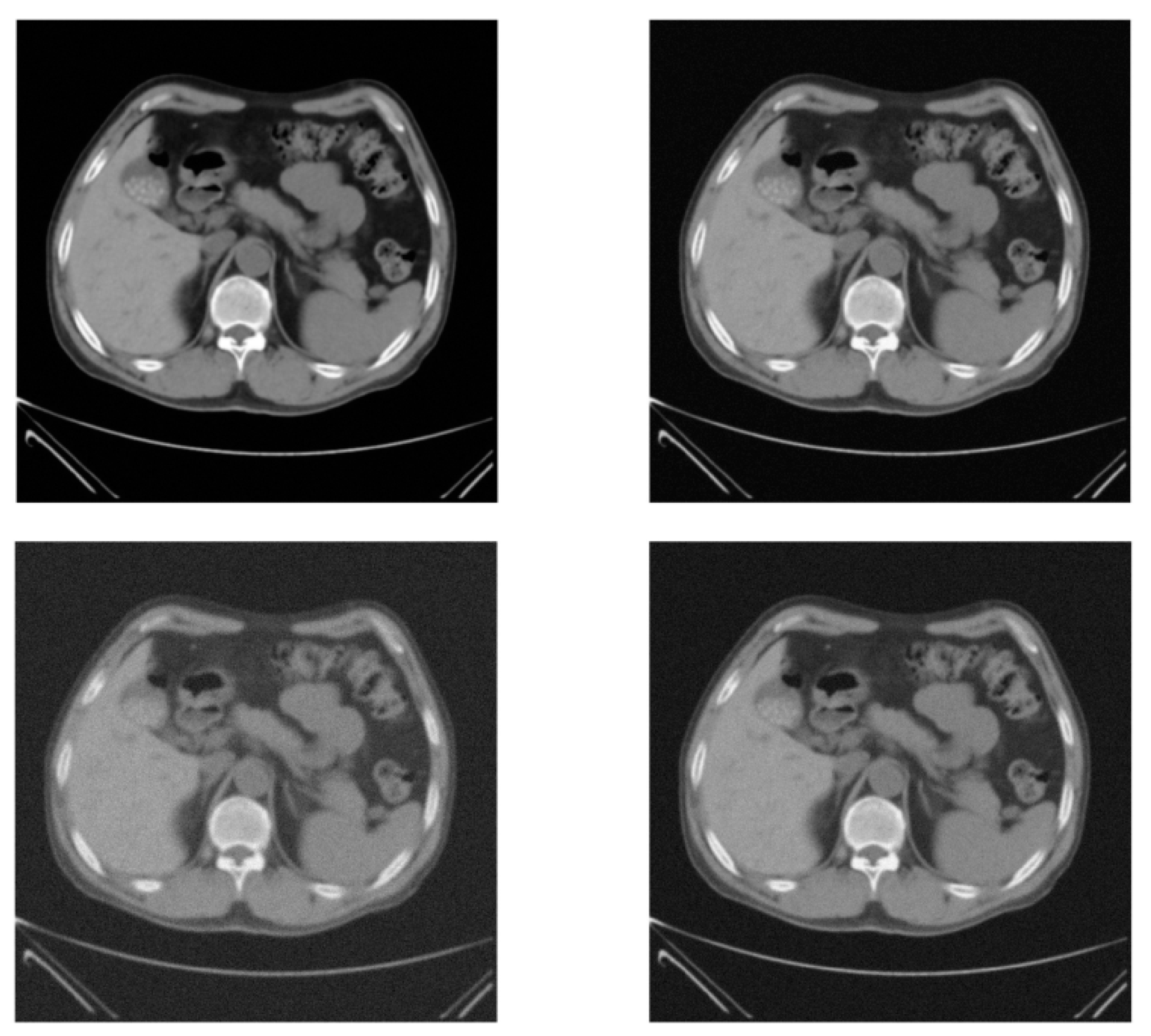
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Turner, M.O.; Mayo, J.R.; Müller, N.L.; Schulzer, M.; FitzGerald, J.M. The Value of Thoracic Computed Tomography Scans in Clinical Diagnosis: A Prospective Study. Can. Respir. J. 2016, 13, 311–316. [Google Scholar] [CrossRef] [PubMed]
- Lv, P.; Liu, J.; Chai, Y.; Yan, X.; Gao, J.; Dong, J. Automatic Spectral Imaging Protocol Selection and Iterative Reconstruction in Abdominal CT with Reduced Contrast Agent Dose: Initial Experience. Eur. Radiol. 2017, 27, 374–383. [Google Scholar] [CrossRef] [PubMed]
- Yan, M. Convergence Analysis of SART: Optimization and Statistics. Int. J. Comput. Math. 2013, 90, 30–47. [Google Scholar] [CrossRef]
- Ferreira, J.C.; Flores, E.L.; Carrijo, G.A. Quantization Noise on Image Reconstruction using Model-based Compressive Sensing. Lat. Am. Trans. IEEE 2015, 13, 1167–1177. [Google Scholar] [CrossRef]
- Lubner, M.G.; Pickhardt, P.J.; Tang, J.; Chen, G.H. Reduced Image Noise at Low-dose Multidetector CT of the Abdomen with Prior Image Constrained Compressed Sensing Algorithm. Radiology 2011, 260, 248–256. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.; Cho, H.; Je, U.; Lee, M.; Kim, H.; Hong, D.; Park, Y.; Lee, S.; Cho, H.; Choi, S.; et al. Experimental Study on the Application of a Compressed-sensing (CS) Algorithm to Dental Cone-beam CT (CBCT) for Accurate, Low-dose Image Reconstruction. J. Korean Phys. Soc. 2013, 62, 834–838. [Google Scholar] [CrossRef]
- Gonzales, B.; Spronk, D.; Cheng, Y.; Tucker, A.W.; Beckman, M.; Zhou, O.; Lu, J. Rectangular Fixed-gantry CT Prototype: Combining CNT X-Ray Sources and Accelerated Compressed Sensing-based Reconstruction. IEEE Access 2014, 2, 971–981. [Google Scholar] [CrossRef]
- Lubner, M.G.; Pickhardt, P.J.; Kim, D.H.; Tang, J.; Del Rio, A.M.; Chen, G.H. Prospective Evaluation of Prior Image Constrained Compressed Sensing (PICCS) Algorithm in Abdominal CT: A Comparison of Reduced Dose with Standard Dose Imaging. Abdom. Imaging 2015, 40, 207–221. [Google Scholar] [CrossRef]
- Bannas, P.; Li, Y.; Motosugi, U.; Li, K.; Lubner, M.; Chen, G.H.; Pickhardt, P.J. Prior Image Constrained Compressed Sensing Metal Artifact Reduction (PICCS-MAR): 2D and 3D image Quality Improvement with Hip Prostheses at CT Colonography. Eur. Radiol. 2016, 26, 2039–2046. [Google Scholar] [CrossRef]
- Lee, K.; Wu, Y.; Bresler, Y. Near-optimal Compressed Sensing of a Class of Sparse Low-rank Matrices via Sparse Power Factorization. IEEE Trans. Inf. Theory 2018, 64, 1666–1698. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, G.; Skinner, M.W.; Rubinstein, J.T.; Vannier, M.W. Blind Deblurring of Spiral CT Images. IEEE Trans. Med. Imaging 2003, 22, 837–845. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Xie, L.; Luo, L.; Nunes, J.C.; Toumoulin, C. L0 constrained Sparse Reconstruction for Multi-slice Helical CT Reconstruction. Phys. Med. Biol. 2011, 56, 1173–1189. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Wang, X.; Xiang, X.; Wei, Z. Convergence of SART + OS + TV Iterative Reconstruction Algorithm for Optical CT Imaging of Gel Dosimeters. Phys. Med. Biol. 2016, 61, 8425–8439. [Google Scholar] [CrossRef] [PubMed]
- Ram, I.; Cohen, I.; Elad, M. Patch-ordering-based Wavelet Frame and its Use in Inverse Problems. IEEE Trans. Image Process. 2014, 23, 2779–2792. [Google Scholar] [CrossRef] [PubMed]
- Shao, W.Z.; Wang, F.; Huang, L.L. Adapting Total Generalized Variation for Blind Image Restoration. Multidimens. Syst. Signal Process. 2019, 30, 857–883. [Google Scholar] [CrossRef]
- Qiu, X.; Dai, M. Blind Restoration of Camera Shake Blurred Image based on L0 Sparse Priors. Opt. Precis. Eng. 2017, 25, 2490–2498. [Google Scholar]
- Treece, G.M.; Poole, K.E.S.; Gee, A.H. Imaging the Femoral Cortex: Thickness, Density and Mass from Clinical CT. Med. Image Anal. 2012, 16, 952–965. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shangguan, H.; Zhang, Q.; Zhu, H.; Shu, H.; Gui, Z. Median Prior Constrained TV Algorithm for Sparse View Low-dose CT Reconstruction. Comput. Biol. Med. 2015, 60, 117–131. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Mohammad-Djafari, A.; Gac, N. Bayesian X-ray Computed Tomography using a Three-level Hierarchical Prior Model. In Proceedings of the AIP Conference, Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Gent, Belgium, 10–15 July 2016. [Google Scholar]
- Pang, J.; Cheung, G. Graph Laplacian Regularization for Image Denoising: Analysis in the Continuous Domain. IEEE Trans. Image Process. 2017, 26, 1770–1785. [Google Scholar] [CrossRef]
- Raj, R.G. A hierarchical Bayesian-MAP Approach to Inverse Problems in Imaging. Inverse Probl. 2016, 32, 075003. [Google Scholar] [CrossRef]
- Hammond, D.K.; Simoncelli, E.P. Image Modeling and Denoising with Orientation-adapted Gaussian Scale Mixtures. IEEE Trans. Image Process. 2008, 17, 2089–2101. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.; Basarab, A.; Kouame, D.; Tourneret, J.Y. Joint Bayesian deconvolution and point spread function estimation for ultrasound imaging. In Proceedings of the 2015 IEEE 12th International Symposium on Biomedical Imaging, New York, NY, USA, 16–19 April 2015. [Google Scholar]
- Li, Y.; Zhang, G. Blind Seismic Deconvolution using Variational Bayesian Method. J. Appl. Geophys. 2014, 110, 82–89. [Google Scholar]
- Cordemans, V.; Kaminski, L.; Banse, X.; Francq, B.G.; Cartiaux, O. Accuracy of a New Intraoperative Cone Beam CT Imaging Technique (Artis zeego II) Compared to Postoperative CT Scan for Assessment of Pedicle Screws Placement and Breaches Detection. Eur. Spine J. 2017, 26, 2906–2916. [Google Scholar] [CrossRef] [PubMed]








| The Proposed Algorithm |
|---|
| 1: Initialize parameters, , as the known CT system matrix, as the known sparse representation matrix, 2: Set is a Dirac delta function |
| 3: Input the known noisy projection data 4: for each iteration do 5: while do |
| 6: Calculating according to (9) |
| 7: Calculating according to (14) 8: Calculating according to |
| 9: Sampling according to (18) and (19) with a Gibbs method [24] |
| 10: end while 11: end for |
| 12: return |
| Sampling Ratio | 0.4 | 0.6 | 0.8 | 1 | |
|---|---|---|---|---|---|
| Figure 1 | SART | ----- | 50.4383 ± 0.1456 | 52.1108 ± 0.1543 | 54.5095 ± 0.1456 |
| SART + TV | ----- | 51.3425 ± 0.1278 | 54.8435 ± 0.1435 | 56.8108 ± 0.1376 | |
| Wavelet | ----- | 52.8898 ± 0.1212 | 57.1615 ± 0.1324 | 58.9218 ± 0.1214 | |
| Proposed approach | 55.1612 ± 0.1231 | 60.1005 ± 0.1109 | 63.0505 ± 0.1302 | 63.5126 ± 0.1087 | |
| Figure 2 | SART | ----- | 51.4795 ± 0.2561 | 53.4909 ± 0.2143 | 55.7349 ± 0.2469 |
| SART + TV | ----- | 53.9238 ± 0.1812 | 55.8124 ± 0.2452 | 56.7012 ± 0.2376 | |
| Wavelet | ----- | 59.8122 ± 0.1316 | 59.5905 ± 0.1243 | 59.1375 ± 0.1412 | |
| Proposed approach | 62.5796 ± 0.1156 | 63.9229 ± 0.1294 | 63.6970 ± 0.1218 | 64.6231 ± 0.1123 | |
| Figure 3 | SART | ----- | 34.1959 ± 0.1048 | 40.2794 ± 0.1098 | 45.4973 ± 0.1239 |
| SART + TV | ----- | 36.4972 ± 0.1345 | 43.4084 ± 0.1324 | 47.8413 ± 0.1267 | |
| Wavelet | ----- | 38.6082 ± 0.1367 | 45.1803 ± 0.1456 | 49.1661 ± 0.1489 | |
| Proposed approach | 42.7369 ± 0.0976 | 43.1990 ± 0.0989 | 46.6093 ± 0.0902 | 50.8476 ± 0.0087 | |
| Figure 4 | SART | ----- | 42.4213 ± 0.2456 | 44.1773 ± 0.2312 | 45.1659 ± 0.3241 |
| SART + TV | ----- | 43.8746 ± 0.2891 | 45.4988 ± 0.2561 | 46.6102 ± 0.2134 | |
| Wavelet | ----- | 45.8239 ± 0.2211 | 46.2769 ± 0.2341 | 48.4986 ± 0.2781 | |
| Proposed approach | 45.2660 ± 0.1561 | 47.3095 ± 0.1861 | 48.3834 ± 0.1734 | 49.6093 ± 0.1709 | |
| Sampling Ratio | 0.4 | 0.6 | 0.8 | 1 | |
|---|---|---|---|---|---|
| Figure 1 | SART | ----- | 0.9499 ± 0.0015 | 0.9615 ± 0.0018 | 0.9703 ± 0.0016 |
| SART + TV | ----- | 0.9661 ± 0.0012 | 0.9682 ± 0.0015 | 0.9841 ± 0.0026 | |
| Wavelet | ----- | 0.9765 ± 0.0012 | 0.9771 ± 0.0011 | 0.9868 ± 0.0014 | |
| Proposed approach | 0.9751 ± 0.013 | 0.9838 ± 0.0009 | 0.9858 ± 0.0012 | 0.9931 ± 0.0009 | |
| Figure 2 | SART | ----- | 0.9461 ± 0.0056 | 0.9607 ± 0.0038 | 0.9771 ± 0.0065 |
| SART + TV | ----- | 0.9553 ± 0.0078 | 0.9674 ± 0.0045 | 0.9833 ± 0.0076 | |
| Wavelet | ----- | 0.9687 ± 0.0052 | 0.9763 ± 0.0060 | 0.9842 ± 0.0098 | |
| Proposed approach | 0.9743 ± 0.0034 | 0.9830 ± 0.0045 | 0.9850 ± 0.0032 | 0.9923 ± 0.0026 | |
| Figure 3 | SART | ----- | 0.9254 ± 0.0089 | 0.9451 ± 0.0085 | 0.9583 ± 0.0090 |
| SART + TV | ----- | 0.9348 ± 0.0078 | 0.9682 ± 0.0091 | 0.9723 ± 0.0089 | |
| Wavelet | ----- | 0.9578 ± 0.0052 | 0.9789 ± 0.0067 | 0.9815 ± 0.0064 | |
| Proposed approach | 0.9451 ± 0.0031 | 0.9687 ± 0.0029 | 0.9812 ± 0.0032 | 0.9994 ± 0.0037 | |
| Figure 4 | SART | ----- | 0.9491 ± 0.0026 | 0.9707 ± 0.0034 | 0.9795 ± 0.0045 |
| SART + TV | ----- | 0.9553 ± 0.0045 | 0.9774 ± 0.0034 | 0.9833 ± 0.0044 | |
| Wavelet | ----- | 0.96 07 ± 0.0022 | 0.9812 ± 0.023 | 0.9901 ± 0.0024 | |
| Proposed approach | 0.9643 ± 0.0023 | 0.9730 ± 0.0021 | 0.9879 ± 0.0032 | 0.9952 ± 0.0027 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, L.; Li, Y.; Meng, J. A Novel Blind Restoration and Reconstruction Approach for CT Images Based on Sparse Representation and Hierarchical Bayesian-MAP. Algorithms 2019, 12, 174. https://doi.org/10.3390/a12080174
Sun Y, Zhang L, Li Y, Meng J. A Novel Blind Restoration and Reconstruction Approach for CT Images Based on Sparse Representation and Hierarchical Bayesian-MAP. Algorithms. 2019; 12(8):174. https://doi.org/10.3390/a12080174
Chicago/Turabian StyleSun, Yunshan, Liyi Zhang, Yanqin Li, and Juan Meng. 2019. "A Novel Blind Restoration and Reconstruction Approach for CT Images Based on Sparse Representation and Hierarchical Bayesian-MAP" Algorithms 12, no. 8: 174. https://doi.org/10.3390/a12080174
APA StyleSun, Y., Zhang, L., Li, Y., & Meng, J. (2019). A Novel Blind Restoration and Reconstruction Approach for CT Images Based on Sparse Representation and Hierarchical Bayesian-MAP. Algorithms, 12(8), 174. https://doi.org/10.3390/a12080174




