An Application of Manifold Learning in Global Shape Descriptors
Abstract
1. Introduction
2. Background
2.1. Spectral Shape Analysis
2.2. Manifold Learning
3. Method
3.1. Laplacian Eigenmap-Based Shape Descriptor
3.2. Scale Normalization
3.3. Algorithm
| Algorithm 1: Laplacian Eigenmap-based scale-invariant global shape descriptor. |
 |
4. Experiments
4.1. Dataset
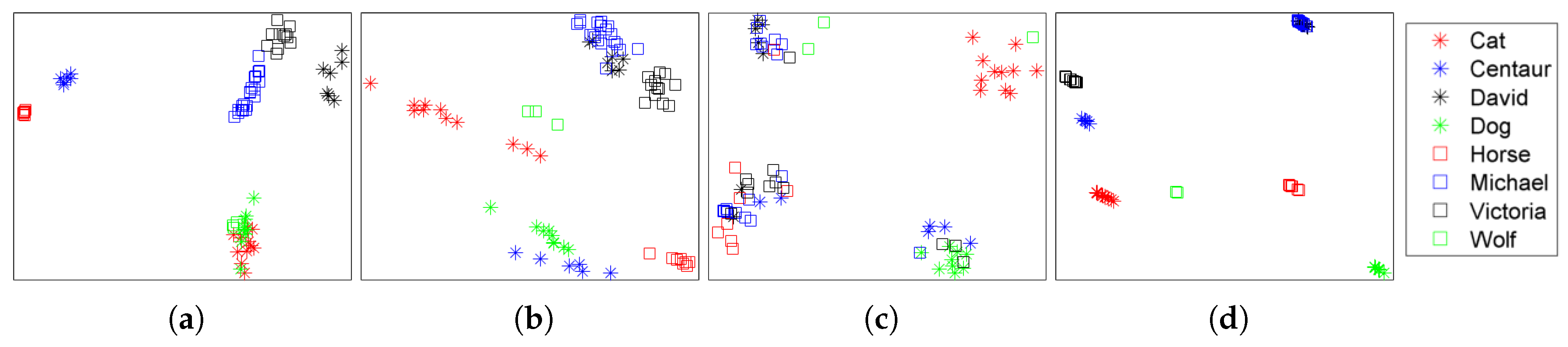
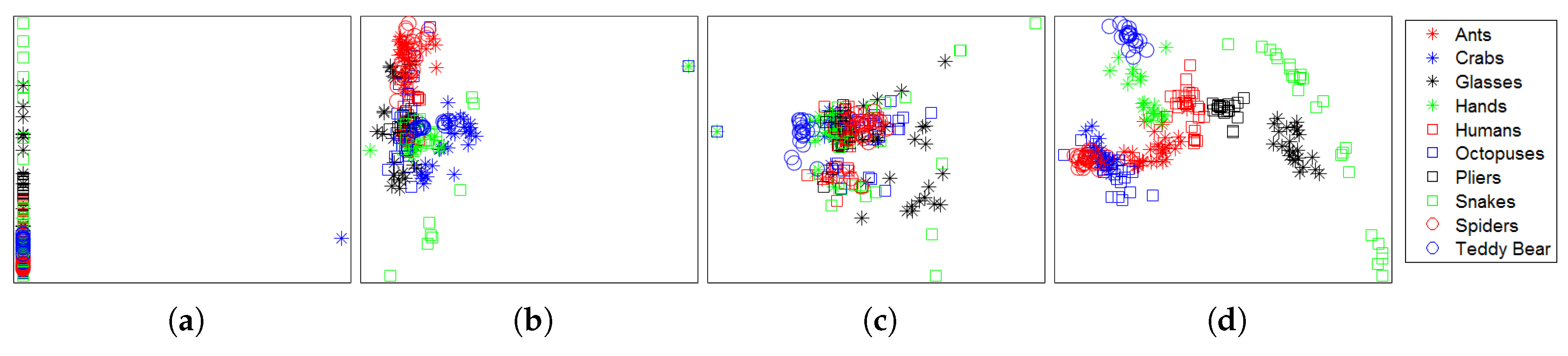
4.2. Retrieval Results
4.3. Multi-Class Classification Results
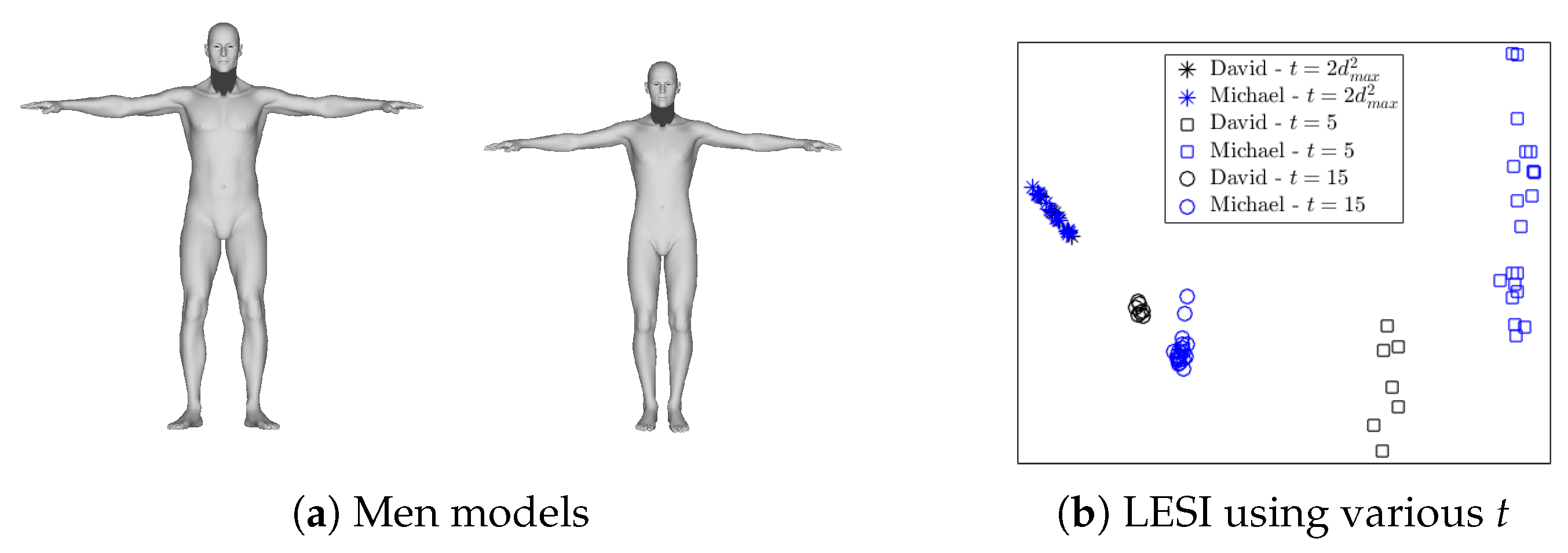
4.4. Robustness
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Omrani, E.; Tafti, A.P.; Fathi, M.F.; Moghadam, A.D.; Rohatgi, P.; D’Souza, R.M.; Yu, Z. Tribological study in microscale using 3D SEM surface reconstruction. Tribol. Int. 2016, 103, 309–315. [Google Scholar] [CrossRef]
- Ng, L.; Pathak, S.; Kuan, C.; Lau, C.; Dong, H.W.; Sodt, A.; Dang, C.; Avants, B.; Yushkevich, P.; Gee, J.; et al. Neuroinformatics for genome-wide 3-D gene expression mapping in the mouse brain. IEEE/ACM Trans. Comput. Biol. Bioinf. (TCBB) 2007, 4, 382–393. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Rostami, R.; Pang, X.; Fu, Z.; Yu, Z. Mesh generation and flexible shape comparisons for bio-molecules. Mol. Based Math. Biol. 2016, 4, 1–13. [Google Scholar] [CrossRef]
- Sosa, G.D.; Rodríguez, S.; Guaje, J.; Victorino, J.; Mejía, M.; Fuentes, L.S.; Ramírez, A.; Franco, H. 3D surface reconstruction of entomological specimens from uniform multi-view image datasets. In Proceedings of the 2016 XXI Symposium on Signal Processing, Images and Artificial Vision (STSIVA), Bucaramanga, Colombia, 31 August–2 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Riehemann, S.; Palme, M.; Kuehmstedt, P.; Grossmann, C.; Notni, G.; Hintersehr, J. Microdisplay-based intraoral 3D scanner for dentistry. J. Disp. Technol. 2011, 7, 151–155. [Google Scholar] [CrossRef]
- Wu, C.; Bradley, D.; Garrido, P.; Zollhöfer, M.; Theobalt, C.; Gross, M.; Beeler, T. Model-based teeth reconstruction. ACM Trans. Graph. (TOG) 2016, 35, 220. [Google Scholar] [CrossRef]
- Aflalo, Y.; Bronstein, A.M.; Bronstein, M.M.; Kimmel, R. Deformable shape retrieval by learning diffusion kernels. In International Conference on Scale Space and Variational Methods in Computer Vision; Springer: Berlin, Germany, 2011; pp. 689–700. [Google Scholar]
- Bronstein, A.M.; Bronstein, M.M.; Guibas, L.J.; Ovsjanikov, M. Shape google: Geometric words and expressions for invariant shape retrieval. ACM Trans. Graph. (TOG) 2011, 30, 1. [Google Scholar] [CrossRef]
- Xie, J.; Fang, Y.; Zhu, F.; Wong, E. Deepshape: Deep learned shape descriptor for 3d shape matching and retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7 June 2015; pp. 1275–1283. [Google Scholar]
- Toldo, R.; Castellani, U.; Fusiello, A. Visual vocabulary signature for 3D object retrieval and partial matching. In Proceedings of the 2nd Eurographics conference on 3D Object Retrieval; Eurographics Association: Aire-la-Ville, Switzerland, 2009; pp. 21–28. [Google Scholar]
- Bu, S.; Liu, Z.; Han, J.; Wu, J.; Ji, R. Learning high-level feature by deep belief networks for 3-D model retrieval and recognition. IEEE Trans. Multimed. 2014, 16, 2154–2167. [Google Scholar] [CrossRef]
- Boscaini, D.; Masci, J.; Rodolà, E.; Bronstein, M.M.; Cremers, D. Anisotropic diffusion descriptors. Comput. Graph. Forum 2016, 35, 431–441. [Google Scholar] [CrossRef]
- Bronstein, A.M. Spectral descriptors for deformable shapes. arXiv 2011, arXiv:1110.5015. [Google Scholar]
- Raviv, D.; Kimmel, R.; Bruckstein, A.M. Graph isomorphisms and automorphisms via spectral signatures. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1985–1993. [Google Scholar] [CrossRef]
- De Youngster, D.; Paquet, E.; Viktor, H.; Petriu, E. An isometry-invariant spectral approach for protein-protein docking. In Proceedings of the 13th IEEE International Conference on BioInformatics and BioEngineering, Chania, Greece, 10–13 December 2013; pp. 1–6. [Google Scholar]
- Ovsjanikov, M.; Ben-Chen, M.; Solomon, J.; Butscher, A.; Guibas, L. Functional maps: A flexible representation of maps between shapes. ACM Trans. Graph. (TOG) 2012, 31, 30. [Google Scholar] [CrossRef]
- Tangelder, J.W.; Veltkamp, R.C. A survey of content based 3D shape retrieval methods. In Proceedings of the 2004 Shape Modeling Applications, Genova, Italy, 7–9 June 2004; pp. 145–156. [Google Scholar]
- Zhang, L.; da Fonseca, M.J.; Ferreira, A.; e Recuperação, C.R.A. Survey on 3D Shape Descriptors; Technical Report, DecorAR (FCT POSC/EIA/59938/2004); Fundação para a Cincia e a Tecnologia: Lisboa, Portugal, 2007. [Google Scholar]
- Rostami, R.; Bashiri, F.; Rostami, B.; Yu, Z. A survey on data-driven 3D shape descriptors. Comput. Graph. Forum 2019, 38, 356–393. [Google Scholar] [CrossRef]
- Reuter, M.; Wolter, F.E.; Peinecke, N. Laplace–Beltrami spectra as ’Shape-DNA’ of surfaces and solids. Comput. Aided Des. 2006, 38, 342–366. [Google Scholar] [CrossRef]
- Sun, J.; Ovsjanikov, M.; Guibas, L. A concise and provably informative multi-scale signature based on heat diffusion. Comput. Graph. Forum 2009, 28, 1383–1392. [Google Scholar] [CrossRef]
- Aubry, M.; Schlickewei, U.; Cremers, D. The wave kernel signature: A quantum mechanical approach to shape analysis. In Proceedings of the IEEE 2011 Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 1626–1633. [Google Scholar]
- Rustamov, R.M. Laplace-Beltrami eigenfunctions for deformation invariant shape representation. In Proceedings of the Fifth Eurographics Symposium on Geometry Processing; Eurographics Association: Aire-la-Ville, Switzerland, 2007; pp. 225–233. [Google Scholar]
- Reuter, M.; Biasotti, S.; Giorgi, D.; Patanè, G.; Spagnuolo, M. Discrete Laplace–Beltrami operators for shape analysis and segmentation. Comput. Graph. 2009, 33, 381–390. [Google Scholar] [CrossRef]
- Belkin, M.; Sun, J.; Wang, Y. Discrete laplace operator on meshed surfaces. In Proceedings of the ACM Twenty-Fourth Annual Symposium on Computational Geometry, College Park, MD, USA, 9–11 June 2008; pp. 278–287. [Google Scholar]
- Goldberg, Y.; Zakai, A.; Kushnir, D.; Ritov, Y. Manifold learning: The price of normalization. J. Mach. Learn. Res. 2008, 9, 1909–1939. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Kokkinos, I. Scale-invariant heat kernel signatures for non-rigid shape recognition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1704–1711. [Google Scholar]
- Kuang, Z.; Li, Z.; Lv, Q.; Weiwei, T.; Liu, Y. Modal function transformation for isometric 3D shape representation. Comput. Graph. 2015, 46, 209–220. [Google Scholar] [CrossRef]
- Gao, Z.; Yu, Z.; Pang, X. A compact shape descriptor for triangular surface meshes. Comput. Aided Des. 2014, 53, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Lévy, B. Laplace-beltrami eigenfunctions towards an algorithm that “understands” geometry. In Proceedings of the IEEE International Conference on Shape Modeling and Applications 2006 (SMI’06), Matsushima, Japan, 14–16 June 2006; p. 13. [Google Scholar]
- Taubin, G. A signal processing approach to fair surface design. In Proceedings of the ACM 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August 1995; pp. 351–358. [Google Scholar]
- Mayer, U.F. Numerical solutions for the surface diffusion flow in three space dimensions. Comput. Appl. Math. 2001, 20, 361–379. [Google Scholar]
- Xu, G. Discrete Laplace–Beltrami operators and their convergence. Comput. Aided Geom. Des. 2004, 21, 767–784. [Google Scholar] [CrossRef]
- Desbrun, M.; Meyer, M.; Schröder, P.; Barr, A.H. Implicit fairing of irregular meshes using diffusion and curvature flow. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 1999; pp. 317–324. [Google Scholar]
- Meyer, M.; Desbrun, M.; Schröder, P.; Barr, A.H. Discrete differential-geometry operators for triangulated 2-manifolds. In Visualization and Mathematics III; Springer: Berlin, Germany, 2003; pp. 35–57. [Google Scholar]
- Xu, G. Convergence analysis of a discretization scheme for Gaussian curvature over triangular surfaces. Comput. Aided Geom. Des. 2006, 23, 193–207. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Silva, V.D.; Tenenbaum, J.B. Global versus local methods in nonlinear dimensionality reduction. In Proceedings of the 15th International Conference on Neural Information Processing Systems (NIPS’02), Vancouver, BC, Canada, 9–14 December 2002; pp. 721–728. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Saul, L.K.; Roweis, S.T. Think globally, fit locally: Unsupervised learning of low dimensional manifolds. J. Mach. Learn. Res. 2003, 4, 119–155. [Google Scholar]
- Coifman, R.R.; Lafon, S. Diffusion maps. Appl. Comput. Harmonic Anal. 2006, 21, 5–30. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Proceedings of the 14th International Conference on Neural Information Processing Systems (NIPS’01), Vancouver, BC, Canada, 3–8 December 2001; pp. 585–591. [Google Scholar]
- Wachinger, C.; Navab, N. Manifold Learning for Multi-Modal Image Registration. In Proceedings of the British Machine Vision Conference (BMVC’10), Aberystwyth, UK, 30 August–2 September 2010; pp. 82.1–82.12. [Google Scholar]
- Wachinger, C.; Navab, N. Structural image representation for image registration. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition—Workshops, San Francisco, CA, USA, 13–18 November 2010; pp. 23–30. [Google Scholar]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef]
- Dulmage, A.L.; Mendelsohn, N.S. Coverings of bipartite graphs. Can. J. Math. 1958, 10, 516–534. [Google Scholar] [CrossRef]
- Weyl, H. Über die asymptotische Verteilung der Eigenwerte. Nachrichten Gesellschaft Wissenschaften Göttingen Mathematisch-Physikalische Klasse 1911, 1911, 110–117. [Google Scholar]
- Bronstein, A.M.; Bronstein, M.M.; Kimmel, R. Numerical Geometry of Non-Rigid Shapes; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Siddiqi, K.; Zhang, J.; Macrini, D.; Shokoufandeh, A.; Bouix, S.; Dickinson, S. Retrieving articulated 3-D models using medial surfaces. Mach. Vis. Appl. 2008, 19, 261–275. [Google Scholar] [CrossRef]
- Mirloo, M.; Ebrahimnezhad, H. Non-rigid 3D object retrieval using directional graph representation of wave kernel signature. Multimed. Tools Appl. 2017, 77, 6987–7011. [Google Scholar] [CrossRef]
- Masoumi, M.; Hamza, A.B. Global spectral graph wavelet signature for surface analysis of carpal bones. arXiv 2017, arXiv:1709.02782. [Google Scholar] [CrossRef] [PubMed]
- Boscaini, D.; Masci, J.; Melzi, S.; Bronstein, M.M.; Castellani, U.; Vandergheynst, P. Learning class-specific descriptors for deformable shapes using localized spectral convolutional networks. Comput. Graph. Forum 2015, 34, 13–23. [Google Scholar] [CrossRef]
- Li, C.; Hamza, A.B. Spatially aggregating spectral descriptors for nonrigid 3D shape retrieval: a comparative survey. Multimed. Syst. 2014, 20, 253–281. [Google Scholar] [CrossRef]
- Lian, Z.; Godil, A.; Bustos, B.; Daoudi, M.; Hermans, J.; Kawamura, S.; Kurita, Y.; Lavoua, G.; Dp Suetens, P. SHREC’11 track: Shape retrieval on non-rigid 3D watertight meshes. In Proceedings of the Eurographics Workshop on 3D Object Retrieval (3DOR), Llandudno, UK, 10 April 2011; pp. 79–88. [Google Scholar]
- Shilane, P.; Min, P.; Kazhdan, M.; Funkhouser, T. The princeton shape benchmark. In Proceedings of the International Conference on Shape Modeling and Applications (SMI’04), Genova, Italy, 7–9 June 2004; pp. 167–178. [Google Scholar]
- Liu, Y.J.; Chen, Z.; Tang, K. Construction of iso-contours, bisectors, and Voronoi diagrams on triangulated surfaces. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1502–1517. [Google Scholar] [PubMed]
- Zhang, Y.; Bajaj, C.; Xu, G. Surface smoothing and quality improvement of quadrilateral/hexahedral meshes with geometric flow. Int. J. Numer. Methods Biomed. Eng. 2009, 25, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Xie, J.; Dai, G.; Wang, M.; Zhu, F.; Xu, T.; Wong, E. 3D deep shape descriptor. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2319–2328. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
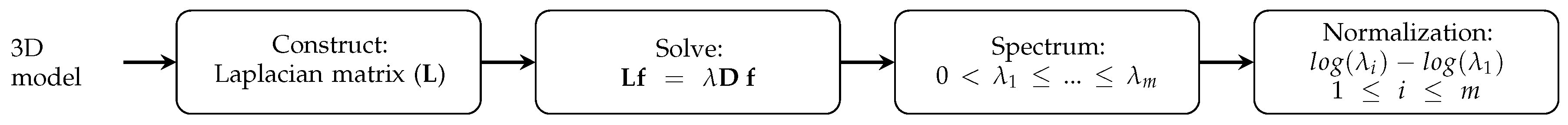


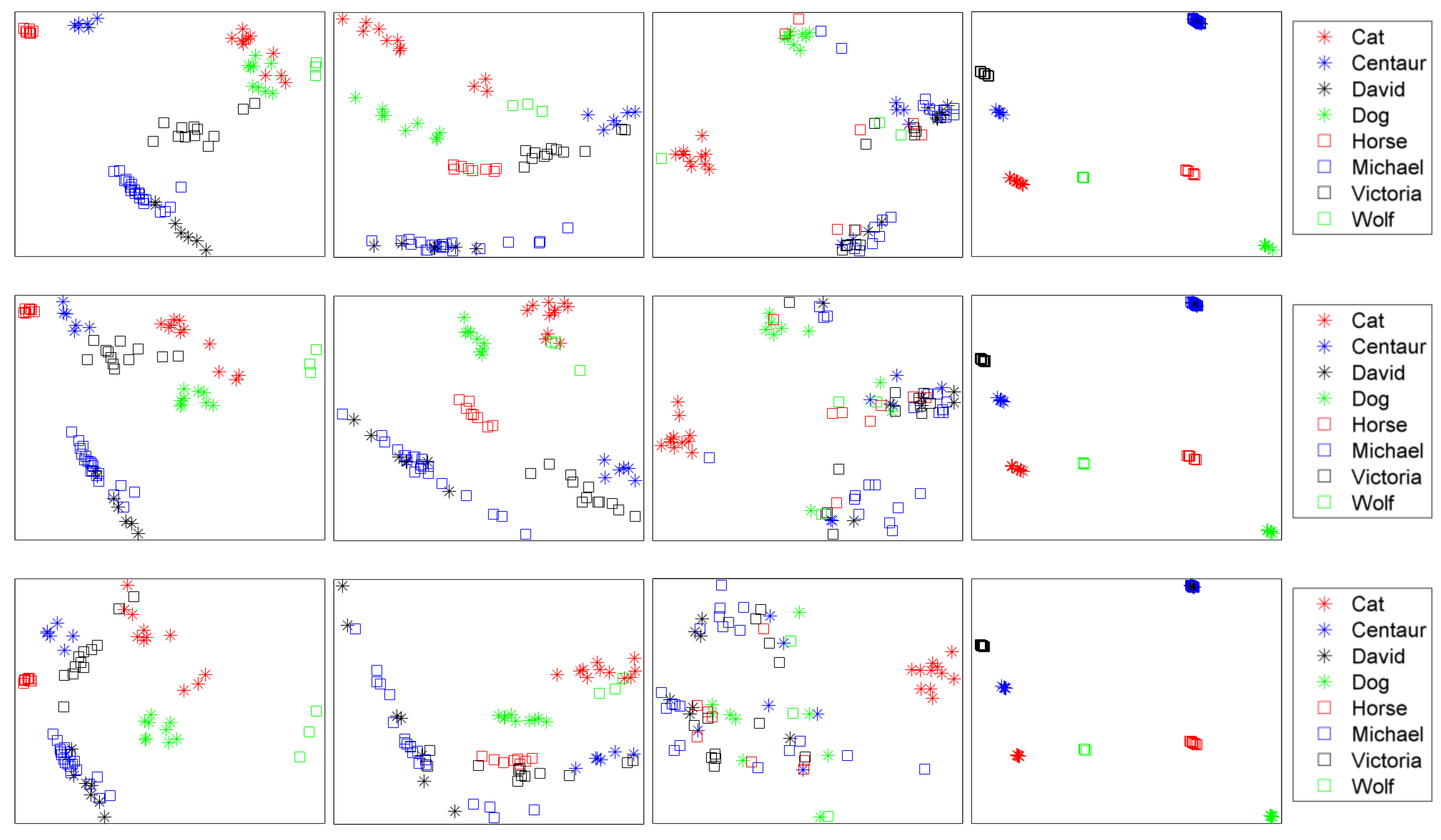

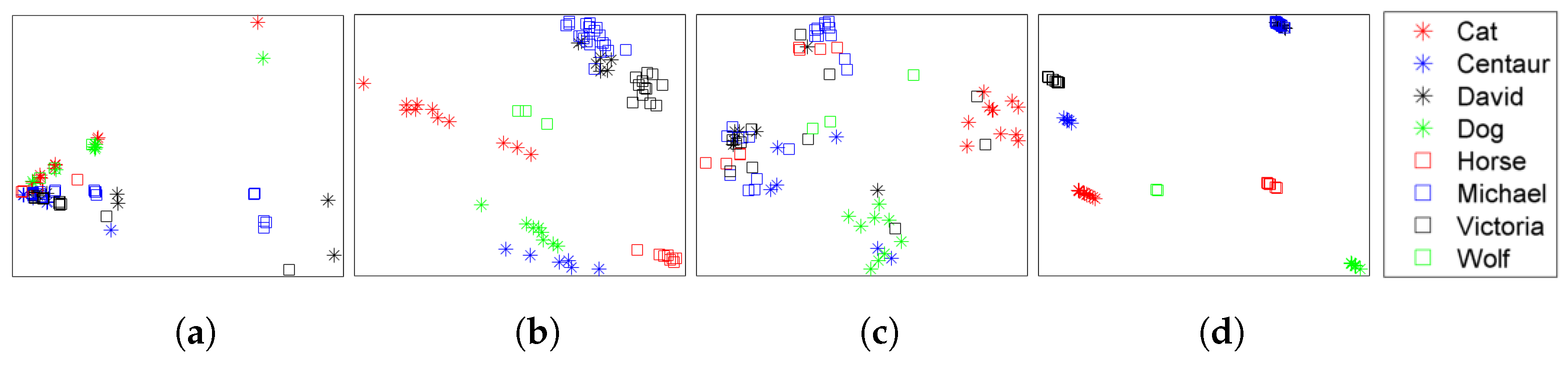

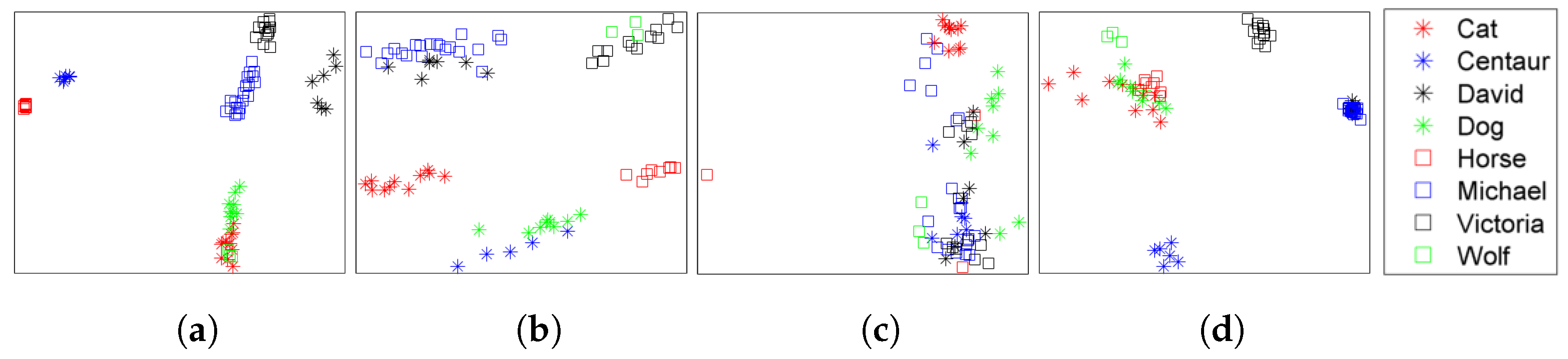

| Dataset | Method | NN | FT | ST | E | DCG |
|---|---|---|---|---|---|---|
| TOSCA | ShapeDNA | 1.0000 | 0.8091 | 0.9391 | 0.4486 | 0.9584 |
| cShapeDNA | 0.9474 | 0.7748 | 0.8984 | 0.4748 | 0.9241 | |
| GPS | 0.4868 | 0.4244 | 0.6320 | 0.3614 | 0.6787 | |
| LESI | 0.8684 | 0.8456 | 0.9430 | 0.4860 | 0.9244 | |
| McGill | ShapeDNA | 0.7922 | 0.3452 | 0.4977 | 0.3411 | 0.7192 |
| cShapeDNA | 0.7882 | 0.3943 | 0.5483 | 0.3852 | 0.7470 | |
| GPS | 0.3843 | 0.2508 | 0.4066 | 0.2588 | 0.6020 | |
| LESI | 0.9647 | 0.7046 | 0.8739 | 0.6644 | 0.9251 |
| Method | Average Accuracy |
|---|---|
| Shape-DNA | 21.02% |
| Shape-DNA (Normalized) | 90.60% |
| cShape-DNA | 71.37% |
| GPS | 50.11% |
| LESI | 95.69% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashiri, F.S.; Rostami, R.; Peissig, P.; D’Souza, R.M.; Yu, Z. An Application of Manifold Learning in Global Shape Descriptors. Algorithms 2019, 12, 171. https://doi.org/10.3390/a12080171
Bashiri FS, Rostami R, Peissig P, D’Souza RM, Yu Z. An Application of Manifold Learning in Global Shape Descriptors. Algorithms. 2019; 12(8):171. https://doi.org/10.3390/a12080171
Chicago/Turabian StyleBashiri, Fereshteh S., Reihaneh Rostami, Peggy Peissig, Roshan M. D’Souza, and Zeyun Yu. 2019. "An Application of Manifold Learning in Global Shape Descriptors" Algorithms 12, no. 8: 171. https://doi.org/10.3390/a12080171
APA StyleBashiri, F. S., Rostami, R., Peissig, P., D’Souza, R. M., & Yu, Z. (2019). An Application of Manifold Learning in Global Shape Descriptors. Algorithms, 12(8), 171. https://doi.org/10.3390/a12080171





