Protograph LDPC Code Design for Asynchronous Random Access †
Abstract
1. Introduction
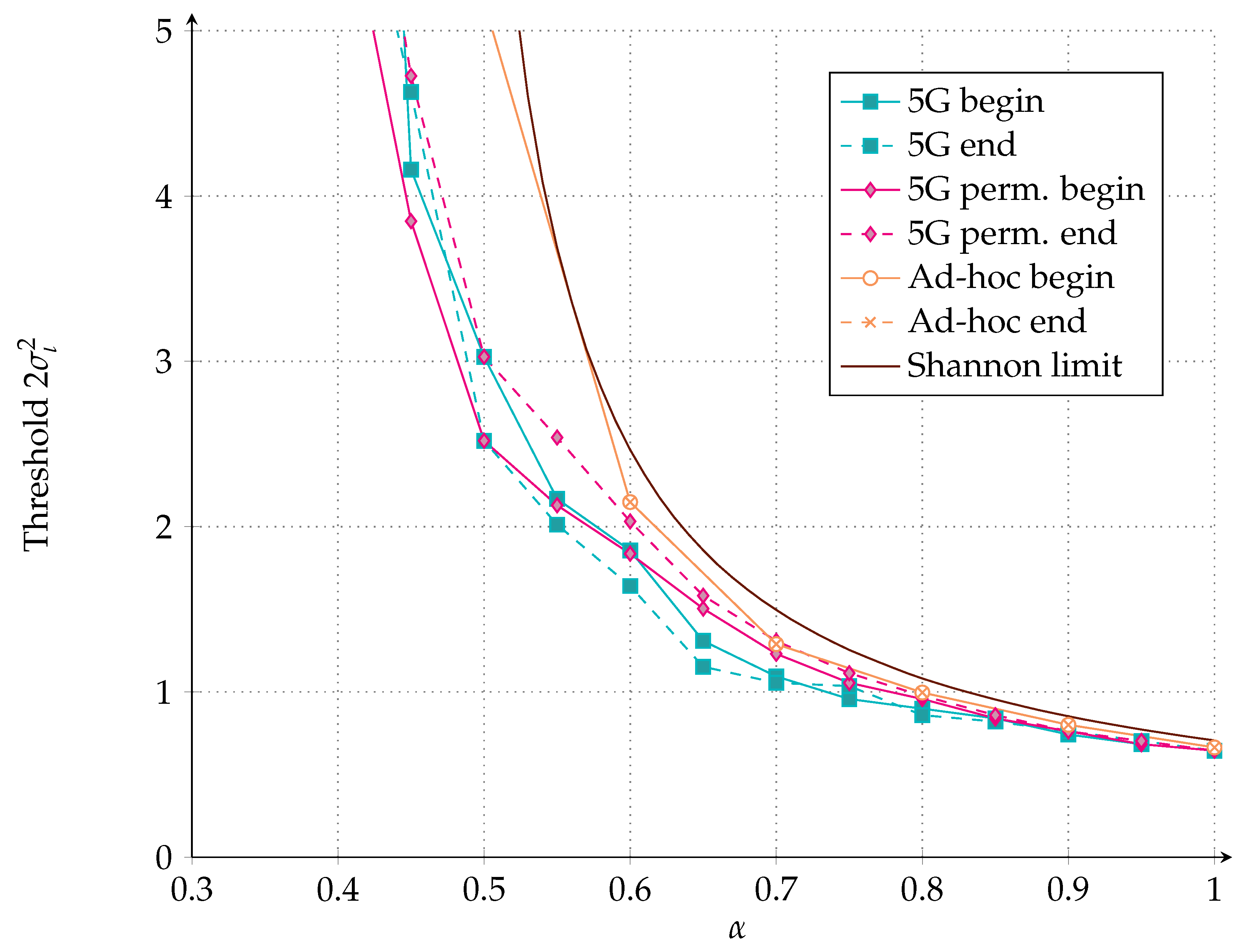
- In Section 3, we present a surrogate channel model, exploited in the code design phase, which assumes constant interference power over a fraction of the codeword. To facilitate code design, we further approximate the aggregate interference contribution, possibly generated by a multitude of terminals, as Gaussian. In Section 3.4, we present a protograph LDPC code design for this channel model, and its iterative decoding threshold is compared with the one of a raptor-like LDPC code design proposed for the recently introduced fifth generation of mobile networks (5G) standard. Both code designs are compared with the Shannon limit.
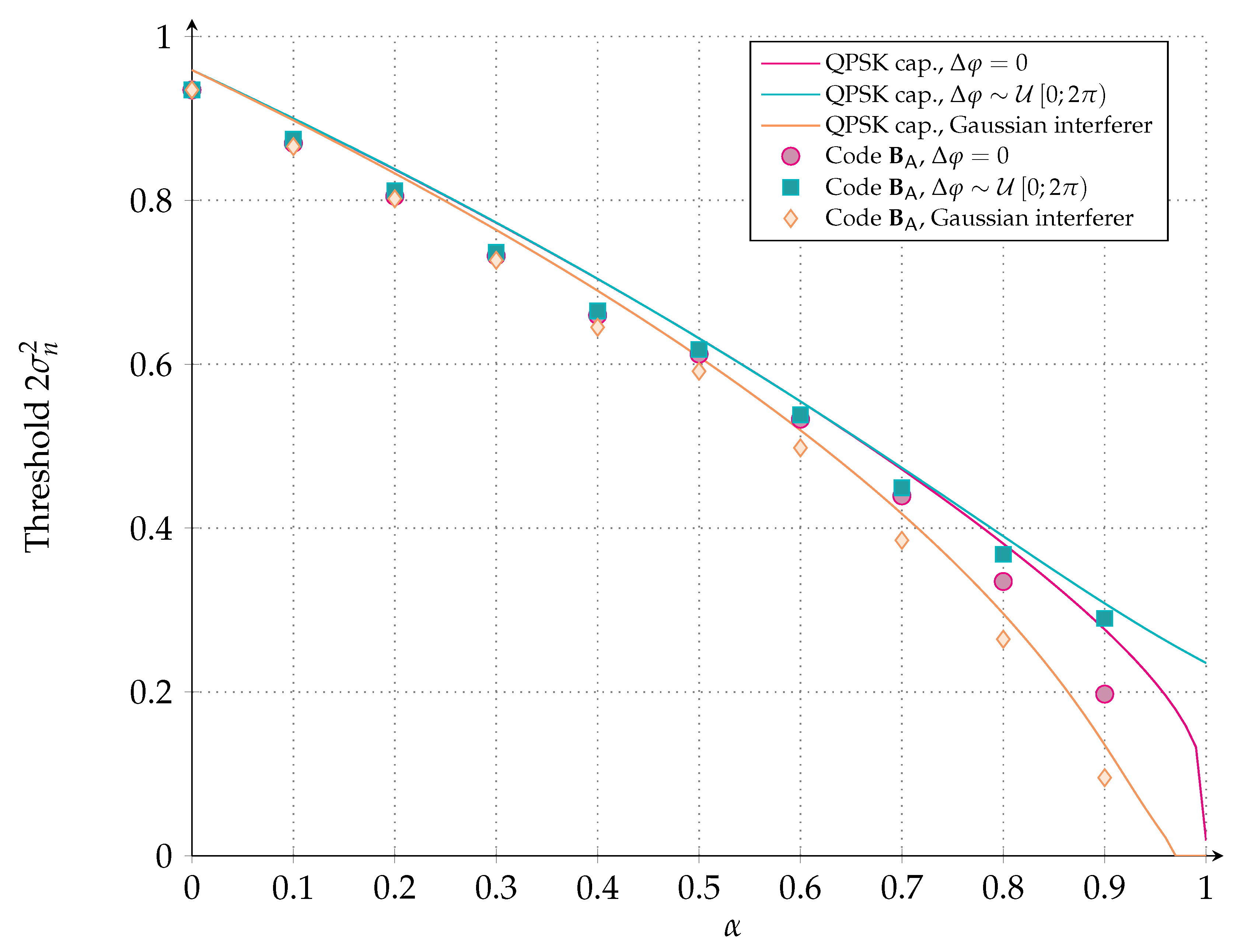
- The impact of the Gaussian interference assumption on the code performance is also considered in Section 3.5. The expression of the log-likelihood ratio (LLR) and the threshold performance, computed with quantized density evolution, are presented for a single interferer when the Gaussian assumption is dropped.
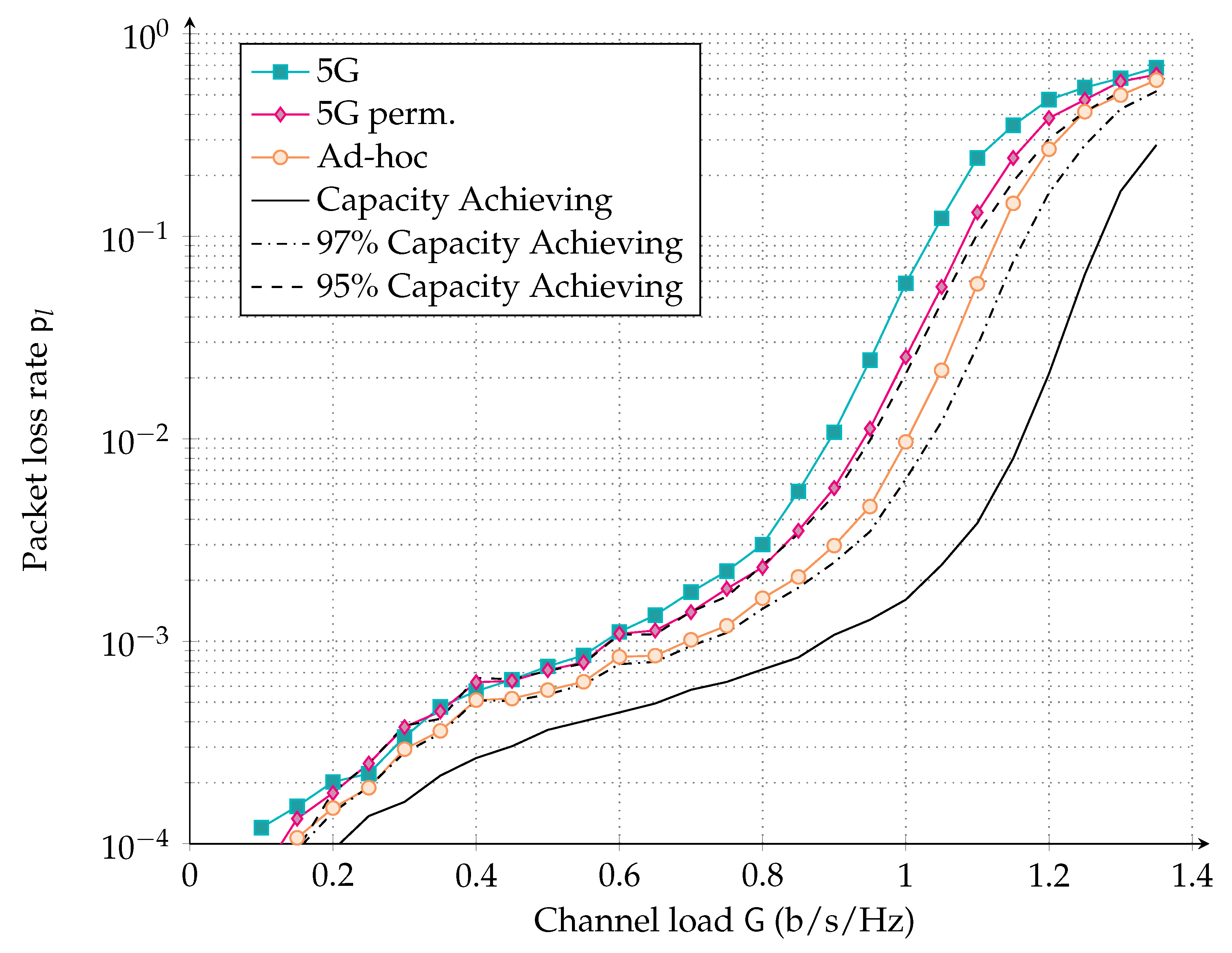
- In order to get a first, yet not fully accurate, performance characteristic for the proposed LDPC codes in the random access (RA) channel, we elaborate on the decoding condition so as to abstract the physical layer in Section 4.1. A decoding region, as a function of the interference pattern for both a random code ensemble and for the LDPC code ensemble is derived. Although more accurate than the surrogate channel model, since the effective interference power and affected codeword position are considered, the abstraction is grounded on the iterative decoding threshold, and thus on large blocks assumption.
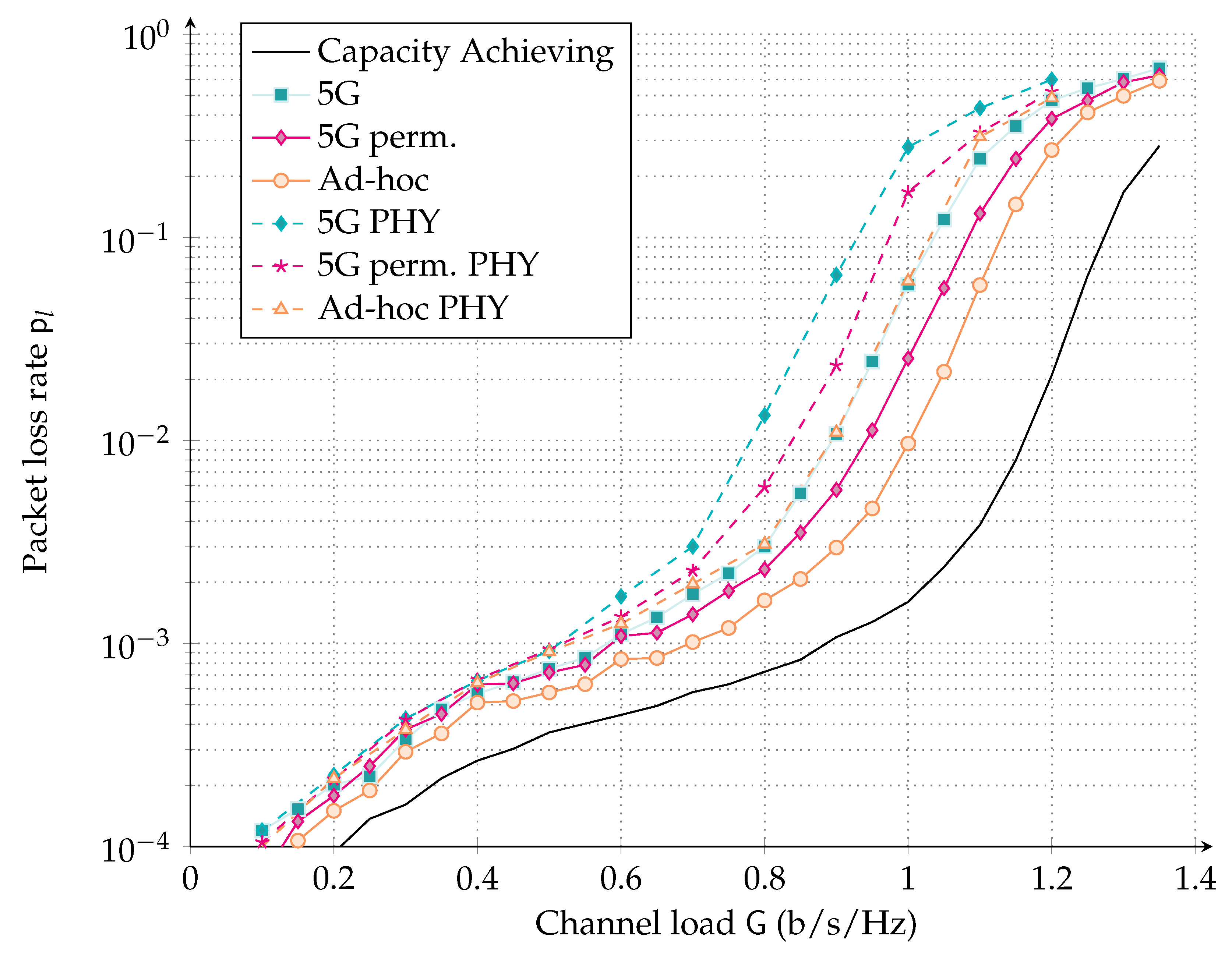
- Since RA is particularly appealing for short packet transmission, we depart from the physical layer abstraction and present in Section 4.2 physical layer simulations considering a finite block length. Interestingly, the codes designed for the surrogate channel model still perform very well on the asynchronous multiple access channel. Moreover, the performance trends and relative performance identified via the simpler simulations with the abstracted physical layer are confirmed.
2. System Model
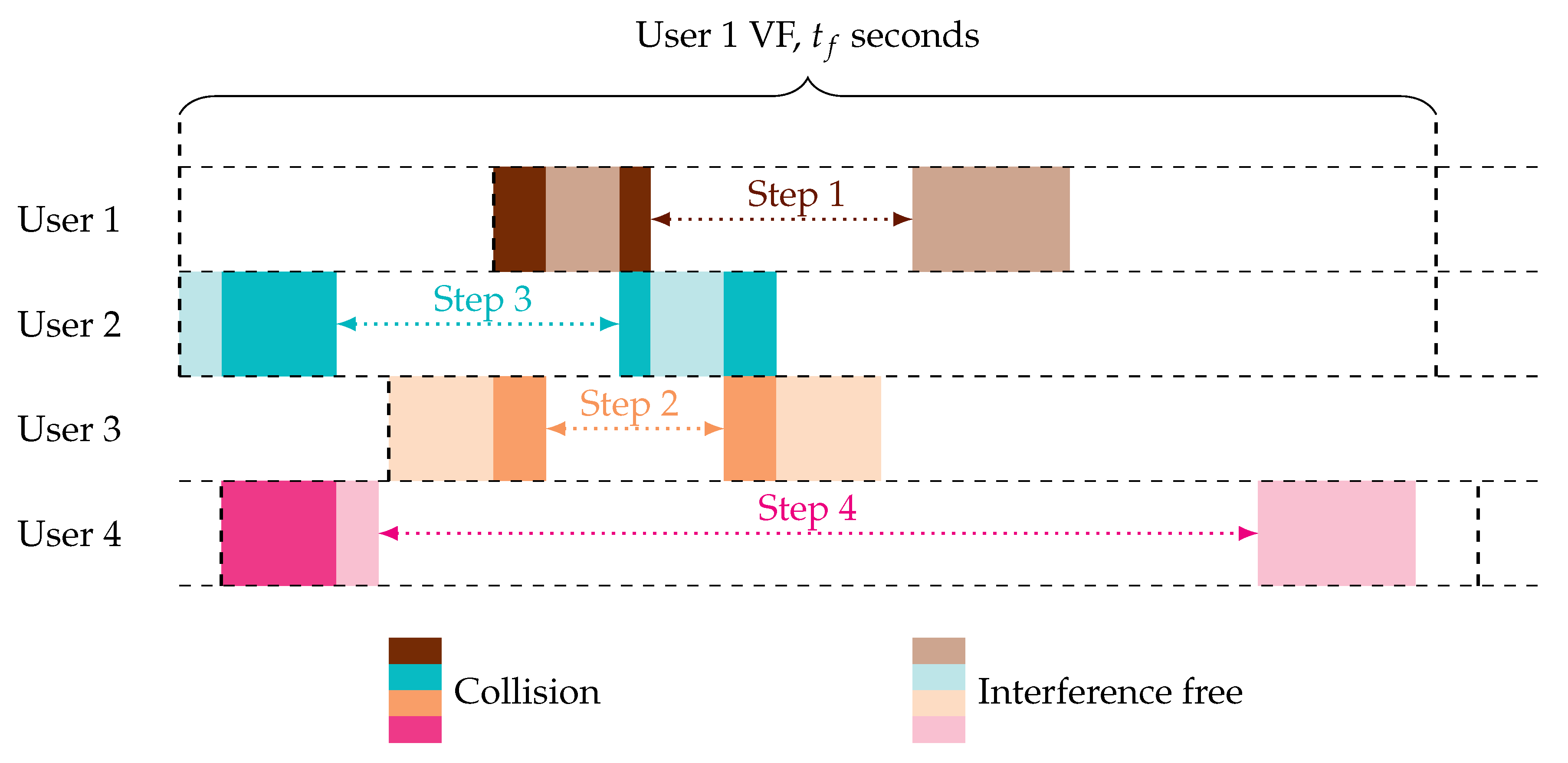
2.1. Asynchronous Random Access Protocol
- self-interference must be avoided, i.e., no portion of the two replicas shall overlap;
- the maximum delay, called virtual frame (VF), between the start of the first replica and the end of the second one shall not exceed seconds;
- the delay between the start of the two replicas is drawn uniformly at random within the interval , with the activation time of User u.
- the replica waveform is reconstructed on a sample level and subtracted from the incoming signal. We will consider ideal interference cancellation, i.e., after cancellation, no residual power is left by the replica;
- the information about the twin location (the time position of the other replica of the same user) is extracted from the header.
2.2. Asynchronous Random Access Channel Model
3. Code Design for the Asynchronous Random Access Channel
3.1. Protograph LDPC Codes
3.2. Code Optimization
3.3. Simplified Channel Models for Code Design
- A fraction , , of a (modulated) codeword is only affected by noise with power .
- A fraction of a (modulated) codeword is affected by noise and interference of constant power over the fraction.
3.3.1. Gaussian Interference Model
3.3.2. Single Interferer Model
3.4. Code Design for Gaussian Interference
3.4.1. Ad-Hoc LDPC Code Design
3.4.2. Raptor-Like LDPC Code Design
3.4.3. Asymptotic Results for Gaussian Interference
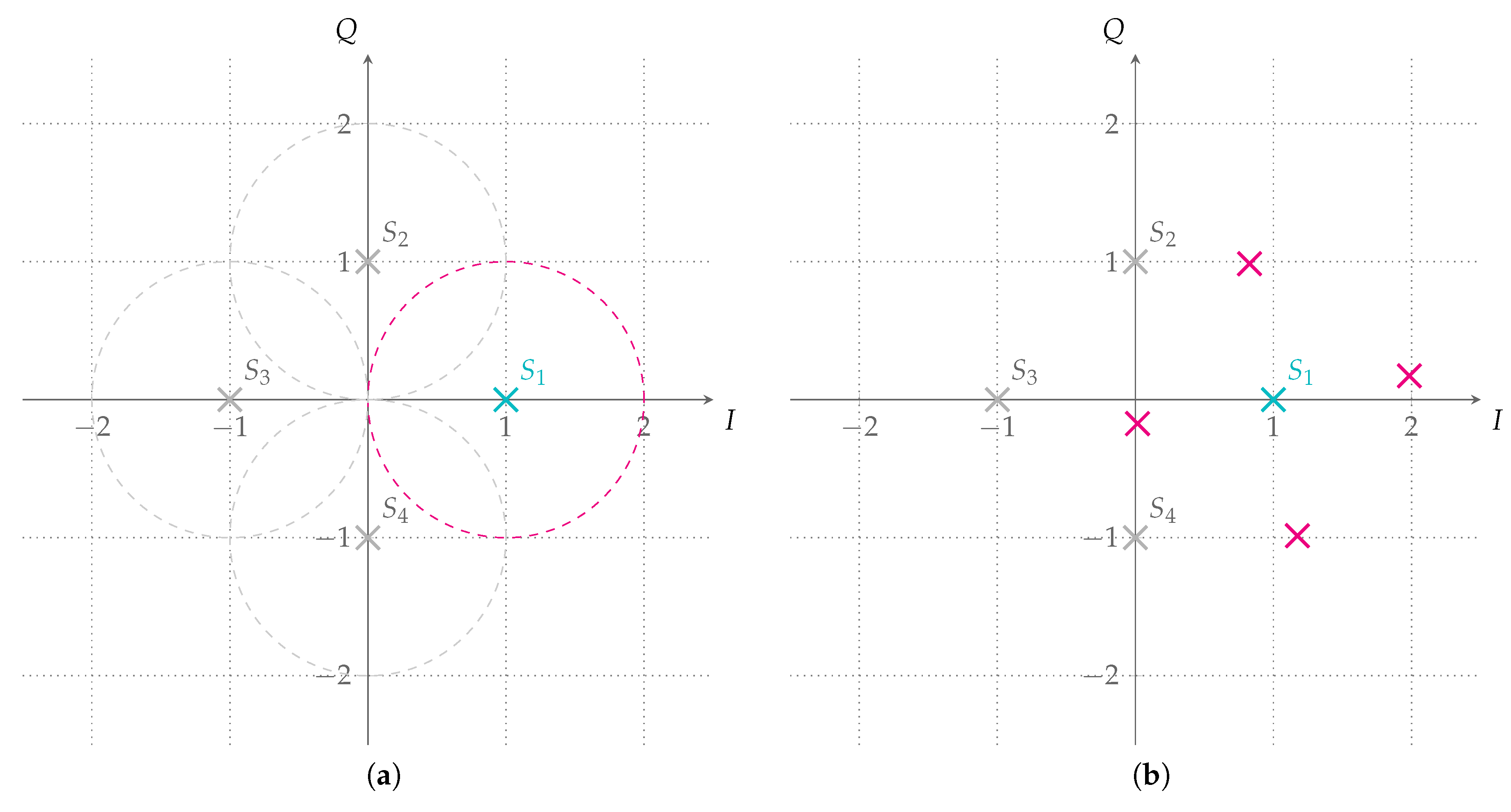
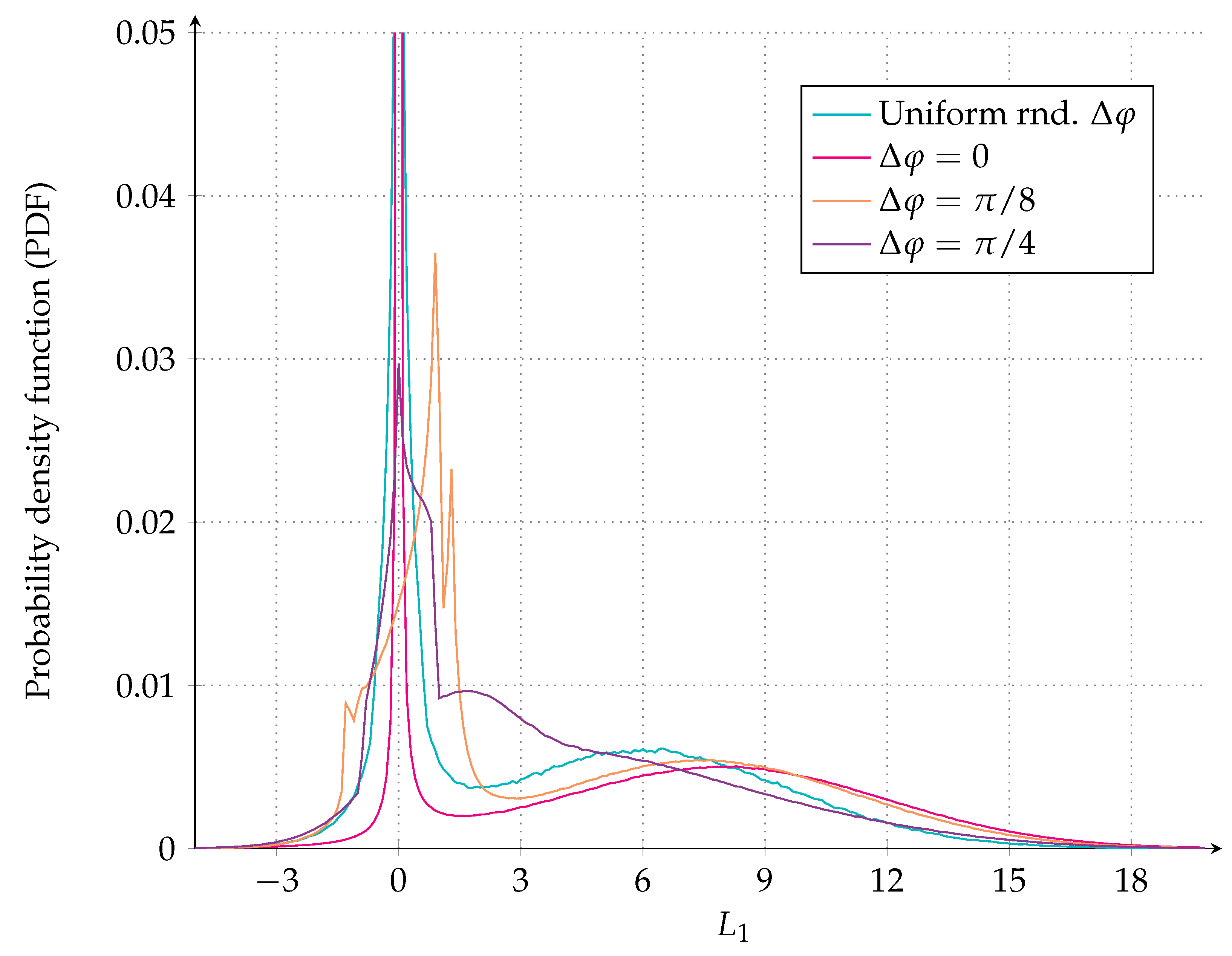
3.5. Asymptotic Results for a Single Non-Gaussian Interferer
- Symbol-synchronous, phase-aligned, equal-power QPSK interferer, i.e., , , .
- Symbol-synchronous, equal-power QPSK interferer uniform at random phase, i.e., , , .
4. Numerical Results
4.1. Abstracted Physical Layer
4.1.1. Decoding Region for Random Code Ensembles
4.1.2. Decoding Region for LDPC Code Ensembles
4.1.3. Simulation Results
4.2. Finite-Length Physical Layer Simulations with the Designed LDPC Codes
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Acronyms
| 5G | fifth generation of mobile networks |
| ACRDA | asynchronous contention resolution diversity ALOHA |
| APP | a posteriori probability |
| ARA | accumulate repeat accumulate |
| AWGN | additive white Gaussian noise |
| CDF | cumulative distribution function |
| CN | check node |
| CRA | contention resolution ALOHA |
| CRC | cyclic redundancy check |
| CRDSA | contention resolution diversity slotted ALOHA |
| CSA | coded slotted ALOHA |
| DAMA | demand assigned multiple access |
| DSA | diversity slotted ALOHA |
| ECRA | enhanced contention resolution ALOHA |
| eMBB | enhanced mobile broadband |
| EXIT | extrinsic information transfer |
| FEC | forward error correction |
| GEO | geostationary orbit |
| IC | interference cancellation |
| IRCRA | irregular repetition contention resolution ALOHA |
| IRSA | irregular repetition slotted ALOHA |
| LDPC | low-density parity-check |
| LLR | log-likelihood ratio |
| LT | Luby transform |
| M2M | machine-to-machine |
| MAC | medium access |
| MF | matched filter |
| MF-TDMA | multi-frequency time division multiple access |
| MRC | maximal-ratio combining |
| mMTC | massive machine-type communications |
| probability density function | |
| PER | packet error rate |
| PLR | packet loss rate |
| PRACH | physical random access channel |
| QPSK | quadrature amplitude shift keying |
| RA | random access |
| RV | random variable |
| SA | slotted ALOHA |
| SB | Shannon bound |
| SC | selection combining |
| SIC | successive interference cancellation |
| SINR | signal-to-interference and noise ratio |
| SNIR | signal-to-noise-plus-interference ratio |
| SNR | signal-to-noise ratio |
| TDMA | time division multiple access |
| TS | time sharing |
| VF | virtual frame |
| VN | variable node |
| WER | word error rate |
References
- Osseiran, A.; Boccardi, F.; Braun, V.; Kusume, K.; Marsch, P.; Maternia, M.; Queseth, O.; Schellmann, M.; Schotten, H.; Taoka, H.; et al. Scenario for 5G mobile and wireless communications: The vision of the METIS project. IEEE Commun. Mag. 2014, 52, 26–35. [Google Scholar] [CrossRef]
- 3GPP. TR 21.915 v1.1.0, Release 15 Description. 2019. Available online: https://www.3gpp.org/DynaReport/21-series.htm (accessed on 14 August 2019).
- Laya, A.; Alonso, L.; Alonso-Zarate, J. Is the Random Access Channel of LTE and LTE-A Suitable for M2M Communications? A Survey of Alternatives. IEEE Commun. Surv. Tutor. 2014, 16, 4–16. [Google Scholar] [CrossRef]
- Abramson, N. The ALOHA system: Another alternative for computer communications. In Proceedings of the Fall Joint Computer Conference (AFIPS), Houston, Texas, 17–19 November 1970; ACM: New York, NY, USA, 1970; Volume 37, pp. 281–285. [Google Scholar]
- Roberts, L.G. ALOHA packet system with and without slots and capture. Proc. SIGCOMM Comput. Commun. Rev. 1975, 5, 28–42. [Google Scholar] [CrossRef]
- Casini, E.; De Gaudenzi, R.; Del Rio Herrero, O. Contention resolution diversity slotted ALOHA (CRDSA): An enhanced random access scheme for satellite access packet networks. IEEE Trans. Wirel. Commun. 2007, 6, 1408–1419. [Google Scholar] [CrossRef]
- Liva, G. Graph-Based Analysis and Optimization of Contention Resolution Diversity Slotted ALOHA. IEEE Trans. Commun. 2011, 59, 477–487. [Google Scholar] [CrossRef]
- Paolini, E.; Liva, G.; Chiani, M. Coded Slotted ALOHA: A Graph-Based Method for Uncoordinated Multiple Access. IEEE Trans. Inf. Theory 2015, 61, 6815–6832. [Google Scholar] [CrossRef]
- Sandgren, E.; i Amat, A.G.; Brännström, F. On Frame Asynchronous Coded Slotted ALOHA: Asymptotic, Finite Length, and Delay Analysis. IEEE Trans. Commun. 2017, 65, 691–703. [Google Scholar] [CrossRef]
- Stefanovic, C.; Popovski, P. ALOHA Random Access that Operates as a Rateless Code. IEEE Trans. Commun. 2013, 61, 4653–4662. [Google Scholar] [CrossRef]
- Yu, Y.; Giannakis, G.B. High-Throughput Random Access Using Successive Interference Cancellation in a Tree Algorithm. IEEE Trans. Inf. Theory 2007, 53, 4628–4639. [Google Scholar] [CrossRef]
- Massey, J.L. Collision-Resolution Algorithm and Random-Access Communication. In Multi-User Communication Systems; Longo, G., Ed.; Springer: Vienna, Austria, 1981; pp. 73–137. [Google Scholar]
- Gallager, R. A perspective on Multiaccess Channels. IEEE Trans. Inf. Theory 1985, 31, 124–142. [Google Scholar] [CrossRef]
- Luby, M.; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.A. Improved Low-Density Parity-Check Codes Using Irregular Graphs. IEEE Trans. Inf. Theory 2001, 47, 585–598. [Google Scholar] [CrossRef]
- Richardson, T.J.; Shokrollahi, A.; Urbanke, R.L. Design of Capacity-Approaching Irregular Low-Density Parity-Check Codes. IEEE Trans. Inf. Theory 2001, 47, 619–637. [Google Scholar] [CrossRef]
- Ivanov, M.; Brännström, F.; i Amat, A.G.; Popovski, P. Error Floor Analysis of Coded Slotted ALOHA Over Packet Erasure Channels. IEEE Commun. Lett. 2015, 19, 419–422. [Google Scholar] [CrossRef]
- i Amat, A.G.; Liva, G. Finite-Length Analysis of Irregular Repetition Slotted ALOHA in the Waterfall Region. IEEE Commun. Lett. 2018, 22, 886–889. [Google Scholar] [CrossRef]
- Narayanan, K.R.; Pfister, H.D. Iterative Collision Resolution for Slotted ALOHA: An Optimal Uncoordinated Transmission Policy. In Proceedings of the 7th International Symposium on Turbo Codes and Iterative Information Processing (ISTC), Gothenburg, Sweden, 27–31 August 2012; pp. 136–139. [Google Scholar]
- Polyanskiy, Y. A Perspecitve on Massive Random-Access. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2523–2527. [Google Scholar]
- Effros, M.; Kostina, V.; Yavas, R.C. Random Access Channel Coding in the Finite Blocklength Regime. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018. [Google Scholar]
- Ordentlich, O.; Polyanskiy, Y. Low Complexity Scheme for the Random Access Gaussian Channel. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2528–2532. [Google Scholar]
- Vem, A.; Narayanan, K.R.; Cheng, J.; Chamberland, J.F. A User-Indipendent Serial Interference Cancellation Based Coding Scheme for the Unsourced Random Access Gaussian Channel. In Proceedings of the 2017 IEEE Information Theory Workshop (ITW), Kaohsiung, Taiwan, 6–10 November 2017; pp. 121–125. [Google Scholar]
- Calderbank, R.; Thompson, A. CHIRRUP: A Practical Algorithm for Unsourced Multiple Access. arXiv 2018, arXiv:1811.00879. [Google Scholar]
- Amalladinne, V.K.; Chamberland, J.F.; Narayanan, K.R. A Coded Compressed Sensing Scheme for Uncoordinated Multiple Access. arXiv 2018, arXiv:1809.04745. [Google Scholar]
- Kissling, C. Performance Enhancements for Asynchronous Random Access Protocols over Satellite. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–6. [Google Scholar]
- De Gaudenzi, R.; del Rio Herrero, O.; Acar, G.; Barrabes, E.G. Asynchronous Contention Resolution Diversity ALOHA: Making CRDSA Truly Asynchronous. IEEE Trans. Wirel. Commun. 2014, 13, 6193–6206. [Google Scholar] [CrossRef]
- Clazzer, F.; Kissling, C.; Marchese, M. Enhancing Contention Resolution ALOHA using Combining Techniques. IEEE Trans. Commun. 2018, 66, 2576–2587. [Google Scholar] [CrossRef]
- Akyildiz, T.; Demirhan, U.; Duman, T.M. Asymptotic Analysis of Contention Resolution ALOHA with Replica Concatenation. In Proceedings of the 2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Kissling, C.; Clazzer, F. LDPC code performance and optimum code rate for Contention Resolution Diversity ALOHA. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 2932–2938. [Google Scholar]
- Matuz, B.; Clazzer, F.; Johnson, S.J.; Jayasooriya, S.; Shirvanimoghaddam, M. LDPC Code Design for Asynchronous Random Access. In Proceedings of the 2018 IEEE 10th International Symposium on Turbo Codes Iterative Information Processing (ISTC), Hong Kong, China, 3–7 December 2018; pp. 1–5. [Google Scholar]
- Masnick, B.; Wolf, J. On linear unequal error protection codes. IEEE Trans. Inf. Theory 1967, 13, 600–607. [Google Scholar] [CrossRef]
- Caire, G.; Biglieri, E. Parallel Concatenated Codes with Unequal Error Protection. IEEE Trans. Commun. 1998, 46, 565–567. [Google Scholar] [CrossRef]
- Boutros, J.J.; i Fabregas, A.G.; Calvanese, E. Analysis of Coding on Non-Ergodic Block fading Channels. In Proceedings of the 2005 Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 28–30 September 2005. [Google Scholar]
- Boutros, J.J.; i Fabregas, A.G.; Biglieri, E.; Zemor, G. Low-Density Parity-Check Codes for Nonergodic Block-Fading Channels. IEEE Trans. Inf. Theory 2010, 56, 4286–4300. [Google Scholar] [CrossRef]
- Chiani, M. Noncoherent Frame Synchronization. IEEE Trans. Commun. 2010, 58, 1536–1545. [Google Scholar] [CrossRef]
- Clazzer, F.; Lázaro, F.; Liva, G.; Marchese, M. Detection and Combining Techniques for Asynchronous Random Access with Time Diversity. In Proceedings of the 11th International ITG Conference on Systems, Communications and Coding (SCC), Hamburg, Germany, 6–9 February 2017; pp. 1–6. [Google Scholar]
- Mengali, U.; D’Andrea, A.N. Synchronization Techniques for Digital Receivers; Springer Science+Business Media: Berlin, Germany, 1997. [Google Scholar]
- Thorpe, J. Low-Density Parity-Check (LDPC) Codes Constructed from Protographs; Ipn Progress Report 42-154; NASA JPL: Pasadena, CA, USA, 2003. [Google Scholar]
- Uchikawa, H. Design of Non-Precoded Protograph-Based LDPC Codes. In Proceedings of the IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2779–2783. [Google Scholar]
- Liva, G.; Chiani, M. Protograph LDPC Codes Design Based on EXIT Analysis. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), Washington, DC, USA, 26–30 November 2007; pp. 3250–3254. [Google Scholar]
- McEliece, R.J.; Stark, W.E. Channels with Block Interference. IEEE Trans. Inf. Theory 1984, IT-30, 44–53. [Google Scholar] [CrossRef]
- Chen, T.Y.; Divsalar, D.; Wang, J.; Wesel, R.D. Protograph-Based Raptor-Like LDPC Codes for Rate Compatibility with Short Blocklengths. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), Kathmandu, Nepal, 5–9 December 2011; pp. 1–6. [Google Scholar]
- Huawei; HiSilicon. R1-1706970 LDPC Design for eMBB Data. 2017. RAN1 #89. Available online: https://www.3gpp.org/DynaReport/TDocExMtg--R1-89--17065.htm (accessed on 14 August 2019).
- Pulini, P.; Liva, G.; Chiani, M. Unequal Diversity LDPC Codes for Relay Channels. IEEE Trans. Wirel. Commun. 2013, 12, 5646–5655. [Google Scholar] [CrossRef]
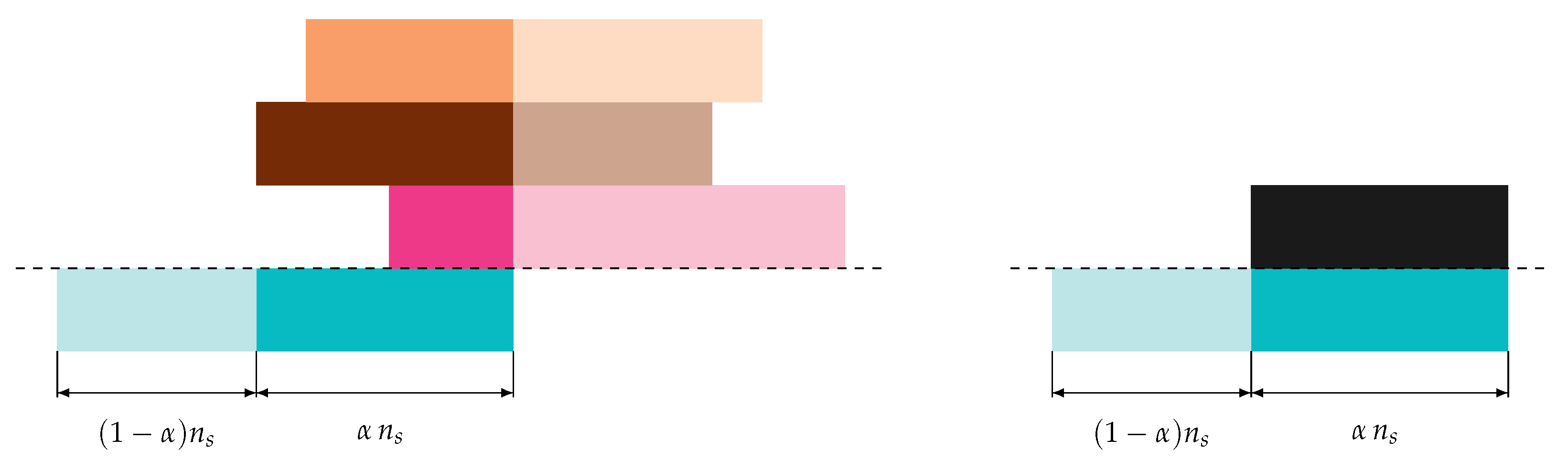

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clazzer, F.; Matuz, B.; Jayasooriya, S.; Shirvanimoghaddam, M.; Johnson, S.J. Protograph LDPC Code Design for Asynchronous Random Access. Algorithms 2019, 12, 170. https://doi.org/10.3390/a12080170
Clazzer F, Matuz B, Jayasooriya S, Shirvanimoghaddam M, Johnson SJ. Protograph LDPC Code Design for Asynchronous Random Access. Algorithms. 2019; 12(8):170. https://doi.org/10.3390/a12080170
Chicago/Turabian StyleClazzer, Federico, Balázs Matuz, Sachini Jayasooriya, Mahyar Shirvanimoghaddam, and Sarah J. Johnson. 2019. "Protograph LDPC Code Design for Asynchronous Random Access" Algorithms 12, no. 8: 170. https://doi.org/10.3390/a12080170
APA StyleClazzer, F., Matuz, B., Jayasooriya, S., Shirvanimoghaddam, M., & Johnson, S. J. (2019). Protograph LDPC Code Design for Asynchronous Random Access. Algorithms, 12(8), 170. https://doi.org/10.3390/a12080170




