Abstract
The significant task for control performance assessment (CPA) is to review and evaluate the performance of the control system. The control system in the semiconductor industry exhibits a complex dynamic behavior, which is hard to analyze. This paper investigates the interesting crossover properties of Hurst exponent estimations and proposes a novel method for feature extraction of the nonlinear multi-input multi-output (MIMO) systems. At first, coupled data from real industry are analyzed by multifractal detrended fluctuation analysis (MFDFA) and the resultant multifractal spectrum is obtained. Secondly, the crossover points with spline fit in the scale-law curve are located and then employed to segment the entire scale-law curve into several different scaling regions, in which a single Hurst exponent can be estimated. Thirdly, to further ascertain the origin of the multifractality of control signals, the generalized Hurst exponents of the original series are compared with shuffled data. At last, non-Gaussian statistical properties, multifractal properties and Hurst exponents of the process control variables are derived and compared with different sets of tuning parameters. The results have shown that CPA of the MIMO system can be better employed with the help of fractional order signal processing (FOSP).
1. Introduction
Control loops are the most significant elements in automation systems. Product quality, operation safety, material and energy consumption, and thus the financial performance, are directly or indirectly linked to the performance of control systems. Control Performance Assessment (CPA) provides a benchmark for detecting and diagnosing root-causes of poor performance, reviewing and evaluating current performance, as well as improving control performance or avoiding performance degradation [1].
However, the mainstream assumption of Gaussian character of process signals contributes to the basis for CPA analysis algorithms and methods. On the contrary, a typical industrial process, which includes thousands of control loops, has witnessed many non-Gaussian behaviors, such as long range dependency (LRD), self-similarity, power-law of autocorrelation, infinite variance, spiky signals. Non-Gaussian signals and noises tend to produce large-amplitude fluctuations from the average value more frequently than Gaussian ones do [2]. Process control systems are very complex, usually encompassing different hierarchical levels, therefore it is inconceivable for plant personals to maintain them on regular basis. For example, control loops are often multivariable and exhibit nonlinear dynamics stemming either from the plant, the transducers, the actuators, or even in some cases the controllers themselves in industrial applications.
To address the above issues, the fractional order signal processing (FOSP) techniques have been proposed to better characterize the control process in the recent years with the notion of fractional calculus [2]. FOSP techniques include fractional order linear systems, autoregressive fractional integrated moving average (ARFIMA), Hurst parameter estimation, fractional order Fourier transformation (FrFT), fractals, Multifractal detrended fluctuation analysis (MFDFA), etc [3]. In addition, fractional order thinking is inevitable to gain more insights to characterize complex objects [4].
CPA is an important asset-management technology to maintain highly efficient operation performance of automation systems in production plants [5]. There are many classic performance assessment approaches, such as mean squared error (MSE), integral absolute error (IAE), statistical indexes, fractal indexes, etc. In addition, they can be various depending on systems under the different conditions, for example, with control action constraints, with deterministic disturbances, with setpoint changes. How to evaluate the quality of the control system performance is an essential issue for process engineers. In recent years, multifractal analysis has become the focus among the control engineering after some researchers gave applied it with CPA. The on-line control loop performance monitoring with non-Gaussian statistical and fractal measure has been proposed in [6]. Domański presents results of the research on alternative CPA measures applied to control quality assessment for SISO loop with generalized predictive control (GPC) controller in [7,8].
However, as mentioned in [8], the above CPA analyses and observations are accomplished with a simple linear SISO case, which cannot capture the monofractal and multifractal properties, since the process complexity, cross-dependencies with varying delays, LRD and human factors are not reflected in simulations. Many intriguing questions are left behind in the above articles, such as multiple input multiple output (MIMO) and systems with significant delays. Moreover, the origins and meaning of multifractal properties with crossover phenomena are still needed to be analyzed. Therefore, it is worth investigating more complex scenarios, such as nonlinear, MIMO and systems with significant delay cases to verify method applicability and effectiveness. The aim of this paper is to cast more light on the new directions for process engineers and provide some novel techniques to assess the process performance.
More specifically, the purposes of this paper are to:
- Use MFDFA to analyze semiconductor data, derive the multifractal spectrum and select the characteristic parameters sensitive to changes of the control system.
- Extract the characteristic parameters from the multifractal spectrum of reference data to form reference feature sets;
- Modify the standard single Hurst exponent estimation by the multiple Hurst exponent fitting method with crossover points;
- Select multifractal properties and modified Hurst exponents to distinguish different types of control actions (tunings).
Section 1 starts with a brief introduction of the current FOSP techniques in CPA. Section 2 provides the definition of the fractional Gaussian noise, Hurst exponent and -stable distribution for readers with zero knowledge. Section 3 proposes the MFDFA algorithm and Hurst spline fit with crossovers. Data analysis with MFDFA for each loop of the real MIMO system is carried in Section 4. The analysis of the results are carried in Section 5. The conclusion is given in Section 6.
2. Preliminaries
2.1. Fractal and Fractional Gaussian Noise
Fractal analysis is especially useful when the data show self-similarity, power-law, scale-invariant and nonlinear properties [9,10,11]. From the fractal theory introduced by Mandelbrot in [9], the traditional concept of three-dimensional space can be extended to the fractal (fractional) dimension (FD).
Based on the definitions of fractional-order differential operators, many complex dynamic systems with complex memory behaviors can be more properly described by the fractional calculus. Some researchers found interesting the analytical results of the linear fractional-order differential equations are represented by the Mittag–Leffler function, which exhibits a power-law asymptotic behavior [12]. Therefore, the fractional calculus is being widely used to analyze the random signals with power-law size distributions or power-law decay of correlations [13,14].
The fractional order integral of the function with is defined
where is the Gamma function, is the fractional integral of order in [14].
Based on fractional order integral, the relationship of white Gaussian noise wGn , fractional Gaussian noise (fGn), -stable noise , fractional stable noise, multifractional Gaussian noise and multifractional stable noise can be described in Figure 1. Besides, the fGn can be expressed as the th order integration of wGn [2,15]:
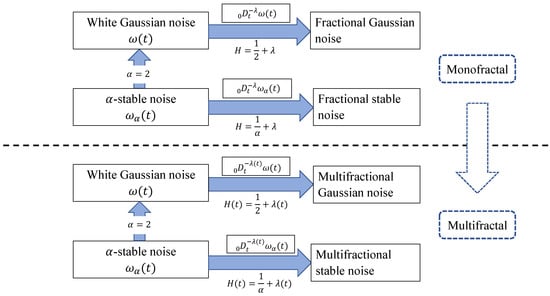
Figure 1.
Fractional Gaussian noise and fractional Brown noise in monofractal analysis and multifractal analysis.
Therefore, from the perspective of fractional signals and fractional-order systems the fGn can be simulated by the dth integrator with wGn as the input in the Figure 1.
From the above figure, the major difference of monofractal and multifracal property is the time-depend variable H. The linear multifractional stable motion is obtained by generalizing the constant Hurst parameter H to a time-dependent local Hölder exponent .
2.2. Hurst Parameter
LRD is characterized by the Hurst exponent H. It means that there is a strong coupling between values at different times. The coupling effect characterized by the autocorrelations functions (ACF) and power spectrum density (PSD) obey the power law, hyperbolically decaying, while the conventional assumptions are based on the exponentially decaying effects. To quantify the level of the coupling, the Hurst exponent and many valuable Hurst exponent estimators have been provided to more accurately characterize the LRD time series.
The rescaled range (R/S) method is one of the time-domain analysis of Hurst parameter defined as follows [16]:
where denotes the expected value of the observations, is the range of the first n values, is their standard deviation, and C is a constant. Alternatively, Whittle’s maximum likelihood estimator (MLE) and wavelet analysis are using periodogram based analysis in the frequency domain [17].
LRD processes appear in many contexts, which is characterized by the Hurst parameter H . The phenomenon of LRD can be observed in hydrology, finance, economics and so on. Unlike with a stationary process, the autocorrelations between observations of a long memory series are slowly decaying to zero. However, according to the survey paper [18], Hurst estimators can be significantly affected by trend and seasonality.
LRD or long memory process can be defined by the autocovariance in the time domain, or defined by the power spectrum in the frequency domain. The power law is observed in the long memory ARFIMA process with , since the asymptotic behaviour of the autocovariance function is given by [19]
In particular, if , then is a long-memory process, or long range positive dependence, since [20]. The process is said to exhibit intermediate memory (anti-persistence) (Also known as a mean-reverting process), or long-range negative dependence, for . In addition, the process is non-stationary for , as it possesses infinite variance and first order difference is needed to get the stationary series. Therefore, the fractional order difference filter is the first step of processing long memory ARFIMA models [21].
Besides, the fractional order difference (integral) coefficient d has a closed relation with Hurst parameter and characteristic exponent :
where H is the Hurst parameter and is from the -stable distribution, which will be introduced in the next subsection. The Hurst parameter of fGn is related to d by the Equation (5).
2.3. Stable Distribution
In the real system, non-stationary, non-Gaussian, spiky signals are usually regarded as outliers and thus discarded by engineers during the signal processing. In fact, however, each point of data from the real system could tell a “story” such as malfunctioning, inappropriate control philosophy, abnormal human intervention, etc. Non-Gaussian signals and noises tend to produce large-amplitude fluctuations from the average value more frequently than Gaussian ones do. Where did non-Gaussian signals come from? Many researchers have found that they are from fractional calculus or even more specifically, -stable processes [22].
The stable distribution, which is the generalization of the Gaussian distribution, is used to model the non-Gaussian distribution. The -stable distribution based techniques have been applied to describe many natural or man-made phenomena in various fields, such as physics, hydrology, biology, financial and network traffic. Stable distributions provide a useful theoretical tool for this type of signals and noises [23]. The -stable characteristic function (or distribution) is determined by four parameters: , , and . A univariate distribution function is stable if and only if its characteristic function has the form:
where
and
is called the characteristic exponent. A small value of will imply considerable probability mass in the tails of the distribution. That is, the smaller is, the heavier are the tails. corresponds to the Gaussian distribution (for any ). is a scaling parameter called the dispersion. It is similar to the variance of the Gaussian distribution. is a symmetry parameter. indicates a distribution symmetric about .
There are two algorithms provide consistent estimators for all four parameters—Koutrouvelis’s method, which is based on empirical characteristic function methods of Koutrouvelis [24] and McCulloch’s method, which is a simpler, faster but less accurate method [25]. In this paper, we apply Koutrouvelis method for estimation of these parameters in Section 4.
3. MFDFA Algorithm
MFDFA is an efficient FOSP technique to detect multifractality in a time series since it does not require any knowledge about the process time delay or other process parameters [26]. MFDFA can estimate the multifractal spectrum of the generalized Hurst exponent from a time series and it does not require any knowledge about the process time delay or other process parameters [27]. Currently, MFDFA has been successfully applied to analyze various data, such as hydrographic data [28], wind records [29], financial time series [30], traffic time series [31], mechanical vibration signals [32], etc. It has proven to be a powerful tool for uncovering the multifractality of non-stationary time series in the complex systems. In this study, MFDFA is applied to detect the presence of multifractal and monofratal properties in the MIMO systems with external disturbance and noise. Then, the origin of the multifractality of control signals, the generalized Hurst exponents of the original series are compared with shuffled data.
3.1. Basic MFDFA Algorithm
Detrended fluctuation analysis (DFA) was first proposed by Peng et al. on the DNA analysis in 1995 [33] and then MFDFA was proposed by Kantelhardt et al. in 2002 [34]. For the calculation methodology, Ihlen developed MATLAB code in [35] and Domański modified the algorithm in [7].
The MFDFA method starts with a possibly non-stationary time series for , where N indicates its length.
- Define the “profile” E and transform original data into mean-reduced cumulative sums,where is the mean of series, such that the aggregated time series are with zero mean.
- Divide time series into non-overlapping segments of equal length s, starting from the beginning. Since the length N of the series is often not a multiple of the considered time scale s, in order to not miss any piece of data, another set of segments starting from the end of data is made from the end coming to the beginning. As a result, segments are obtained covering the whole dataset.
- Calculate the local trend for each of the segments by a least-square fit of the series.
- Calculate the mean square error for the estimate of each segment k of length s.for each segment andfor each segment .
- Average over all segments to obtain the qth order variance (or fluctuation) function for each size s:For use
- Repeat steps (2)–(5) for different s evaluating new sets of variances .
- Plot for each q in log-log scale and estimate the linear fit with least squares. If slope varies with q, multifractality is suspected. Single slope shows monofractal scaling.
- Calculate multifractal exponent as
- Use Legendre transform to evaluate Hölder exponent and multifractal spectrum :
The slope of scaling function with different q order demonstrates the LRD behavior of signals. The multifractal spectrum indicates how much dominant are the various fractal exponents present in the series. The width of the singularity spectrum denotes the range of the generalized Hurst (Hölder) exponent, which is defined as
It is often used to quantitatively measure the degree of multifractality of the series. Thus, the wider the spectrum the more multifractal series is.
3.2. Defining the Source of the Multifractality
The origin of multifractality of a time series can be distinguished as two different types, i.e., the multifractality due to: (i) the different long-range correlations of the number fluctuations; and (ii) the broadness of probability density function (PDF) of the distributions [34].
The easiest way to eliminate the correlations for (i) is shuffling the original series into random order, since the multifractality is due to the probability density, which is not affected by the shuffling procedure. For (ii), the surrogate process of data, defined as replacing the phase of discrete Fourier transform (DFT) coefficients of the original data with a set of pseudo independent and identically distributed quantities in , can change the broad PDF of the original data into the Gaussian distribution and seldom destroys the intrinsic long-range correlations of the original data [34].
3.3. Plot Fitting Hurst Exponents with Crossovers
Generally, the conventional R/S plot fitting is performed by Equation (3). The standard estimation with least squares using QR factorization is used for single Hurst exponent estimation. In the current study, the curve is assumed to be piece-wise linear, which is achieved by solving the first-order spline least squares (LSQ) fitting problem with graph log() versus log(s) identifying crossovers. Each plot includes one, two, and three linear approximations. In the next section, the red line represents single line and estimation of one memory scale, which is the conventional single Hurst exponent . The green line represents two memory scales with one crossover. The blue line represents three memory scales separated with two crossovers. Short-term is important from the perspective of the controller tuning, while the long-term scale indicates the control system structure. Therefore, the asymptotic and transient behavior of the system can be characterized with multiple Hurst exponents.
4. Case Studies
Semiconductor products are characterized by rapid changes in both improvement and deterioration of quality. Moreover, the embedded seasonal property of the high power plasma etching makes it difficult to analyze the real-time data since the process is nonlinear and non-stationary.
Thousands of runs are performed overnight for each recipe and they might be subject to unknown interventions. The precise control of coolant temperature is the key to the wafer uniformity during the etching process. Data from the process of dynamic coolant supply temperature are anonymously selected out of hundreds of control loops. The industrial part of the analysis is based on the real data stem from etching equipment in semiconductor manufacturing.
For thousands of data logs from different chambers, how to assess the control performance is a thorny problem for process engineers in semiconductor industry. In addition, the tuning of the MIMO system is a challenging task, because the optimization of PID parameters can be unachievable under coupled loops and nonlinearities. In Figure 2, , are set-points and outputs of the control system respectively. The three PID controllers are designed to control the temperature, flow and coolant level in the tank accordingly. Therefore, it is a MIMO system with internal coupling loops and external disturbance and noise with significant delays. In the article, we use Var1, Var2, Var3 to represent the error signals ( ) from each loop depicted in Figure 3.
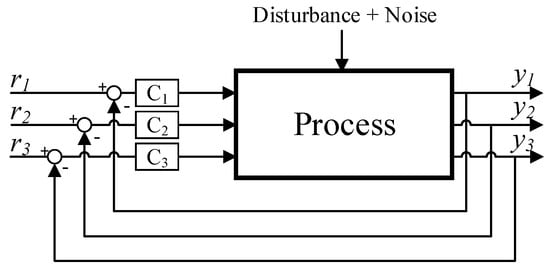
Figure 2.
Control structure of the MIMO system.
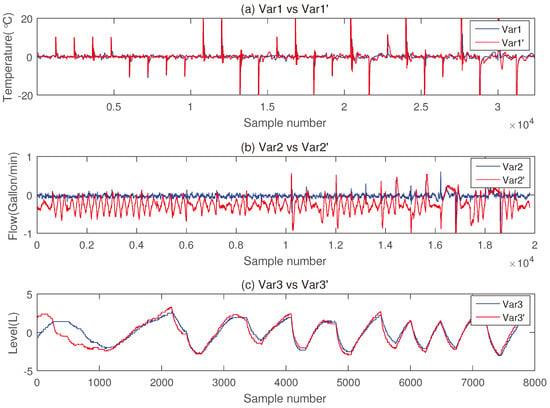
Figure 3.
Output errors of three loops: Var1, Var2, Var3 with first tuning parameters in blue; Var1’, Var2’, Var3’ with second tuning parameters in red.
4.1. Non-Gaussian Statistical Analysis
First, the histogram plot Var1, Var2, Var3 with a probabilistic distribution function (PDF) fitting is frequently carried out to detect if the data are impacted by non-Gaussian noises or subject to human interventions. It is often used to measure the heavy-tailedness underlying process during assessment and frequently the a suitable moment to call for further insight. Histogram fitting is significant since some parts of the process can be more impacted by the disturbances or can be more exposed to the process nonstationarity, can be cross-correlated or might be subject to human interventions. In real situations it is a challenge to have similar properties for all the loops.
The etching process requires uniform temperature behaviors from batch to batch, therefore Var1 is the major concern in the current MIMO system. As introduced in Section 2.3, the -stable distribution is performed to detect whether the distributions are Gaussian, Lévy or else. In Figure 4, time series Var1 of the MIMO system has significant fat tail properties. Therefore, it can be inferred that there are non-Gaussian noises coming to the system.
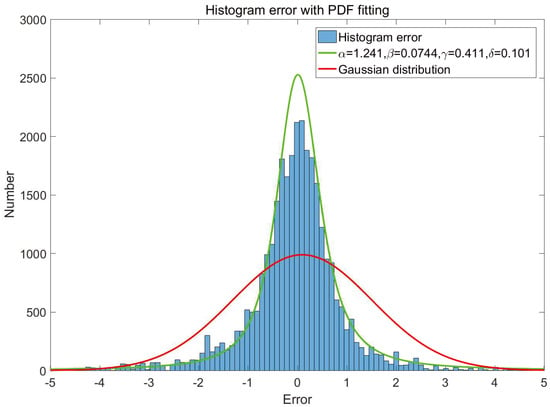
Figure 4.
Histogram of Var1 with PDF fitting.
Var2 is the variable of errors from flow loop. The higher flow rate can exchange heat efficiently whereas more turbulence could be introduced at the same time. Therefore, the flow loop is interacted with the temperature loop. From the Figure 4 and Figure 5, we could see the clear correlations between Var1 and Var2.
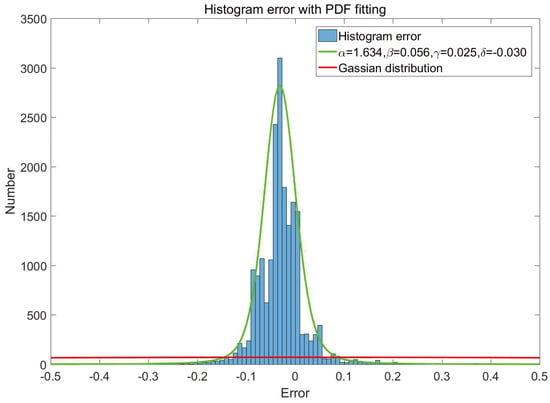
Figure 5.
Histogram of Var2 with PDF fitting.
The histogram of the Var3 explicitly shows very poor or even not working control. The histogram is highly scattered, almost uniform. The loop is uncontrolled with possible oscillations and operating on the edge of the stability region or manually operated.
4.2. Hurst Exponents Fitting with Crossovers
Second, in Figure 6, Figure 7 and Figure 8 the red line represents single memory scale estimation, i.e., one Hurst exponent fitting without crossover . Green line represents two memory scales with one crossover. Blue line represents three memory scales with two crossovers. All the crossover points are marked in circles. The phenomenon of the multiple memory scales in Var1 and Var2 are observed in Figure 6 and Figure 7. Therefore, the variation of the memory scales with crossovers cannot be captured by the conventional Hurst R/S fitting method with the constant value. After processing data with MFDFA, the multiple Hurst exponents, along with crossover point position might carry on information of multifractality of the control performance.
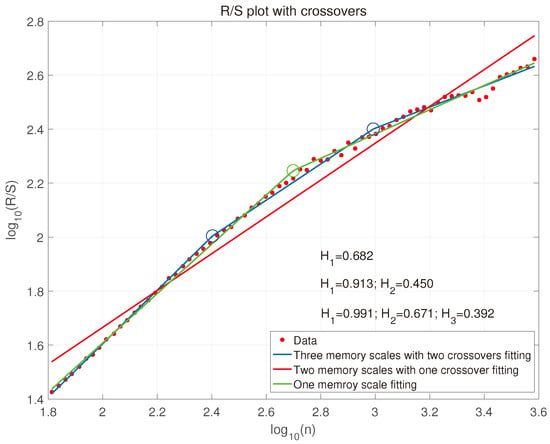
Figure 6.
R/S plot Var1 with crossovers.
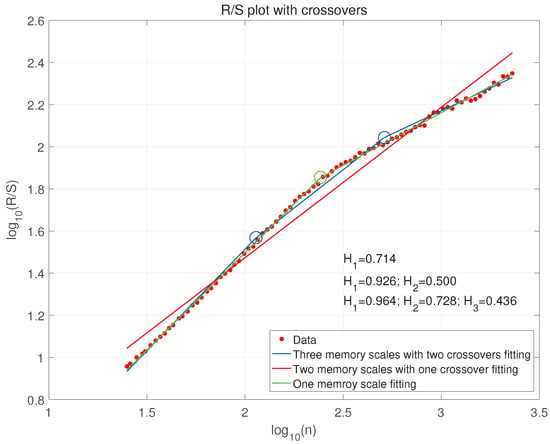
Figure 7.
R/S plot Var2 with crossovers.
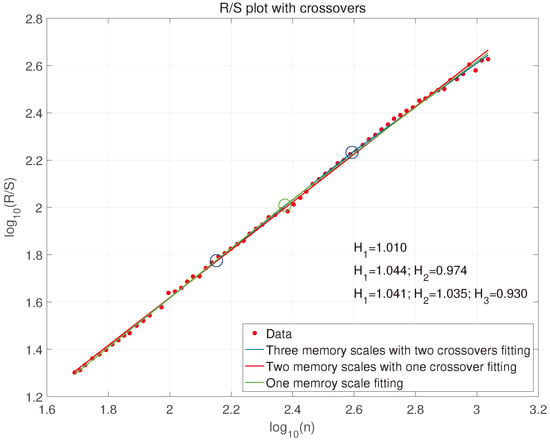
Figure 8.
R/S plot Var3 with crossovers.
Var3 is the variable of errors from coolant level loop, which in reality to keep the coolant away from the alarm levels. It should be noted that the control priority is comparatively lower in the design of the MIMO system. Compared with Var1, Var2, however, the monofractal behavior of Var3 can be validated through Figure 8, Figure 9 and Figure 10.
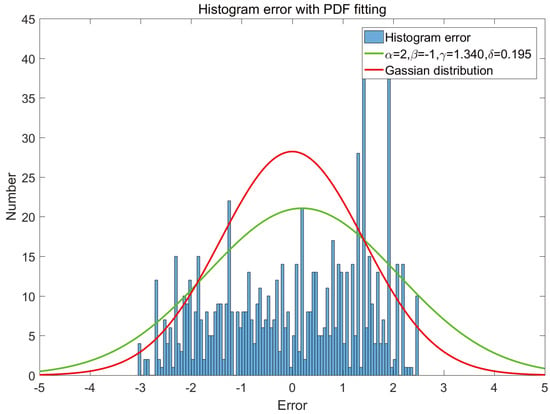
Figure 9.
Histogram of Var3 with PDF fitting.
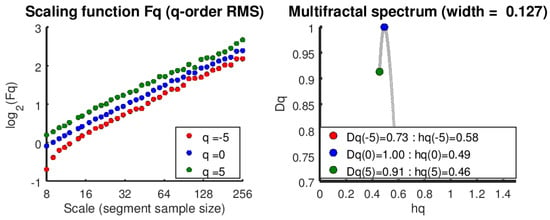
Figure 10.
Multifractal spectrum for shuffled Var3. The parallel behavior with different scales (left plot) and the tiny arch (right plot) indicate the monofractal behaviors of Var3 in the MIMO system.
There might be done further conclusions on the control quality of the loops. Var1 and Var2 show multi-persistence behaviour with different Hurst exponents in different memory scales. In contrary Var3 is clearly mono-persistent. It means that this loop is rather not coupled with the other ones. Its Hurst exponent is approximately equal to 1. Its tuning is highly sluggish, almost not existent. It confirms initial observation done using the histogram. The other two loops are the most probably close coupled. Observation of the R/S plots and the shortest Hurst exponent also reveals dynamically sluggish control, however in the longer memory scale control improves and is back to the neutral one.
4.3. Multifractal Analysis
In order to clearly derive the origin of the multifractal property, the shuffled datasets of Var1, Var2, Var3 can remove correlations from data and any remaining scaling is caused by probability density function broadness. It is shown that the multifractal behaviors can be captured by the multifractal spectrum analysis with the shuffled datasets in Figure 11.
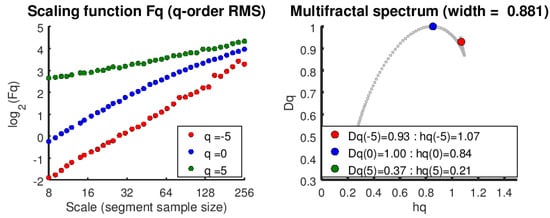
Figure 11.
Multifractal spectrum for shuffled Var1. The non-parallel behavior with different scales (left plot) and the arch with large width (right plot) indicate the multifractal behaviors of Var1 in the MIMO system.
From multifractal spectrum in Figure 10, Figure 11 and Figure 12, the multifractal spectrum width is significantly different. Notice the tiny arcs in Figure 10 demonstrate the constant for monofractal property in Var3, while the wider arcs of Var1, Var2 shows the multifractality in MIMO system. Moreover, the multifractality of the MIMO process have been detected and analyzed for the each loop with shuffled datasets Var1, Var2, Var3.
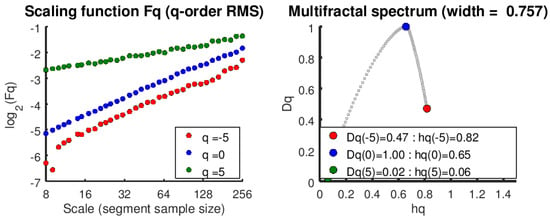
Figure 12.
Multifractal spectrum for shuffled Var2. The non-parallel behavior with different scales (left plot) and the arch with large width (right plot) indicate the multifractal behaviors of Var2 in the MIMO system.
5. Results and Discussion
This paper presented a CPA method with non-Gaussian statistical factors. First, we extracted four parameters , , , with stable distribution and calculated the multifractal spectrum width .
It is well known that the PID tuning of the MIMO system is a time consuming and arduous work. Two sets of real data Var1, Var2, Var3 and Var1’, Var2’, Var3’ with different PID parameters are compared in the end of article, in which the former settings are conservative and latter ones are more aggressive. In Table 1, the proposed FOSP method has been conducted according to the previous sections. The aggressive tuning with small depicts the broadness and fat tails of the distribution of the underlying process. Moreover, the absolute values of , , indicate the worse behavior with the latter tuning.

Table 1.
Indexes for variables with different PID tunings.
In addition, the multi-scale Hurst spline fit with crossovers are located, compared with single Hurst estimation. Using multiple Hurst exponent fitting at different scales representing the dynamic behavior of the system with noise in Table 2.

Table 2.
Hurst exponents at different memory scales.
Review of the persistence properties of the data reveals visible effects of tuning and we observe changes in . For the first loop it moved from more sluggish value of towards neutral tuning, while the second loop Var2 is slightly more sluggish. Loop Var3 is unchanged. However, the effect of tuning (whatever the set is) is evident in comparison with original MIMO system presented in R/S plots (Figure 6, Figure 7 and Figure 8). Var1, Var2 require disturbance decoupling compared with aggressive tuning while Var3 requires possible redesign of the control philosophy and fine tuning.
As it is well known there is no single universal measure that handles and detects all possible features that may be encountered in the industrial control. Each method well suites to the specific loop properties. Classical methods, such as integral, statisitical or minimum variance methods cover wide are of the applications. However, they may have difficulties in case of nonlinear and complex processes. FOSP approach enables to address controller performance, which depends on the controller tuning and control philosophy suitability. It allows to incorporate into the research the stable properties of the control error histogram. As distribution fitting may be inefficient, the multifractal spectrum can disclose further information about control properties. Complex cascaded properties of the overall system, human impact or superposition of various impacts and oscillations (non-concave spectra) may be additionally assessed.
6. Conclusions
The multifractal properties of process control variables exhibit fractional order system dynamics. In this paper, we have described the origin of multifractal properties and how the FOSP techniques relate to complex phenomena in the control system. More significantly, CPA of the MIMO control system is first proposed with the help of FOSP through the real semiconductor industry data. Indications for the control improvement are defined and the conclusions upon the control performance of the MIMO system are subsequently derived. The FOSP analysis makes it possible to perform analysis in different scales, allowing to address controller dynamics (short scale) and system cross-dependencies (mostly reflected in longer scales). Similar phenomena have been already analyzed in time-delayed systems and networks, allowing to assess both system parametrization and its structure. Therefore, it is believed that FOSP will find a unique place that conventional signal processing methods cannot even reach the answer to.
Author Contributions
K.L. performed the experiment and wrote the paper; Y.C. proposed the method; P.D.D. analyzed the data; X.Z. designed the experiment.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jelali, M. Control Performance Management in Industrial Automation: Assessment, Diagnosis and Improvement of Control Loop Performance; Springer Science & Business Media: London, UK, 2012. [Google Scholar]
- Sheng, H.; Chen, Y.; Qiu, T. Fractional Processes and Fractional-Order Signal Processing: Techniques and Applications; Springer Science & Business Media: London, UK, 2011. [Google Scholar]
- Chen, Y.; Sun, R.; Zhou, A. An overview of fractional order signal processing (FOSP) techniques. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007; pp. 1205–1222. [Google Scholar]
- West, B.J. Fractional Calculus View of Complexity: Tomorrow’s Science; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Jelali, M. An overview of control performance assessment technology and industrial applications. Control Eng. Pract. 2006, 14, 441–466. [Google Scholar] [CrossRef]
- Domański, P.D. On-line control loop assessment with non-Gaussian statistical and fractal measures. In Proceedings of the American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 555–560. [Google Scholar]
- Domański, P.D. Multifractal Properties of Process Control Variables. Int. J. Bifurc. Chaos 2017, 27, 1750094. [Google Scholar] [CrossRef]
- Domański, P.D.; Ławryńczuk, M. Assessment of predictive control performance using fractal measures. Nonlinear Dyn. 2017, 89, 773–790. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1983. [Google Scholar]
- Feder, J. Fractals; Springer Science & Business Media: London, UK, 2013. [Google Scholar]
- Schmitt, D.T.; Ivanov, P.C. Fractal scale-invariant and nonlinear properties of cardiac dynamics remain stable with advanced age: A new mechanistic picture of cardiac control in healthy elderly. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 293, R1923–R1937. [Google Scholar] [CrossRef] [PubMed]
- Kilbas, A.A.; Saigo, M.; Saxena, R. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transf. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1998; Volume 198. [Google Scholar]
- Mandelbrot, B.B.; van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; CRC Press: Boca Raton, FL, USA, 1994; Volume 1. [Google Scholar]
- Ye, X.; Xia, X.; Zhang, J.; Chen, Y. Effects of trends and seasonalities on robustness of the Hurst parameter estimators. IET Signal Process. 2012, 6, 849–856. [Google Scholar] [CrossRef]
- Inoue, A. Asymptotic behavior for partial autocorrelation functions of fractional ARIMA processes. Ann. Appl. Probabil. 2002, 12, 1471–1491. [Google Scholar] [CrossRef]
- Woodward, W.A.; Gray, H.L.; Elliott, A.C. Applied Time Series Analysis with R, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Liu, K.; Chen, Y.; Zhang, X. An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs. Axioms 2017, 6, 16. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional calculus and stable probability distributions. Arch. Mech. 1998, 50, 377–388. [Google Scholar]
- Nikias, C.L.; Shao, M. Signal Processing With Alpha-Stable Distributions and Applications; Wiley-Interscience: New York, NY, USA, 1995. [Google Scholar]
- Koutrouvelis, I.A. Regression-type estimation of the parameters of stable laws. J. Am. Stat. Assoc. 1980, 75, 918–928. [Google Scholar] [CrossRef]
- McCulloch, J.H. Simple consistent estimators of stable distribution parameters. Commun. Stat. Simul. Comput. 1986, 15, 1109–1136. [Google Scholar] [CrossRef]
- Movahed, M.S.; Jafari, G.; Ghasemi, F.; Rahvar, S.; Tabar, M.R.R. Multifractal detrended fluctuation analysis of sunspot time series. J. Stat. Mech. Theory Exp. 2006, 2006, P02003. [Google Scholar] [CrossRef]
- Srinivasan, B.; Spinner, T.; Rengaswamy, R. Control loop performance assessment using detrended fluctuation analysis (DFA). Automatica 2012, 48, 1359–1363. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Chen, Y.D.; Yu, Z. Multifractal detrended fluctuation analysis of streamflow series of the Yangtze River basin, China. Hydrol. Process. 2008, 22, 4997–5003. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M. Analysis of the time dynamics in wind records by means of multifractal detrended fluctuation analysis and the Fisher–Shannon information plane. J. Stat. Mech. Theory Exp. 2011, 7, P07001. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Y.; Wu, C. Analysis of the efficiency and multifractality of gold markets based on multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Appl. 2011, 390, 817–827. [Google Scholar] [CrossRef]
- Shang, P.; Lu, Y.; Kamae, S. Detecting long-range correlations of traffic time series with multifractal detrended fluctuation analysis. Chaos Solitons Fractals 2008, 36, 82–90. [Google Scholar] [CrossRef]
- Lin, J.; Chen, Q. Fault diagnosis of rolling bearings based on multifractal detrended fluctuation analysis and Mahalanobis distance criterion. Mech. Syst. Signal Process. 2013, 38, 515–533. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Ihlen, E.A. Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Physiol. 2012, 3, 141. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).