Abstract
Many approaches that model specific intelligent behaviors perform excellently in solving complex optimization problems. Game theory is widely recognized as an important tool in many fields. This paper introduces a game theory-inspired evolutionary algorithm for global optimization (GameEA). A formulation to estimate payoff expectations is provided, which is a mechanism to make a player become a rational decision-maker. GameEA has one population (i.e., set of players) and generates new offspring only through an imitation operator and a belief-learning operator. An imitation operator adopts learning strategies and actions from other players to improve its competitiveness and applies these strategies to future games where one player updates its chromosome by strategically copying segments of gene sequences from a competitor. Belief learning refers to models in which a player adjusts his/her strategies, behavior or chromosomes by analyzing the current history information to improve solution quality. Experimental results on various classes of problems show that GameEA outperforms the other four algorithms on stability, robustness, and accuracy.
1. Introduction
Several approaches have been proposed to model the specific intelligent behavior, such as the ant colony algorithm [1] based on the behavior of ants searching for food; the firefly algorithm, inspired by the flashing behavior of fireflies [2]; the fish swarm algorithm, inspired by the collective movement of the fish and their various social behaviors [3,4]; artificial bee colony [5], and its variants [6]; cuckoo search [7]; and artificial immune system [8], etc. Some other kinds of algorithms, like neural computation [9] or brainstorming algorithms [10], are enlightened from the advanced activities of human brain, which focus on the intelligence of cell behaviors. Obviously, those studies are concentrated on the simulated biologic behavior rule or biological mechanism.
Game theory, which is a theory for the science of logical decision-making in humans and computers, is applied to an extensive range of behavioral relations [11]. A game typically involves several players, strategies or actions, orders, and payoffs, which are similar to the individuals, genetic operators (selection, crossover and mutation), and fitness involved in evolutionary algorithms. Players usually select a strategy based on the expected payoffs. Otherwise, they apply learning methods, such as reinforcement learning [12], belief learning [13], imitation [14], directional learning [15,16], and rule learning [17], to guarantee gains. A player makes a decision based on his/her perception of the actions of other players. Evolution through natural selection is typically attributed to improvement and progress, and game-theoretic arguments are more appropriate than optimization algorithms in studying frequency-dependent selection [18]. Replicator and adaptive dynamics describe short- and long-term evolution in the phenotype space and have been applied in a variety of fields ranging from animal behavior and ecology to speciation, macroevolution, and human language. Evolutionary game theory is an essential component of a mathematical and computational approach to biology. In addition to focus on agent-based automated negotiation research, there are studies [19,20] on searching the strategies through co-evolutionary learning using EAs and game-theoretic analysis. Additionally, recent research [21] suggests that predictive adaptive responses can lead to differential development among initially-similar individuals and increase evolutionary fitness, which is an adaptive change in long-term behavior or development because it is triggered by environmental exposure. The use of a learning strategy can help an entity win against the top entries from the Othello League without explicitly applying human knowledge [22]. Aimed at obtaining an optimization approach embodied the mechanism of behavior game fully, a game evolutionary model used to calculate the payoffs expectation was established [23]. Game mechanisms can be used to devolve a new intelligent algorithm. Thus, this work investigates a game theory-inspired evolutionary algorithm for global optimization (GameEA), which is an optimization approach based on behavioral expectation.
The contributions of this study are summarized as follows.
- A novel game evolutionary algorithm (GameEA) is introduced which is a framework to simulate human game behavior. GameEA includes imitation and belief learning strategies and a payoff expectation mechanism. Learning strategies are used to improve competitiveness of the players, while the payoff expectation formulation is employed to estimate and master the information of the players.
- We compared GameEA with the standard genetic algorithm (StGA) [24], island-model genetic algorithms (IMGA) [25], finding multimodal solutions using restricted tournament selection (RTS) [26], dual-population genetic algorithm (DPGA) [27], and GameEA outperforms the compared four algorithms in terms of stability and accuracy.
The remainder of this paper is organized as follows: Section 2 presents some related works. Section 3 is devoted to the description of the fundamentals of our proposed algorithm and details the proposed algorithm’s procedures. Section 4 presents the comprehensive experiments and analysis. Finally, Section 5 concludes this paper and threads some future research issues.
2. Related Works
Evolutionary game theory [28] refers to the strategic interactions among large populations of agents who base their decisions on simple and myopic rules to determine broad classes of decision procedures. These procedures provide plausible descriptions for selfish behavior and include appealing forms of aggregate behavior.
Game-theoretic differential evolution (GTDE) [29] was developed from differential evolution (DE) by adopting cooperative and defective strategies. The poor strategy was used to reduce the influence of a child vector on the principle parent at each generation and to modify relations to increase the mutation degree for the child vector. Cooperative strategies are adopted to increase or decrease the mutation factor of a child vector. GTDE was conducted in the framework of DE with the strategies and two computational times of DE.
A particle swarm optimizer based on evolutionary game (EGPSO) [30] uses replicator dynamics to model the behavior of particles to players who aim to achieve maximum utility. The author claims that EGPSO can overcome premature convergence and has an excellent convergence property unlike traditional particle swarm optimization with limited experiments. An evolutionary algorithm based on Nash dominance for equilibrium problems with equilibrium constraints [31] was developed. However, its largest labels are Nash dominance and the creation of a child vector via DE. The game-theoretic approach for designing evolutionary programming is a strategy that uses a combination of Gaussian and Cauchy mutations [32]. Although the framework of the algorithm is similar to popular evolutionary programming, its mutation operation is similar to game strategy. With the ever-increasing complexity of design engineering problems, game strategies have been proposed to save CPU usage and increase model quality [33,34], in which game strategies are hybridized and coupled with multi-objective evolutionary algorithms to improve the quality of solutions.
Evolutionary algorithms based on game theory and cellular automata with coalitions (EACO) [35] was implemented in an adaptive technique based on cellular automata, in which the game theory and coalitions are employed to manage dynamic neighborhoods. Although EACO outperforms the compared cellular genetic algorithm in most of the cases, it is worse for some benchmarks of combinatorial optimization problems.
Recently, David et al. [36] reviewed game theory-based EA techniques and the use of its application to solving game theory issues and the problems of computational engineering. Here, its extended application also introduced. Otherwise, they compared panmictic EAs and Nash EAs, and their experiments showed the preponderance of the Nash EAs approach.
Game theory has also been adopted to solve complex problems. A game-theoretic framework was proposed to investigate network dynamics under different system parameter settings and perturbations regarding spectrum trading with multiple licensed users selling spectrum opportunities to multiple unlicensed users [37]. This framework was designed to model interactions among multiple primary and secondary users. Evolutionary game theory is used to model the evolution and dynamic behavior of secondary users, and a non-cooperative game has been formulated to model competition among primary users. An evolutionary mechanism is designed by introducing a Nash equilibrium [38] based on a practically approximated solution for the quality of a service-constrained resource allocation problem. Nash equilibrium always exists if the resource allocation game has feasible solutions. The steps to develop an evolutionary mechanism are as follows: Concentrate on the optimum wireless network, i.e., the evolutionary game framework, to enable an arbitrary number of mobiles involved in a local interaction to be extended towards the evolution of dynamics and equilibrium [39,40]. Trying to explain the evolution of structured meaning-signal mappings why the evolutionary dynamics are trapped in a local maxima that do not reflect the structure of the meaning and signal spaces, a simple game theoretical model is used, which can show analytically that when individuals adopting the same communication code meet more frequently than individuals using different codes (a result of the spatial organization of the population) then advantageous linguistic innovations can spread and take over the population [41]. The game theoretic trust model [42] for online distributed evolution of cooperation adapts effectively to environmental changes, but relies on a bacteria-like algorithm to allow nodes to quickly learn appropriate cooperation behavior. A game-theoretic approach to partial clique enumeration [43] announced its effectiveness, which can avoid extracting the same clique multiple times by casting the problem into a game-theoretic framework. Recently, a constant model hawk-dove game [44] is designed to ensure prioritizing the local data processing units in wireless body area networks during medical emergency situations. Furthermore, game theory has raised attention in many other fields like data mining [45] and knowledge discovery [46].
3. Proposed Algorithm: GameEA
3.1. Fundamentals of GameEA
Game theory states that players make a decision based on obtained information and expert opinion to achieve optimal payoffs. Under non-cooperative gaming, John Nash verified that one player could gain worse payoffs unless the best strategy was adopted and if the other participants did not change their decisions. A rational player will obtain consistent predictions by analyzing information. A repeated game is a massive game composed of a number of repetitions of several stage games. This idea implies that one person will consider the influence of his/her current action on the later actions of other players. Every strategy with a payoff greater than the minimum payoff can be a Nash equilibrium, which is a large set of strategies. Payoff is the evaluative criterion when players choose a certain strategy and the payoff of the repeated game is distinguished from the unique game. Each stage of the repeated game obtains a payoff. When a repeated game is assigned to each game turn, it is considered a single game. Thus, the payoffs of a repeated game are related to the strategies used and current total payoffs.
For base game G (a static or dynamic game), T is the number of repeating games. The game results can be observed before starting a new G. This event called a T-repeated game of G, which is marked as G(T). A presupposition typically assumes that players act rationally and make decisions intelligently. However, human behavior frequently deviates from absolute rationality and intelligence, and the concept of learning is integrated into game theory.
Rational and intelligent players can gain insight into the optimal strategies by obtaining and analyzing information to earn the highest payoffs. Furthermore, the final payoffs of all players are related to stage gains in a repeated game. Players can scrutinize historical stage information, and participants can choose an appropriate strategy, which can be different equilibrium strategies for long-term interests. Learning is an important task to achieve a competitive edge when a player is not rational and intelligent. Thus, a new computational intelligent algorithm, which is based on game theory, is proposed.
In extensive form, repeated games can be presented as a game with complete but imperfect information using the Harsanyi Transformation [47]. This transformation introduces the notion of nature’s choice to the game. Hence, when a challenger competes with opponents, all candidates are considered part of nature and the challenger is chosen by nature. The challenger does not know what part of nature is moved. The probability distribution under various options and winner payoffs are known to every player. The action or strategy of a player is traditionally the most important factor, but some differences may be observed:
- Stable payoffs are achieved by a player after winning against an opponent and another challenger.
- If a player accepts a game, then he/she can learn something from the opponent whether he/she losses or wins, which indirectly influences future competition.
- If a player gives up in a competition, then he/she can improve by self-training.
Let w1 and w2 indicate the payoffs from fighting with nature’s choice and the gains from self-training, respectively. Nature has a probability of p to choose a weaker rival and provides a stronger opponent with a probability of 1 − p. Nature’s choice with a probability of p, which is characterized as weaker, exhibits different performances for various challengers even for homogenous challengers in different stages. Thus, payoffs w1 and w2 are undetermined. The participant chosen by nature can achieve gains, which is distinct from the traditional Harsanyi Transformation. Nature’s choice is a virtual player who does not benefit from the game in the traditional Harsanyi Transformation.
When the challenger is not sure about competitiveness of a competitor, mathematical expectation is used to estimate the payoff for a risk preference player. If a challenger decides to fight with nature’s choice, then its expectation payoffs can be presented as (1 − p) × w1 + p × (w1 + 1). Otherwise, if the challenger gives up in the competition, then its expectation payoffs can be calculated using (1 − p) × w2 + p × w2. Thus, total expectation payoff E is calculated using Equation (1). Let w = w2 − w1 be substituted into Equation (1). Hence, we can obtain Equation (2):
We adopt Equation (2) as the criterion for one challenger. Thus, if E ≤ 0, then the challenger gives up in the competition. Otherwise, if E > 0, then the challenger has to compete with a randomly-selected sample (nature’s choice).
Additionally, in traditional game theory, discussions on achieving equilibrium are avoided. Equilibrium reasoning assumes that participants are rational or can approximate equilibrium by learning [48]. Considering that a perfectly rational player exists only in an ideal state, learning is vital for a player in the wrestling model. In our research, we design learning strategies for the wrestling model. This model includes imitation and belief learning. Imitation involves learning strategies and actions from other players to improve competitiveness and applying these strategies to the next game. One player updates its chromosome by copying segments of gene sequences from opponents, which are characterized with positive feedback. In the context of learning in games, belief learning refers to models in which players are engaged in a repeated game, and each player adjusts his/her strategies, behavior or chromosomes by analyzing current history information to consider improvements in payoffs and competitiveness against opponent behavior for the next period.
3.2. Framework of Proposed Algorithm
Some symbols are defined in Table 1. Algorithm 1 presents the general framework of GameEA. The initialization procedure initially generates N initial players and initializes the active payoff of the game and the passive payoff of the match for each player. Within the main loop, in case the termination condition is not met, each player Ii selects an opponent Ij as his/her challenger, and the challenger makes a decision by carefully checking the selected player. At the beginning of the game evolution, considering that the players are very weak, namely Iiv = 0, we let the player perform the imitation operation with P1 to produce a new individual (shown in step 7). Evolving ahead, the challenger Ii makes a decision by carefully checking the selected player Ij, then the imitation or the belief learning procedure is employed for offspring generation. If player Ij is more competitiveness then player Ii, player Ii decides to imitate some genes from player Ij by applying the imitation operator. Otherwise, player Ii insists that it will become more competitiveness by applying the belief learning operator. GameEA has only one population (set of players) and generates new offspring through the imitation operator between the challenger and the opponent and the belief learning operator via self-training strategies. In GameEA, the objective values are not used to calculate the dominance among the players, and the total expectation payoffs based on the history information are employed to facilitate the player becoming a rational decision-maker. The implementation details of each component in GameEA are described in the succeeding paragraphs.
| Algorithm 1. GameEA. |
| Begin |
| 1. t: = 1; // iteration number |
| 2. Initialize players set I, Iia:= 0, and Iip:= 0 (|It| = N, 0 < I < N); // Initialize players population for iteration |
| 3. Evaluate f(I); // for each Ii of I, evaluate Iiobj; |
| 4. while t > Tmax do |
| 5. Select 2 different competitors Ii and Ij from I; |
| 6. Refresh the payoff of Ii and Ij: Iiv:= Iia + Iip, Ijv:= Ija + Ijp; // the following steps are responsible to reproduce a new player Ii |
| 7. if Iiv == 0 && random() < P1 then Perform imitation operator : Ii = imitation(Ii, Ij); |
| 8. else |
| 9. Calculate the expectation payoffs E(Ii) of Ii using Equation (3); |
| 10. if E(Ii) > 0 then Perform imitation operator: Ii = imitation(Ii, Ij); |
| 11. else if random() < P2 then Perform belief learning operator: Ii = beliefLearning(Ii); |
| 12. t: = t + 1; |
| 14. end while |
| end |

Table 1.
Definition of symbols.
3.3. Initialization Players Population
The initialization procedure of GameEA includes three aspects: (1) the decision space and the objective function; (2) the initialization of set of players I; and (3) the assignment of the passive and active payoffs of each player to zero. For the optimization problems, the set of players I should be randomly sampled from the decision space Rn via a uniform distribution using a real-value representation. The objective value of each player is calculated using the objective function.
3.4. Imitation Operator
According to Harsanyi Transformation, nature should make a choice before applying the imitation procedure, which relates to line 5 of Algorithm 1. Equation (3) is described to calculate the expectation payoffs of Ii:
where μ ∈ (0, 1) is a random decimal that is generated by the random function. During the initial evolution, players with zero total payoffs are not intelligent. Thus, a player imitates the selected player under probability P1, which is a very high number, such as 0.9. The weak challenger Ii must compete with the selected Ij and imitate useful information from others by using operator imitation (Ii, Ij). However, the challenger may do nothing at the current game to survive some schema. This approach is a special strategy with varying conditions and unchanging genes when the player does not have substantial information about others.
The calculation of payoffs expectation (line 9 of Algorithm 1) is highly significant. This process is a mechanism of an attempt to master the information of others because the total payoff indicates the historical strategies of an individual. This mechanism allows a player to become more rational and helps him/her make rational decisions. A player frequently sets goals based on his/her experiences with different actions and opponents. Payoff rewards are either reinforced or deterred depending on whom these rewards are compared with; decision-makers adjust their aspirations as they gain experience [49]. Algorithm 2 presents the general procedure for imitation. The objective value comparison between a pair of players (line 1, Algorithm 2) is the basis of historical performance. However, the comparison result affects active or passive payoffs. A temporary variable is adopted to breed new individuals based on imitation strategies according to a past action. An offspring replaces its parent only when the offspring is better than its parent, thereby facilitating global convergence.
In the real word, if one person feels that others have competitive skills, then he/she may attempt to learn these skills. Otherwise, the final decision is influenced by the attraction of the skills and initiative of an individual. A random value, which is denoted as random(), is adopted to present the degree of individual initiative, ratio of succeeding imitation number (Ha + 1) and the total number of imitations (2Hs + 1). If random() × (Ha + 1)/(2Hs + 1) < P3, then all the conditions indicate that the player should improve by speculatively learning from others. For example, using one method that exhibits perfect performance in solving a problem in a specific field to address a problem in another field frequently yields good and unexpected result. This outcome is related to speculative learning because it is based on guesses or ideas about what may happen or be true rather than what are factual. Strategically copying a segment of genes entails obtaining chromosomes from others, which may result in certain improvement. Companies achieve substantial success by investing in new technology. Other companies allocate resources to follow their investment strategies. Followers are likely to benefit. Thus, strategic copying or learning is proposed.
Different imitation strategies can be implemented according to the properties of a problem. For function optimization problems:
If r1 = rand(0, n − 1), r2 = rand(0, n − 1), and β = random(), then if β < 0.5 then .
Otherwise .
Hence, we use the following strategy to implement Ii, which speculatively learns from Ij (line 5, Algorithm 2):
- (1)
- Ip.gen[r2] = 0.5(1 − τ) Ii.gen[r2] + (1 + τ) Ij.gen[r1].
- (2)
- If the value of Ip.gen[r2] is out of range, then a random value must be assigned to Ip.gen[r2].
- (3)
- Ii strategically copies a segment of genes from Ij via Ip.gen[r1] = 0.5(1 − τ) Ii.gen[r1] + (1 + τ) Ij.gen[r1].
- (4)
- If the value of Ip.gen[r1] is out of the decision space, then a random value must be assigned to Ip.gen[r1].
| Algorithm 2. Imitation (Ii, Ij). |
| Begin |
| 1. if Iiobj < Ijobj then Iia:= Iia + 1; |
| 2. else Ijp = Ijp + 1; |
| 3. Initialize temporary variable Ip = Ii and B:= 0; |
| 4. if (random() × (Ha + 1)/(2Hs + 1)) < P3 then |
| 5. Modify genes of Ip by speculatively learning from Ij; |
| 6. B = 1 and Ha = Ha + 1; |
| 7. else change genes of Ii by strategically copying a segment of genes from Ij; |
| 8. update the objectives value Ipobj; |
| 9. if Ipobj < Iiobj then Ii = Ip ; |
| 10. if B == 1 then Hs = Hs + 1; |
| 11. return Ii; |
| end |
3.5. Belief Learning Operator
Belief learning refers to models in which each player adjusts his/her strategies to increase payoffs and competitiveness against opponent behavior for the next period. The player posits that one strategy will facilitate positive feedback and insists on using the strategy to train himself/herself with the expectation of improving future competitiveness. This type of self-training is associated with training methods and duration. A decision-maker is not usually completely committed to one set of ideas or one way of behavior. Several systems of ideas or several possible ways of behaving may be simultaneously perceived; which of these ideas predominate and which are given less attention depend on the experiences of an individual [49].
Thus, the operator performs under given probability P2. If belief learning is expected to run for a significant amount of time, then P2 is assigned a high value. Otherwise, P2 is given a low value. If a characteristic of a solution must be emphasized, then special knowledge can be used to specify a belief learning algorithm. Algorithm 3 presents a belief learning procedure for real-value presentation problems. An offspring replaces its parent only when the offspring is better than its parent and, thus, the eliting conservation strategy is implemented. The belief learning operator differs from the belief space of a cultural algorithm [50], which is divided into distinct categories that represent different fields of knowledge that the population has regarding the search space. The belief space is updated after each iteration by the best individuals of the population.
| Algorithm 3. Belieflearning(Ii). // for real-valued presentation. |
| Begin |
| 1. r1:= rand(0, n − 1), β:= random() |
| 2. Δ:= difference of maximum and minimum value of r1th dimension |
| 3. if β < 0.5 then τ = (2β)1/21 − 1 |
| 4. else τ =1 − (2 − 2β)1/21 |
| 5. Ii.gen[r1] = Ii.gen[r1] + τ × Δ |
| 6. if the value of Ip.gen[r1] out of the given ranges |
| 7. then assign a required random value to Ip.gen[r1] |
| end |
3.6. Players Set Updating Strategy
The algorithm GameEA, which is inspired by the game of human behavior, was proposed in this work. Human society, as well as the game or competition among individuals, is simulated. In biology, individuals of all ages live in the same environment and compete with one another. Parents are exploited by their offspring even within the surviving space. In environments, individual learning behavior possibly differs from biological evolution (for example, individuals adjust rapidly); at the population level, however, a process that is analogous to biological evolution occurs. Decision-makers observe and imitate each other in different roles (challenger or opponent); they lean onto and change one another. These processes may imply that the distribution of ideas and strategies in a population of agents changes over time in a manner that is analogous to biological evolution [49]. The existence of a parent is justified and competitive. An offspring has the capability to survive if it is stronger or better than its parents. Thus, GameEA uses a simple strategy to update the set of players. An offspring replaces its parent and inherit their fortune, such as payoffs and behavior, only when the offspring is better than its parent, thereby implementing the eliting conservation strategy and facilitating global convergence. For each repeat loop (line 5–12 of Algorithm 1), a new player does not shy away from other players, and the game is available for all players regardless of whether an individual is experienced or not.
4. Performance Comparison and Experimental Results
4.1. Test Problems and Compared Algorithms
The C++ language was used to implement GameEA. Our program uses the .NET platform, and the PC was an AMD Phenom™ II X4 810 CPU (2.59 GHz) with 2 GB RAM. To evaluate the improvement of the performance of our method, the proposed algorithm was compared with four kinds of algorithms: standard genetic algorithm (StGA) [24], island-model genetic algorithms (IMGA) [25], finding multimodal solutions using restricted tournament selection (RTS) [26], and dual-population genetic algorithm (DPGA) for adaptive diversity control [27], which are famous for their unique performance with different characteristics.
IMGA is a typical example of multi-population genetic algorithms. This type of algorithm evolves two or more subpopulations and uses periodic migration for the exchange of information among subpopulations. IMGA has multiple subpopulations that evolve separately.
Regarding RTS, a crowding method that is slightly different from standard crowding is used. This approach randomly selects parents and allows the latest offspring to replace the most similar one using a specific strategy.
DPGA uses two populations. Among which, the main population evolves to identify a good solution for a given problem, whereas the reserve population evolves to provide controlled diversity to the main population.
To focus on the searching accuracy and stability, thirteen benchmark functions f1–f13 shown in Table 2 have been considered in our experiments on real-valued representations, which are widely adopted for comparing the capabilities of evolutionary algorithms. The functions f1–f7 are unimodal distribution functions with one peak within the entire given domain, the functions f8–f13 are multimodal functions with a large number of local optima in the searching space. Column n in Table 2 indicates the dimensions used.

Table 2.
Test functions used for the experiments.
4.2. Experimental Setup
Specifically, we continue to use the parameters and strategies that StGA, IMGA, RTS, and DPGA have used. IMGA has multiple subpopulations each of which evolves separately. RTS uses a crowding method which is somewhat different from the standard crowding, which selects parents randomly and lets the latest offspring replace the most similar one by using a specific strategy. DPGA also uses an additional population as a reservoir of diversity. Additional details of these algorithms can be found in [24,25,26,27].
The players size N was set to 50 for GameEA, the payoff weight W1, losses weight W2, learning probability P1, mutation probability P2 and the speculative probability P3 were set to 0.9, 0.01, 0.9, 0.1, and 0.1, respectively. For each function, the maximum iteration of GameEA was set to a homogeneous iteration with the compared algorithm. Table 3 summarizes iterations used for each function, which are indicated in the iteration column of the table. The following sections present the statistical experimental results obtained for the functions mentioned above.

Table 3.
Fifty independent experimental statistics results based on StGA, IMGA, RTS, DPGA, and GameEA using real-valued representations of functions .
4.3. Results and Comparision Analysis
For each test problem, 50 independent experiments have been executed and the averaged results are shown in Table 3.
For functions f1, f2, and f4, the GameEA obtains the best results with an average result of 4.33 × 10−96, 1.52 × 10−66, and 0.0374, respectively. The DPGA shows the second-best results with an average result of 1.47 × 10−52 for function f1, and the RTS is third on the list. The StGA convergence accuracy is slightly worse than that of the IMGA for functions f1 and f2, but the IMGA is worse than the StGA for function f4.
For function f4, the RTS with an average of 1.391 is the silver medalist, but the GameEA’s average is less than 3% of the RTS.
For function f6, the GameEA is significantly better than the StGA and the DPGA. The GameEA is similar to the IMGA and the RTS, but it has a smaller standard deviation. For function f5 and f7, all the mentioned algorithms above converge to the global minimum.
To make a careful observation of the results on the highly-multimodal functions f8–f13, which have a large number of local optima, all the algorithms converge to the global minimum on the functions f8 and f9. The RTS, the DPGA and the GameEA show no significant difference with the convergence of the global optimum in each independent trial on function f10, which means that all the algorithms can solve such problems.
The GameEA won a landslide victory with the best stability convergence in 50 independent trials for the functions f11–f13, which demonstrates the search ability, stability, and robustness. It is a remarkable fact that the StGA and the DPGA do not converge to the global optimal solution with the same standard deviation of zero in all the trials for function f13, which indicates that those algorithms stalled at the local optimum points, whereas the GameEA escapes and continually evolves to the global minimum. We also observed the final solutions of the GameEA with respect to the f13, although its average optimums are not perfect, thirty-nine parts in fifty obtain the global optimum.
With respect to function f3, the GameEA is obviously worse than other four algorithms. When we scrutinize the 50 experimental outputs, we find that the best solutions are set to 4.43 × 10−12 and the worst optimum is set to 0.0122, which means that the final results have a wide range and, thus, a poor average and standard deviation.
Furthermore, based on those results, the Friedman test [51,52,53], which is a non-parametric alternative to ANOVA, is conducted with SPSS 22 to check whether the StGA, the IMGA, the RTS, the DPGA, and GameEA have similar performances. The null hypothesis is set to: “the distributions of StGA, IMGA, RTS, DPGA, and GameEA are the same”. This null hypothesis states that the observed algorithms output the same distribution and, therefore, have the same mean ranking. Table 4 shows the results of the pairwise comparisons in the hypothesis test summary. Especially, all the observed algorithms reported the optimal solution for functions f5, f7, f8, and f9, so we do not check the Friedman test on those functions.

Table 4.
Hypothesis test summary and results of the pairwise comparisons.
As seen from Table 4, all the algorithms could offer different performance for all the used functions, except f6 and f13, on the whole. It is clear that the GameEA has given the best performance amongst all four algorithms according to Table 3. For function f2, the decision rejected the null hypothesis according to Table 4, and the GameEA has the best performance according to Table 3, but the results of the pairwise comparison was only rejected in the case of the StGA. In addition, for function f3, it indicates that the GameEA has given the worst performance according to Table 3, but the Friedman test results shows that the distribution of IMGA, RTS, DPGA, and GameEA are the same according to Table 4. The null hypothesis of pairwise comparison was only rejected in the case of StGA. Additionally, for functions f6 and f13, although all the algorithms show different distributions according to the statistic results shown in Table 3, their null hypothesizes were not rejected, which means that all the algorithms could offer similar performances.
In addition, for function f1, we checked its detailed Friedman test results, and Figure 1 and Table 5 show the detailed statistics of the Friedman test.
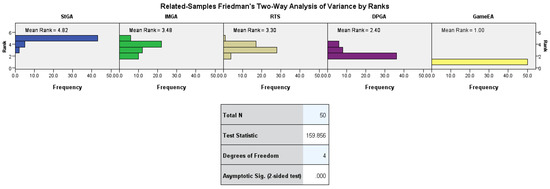
Figure 1.
Related samples test view.

Table 5.
Pairwise comparisons. Each row tests the null hypothesis that the Sample 1 and Sample 2 distributions are the same. Asymptotic significances (2-sided tests) are displayed. The significance level is 0.05.
According to Figure 1, it can be found that the GameEA states the smallest average ranking of 1.00 and the StGA reports the largest mean ranking of 4.82. According to the definition of the Friedman test, the mean ranking can be employed as an indicator as to how successful the considered algorithm is. The first place belongs to GameEA, followed by DPGA, RTS, IMGA, and StGA. The GameEA has the lower mean ranking, which means that the GameEA outperforms the compared algorithms. Additionally, the pairwise comparisons in Table 5 also state that similar conclusion.
From these results, we conclude that the GameEA is more powerful than the compared algorithms, and GameEA has better performance, such as the stability, robustness, and accuracy of solutions, than the compared algorithms on function optimization problems.
5. Conclusions
This paper proposed a new framework to simulate human game behavior, and its software code in C++ of GameEA can be found at [54]. GameEA is a population-based algorithm, in which the player makes decisions according to the payoff expectation, and then learning strategies are used to evaluate the chromosome genes of the players. GameEA employs a simple strategy to update the player set, which is that the offspring replaces its parents and inherits the parents’ information only when the offspring is better than its parent to implement the eliting conservation strategy to facilitate convergence. Experimental results show that GameEA outperforms the compared algorithms. In our future work, we will study what the parameters are that affect the GameEA and how to select better parameters. We will also conduct intensive experiments using well-established benchmarks with rotated and shifted functions, including multi-objective optimization problems involving more complicated applications. Additionally, we will conduct more intensive compressions with some other metaheuristics. Additionally, this work is also part of our ongoing research that explores social robots in the smart home. We will investigate how to use GameEA to improve the accuracy of activity recognition and privacy detection [55].
Acknowledgments
This research was partially supported by National Natural Science Foundation of China under Grant 61640209, Foundation for Distinguished Young Talents of Guizhou Province under grant QKHRZ[2015]13, Science and Technology Foundation of Guizhou Province under grant JZ[2014]2004, JZ[2014]2001, ZDZX[2013]6020, and LH[2016]7433.
Conflicts of Interest
The author declared no conflict of interest.
References
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Yang, X. Firefly algorithm, stochastic test functions and design optimisation. Int. J. BioInspir. Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Li, X.; Shao, Z.; Qian, J. An optimizing method based on autonomous animats: Fish-swarm algorithm. Syst. Eng. Theory Pract. 2002, 22, 32–38. [Google Scholar]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial fish swarm algorithm: A survey of the state-of-the-art, hybridization, combinatorial and indicative applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Mernik, M.; Liu, S.; Karaboga, D.; Črepinšek, M. On clarifying misconceptions when comparing variants of the Artificial Bee Colony Algorithm by offering a new implementation. Inf. Sci. 2015, 291, 115–127. [Google Scholar] [CrossRef]
- Yang, X.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009. [Google Scholar]
- Woldemariam, K.M.; Yen, G.G. Vaccine-Enhanced Artificial Immune System for Multimodal Function Optimization. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2010, 40, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Maass, W.; Natschläger, T.; Markram, H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y. Brain storm optimization algorithm. In Advances in Swarm Intelligence; Springer: Berlin, Germany, 2011; pp. 303–309. [Google Scholar]
- Wikipedia. Game Theory. Available online: https://en.wikipedia.org/wiki/Game_theory (accessed on 3 March 2016).
- Madani, K.; Hooshyar, M. A game theory-reinforcement learning (GT-RL) method to develop optimal operation policies for multi-operator reservoir systems. J. Hydrol. 2014, 519, 732–742. [Google Scholar] [CrossRef]
- Spiliopoulos, L. Pattern recognition and subjective belief learning in a repeated constant-sum game. Games Econ. Behav. 2012, 75, 921–935. [Google Scholar] [CrossRef]
- Friedman, D.; Huck, S.; Oprea, R.; Weidenholzer, S. From imitation to collusion: Long-run learning in a low-information environment. J. Econ. Theory 2015, 155, 185–205. [Google Scholar] [CrossRef]
- Nax, H.H.; Perc, M. Directional learning and the provisioning of public goods. Sci. Rep. 2015, 5, 8010. [Google Scholar] [CrossRef] [PubMed]
- Anderson, S.P.; Goeree, J.K.; Holt, C.A. Stochastic Game Theory: Adjustment to Equilibrium under Noisy Directional Learning; University of Virginia: Charlottesville, VA, USA, 1999. [Google Scholar]
- Stahl, D.O. Rule learning in symmetric normal-form games: Theory and evidence. Games Econ. Behav. 2000, 32, 105–138. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Evolutionary Dynamics of Biological Games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef] [PubMed]
- Gwak, J.; Sim, K.M. A novel method for coevolving PS-optimizing negotiation strategies using improved diversity controlling EDAs. Appl. Intell. 2013, 38, 384–417. [Google Scholar] [CrossRef]
- Gwak, J.; Sim, K.M.; Jeon, M. Novel dynamic diversity controlling EAs for coevolving optimal negotiation strategies. Inf. Sci. 2014, 273, 1–32. [Google Scholar] [CrossRef]
- Rosenstrom, T.; Jylha, P.; Pulkki-Raback, L.; Holma, M.; Raitakari, I.T.; Isometsa, E.; Keltikangas-Jarvinen, L. Long-term personality changes and predictive adaptive responses after depressive episodes. Evol. Hum. Behav. 2015, 36, 337–344. [Google Scholar] [CrossRef]
- Szubert, M.; Jaskowski, W.; Krawiec, K. On Scalability, Generalization, and Hybridization of Coevolutionary Learning: A Case Study for Othello. IEEE Trans. Comput. Intell. AI Games 2013, 5, 214–226. [Google Scholar] [CrossRef]
- Yang, G.C.; Wang, Y.; Li, S.B.; Xie, Q. Game evolutionary algorithm based on behavioral game theory. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2016, 7, 68–73. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Alba, E.; Tomassini, M. Parallelism and evolutionary algorithms. IEEE Trans. Evol. Comput. 2002, 6, 443–462. [Google Scholar] [CrossRef]
- Harik, G.R. Finding Multimodal Solutions Using Restricted Tournament Selection. In Proceedings of the 6th International Conference on Genetic Algorithms, San Francisco, CA, USA, 15–19 July 1995. [Google Scholar]
- Park, T.; Ryu, K.R. A Dual-Population Genetic Algorithm for Adaptive Diversity Control. IEEE Trans. Evol. Comput. 2010, 14, 865–884. [Google Scholar] [CrossRef]
- Kontogiannis, S.; Spirakis, P. Evolutionary games: An algorithmic view. In Lecture Notes in Computer Science; Babaoglu, O., Jelasity, M., Montresor, A., Eds.; Springer: Berlin, Germany, 2005; pp. 97–111. [Google Scholar]
- Ganesan, T.; Elamvazuthi, I.; Vasant, P. Multiobjective design optimization of a nano-CMOS voltage-controlled oscillator using game theoretic-differential evolution. Appl. Soft Comput. 2015, 32, 293–299. [Google Scholar] [CrossRef]
- Liu, W.; Wang, X. An evolutionary game based particle swarm optimization algorithm. J. Comput. Appl. Math. 2008, 214, 30–35. [Google Scholar] [CrossRef]
- Koh, A. An evolutionary algorithm based on Nash Dominance for Equilibrium Problems with Equilibrium Constraints. Appl. Soft Comput. 2012, 12, 161–173. [Google Scholar] [CrossRef]
- He, J.; Yao, X. A game-theoretic approach for designing mixed mutation strategies. In Lecture Notes in Computer Science; Wang, L., Chen, K., Ong, Y.S., Eds.; Springer: Berlin, Germany, 2005; pp. 279–288. [Google Scholar]
- Periaux, J.; Chen, H.Q.; Mantel, B.; Sefrioui, M.; Sui, H.T. Combining game theory and genetic algorithms with application to DDM-nozzle optimization problems. Finite Elem. Anal. Des. 2001, 37, 417–429. [Google Scholar] [CrossRef]
- Lee, D.; Gonzalez, L.F.; Periaux, J.; Srinivas, K.; Onate, E. Hybrid-Game Strategies for multi-objective design optimization in engineering. Comput. Fluids 2011, 47, 189–204. [Google Scholar] [CrossRef]
- Dorronsoro, B.; Burguillo, J.C.; Peleteiro, A.; Bouvry, P. Evolutionary Algorithms Based on Game Theory and Cellular Automata with Coalitions. In Handbook of Optimization: From Classical to Modern Approach; Zelinka, I., Snášel, V., Abraham, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 481–503. [Google Scholar]
- Greiner, D.; Periaux, J.; Emperador, J.M.; Galván, B.; Winter, G. Game Theory Based Evolutionary Algorithms: A Review with Nash Applications in Structural Engineering Optimization Problems. Arch Comput. Method E 2016. [Google Scholar] [CrossRef]
- Niyato, D.; Hossain, E.; Zhu, H. Dynamics of Multiple-Seller and Multiple-Buyer Spectrum Trading in Cognitive Radio Networks: A Game-Theoretic Modeling Approach. IEEE Trans. Mob. Comput. 2009, 8, 1009–1022. [Google Scholar] [CrossRef]
- Wei, G.; Vasilakos, A.V.; Zheng, Y.; Xiong, N. A game-theoretic method of fair resource allocation for cloud computing services. J. Supercomput. 2010, 54, 252–269. [Google Scholar] [CrossRef]
- Jiang, G.; Shen, S.; Hu, K.; Huang, L.; Li, H.; Han, R. Evolutionary game-based secrecy rate adaptation in wireless sensor networks. Int. J. Distrib. Sens. N 2015, 2015, 25. [Google Scholar] [CrossRef]
- Tembine, H.; Altman, E.; El-Azouzi, R.; Hayel, Y. Evolutionary Games in Wireless Networks. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2010, 40, 634–646. [Google Scholar] [CrossRef] [PubMed]
- Fontanari, J.F.; Perlovsky, L.I. A game theoretical approach to the evolution of structured communication codes. Theory Biosci. 2008, 127, 205–214. [Google Scholar] [CrossRef] [PubMed]
- Mejia, M.; Pena, N.; Munoz, J.L.; Esparza, O.; Alzate, M.A. A game theoretic trust model for on-line distributed evolution of cooperation in MANETs. J. Netw. Comput. Appl. 2011, 34, 39–51. [Google Scholar] [CrossRef]
- Bulo, S.R.; Torsello, A.; Pelillo, M. A game-theoretic approach to partial clique enumeration. Image Vis. Comput. 2009, 27, 911–922. [Google Scholar] [CrossRef]
- Misra, S.; Sarkar, S. Priority-based time-slot allocation in wireless body area networks during medical emergency situations: An evolutionary game-theoretic perspective. IEEE J. Biomed. Health 2015, 19, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Qin, Z.; Wan, T.; Dong, Y.; Du, Y. Evolutionary collective behavior decomposition model for time series data mining. Appl. Soft Comput. 2015, 26, 368–377. [Google Scholar] [CrossRef]
- Hausknecht, M.; Lehman, J.; Miikkulainen, R.; Stone, P. A neuroevolution approach to general atari game playing. IEEE Trans. Comput. Intell. AI Games 2014, 6, 355–366. [Google Scholar] [CrossRef]
- Hu, H.; Stuart, H.W. An epistemic analysis of the Harsanyi transformation. Int. J. Game Theory 2002, 30, 517–525. [Google Scholar] [CrossRef]
- Colman, A.M. Cooperation, psychological game theory, and limitations of rationality in social interaction. Behav. Brain Sci. 2003, 26, 139. [Google Scholar] [CrossRef] [PubMed]
- Borgers, T.; Sarin, R. Learning through reinforcement and replicator dynamics. J. Econ. Theory 1997, 77, 1–14. [Google Scholar] [CrossRef]
- Reynolds, R.G. Cultural algorithms: Theory and applications. In New Ideas in Optimization; Corne, D., Dorigo, M., Glover, F., Eds.; McGraw-Hill Ltd.: Maidenhead, UK, 1999; pp. 367–378. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Draa, A. On the performances of the flower pollination algorithm—Qualitative and quantitative analyses. Appl. Soft Comput. 2015, 34, 349–371. [Google Scholar] [CrossRef]
- Veček, N.; Mernik, M.; Črepinšek, M. A chess rating system for evolutionary algorithms: A new method for the comparison and ranking of evolutionary algorithms. Inf. Sci. 2014, 277, 656–679. [Google Scholar] [CrossRef]
- GitHub, Inc. (US). Available online: https://github.com/simonygc/GameEA.git (accessed on 14 July 2017).
- Fernandes, F.E.; Guanci, Y.; Do, H.M. Detection of privacy-sensitive situations for social robots in smart homes. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).