Scale Reduction Techniques for Computing Maximum Induced Bicliques

Abstract

Given a simple, undirected graph G, a biclique is a subset of vertices inducing a complete bipartite subgraph in G. In this paper, we consider two associated optimization problems, the maximum biclique problem, which asks for a biclique of the maximum cardinality in the graph, and the maximum edge biclique problem, aiming to find a biclique with the maximum number of edges in the graph. These NP-hard problems find applications in biclustering-type tasks arising in complex network analysis. Real-life instances of these problems often involve massive, but sparse networks. We develop exact approaches for detecting optimal bicliques in large-scale graphs that combine effective scale reduction techniques with integer programming methodology. Results of computational experiments with numerous real-life network instances demonstrate the performance of the proposed approach.

1. Introduction

Network-based analysis offers a powerful approach for modeling elements and their interactions in complex systems. In particular, network models make it possible to take advantage of graph algorithms for mining massive datasets. For example, in protein-protein interaction networks, proteins are represented as vertices and interaction between pairs of proteins are represented by edges [1,2,3]. In genome research, the relationship between genes and diseases can be modeled using graphs in which vertices represent genes and diseases and edges represent a meaningful or hypothetical relationship between a gene and a disease [4,5]. The World Wide Web can be represented using a graph in which vertices are documents and edges are the hyperlinks between documents [6,7]. Network models provide a valuable description of such systems and allow us to apply advanced techniques for identification of some of the global structural properties of the system and prediction of their future behavior. Biclique community detection has been studied extensively in recent years due to its various applications in automata and language theory, biology and genome research, clustering and data mining, artificial intelligence and graph compression [4,8,9,10,11,12,13,14]. Several different variants of the biclique community detection problems have been introduced and studied in the literature in this context. Next, we provide formal definitions and briefly review related literature.

Let $G=(V,E)$ be a simple, undirected graph, where $V=\{1,\dots ,n\}$ is the vertex set, and $E\subseteq \{\{i,j\}:i,j\in V,i\ne j\}$ is the edge set. Let $N_G(i)=\{j\in V:\{i,j\}\in E\}$ denote the neighborhood of a vertex i in G, and let $N_G[i]=N_G(i)\cup \{i\}$ be the closed neighborhood of i. For $C\subseteq V$, let $G[C]=(C,E(C))$, where $E(C)=\{\{i,j\}\in E:i,j\in C,i\ne j\}$, denote the subgraph induced by C in G. The set C is called an independent set if $G[C]$ is edgeless, and C is a clique if $G[C]$ is a complete graph (i.e., has all possible edges). Let $\alpha (G)$ be the independence number of G, which is the cardinality of a maximum independent set in G. A graph is called bipartite if its set of vertices can be partitioned into two non-overlapping independent sets, referred to as parts.

Definition 1.

A set $C\subseteq V$ is called a biclique if $G[C]$ is a complete bipartite graph, which is a bipartite graph with all possible edges between the parts.

A biclique is called maximal if it is not a subset of a larger biclique and, maximum if there is no larger biclique in G. Note that according to Definition 1, an independent set is a biclique with one of the parts being an empty set. However, from a practical perspective, one is not interested in independent set solutions when searching for large bicliques in a graph. This observation is reflected in the definitions of the corresponding optimization problems given next.

Definition 2.

Given a simple, undirected graph $G=(V,E)$, the maximum biclique (MB) problem is to find a maximum cardinality biclique in G that is not an independent set.

Definition 3.

Given a simple, undirected graph $G=(V,E)$, the maximum edge biclique (MEB) problem is to find a biclique with the maximum number of edges in G.

Different algorithms have been proposed for biclique community detection ranging from enumeration of all maximal (non-induced) bicliques of a graph [13,15,16,17,18], finding a maximum edge cardinality biclique [5] and maximum balanced bicliques [19] to exact, exponential-time methods [20], approximation algorithms [21] and mining quasi-bicliques [22,23]. In particular, the MB problem has been proved to be NP-hard in general graphs, but polynomial-time solvable in bipartite graphs [21]. The maximum edge biclique (MEB) problem has been successfully used for biclustering and formal concept analysis [4,5,24]. It has been proved to be NP-hard in general and hard to approximate even for bipartite graphs [25,26], but polynomial time solvable in convex bipartite and biconvex graphs [5] (A bipartite graph $G=(V_1,V_2,E)$ is called convex on $V_2$ if there exists an ordering of the vertices of $V_2$ such that for any $v\in V_1$, $N_G(v)$ consists of vertices that are consecutive in $V_2$. The graph G is biconvex if it is convex on both $V_1$ and $V_2$). The maximum edge weight biclique problem, an edge-weighted generalization of MEB, has also been considered in the literature [11,27].

It should be noted that the NP-hardness of the MB problem in some of the previous publications [21,25] has been claimed based on a more general result by Yannakakis [28], as discussed next. A graph property $\Pi$ is said to be hereditary on induced subgraphs if for a graph G with property $\Pi$, the deletion of any subset of vertices does not produce a graph violating $\Pi$. A property $\Pi$ is said to be nontrivial if it is true for a single-vertex graph and is not satisfied by every graph. Also a property is said to be interesting if there are arbitrarily large graphs satisfying $\Pi$. The maximum $\Pi$ problem is to find the largest order induced subgraph that does not violate property $\Pi$. Yannakakis [28] proved that the maximum $\Pi$ problem for nontrivial, interesting graph properties that are hereditary on induced subgraphs is NP-hard. If an independent set is accepted as a feasible solution for the MB problem, then clearly the property “a graph whose set of vertices is a biclique” is nontrivial, interesting and hereditary on induced subgraphs, which proves that this version of the MB problem (that accepts independent set solutions) is NP-hard. However, requiring bicliques to have two nonempty parts (as in this paper and in [21]) violates the heredity property, since removing the central vertex of a star graph gives an independent set, which is infeasible under this requirement. Thus, the result of Yannakakis is not applicable for this, more practically reasonable version of the MB problem. Nonetheless, the reduction from the independent set problem used in [21] does prove that the non-hereditary version of the MB problem is indeed NP-hard. On a practical note, the lack of heredity implies that the general-purpose combinatorial branch-and bound framework known as Russian Doll Search (RDS) [29,30] is not directly applicable to the problems considered in this paper.

The focus of this paper is on developing effective scale reduction techniques for the MB and MEB problems that can be used in combination with an exact algorithm in order to solve this problem to optimality on large, sparse networks. Simple scale reduction techniques have been successfully applied to other important combinatorial optimization problems, including the maximum clique and minimum vertex coloring problems [31,32], the maximum independent set problem [33], and the minimum vertex cover problem [34] among others. The ideas behind these methods are similar to some of those used to develop parameterized algorithms for hard optimization problems [35]. In parameterized approaches, one considers a parameter k (e.g., the target size of a solution) along with the usual input size n [36]. A parameterized problem is called fixed-parameter tractable if there exists an algorithm (called an fpt-algorithm) solving this problem in $f(k)·n^{O(1)}$ time, where f is a computable function depending only on k (typically exponentially). The first result on parameterized complexity of a problem dealing with finding bicliques has only been established recently, after numerous previous attempts. More specifically, Lin [37] has proved that the problem of deciding whether a given graph G contains a complete bipartite subgraph $K_{k,k}$ is W[1]-hard, meaning that an fpt-algorithm is unlikely to exist. In another recent paper, Feng et al. [38] studied the parameterized edge biclique problem, which asks if a given bipartite graph G contains a biclique subgraph with at least k edges, where k is a given integer parameter. To the best of our knowledge, the MB and MEB problems considered in this paper have not been studied from a parameterized complexity perspective and the exact approach proposed in this paper is the first reported attempt of solving these problems computationally.

The remainder of the paper is organized as follows. Section 2 provides integer programming formulations of the considered problems. A global optimization approach is proposed in Section 3, which employs a novel scale reduction technique that empowers exact solution methods to handle large-scale instances of the MB and MEB problems. Results of computational experiments with proposed method are reported in Section 4. The paper is concluded in Section 5.

2. Integer Programming Formulations

In this section, we provide integer programming (IP) formulations for the problems of interest. Consider a simple, undirected graph $G=(V,E)$. Let $x_{ij}$ be a binary decision variable indicating whether a vertex $i\in V$ belongs to either of the two parts $j\in \{1,2\}$. Then the MB problem can be formulated as follows:

$$\begin{array}{cc}\hfill \mathrm{Maximize}& \sum _{i\in V}(x_{i1}+x_{i2})\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \mathrm{subject}\mathrm{to}:& x_{i1}+x_{i2}\le 1\hfill & \forall i\in V\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& \sum _{i\in V}{x}_{ij}\ge 1\hfill & \forall j\in \{1,2\}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& x_{ij}+x_{kj}\le 1\hfill & \forall \{i,k\}\in E,j\in \{1,2\}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& x_{i1}+x_{k2}\le 1\hfill & \forall \{i,k\}\notin E\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& x_{ij}\in \{0,1\}\hfill & \forall i\in V,j\in \{1,2\}\hfill \end{array}$$

(6)

In this formulation, constraints (2) make sure that each vertex belongs to at most one part, and constraints (3) rule out solutions with empty parts, which correspond to independent sets. Constraints (4) ensure that each of the two parts forms an independent set, and constraints (5) guarantees that non-adjacent vertices cannot belong to different parts. Considering an instance with $n=\left|V\right|$ vertices and $m=\left|E\right|$ edges, the above formulation has 2n binary variables and $n^2+2$ constraints.

To develop an IP formulation for the MEB problem, we introduce m new binary variables $z_{ik},\{i,k\}\in E,i<k$ indicating whether edge $\{i,k\}$ is included in the optimal solution. We have:

$$\begin{array}{cc}\hfill \mathrm{Maximize}& {\displaystyle \sum _{\{i,k\}\in E}{z}_{ik}}\hfill \\ \hfill \mathrm{subject}\mathrm{to}:& (2)-(5)\hfill \end{array}$$

(7)

$$\begin{array}{ccc}& z_{ik}\le x_{i1}+x_{i2},z_{ik}\le x_{k1}+x_{k2}\hfill & \forall \{i,k\}\in E,k>i\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& x_{ij},z_{ik}\in \{0,1\}\hfill & \forall i\in V,j\in \{1,2\},\{i,k\}\in E,k>i\hfill \end{array}$$

(9)

In this model, constraints (8) ensure that an edge is in the solution only if its incident vertices are selected to be in the solution. Note that the integrality of $z_{ik}$ can be relaxed due to the fact that these variables are bounded by $x_{ij}$ variables and the objective function is maximization. This formulation has $2n+m$ variables and $n^2+2m+2$ constraints.

The proposed IP formulations can be employed in off-the-shelf solvers to find optimal solutions of the problems of interest. However, the practical applicability of this approach is limited to small-scale instances, unless the formulations are strengthened based on their detailed polyhedral study. In the next section, we propose an alternative global optimization approach that employs effective scale reduction techniques to solve large-scale real-life instances.

3. Exact Algorithm Based on the Proposed Scale Reduction

Due to the NP-hardness of the considered problems, solving large-scale instances arising in practice is a formidable challenge. However, many real-life networks are characterized by sparsity, which can be exploited in designing exact, global optimization algorithms. Namely, instead of directly applying standard solution techniques, such as branch-and-bound method, we will aim to reduce large-scale instances to manageable sizes first. Using structural properties of bicliques, we propose a scale reduction technique that attempts to shrink the feasible region of a given instance of the problem while ensuring that the reduced instance contains a global optimal solution to the original problem. The overall structure of the proposed global optimization algorithm consists of the following steps.

• Find a lower bound. Use a heuristic algorithm to obtain a lower bound on the optimal solution.
• Apply scale reduction. Given a heuristic solution, recursively identify and remove vertices that cannot be included in a globally optimal solution, until no further reduction is possible.
• Solve. Apply a standard exact algorithm to find a globally optimal solution in the residual graph.

The procedure starts with finding a lower bound solution using a heuristic algorithm described in the next subsection. Given this lower bound, the scale reduction algorithm iteratively identifies and removes edges that cannot be present in the optimal solution (Section 3.2). If no further reduction is possible, the residual graph is extracted and updated. Lastly, an IP model is developed based on residual graph, certain valid inequalities (described below) are added, and the model is solved using a standard solver. Next, we describe the algorithm in detail.

3.1. Finding a Lower Bound

The scale reduction algorithm employs a feasible lower bound on the optimal objective value and iteratively identifies edges that cannot be part of the optimal solution. To obtain a lower bound, we find an induced star subgraph of G by applying a simple degree-based greedy heuristic to compute an independent set in the neighborhood of each vertex. The algorithm is outlined in Algorithm 1.

Algorithm 1 Greedy induced star construction heuristic.

1: Initialization: Sort vertices based on non-increasing order of their degree in G; $\mathcal{L}\leftarrow 0$; 2: for $i\leftarrow 1$ to $\left|V\right|$ do 3:  if $|N_G[i]|>\mathcal{L}$ then 4:   $S_i=\{i\}$; 5:   $C_i\leftarrow N_G(i)$; 6:   while $|C_i|>0$ do 7:    $j\leftarrow$ a least degree vertex in $G[C_i]$; 8:    $S_i=S_i\cup \{j\}$; 9:    $C_i=C_i\backslash N_{G[C_i]}[j]$; 10:   end while 11:   if $|S_i|>\mathcal{L}$ then 12:    $\mathcal{L}\leftarrow |S_i|$; 13:   end if 14:  end if 15: end for 16: return $\mathcal{L}$;

The vertices in G are sorted in a non-increasing order of their degrees in the initialization step and the subgraph induced by the neighborhood $C_i$ of each vertex $i\in V$ is then considered. Starting with $S_i=\{i\}$, we recursively add a least degree vertex j from $G[C_i]$ to $S_i$ and update $C_i$ by removing j and its neighbors. The output of this procedure is the number $\mathcal{L}$ of vertices in the induced star subgraph found.

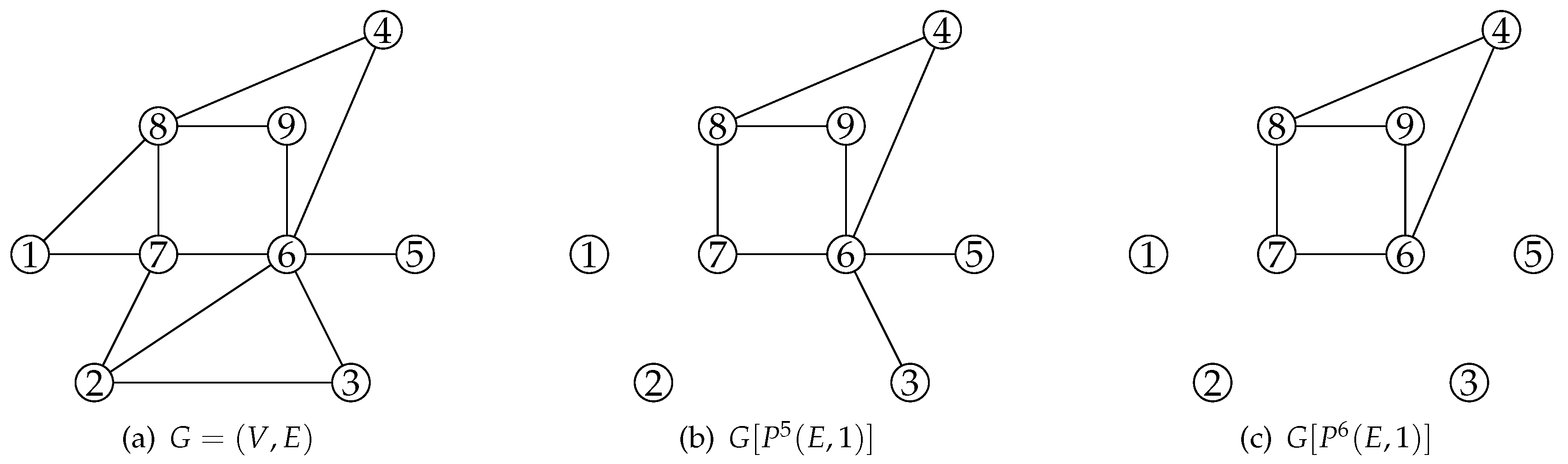
3.2. Scale Reduction Techniques

For $G=(V,E)$, let $G^{\prime }=(V^{\prime },E^{\prime })$ be a subgraph of G induced by a biclique $V^{\prime }=V_1^{\prime }\cup V_2^{\prime }$ with parts $V_1^{\prime }$ and $V_2^{\prime }$, i.e., $V_1^{\prime }$ and $V_2^{\prime }$ are independent sets in G and $E^{\prime }=\{\{i,j\}\in E:i\in V_1^{\prime },j\in V_2^{\prime }\}$. Then $\mathcal{L}=|V_1^{\prime }\cup V_2^{\prime }|$ is a lower bound on the size of a maximum biclique in G. In addition, for any given edge $\{i,j\}\in E^{\prime }$, where $i\in V_1^{\prime }$ and $j\in V_2^{\prime }$, we have $\alpha (G^{\prime }[N(i)])=\left|V_2^{\prime }\right|$ and $\alpha (G^{\prime }[N(j)])=\left|V_1^{\prime }\right|$, so

$$\alpha (G^{\prime }[N(i)])+\alpha (G^{\prime }[N(j)])=|V_1^{\prime }\cup V_2^{\prime }|=|V_1^{\prime }|+|V_2^{\prime }|.$$

3.2.1. Scale Reduction for the MB Problem

For a subset of edges $H\subset E$, the corresponding edge-induced subgraph $G[H]$ of G is given by $G[H]=(V(H),H)$, where $V(H)=\{i\in V:\exists j\in V\mathrm{such}\mathrm{that}\{i,j\}\in H\}$. Consider $G=(V,E)$, a biclique $V^{\prime }$ of size $\mathcal{L}$ in G, a subset of edges $H\subset E$ and induced subgraph $G[H]$. Define the following operator function for $\{u,v\}\in H$:

$$P_G^{\mathcal{L}}(H,\{u,v\})=\left\{\begin{array}{cc}\{u,v\},\hfill & \mathrm{if}\alpha (G[N_{G[H]}(u)\backslash N_G(v)])+\alpha (G[N_{G[H]}(v)\backslash N_G(u)])\ge \mathcal{L},\hfill \\ \varnothing ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(10)

The operator function determines whether two adjacent vertices u and v can be simultaneously included in a biclique with at least $\mathcal{L}$ vertices in $G[H]$. If $P_G^{\mathcal{L}}(H,\{u,v\})=\varnothing$ we will call $\{i,j\}$ a conflict edge with respect to H, since at most one of its two vertices can be included in a biclique with at least $\mathcal{L}$ vertices in $G[H]$. Then

$$P_G^{\mathcal{L}}(H)=\bigcup _{\{u,v\}\in H}{P}_G^{\mathcal{L}}(H,\{u,v\})$$

(11)

gives a subset of edges in H that results from excluding all the conflict edges. This process can be applied recursively until there are no more conflict edges with respect to the remaining set of edges. More formally, for a given lower bound $\mathcal{L}$ and a positive integer k, denote by $P^{\mathcal{L}}(E,k)$ the following recursively defined set:

$$P^{\mathcal{L}}(E,k)=\left\{\begin{array}{cc}{P}_G^{\mathcal{L}}(E),\hfill & \mathrm{if}k=1,\hfill \\ P_G^{\mathcal{L}}(P^{\mathcal{L}}(E,k-1)),\hfill & \mathrm{if}k\ge 2.\hfill \end{array}\right.$$

(12)

For $k\ge 1$, $P^{\mathcal{L}}(E,k)$ is a subset of edges in E that were not labeled as conflict edges during k rounds of the process.

Example 1.

Figure 1 illustrates this process on a 9-vertex graph G with a known biclique (obtained using Algorithm 1) $V^{\prime }=V_1^{\prime }\cup V_2^{\prime }$, where $V_1^{\prime }=\{\mathit{6}\}$ and $V_2^{\prime }=\{\mathit{3},\mathit{4},\mathit{5},\mathit{7},\mathit{9}\}$ giving a lower bound $\mathcal{L}=|V_1^{\prime }\cup V_2^{\prime }|$ = 6 on the size of a MB in G. We find $P^{\mathcal{L}}(E,k)$ for $k=$ 1. For the edge {1, 8}, we have $G[N_G(\mathit{1})\backslash N_G($8$)]=\{\mathit{8}\}$ and $\alpha (G[N_G(\mathit{1})\backslash N_G(\mathit{8})])=1$. Likewise, $G[N_G(\mathit{8})\backslash N_G(\mathit{1})]=\{\mathit{1},\mathit{4},\mathit{9}\}$ and $\alpha (G[N_G(\mathit{8})\backslash N_G(\mathit{1})])=\mathit{3}$. As a result, $\alpha (G[N_G(\mathit{1})\backslash N_G(\mathit{8})])+\alpha (G[N_G(\mathit{8})\backslash N_G(\mathit{1})])=\mathit{4}<\mathcal{L}=\mathit{6}$. Therefore, $P_G^{\mathcal{L}}(E,\{$1, 8$\})=\varnothing$ and {1, 8} is a conflict edge. On the other hand, for {6, 7}, $G[N_G(\mathit{7})\backslash N_G(\mathit{6})]=\{\mathit{1},\mathit{6},\mathit{8}\}$, $G[N_G(\mathit{6})\backslash N_G(\mathit{7})]=\{\mathit{3},\mathit{4},\mathit{5},\mathit{7},\mathit{9}\}$ and $\alpha (G[\{\mathit{1},\mathit{6},\mathit{8}\})+\alpha (G[\{\mathit{3},\mathit{4},\mathit{5},\mathit{7},\mathit{9}\}])=\mathit{7}>\mathcal{L}=\mathit{6}$, so $P_G^{\mathcal{L}}(E,\{$6, 7$\})=\{\mathit{6},\mathit{7}\}$ meaning that the edge {6, 7} is not a conflict edge. After performing the recursive procedure for $k=$ 1 and $k=$ 2, we obtain a graph $G[P^{\mathcal{L}}(E,\mathit{2})]$ with no conflict edges. Clearly, vertices 1, 2 and 8 cannot be a part of a biclique with at least 6 vertices, so they can be permanently removed, and a MB of G must be a part of $G[\{$3, 4, 5, 6, 7, 9$\}]$. Since the latter graph is complete bipartite, its set of vertices is the maximum biclique of G. This shows that our lower bound solution is, in fact, optimal for this graph.

Next, we discuss some properties of the proposed scale reduction process. The following lemma follows directly from the definition of $P^{\mathcal{L}}(E,k)$.

Lemma 1.

Let $V^{\prime }=(V_1^{\prime }\cup V_2^{\prime },E^{\prime })$ and $V^{\ast }=(V_1^{\ast }\cup V_2^{\ast },E^{\ast })$ be bicliques in $G=(V,E)$ with $|V^{\prime }|=\mathcal{L}$, $|V^{\ast }|={\mathcal{L}}^{\ast }$, such that $\mathcal{L}\le {\mathcal{L}}^{\ast }$. Then for any integer $k\ge 1$ the following inclusions hold:

1. 

$P^{{\mathcal{L}}^{\ast }}(E,k+1)\subseteq P^{{\mathcal{L}}^{\ast }}(E,k)\subseteq P^{\mathcal{L}}(E,k).$

2. 

$E^{\ast }\subseteq P^{\mathcal{L}}(E,k)$ for all k.

In particular, this lemma implies that an edge from a subgraph induced by a maximum biclique will never be labeled as a conflict edge during the scale reduction process. Hence, it is tempting to remove all the conflict edges and restrict the search for a maximum biclique to the residual graph. Unfortunately, this cannot always be done since removing a conflict edge may increase the size of a maximum biclique. Consider, for example, a star graph on $n\ge 4$ nodes with an extra edge $\{u,v\}$ between two leaf nodes. Clearly, dropping either u or v gives a maximum biclique on $n-1$ vertices. However, for $\mathcal{L}=n-1$ the scale reduction process will label $\{u,v\}$ as a conflict edge, resulting in $G[P^{\mathcal{L}}(E,1)]$ given by a star on n vertices, which is an n-vertex biclique. On a positive side, it is safe to remove nodes adjacent to conflict edges only, i.e., the nodes that would become isolated if all the conflict edges were removed. This provides basis for the proposed scale reduction technique. The algorithm, outlined in Algorithm 2, proceeds by computing $P^{\mathcal{L}}(E,k)$ until no new edges are labeled as conflict edges, at which point we compute $\widehat{V}=V(G[P^{\mathcal{L}}(E,k)])$, which is the set of vertices in the subgraph induced by non-conflict edges (this essentially removes the vertices that become isolated if all conflict edges are removed). The subgraph induced by $\widehat{V}$ is output as the residual graph.

Algorithm 2 Scale reduction algorithm.

1: Input: $G=(V,E)$, $\mathcal{L}:$ a feasible lower bound 2: $k\leftarrow 1$; 3: $P^{\mathcal{L}}(E,0)=E$; 4: repeat 5:   $k\leftarrow k+1$; 6: until $P^{\mathcal{L}}(E,k)=P^{\mathcal{L}}(E,k-1)$ 7: $\widehat{V}\leftarrow V(G[P^{\mathcal{L}}(E,k)])$; $⊳$ set of vertices of $G[P^{\mathcal{L}}(E,k)]$ 8: return $G[\widehat{V}]$;

Even though not all conflict edges can be removed as a result of the scale reduction procedure, the fact that they cannot be included in a subgraph induced by an optimal biclique can be used to develop optimality cuts and thus strengthen the IP formulation of the MB problem for the residual graph. Indeed, let $\{i,j\}$ be a conflict edge that was included in the residual graph. Since $\{i,j\}$ cannot be included in the optimal solution, at most one of the two vertices i and j can belong to a maximum biclique, and since each vertex can only be in one part of a bipartite clique, it implies that

$$\begin{array}{c}\hfill x_{i1}+x_{i2}+x_{j1}+x_{j2}\le 1\end{array}$$

(13)

for any optimal solution of (1)–(6). The inequality (13) is added to the IP for the residual graph for each remaining conflict edge $\{i,j\}$.

3.2.2. Scale Reduction for the MEB Problem

The scale reduction used for the MEB problem is very similar to the one just described for the MB problem. Given $G=(V,E)$, consider a biclique $V^{\prime }$ of size $\mathcal{L}$ in G, a subset of edges $H\subset E$ and the corresponding induced subgraph $G[H]$. Let

$$\overline{E}(H,\{u,v\})=\{\{i,j\}\in E:i\in N_{G[H]}(u)\backslash N_G(v),j\in N_{G[H]}(v)\backslash N_G(u)\}$$

be the set of edges between $N_{G[H]}(u)\backslash N_G(v)$ and $N_{G[H]}(v)\backslash N_G(u)$ in G. We will abuse the notation to define the analog of operator $P_G^{\mathcal{L}}(H,\{u,v\})$ introduced for the MB problem in (10) as follows:

$$P_G^{\mathcal{L}}(H,\{u,v\})=\left\{\begin{array}{cc}\{u,v\},\hfill & \mathrm{if}min\{|\overline{E}|,A\}\ge \mathcal{L},\hfill \\ \varnothing ,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(14)

where $\overline{E}\equiv \overline{E}(H,\{u,v\})$, $A\equiv \alpha (G[N_{G[H]}(u)\backslash N_G(v)])\times \alpha (G[N_{G[H]}(v)\backslash N_G(u)])$. Whenever we discuss the MB problem, the definition of $P_G^{\mathcal{L}}(H,\{u,v\})$ given in (10) applies, whereas for the MEB problem we will use the definition of $P_G^{\mathcal{L}}(H,\{u,v\})$ from (14). This allows us to use definitions of $P_G^{\mathcal{L}}(H)$ in (11) and $P^{\mathcal{L}}(E,k)$ in (12) for the MEB problem as well. All the properties of the scale reduction process for the MB problem hold for the case of MEB as well. This includes Lemma 1, Algorithm 2, and the Inequality (13), which is now valid for every optimal solution of the MEB Formulation (7)–(9).

Note that in this case the operator function keeps an edge if the minimum among $|\overline{E}|$ and the total possible number of edges between maximum independent sets of $G[N_{G[H]}(u)\backslash N_G(v)]$ and $G[N_{G[H]}(v)\backslash N_G(u)]$, required to form a biclique, is at least $\mathcal{L}$. In practice for sparse networks, it is often sufficient to count the number of edges in $\overline{E}$, which can be done efficiently. We will only need to compute the independence numbers if $|\overline{E}|\ge \mathcal{L}$.

Example 2.

Figure 2 illustrates the process for the same example as in Figure 1. We consider the same lower bound solution $V^{\prime }=V_1^{\prime }\cup V_2^{\prime }$, where $V_1^{\prime }=${6} and $V_2^{\prime }=${3, 4, 5, 7, 9}. This time it yields a lower bound $\mathcal{L}=|V_1^{\prime }|·|V_2^{\prime }|=\mathit{5}$ on the size of a MEB in G. For edge {1, 7}, observe that $G[N_G(\mathit{1})\backslash N_G(\mathit{7})]=${7}, $G[N_G(\mathit{7})\backslash N_G(\mathit{1})]=${1, 2, 6} and $\overline{E}\equiv \overline{E}(E,\{$1, 7$\})=\{\{$1, 7$\},\{$2, 7$\},\{$6, 7$\}\}$, so $|\overline{E}|=\mathit{3}<\mathcal{L}=\mathit{5}$. Therefore, $P_G^{\mathcal{L}}(E,\{$1, 7$\})=\varnothing$. For edge {4, 8}, $G[N_G(\mathit{4})\backslash N_G(\mathit{8})]=${6, 8}, $G[N_G(\mathit{8})\backslash N_G(\mathit{4})]=${1, 4, 7, 9} and $\overline{E}\equiv \overline{E}(E,\{$4, 8$\})=\{\{$4, 6$\},\{$6, 7$\},\{$6, 9$\},\{$1, 8$\},\{$4, 8$\},\{$7, 8$\},\{$8, 9$\}\}$, so $|\overline{E}|=\mathit{7}>\mathcal{L}=\mathit{5}$. Next, we need to compute the independence numbers for $G[\{$6, 8$\}]$ and $G[\{$1, 4, 7, 9$\}]$. We have: $\alpha (G[\{\mathit{6},\mathit{8}\}])=\mathit{2}$, $\alpha (G[\{\mathit{1},\mathit{4},\mathit{7},\mathit{9}\}])=\mathit{3}$. Since $min\{\mathit{7},\mathit{2}\times \mathit{3}\}=\mathit{6}>\mathcal{L}=\mathit{5}$, we obtain $P_G^{\mathcal{L}}(E,\{$4, 8$\})=${4, 8}. After performing the recursive procedure for $k=$ 1, we obtain a graph $G[P^{\mathcal{L}}(E,\mathit{1})]$ with no conflict edges (Figure 2b). Clearly, vertices 1 and 2 cannot be a part of a biclique with at least 5 edges, so they can be permanently removed, and a MEB of G must be a part of $G[\{$3, 4, 5, 6, 7, 8, 9$\}]$.

If we assume that the graph contains a biclique with 6 edges and set the lower bound to $\mathcal{L}=\mathit{6}$, we obtain a graph $G[P^{\mathcal{L}}(E,\mathit{1})]$ with no conflict edges (Figure 2c). Removing the isolated vertices 1, 2, 3 and 5 from this graph we obtain a biclique ({6, 8}, {4, 7, 9}) with 6 edges. This shows that our assumption that there is a biclique with 6 edges in the graph is correct, moreover, the biclique found is the optimal solution for the MEB problem in this instance.

4. Computational Experiments

To evaluate the effectiveness of the proposed methodology, we conducted extensive computational experiments. The proposed approach was implemented in C++. Östergård’s well-known algorithm [39] has been adapted to compute the independence number within the scale reduction procedure. This algorithm was chosen due to its simplicity and effectiveness on instances of small to medium scale, however, it should be noted that other recently developed algorithms, such as MCS [40] could be used instead. To solve the IP model for the residual graph resulting from the scale reduction algorithm, IBM ILOG CPLEX OPTIMIZER 12.6.3^® has been employed with default settings for preprocessing, branching strategy and cutting planes. The proposed method was implemented in C++11 language and compiled using gcc 4.8.1 in Microsoft Visual Studio 2013. All experiments were executed on a 64-bit Windows 7 computer with 2.60 GHz Intel(R) Core(TM) i7-5600U CPU and 16 GB RAM. The total of 33 instances from two different sources were used for the experiments. The first set includes test instances from the Stanford Large Network Dataset Collection (SNAP) and contains both directed and undirected real life instances from collaboration networks, peer-to-peer file sharing and route networks [41]. The directed instances used in the experiments have been converted to undirected instances. The second group of test instances is from the tenth DIMACS implementation challenge [42]. This choice of testbeds is motivated by the fact that many real-life networks have similar structural characteristics (large and sparse), which is also the type of networks our methodology is tailored to. The proposed scale reduction technique is unlikely to be effective in graphs with high edge density because independent sets and lower bound solution for MB and MEB problems in such graphs tend to have small cardinality. As a result, scale reduction is not effective in shrinking the instance size. Other approaches need to be developed to address this case.

The results of computational experiments are reported in

Table 1. Computational results for the MB problem on instances from DIMACS Clustering challenge and Stanford Large Network Dataset Collection (SNAP) dataset.

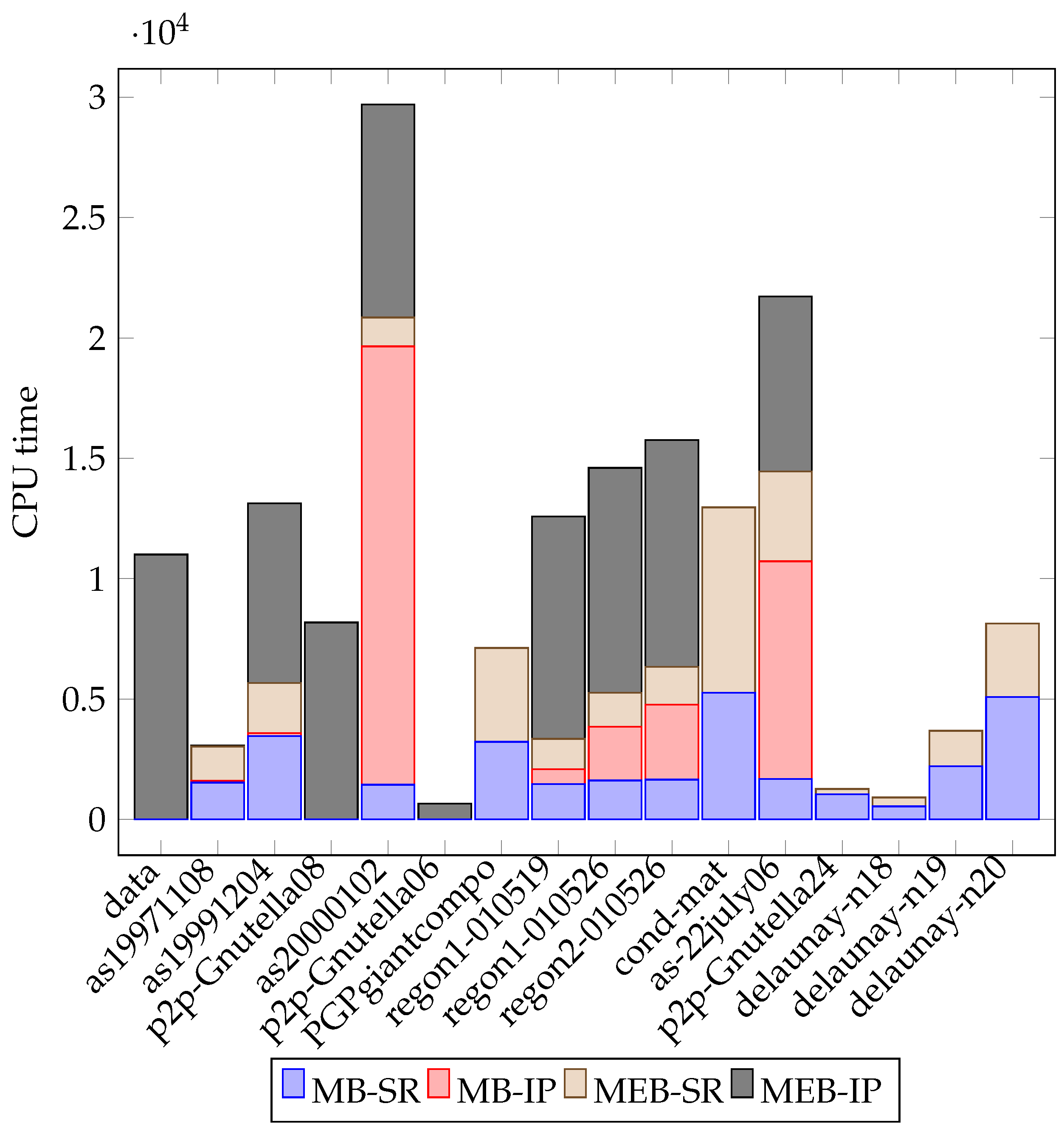
Graph	$\left|\mathit{V}\right|$	$\left|\mathit{E}\right|$	LB	$|{\mathit{V}}^{\prime }|$	$|{\mathit{E}}^{\prime }|$	SR-CPU(s)	Opt. Obj.	CPU (s)
jazz	198	2742	18	85	704	0.44	20	0.67
email	1133	5451	34	35	35	0.61	34	0.64
netscience	1589	2742	16	26	42	0.02	16	0.03
add20	2395	7462	30	68	186	464.66	30	464.73
data	2851	15,093	8	41	99	1.09	8	1.36
as19971108	3015	5347	540	583	740	1531.77	540	1602.59
add32	4960	9462	16	66	108	0.17	16	0.42
CA-GrQC	5242	14,490	29	35	41	0.39	29	0.42
as19991204	6296	12,830	1294	1407	2234	3461.69	1294	3582.89
p2p-Gnutella08	6301	20,777	88	88	87	1.36	88	1.48
as20000102	6474	13,233	1338	1454	2430	1440.82	1340	19,645.00
p2p-Gnutella09	8114	26,013	98	98	97	1.09	98	1.47
hep-th	8361	15,751	22	81	151	0.40	23	0.66
p2p-Gnutella06	8717	31,525	104	113	121	0.21	104	0.44
p2p-Gnutella05	8846	31,839	87	88	88	0.76	87	1.11
CA-HepTH	9877	25,973	32	43	59	4.18	32	4.42
PGPgiantcompo	10,680	24,316	105	114	122	3223.57	105	3223.85
p2p-Gnutella04	10,876	39,994	97	100	102	0.12	97	0.42
oregon1-010519	11,051	22,724	2203	2384	4289	1466.45	2207	2085.01
oregon1-010526	11,173	23,409	2199	2385	4308	1619.41	2203	3852.24
oregon2-010526	11,460	16,365	2230	2428	4676	1652.65	2234	4762.25
cond-mat	16,726	47,594	41	55	72	5257.99	41	5258.05
p2p-Gnutella25	22,687	54,705	64	66	67	0.22	64	0.33
as-22july06	22,963	48,436	2243	2387	4125	1678.23	2245	10,722.34
p2p-Gnutella24	26,518	65,369	304	356	426	1040.93	304	1043.72
p2p-Gnutella30	36,682	88,328	54	54	53	0.59	54	0.70
p2p-Gnutella31	62,586	147,892	90	95	100	0.41	90	0.70
delaunay-n14	16,384	49,122	9	26	39	4.15	9	4.23
delaunay-n16	65,536	196,575	9	18	34	61.05	9	61.13
delaunay-n17	131,072	393,176	9	67	123	243.29	10	244.00
delaunay-n18	262,144	786,396	11	65	123	541.73	12	542.29
delaunay-n19	524,288	1,572,823	11	54	92	2205.50	11	2206.09
delaunay-n20	1,048,576	3,145,686	12	24	45	5086.75	13	5087.06

and

Table 2. Computational results for the MEB problem on instances from DIMACS Clustering challenge and SNAP dataset.

Graph	$\left|\mathit{V}\right|$	$\left|\mathit{E}\right|$	LB	$|{\mathit{V}}^{\prime }|$	$|{\mathit{E}}^{\prime }|$	SR-CPU(s)	Opt. Obj.	CPU (s)
jazz	198	2742	17	85	704	0.67	19	2.67
email	1133	5451	33	35	35	1.42	33	1.45
netscience	1589	2742	15	26	42	0.01	15	0.03
add20	2395	7462	29	68	186	306.95	29	307.45
data	2851	15,093	7	1944	11,290	0.78	-	>11,000
as19971108	3015	5347	539	583	740	1430.57	539	1462.28
add32	4960	9462	15	66	108	0.17	15	0.89
CA-GrQC	5242	14,490	28	35	41	0.47	28	0.51
as19991204	6296	12,830	1293	1407	2234	2081.83	1293	9542.64
p2p-Gnutella08	6301	20,777	87	448	3194	9.19	87	8177.89
as20000102	6474	13,233	1337	1454	2430	1201.03	1339	10,044.40
p2p-Gnutella09	8114	26,013	97	98	97	12.37	97	12.51
hep-th	8361	15,751	21	81	151	0.50	22	1.26
p2p-Gnutella06	8717	31,525	103	305	1283	2.53	138	654.47
p2p-Gnutella05	8846	31,839	86	136	203	5.74	92	8.38
CA-HepTH	9877	25,973	31	43	59	6.19	31	6.51
PGPgiantcompo	10,680	24,316	104	114	122	3899.91	104	3900.27
p2p-Gnutella04	10,876	39,994	96	100	102	0.56	96	0.78
oregon1-010519	11,051	22,724	2202	2384	4289	1262.38	2206	10,494.20
oregon1-010526	11,174	23,409	2198	2385	4308	1415.75	2202	10,750.50
oregon2-010526	11,460	16,365	2229	2428	4676	1579.16	-	>11,000
cond-mat	16,726	47,594	40	55	72	7703.95	40	7704.02
p2p-Gnutella25	22,687	54,705	63	66	67	0.31	63	0.44
as-22july06	22,963	48,436	2242	2387	4125	3735.30	-	>11,000
p2p-Gnutella24	26,518	65,369	303	356	426	220.50	303	225.52
p2p-Gnutella30	36,682	88,328	53	54	53	2.06	53	2.12
p2p-Gnutella31	62,586	147,892	89	95	100	0.98	89	1.30
delaunay-n14	16,384	49,122	8	26	39	5.57	8	5.70
delaunay-n16	65,536	196,575	8	18	34	80.41	8	80.54
delaunay-n17	131,072	393,176	8	67	123	315.68	9	316.55
delaunay-n18	262,144	786,396	10	65	123	373.68	11	374.53
delaunay-n19	524,288	1,572,823	10	54	92	1478.44	10	1479.16
delaunay-n20	1,048,576	3,145,686	11	24	45	3044.67	12	3045.02

. The columns of these tables show the graph’s name (“Graph”), number of vertices (“$\left|V\right|$”), number of edges (“$\left|E\right|$”), the objective value of a solution found using the heuristic described in Algorithm 1 (“LB”), the number of vertices (“$|V^{\prime }|$”) and edges (“$|E^{\prime }|$”) in the residual graph obtained after applying the scale reduction procedure described in Algorithm 2, the time solely used by the scale reduction procedure (“SR-CPU(s)”) in CPU seconds, the optimal objective value (“Opt. Obj.”), and, finally, the total time, in CPU seconds, used to solve the corresponding instance (“CPU(s)”). The last figure includes the time taken by the scale reduction procedure.

Note that since the greedy induced star construction heuristic was used to find an initial solution for both the MB and MEB problems, the lower bound values always differ by 1 (for a star on k vertices, the corresponding lower bounds for MB and MEB objective values are k and $(k-1)\times 1=k-1$, respectively). Comparing the size of the original and residual graphs in each of the test cases shows that scale reduction technique is successful in shrinking the instance size, which is essential for applicability of the IP-based approach. Also, in all but four instances (“data”, “p2p-Gnutella08”, “p2p-Gnutella06”, and “p2p-Gnutella05”) the scale reduction process yielded the same residual graph for both problems. The most dramatic difference in effectiveness of the scale reduction process was observed for the “data” graph. In this case, the MB residual graph had only 41 vertices and 99 edges, while the MEB residual graph had 1944 vertices and 11,290 edges. As a result, we were not able to solve the MEB problem for this instance within the 11,000-s time limit (The 11,000-s time limit for the MEB problem was chosen based on the results obtained for the MB problem, for which all but one instances were solved in under 11,000 s, while one instance took over 19,000 s). This was also the case with two other instances, “oregon2-010526” and “as-22july06” for the MEB problem. All other instances of both MB and MEB problems were solved to optimality, and in all but four cases the MB problem was solved faster than the MEB problem. This is not surprising, since the residual graph is always at least as large for MEB as it is for MB, and the IP formulation for MEB has more variables and constraints.

The CPU times taken by the scale reduction and IP steps of the exact approaches are illustrated in Figure 3 for 16 instances for which at least one of the four times (scale reduction for MB (MB-SR), IP solution for MB (MB-IP), scale reduction for MEB (MEB-SR), or IP solution for MB (MEB-IP)) exceeded 500 s. It can be seen that for 7 of these instances MEB-IP takes the longest, while MB-IP is the most time-consuming step for 2 more instances. The scale reduction techniques dominate the CPU time taken for the remaining 7 instances. Not surprisingly, the construction heuristic yielded optimal solutions for both the MB and MEB problems for 5 of these 7 instances, and was just short of optimum by 1 unit in the remaining two cases. For all these cases, the scale reduction procedure outputs a small residual graph that is easily handled by CPLEX.

It should be noted that the lower bound heuristic yielded optimal solution in most cases (23 and 20 out of 33 instances for the MB and MEB problems, respectively) and close to optimal solution in most of the remaining cases. This shows that the optimal bicliques tend to have a star structure and can often be found by analyzing the neighborhoods of individual vertices. The only two exceptions were “p2p-Gnutella06” and “p2p-Gnutella05” networks. The optimal MEB solutions for these instances had parts consisting of 23 and 6 vertices (yielding $23\times 6=138$ edges) and 46 and 2 vertices ($46\times 2=92$ edges), respectively. Observe that despite a relatively large gap between the optimal objective value and the heuristic lower bound, the combination of the scale reduction and the IP-based approach was quite effective in finding optimal solution for both of these instances.

On the one hand, the observation that the optimal induced bicliques in real-life networks often correspond to star graphs can be used as yet another evidence of “global structural imbalance” in the so-called scale-free networks, which typically have a few high degree, and a large number of low-degree vertices. On the other hand, this motivates using bipartite and multipartite versions of clique relaxation models, such as s-plexes, s-defective cliques, and $\gamma$-quasicliques, which allow some missing edges between the parts and hence are less restrictive [43].

5. Conclusions

In this paper, we proposed a scale reduction technique for the MB and MEB problems, which can be used to expand the applicability of exact algorithms for this problem to larger instances. Through experiments with 33 real-life instances with the number of vertices ranging from 198 to 1,048,576, we have shown that the proposed method is very effective in reducing the considered instances to scales that can be handled by modern mixed integer programming (MIP) solvers. To further improve the IP solution time, one could perform a polyhedral study, explore and exploit the symmetries in the IP formulations, as well as take advantage of the high-quality heuristic solutions for warm-starting the MIP solvers. In addition, the proposed scale-reduction schemes with $\mathcal{L}$ values high enough to yield the empty edge set in the residual graph could be used to obtain upper bounds on the MB and MEB size, as it was successfully done in [32] for the maximum clique problem.

In terms of the structure of the obtained optimal solutions, we observe that oftentimes optimal bicliques in real-life networks induce star subgraphs, which, on the one hand can be thought of as a global structural characteristic of scale-free networks, but on the other hand, may make one question the practicality of searching for maximum bicliques in the context of complex network analysis, where the instances are typically very sparse. These models may be more practical on denser networks, however, the proposed scale reduction technique will not be applicable in this case, calling for alternative solution methods, such as a combinatorial branch-and-bound method similar to RDS [29,44]. As noted above, RDS is not directly applicable due to the lack of heredity property, however, it can be modified to address the cases when heredity is violated. Other, more practical alternatives of bicliques that would be interesting to consider in future research are bipartite and multipartite versions of clique relaxations [43].