Determination of Specific Heat Capacity on Composite Shape-Stabilized Phase Change Materials and Asphalt Mixtures by Heat Exchange System
Abstract
:1. Introduction
2. Materials
3. Experiment Methods
3.1. Heat Exchange Test
3.1.1. Principle and Determination of Specific Heat Capacity
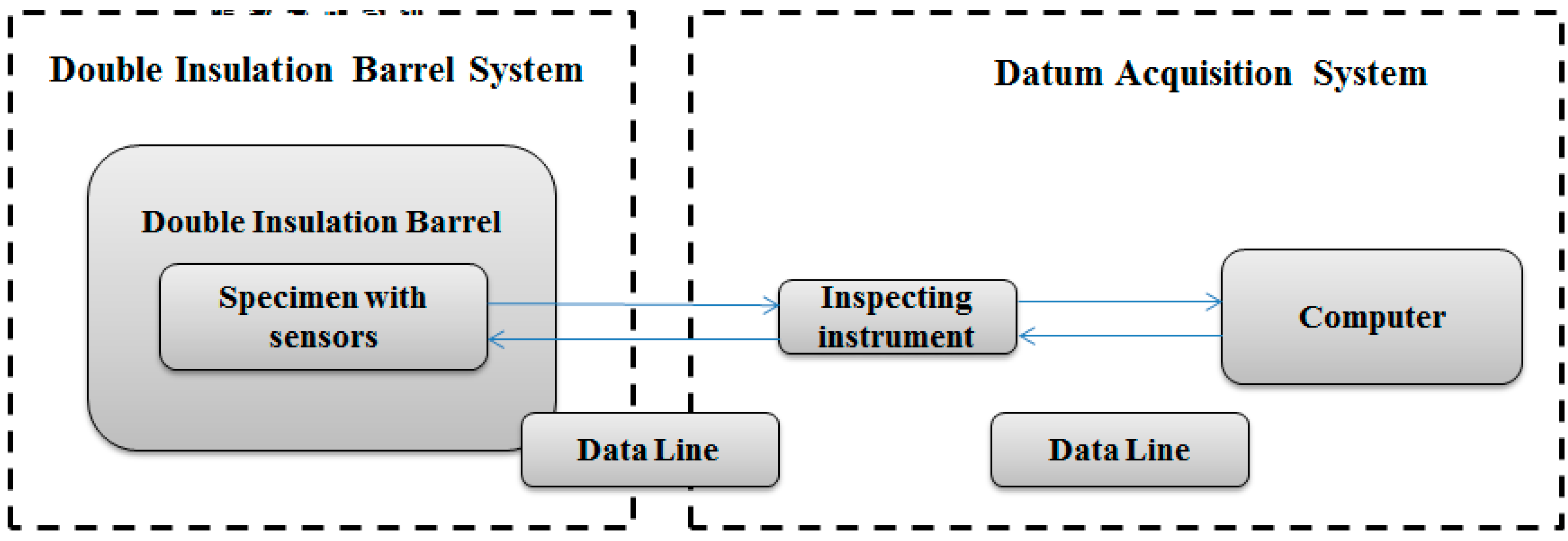
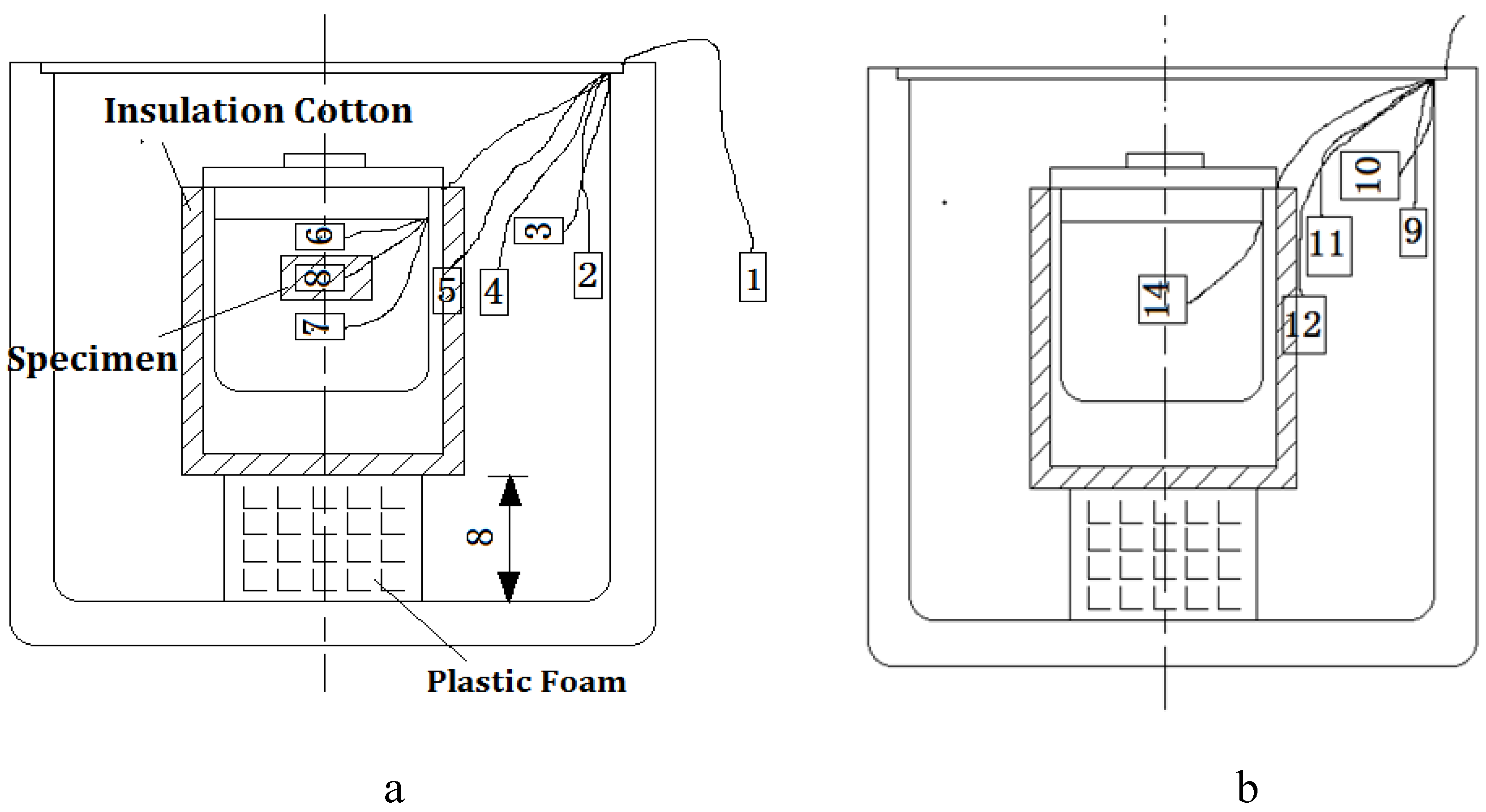
3.1.2. Heat Exchange Test Equipment
3.1.3. Measuring Method of Real-Time Temperature
- (1)
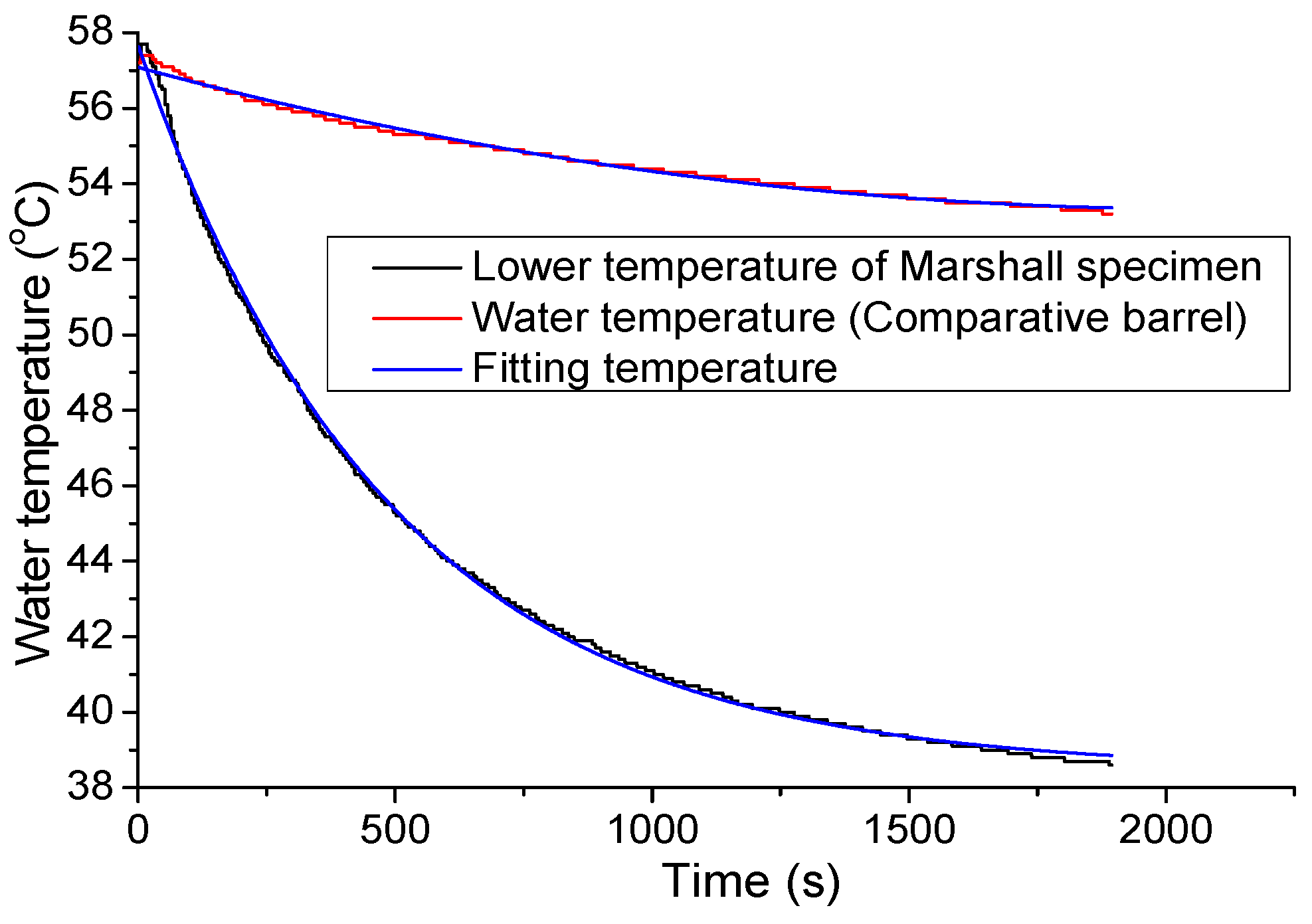
- The heat exchange barrel was used to exchange heat from a high temperature object to a low temperature object; the comparative barrel was applied to correct the temperature loss caused by the system during the heating process.In Figure 5, sensor 1 was used to observe the temperature of the environment, sensor 2 and sensor 9 were used to observe the internal wall temperature of the two big insulation barrels, sensor 3 and sensor 10 were used to observe the cavity temperature of the two insulation barrel systems, sensor 6 and sensor 7 were used to observe the upper and lower temperature of the heat exchange barrel, sensor 14 was used to observe water temperature of the comparative barrel, and sensor 8 was used to observe the central temperature of the tested specimen.
- (2)
- After placing the temperature sensors correctly, a certain quantity of hot water at 60 °C was poured into the two little insulation barrels, successively and quickly.
- (3)
- Next, the specimen was placed into the little insulation barrel of the heat exchange barrel, then sealed and put into the big insulation barrel.
- (4)
- The heat exchange process finished when the water temperature was equal to the specimen’s temperature.
- (5)
- Finally, data were extracted from the computer to analyze the temperature change behaviors and calculate the specific heat capacity using Equation (3).
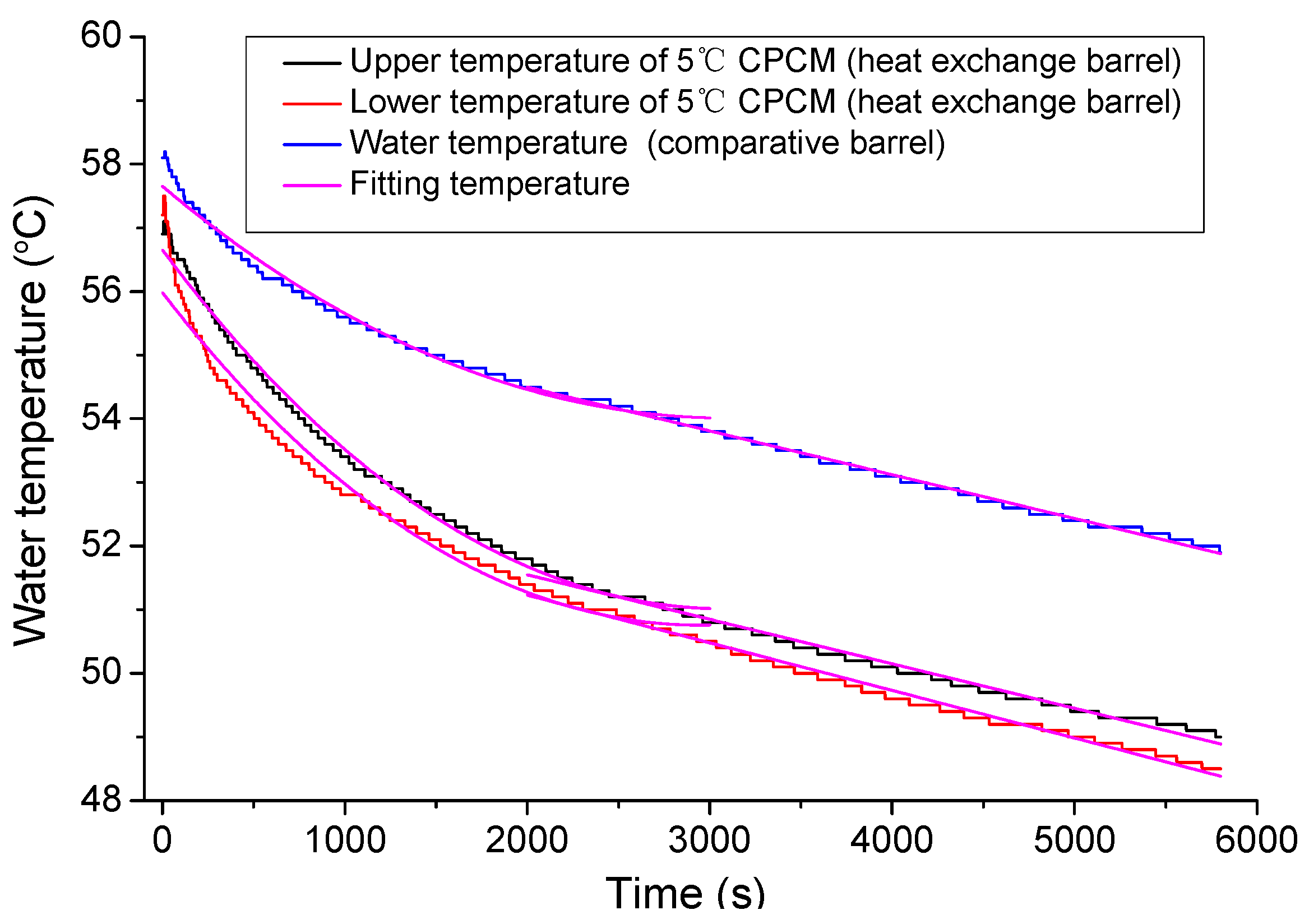
3.2. Water Temperature Correction
3.3. Experiment Plan
4. Results and Analysis
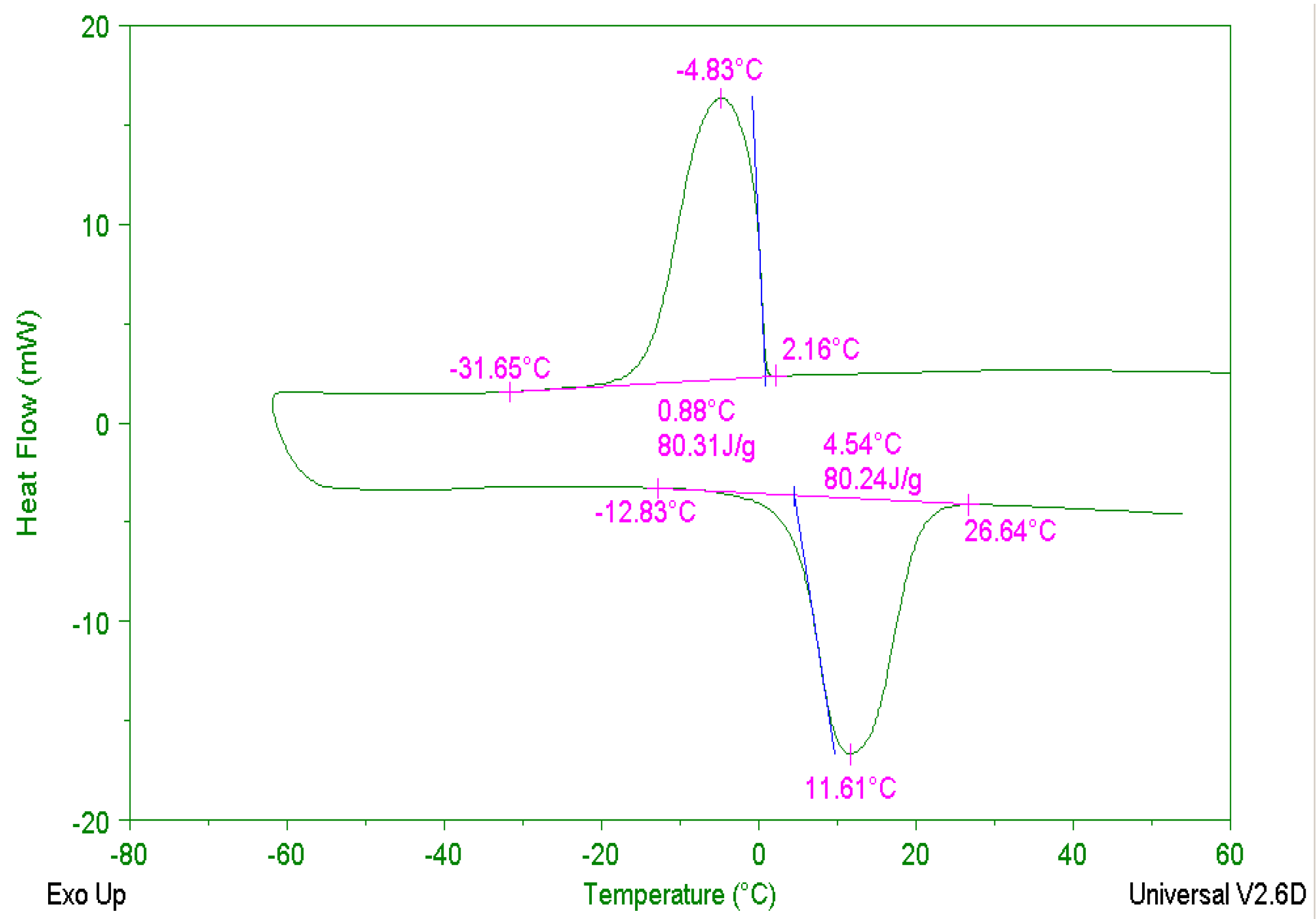
4.1. Results and Analysis of 5 °C CPCM Specimen
4.1.1. Temperature Changing Behaviors of 5 °C CPCM Specimen
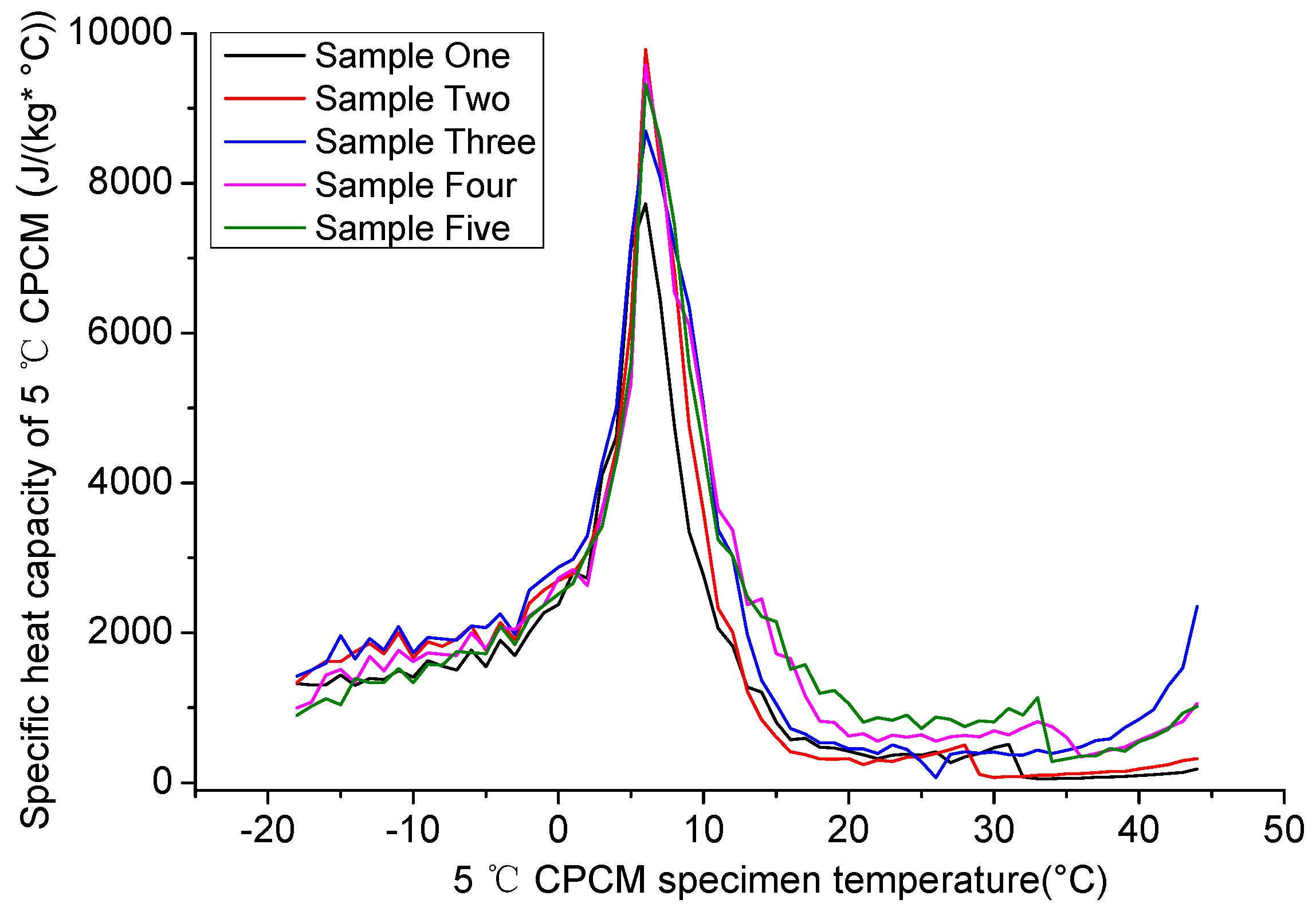
4.1.2. Specific Heat Capacity of 5 °C CPCM Specimen
4.1.3. Recommended Parameters of 5 °C CPCM Specimen Specific Heat Capacity
4.2. Results and Analysis of Asphalt Mixture Mixed with 5 °C CPCM
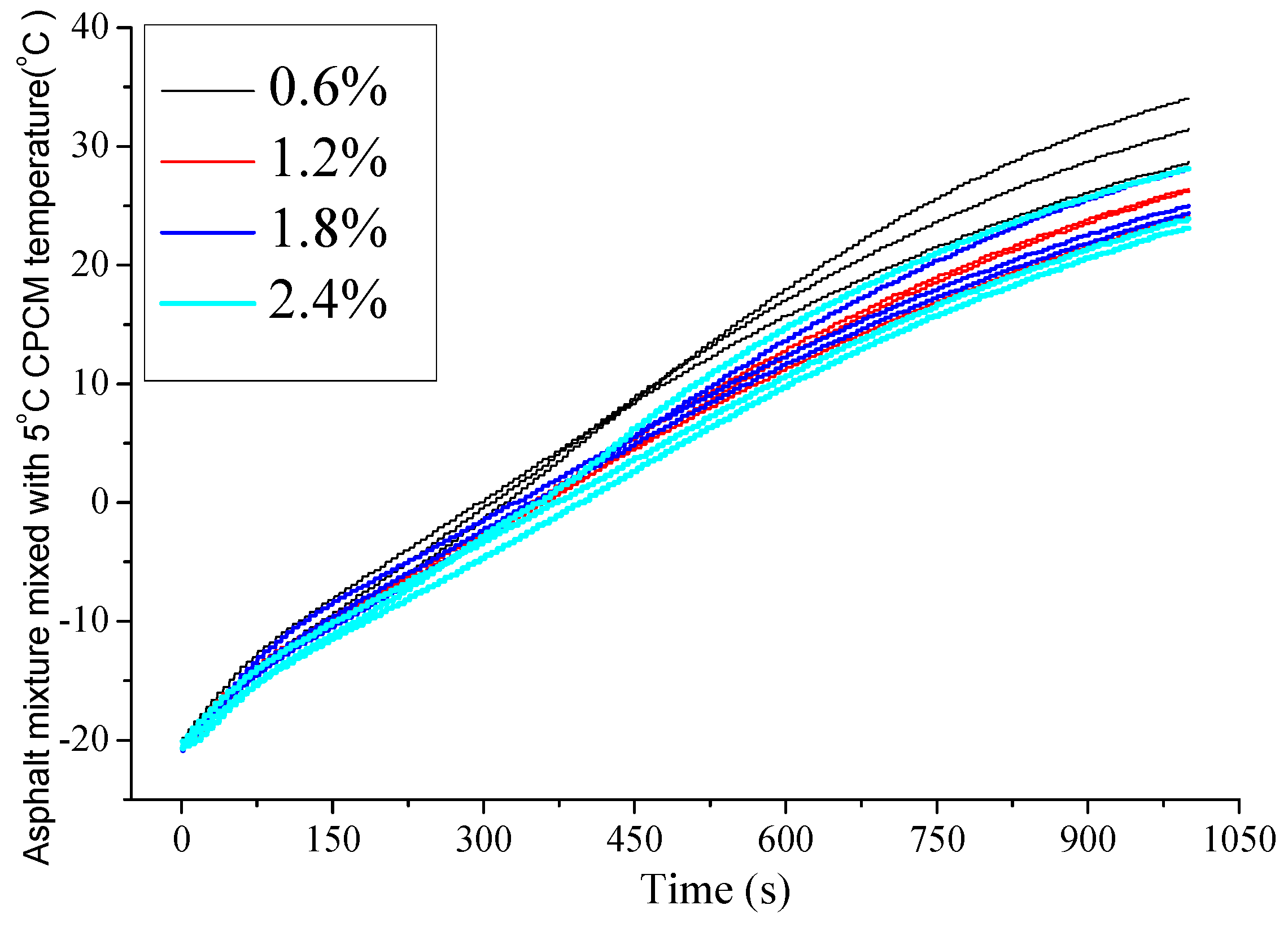
4.2.1. Temperature Changing Behaviors of Asphalt Mixture Mixed with 5 °C CPCM
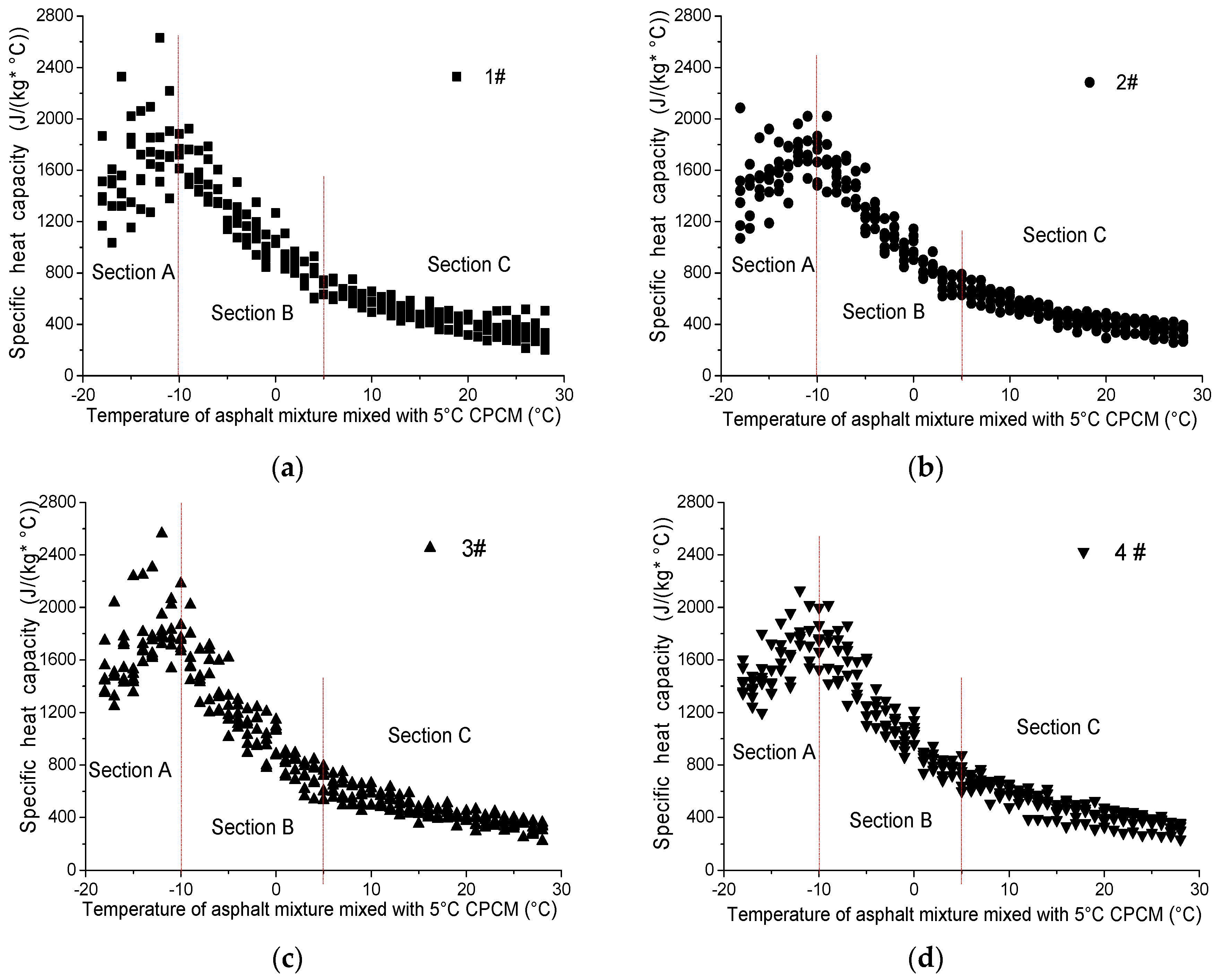
4.2.2. Specific Heat Capacity of Asphalt Mixture Mixed with 5 °C CPCM
4.2.3. Recommended Parameters of Asphalt Mixture Mixed with 5 °C CPCM
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yoder, E.J.; Witzak, M.W. Principles of Pavement Design; Wiley and Sons: New York, NY, USA, 1975. [Google Scholar]
- Huang, Y.H. Pavement Analysis and Design, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Zhang, D.L. Asphalt Pavement; China Communications Press: Beijing, China, 1999. [Google Scholar]
- Stritih, U. An experimental study of enhanced heat transfer in rectangular PCM thermal storage. Int. J. Heat Mass Trans. 2004, 47, 2841–2847. [Google Scholar] [CrossRef]
- Trp, A. An experimental and numerical investigation of heat transfer during technical grade paraffin melting and solidification in a shell-and-tube latent thermal energy storage unit. Sol. Energy 2005, 79, 648–660. [Google Scholar] [CrossRef]
- Wei, J.; Kawaguchi, Y.; Hirano, S.; Takeuchi, H. Study on a PCM heat storage system for rapid heat supply. Appl. Therm. Eng. 2005, 25, 2903–2920. [Google Scholar] [CrossRef]
- Ma, B.; Wang, S.; Li, J. Study on application of PCM in asphalt mixture. Adv. Mater. Res. 2011, 168–170, 2625–2630. [Google Scholar] [CrossRef]
- Si, W.; Ma, B.; Li, N.; Ren, J.; Wang, H. Reliability-based assessment of deteriorating performance to asphalt pavement under freeze-thaw cycles in cold regions. Constr. Build. Mater. 2014, 68, 572–579. [Google Scholar] [CrossRef]
- Ma, B.; Li, J.; Liu, R.; Ma, J. Study on road performance of phase-change temperature-adjusting asphalt mixture. Adv. Mater. Res. 2011, 287, 978–981. [Google Scholar] [CrossRef]
- Ma, B.; Li, J.; Wang, X.; Xiao, N. Effect of composite shape-stabilized phase change material on asphalt mixture temperature. Adv. Mater. Res. 2011, 311, 2151–2154. [Google Scholar] [CrossRef]
- Ma, B.; Si, W.; Ren, J.; Wang, H.; Liu, F.; Li, J. Exploration of road temperature-adjustment material in asphalt mixture. Road Mater. Pavement 2014, 15, 659–673. [Google Scholar] [CrossRef]
- Ma, B.; Adhikari, S.; Chang, Y.; Ren, J.; Liu, J.; You, Z. Preparation of composite shape-stabilized phase change materials for highway pavements. Constr. Build. Mater. 2013, 42, 114–121. [Google Scholar] [CrossRef]
- Ma, B.; Ma, J.; Wang, D.; Peng, S. Preparation and properties of composite shape-stabilized phase change material for asphalt mixture. AMM 2011, 71, 118–121. [Google Scholar] [CrossRef]
- Si, W.; Zhou, X.; Ma, B.; Li, N. The mechanism of different thermoregulation types of composite shape-stabilized phase change materials used in asphalt pavement. Constr. Build. Mater. 2015, 98, 547–558. [Google Scholar] [CrossRef]
- Alvarado, J.; Marsh, C.; Sohn, C.; Vilceus, M.; Hock, V.; Phetteplace, G.; Newell, T. Characterization of super cooling suppression of microencapsulated phase change material by using DSC. Therm. Anal. Calorim. 2006, 86, 505–509. [Google Scholar] [CrossRef]
- Cemil, A.; Ahmet, S.; Ali, K.; Orhan, U. Preparation, characterization, and thermalproperties of microencapsulated phase change material for thermal energy storage. Sol. Energy Mater. Sol. Cells 2009, 93, 143–147. [Google Scholar]
- He, B.; Martin, V.; Setterwall, F. Liquid-solid phase equilibrium study of tetradecane and hexadecane binary mixtures as phase change materials (PCMs) for comfort cooling storage. Fluid Phase Equilibr. 2003, 212, 97–109. [Google Scholar] [CrossRef]
- Peck, J.H.; Kim, J.-J.; Kang, C.; Hong, H. A study of accurate latent heatmcasurement for a PCM with a low melting temperature using t-history method. Int. J. Refrig. 2006, 29, 1225–1232. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.; Jiang, Y. A simple method, the -history method, of determining the heat of fusion, specific heat and thermal conductivity of phase-change materials. Meas. Sci. Technol. 1999, 10, 201. [Google Scholar]
- Yang, S. General Physics Experiment; Higher Education Press: Beijing, China, 1982; pp. 223–228. [Google Scholar]
- Tan, J.; Zhang, H. University Physics Experiment; Beijing University of Posts and Telecommunications Press: Beijing, China, 2006. [Google Scholar]
- Hong, H.; Park, C.H.; Choi, J.H.; Peck, J.H. Improvement of the t-history method to measure heat of fusion for phase change materials. J. Air-Cond. Ref. 2003, 11, 32–39. [Google Scholar]
- Zhang, D.; Li, K. Testing methods of thermal property of phase change materials. Mater. Rev. 2007, 12, 103–106. [Google Scholar]
- Research Institute of Highway Ministry of Transport. Technical Specification for Construction of Highway Asphalt Pavements; China Communications Press: Beijing, China, 2004. [Google Scholar]
- Research Institute of Highway Ministry of Transport. Standard Methods of Bitumen and Bituminous Mixture for Highway Engineering; China Communications Press: Beijing, China, 2009. [Google Scholar]



| Temperature | Water Cp Values |
|---|---|
| 0 °C | 4212 J/(kg·°C) |
| 20 °C–60 °C | 4179 J/(kg·°C) |
| 100 °C | 4220 J/(kg·°C) |
| c = b + kT | y Intercept | Slope | R2 | F | P | ||
|---|---|---|---|---|---|---|---|
| b | σ | k | σ | ||||
| 0.6% | 2266.25306 | 98.88348 | 45.34586 | 6.98557 | 0.64140 | 42.13775 | 1.5718E-6 |
| 1.2% | 2192.90216 | 71.85695 | 42.42836 | 4.90949 | 0.73918 | 74.68605 | 5.58995E-9 |
| 1.8% | 2000.60122 | 78.97311 | 47.90939 | 5.48087 | 0.71288 | 72.43339 | 5.14278E-9 |
| 2.4% | 2250.58206 | 56.12908 | 46.13190 | 4.36640 | 0.81838 | 80.91606 | 1.0 0332E-8 |
| c = b + kT | y Intercept | Slope | R2 | F | P | ||
|---|---|---|---|---|---|---|---|
| b | σ | k | σ | ||||
| 0.6% | 1007.76487 | 14.55219 | −67.51472 | 2.75011 | 0.8775 | 602.69612 | 0 |
| 1.2% | 982.59219 | 12.80987 | −69.688 | 2.42084 | 0.89124 | 828.67598 | 0 |
| 1.8% | 889.48133 | 21.90015 | −72.15694 | 4.13874 | 0.85834 | 603.96246 | 0 |
| 2.4% | 995.88062 | 22.68982 | −72.37224 | 4.28797 | 0.85024 | 584.86557 | 0 |
| c = b + kT | y Intercept | Slope | R2 | F | P | ||
|---|---|---|---|---|---|---|---|
| b | σ | k | σ | ||||
| 0.6% | 742.48076 | 12.11364 | −16.21584 | 0.68991 | 0.8375 | 552.45665 | 0 |
| 1.2% | 698.87274 | 10.66406 | −13.62437 | 0.58443 | 0.80191 | 543.46803 | 0 |
| 1.8% | 617.33916 | 10.80598 | −11.88699 | 0.60392 | 0.84478 | 487.42904 | 0 |
| 2.4% | 751.29099 | 17.39458 | −15.88174 | 0.93331 | 0.83264 | 389.56278 | 0 |
| c = b + kT | y Intercept | Slope |
|---|---|---|
| Section A | 2177.585 | 45.454 |
| Section B | 968.930 | −70.433 |
| Section C | 702.496 | V14.402 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, B.; Zhou, X.-y.; Liu, J.; You, Z.; Wei, K.; Huang, X.-f. Determination of Specific Heat Capacity on Composite Shape-Stabilized Phase Change Materials and Asphalt Mixtures by Heat Exchange System. Materials 2016, 9, 389. https://doi.org/10.3390/ma9050389
Ma B, Zhou X-y, Liu J, You Z, Wei K, Huang X-f. Determination of Specific Heat Capacity on Composite Shape-Stabilized Phase Change Materials and Asphalt Mixtures by Heat Exchange System. Materials. 2016; 9(5):389. https://doi.org/10.3390/ma9050389
Chicago/Turabian StyleMa, Biao, Xue-yan Zhou, Jiang Liu, Zhanping You, Kun Wei, and Xiao-feng Huang. 2016. "Determination of Specific Heat Capacity on Composite Shape-Stabilized Phase Change Materials and Asphalt Mixtures by Heat Exchange System" Materials 9, no. 5: 389. https://doi.org/10.3390/ma9050389
APA StyleMa, B., Zhou, X.-y., Liu, J., You, Z., Wei, K., & Huang, X.-f. (2016). Determination of Specific Heat Capacity on Composite Shape-Stabilized Phase Change Materials and Asphalt Mixtures by Heat Exchange System. Materials, 9(5), 389. https://doi.org/10.3390/ma9050389







