One-Dimensional Four-Layered Photonic Heterostructures: Analysis of Transmittance
Abstract
1. Introduction
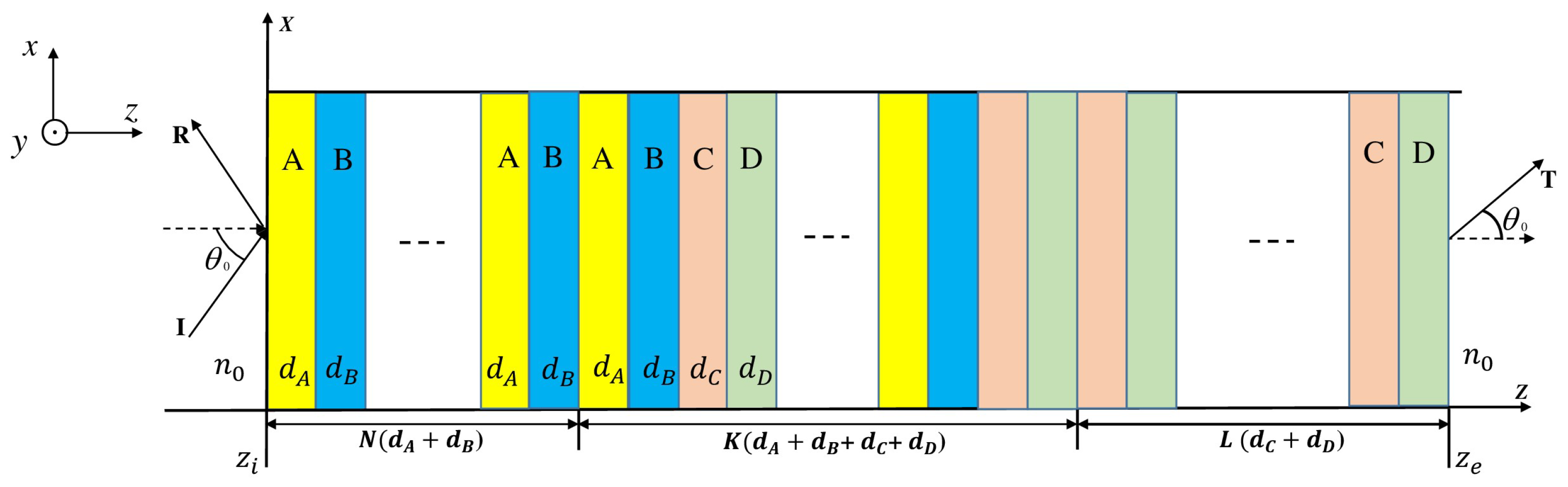
2. Transfer Matrix Method for Photonic Crystal Heterostructures
3. Numerical Results and Discussion
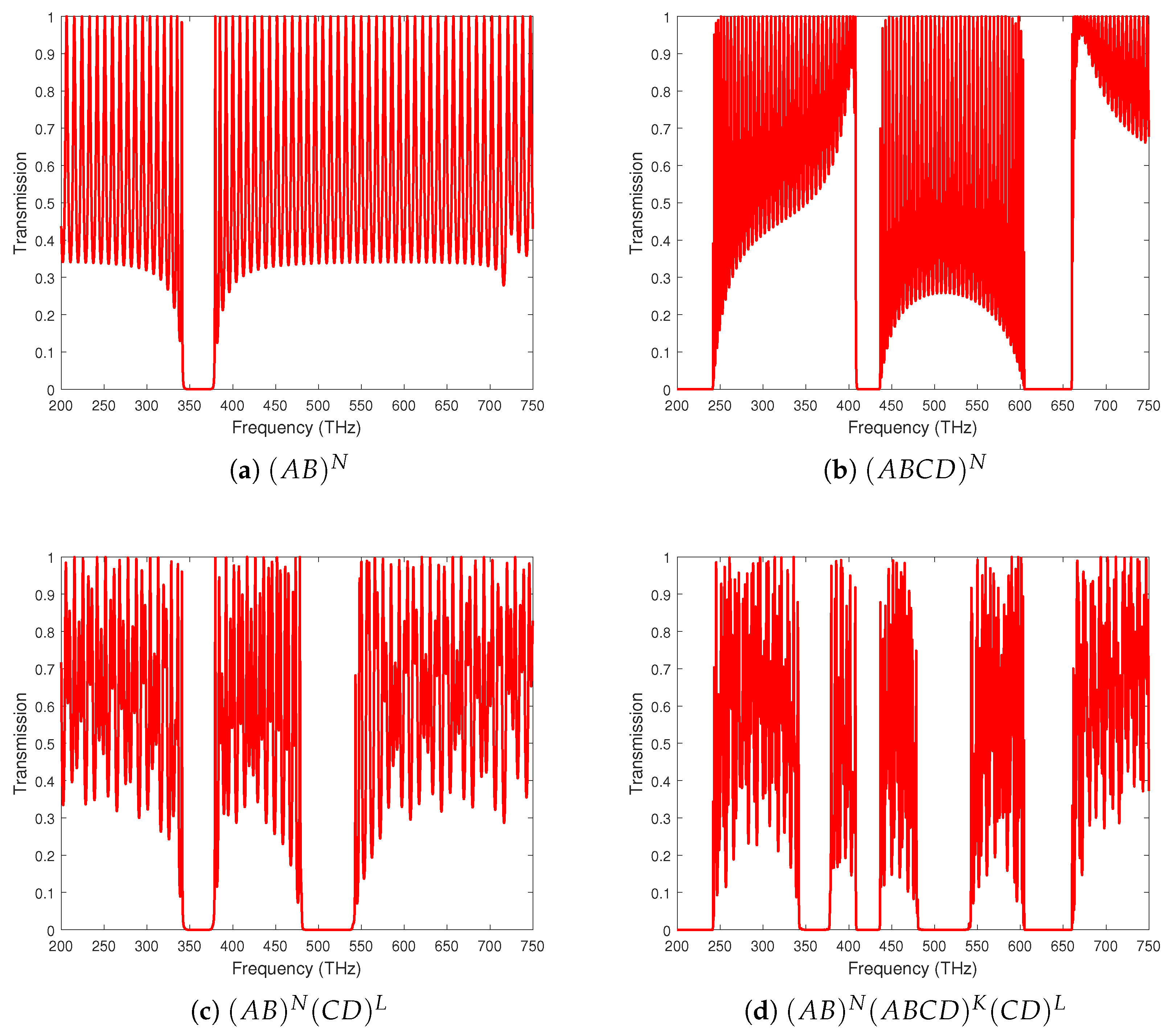
3.1. Effect of Composite Dielectrics
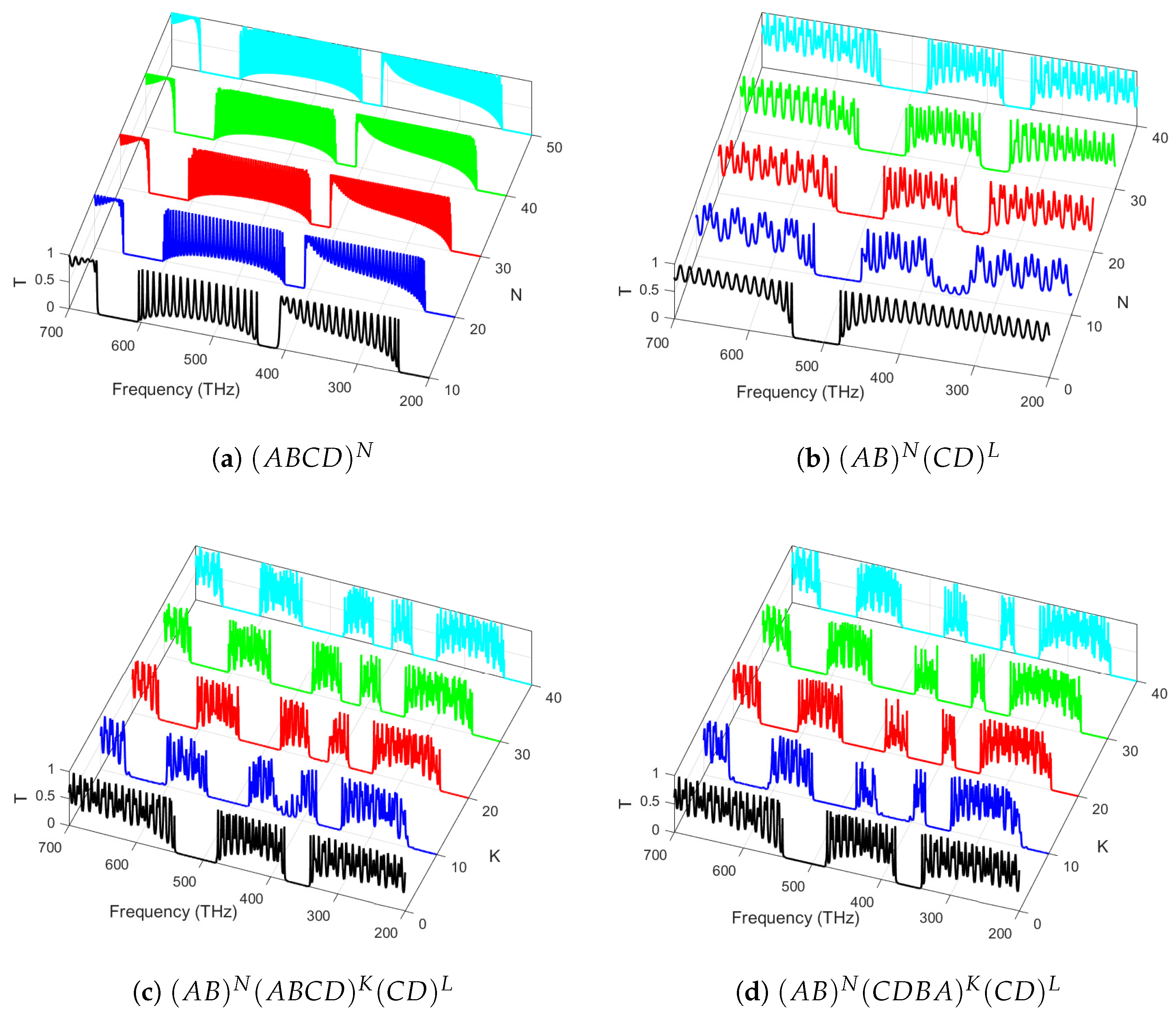
3.2. Effect of Periodicity
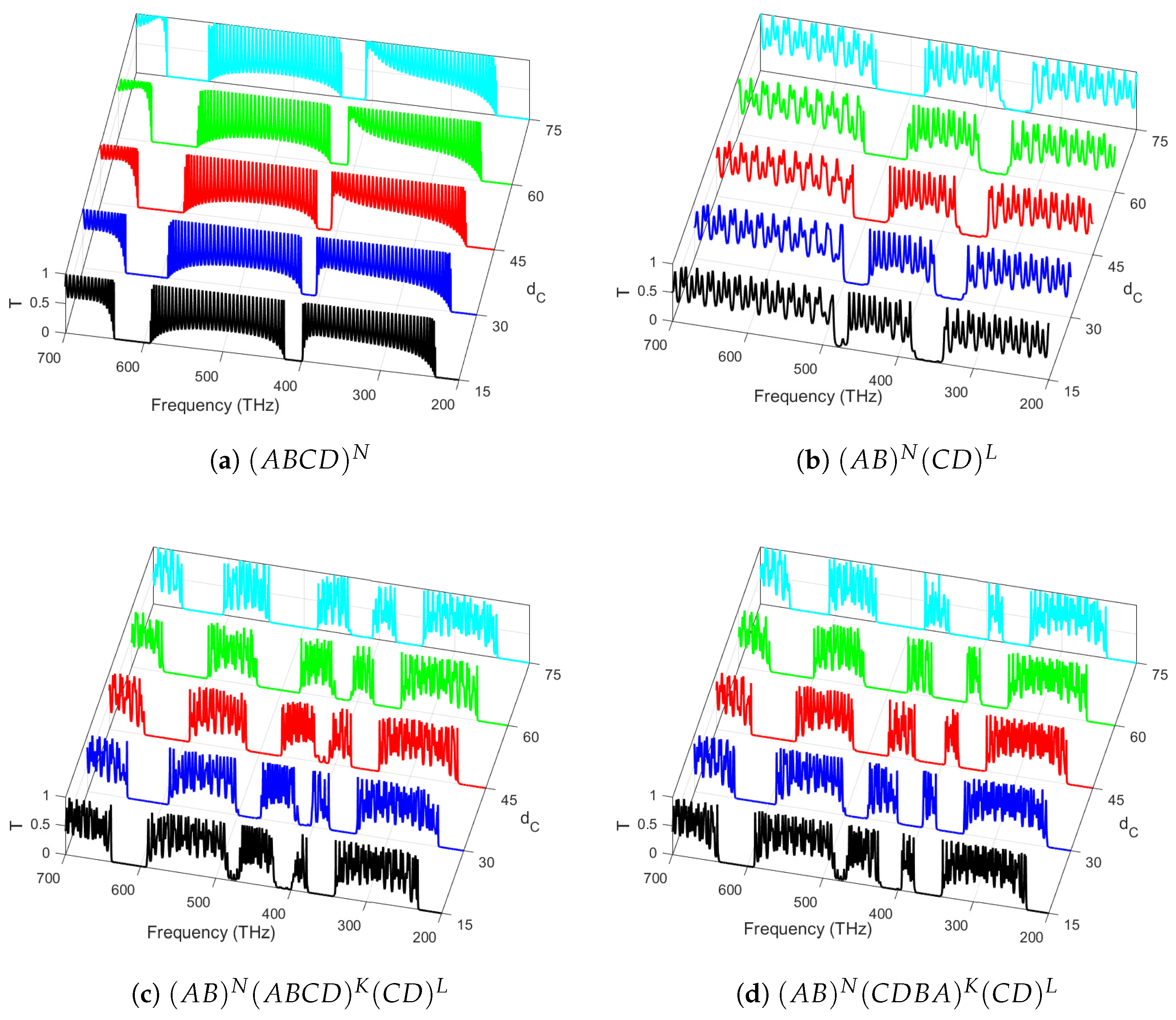
3.3. Effect of Sub-Layer Thicknesses
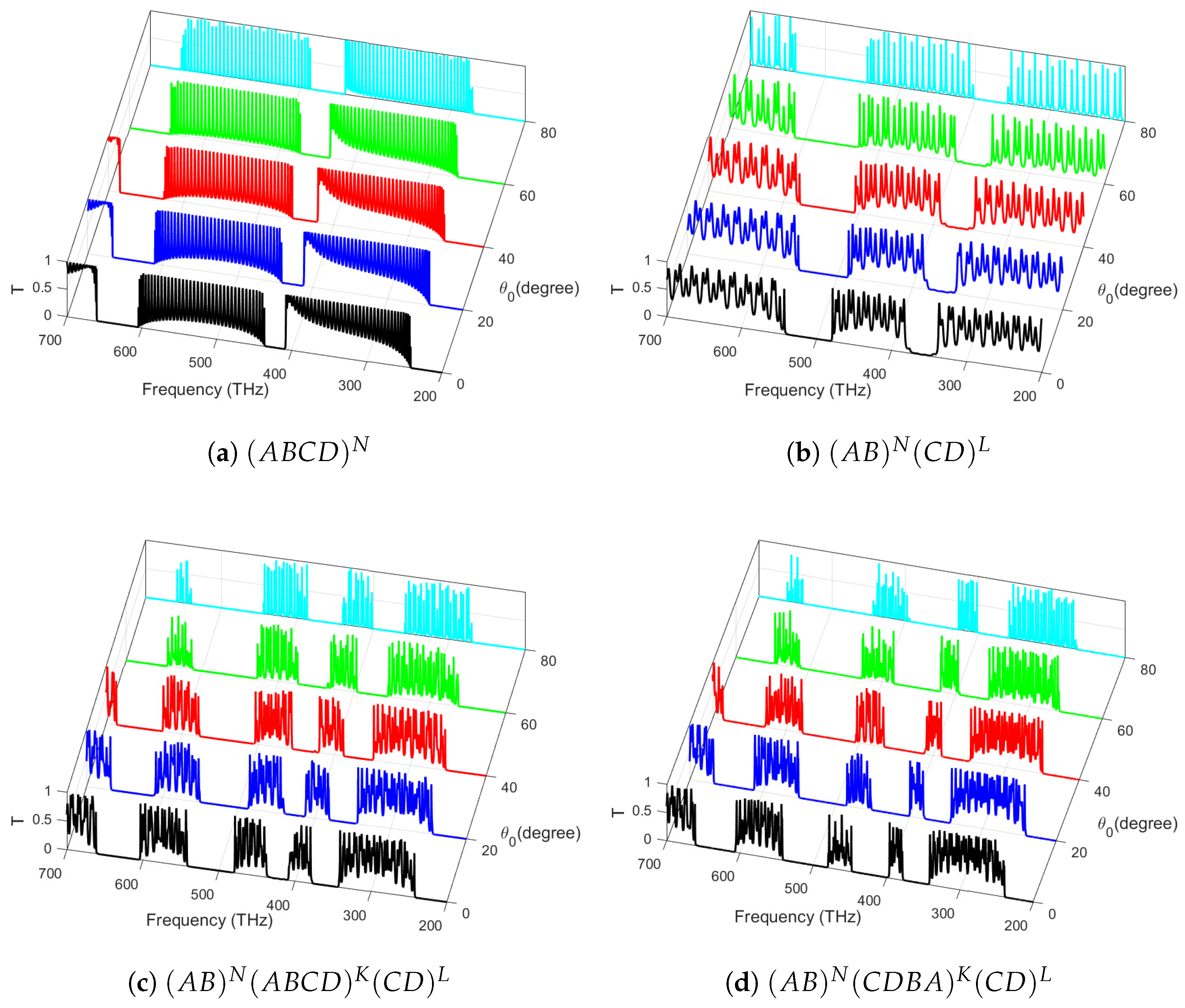
3.4. Effect of Incident Angle ()
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 1D | One-dimensional |
| PC | Photonic crystal |
| PBG | Photonic bandgap |
| FBG | Fiber Bragg grating |
| EMW | Electromagnetic waves |
| PCH | Photonic heterostructure |
| TO | Transverse optical |
| LO | Longitudinal optical |
| GHz | Gigahertz |
| PHz | Petahertz |
| THz | Terahertz |
| TMM | Transfer matrix method |
| TE | Transverse electric |
| WDM | Wavelength division multiplexer |
| NIR | Near-infrared region |
References
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486. [Google Scholar]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Michel, J.; Joannopoulos, J.D.; Thomas, E.L. A Dielectric Omnidirectional Reflector. Science 1998, 282, 1679–1682. [Google Scholar] [CrossRef] [PubMed]
- Chigrin, D.N.; Lavrinenko, A.; Yarotsky, D.; Gaponenko, S. Observation of total omnidirectional reflection from a one-dimensional dielectric lattice. Appl. Phys. A 1999, 68, 25–28. [Google Scholar]
- Joannopoulos, J.D.; Meade, R.D.; Winn, J. Photonic Crystals-Molding the flow of light. Nature 1996, 381, 290. [Google Scholar]
- Biswas, R.; Chan, C.; Sigalas, M.; Soukoulis, C.; Ho, K. Photonic band gap materials. In Photonic Band Gap Materials; Springer: Berlin/Heidelberg, Germany, 1996; pp. 23–40. [Google Scholar]
- Elsayed, H.A.; Aly, A.H. Terahertz frequency superconductor-nanocomposite photonic band gap. Int. J. Mod. Phys. B 2018, 32, 1850056. [Google Scholar]
- Gong, Q.; Hu, X. Photonic Crystals: Principles and Applications; Jenny Stanford Publishing: Singapore, 2014. [Google Scholar]
- Shaban, S.M.; Mehaney, A.; Aly, A.H. Determination of 1-propanol, ethanol, and methanol concentrations in water based on a one-dimensional phoxonic crystal sensor. Appl. Opt. 2020, 59, 3878–3885. [Google Scholar]
- Vakhrushev, A. Theoretical Foundations and Application of Photonic Crystals; BoD–Books on Demand: Norderstedt, DE, USA, 2018. [Google Scholar]
- Nouman, W.M.; Abd El-Ghany, S.E.S.; Sallam, S.M.; Dawood, A.F.B.; Aly, A.H. Biophotonic sensor for rapid detection of brain lesions using 1D photonic crystal. Opt. Quantum Electron. 2020, 52, 287. [Google Scholar]
- Bazian, M. Photonic crystal add–drop filter: A review on principles and applications. Photonic Netw. Commun. 2021, 41, 57–77. [Google Scholar] [CrossRef]
- Aly, A.H.; Zaky, Z.A.; Shalaby, A.S.; Ahmed, A.M.; Vigneswaran, D. Theoretical study of hybrid multifunctional one-dimensional photonic crystal as a flexible blood sugar sensor. Phys. Scr. 2020, 95, 035510. [Google Scholar]
- Arregui, G.; Lanzillotti-Kimura, N.D.; Sotomayor-Torres, C.M.; García, P.D. Anderson photon-phonon colocalization in certain random superlattices. Phys. Rev. Lett. 2019, 122, 043903. [Google Scholar]
- Biswal, A.; Kumar, R.; Nayak, C.; Samiappan, D. Photonic transmission spectra in an extrinsic semiconductor based Gaussian random multilayer. Opt. Mater. 2020, 102, 109799. [Google Scholar]
- Biswal, A.; Kumar, R.; Nayak, C.; Dhanalakshmi, S. Photonic bandgap characteristics of GaAs/AlAs-based one-dimensional quasi-periodic photonic crystal. Optik 2021, 234, 166597. [Google Scholar]
- Biswal, A.; Kumar, R.; Nayak, C.; Samiappan, D. n-GaAs based extrinsic Dodecanacci photonic quasicrystal. Phys. B Condens. Matter 2020, 595, 412340. [Google Scholar]
- Kim, S.; Yoon, S.; Seok, H.; Lee, J.; Jeon, H. Band-edge lasers based on randomly mixed photonic crystals. Opt. Express 2010, 18, 7685–7692. [Google Scholar]
- Ilegems, M.; Pearson, G. Infrared Reflection Spectra of Ga 1- x Al x As Mixed Crystals. Phys. Rev. B 1970, 1, 1576. [Google Scholar]
- Istrate, E.; Sargent, E.H. Photonic crystal heterostructures and interfaces. Rev. Mod. Phys. 2006, 78, 455. [Google Scholar]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. 2D-Photonic crystal heterostructures for the realization of compact photonic devices. Photonics Nanostruct.-Fundam. Appl. 2021, 44, 100903. [Google Scholar]
- Amaolo, A.; Chao, P.; Maldonado, T.J.; Molesky, S.; Rodriguez, A.W. Can photonic heterostructures provably outperform single-material geometries? Nanophotonics 2024, 13, 283–288. [Google Scholar]
- Minden, H. Some Optical Properties of Aluminum Arsenide. Appl. Phys. Lett. 1970, 17, 358–360. [Google Scholar]
- Chen, X.; Xiong, S. Optical properties of GaAs/AlAs superlattices with randomly distributed layer thicknesses. Phys. Rev. B 1993, 47, 7146. [Google Scholar] [CrossRef] [PubMed]
- Ohnuma, T.; Nagano, M. Electronic, structural and optical properties of AlAs/GaP strained short-period superlattices. Jpn. J. Appl. Phys. 2003, 42, 4237. [Google Scholar] [CrossRef]
- Kim, O.; Spitzer, W. Infrared reflectivity spectra and Raman spectra of Ga1- x Al x As mixed crystals. J. Appl. Phys. 1979, 50, 4362–4370. [Google Scholar] [CrossRef]
- Dumelow, T.; Parker, T.; Smith, S.; Tilley, D. Far-infrared spectroscopy of phonons and plasmons in semiconductor superlattices. Surf. Sci. Rep. 1993, 17, 151–212. [Google Scholar] [CrossRef]
- Adachi, S. GaAs and Related Materials: Bulk Semiconducting and Superlattice Properties; World Scientific: Singapore, 1994. [Google Scholar]
- Panyaev, I.S.; Yafarova, L.R.; Sannikov, D.G.; Dadoenkova, N.N.; Dadoenkova, Y.S.; Lyubchanskii, I.L. One-dimensional multiperiodic photonic structures: A new route in photonics (four-component media). J. Appl. Phys. 2019, 126, 103102. [Google Scholar] [CrossRef]
- Mohamed, A.G.; Elsayed, H.A.; Mehaney, A.; Aly, A.H.; Sabra, W. Transmittance properties of one-dimensional metamaterial nanocomposite photonic crystal in GHz range. Sci. Rep. 2022, 12, 18331. [Google Scholar] [CrossRef]
- Dadoenkova, Y.S.; Dadoenkova, N.N.; Lyubchanskii, I.L.; Kłos, J.W.; Krawczyk, M. Faraday effect in bi-periodic photonic-magnonic crystals. IEEE Trans. Magn. 2017, 53, 1–5. [Google Scholar] [CrossRef]
- Jafarpour, A.; Chow, E.; Reinke, C.; Huang, J.; Adibi, A.; Grot, A.; Mirkarimi, L.; Girolami, G.; Lee, R.; Xu, Y. Large-bandwidth ultra-low-loss guiding in bi-periodic photonic crystal waveguides. Appl. Phys. B 2004, 79, 409–414. [Google Scholar] [CrossRef]
- Hernández-Acosta, M.; Trejo-Valdez, M.; Castro-Chacón, J.; Torres-San Miguel, C.; Martínez-Gutiérrez, H.; Torres-Torres, C. Chaotic signatures of photoconductive Cu2ZnSnS4 nanostructures explored by Lorenz attractors. New J. Phys. 2018, 20, 023048. [Google Scholar] [CrossRef]
- Biswal, A.; Kumar, R.; Nayak, C.; Dhanalakshmi, S.; Behera, H.; Lyubchanskii, I. Analysis of transmission spectra in one-dimensional ternary photonic crystals with complex unit cell. Optik 2022, 261, 169169. [Google Scholar] [CrossRef]
- Amiri, I.S.; Paul, B.K.; Ahmed, K.; Aly, A.H.; Zakaria, R.; Yupapin, P.; Vigneswaran, D. Tri-core photonic crystal fiber based refractive index dual sensor for salinity and temperature detection. Microw. Opt. Technol. Lett. 2019, 61, 847–852. [Google Scholar]
- Lyu, W.; An, J.; Lin, Y.; Qiu, P.; Wang, G.; Chao, J.; Fu, B. Fabrication and applications of heterostructure materials for broadband ultrafast photonics. Adv. Opt. Mater. 2023, 11, 2300124. [Google Scholar] [CrossRef]
- Dixon, K.Y.; Loring, T.A.; Cerjan, A. Classifying topology in photonic heterostructures with gapless environments. Phys. Rev. Lett. 2023, 131, 213801. [Google Scholar] [CrossRef]
- Sui, J.Y.; Liao, S.Y.; Li, B.; Zhang, H.F. High sensitivity multitasking non-reciprocity sensor using the photonic spin Hall effect. Opt. Lett. 2022, 47, 6065–6068. [Google Scholar]
- Panyaev, I.S.; Sannikov, D.G.; Dadoenkova, N.N.; Dadoenkova, Y.S. Three-periodic 1D photonic crystals for designing the photonic optical devices operating in the infrared regime. Appl. Opt. 2021, 60, 1943–1952. [Google Scholar] [CrossRef]
- Biswal, A.; Jwo, D.J. Analysis of photonic band gap in a one-dimensional photonic crystal with multiple semiconductor bilayers. In Waves in Random and Complex Media; Taylor & Francis: Abingdon, UK, 2023; pp. 1–12. [Google Scholar]
- Yeh, P. Optical Waves in Layered Media; Wiley Online Library: Hoboken, NJ, USA, 1988; Volume 95. [Google Scholar]
- Morozov, G.V. Two forms of transfer matrix for one-dimensional optical structures. Opt. Quantum Electron. 2023, 55, 1120. [Google Scholar]
- Malitson, I.H. Refraction and dispersion of synthetic sapphire. JOSA 1962, 52, 1377–1379. [Google Scholar]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3. [Google Scholar]
- Jain, N.; Kumar, D.; Bhardwaj, K.; Sharma, R.K.; Holovsky, J.; Mishra, M.; Mishra, Y.K.; Sharma, S.K. Heterostructured core-shell metal oxide-based nanobrushes for ultrafast UV photodetectors. Mater. Sci. Eng. R Rep. 2024, 160, 100826. [Google Scholar]
- Vyas, K.; Espinosa, D.H.; Hutama, D.; Jain, S.K.; Mahjoub, R.; Mobini, E.; Awan, K.M.; Lundeen, J.; Dolgaleva, K. Group III-V semiconductors as promising nonlinear integrated photonic platforms. Adv. Phys. X 2022, 7, 2097020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biswal, A.; Behera, H.; Jwo, D.-J.; Hsu, T.-W. One-Dimensional Four-Layered Photonic Heterostructures: Analysis of Transmittance. Materials 2025, 18, 1433. https://doi.org/10.3390/ma18071433
Biswal A, Behera H, Jwo D-J, Hsu T-W. One-Dimensional Four-Layered Photonic Heterostructures: Analysis of Transmittance. Materials. 2025; 18(7):1433. https://doi.org/10.3390/ma18071433
Chicago/Turabian StyleBiswal, Amita, Harekrushna Behera, Dah-Jing Jwo, and Tai-Wen Hsu. 2025. "One-Dimensional Four-Layered Photonic Heterostructures: Analysis of Transmittance" Materials 18, no. 7: 1433. https://doi.org/10.3390/ma18071433
APA StyleBiswal, A., Behera, H., Jwo, D.-J., & Hsu, T.-W. (2025). One-Dimensional Four-Layered Photonic Heterostructures: Analysis of Transmittance. Materials, 18(7), 1433. https://doi.org/10.3390/ma18071433








