Recent Developments in Novel TPMS Lattice Materials: Design Optimization, Performance Control, and Applications in Biomimetic Scaffolds
Abstract
1. Introduction
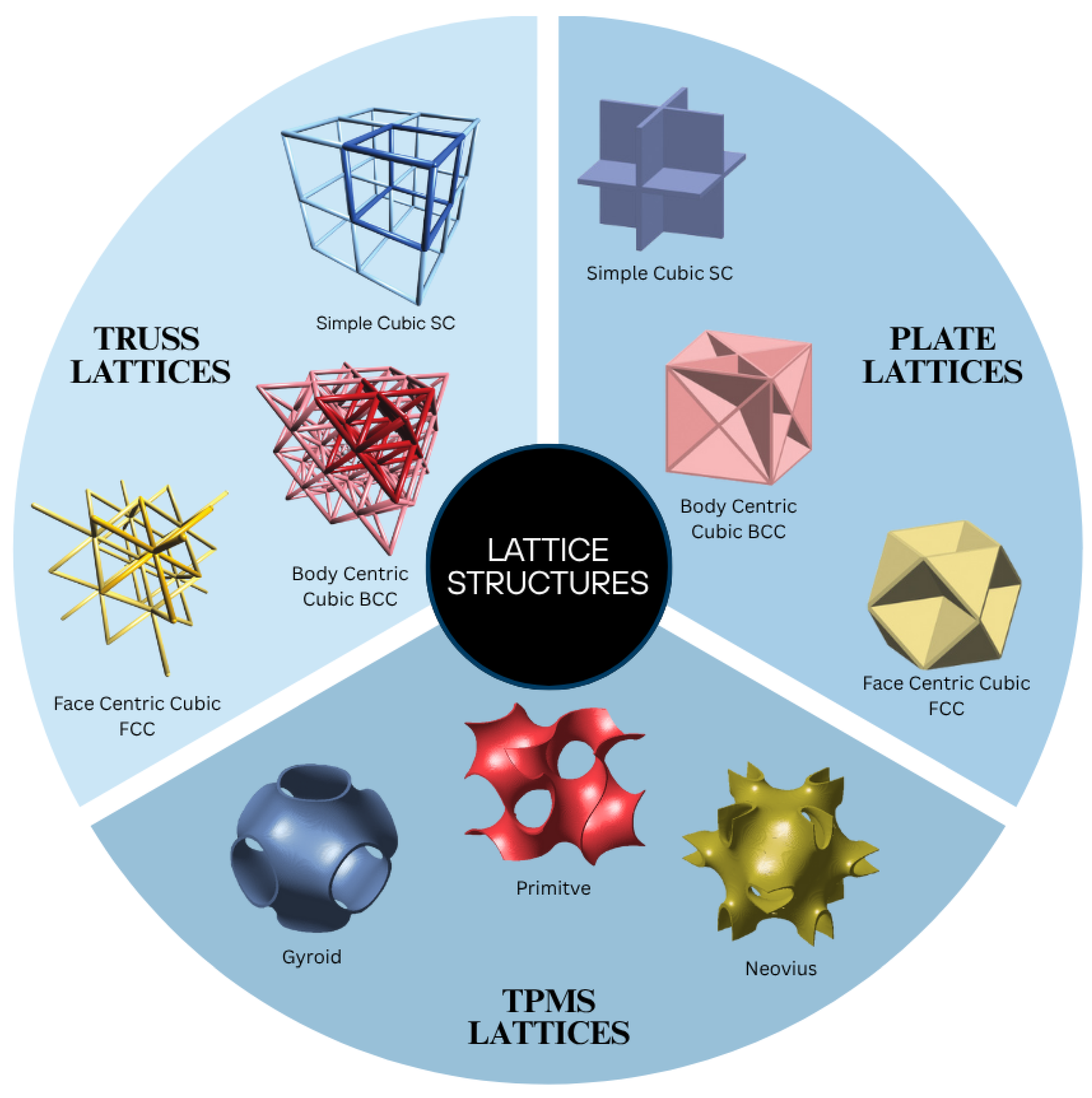
2. Classification of Lattice Structures
2.1. Truss Lattices
2.2. Plate Lattices
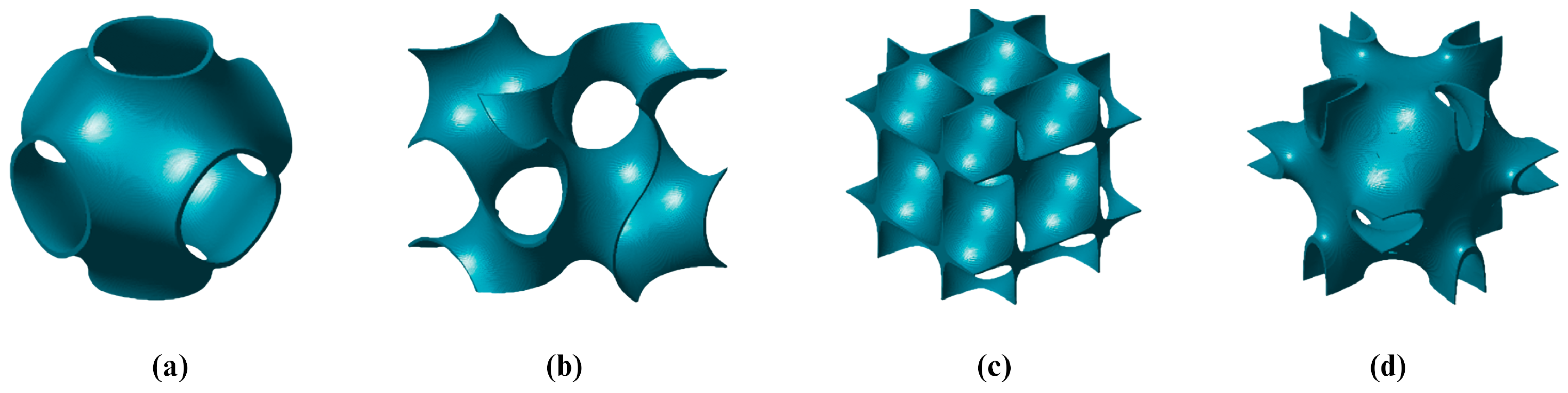
2.3. TPMS Lattices
2.4. Performance of TPMS Lattices
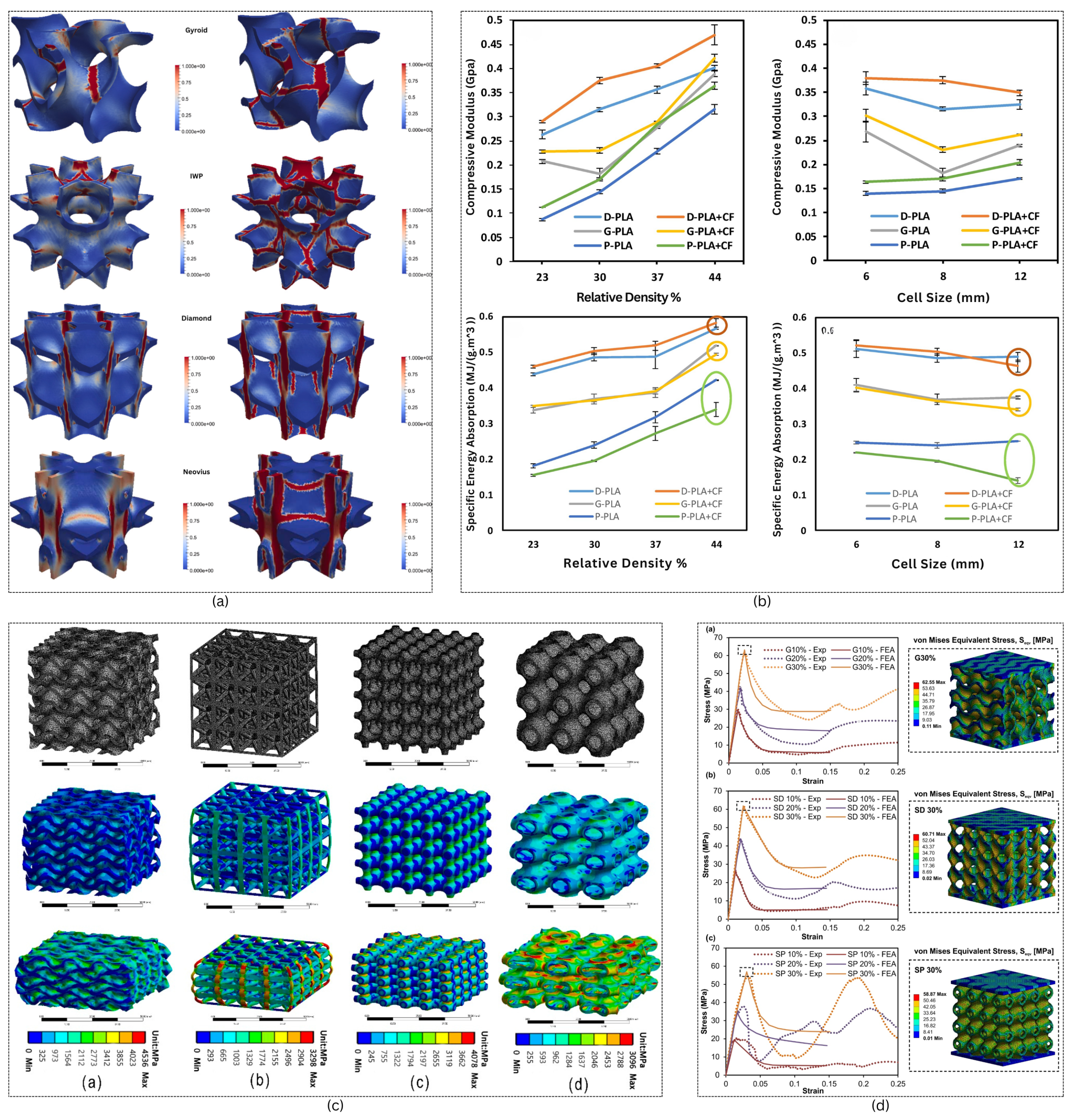
2.4.1. Mechanical Performance
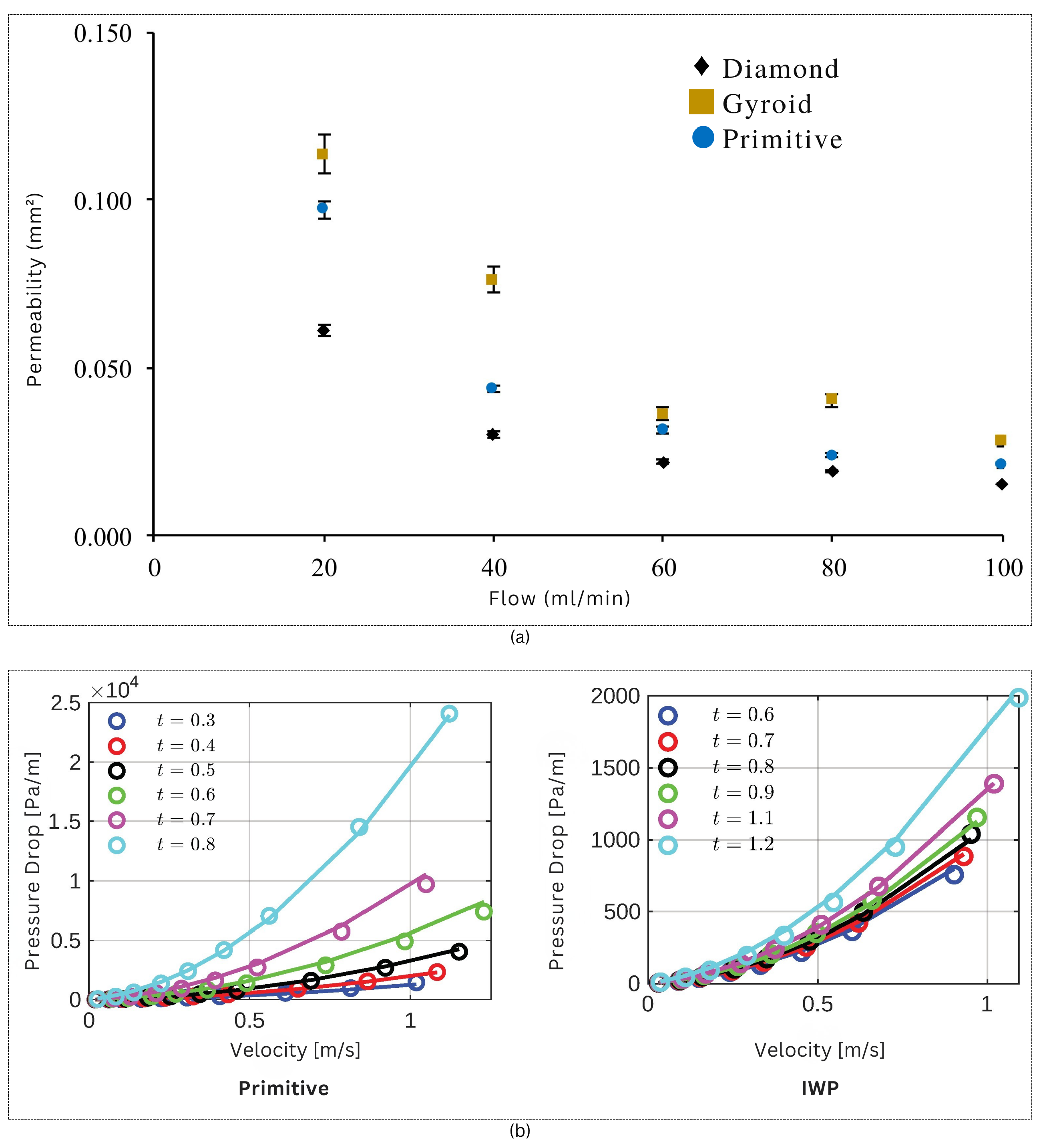
2.4.2. Mass Transfer
2.4.3. Thermal Conductivity
3. Design and Performance Optimization of TPMS
3.1. Functional Grading
3.1.1. Relative Density Grading
3.1.2. Unit Cell Size Grading

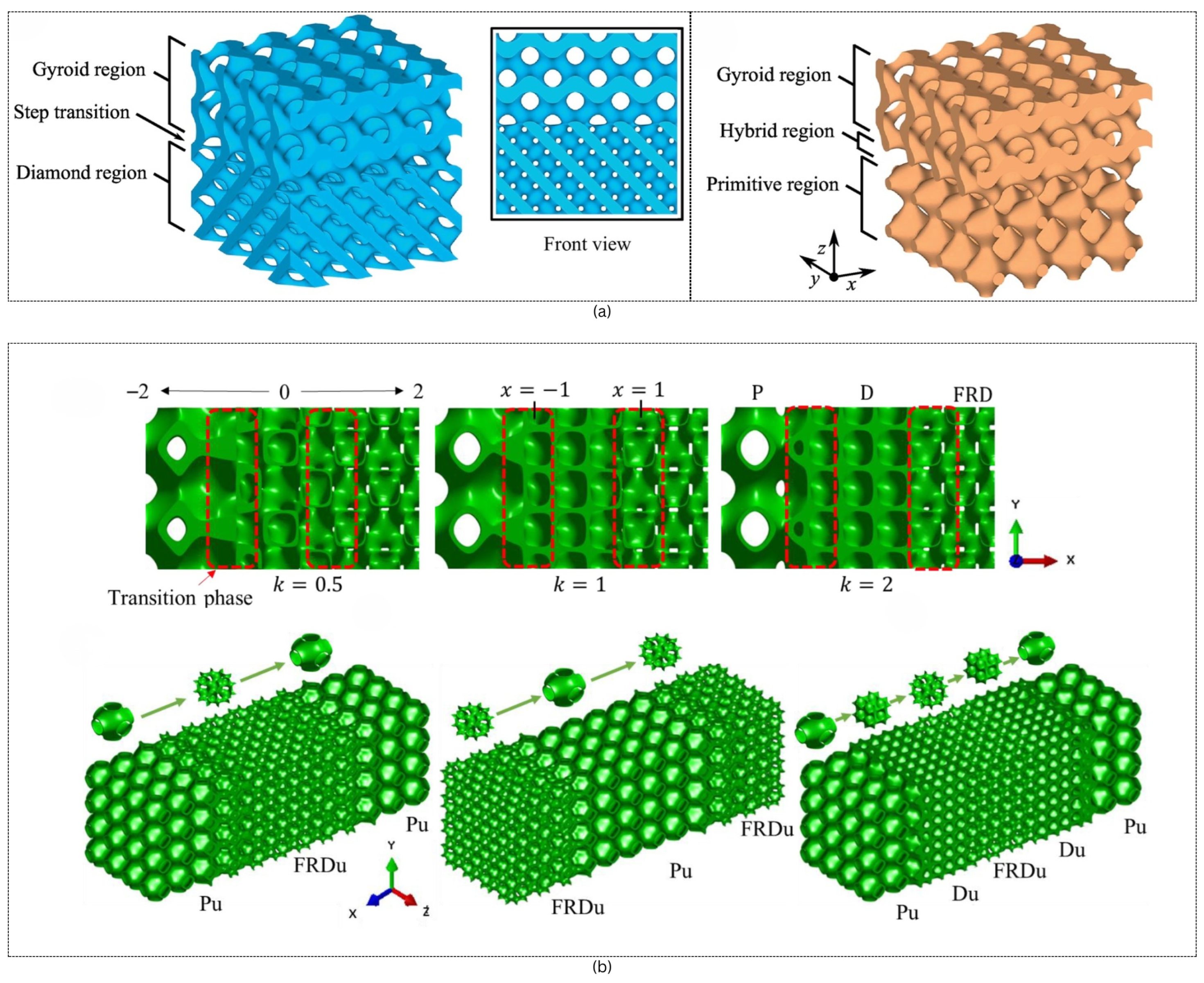
3.2. Hybridization
3.2.1. Sigmoid Function
3.2.2. Radial Basis Function
3.3. Computational Methods
3.3.1. Level-Set Methods
3.3.2. Density-Based Methods
3.3.3. Geometric Projection-Based Methods
3.3.4. Genetic Algorithms
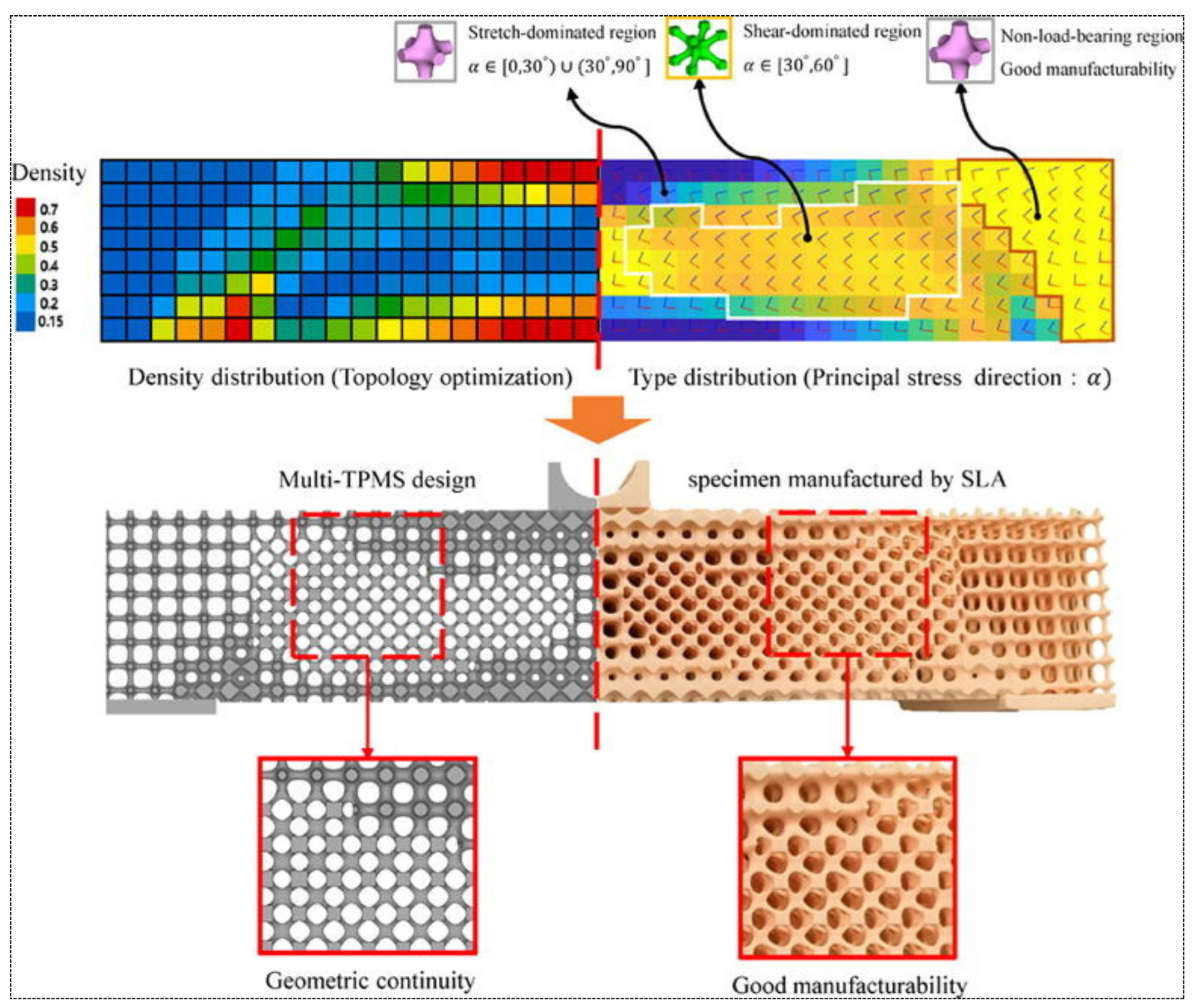
3.4. Advancement in Topology Optimization Methods
4. Topology Optimization of TPMS Structures
5. Manufacturing Methods for TPMS-Based Structures
5.1. Stereolithography (SLA)
5.2. Digital Light Processing (DLP)
5.3. Selective Laser Melting (SLM)
5.4. Selective Laser Sintering (SLS)
5.5. Electron Beam Melting (EBM)
5.6. Fused Deposition Modeling (FDM)
5.7. Other Special Fabrication Methods
5.8. Projection Micro-Stereolithography (PµSL)
5.8.1. Two-Photon Polymerization (2PP)/Direct Laser Writing (DLW)
5.8.2. Robocasting
6. Applications of TPMS Lattice Structures
6.1. Heat Sink
6.1.1. Conventional Heat Sinks
6.1.2. Emergence of TPMS-Based Heat Sinks
6.1.3. Optimization of TPMS Structures for Thermal Efficiency
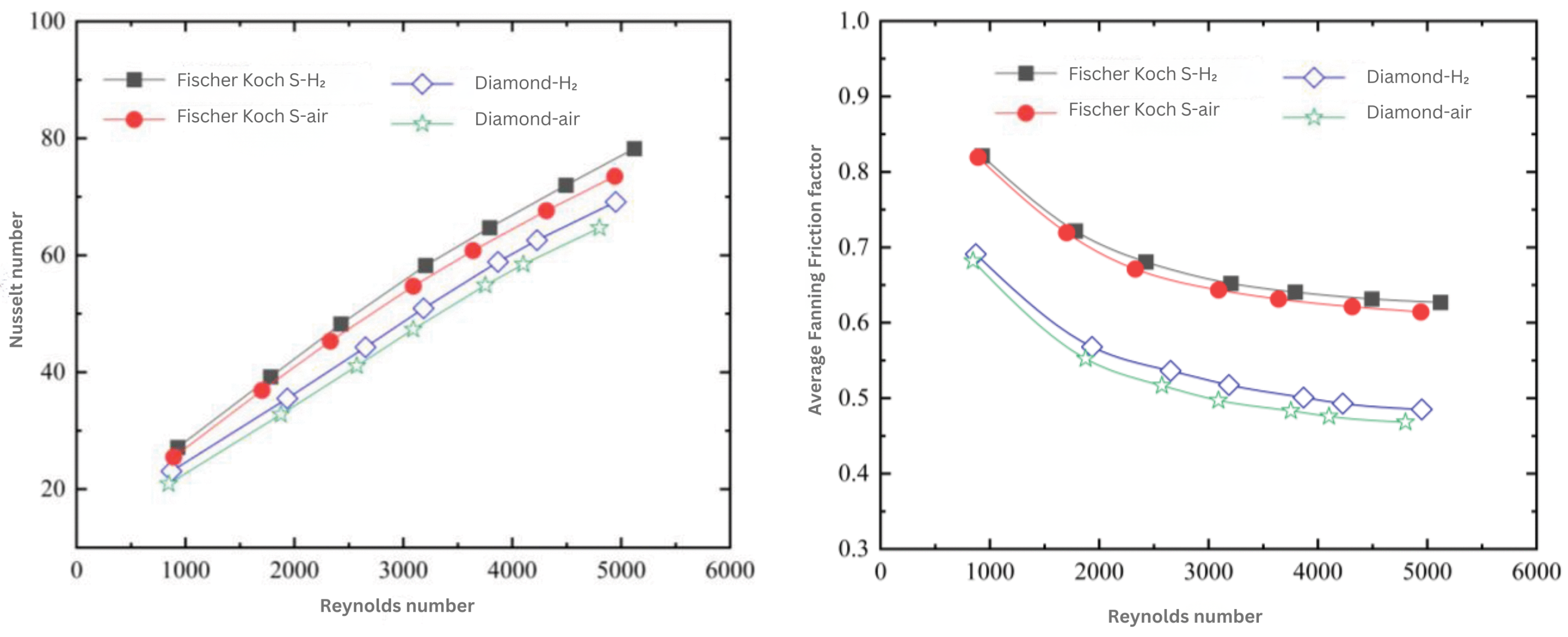
6.1.4. Summary of TPMS-Based Heat Sinks Performance
6.2. Interpenetrating Phase Composites
6.2.1. Mechanical Advantages of IPC Structures
6.2.2. Role of Additive Manufacturing and TPMS Integration
6.2.3. Performance Comparison of TPMS-Based IPCs
6.3. Biomimetic Scaffolds
6.3.1. Orthopedic Applications
6.3.2. Dental Applications
6.3.3. Chondral Applications
7. Limitations and Practical Barriers
8. Discussion and Future Prospects
9. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| L | Unit cell size of TPMS |
| W | Spatial frequency or wavenumber, given by |
| Level-set approximation | |
| c | Threshold value or level-set constant which defines the relative density of TPMS |
| , , | Parameters controlling cell size and shape |
| G | Spatial coordinate function defining the shape of the transition between different regions |
| k | Parameter controlling the width of the transition region |
| Stiffness matrix of the domain , dependent on material distribution | |
| Displacement field in domain , dependent on material distribution | |
| External load vector applied at position x | |
| Material indicator function: 1 if , 0 if | |
| Design domain where material is present | |
| Total domain including both material and void regions |
References
- Ha, N.S.; Lu, G. A review of recent research on bio-inspired structures and materials for energy absorption applications. Compos. Part B Eng. 2020, 181, 107496. [Google Scholar] [CrossRef]
- Guddati, S.; Kiran, A.S.K.; Leavy, M.; Ramakrishna, S. Recent advancements in additive manufacturing technologies for porous material applications. Int. J. Adv. Manuf. Technol. 2019, 105, 193–215. [Google Scholar] [CrossRef]
- Schoen, A.H. Infinite Periodic Minimal Surfaces Without Self-Intersections. 1970. Available online: https://ntrs.nasa.gov/citations/19700020472 (accessed on 9 November 2025).
- Wein, F.; Dunning, P.D.; Norato, J.A. A review on feature-mapping methods for structural optimization. Struct. Multidiscip. Optim. 2020, 62, 1597–1638. [Google Scholar] [CrossRef]
- Rade, J.; Balu, A.; Herron, E.; Pathak, J.; Ranade, R.; Sarkar, S.; Krishnamurthy, A. Algorithmically-consistent deep learning frameworks for structural topology optimization. Eng. Appl. Artif. Intell. 2021, 106, 104483. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Baobaid, N.; Ali, M.I.; Khan, K.A.; Al-Rub, R.K.A. Fluid flow and heat transfer of porous TPMS architected heat sinks in free convection environment. Case Stud. Therm. Eng. 2022, 33, 101944. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, Y.; Hu, J.; Fan, X.; Luo, Z.; Liu, Y.; Liu, L. Efficient Representation and Optimization of TPMS-Based Porous Structures for 3D Heat Dissipation. Comput.-Aided Des. 2022, 142, 103123. [Google Scholar] [CrossRef]
- Modrek, M.; Viswanath, A.; Khan, K.A.; Ali, M.I.; Al-Rub, R.K.A. An optimization case study to design additively manufacturable porous heat sinks based on triply periodic minimal surface (TPMS) lattices. Case Stud. Therm. Eng. 2022, 36, 102161. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Salman, B.; Kherbeet, A.; Ahmed, M. Optimization of thermal design of heat sinks: A review. Int. J. Heat Mass Transf. 2018, 118, 129–153. [Google Scholar] [CrossRef]
- Santos, S.; Matos, C.; Duarte, I.; Olhero, S.M.; Miranda, G. Effect of TPMS reinforcement on the mechanical properties of aluminium—Alumina interpenetrating phase composites. Prog. Addit. Manuf. 2025, 10, 1187–1199. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Sun, Y.; Yang, J.; Chen, R.; Xiong, Y.; Hou, W.; Bai, L. Design of a biomimetic graded TPMS scaffold with quantitatively adjustable pore size. Mater. Des. 2022, 218, 110665. [Google Scholar] [CrossRef]
- Pugliese, R.; Graziosi, S. Biomimetic scaffolds using triply periodic minimal surface-based porous structures for biomedical applications. SLAS Technol. 2023, 28, 165–182. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Qin, Q.; Wang, J. A Review of Stereolithography: Processes and Systems. Processes 2020, 8, 1138. [Google Scholar] [CrossRef]
- Zhu, L.; Li, L.; Li, Z.; Shi, J.; Tang, W.; Yang, J.; Jiang, Q. Design and biomechanical characteristics of porous meniscal implant structures using triply periodic minimal surfaces. J. Transl. Med. 2019, 17, 89. [Google Scholar] [CrossRef]
- Timoshenko, A.B.; Ghasemkhani, A.; Kim, C.; Cordova, D.J.; Potes, M.A.; Aceves, V.; Mitra, I.; Bird, J.E.; Gray, R.S.; Seidlits, S.K.; et al. Visible Light Induced DLP-Printed Oxygen-Releasing TPMS Scaffolds Mitigate Early Hypoxia in Bone Defects. Adv. Healthc. Mater. 2025, e02735. [Google Scholar] [CrossRef]
- Ataee, A.; Li, Y.; Brandt, M.; Wen, C. Ultrahigh-strength titanium gyroid scaffolds manufactured by selective laser melting (SLM) for bone implant applications. Acta Mater. 2018, 158, 354–368. [Google Scholar] [CrossRef]
- Khrapov, D.; Kozadayeva, M.; Manabaev, K.; Panin, A.; Sjöström, W.; Koptyug, A.; Mishurova, T.; Evsevleev, S.; Meinel, D.; Bruno, G.; et al. Different Approaches for Manufacturing Ti-6Al-4V Alloy with Triply Periodic Minimal Surface Sheet-Based Structures by Electron Beam Melting. Materials 2021, 14, 4912. [Google Scholar] [CrossRef]
- Abou-Ali, A.M.; Lee, D.W.; Abu Al-Rub, R.K. On the Effect of Lattice Topology on Mechanical Properties of SLS Additively Manufactured Sheet-, Ligament-, and Strut-Based Polymeric Metamaterials. Polymers 2022, 14, 4583. [Google Scholar] [CrossRef]
- Diez-Escudero, A.; Harlin, H.; Isaksson, P.; Persson, C. Porous polylactic acid scaffolds for bone regeneration: A study of additively manufactured triply periodic minimal surfaces and their osteogenic potential. J. Tissue Eng. 2020, 11, 2041731420956541. [Google Scholar] [CrossRef] [PubMed]
- Baumer, V.; Gunn, E.; Riegle, V.; Bailey, C.; Shonkwiler, C.; Prawel, D. Robocasting of Ceramic Fischer–Koch S Scaffolds for Bone Tissue Engineering. J. Funct. Biomater. 2023, 14, 251. [Google Scholar] [CrossRef]
- Zok, F.W.; Latture, R.M.; Begley, M.R. Periodic truss structures. J. Mech. Phys. Solids 2016, 96, 184–203. [Google Scholar] [CrossRef]
- Yang, C.; Xu, P.; Xie, S.; Yao, S. Mechanical performances of four lattice materials guided by topology optimisation. Scr. Mater. 2020, 178, 339–345. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Diamantopoulou, M.; Gorji, M.B.; Bonatti, C.; Mohr, D. 3D Plate-Lattices: An Emerging Class of Low-Density Metamaterial Exhibiting Optimal Isotropic Stiffness. Adv. Mater. 2018, 30, 1803334. [Google Scholar] [CrossRef] [PubMed]
- Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Jarrar, F.; Abu Al-Rub, R.; Cantwell, W. Additive manufactured semi-plate lattice materials with high stiffness, strength and toughness. Int. J. Solids Struct. 2021, 230–231, 111153. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, Z.; Hu, X.; Kuang, H.; Zhai, J. The effect of porosity on the mechanical properties of 3D-printed triply periodic minimal surface (TPMS) bioscaffold. Bio-Des. Manuf. 2019, 2, 242–255. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Abu Al-Rub, R.K. Multifunctional Mechanical Metamaterials Based on Triply Periodic Minimal Surface Lattices. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- Kapfer, S.C.; Hyde, S.T.; Mecke, K.; Arns, C.H.; Schröder-Turk, G.E. Minimal surface scaffold designs for tissue engineering. Biomaterials 2011, 32, 6875–6882. [Google Scholar] [CrossRef]
- Speirs, M.; Hooreweder, B.V.; Humbeeck, J.V.; Kruth, J.P. Fatigue behaviour of NiTi shape memory alloy scaffolds produced by SLM, a unit cell design comparison. J. Mech. Behav. Biomed. Mater. 2017, 70, 53–59. [Google Scholar] [CrossRef]
- Khan, K.A.; Al-Rub, R.K.A. Time dependent response of architectured Neovius foams. Int. J. Mech. Sci. 2017, 126, 106–119. [Google Scholar] [CrossRef]
- Wang, N.; Meenashisundaram, G.K.; Chang, S.; Fuh, J.Y.H.; Dheen, S.T.; Kumar, A.S. A comparative investigation on the mechanical properties and cytotoxicity of Cubic, Octet, and TPMS gyroid structures fabricated by selective laser melting of stainless steel 316L. J. Mech. Behav. Biomed. Mater. 2022, 129, 105151. [Google Scholar] [CrossRef]
- Teng, F.; Sun, Y.; Guo, S.; Gao, B.; Yu, G. Topological and mechanical properties of different lattice structures based on additive manufacturing. Micromachines 2022, 13, 1017. [Google Scholar] [CrossRef] [PubMed]
- Maharjan, G.K.; Khan, S.Z.; Riza, S.H.; Masood, S.H. Compressive Behaviour of 3D Printed Polymeric Gyroid Cellular Lattice Structure. IOP Conf. Ser. Mater. Sci. Eng. 2018, 455, 012047. [Google Scholar] [CrossRef]
- Khan, S.Z.; Masood, S.H.; Essam, I.; Ahmad, Z. Compressive Behaviour of Neovius Triply Periodic Minimal Surface Cellular Structure Manufactured by Fused Deposition Modelling. Virtual Phys. Prototyp. 2019, 14, 360–370. [Google Scholar] [CrossRef]
- Préve, D.; Lenarda, P.; Maskery, I.; Paggi, M. A comprehensive characterization of fracture in unit cell open foams generated from Triply Periodic Minimal Surfaces. Eng. Fract. Mech. 2023, 277, 108949. [Google Scholar] [CrossRef]
- Iandiorio, C.; Mattei, G.; Marotta, E.; Costanza, G.; Tata, M.E.; Salvini, P. The Beneficial Effect of a TPMS-Based Fillet Shape on the Mechanical Strength of Metal Cubic Lattice Structures. Materials 2024, 17, 1553. [Google Scholar] [CrossRef]
- Saleh, M.; Anwar, S.; Al-Ahmari, A.M.; Alfaify, A. Compression Performance and Failure Analysis of 3D-Printed Carbon Fiber/PLA Composite TPMS Lattice Structures. Polymers 2022, 14, 4595. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Tzetzis, D. Mechanical and FEA-Assisted Characterization of Fused Filament Fabricated Triply Periodic Minimal Surface Structures. J. Compos. Sci. 2021, 5, 58. [Google Scholar] [CrossRef]
- Montazerian, H.; Zhianmanesh, M.; Davoodi, E.; Milani, A.; Hoorfar, M. Longitudinal and radial permeability analysis of additively manufactured porous scaffolds: Effect of pore shape and porosity. Mater. Des. 2017, 122, 146–156. [Google Scholar] [CrossRef]
- Castro, A.P.G.; Pires, T.; Santos, J.E.; Gouveia, B.P.; Fernandes, P.R. Permeability versus Design in TPMS Scaffolds. Materials 2019, 12, 1313. [Google Scholar] [CrossRef]
- Piedra, S.; Gomez-Ortega, A.; Perez-Barrera, J. Prediction of Flow Properties of Porous Triply Periodic Minimal Surface (TPMS) Structures. Fluids 2023, 8, 312. [Google Scholar] [CrossRef]
- Zhianmanesh, M.; Varmazyar, M.; Montazerian, H. Fluid Permeability of Graded Porosity Scaffolds Architectured with Minimal Surfaces. ACS Biomater. Sci. Eng. 2019, 5, 1228–1237. [Google Scholar] [CrossRef]
- Catchpole-Smith, S.; Sélo, R.; Davis, A.; Ashcroft, I.; Tuck, C.; Clare, A. Thermal conductivity of TPMS lattice structures manufactured via laser powder bed fusion. Addit. Manuf. 2019, 30, 100846. [Google Scholar] [CrossRef]
- Li, N.; Wang, M.; Zhao, J.; Sun, K.; Bi, C.; Du, M.; You, E.; Yang, M. Heat Transfer Characterization of TPMS Heat Exchangers Applied to the Aerospace Field. Front. Heat Mass Transf. 2025, 23, 601–614. [Google Scholar] [CrossRef]
- Bragin, D.; Popov, A.; Eremin, A. The thermal conductivity properties of porous materials based on TPMS. Int. J. Heat Mass Transf. 2024, 231, 125863. [Google Scholar] [CrossRef]
- Yu, S.; Sun, J.; Bai, J. Investigation of functionally graded TPMS structures fabricated by additive manufacturing. Mater. Des. 2019, 182, 108021. [Google Scholar] [CrossRef]
- Ejeh, C.J.; Barsoum, I.; Abu Al-Rub, R.K. Flexural properties of functionally graded additively manufactured AlSi10Mg TPMS latticed-beams. Int. J. Mech. Sci. 2022, 223, 107293. [Google Scholar] [CrossRef]
- Liu, F.; Mao, Z.; Zhang, P.; Zhang, D.Z.; Jiang, J.; Ma, Z. Functionally graded porous scaffolds in multiple patterns: New design method, physical and mechanical properties. Mater. Des. 2018, 160, 849–860. [Google Scholar] [CrossRef]
- Zhou, X.; Jin, Y.; Du, J. Functionally Graded Scaffolds with Programmable Pore Size Distribution Based on Triply Periodic Minimal Surface Fabricated by Selective Laser Melting. Materials 2020, 13, 5046. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, C.; Deng, M.; Li, Y.; Li, J.; Wang, D. Graded Minimal Surface Structures with High Specific Strength for Broadband Sound Absorption Produced by Laser Powder Bed Fusion. Coatings 2023, 13, 1950. [Google Scholar] [CrossRef]
- Yang, N.; Quan, Z.; Zhang, D.; Tian, Y. Multi-morphology transition hybridization CAD design of minimal surface porous structures for use in tissue engineering. CAD Comput. Aided Des. 2014, 56, 11–21. [Google Scholar] [CrossRef]
- Maskery, I.; Aremu, A.; Parry, L.; Wildman, R.; Tuck, C.; Ashcroft, I. Effective design and simulation of surface-based lattice structures featuring volume fraction and cell type grading. Mater. Des. 2018, 155, 220–232. [Google Scholar] [CrossRef]
- Michell, A. LVIII. The limits of economy of material in frame-structures. London Edinburgh Dublin Philos. Mag. J. Sci. 1904, 8, 589–597. [Google Scholar] [CrossRef]
- Strömberg, N. Optimal grading of TPMS-based lattice structures with transversely isotropic elastic bulk properties. Eng. Optim. 2021, 53, 1871–1883. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Stolpe, M.; Svanberg, K. An alternative interpolation scheme for minimum compliance topology optimization. Struct. Multidiscip. Optim. 2001, 22, 116–124. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Hajela, P.; Lee, E.; Lin, C.Y. Genetic Algorithms in Structural Topology Optimization. In Topology Design of Structures; Bendsøe, M.P., Soares, C.A.M., Eds.; Springer: Dordrecht, The Netherlands, 1993; pp. 117–133. [Google Scholar] [CrossRef]
- Li, Z.; Hou, X.; Ke, Y.; Tao, M. Topology optimization with a genetic algorithm for the structural design of composite porous acoustic materials. Appl. Acoust. 2022, 197, 108917. [Google Scholar] [CrossRef]
- Bobby, S.; Spence, S.M.; Kareem, A. Data-driven performance-based topology optimization of uncertain wind-excited tall buildings. Struct. Multidiscip. Optim. 2016, 54, 1379–1402. [Google Scholar] [CrossRef]
- Ulu, E.; Zhang, R.; Kara, L.B. A data-driven investigation and estimation of optimal topologies under variable loading configurations. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2016, 4, 61–72. [Google Scholar] [CrossRef]
- Ulu, E.; Mccann, J.; Kara, L.B. Lightweight structure design under force location uncertainty. ACM Trans. Graph. (TOG) 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Martínez-Frutos, J.; Martínez-Castejón, P.J.; Herrero-Pérez, D. Efficient topology optimization using GPU computing with multilevel granularity. Adv. Eng. Softw. 2017, 106, 47–62. [Google Scholar] [CrossRef]
- Challis, V.J.; Roberts, A.P.; Grotowski, J.F. High resolution topology optimization using graphics processing units (GPUs). Struct. Multidiscip. Optim. 2014, 49, 315–325. [Google Scholar] [CrossRef]
- Yu, Y.; Hur, T.; Jung, J.; Jang, I.G. Deep learning for determining a near-optimal topological design without any iteration. Struct. Multidiscip. Optim. 2019, 59, 787–799. [Google Scholar] [CrossRef]
- Jeong, H.; Bai, J.; Batuwatta-Gamage, C.P.; Rathnayaka, C.; Zhou, Y.; Gu, Y.T. A Physics-Informed Neural Network-based Topology Optimization (PINNTO) framework for structural optimization. Eng. Struct. 2023, 278, 115484. [Google Scholar] [CrossRef]
- Yan, K.; Yan, J.; Luo, C.; Chen, L.; Lin, Q.; Zhang, D. A Surrogate Objective Framework for Prediction+Optimization with Soft Constraints. arXiv 2021, arXiv:2111.11358. [Google Scholar]
- Wu, J.; Sigmund, O.; Groen, J.P. Topology optimization of multi-scale structures: A review. Struct. Multidiscip. Optim. 2021, 63, 1455–1480. [Google Scholar] [CrossRef]
- Sivapuram, R.; Dunning, P.D.; Kim, H.A. Simultaneous material and structural optimization by multiscale topology optimization. Struct. Multidiscip. Optim. 2016, 54, 1267–1281. [Google Scholar] [CrossRef]
- Chen, W.; Tong, L.; Liu, S. Concurrent topology design of structure and material using a two-scale topology optimization. Comput. Struct. 2017, 178, 119–128. [Google Scholar] [CrossRef]
- Yan, X.; Huang, X.; Zha, Y.; Xie, Y.M. Concurrent topology optimization of structures and their composite microstructures. Comput. Struct. 2014, 133, 103–110. [Google Scholar] [CrossRef]
- Lu, Y.; Tong, L. Concurrent topology optimization of cellular structures and anisotropic materials. Comput. Struct. 2021, 255, 106624. [Google Scholar] [CrossRef]
- Chen, J.; Baldwin, M.; Prabha Narra, S.; McComb, C. Multi-Lattice Topology Optimization Via Generative Lattice Modeling. J. Mech. Des. 2025, 147, 051707. [Google Scholar] [CrossRef]
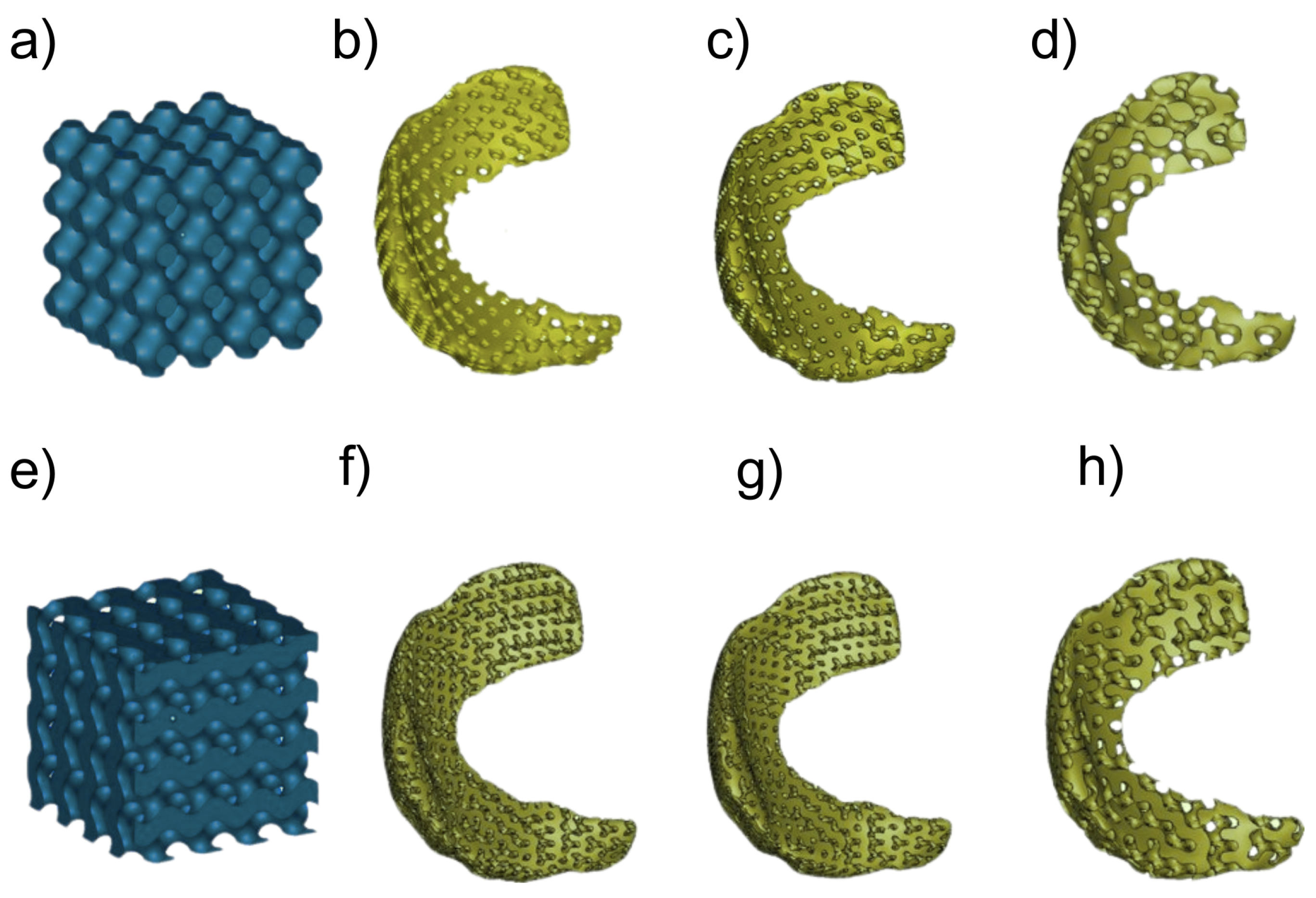
- Li, D.; Liao, W.; Dai, N.; Dong, G.; Tang, Y.; Xie, Y.M. Optimal design and modeling of gyroid-based functionally graded cellular structures for additive manufacturing. CAD Comput. Aided Des. 2018, 104, 87–99. [Google Scholar] [CrossRef]
- Fangxi, R.; Changdong, Z.; Wenhe, L.; Tingting, L.; Dawei, L.; Xin, S.; Weiming, J.; Cong, W.; Junfeng, Q.; Yi, C.; et al. Transition Boundaries and Stiffness Optimal Design for Multi-TPMS Lattices. Mater. Des. 2021, 210, 110062. [Google Scholar] [CrossRef]
- Feng, J.; Fu, J.; Yao, X.; He, Y. Triply periodic minimal surface (TPMS) porous structures: From multi-scale design, precise additive manufacturing to multidisciplinary applications. Int. J. Extrem. Manuf. 2022, 4, 022001. [Google Scholar] [CrossRef]
- Matsuda, T.; Mizutani, M.; Arnold, S.C. Molecular Design of Photocurable Liquid Biodegradable Copolymers. 1. Synthesis and Photocuring Characteristics. Macromolecules 2000, 33, 795–800. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; He, F.; Zuo, F.; Shi, X. Fabrication of cancellous-bone-mimicking β-tricalcium phosphate bioceramic scaffolds with tunable architecture and mechanical strength by stereolithography 3D printing. J. Eur. Ceram. Soc. 2022, 42, 6713–6720. [Google Scholar] [CrossRef]
- Lan, P.X.; Lee, J.W.; Seol, Y.J.; Cho, D.W. Development of 3D PPF/DEF scaffolds using micro-stereolithography and surface modification. J. Mater. Sci. Mater. Med. 2009, 20, 271–279. [Google Scholar] [CrossRef]
- Araya, M.; Murillo, J.; Vindas, R.; Guillén, T. Compressive behavior of SLA open-cell lattices: A comparison between triply periodic minimal surface gyroid and stochastic structures for artificial bone. Materialia 2024, 38, 102233. [Google Scholar] [CrossRef]
- Kavafaki, S.; Maliaris, G. Mechanical Characterization of Triply Periodic Minimal Surface Structures Fabricated via SLA 3D Printing Using Tough Resin: Influence of Geometry on Performance. Eng. Proc. 2025, 87, 46. [Google Scholar] [CrossRef]
- Gabrieli, R.; Wenger, R.; Mazza, M.; Verné, E.; Baino, F. Design, Stereolithographic 3D Printing, and Characterization of TPMS Scaffolds. Materials 2024, 17, 654. [Google Scholar] [CrossRef]
- Yang, C.; Wu, W.; Fu, Z.; Zheng, H. Preparation and thermal insulation properties of TPMS 3Y-TZP ceramics using DLP 3D printing technology. J. Mater. Sci. 2023, 58, 11992–12007. [Google Scholar] [CrossRef]
- Guo, W.; Li, P.; Wei, Y.; Zhao, L.; Pang, Y.; Huang, Y.; Ye, X.; Wang, S.; Liu, B.; You, H.; et al. Ionic substitution through bredigite doping for microstructure and performance adjustment in DLP 3D-printed TPMS porous HA bone scaffolds. Virtual Phys. Prototyp. 2024, 19, e2423840. [Google Scholar] [CrossRef]
- Lumba, L.T.; Chernyshikhin, S.; Mahato, B.; Abaimov, S.G.; Shishkovsky, I. The assessment of permeability of biological implant structure using DLP-manufactured TPMS lattice physical models. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Shen, M.; Li, Y.; Lu, F.; Gou, Y.; Zhong, C.; He, S.; Zhao, C.; Yang, G.; Zhang, L.; Yang, X.; et al. Bioceramic scaffolds with triply periodic minimal surface architectures guide early-stage bone regeneration. Bioact. Mater. 2023, 25, 374–386. [Google Scholar] [CrossRef]
- Park, K.S.; Jin, H.; Shin, Y.A.; Gupta, A.; Kim, J.K.; Rhee, H.N.; Son, Y.J.; Choi, S.H. A Study on the Effect of Bulk Porosity and Surface Roughness on the Biocompatibility of TPMS Gyroid Structures Fabricated via the SLM Process. Met. Mater. Int. 2025, 31, 3455–3473. [Google Scholar] [CrossRef]
- Lv, S.; Chai, Y.; Feng, H.; Lou, W.; Xiao, C.; Li, S. Numerical and experimental study of stress-field-driven TPMS hybrid-gradient SLM lattice for impact cushioning. J. Mater. Res. Technol. 2025, 38, 3830–3850. [Google Scholar] [CrossRef]
- Abou-Ali, A.M.; Al-Ketan, O.; Lee, D.W.; Rowshan, R.; Al-Rub, R.K.A. Mechanical behavior of polymeric selective laser sintered ligament and sheet based lattices of triply periodic minimal surface architectures. Mater. Des. 2020, 196, 109100. [Google Scholar] [CrossRef]
- Shevchenko, V.; Balabanov, S.; Sychov, M.; Karimova, L. Prediction of Cellular Structure Mechanical Properties with the Geometry of Triply Periodic Minimal Surfaces (TPMS). ACS Omega 2023, 8, 26895–26905. [Google Scholar] [CrossRef]
- Liu, F.; Gan, D.; Zhang, K.; Zhang, P.; Zhang, C.; Li, S.; Xie, H.; Tang, K. A selective strategy for determining suitable structure and fatigue behavior study of minimal surface scaffolds fabricated by EBM. Int. J. Fatigue 2023, 167, 107380. [Google Scholar] [CrossRef]
- Mishra, A.K.; Chavan, H.; Kumar, A. Effect of material variation on the uniaxial compression behavior of FDM manufactured polymeric TPMS lattice materials. Mater. Today Proc. 2021, 46, 7752–7759. [Google Scholar] [CrossRef]
- Li, M.; Xu, Y.; Wu, C.; Li, Q.; Wu, C.; Fang, J. Mechanical performance of FDM-printed PLA TPMS lattices under hydrothermal aging. Thin-Walled Struct. 2026, 218, 113924. [Google Scholar] [CrossRef]
- Cao, X.; Yang, H.; Ren, X.; Wu, W.; Xi, L.; Li, Y.; Fang, D. Mechanical performance and defect analysis of the imperfect micro smooth gyroid cylinder shell structure. Compos. Struct. 2021, 273, 114320. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.S.A.; Abu Al-Rub, R.K.; Jasiuk, I.M. Compression and buckling of microarchitectured Neovius-lattice. Extrem. Mech. Lett. 2020, 37, 100688. [Google Scholar] [CrossRef]
- Hauptmann, N.; Lian, Q.; Ludolph, J.; Rothe, H.; Hildebrand, G.; Liefeith, K. Biomimetic Designer Scaffolds Made of D,L-Lactide-ɛ-Caprolactone Polymers by 2-Photon Polymerization. Tissue Eng. Part B Rev. 2019, 25, 167–186. [Google Scholar] [CrossRef] [PubMed]
- Baumer, V.; Isaacson, N.; Kanakamedala, S.; McGee, D.; Kaze, I.; Prawel, D. Comparing ceramic Fischer-Koch-S and gyroid TPMS scaffolds for potential in bone tissue engineering. Front. Bioeng. Biotechnol. 2024, 12, 1410837. [Google Scholar] [CrossRef]
- Moore, A.L.; Shi, L. Emerging challenges and materials for thermal management of electronics. Mater. Today 2014, 17, 163–174. [Google Scholar] [CrossRef]
- Khalaj, A.H.; Halgamuge, S.K. A Review on efficient thermal management of air- and liquid-cooled data centers: From chip to the cooling system. Appl. Energy 2017, 205, 1165–1188. [Google Scholar] [CrossRef]
- Hung, T.C.; Huang, Y.X.; Yan, W.M. Thermal performance analysis of porous-microchannel heat sinks with different configuration designs. Int. J. Heat Mass Transf. 2013, 66, 235–243. [Google Scholar] [CrossRef]
- Hajialibabaei, M.; Saghir, M.Z. Experimental Study on Heat Transfer Performance of FKS-TPMS Heat Sink Designs and Time Series Prediction. Energies 2025, 18, 3459. [Google Scholar] [CrossRef]
- Clarke, D.R. Interpenetrating Phase Composites. J. Am. Ceram. Soc. 1992, 75, 739–758. [Google Scholar] [CrossRef]
- Liu, W.; Köster, U. Microstructures and properties of interpenetrating alumina/aluminium composites made by reaction of SiO2 glass preforms with molten aluminium. Mater. Sci. Eng. A 1996, 210, 1–7. [Google Scholar] [CrossRef]
- Jhaver, R.; Tippur, H. Processing, compression response and finite element modeling of syntactic foam based interpenetrating phase composite (IPC). Mater. Sci. Eng. A 2009, 499, 507–517. [Google Scholar] [CrossRef]
- Kouzeli, M.; Dunand, D. Effect of reinforcement connectivity on the elasto-plastic behavior of aluminum composites containing sub-micron alumina particles. Acta Mater. 2003, 51, 6105–6121. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, H.; Yuan, R.; Wang, S.; Fan, T.; Rezgui, Y.; Zhang, D. The near-isotropic elastic properties of interpenetrating composites reinforced by regular fibre-networks. Mater. Des. 2022, 221, 110923. [Google Scholar] [CrossRef]
- Liu, Z.; Gong, H.; Gao, J.; Liu, L. Bio-inspired design, mechanical and mass-transport characterizations of orthotropic TPMS-based scaffold. Compos. Struct. 2023, 321, 117256. [Google Scholar] [CrossRef]
- Shahid, M.N.; Shahid, M.U.; Rasheed, S.; Irfan, M.; Obeidi, M.A. Computational Investigation of the Fluidic Properties of Triply Periodic Minimal Surface (TPMS) Structures in Tissue Engineering. Designs 2024, 8, 69. [Google Scholar] [CrossRef]
- Maevskaia, E.; Ghayor, C.; Bhattacharya, I.; Guerrero, J.; Weber, F.E. TPMS Microarchitectures for Vertical Bone Augmentation and Osteoconduction: An In Vivo Study. Materials 2024, 17, 2533. [Google Scholar] [CrossRef]
- Günther, F.; Wagner, M.; Pilz, S.; Gebert, A.; Zimmermann, M. Design procedure for triply periodic minimal surface based biomimetic scaffolds. J. Mech. Behav. Biomed. Mater. 2022, 126, 104871. [Google Scholar] [CrossRef]
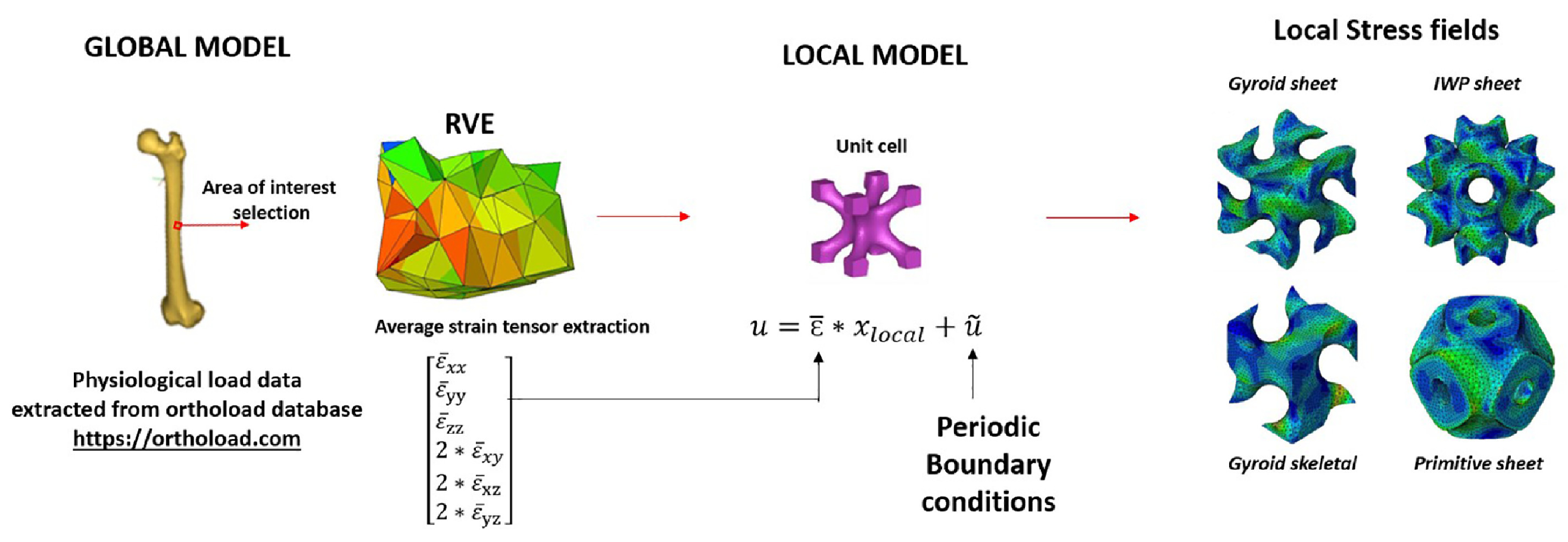
- Chatzigeorgiou, C.; Piotrowski, B.; Meraghni, F.; Chemisky, Y. Multiscale mechanical analysis for biomimetic implant design based on Triply Periodic Minimal Surfaces (TPMS) lattices: Application to partial replacement of femoral bone. Results Eng. 2025, 25, 103984. [Google Scholar] [CrossRef]
- Gao, T.; Liu, K.; Wang, X.; Wei, K.; Wang, Z. Multi-level mechanism of biomimetic TPMS hybridizations with tailorable global homogeneity and heterogeneity. Extrem. Mech. Lett. 2024, 68, 102136. [Google Scholar] [CrossRef]
- Dong, X.; Wang, G.; Wang, S.; Yang, X.; Wen, D.; Zhang, L. Designing and additive manufacturing of biomimetic interpenetrating phase zirconia-resin composite dental restorations with TPMS structure. J. Mech. Behav. Biomed. Mater. 2024, 160, 106718. [Google Scholar] [CrossRef]
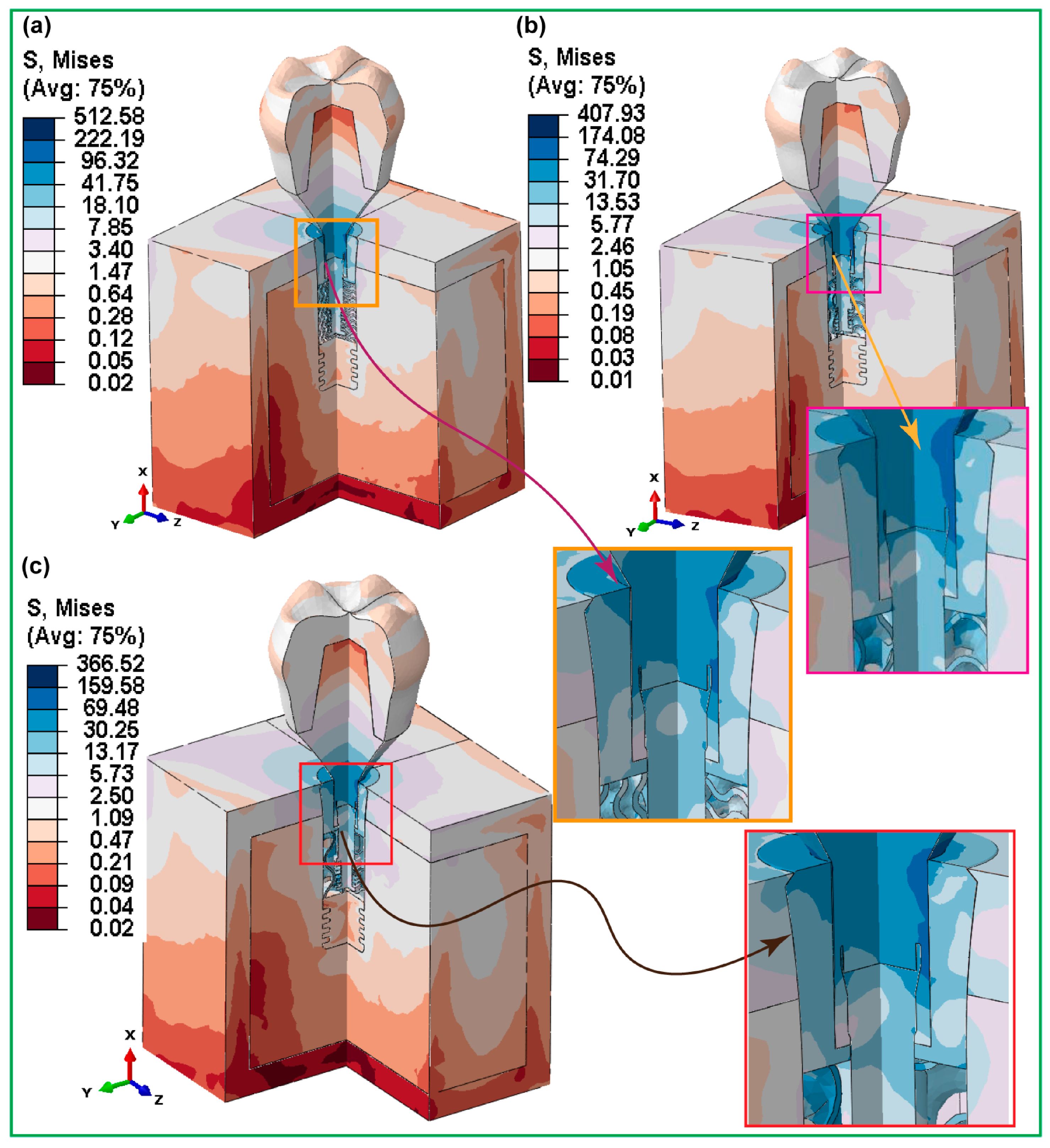
- Alemayehu, D.B.; Todoh, M.; Huang, S.J. Hybrid Biomechanical Design of Dental Implants: Integrating Solid and Gyroid Triply Periodic Minimal Surface Lattice Architectures for Optimized Stress Distribution. J. Funct. Biomater. 2025, 16, 54. [Google Scholar] [CrossRef]
- Li, L.; Wang, P.; Jin, J.; Xie, C.; Xue, B.; Lai, J.; Zhu, L.; Jiang, Q. The triply periodic minimal surface-based 3D printed engineering scaffold for meniscus function reconstruction. Biomater. Res. 2022, 26, 45. [Google Scholar] [CrossRef]
- Dong, Z.; Zhao, X. Application of TPMS structure in bone regeneration. Eng. Regen. 2021, 2, 154–162. [Google Scholar] [CrossRef]






| Manufacturing Technique | Key Findings/ Achievements | Common Defects/ Limitations | Best Application Area | Achieved Scale/Resolution | Availability/Cost |
|---|---|---|---|---|---|
| SLA (Stereolithography) | High precision and smooth surface finish; ideal for polymer TPMS scaffolds. | Brittle resin, shrinkage, limited build size. | Bone scaffolds, tissue engineering—smooth surface enhances cell adhesion and biological response. | Layer thickness: 25–50 µm | Widely available; moderate cost |
| DLP (Digital Light Processing) | High-resolution ceramic/polymer TPMS with tunable porosity and strength up to 937 MPa. | Light scattering, sintering shrinkage, small build area. | Biomedical scaffolds, thermal ceramics—precise control for bioactive materials. | Grain size: 1–8 µm | Commercial; medium cost |
| FDM (Fused Deposition Modeling) | Cost-effective fabrication; tunable porosity via infill patterns. | Poor surface finish, anisotropy, limited resolution. | Structural prototypes, polymer scaffolds—low-cost for functional TPMS models. | Pore size: 650–1000 µm; layer height: 0.12 mm | Highly available; very low cost |
| SLS (Selective Laser Sintering) | Complex polymer/metal TPMS with good accuracy and strength. | Surface roughness, incomplete sintering, powder waste. | Aerospace lattice cores—strong, lightweight designs with complex geometries. | Layer thickness: 50–80 µm | Commercial; high cost |
| SLM (Selective Laser Melting) | Fully dense metallic TPMS; adjustable porosity for strength/stiffness control. | Residual stress, high roughness, post-processing required. | Load-bearing implants, metallic lattices—excellent mechanical and biocompatibility performance. | Layer thickness: 30 µm | Commercial industrial; very high cost |
| EBM (Electron Beam Melting) | Produces high-strength metal TPMS with lower residual stresses. | High surface roughness, limited resolution. | Orthopedic and aerospace parts—dense, stress-free metallic lattices. | Layer thickness: 50 µm | Industrial; very high cost |
| 2PP (Two-Photon Polymerization) | Ultra-high precision sub-micron TPMS fabrication. | Small build volume, slow, expensive. | Micro-tissue scaffolds, photonics—ideal for cellular-level control. | 0.2 µm voxel size | Lab-scale; extremely high cost |
| Robocasting (Direct Ink Writing) | Bioceramic TPMS with gradient porosity and bioactivity. | Cracking during drying/sintering, low mechanical strength. | Bone tissue engineering—tunable degradation and pore structure. | Nozzle Ø 0.41 mm | Lab to pilot scale; low–medium cost |
| Micro-SLA | Fine polymeric TPMS scaffolds with high surface quality and accuracy. | Shrinkage, polymerization defects, low mechanical load capacity. | Soft-tissue scaffolds—precise, smooth features for biocompatibility. | Layer thickness: 5 µm | Laboratory-scale; moderate cost |
| Sr# | Author(s) | Structure Type | Primary Application | Analysis Method/ Manufacturing Process | Comparison/ Benchmark | Methodology & Validation | Key Findings | Limitations or Future Works | Source DOI |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Mian et al., 2025 | Schwarz-P | Electronics heat sink cooling | CFD on AM materials, no physical fabrication | Compared with traditional plate-fin heat sink; validated via pin-fin model | Simulated flow and thermal performance using SST k-ω model; varied unit cell sizes (5–20 mm) and porosity (65–75%); validation done | Smaller cell sizes improve heat transfer but increase pressure drop; 5 mm Schwarz-P is 50% more efficient; lower porosity improves resistance | AM limits: surface defects, high computation; needs experimental validation | https://doi.org/10.1016/j.csite.2025.106273 |
| 2 | Ansari & Duwig 2024 | Gyroid | Microprocessor cooling | CFD on AM materials, no physical fabrication | Compared Gyroid (GHS) vs. pin-fin (PHS) under porosity 0.5–0.8 | Conjugate heat transfer; analyzed flow, temperature, pressure via streamlines; hotspot analysis | GHS outperformed PHS by 30% lower resistance; 3D helical flow enhanced transfer; lower porosity, higher flow rate improved performance | Limited porosity range; high pressure drop; explore graded porosity, roughness, TPMS orientation | https://doi.org/10.1016/j.enconman.2024.118918 |
| 3 | Modrek et al., 2022 | Gyroid | Thermal management in AM heat sinks | Modeled in nTopology + Abaqus thermal simulation | Compared SIMP and homogenized gyroid (solid/sheet) designs | Topology optimization (SIMP & homogenized); FE homogenization; thermal conductivity simulations | Gradient-mapped gyroid-sheet had highest conductivity, lowest temperature; outperformed SIMP/solid | Experimental validation pending; only steady-state conduction studied; explore other TPMS (D/P) | https://doi.org/10.1016/j.csite.2022.102161 |
| 4 | Baobaid et al., 2022 | Diamond, Gyroid | Passive natural convection cooling | CFD (Star-CCM+); AlSi10Mg properties | Compared with pin-fin and metal foam heat sinks; orientation studied | Simulations under enclosures; radiation included; derived Nu–Ra correlation | Gyroid-sheet 50% better than pin-fin; radiation 17–23% of heat dissipation; horizontal 11.5% better; outperformed Al foam by 44% | Future work: porosity effects with varied TPMS geometries | https://doi.org/10.1016/j.csite.2022.101944 |
| 5 | Saghir & Rahman 2024 | Gyroid | Forced convection cooling (water) | COMSOL simulation + experiments vs. Al 6061-T6 foam | Compared TPMS vs. metal foam; parallel vs. perpendicular flow | FEM (Navier–Stokes, conduction); varied porosities, flow directions | TPMS superior to foam; gyroid gave uniform cooling; parallel flow more effective; optimal PEC at ɸ = 0.8 | Impingement jets less effective; test 3D-printed TPMS; study turbulent regimes | https://doi.org/10.3390/fluids9120297 |
| 6 | Chen et al., 2025 | Gyroid | Thermal dissipation | SLM (AlSi10Mg, 33 µm avg.) | Compared TPMS vs. plate-fin heat sink | CFD (COMSOL) + experiments (1–10 L/min, 500 W load) | TPMS had 60% higher efficiency, lower pressure drop/pump power; improved temperature uniformity | Focused on Gyroid only; future work: other TPMS, thinner fins, turbulent flow | https://doi.org/10.1016/j.tsep.2025.103499 |
| 7 | Wang et al., 2024 | Gyroid | Electronics cooling | 3D-printed TPMS samples | Compared 3 TPMS geometries + baseline | Simulations + experiments under cycling; temperature and HTC analyzed | TPMS outperformed conventional; better uniformity; 12.9–16.6% HTC improvement | Limited to one PCM type/power; future work on PCM enhancement, variable heat loads | https://doi.org/10.1016/j.ijheatmasstransfer.2024.126078 |
| Sr# | Author(s) | Structure Type | Primary Application | Manufacturing Process | Comparison/ Benchmark | Methodology & Validation | Key Findings | Limitations or Future Works | Source DOI |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Song et al., 2023 | Diamond, IWP, Gyroid | Mechanical energy absorption, impact protection | PolyJet-based multi-material 3D printing (VB+ as reinforcement, PP as matrix) | Compared IPCs with single-phase matrix/reinforcement; validated via FEM | Experimental compression testing + FEM (RVE and full model) validation; IPC strength and SEA compared with sum of constituents; studied effect of equivalent density and deformation modes | IPCs showed up to 497% strength increase over constituent phases; 33% SEA improvement; Diamond best SEA (24.6 J/g), Gyroid highest strength (84 MPa); strong synergistic effect | FEM assumes perfect bonding; dynamic/turbulent loads not explored; future work could explore more material combinations and real-world loads | https://doi.org/10.1016/j.tws.2023.111210 |
| 2 | Singh & Karathanasopoulos 2024 | Gyroid, IWP, P-Cell TPMS and stochastic spinodal | Mechanical and dynamic damping performance of architected IPCs | Additive manufacturing with ceramic-epoxy co-continuous phases; with and without whisker reinforcement | Compared SEA and damping performance against advanced architected materials (steel TPMS, Ti TPMS, TPU, CNT foams, PA) using Ashby plots | Static & dynamic tests (SEA, stress-strain, DMA 25–70 Hz); FEA & DIC for stress and crack analysis | IPCs show 10–30× strength over ceramic alone (peak > 140 MPa); SEA up to 18.5 J/g; damping matches wood/bone; spinodal better at 20%, TPMS better at 30% content | Dynamic tests limited to 70 Hz; only 20–30% phase content studied; no biomedical validation; needs calibrated dynamic IPC models | https://doi.org/10.1016/j.compscitech.2024.110632 |
| 3 | Xie et al., 2024 | Primitive, IWP | Bone scaffolds—improved strength, toughness, energy absorption | Photopolymerization-based additive manufacturing and PUF foaming | Compared IPCs with constituent scaffolds (PMMA, PUF); benchmarked with trabecular bone (2.96–4.01 MPa, 4–430 MPa modulus); validated simulation | Compression tests; SEM, CT, DIC, FEA; analyzed stress distribution, failure, and crack propagation | I-WP IPCs improved strength (134%), toughness (73%), and energy absorption (236%); within human trabecular bone range; better stress uniformity and synergy than Primitive | Tensile/fatigue testing missing; reduced PUF at high density affects performance; further study needed for crack propagation and bone integration | https://doi.org/10.1016/j.compstruct.2024.118526 |
| 4 | Santos et al., 2024 | Gyroid, Diamond, Primitive; Aluminium–Alumina | Mechanical performance improvement; energy absorption | DLP-based 3D printing of alumina TPMS + aluminium infiltration via investment casting | Compared different TPMS geometries and volume fractions; evaluated against cast aluminium | Compression testing (ISO 13314); SEM; Micro-CT; XRD; densification & shrinkage measurements | Diamond and Gyroid IPCs showed 10% higher plateau stress and 6.8% higher SEA vs. Primitive; IPCs improved compressive offset stress by 6% over Al alloy; pseudo-ductile failure in ceramics | Fatigue/tensile testing missing; Al–Al2O3 interface issues; further study needed on bonding and alternative materials | https://link.springer.com/article/10.1007/s40964-024-00698-7 |
| 5 | Guo et al., 2023 | Primitive | Structural composites with enhanced compressive strength and energy absorption | Metal AM via Micro-SLM (SS316L); epoxy (EPOLAM 2040) injection molding to form IPCs | Compared empty P-lattices and IPCs; modified vs. original P-lattice; FEM validation; benchmarked against linear sum of epoxy + lattice | Quasi-static compression testing; SEM imaging; FEM via Abaqus; evaluated internal energy of lattice, epoxy, and IPC | Modified TPMS (SP & BP) enhanced SEA (up to 49.6 J/g) and strength; improved crushing resistance; FEM showed 136% ↑ in lattice energy and 21% ↑ in epoxy contribution | Limited to static compression; not tested for fatigue; fracture/delamination observed; mechanical behavior depends on lattice direction; explore multi-axial loading | https://doi.org/10.1016/j.compositesb.2022.110351 |
| Sr# | Author(s) | Structure Type | Primary Application | Manufacturing Process | Comparison/ Benchmark | Methodology & Validation | Key Findings | Limitations or Future Works | Source DOI |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Raffaele Pugliese et al., 2024 | Primitive, Gyroid | Knee meniscal implants | FDM printing proposed | Compared to healthy knee | FEA for stress analysis | TPMS-based meniscal implants prevent higher magnitude compression and shear stress on articular cartilage | Effects of variations in pore size, porosity, and pore shape of the meniscal implant should be studied | https://doi.org/10.1016/j.slast.2023.04.004 |
| 2 | Rati Verma et al., 2022 | Primitive, Gyroid | Segmental bone defect (Femur) | Designed for AM using Ti6Al4V, not fabricated | Compared with solid scaffold | FEA for porosity-dependent stress & modulus; biomechanical model of femur used | P scaffold improved stress transfer by 76% vs. solid; stiffness reduced from 107 GPa (solid) to 4.2–29.6 GPa matching bone; stretching-dominant deformation | Need experimental validation; suggested experimental permeability analysis and clinical validation | https://doi.org/10.3390/coatings12060839 |
| 3 | Hou et al., 2022 | Graded Primitive | Dental implants | SLM (CP-Ti; Porosities: 48–68%) | Compared P50–P70 vs. human bone | FEA simulation, compression testing, permeability testing, in vitro biocompatibility, PCR analysis for osteogenic genes | P60 scaffold showed optimal mechanical properties (E = 9.7 GPa, σy = 163 MPa); permeability within bone range; strong osteogenic differentiation | Slight porosity deviation, surface roughness reduced permeability, clinical validation needed | https://doi.org/10.1016/j.bioadv.2022.213018 |
| 4 | Dabaja et al., 2025 | Gyroid, Voronoi Stochastic Lattice | Dental implants | SLM with Ti6Al4V ELI Grade 23 | Compared 3 porous architectures vs. dense implant | MicroCT, SEM, confocal microscopy, RNA extraction, CFD for permeability | TPMS solid gyroid showed highest resolution, controlled porosity (220 µm), 4× higher RNA, best cell adhesion, uniform distribution, highest permeability | In vitro only; SLM-induced partially melted particles; future CFD needed with real blood conditions | https://link.springer.com/article/10.1186/s40729-025-00618-6 |
| 5 | Jiaqi Ma et al., 2024 | Primitive, Gyroid, I-WP, Diamond, Fischer–Koch S | Bone regeneration (dental, cortical, trabecular, breast, ocular) | 3D printing (primarily FDM); hydrogel infusion for soft tissue | Compared TPMS scaffolds with conventional implants and natural bone | Literature review of clinical & experimental findings; mechanical behavior, permeability, antibacterial use, anisotropic behavior | TPMS scaffolds offer high permeability, bone-mimicking structure, favorable mechanical properties (20–60 MPa), enhanced osseointegration | Limited to 3D printing; deviation between designed and printed geometry; rough surface; small-aperture clogging; only preclinical studies | https://doi.org/10.1177/20417314241263689 |
| 6 | Shen et al., 2023 | Diamond, Gyroid, IWP, Diamond, Gyroid | Femoral bone defect regeneration in rabbits | DLP-based 3D printing of Ca0.94Mg0.06SiO3 scaffolds (>50% porosity, >500 µm) | Compared 5 TPMS geometries (3 non-sheet vs. 2 sheet-type) | In vivo rabbit model, µCT, histology, mechanical testing, BV/TV, Tb.N, Tb.Th, BS/TS | Diamond and Gyroid scaffolds showed highest bone ingrowth; sheet-type better compressive strength but lower osteoconductivity | Early-stage bone formation inhibited in sheet-type pores; osteoconductivity strongly depends on pore geometry; further studies on remodeling needed | https://doi.org/10.1016/j.bioactmat.2023.02.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, S.Z.; Masood, M.H.; Khattab, M.U.; Ahmad, S.S.; Zaidi, S.A.A.; Khan, S.Z. Recent Developments in Novel TPMS Lattice Materials: Design Optimization, Performance Control, and Applications in Biomimetic Scaffolds. Materials 2025, 18, 5209. https://doi.org/10.3390/ma18225209
Ahmad SZ, Masood MH, Khattab MU, Ahmad SS, Zaidi SAA, Khan SZ. Recent Developments in Novel TPMS Lattice Materials: Design Optimization, Performance Control, and Applications in Biomimetic Scaffolds. Materials. 2025; 18(22):5209. https://doi.org/10.3390/ma18225209
Chicago/Turabian StyleAhmad, Syed Zahid, Muhammad Hassan Masood, Muhammad Umar Khattab, Syed Sulman Ahmad, Syed Asad Ali Zaidi, and Shoaib Z. Khan. 2025. "Recent Developments in Novel TPMS Lattice Materials: Design Optimization, Performance Control, and Applications in Biomimetic Scaffolds" Materials 18, no. 22: 5209. https://doi.org/10.3390/ma18225209
APA StyleAhmad, S. Z., Masood, M. H., Khattab, M. U., Ahmad, S. S., Zaidi, S. A. A., & Khan, S. Z. (2025). Recent Developments in Novel TPMS Lattice Materials: Design Optimization, Performance Control, and Applications in Biomimetic Scaffolds. Materials, 18(22), 5209. https://doi.org/10.3390/ma18225209







