Study on Restraint Effect of Post-Casting Belt in Full-Section Interval Casting Immersed Tube
Abstract
1. Introduction
2. Field Test Analysis
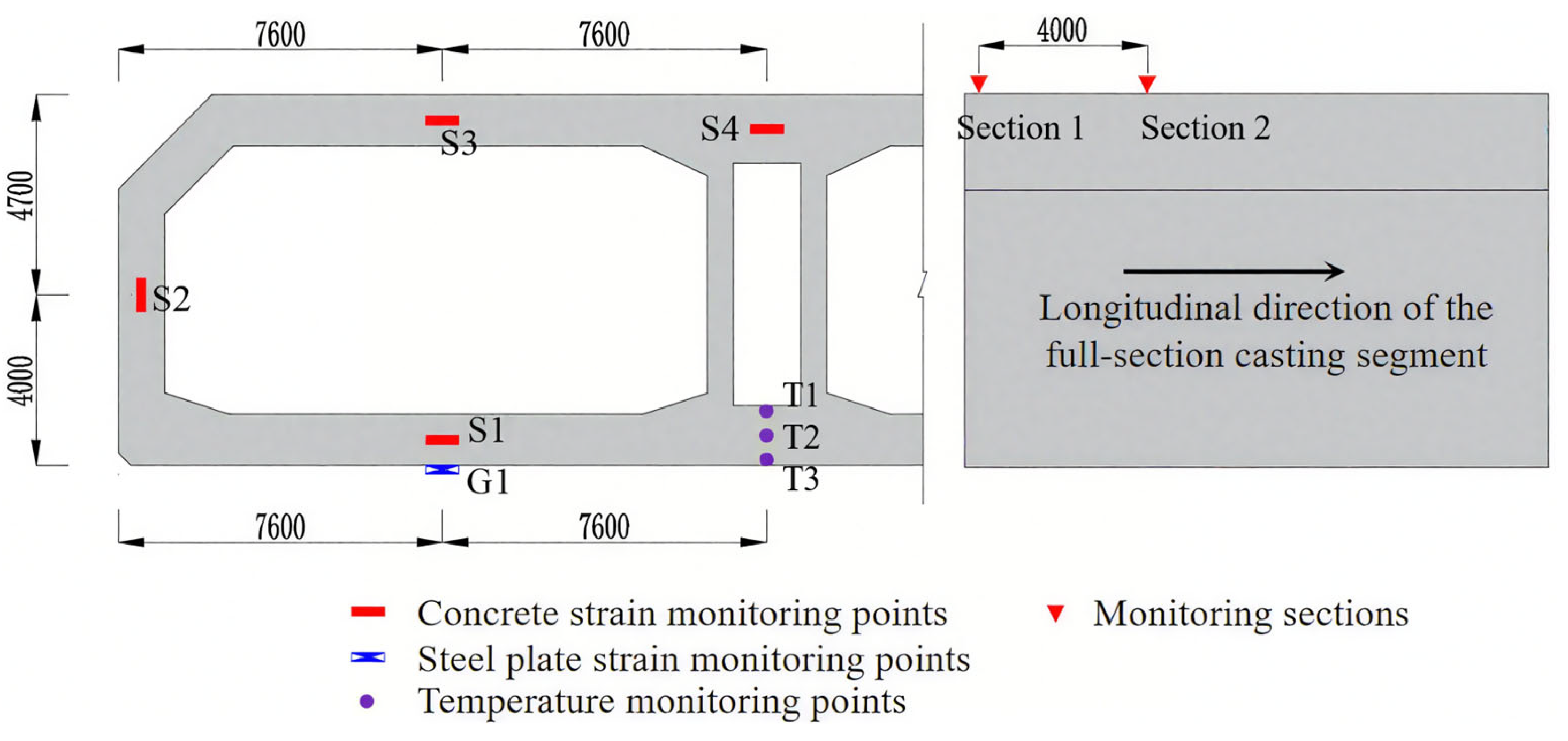
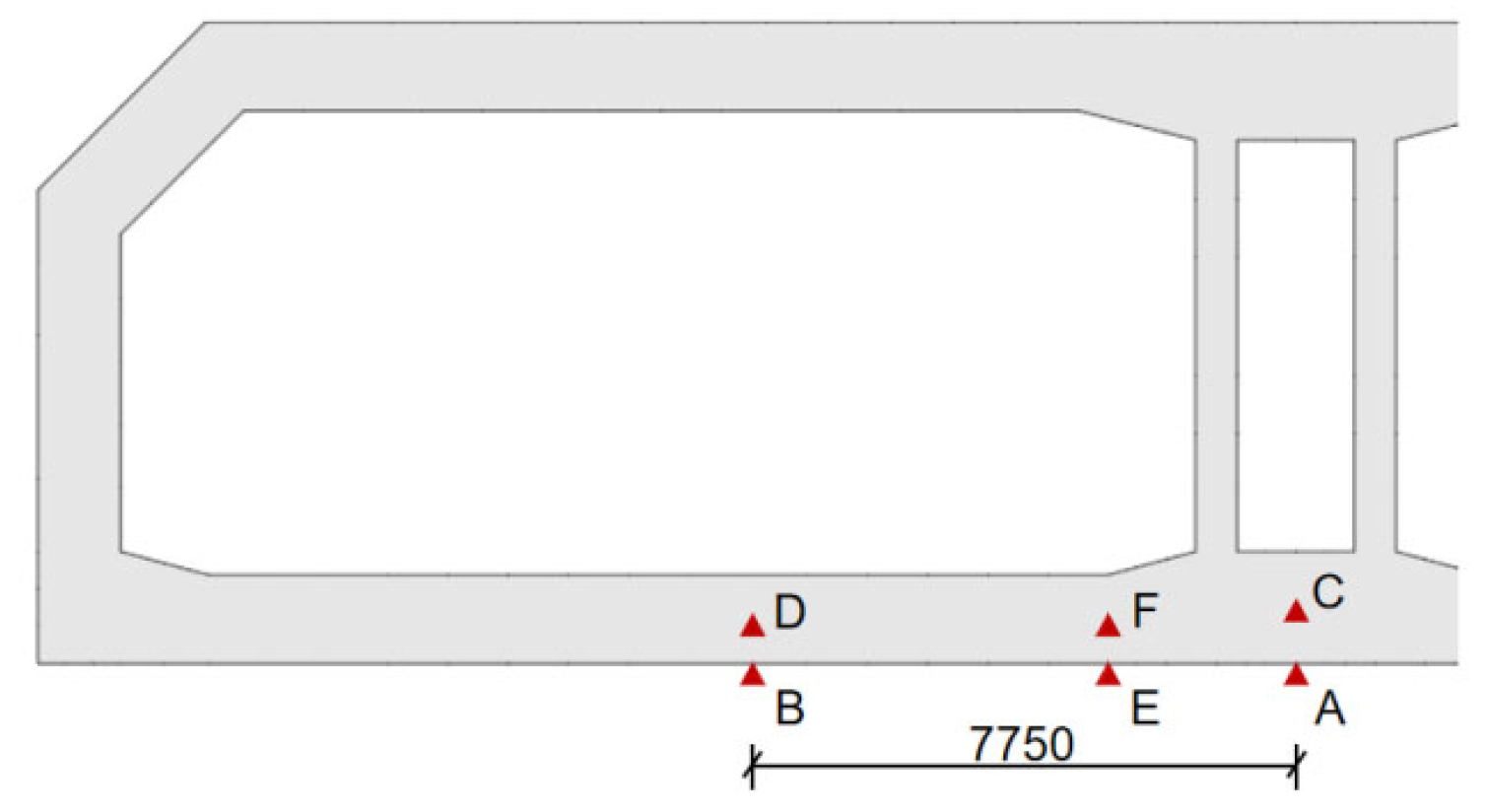
2.1. Instrumentation
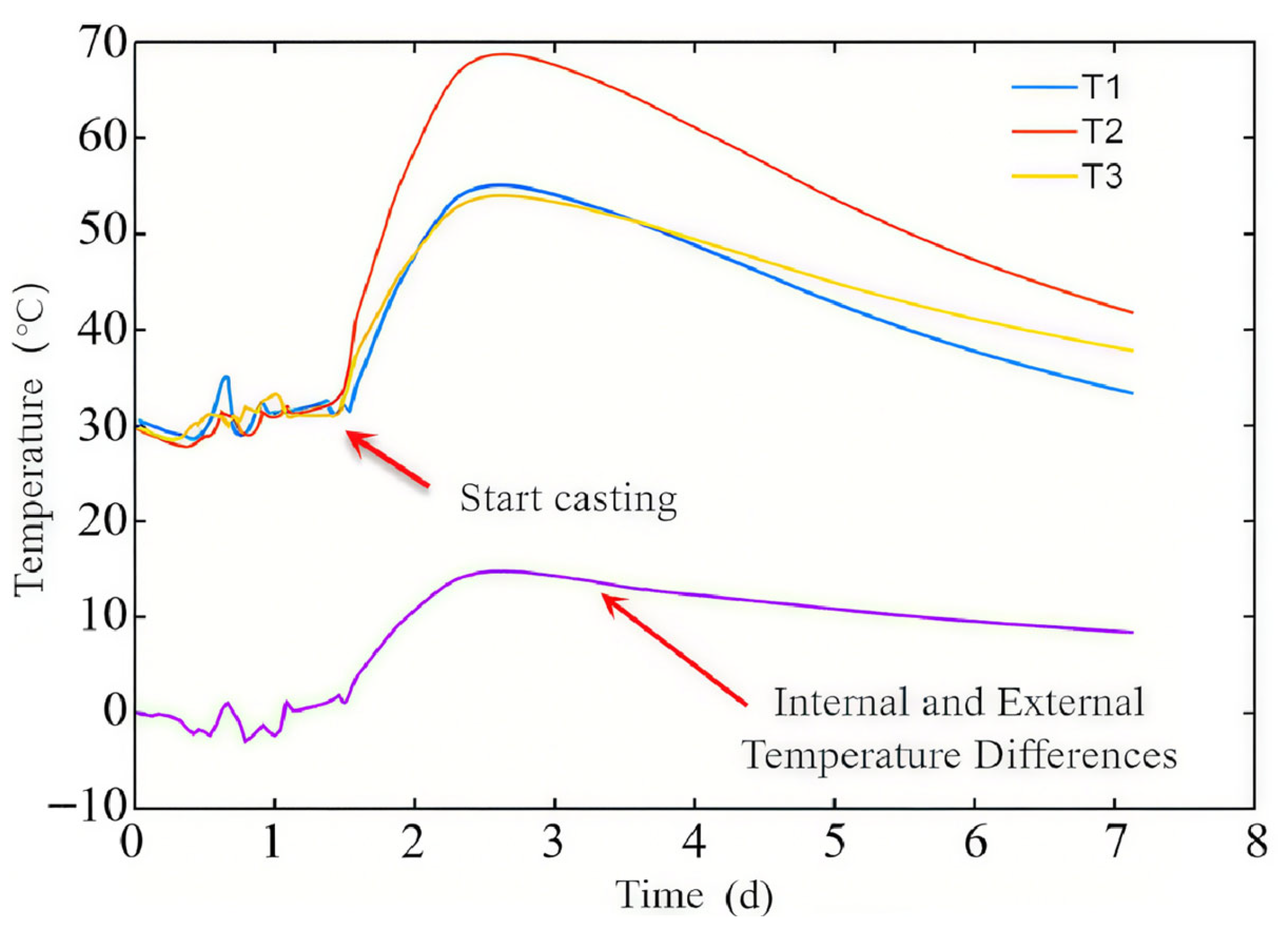
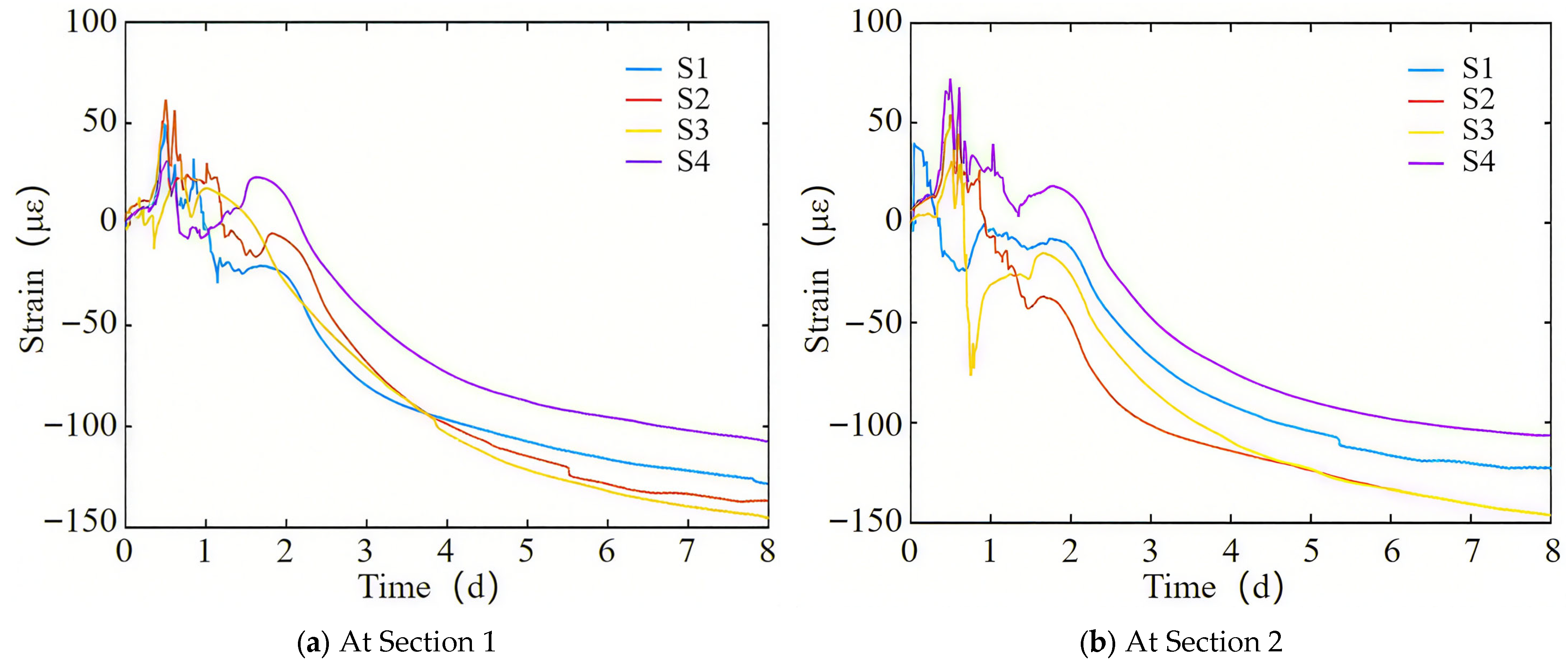
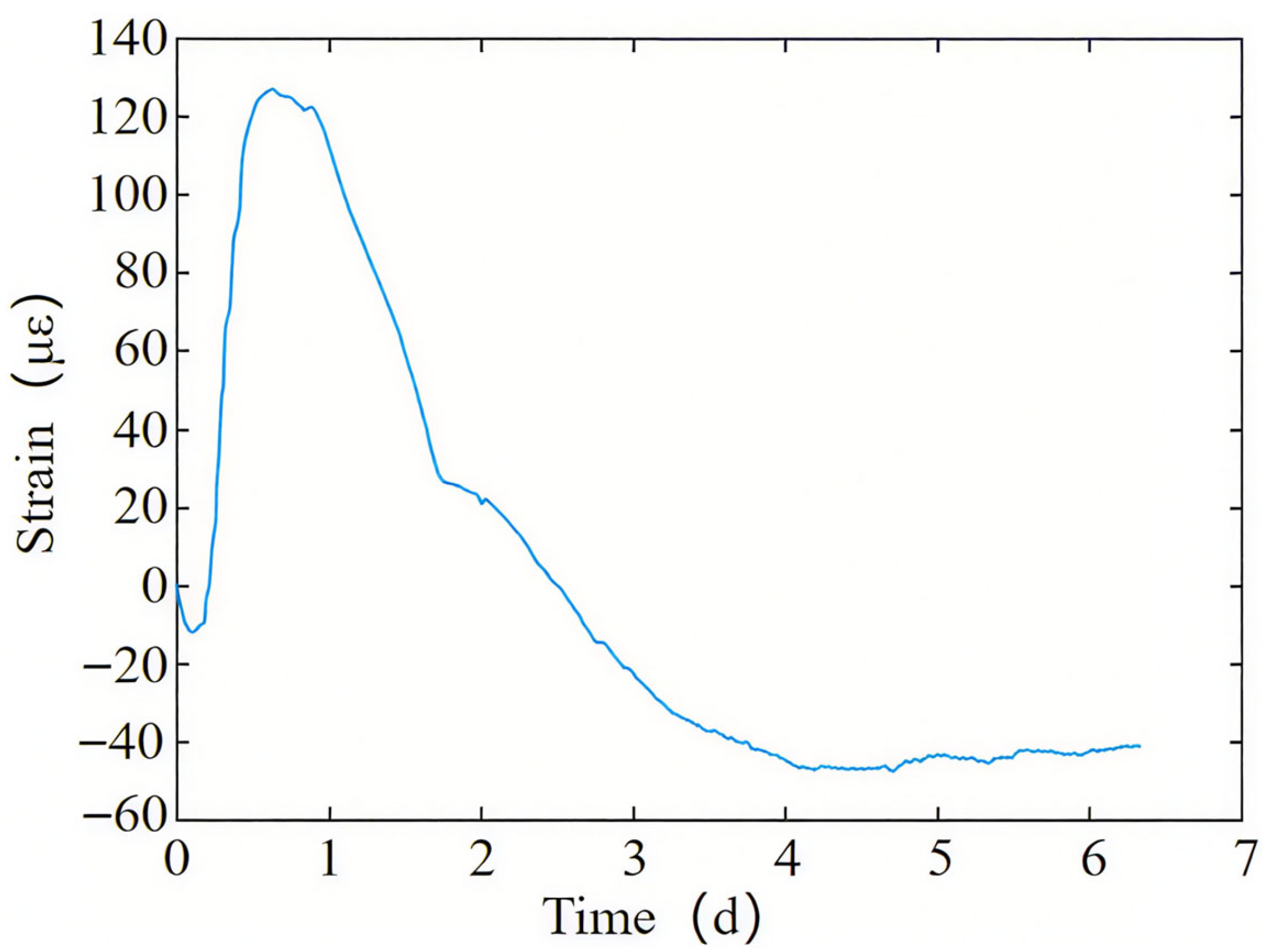
2.2. Field Test Data Analysis
3. Numerical Calculation Analysis
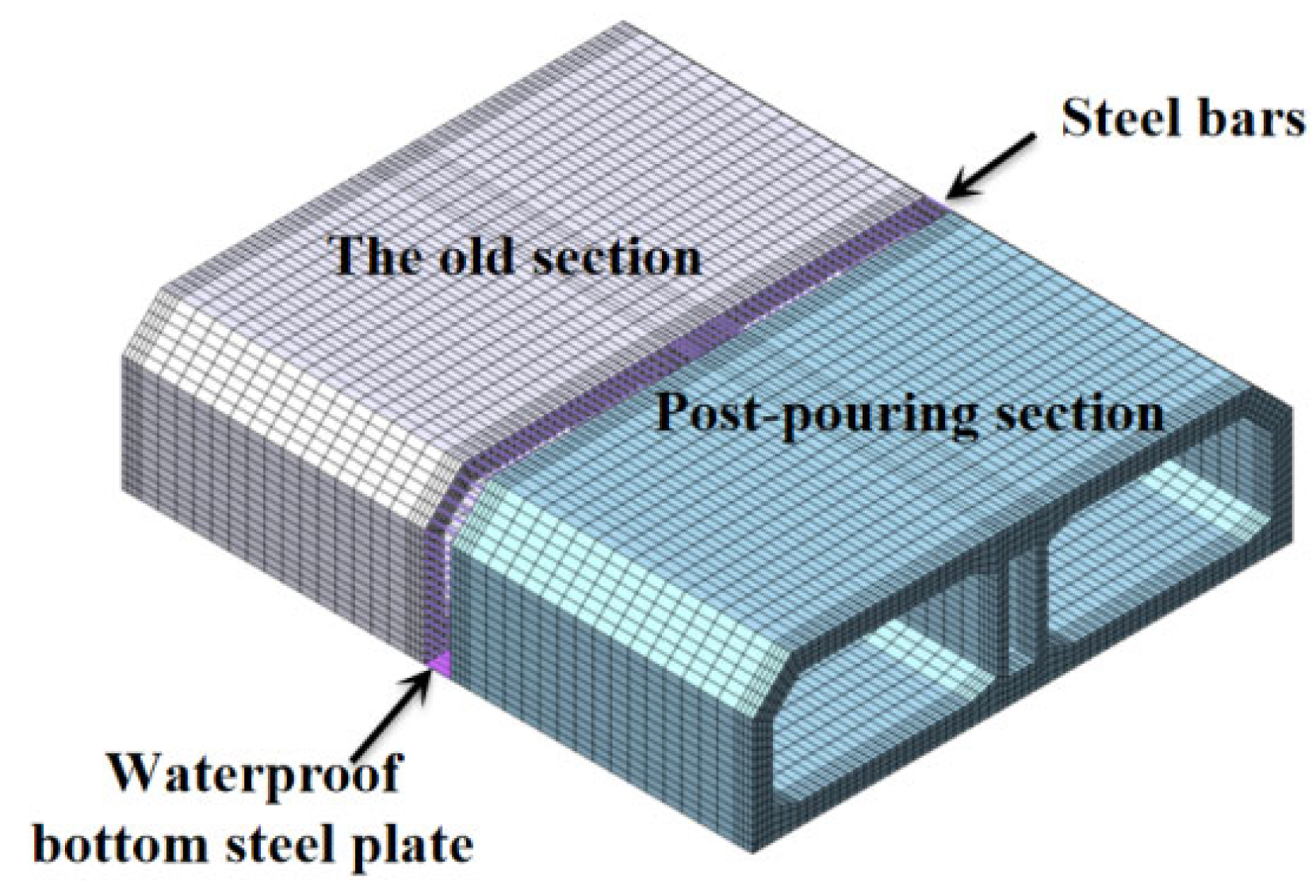
3.1. Finite Element Model
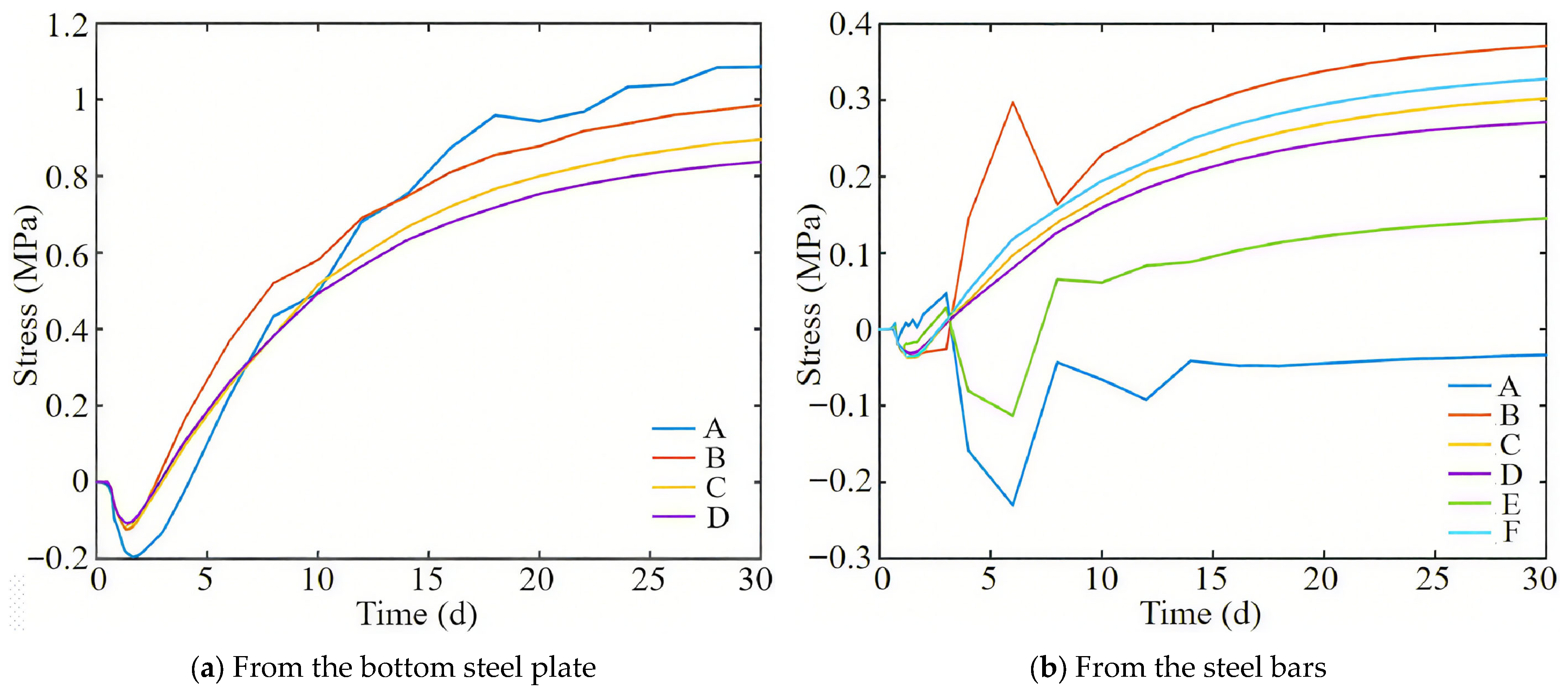
3.2. Calculation Results Analysis
4. Analysis of Constraint Effect of the Post-Casting Belt
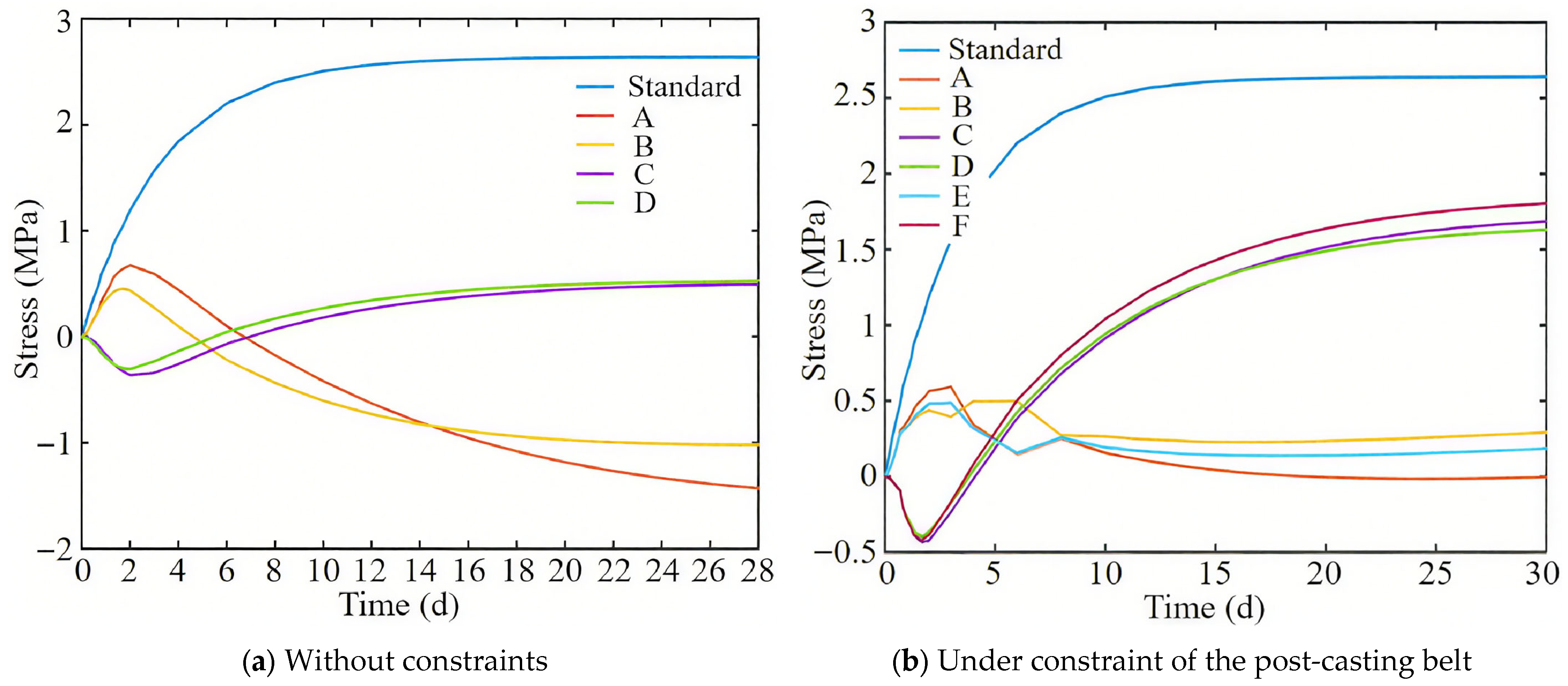
4.1. Stress Analysis of the Full-Section Casting Segment Without Constraints
4.2. Stress Analysis of the Full-Section Casting Segment Under Constraint of Post-Casting Belt
4.3. Analysis of the Requirements for Setting the Length of the Post-Casting Belt
5. Conclusions
- (1)
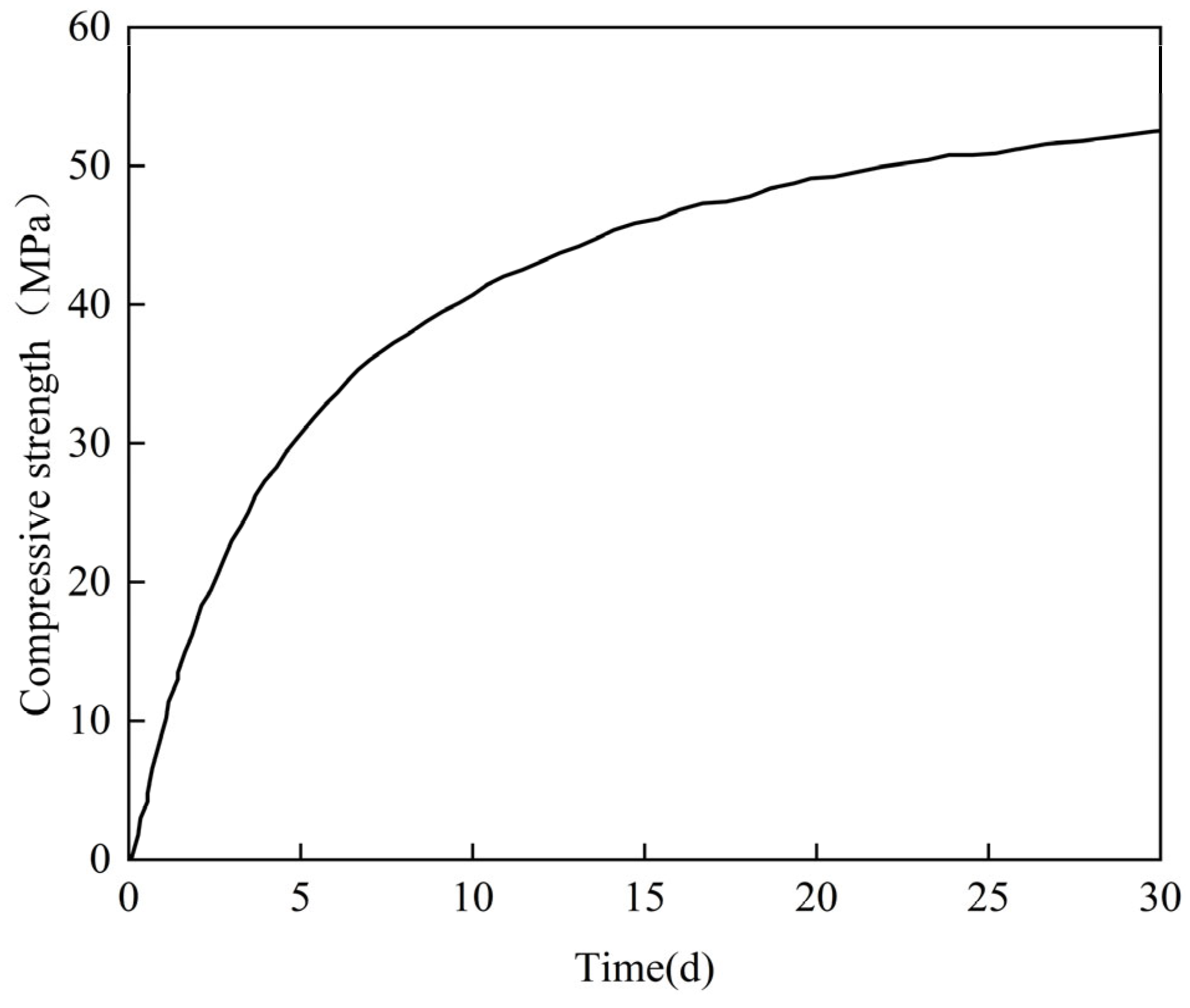
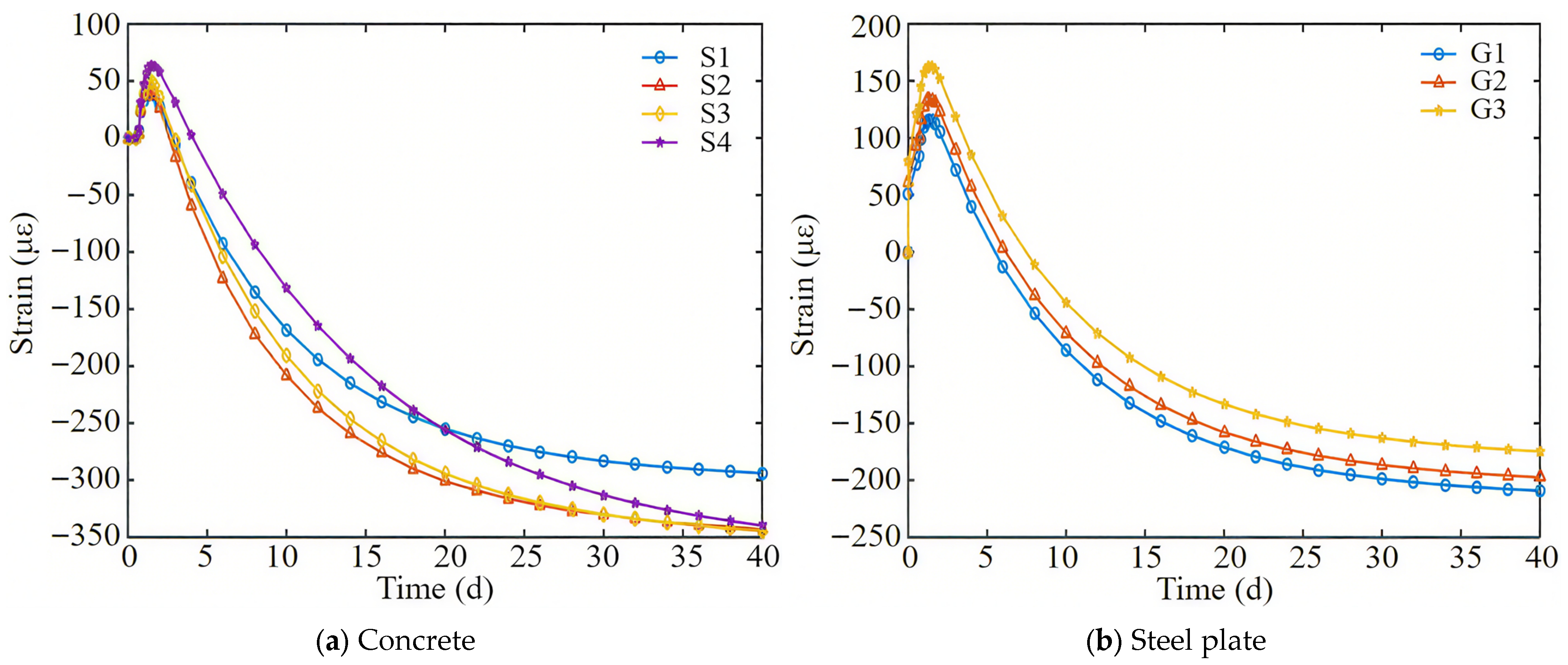
- Due to the combined effects of hydration, heat temperature field, and concrete shrinkage, the full-section casting segment first expands and then shrinks, with a final strain of 348 με. The strain caused by concrete temperature drop and shrinkage accounts for 59% and 41%, respectively.
- (2)
- When the hydration heat temperature rises, due to the plastic flow state of the concrete, the expansion of the bottom steel plate is greater than that of the concrete. Subsequently, as the strength of the concrete increases, the bottom steel plate and the concrete form a force-bearing whole and shrink together with the temperature drop.
- (3)
- This article proposes a method for determining the thermal expansion coefficient during the concrete pouring process through on-site testing and analysis, and verifies its reliability through numerical calculation and comparative analysis. However, due to limited monitoring data, we will verify the reliability of the calculation formula through data from multiple projects in the future.
- (4)
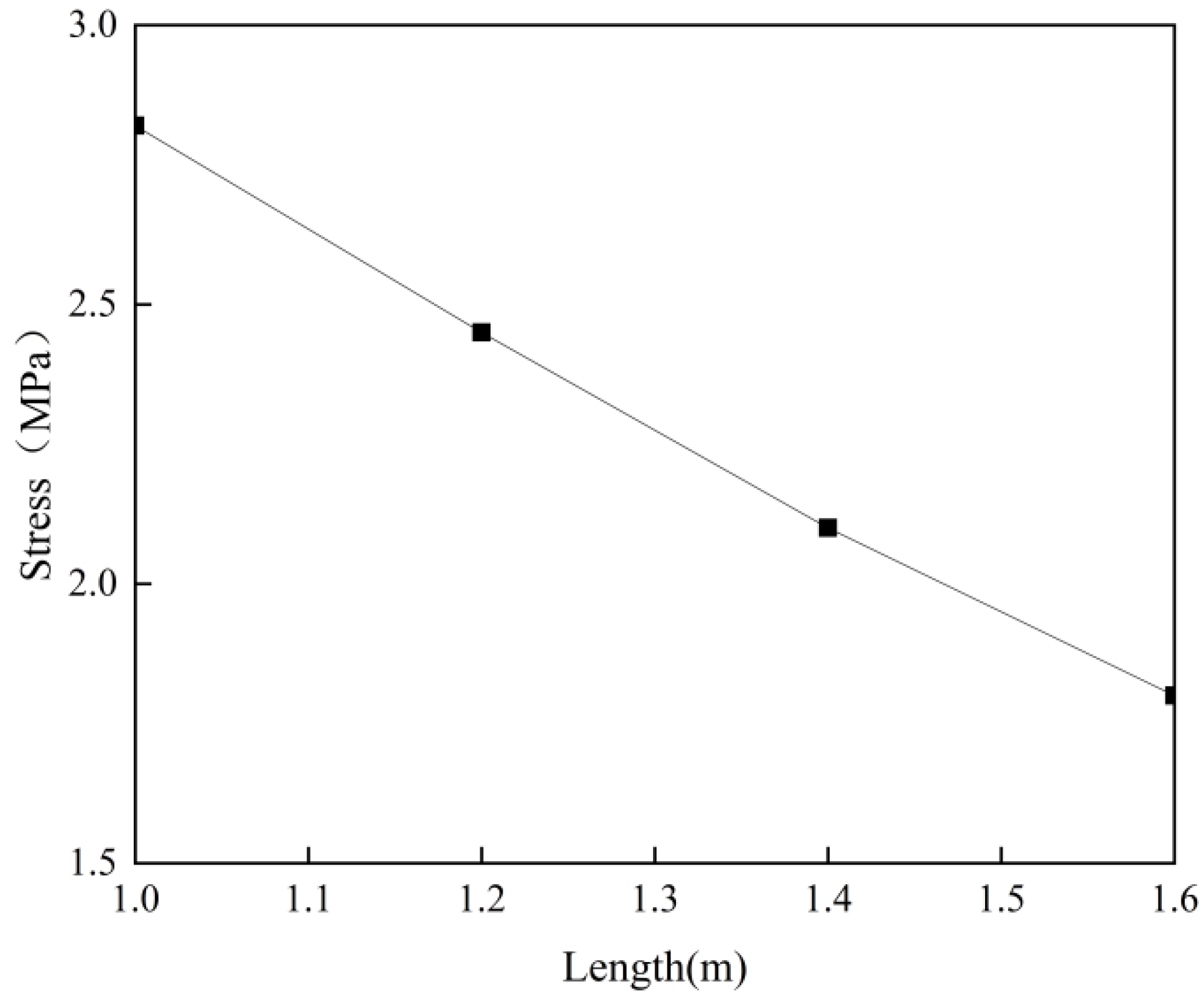
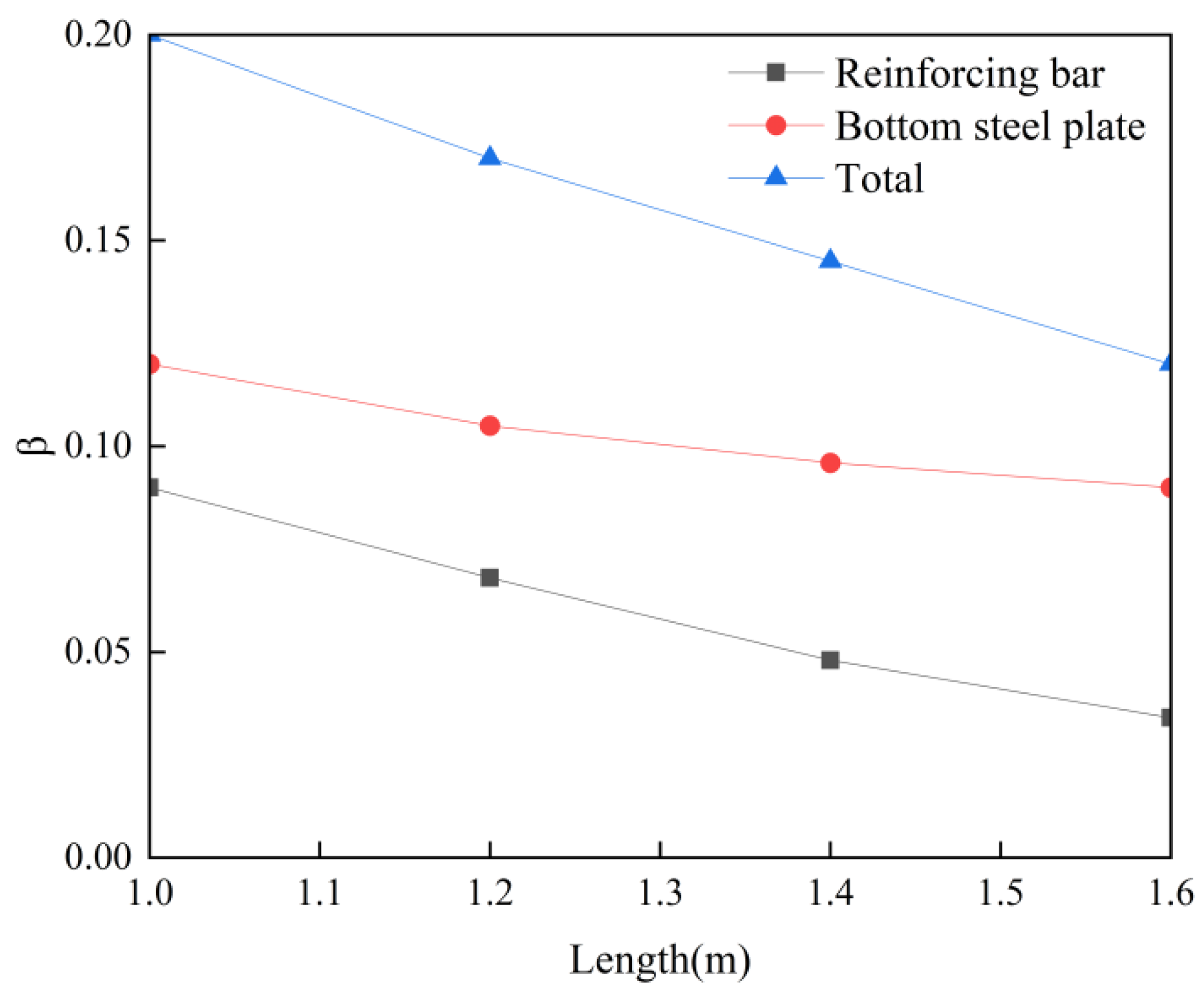
- The post-casting belt exerts a restraining effect on the full-section casting segment, and the shorter the post-casting belt, the greater the restraining effect. The post-casting belt length of the Chebei Tunnel is 1.6 m, and the post-casting belt restraint causes an increase of 1.4 MPa in the tensile stress of the full-section casting segment. Based on comparative analysis of on-site monitoring data, the contribution of the bottom steel plate and steel bars restraint accounts for about 70% and 30%, respectively. And as the post-casting belt length becomes shorter, the contribution of steel bars will increase.
- (5)
- In practical engineering, the post-casting belt is often set at around 1.5 m, and the constraint coefficient of the post-casting belt can be taken as 0.13.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, E.; Li, P.; Lin, M.; Liu, X. The rationality of semi-rigid immersed tunnel element structure scheme and its first application in Hong Kong Zhuhai Macao bridge project. Tunn. Undergr. Space Technol. 2018, 82, 6–169. [Google Scholar] [CrossRef]
- Lin, M.; Lin, W. Hong Kong-Zhuhai-Macao Island and Tunnel Project; Engineering: Beijing, China, 2017. [Google Scholar]
- Zhao, J.; Gan, C.J.; Li, W.J. Seismic analysis of the south bank section and wind tower structures of Dalian Bay subsea immersed tube tunnel. J. Earthg. Eng. 2023, 45, 772–779+791. [Google Scholar]
- Zeng, B.C.; Pan, C.Z.; Ren, Y.P. Study on Scheme Selection of Supporting Structure Design for Deep Foundation Excavation of Dry Dock on Immersed Tunnel Axis. Constr. Technol. 2023, 52, 42–48. [Google Scholar]
- He, Y. Key Construction Technologies for Honggu Immersed Tunnel Located in Inland River in Nanchang. J. Tunn. Constr. 2016, 36, 1085–1094. [Google Scholar]
- Chen, Y. Application and Developing Trends of Immersed Tunnel. J. Mod. Tunn. Technol. 2017, 37, 387–393. [Google Scholar]
- Zhou, H.; Wang, L.; Wang, Y.; Min, X. Improved Deformation Calculation Method for Immersed Tunnels Considering Siltation Effects: A Case Study of the Yongjiang Immersed Tunnel in Ningbo, Zhejiang Province, China. Int. J. Geomech. 2025, 6, 04025105. [Google Scholar] [CrossRef]
- Adilkhodzhaev, A.I.; Kadirov, I.A.; Abdullaev, U.K. Some Issues of Moisture Transfer in Concrete. J. Eur. J. Humanit. Educ. Adv. 2021, 2, 20–23. [Google Scholar]
- Wu, Z.J.; Ma, Q.J.; Zhu, Y. Numerical Simulation Study on Thermal Damage of Concrete. Numer. Simul. Study Therm. Damage Concr. 2023, 8, 114–117. [Google Scholar]
- Gilbert, R.I. Cracking Caused by Early-Age Deformation of Concrete-Prediction and Control. J. Procedia Eng. 2017, 172, 13–22. [Google Scholar] [CrossRef]
- Samouh, H.; Roziere, E.; Loukili, A. Experimental and numerical study of the relative humidity effect on drying shrinkage and cracking of self-consolidating concrete. J. Cem. Concr. Res. 2019, 115, 519–529. [Google Scholar] [CrossRef]
- Podhajecky, A.L.; Oneschkow, N.; Kern, B. Influence of initial moisture content on creep and shrinkage of concrete at constant and cyclic ambient humidity. J. Mater. Struct. 2023, 56, 170. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, X.; Jiao, Y.; Zeng, B.; Tan, F.; Li, T.; Wei, P. Development and application of a new ballast water system for immersed tunnel installation: A case study of the Yuliangzhou tunnel in Xiangyang, China. Tunn. Undergr. Space Technol. 2022, 119, 104261. [Google Scholar] [CrossRef]
- Sun, Y.; Song, S.; Yu, H.; Ma, H.; Xu, Y.; Zu, G.; Ruan, Y. Experimental Study on the Strength and Durability of Manufactured Sand HPC in the Dalian Bay Undersea Immersed Tube Tunnel and Its Engineering Application. Materials 2024, 17, 5003. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.H.; Chen, R.Y.; Yuan, J. Experimental Study and Numerical Simulation on Hydration Heat of Large-volume Iron Tailings Concrete. J. Shandong Agric. Univ. 2023, 54, 440–446. [Google Scholar]
- Liu, J.; Sun, C.; Zhao, S. Simulation of thermal performance of composite insulated blocks with recycled aggregate concrete. Concrete 2022, 8, 119–124. [Google Scholar]
- Li, W.C.; Hu, L.M.; Zeng, Y. Numerical Simulation Analysis of Onshore Wind Turbine Foundation and Reinforcement Body Hydration Heat Based on ABAOUS. Water Resour. Power 2021, 39, 192–195+200. [Google Scholar]
- Liang, B.-Y.; Sun, W.-H.; Deng, C.-L.; Hu, Q.; Huang, Y.-H. Experimental Study on Low-Shrinkage Concrete Mix Proportion for Post-Casting Belt of Full-Section Casting in Immersed Tube. Materials 2025, 18, 3315. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Su, X.; Chen, Y.; An, L. New Technologies and Challenges in the Construction of the Immersed Tube Tunnel of the Hong Kong-Zhuhai-Macao Link. Struct. Eng. Int. 2021, 32, 455–464. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Architecture & Concrete Structures. China Architecture & Building Press: Beijing, China, 2010. (In Chinese)
- Dong, F.Q.; Huang, G.S. Simulation Analysis and Temperature Control Research on Hydration Heat of Mass Concrete in Pile Caps Based on MIDAS/FEA. Pet. Chem. Constr. 2021, 43, 131–133. [Google Scholar]
- GB50496-2018; Standard for Construction of Mass Concrete. China Architecture & Building Press: Beijing, China, 2018. (In Chinese)
- Sun, M.; Bennett, T.; Visintin, P. Dataset on plastic and early-age shrinkage of ultra-high performance concrete with corresponding chemical shrinkage, temperature, relative humidity, reaction degree and material properties changes. J. Data Brief 2022, 42, 108053. [Google Scholar] [CrossRef] [PubMed]

| Binder Content (kg/m3) | Water-to-Binder Ratio | Cement (kg/m3) | Fly Ash (kg/m3) | Slag Powder (kg/m3) | Sand Ratio | Water Reducer Content | Density (kg/m3) |
|---|---|---|---|---|---|---|---|
| 400 | 0.39 | 210 | 80 | 110 | 40% | 1.2% | 2360 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, B.-Y.; Sun, W.-H.; Huang, Y.-H.; Wang, K. Study on Restraint Effect of Post-Casting Belt in Full-Section Interval Casting Immersed Tube. Materials 2025, 18, 4665. https://doi.org/10.3390/ma18204665
Liang B-Y, Sun W-H, Huang Y-H, Wang K. Study on Restraint Effect of Post-Casting Belt in Full-Section Interval Casting Immersed Tube. Materials. 2025; 18(20):4665. https://doi.org/10.3390/ma18204665
Chicago/Turabian StyleLiang, Bang-Yan, Wen-Huo Sun, Yong-Hui Huang, and Kai Wang. 2025. "Study on Restraint Effect of Post-Casting Belt in Full-Section Interval Casting Immersed Tube" Materials 18, no. 20: 4665. https://doi.org/10.3390/ma18204665
APA StyleLiang, B.-Y., Sun, W.-H., Huang, Y.-H., & Wang, K. (2025). Study on Restraint Effect of Post-Casting Belt in Full-Section Interval Casting Immersed Tube. Materials, 18(20), 4665. https://doi.org/10.3390/ma18204665








