Stabilization of Charge Density Waves in Atomic Chains on Xenes
Abstract
1. Introduction
2. Theoretical Description
2.1. DFT Calculations
2.2. TB Calculations
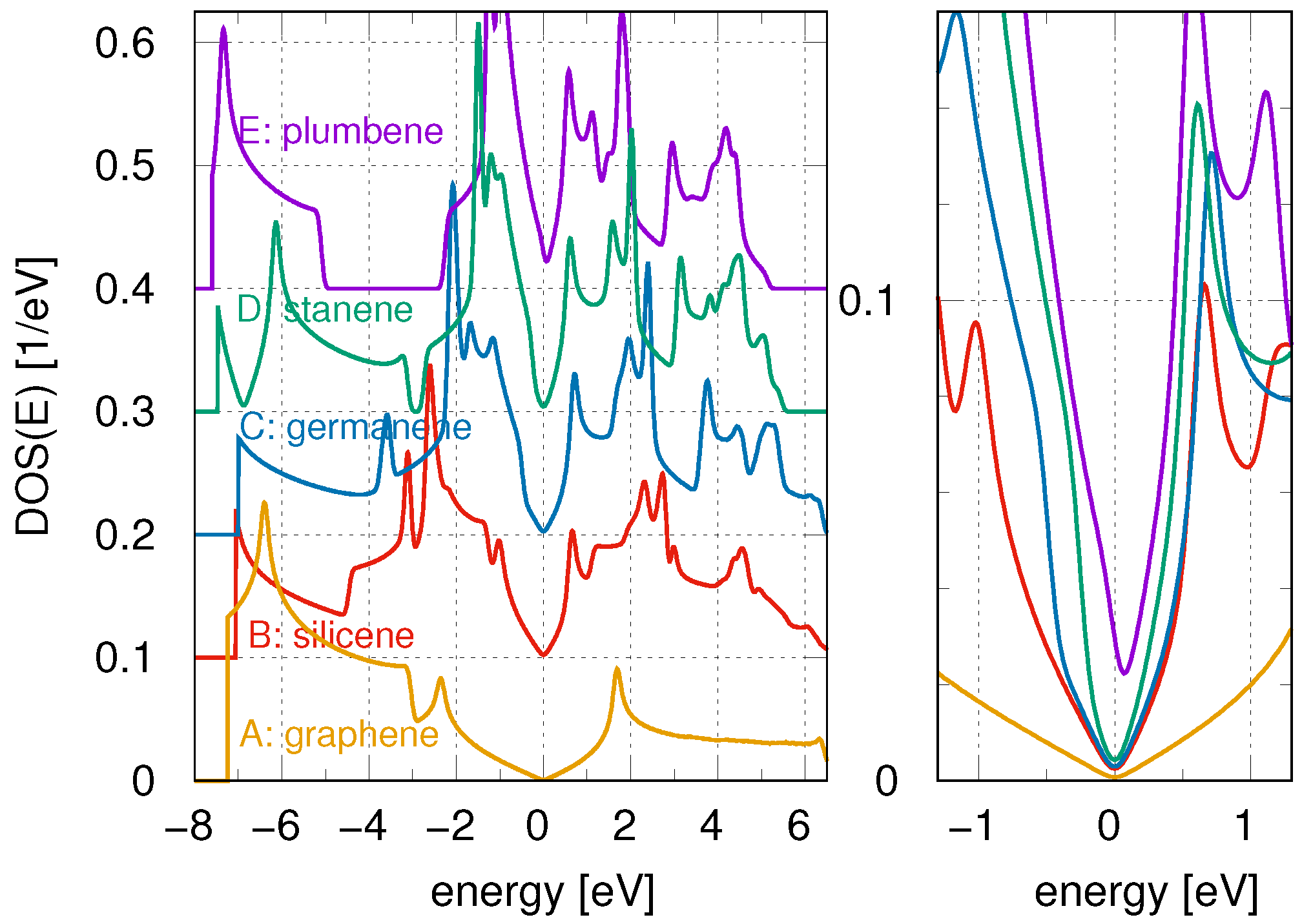
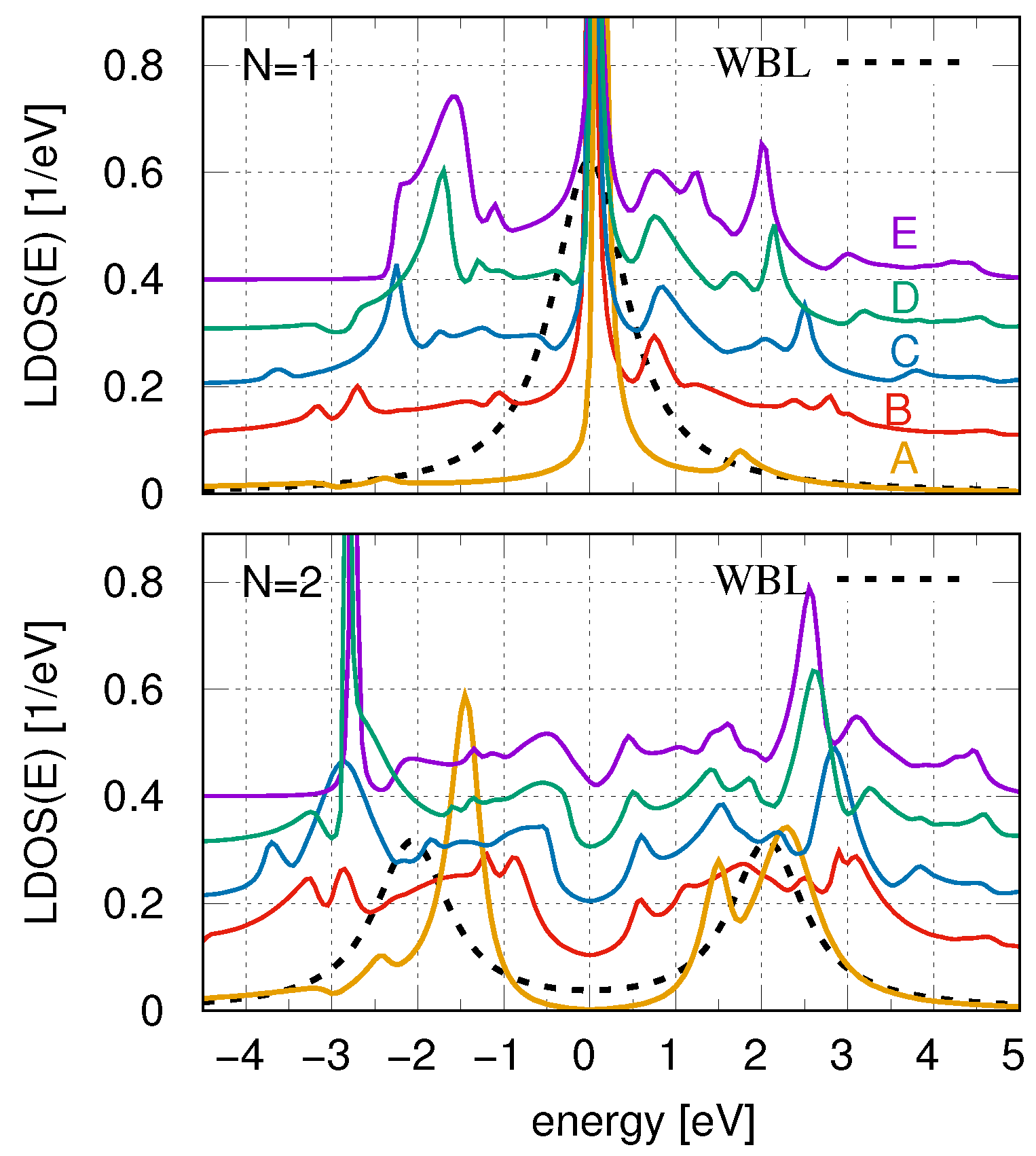
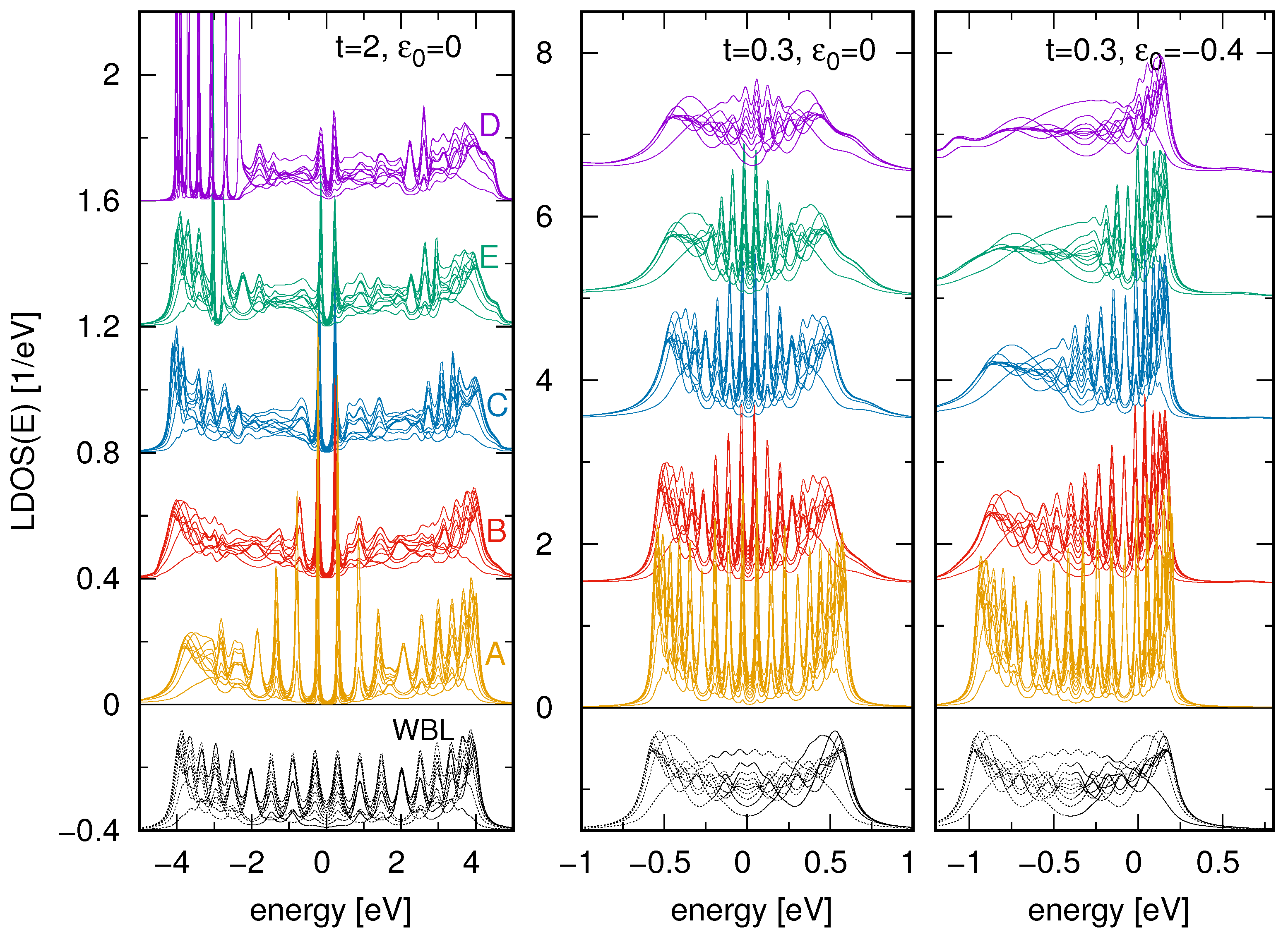
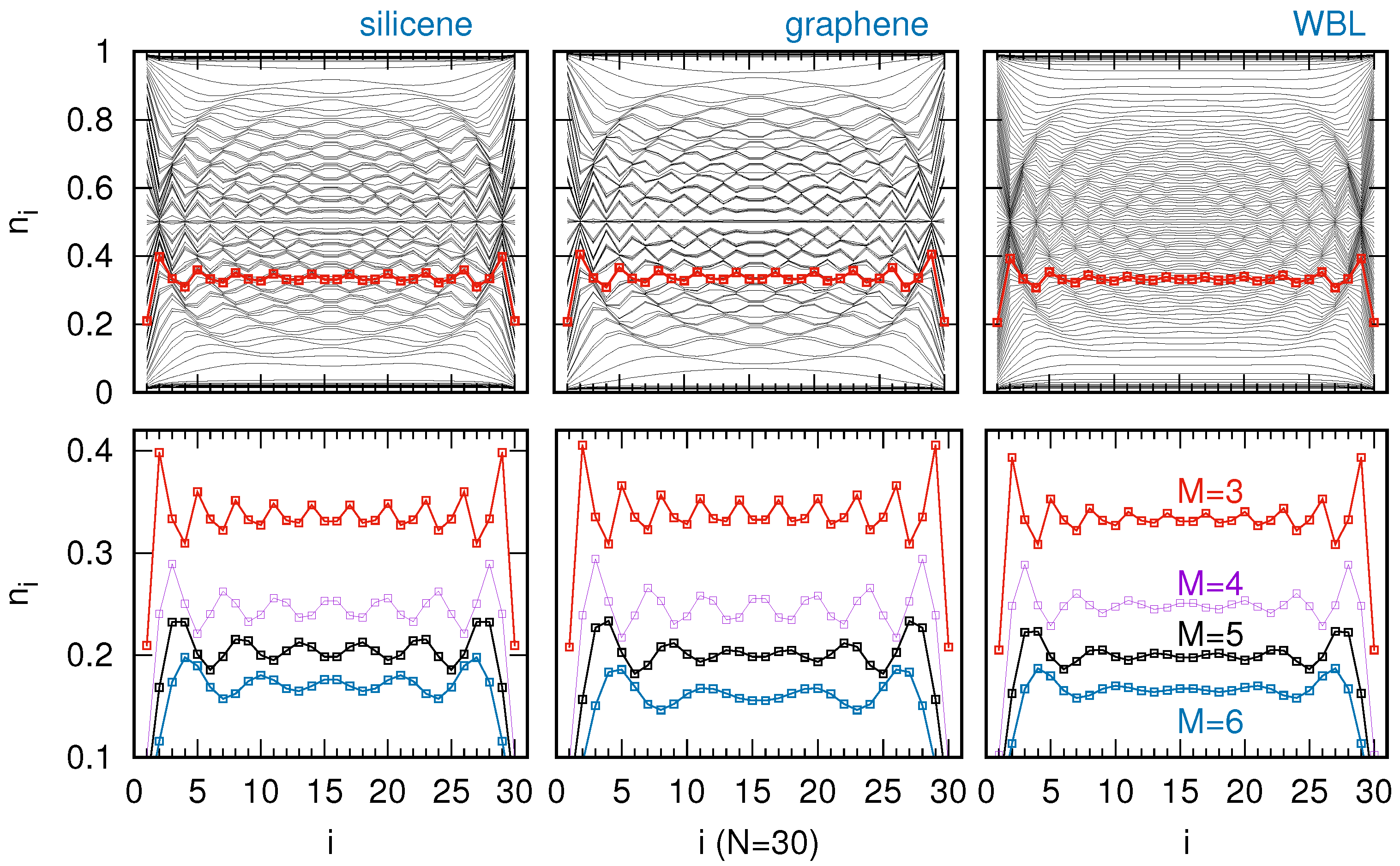
3. Results and Discussion
3.1. Few-Atom Systems
3.2. Atomic Chains on Various 2D Substrates
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Auslaender, O.M.; Steinberg, H.; Yacoby, A.; Tserkovnyak, Y.; Halperin, B.I.; Baldwin, K.W.; Pfeiffer, L.N.; West, K.W. Spin-Charge Separation and Localization in One Dimension. Science 2005, 308, 88–92. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.S.; Ryang, K.D.; Yeom, H.W. Finite-length charge-density waves on terminated atomic wires. Phys. Rev. B 2012, 85, 073401. [Google Scholar] [CrossRef]
- Stefanucci, G.; Kurth, S.; Rubio, A.; Gross, E.K.U. Time-dependent approach to electron pumping in open quantum systems. Phys. Rev. B 2008, 77, 075339. [Google Scholar] [CrossRef]
- Nadj-Perge, S.; Drozdov, I.K.; Li, J.; Chen, H.; Jeon, S.; Seo, J.; MacDonald, A.H.; Bernevig, B.A.; Yazdani, A. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 2014, 346, 602–607. [Google Scholar] [CrossRef]
- Pawlak, R.; Kisiel, M.; Klinovaja, J.; Meier, T.; Kawai, S.; Glatzel, T.; Loss, D.; Meyer, E. Probing atomic structure and Majorana wavefunctions in mono-atomic Fe chains on superconducting Pb surface. npj Quantum Inf. 2016, 2, 16035. [Google Scholar] [CrossRef]
- Lindner, N.H.; Refael, G.; Galitski, V. Floquet topological insulator in semiconductor quantum wells. Nat. Phys. 2011, 7, 490–495. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum Time Crystals. Phys. Rev. Lett. 2012, 109, 160401. [Google Scholar] [CrossRef]
- Żurawek, L.; Kopciuszyński, M.; Dachniewicz, M.; Stróżak, M.; Krawiec, M.; Jałochowski, M.; Zdyb, R. Partially embedded Pb chains on a vicinal Si(113) surface. Phys. Rev. B 2020, 101, 195434. [Google Scholar] [CrossRef]
- Krawiec, M.; Kwapiński, T.; Jałochowski, M. Scanning tunneling microscopy of monoatomic gold chains on vicinal Si(335) surface: Experimental and theoretical study. Phys. Stat. Sol. 2005, 242, 332–336. [Google Scholar] [CrossRef]
- Jałochowski, M. Strozak, M.; Zdyb, R. Gold-induced ordering on vicinal Si(111). Surf. Sci. 1997, 375, 203–209. [Google Scholar] [CrossRef]
- Pfnür, H.; Tegenkamp, C.; Sanna, S.; Jeckelmann, E.; Horn-von Hoegen, M.; Bovensiepen, U.; Esser, N.; Schmidt, W.G.; Dähne, M.; Wippermann, S.; et al. Atomic wires on substrates: Physics between one and two dimensions. Surf. Sci. Rep. 2024, 573, 151501. [Google Scholar] [CrossRef]
- Crain, J.N.; McChesney, J.L.; Zheng, F.; Gallagher, M.C.; Snijders, P.C.; Bissen, M.; Gundelach, C.; Erwin, S.C.; Himpsel, F.J. Chains of gold atoms with tailored electronic states. Phys. Rev. B 2004, 69, 125401. [Google Scholar] [CrossRef]
- Krawiec, M. Structural model of the Au-induced Si(553) surface: Double Au rows. Phys. Rev. B 2010, 81, 115436. [Google Scholar] [CrossRef]
- Miro, P.; Audiffred, M.; Heine, T. An atlas of two-dimensional materials. Chem. Soc. Rev. 2014, 43, 6537. [Google Scholar] [CrossRef]
- Molle, A. Xenes: A new emerging two-dimensional materials platform for nanoelectronics. ECSP Trans. 2016, 75, 163. [Google Scholar] [CrossRef]
- Molle, A.; Goldberger, J.; Houssa, M.; Xu, Y.; Zhang, S.C.; Akinwande, D. Buckled two-dimensional Xene sheets. Nat. Mater. 2017, 16, 163. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Rubio, A.; Le Lay, G. Emergent elemental two-dimensional materials beyond graphene. J. Phys. D. Appl. Phys. 2017, 50, 053004. [Google Scholar] [CrossRef]
- Krawiec, M. Functionalization of group-14 two-dimensional materials. J. Phys. Condens. Matter 2018, 30, 233003. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666. [Google Scholar] [CrossRef]
- Gorczyca, A.; Maśka, M.M.; Mierzejewski, M. Friedel oscillations in the presence of transport currents in a nanowire. Phys. Rev. B 2007, 76, 165419. [Google Scholar] [CrossRef]
- Brazovskii, S.; Brun, C.; Wang, Z.Z.; Monceau, P. Scanning-Tunneling Microscope Imaging of Single-Electron Solitons in a Material with Incommensurate Charge-Density Waves. Phys. Rev. Lett. 2012, 108, 096801. [Google Scholar] [CrossRef] [PubMed]
- Dora, B. Boundary effect on CDW: Friedel oscillations, STM image. Europhys. Lett. 2005, 70, 362. [Google Scholar] [CrossRef]
- Kwapiński, T. Charge fluctuations in a perfect and disturbed quantum wire. J. Phys. Condens. Matter 2006, 18, 7313. [Google Scholar] [CrossRef]
- Chatterjee, B.; Byczuk, K. Screening of a single impurity and Friedel oscillations in Fermi liquids. J. Phys. Conf. Ser. 2015, 592, 012059. [Google Scholar] [CrossRef]
- Friedel, J. Metallic alloys. Il Nuovo C. 1958, 7, 287. [Google Scholar] [CrossRef]
- Crommie, M.F.; Lutz, C.P.; Eigler, D.M. Imaging standing waves in a two-dimensional electron gas. Nature 1993, 363, 524–527. [Google Scholar] [CrossRef]
- Jia, Y.; Wu, B.; Li, C.; Einstein, T.L.; Weitering, H.H.; Zhang, Z. Strong Quantum Size Effects in Pb(111) Thin Films Mediated by Anomalous Friedel Oscillations. Phys. Rev. Lett. 2010, 105, 066101. [Google Scholar] [CrossRef]
- Kwapiński, T.; Kohler, S.; Hänggi, P. Electron transport across a quantum wire in the presence of electron leakage to a substrate. Eur. Phys. J. B 2010, 78, 75–81. [Google Scholar] [CrossRef]
- Stojchevska, L.; Vaskivskyi, I.; Mertelj, T.; Kusar, P.; Svetin, D.; Brazovskii, S.; Mihailovic, D. Ultrafast Switching to a Stable Hidden Quantum State in an Electronic Crystal. Science 2014, 344, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Vaskivskyi, I.; Gospodaric, J.; Brazovskii, S.; Svetin, D.; Sutar, P.; Goreshnik, E.; Mihailovic, I.A.; Mertelj, T.; Mihailovic, D. Controlling the metal-to-insulator relaxation of the metastable hidden quantum state in 1T-TaS2. Sci. Adv. 2015, 1, e1500168. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, M.; Suzuki, R.; Zhang, Y.; Nakano, M.; Iwasa, Y. Memristive phase switching in two-dimensional 1T-TaS2 crystals. Sci. Adv. 2015, 1, e1500606. [Google Scholar] [CrossRef]
- Miller, J.H.; Wijesinghe, A.I.; Tang, Z.; Guloy, A.M. Coherent quantum transport of charge density waves. Phys. Rev. B 2013, 87, 115127. [Google Scholar] [CrossRef]
- Kogan, E.; Gumbs, G. Green’s Functions and DOS for Some 2D Lattices. Graphene 2021, 10, 1–12. [Google Scholar] [CrossRef]
- Choy, T.C. Density of states for a two-dimensional Penrose lattice: Evidence of a strong Van-Hove singularity. Phys. Rev. Lett. 1985, 55, 2915–2918. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculat ions using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augumented-wav e method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augumented-Wave Metchod. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge Studies in Semiconductor Physics and Microelectronic Engineering, Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Podloucky, R. M. C. Desjonquères and D. Spanjaard: Concepts in surface physics, 2nd edition, Springer Verlag, Berlin Heidelberg, 1996, ISBN-3-450-58622-9, DM 98,00. Berichte Bunsenges. Phys. Chem. 1997, 101, 1081–1082. [Google Scholar] [CrossRef]
- Newns, D.; Read, N. Mean-field theory of intermediate valence/heavy fermion systems. Adv. Phys. 1987, 36, 799–849. [Google Scholar] [CrossRef]
- Kwapiński, T. Conductance oscillations of a quantum wire disturbed by an adatom. J. Phys. Condens. Matter 2007, 19, 176218. [Google Scholar] [CrossRef] [PubMed]
- Park, J.W.; Do, E.; Shin, J.S.; Song, S.K.; Stetsovych, O.; Jelinek, P.; Yeom, H.W. Creation and annihilation of mobile fractional solitons in atomic chains. Nat. Nanotechnol. 2022, 17, 244. [Google Scholar] [CrossRef]
- Jałochowski, M.; Kwapiński, T. Distribution of Electron Density in Self-Assembled One-Dimensional Chains of Si Atoms. Materials 2023, 16, 6044. [Google Scholar] [CrossRef]
- Krawiec, M. Protecting Au-stabilized vicinal Si surfaces from degradation: Graphene on the Si(553)-Au surface. Appl. Surf. Sci. 2014, 304, 44–49. [Google Scholar] [CrossRef]
- Krawiec, M. Undercover diffusion of atoms: Pb on Si(553)-Au surface covered by graphene. J. Phys. Condens. Matter 2015, 27, 125003. [Google Scholar] [CrossRef]
- Srut Rakic, I.; Kralj, M.; Jolie, W.; Lazic, P.; Sun, W.; Avila, J.; Asensio, M.C.; Craes, F.; Miksic Trontl, V.; Busse, C.; et al. Step-induced faceting and related electronic effects for graphene on Ir(332). Carbon 2016, 110, 267–277. [Google Scholar] [CrossRef]
- Jałochowski, M.; Krawiec, M.; Kwapiński, T. Implementation of the Su-Schrieffer-Heeger Model in the Self-Assembly Si-In Atomic Chains on the Si(553)-Au Surface. ACS Nano 2024, 18, 12861–12869. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwapiński, T.; Kurzyna, M.; Krawiec, M. Stabilization of Charge Density Waves in Atomic Chains on Xenes. Materials 2025, 18, 3843. https://doi.org/10.3390/ma18163843
Kwapiński T, Kurzyna M, Krawiec M. Stabilization of Charge Density Waves in Atomic Chains on Xenes. Materials. 2025; 18(16):3843. https://doi.org/10.3390/ma18163843
Chicago/Turabian StyleKwapiński, Tomasz, Marcin Kurzyna, and Mariusz Krawiec. 2025. "Stabilization of Charge Density Waves in Atomic Chains on Xenes" Materials 18, no. 16: 3843. https://doi.org/10.3390/ma18163843
APA StyleKwapiński, T., Kurzyna, M., & Krawiec, M. (2025). Stabilization of Charge Density Waves in Atomic Chains on Xenes. Materials, 18(16), 3843. https://doi.org/10.3390/ma18163843







