The Quantum Transport of Dirac Fermions in Selected Graphene Nanosystems Away from the Charge Neutrality Point
Abstract
1. Introduction
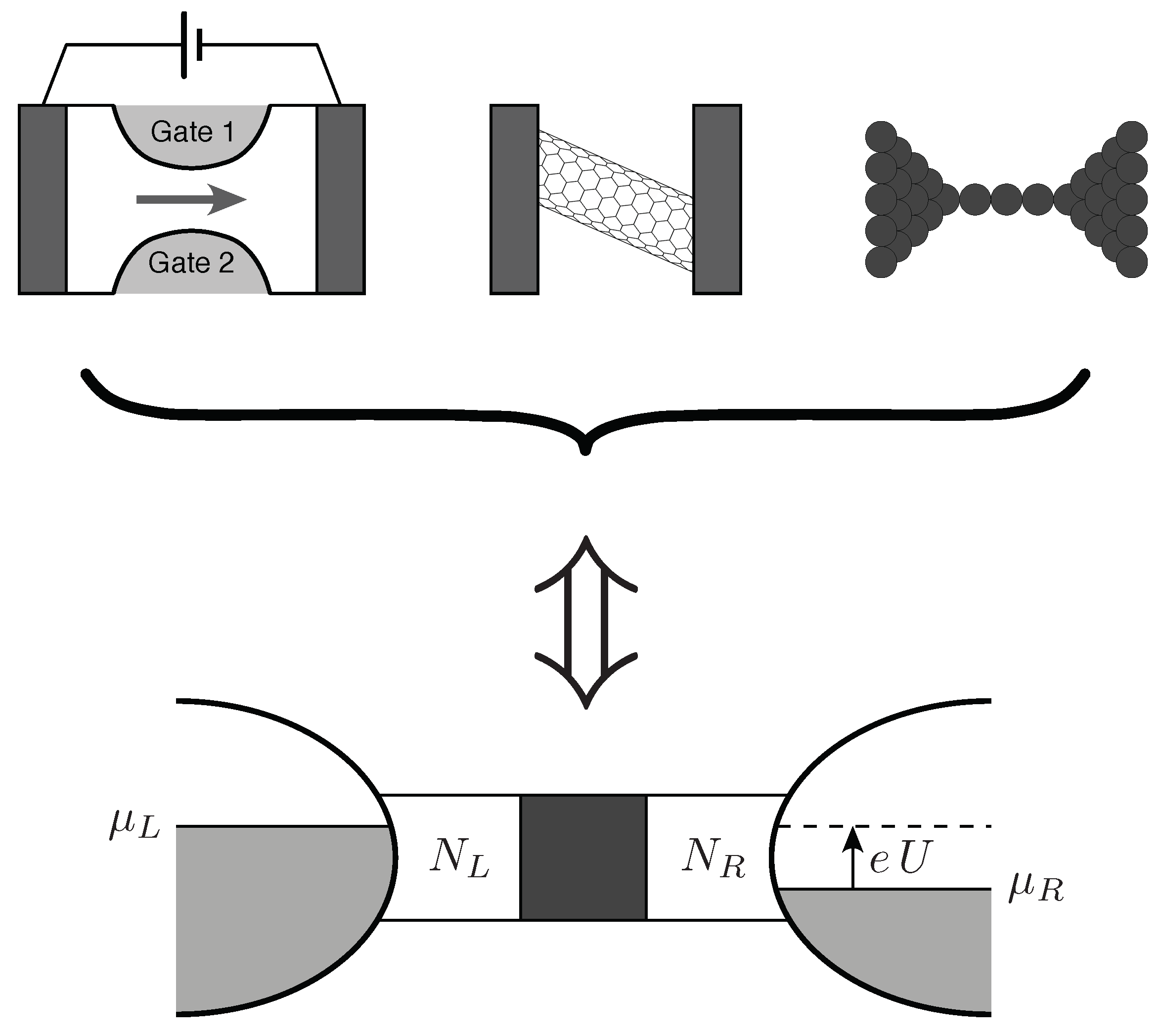
2. Landauer–Büttiker Transport in Nanoscopic Systems and Graphene
2.1. Remark on the Origin of Zero-Temperature Landauer–Sharvin Resistance
2.2. The Landauer–Büttiker Formula
2.3. Shot Noise and Counting Statistics
2.4. Scattering of Dirac Fermions in Two Dimensions
2.5. The Conductivity, Shot Noise, and Higher Cumulants for Ballistic Graphene Strip
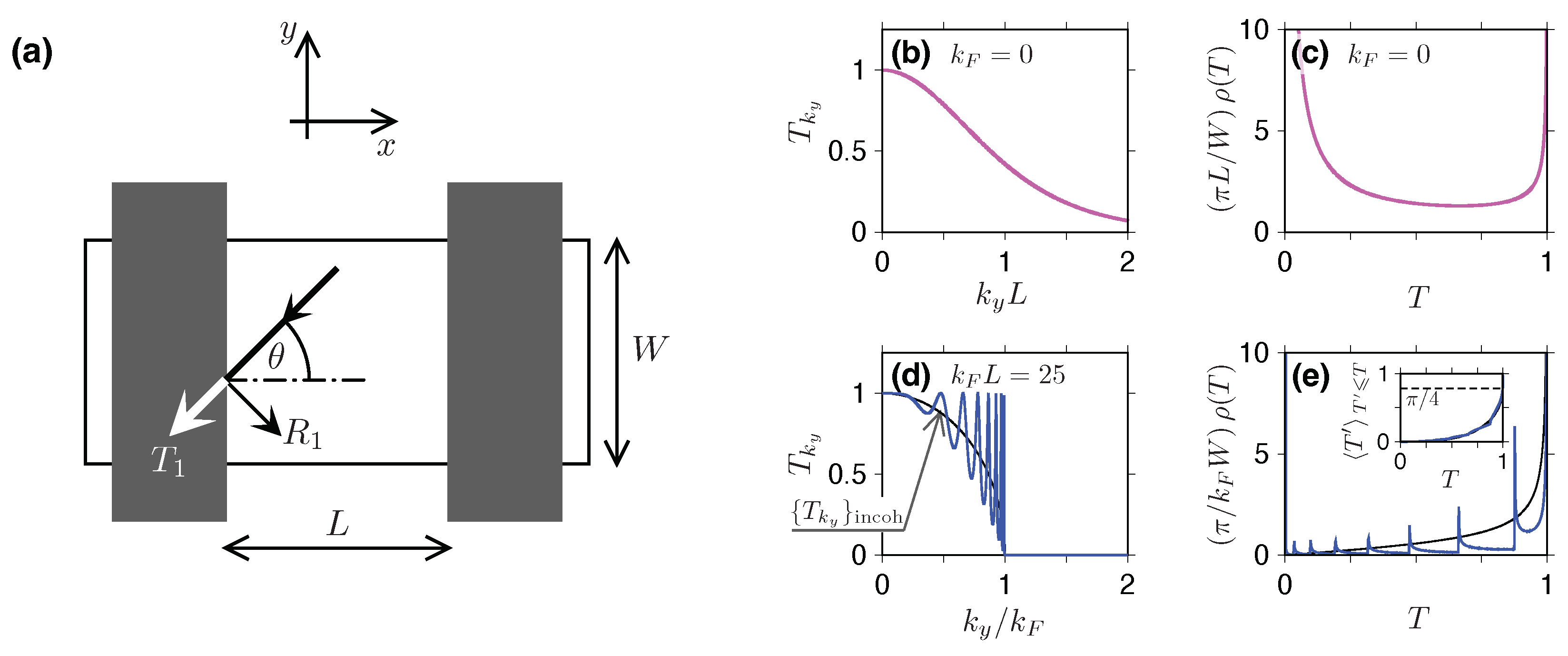
2.6. The Narrow Opening Limit
3. Distributions of Transmission Probabilities
4. Numerical Results and Discussion
4.1. Tight Binding Model
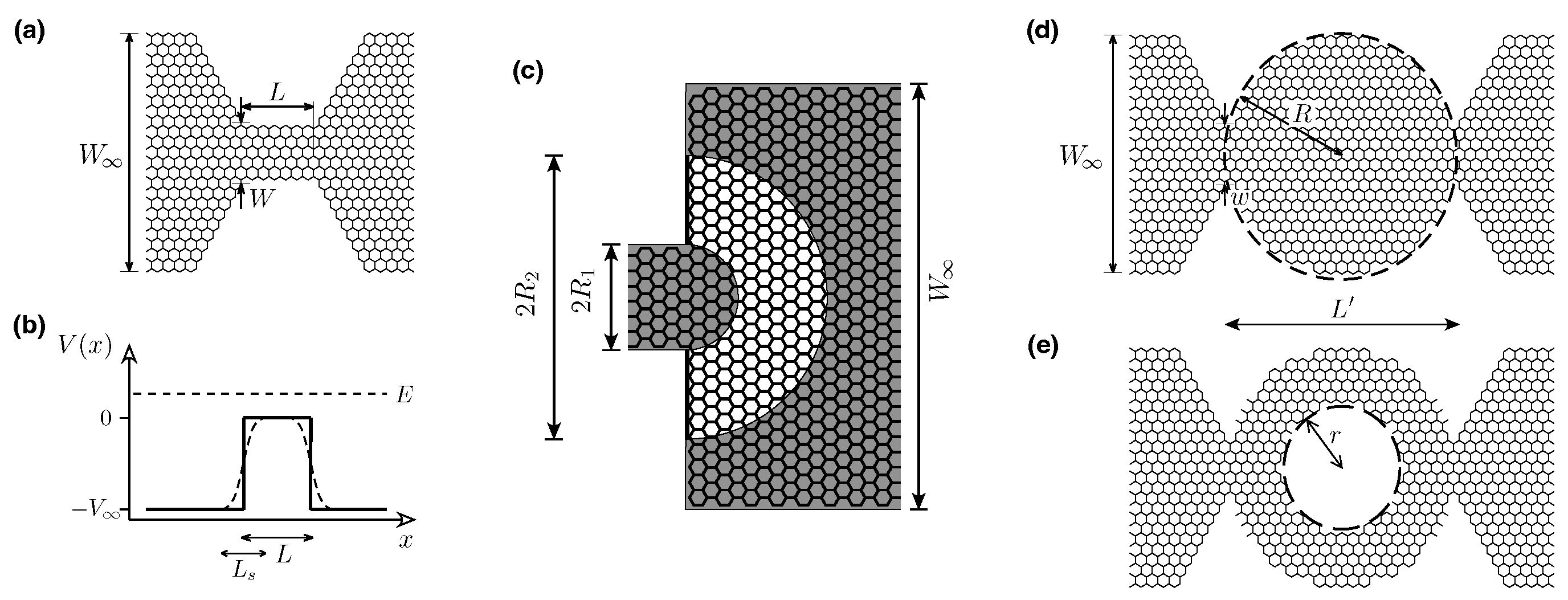
4.2. Constriction with Zigzag Edges
4.3. Half-Disk and Circular Quantum Dots
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Numerical Mode-Matching for the Honeycomb Lattice
Appendix A.1. The Nanosystem
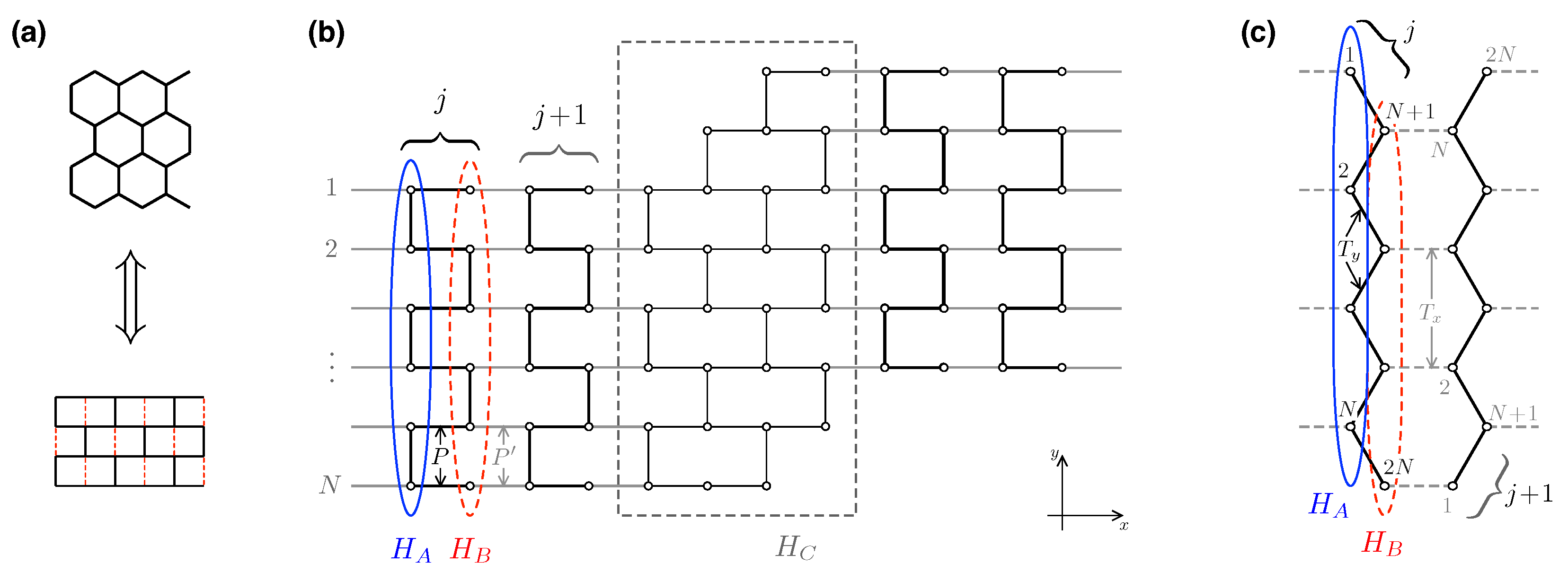
Appendix A.2. Solutions in the Leads
Appendix A.3. Basis for the Scattering Matrix
Appendix A.4. The Scattering Problem
References
- Duff, M.J.; Okun, L.B.; Veneziano, G. Trialogue on the number of fundamental constants. J. High Energy Phys. 2002, 2002, 023. [Google Scholar] [CrossRef]
- Lévy-Leblond, J.-M. On the Conceptual Nature of the Physical Constants. In The Reform of the International System of Units (SI): Philosophical, Historical and Sociological Issues; Routledge: London, UK, 2019; pp. 125–149. [Google Scholar] [CrossRef]
- Ando, T.; Matsumoto, Y.; Uemura, Y. Theory of Hall Effect in a Two-Dimensional Electron System. J. Phys. Soc. Jpn. 1975, 39, 279. [Google Scholar] [CrossRef]
- Klitzing, K.v.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494. [Google Scholar] [CrossRef]
- Laughlin, R.B. Quantized Hall conductivity in two dimensions. Phys. Rev. B 1981, 23, 5632–5633. [Google Scholar] [CrossRef]
- Tsui, D.C.; Stormer, H.L.; Gossard, A.C. Two-Dimensional Magnetotransport in the Extreme Quantum Limit. Phys. Rev. Lett. 1982, 48, 1559. [Google Scholar] [CrossRef]
- Josephson, B.D. The discovery of tunneling supercurrents. Rev. Mod. Phys. 1974, 46, 251. [Google Scholar] [CrossRef]
- Payagala, S.; Rigosi, A.; Panna, A.; Pollarolo, A.; Kruskopf, M.; Schlamminger, S.; Jarrett, D.; Brown, R.; Elmquist, R.; Brown, D.; et al. Comparison between Graphene and GaAs Quantized Hall Devices with a Dual Probe. IEEE Trans. Instrum. Meas. 2020, 69, 9374. [Google Scholar] [CrossRef]
- Tang, Y.; Wachter, J.; Rufenacht, A.; FitzPatrick, G.; Benz, S. 10 V Programmable Josephson Voltage Standard and its Application in Direct Comparison with the Conventional Josephson Voltage Standard. IEEE Trans. Instrum. Meas. 2015, 64, 3458. [Google Scholar] [CrossRef]
- Novoselov, K.; Geim, A.; Morozov, S.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201. [Google Scholar] [CrossRef]
- Titov, M.; Beenakker, C.W.J. Josephson effect in ballistic graphene. Phys. Rev. B 2006, 74, 041401(R). [Google Scholar] [CrossRef]
- Salim, S.; Marathe, R.; Gosh, S. Revisiting Andreev processes in superconductor-graphene-superconductor (SGS) Josephson junctions: Comparison with experimental results. Phys. Scr. 2023, 98, 065935. [Google Scholar] [CrossRef]
- Katsnelson, M.I. Zitterbewegung, chirality, and minimal conductivity in graphene. Eur. Phys. J. B 2006, 51, 157. [Google Scholar] [CrossRef]
- Katsnelson, M.I. The Physics of Graphene, 2nd ed.; Cambridge University Press: Cambridge, UK, 2020; Chapter 3. [Google Scholar]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef]
- Skulason, H.S.; Gaskell, P.E.; Szkopek, T. Optical reflection and transmission properties of exfoliated graphite from a graphene monolayer to several hundred graphene layers. Nanotechnology 2010, 21, 295709. [Google Scholar] [CrossRef]
- Tworzydło, J.; Trauzettel, B.; Titov, M.; Rycerz, A.; Beenakker, C.W.J. Sub-Poissonian shot noise in graphene. Phys. Rev. Lett. 2006, 96, 246802. [Google Scholar] [CrossRef]
- Danneau, R.; Wu, F.; Craciun, M.F.; Russo, S.; Tomi, M.Y.; Salmilehto, J.; Morpurgo, A.F.; Hakonen, P.J. Shot Noise in Ballistic Graphene. Phys. Rev. Lett. 2008, 100, 196802. [Google Scholar] [CrossRef]
- Rycerz, A.; Recher, P.; Wimmer, M. Conformal mapping and shot noise in graphene. Phys. Rev. B 2009, 80, 125417. [Google Scholar] [CrossRef]
- Laitinen, A.; Paraoanu, G.S.; Oksanen, M.; Craciun, M.F.; Russo, S.; Sonin, E.; Hakonen, P. Contact doping, Klein tunneling, and asymmetry of shot noise in suspended graphene. Phys. Rev. B 2016, 93, 115413. [Google Scholar] [CrossRef]
- Yoshino, H.; Murata, K. Significant Enhancement of Electronic Thermal Conductivity of Two-Dimensional Zero-Gap Systems by Bipolar-Diffusion Effect. J. Phys. Soc. Jpn. 2015, 84, 024601. [Google Scholar] [CrossRef]
- Crossno, J.; Shi, J.K.; Wang, K.; Liu, X.; Harzheim, A.; Lucas, A.; Sachdev, S.; Kim, P.; Taniguchi, T.; Watanabe, K.; et al. Observation of the Dirac fluid and the breakdown of the Wiedemann-Franz law in graphene. Science 2016, 351, 1058. [Google Scholar] [CrossRef] [PubMed]
- Rycerz, A. Wiedemann–Franz Law for Massless Dirac Fermions with Implications for Graphene. Materials 2021, 14, 2704. [Google Scholar] [CrossRef] [PubMed]
- Tu, Y.-T.; Das Sarma, S. Wiedemann-Franz law in graphene. Phys. Rev. B 2023, 107, 085401. [Google Scholar] [CrossRef]
- Semenoff, G.W. Condensed-Matter Simulation of a Three-Dimensional Anomaly. Phys. Rev. Lett. 1984, 53, 2449. [Google Scholar] [CrossRef]
- Di Vincenzo, D.P.; Mele, E.J. Self-consistent effective-mass theory for intralayer screening in graphite intercalation compounds. Phys. Rev. B 1984, 29, 1685. [Google Scholar] [CrossRef]
- Zor, E.; Bingol, H.; Ramanaviciene, A.; Ramanavicius, A.; Ersoz, M. An electrochemical and computational study for discrimination of D- and L-cystine by reduced graphene oxide/β-cyclodextrin. Analyst 2015, 140, 313. [Google Scholar] [CrossRef]
- Yaghouti Niyat, F.; Shahrokh Abadi, M. COMSOL-Based Modeling and Simulation of SnO2/rGO Gas Sensor for Detection of NO2. Sci. Rep. 2018, 8, 2149. [Google Scholar] [CrossRef]
- Suszalski, D.; Rut, G.; Rycerz, A. Lifshitz transition and thermoelectric properties of bilayer graphene. Phys. Rev. B 2018, 97, 125403. [Google Scholar] [CrossRef]
- Du, M.; Du, L.; Wei, N.; Liu, W.; Bai, X.; Sun, Z. Dual-gated mono–bilayer graphene junctions. Nanoscale Adv. 2021, 3, 399. [Google Scholar] [CrossRef]
- Hadadi, N.; Belayadi, A.; AlRabiah, A.; Ly, O.; Ashu Akosa, C.; Vogl, M.; Bahlouli, H.; Manchon, A.; Abbout, A. Pseudo electric field and pumping valley current in graphene nanobubbles. Phys. Rev. B 2023, 108, 195418. [Google Scholar] [CrossRef]
- Rycerz, A.; Witkowski, P. Sub-Sharvin conductance and enhanced shot noise in doped graphene. Phys. Rev. B 2021, 104, 165413. [Google Scholar] [CrossRef]
- Rycerz, A.; Witkowski, P. Theory of sub-Sharvin charge transport in graphene disks. Phys. Rev. B 2022, 106, 155428. [Google Scholar] [CrossRef]
- Sharvin, Y.V. A possible method for studying Fermi surfaces. Sov. Phys. J. Exp. Theor. Phys. 1965, 21, 655, Russian original in Zh. Eksp. Teor. Fiz. 1965, 48, 984. Available online: http://www.jetp.ras.ru/cgi-bin/e/index/e/21/3/p655?a=list (accessed on 1 April 2025).
- van Wees, B.J.; van Houten, H.; Beenakker, C.W.J.; Williamson, J.G.; Kouwenhoven, L.P.; van der Marel, D.; Foxon, C.T. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 1988, 60, 848. [Google Scholar] [CrossRef]
- Glazman, L.I.; Lesovik, G.B.; Khmel’nitskii, D.E.; Shekhter, R.I. Reflectionless quantum transport and fundamental ballistic-resistance steps in microscopic constrictions. JETP Lett. 1988, 48, 238, Russian original in Pi’sma Zh. Eksp. Teor. Fiz. 1988, 48, 218. Available online: http://jetpletters.ru/ps/1104/article_16696.shtml (accessed on 1 April 2025).
- Bezák, V. Conductance quantization of an ideal Sharvin contact. Ann. Phys. 2007, 322, 2603. [Google Scholar] [CrossRef]
- Rycerz, A.; Rycerz, K.; Witkowski, P. Thermoelectric Properties of the Corbino Disk in Graphene. Materials 2023, 16, 4250. [Google Scholar] [CrossRef]
- Rycerz, A.; Rycerz, K.; Witkowski, P. Sub-Sharvin Conductance and Incoherent Shot-Noise in Graphene Disks at Magnetic Field. Materials 2024, 17, 3067. [Google Scholar] [CrossRef]
- Das Sarma, S.; Yang, K. The enigma of the nu=0 quantum Hall effect in graphene. Solid State Commun. 2009, 149, 1502. [Google Scholar] [CrossRef][Green Version]
- Rycerz, A. Magnetoconductance of the Corbino disk in graphene. Phys. Rev. B 2010, 81, 121404(R). [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.I.A.; Dietrich, S.A.; Ghosh, O.M.; Watanabe, K.; Taniguchi, T.; Hone, J.; Dean, C.R. High-Quality Magnetotransport in Graphene Using the Edge-Free Corbino Geometry. Phys. Rev. Lett. 2019, 122, 137701. [Google Scholar] [CrossRef] [PubMed]
- Suszalski, D.; Rut, G.; Rycerz, A. Mesoscopic valley filter in graphene Corbino disk containing a p-n junction. J. Phys. Mater. 2020, 3, 015006. [Google Scholar] [CrossRef]
- Kamada, M.; Gall, V.; Sarkar, J.; Kumar, M.; Laitinen, A.; Gornyi, I.; Hakonen, P. Strong magnetoresistance in a graphene Corbino disk at low magnetic fields. Phys. Rev. B 2021, 104, 115432. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Willey and Sons: New York, NY, USA, 2005; Chapter 6. [Google Scholar]
- White, C.T.; Todorov, T.N. Carbon nanotubes as long ballistic conductors. Nature 1998, 393, 240. [Google Scholar] [CrossRef]
- Agraït, N.; Levy Yeyati, A.; van Ruitenbeek, J.M. Quantum properties of atomic-sized conductors. Phys. Rep. 2003, 377, 81. [Google Scholar] [CrossRef]
- Landauer, R. Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction. IBM J. Res. Dev. 1957, 1, 223. [Google Scholar] [CrossRef]
- Büttiker, M.; Imry, Y.; Landauer, R.; Pinhas, S. Generalized many-channel conductance formula with application to small rings. Phys. Rev. B 1985, 31, 6207. [Google Scholar] [CrossRef]
- Meir, Y.; Wingreen, N.S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 1992, 68, 2512. [Google Scholar] [CrossRef]
- Kumar, C.; Birkbeck, J.; Sulpizio, J.A.; Perello, D.J.; Taniguchi, T.; Watanabe, K.; Reuven, O.; Scaffidi, T.; Stern, A.; Geim, A.K.; et al. Imaging hydrodynamic electrons flowing without Landauer-Sharvin resistance. Nature 2022, 609, 276. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. [Google Scholar] [CrossRef] [PubMed]
- Fidrysiak, M.; Zegrodnik, M.; Spałek, J. Unconventional topological superconductivity and phase diagram for an effective two-orbital model as applied to twisted bilayer graphene. Phys. Rev. B 2018, 98, 085436. [Google Scholar] [CrossRef]
- Nazarov, Y.V.; Blanter, Y.M. Quantum Transport: Introduction to Nanoscience; Cambridge University Press: Cambridge, UK, 2009; Chapter 1. [Google Scholar]
- Blanter, Y.M.; Martin, I. Transport through normal-metal-graphene contacts. Phys. Rev. B 2007, 76, 155433. [Google Scholar] [CrossRef]
- Robinson, J.P.; Schomerus, H. Electronic transport in normal-conductor/graphene/normal-conductor junctions and conditions for insulating behavior at a finite charge-carrier density. Phys. Rev. B 2007, 76, 115430. [Google Scholar] [CrossRef]
- Kemble, E.C. A Contribution to the Theory of the B. W. K. Method. Phys. Rev. 1935, 48, 549. [Google Scholar] [CrossRef]
- Das Sarma, S.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two dimensional graphene. Rev. Mod. Phys. 2011, 83, 407. [Google Scholar] [CrossRef]
- Koshino, M.; Ando, T. Electronic Properties of Monolayer and Multilayer Graphene. In Physics of Graphene. NanoScience and Technology; Aoki, H., Dresselhaus, M.S., Eds.; Springer: Cham, Switzerland, 2014; pp. 173–211. [Google Scholar] [CrossRef]
- Takimoto, N.; Yamamura, S.; Funayama, K. Generation of Non-Equilibrium 1/f Temperature Noise. J. Phys. Soc. Jpn. 1993, 62, 3077. [Google Scholar] [CrossRef]
- Schönhammer, K. Full counting statistics for noninteracting fermions: Exact results and the Levitov-Lesovik formula. Phys. Rev. B 2007, 75, 205329. [Google Scholar] [CrossRef]
- Berry, M.V.; Mondragon, R.J. Neutrino billiards: Time-reversal symmetry-breaking without magnetic fields. Proc. R. Soc. Lond. A 1987, 412, 53. [Google Scholar] [CrossRef]
- Robinson, T.R. On Klein tunneling in graphene. Am. J. Phys. 2012, 80, 141. [Google Scholar] [CrossRef]
- Gutiérrez, C.; Brown, L.; Kim, C.J.; Park, J.; Pasupathy, A.N. Klein tunnelling and electron trapping in nanometre-scale graphene quantum dots. Nat. Phys. 2016, 12, 1069. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1997; Chapter 3. [Google Scholar]
- Schuessler, A.; Ostrovsky, P.M.; Gornyi, I.V.; Mirlin, A.D. Full counting statistics in disordered graphene at Dirac point: From ballistics to diffusion. Phys. Rev. B 2010, 82, 085419. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: New York, NY, USA, 2007; Eq. 2.553.3. [Google Scholar]
- Miao, F.; Wijeratne, S.; Zhang, Y.; Coscun, U.C.; Bao, W.; Lau, C.N. Phase Coherent Transport in Graphene Quantum Billiards. Science 2007, 317, 1530. [Google Scholar] [CrossRef] [PubMed]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover Publications, Inc.: New York, NY, USA, 1965; Chapter 15. [Google Scholar]
- Chan, W.J.; Ang, L.K.; Ang, Y.S. Quantum transport and shot noise in two-dimensional semi-Dirac system. Appl. Phys. Lett. 2023, 122, 163102. [Google Scholar] [CrossRef]
- DiCarlo, L.; Williams, J.R.; Zhang, Y.; McClure, D.T.; Marcus, C.M. Shot Noise in Graphene. Phys. Rev. Lett. 2008, 100, 156801. [Google Scholar] [CrossRef]
- Onac, E.; Balestro, F.; Trauzettel, B.; Lodewijk, C.F.J.; Kouwenhoven, L.P. Shot-Noise Detection in a Carbon Nanotube Quantum Dot. Phys. Rev. Lett. 2006, 96, 026803. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Guinea, F. Transport through evanescent waves in ballistic graphene quantum dots. Phys. Rev. B 2008, 78, 075417. [Google Scholar] [CrossRef]
- Rycerz, A.; Suszalski, D. Graphene disk in a solenoid magnetic potential: Aharonov-Bohm effect without a two-slit-like setup. Phys. Rev. B 2020, 101, 245429. [Google Scholar] [CrossRef]
- Beenakker, C.W.J.; Büttiker, M. Suppression of shot noise in metallic diffusive conductors. Phys. Rev. B 1992, 46, 1889(R). [Google Scholar] [CrossRef]
- Nagaev, K.E. On the shot noise in dirty metal contacts. Phys. Lett. A 1992, 169, 103. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Random-matrix theory of quantum transport. Rev. Mod. Phys. 1997, 69, 731. [Google Scholar] [CrossRef]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Karpan, V.M.; van den Brink, J.; Kelly, P.J. Doping Graphene with Metal Contacts. Phys. Rev. Lett. 2008, 101, 026803. [Google Scholar] [CrossRef] [PubMed]
- Cusati, T.; Fiori, G.; Gahoi, A.; Passi, V.; Lemme, M.C.; Fortunelli, A.; Iannaccone, G. Electrical properties of graphene-metal contacts. Sci. Rep. 2017, 7, 5109. [Google Scholar] [CrossRef]
- Martelo, L.M.; Dzierzawa, M.; Siffert, L.; Baeriswyl, D. Mott-Hubbard transition and antiferromagnetism on the honeycomb lattice. Z. Phys. B 1997, 103, 335. [Google Scholar] [CrossRef]
- Sorella, S.; Otsuka, Y.; Yunoki, S. Absence of a Spin Liquid Phase in the Hubbard Model on the Honeycomb Lattice. Sci. Rep. 2012, 2, 992. [Google Scholar] [CrossRef]
- Schüler, M.; Rösner, M.; Wehling, T.O.; Lichtenstein, A.I.; Katsnelson, M.I. Optimal Hubbard models for materials with nonlocal Coulomb interactions: Graphene, silicene and benzene. Phys. Rev. Lett. 2013, 111, 036601. [Google Scholar] [CrossRef]
- Rowlands, D.A.; Zhang, Y.-Z. Disappearance of the Dirac cone in silicene due to the presence of an electric field. Chin. Phys. B 2014, 23, 037101. [Google Scholar] [CrossRef][Green Version]
- Tang, H.-K.; Laksono, E.; Rodrigues, J.N.B.; Sengupta, P.; Assaad, F.F.; Adam, S. Interaction-Driven Metal-Insulator Transition in Strained Graphene. Phys. Rev. Lett. 2015, 115, 186602. [Google Scholar] [CrossRef]
- Rut, G.; Fidrysiak, M.; Goc-Jagło, D.; Rycerz, A. Mott Transition in the Hubbard Model on Anisotropic Honeycomb Lattice with Implications for Strained Graphene: Gutzwiller Variational Study. Int. J. Mol. Sci. 2023, 24, 1509. [Google Scholar] [CrossRef]
- Potasz, P.; Güçlü, A.D.; Wójs, A.; Hawrylak, P. Electronic properties of gated triangular graphene quantum dots: Magnetism, correlations, and geometrical effects. Phys. Rev. B 2012, 85, 075431. [Google Scholar] [CrossRef]
- Rosenzweig, P.; Karakachian, H.; Marchenko, D.; Küster, K.; Starke, U. Overdoping Graphene beyond the van Hove Singularity. Phys. Rev. Lett. 2020, 125, 176403. [Google Scholar] [CrossRef]
- Fabian, T.; Walzek, L.; Burgdörfer, J.; Libisch, F.; Datseris, G. Particlelike valleytronics in graphene. Phys. Rev. B 2022, 106, 125419. [Google Scholar] [CrossRef]
- Vidarte, K.J.U.; Lewenkopf, C. High-energy Landau levels in graphene beyond nearest-neighbor hopping processes: Corrections to the effective Dirac Hamiltonian. Phys. Rev. B 2022, 106, 155414. [Google Scholar] [CrossRef]
- Rycerz, A.; Tworzydło, J.; Beenakker, C.W.J. Valley filter and valley valve in graphene. Nat. Phys. 2007, 3, 172. [Google Scholar] [CrossRef]
- Wimmer, M.; Adagideli, İ.; Berber, S.; Tománek, D.; Richter, K. Spin Currents in Rough Graphene Nanoribbons: Universal Fluctuations and Spin Injection. Phys. Rev. Lett. 2008, 100, 177207. [Google Scholar] [CrossRef] [PubMed]
- Grujić, M.M.; Tadić, M.Ž.; Peeters, F.M. Spin-Valley Filtering in Strained Graphene Structures with Artificially Induced Carrier Mass and Spin-Orbit Coupling. Phys. Rev. Lett. 2014, 113, 046601. [Google Scholar] [CrossRef]
- Bao, W.; Liu, G.; Zhao, Z.; Zhang, H.; Yan, D.; Deshpande, A.; LeRoy, B.J.; Lau, C.N. Lithography-free Fabrication of High Quality Substrate-supported and Freestanding Graphene devices. Nano Res. 2010, 3, 98. [Google Scholar] [CrossRef]
- Ando, T. Quantum point contacts in magnetic fields. Phys. Rev. B 1991, 44, 8017. [Google Scholar] [CrossRef]
- Wakabayashi, K.; Aoki, T. Electrical conductance of zigzag nanographite ribbons with locally applied gate voltage. Int. J. Mod. Phys. B 2002, 16, 4897. [Google Scholar] [CrossRef]
- Wakabayashi, K.; Sasaki, K.; Nakanishi, T.; Enoki, T. Electronic states of graphene nanoribbons and analytical solutions. Sci. Technol. Adv. Mater. 2010, 11, 054504. [Google Scholar] [CrossRef]
- Schelter, J.; Recher, P.; Trauzettel, B. The Aharonov-Bohm effect in graphene rings. Solid State Comm. 2012, 152, 1411. [Google Scholar] [CrossRef]
- Hung Nguyen, V.; Niquet, Y.M.; Dollfus, P. Aharonov-Bohm effect and giant magnetoresistance in graphene nanoribbon rings. Phys. Rev. B 2013, 88, 035408. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, S.; Osuala, C.I.; Sarkar, A.S.; Hader, G.; Cummings, A.; Strauf, S.; Qu, C.; Yang, E.-H. Observations of Aharonov-Bohm Conductance Oscillations in CVD-Grown Graphene Rings at 4K. IEEE Open J. Nanotech. 2023, 4, 208. [Google Scholar] [CrossRef]
- Ezawa, M. Monolayer Topological Insulators: Silicene, Germanene, and Stanene. J. Phys. Soc. Jpn. 2015, 84, 121003. [Google Scholar] [CrossRef]
- Hartman, T.; Sofer, Z. Beyond Graphene: Chemistry of Group 14 Graphene Analogues: Silicene, Germanene, and Stanene. ACS Nano 2019, 13, 8566. [Google Scholar] [CrossRef]
- Cserti, J. Minimal longitudinal dc conductivity of perfect bilayer graphene. Phys. Rev. B 2007, 75, 033405. [Google Scholar] [CrossRef]
- Suszalski, D.; Rut, G.; Rycerz, A. Conductivity scaling and the effects of symmetry-breaking terms in bilayer graphene Hamiltonian. Phys. Rev. B 2020, 101, 125425. [Google Scholar] [CrossRef]
- Kashiwaya, S.; Shi, Y.; Lu, J.; Sangiovanni, D.G.; Greczynski, G.; Magnuson, M.; Andersson, M.; Rosen, J.; Hultman, L. Synthesis of goldene comprising single-atom layer gold. Nat. Synth. 2024, 3, 744. [Google Scholar] [CrossRef]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Croz, J.D.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide, 3rd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Lewenkopf, C.H.; Mucciolo, E.R. The recursive Green’s function method for graphene. J. Comput. Eletron. 2013, 12, 203. [Google Scholar] [CrossRef]
- Groth, C.W.; Wimmer, M.; Akhmerov, A.R.; Waintal, X. Kwant: A software package for quantum transport. New J. Phys. 2014, 16, 063065. [Google Scholar] [CrossRef]
- João, S.M.; Anđelković, M.; Covaci, L.; Rappoport, T.G.; Lopes, J.M.V.P.; Ferreira, A. KITE: High-performance accurate modelling of electronic structure and response functions of large molecules, disordered crystals and heterostructures. R. Soc. Open Sci. 2020, 7, 191809. [Google Scholar] [CrossRef]


| Transport Regime (or Approximation) | ||||
|---|---|---|---|---|
| Cumulant | Pseudodiffusive, | Sub-Sharvin, | , | Narrow Opening, |
| (a) | (b) | see Equation (62) (c) | (d) | |
| 1 | ||||
| ∞ (e) | ||||
| Transport Regime | System | G | F | Refs. | |
|---|---|---|---|---|---|
| Standard ballistic | Sharvin contact in 2DEG, width W | [36,37] | |||
| (Pseudo)-diffusive | Diffusive conductor | [77,78] | |||
| Charge-neutral graphene sample (width W, length L) | , | [18,19] | |||
| Charge-neutral graphene disk (inner radii , outer radii ) | [20] | ||||
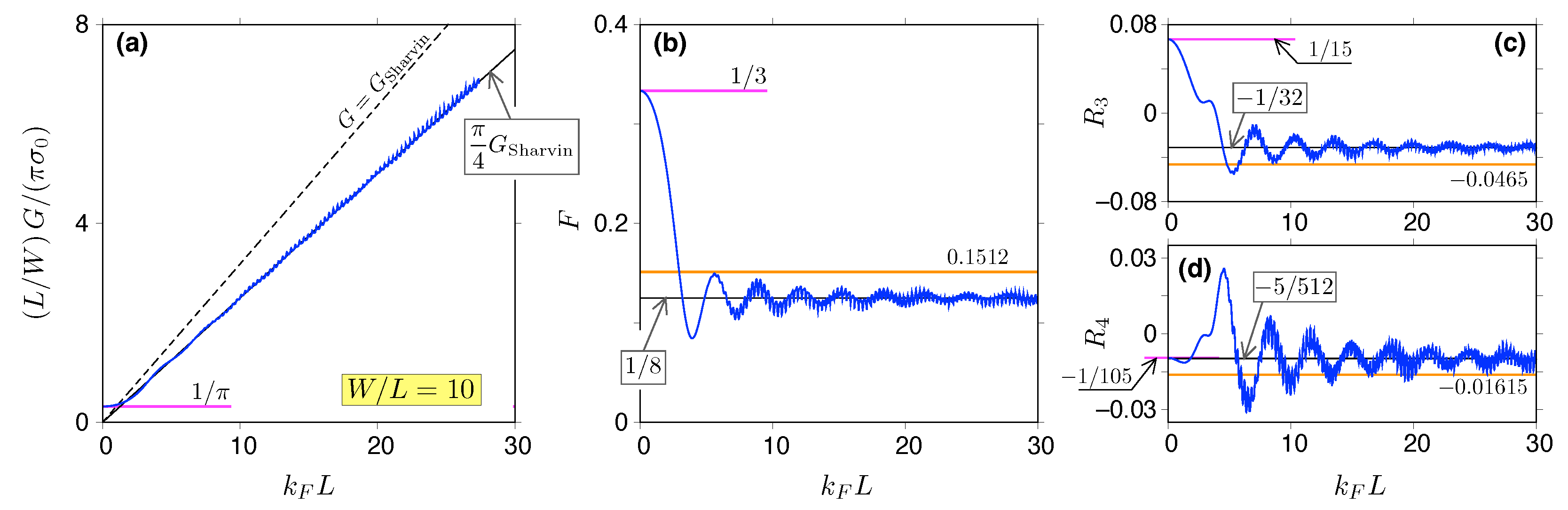
| Sub-Sharvin | Doped graphene sample (width W, length L) | [33], this work | |||
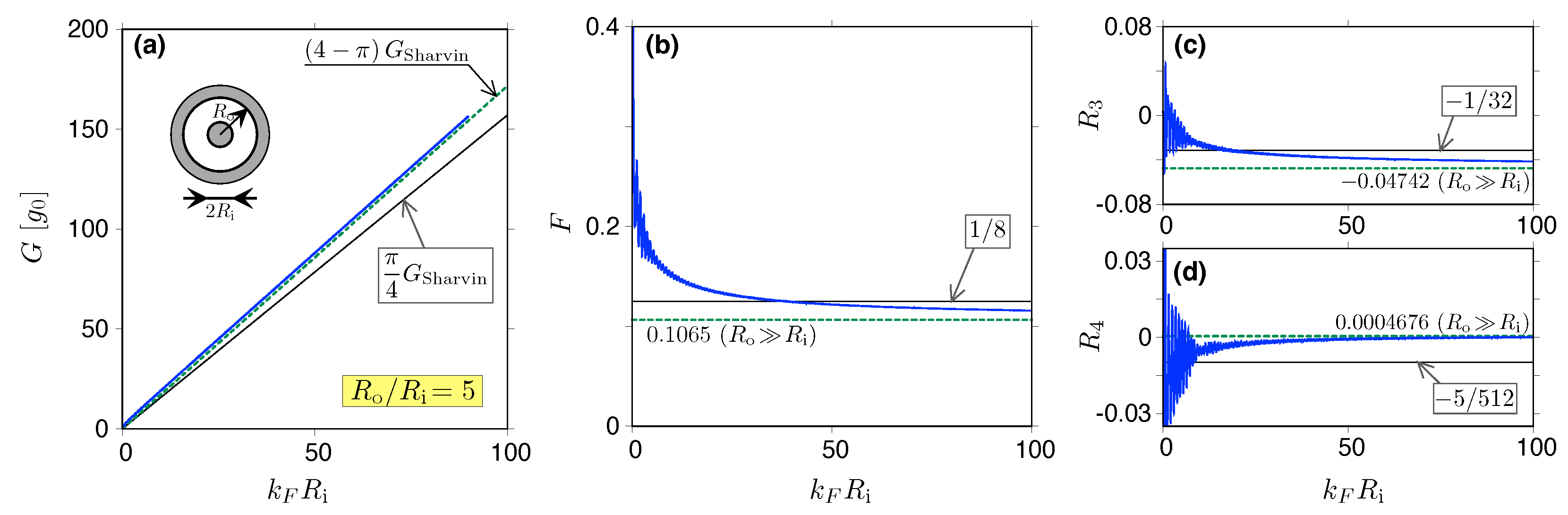
| Doped graphene disk, (inner radii , outer radii ) | (a) (c) | (a) (c) | (c) | [34], this work | |
| Doped graphene disk, (d) | (a) (c) | — | [40] | ||
| Chaotic | Symmetric cavity | (e) | [79] |
| System | Defining Parameters | System (Sample) Length, (a) | No. of Sites (b) |
|---|---|---|---|
| Constriction with zigzag edges | nm | 105,452 | |
| (24,960) | |||
| Half-Corbino disk | nm | 336,000 | |
| (136,035) | |||
| Circular quantum dot | nm | 320,881 | |
| (240,389) | |||
| Circular quantum dot with a circular hole | nm | 301,148 | |
| (220,656) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rycerz, A. The Quantum Transport of Dirac Fermions in Selected Graphene Nanosystems Away from the Charge Neutrality Point. Materials 2025, 18, 2036. https://doi.org/10.3390/ma18092036
Rycerz A. The Quantum Transport of Dirac Fermions in Selected Graphene Nanosystems Away from the Charge Neutrality Point. Materials. 2025; 18(9):2036. https://doi.org/10.3390/ma18092036
Chicago/Turabian StyleRycerz, Adam. 2025. "The Quantum Transport of Dirac Fermions in Selected Graphene Nanosystems Away from the Charge Neutrality Point" Materials 18, no. 9: 2036. https://doi.org/10.3390/ma18092036
APA StyleRycerz, A. (2025). The Quantum Transport of Dirac Fermions in Selected Graphene Nanosystems Away from the Charge Neutrality Point. Materials, 18(9), 2036. https://doi.org/10.3390/ma18092036






