Trans-Scale Progressive Failure Analysis Methodology for Composite Materials Incorporating Interfacial Phase Effect
Abstract
1. Introduction
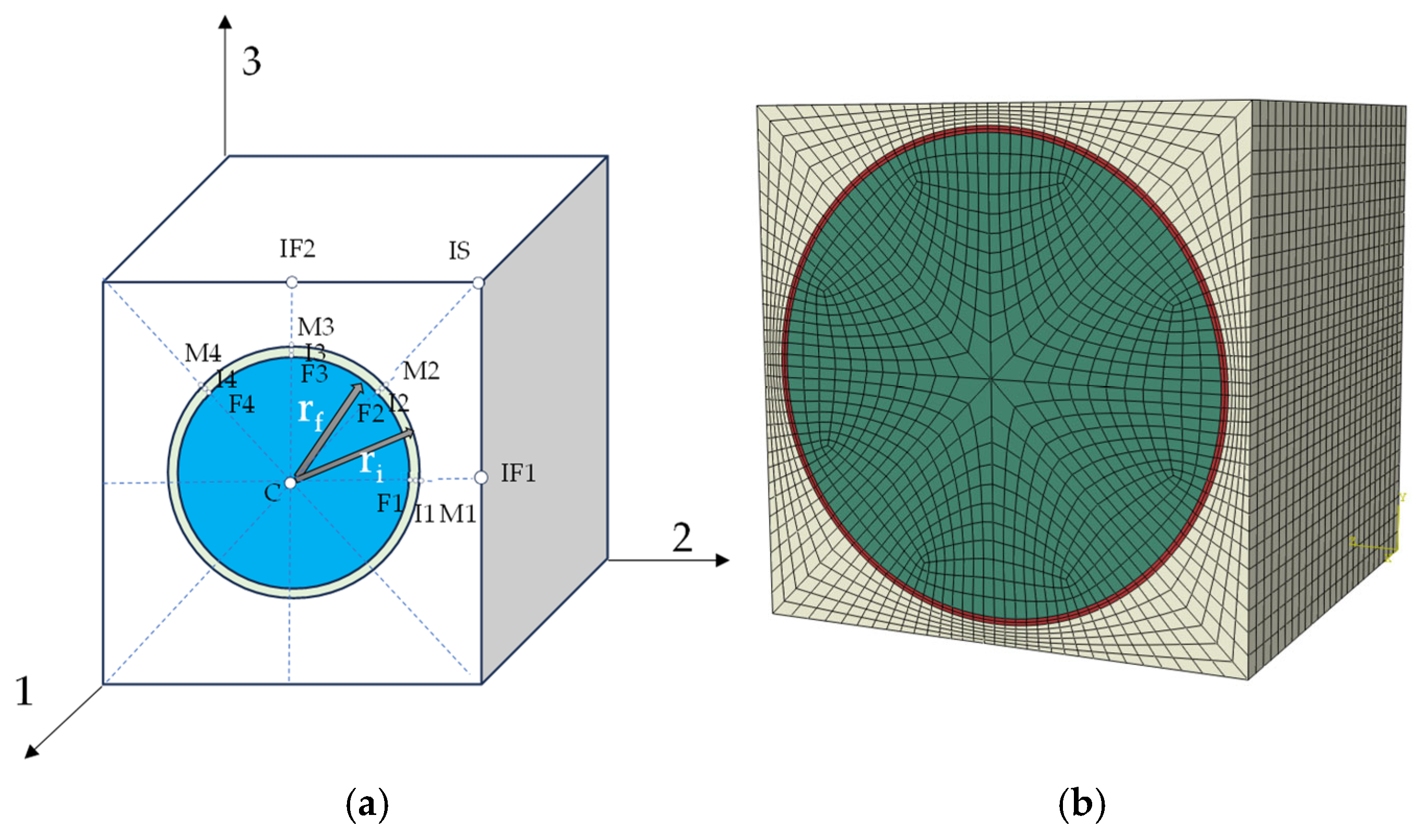
2. Calculation of Equivalent Mechanical Properties of Interface
3. Trans-Scale Failure Analysis Method Based on New RVE Model
3.1. Macro–Micro Strain Transformation
3.2. Trans-Scale Progressive Failure Analysis Methodology Incorporating Interfacial Phase Effect (TFAMII)
3.3. Microscopic Failure Criteria
- (1)
- Fiber Failure
- (2)
- Matrix failure
- (3)
- Interface failure
3.4. Damage Evolution Model
4. Example Analysis
4.1. Finite Element Modeling of Open-Hole Laminate
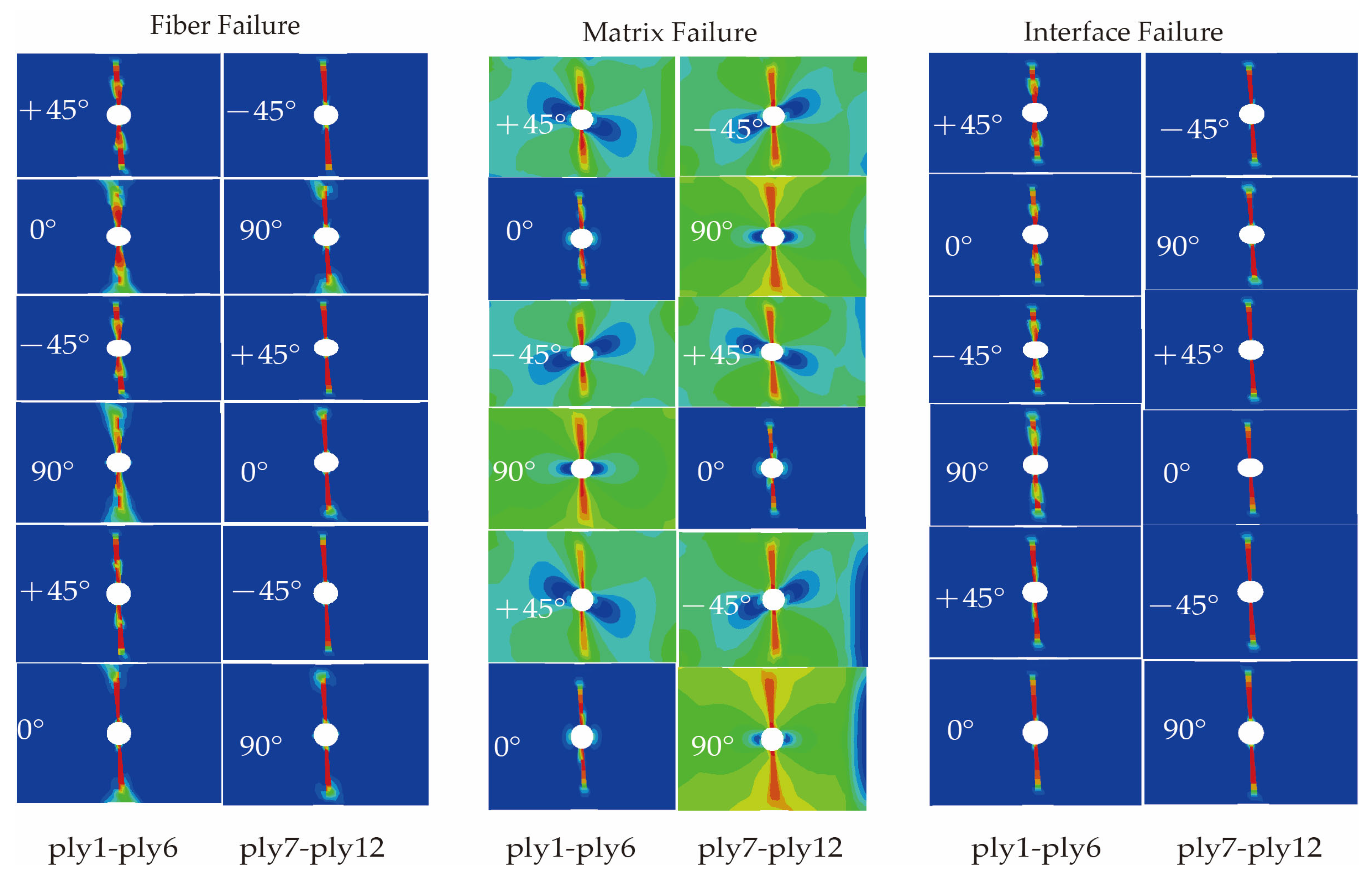
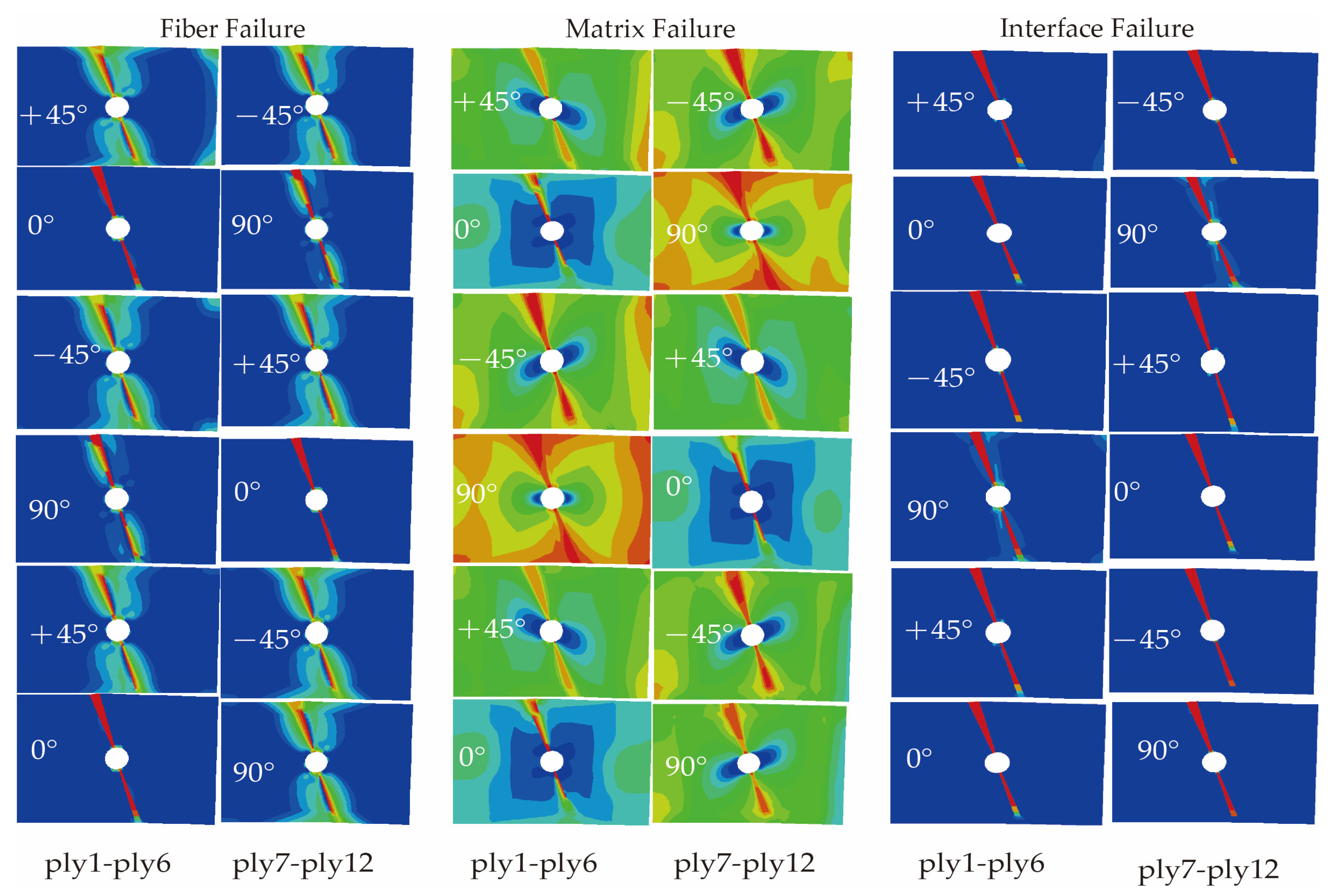
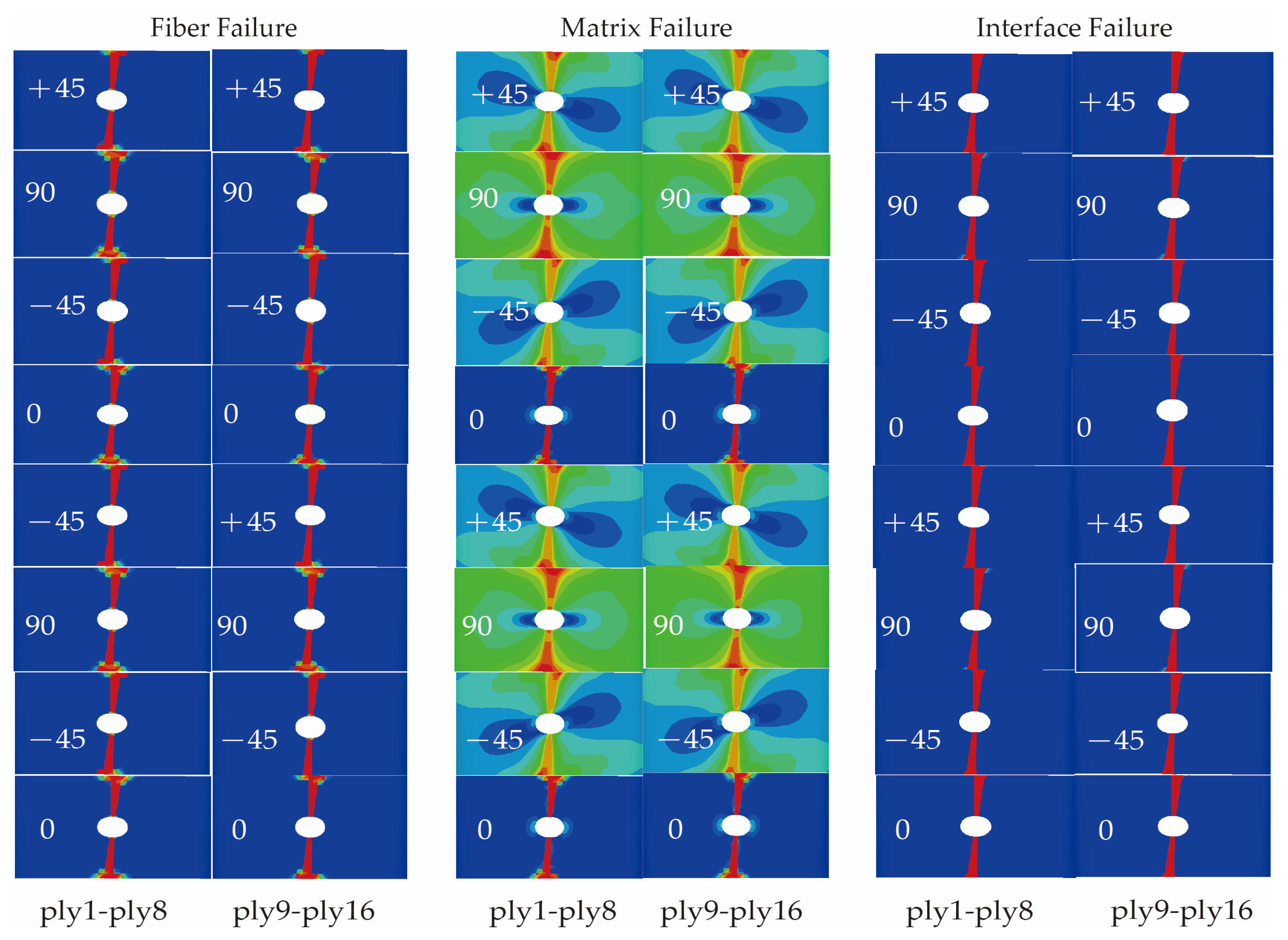
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hill, R. A Self-Consistent Mechanics of Composite Materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Tsai, S.W.; Wu, E.M. A General Theory of Strength for Anisotropic Materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Falzon, B.G.; Apruzzese, P. Numerical Analysis of Intralaminar Failure Mechanisms in Composite Structures. Part II: Applications. Compos. Struct. 2011, 93, 1047–1053. [Google Scholar] [CrossRef]
- Joseph, A.P.K.; Waas, A.M.; Ji, W.; Pineda, E.J.; Liguore, S.L.; Wanthal, S.P. Progressive Damage and Failure Prediction of Open Hole Tension and Open Hole Compression Specimens. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5 January 2015; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015. [Google Scholar]
- Tarfaoui, M.; El Moumen, A.; Lafdi, K. Progressive Damage Modeling in Carbon Fibers/Carbon Nanotubes Reinforced Polymer Composites. Compos. Part B Eng. 2017, 112, 185–195. [Google Scholar] [CrossRef]
- Ud Din, I.; Hao, P.; Franz, G.; Panier, S. Elastoplastic CDM Model Based on Puck’s Theory for the Prediction of Mechanical Behavior of Fiber Reinforced Polymer (FRP) Composites. Compos. Struct. 2018, 201, 291–302. [Google Scholar] [CrossRef]
- Ud Din, I.; Tu, S.; Hao, P.; Panier, S.; Khan, K.A.; Umer, R.; Shah, S.Z.H.; Franz, G.; Aamir, M. Sequential Damage Study Induced in Fiber Reinforced Composites by Shear and Tensile Stress Using a Newly Developed Arcan Fixture. J. Mater. Res. Technol. 2020, 9, 13352–13364. [Google Scholar] [CrossRef]
- Gosse, J.; Christensen, S. Strain Invariant Failure Criteria for Polymers in Composite Materials. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, Anaheim, CA, USA, 11 June 2001; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar]
- Yudhanto, A. Effects of Micromechanical Factors in the Strain Invariant Failure Theory for Composites. Master’s Thesis, National University of Singapore, Singapore, 2005. [Google Scholar]
- Tay, T.E.; Liu, G.; Yudhanto, A.; Tan, V.B.C. A Micro—Macro Approach to Modeling Progressive Damage in Composite Structures. Int. J. Damage Mech. 2008, 17, 5–28. [Google Scholar] [CrossRef]
- Jin, K.-K.; Huang, Y.; Lee, Y.-H.; Ha, S.K. Distribution of Micro Stresses and Interfacial Tractions in Unidirectional Composites. J. Compos. Mater. 2008, 42, 1825–1849. [Google Scholar] [CrossRef]
- Ha, S.K.; Jin, K.K.; Huang, Y. Micro-Mechanics of Failure (MMF) for Continuous Fiber Reinforced Composites. J. Compos. Mater. 2008, 42, 1873–1895. [Google Scholar] [CrossRef]
- Ha, S.K.; Huang, Y.; Han, H.H.; Jin, K.K. Micromechanics of Failure for Ultimate Strength Predictions of Composite Laminates. J. Compos. Mater. 2010, 44, 2347–2361. [Google Scholar] [CrossRef]
- Buchanan, D.L.; Gosse, J.H.; Wollschlager, J.A.; Ritchey, A.; Byron Pipes, R. Micromechanical Enhancement of the Macroscopic Strain State for Advanced Composite Materials. Compos. Sci. Technol. 2009, 69, 1974–1978. [Google Scholar] [CrossRef]
- Sun, X.S.; Tan, V.B.C.; Tay, T.E. Micromechanics-Based Progressive Failure Analysis of Fibre-Reinforced Composites with Non-Iterative Element-Failure Method. Comput. Struct. 2011, 89, 1103–1116. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, L.; Kyu Ha, S. Prediction of Three-Dimensional Composite Laminate Response Using Micromechanics of Failure. J. Compos. Mater. 2012, 46, 2431–2442. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, C.; Ha, S.K. Strength Prediction of Triaxially Loaded Composites Using a Progressive Damage Model Based on Micromechanics of Failure. J. Compos. Mater. 2013, 47, 777–792. [Google Scholar] [CrossRef]
- Li, W.; Cai, H.; Li, C.; Wang, K.; Fang, L. Progressive Failure of Laminated Composites with a Hole under Compressive Loading Based on Micro-Mechanics. Adv. Compos. Mater. 2014, 23, 477–490. [Google Scholar] [CrossRef]
- Li, W.; Cai, H.; Li, C. Static Compressive Strength Prediction of Open-Hole Structure Based on Non-Linear Shear Behavior and Micro-Mechanics. Mech. Time-Depend. Mater. 2014, 18, 643–662. [Google Scholar] [CrossRef]
- Li, X.; Guan, Z.; Li, Z.; Liu, L. A New Stress-Based Multi-Scale Failure Criterion of Composites and Its Validation in Open Hole Tension Tests. Chin. J. Aeronaut. 2014, 27, 1430–1441. [Google Scholar] [CrossRef]
- Wang, L.; Wang, B.; Wei, S.; Hong, Y.; Zheng, C. Prediction of Long-Term Fatigue Life of CFRP Composite Hydrogen Storage Vessel Based on Micromechanics of Failure. Compos. Part B Eng. 2016, 97, 274–281. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, C.; Wei, S.; Wei, Z. Micromechanics-Based Progressive Failure Analysis of Carbon FIber/Epoxy Composite Vessel under Combined Internal Pressure and Thermomechanical Loading. Compos. Part B Eng. 2016, 89, 77–84. [Google Scholar] [CrossRef]
- Liao, B.B.; Tan, H.C.; Zhou, J.W.; Jia, L.Y. Multi-Scale Modelling of Dynamic Progressive Failure in Composite Laminates Subjected to Low Velocity Impact. Thin-Walled Struct. 2018, 131, 695–707. [Google Scholar] [CrossRef]
- Liu, Z.; Guan, Z.; Tan, R.; Xu, J. Analysis of Open-Hole Compressive CFRP Laminates at Various Temperatures Based on a Multiscale Strategy. Appl. Compos. Mater. 2019, 26, 923–944. [Google Scholar] [CrossRef]
- Lou, X.; Han, X.; Cai, H. A High-Efficient Model for Interface Debonding Analysis of Carbon Fiber-Reinforced Polymer Composite. Compos. Interfaces 2020, 27, 87–109. [Google Scholar] [CrossRef]
- Lou, X.; Han, X.; Cai, H. A Micromechanics-Based Damage Model for Compressive Behavior Analysis of Impacted Composite Laminates. Int. J. Damage Mech. 2020, 29, 369–387. [Google Scholar] [CrossRef]
- Sun, J.; Wang, A.; Cai, H.; Han, X.; Wei, Z.; Huang, Y. Multiscale Progressive Damage Model for Plain Woven Composites. Int. J. Mech. Sci. 2023, 259, 108604. [Google Scholar] [CrossRef]
- Lee, S.-M.; Baek, J.-H.; Yu, M.-H.; Jeon, S.-W.; Choi, W.-S.; Heo, S.-P.; Yang, M.-H.; Park, J.-H.; Kim, H.-S. Multi-Scale (Macro-Meso-Micro) Progressive Failure Simulation of the Carbon Fiber Braided Structure Under Quasi-Static Mechanical Loading. Int. J. Precis. Eng. Manuf. Green Technol. 2024. [Google Scholar] [CrossRef]
- Zheng, T.; Guo, L.; Ding, J.; Li, Z. An Innovative Micromechanics-Based Multiscale Damage Model of 3D Woven Composites Incorporating Probabilistic Fiber Strength Distribution. Compos. Struct. 2022, 287, 115345. [Google Scholar] [CrossRef]
- Zheng, T.; Huang, J.; Guo, L.; Sun, R.; Huang, T.; Zhou, J.; Jia, F.; Hong, C. A Combined Experimental and Numerical Approach to Investigate the Failure Behaviors of 3D Woven Composites under Biaxial Tensile Loading. Compos. Sci. Technol. 2023, 236, 109974. [Google Scholar] [CrossRef]
- Zheng, T.; Guo, L.; Sun, R.; Wang, T.; Hong, C.; Benedictus, R.; Pascoe, J.-A. Investigation on the Effect of Interface Properties on Compressive Failure Behavior of 3D Woven Composites through Micromechanics-Based Multiscale Damage Model. Compos. Struct. 2023, 320, 117186. [Google Scholar] [CrossRef]
- Zheng, T.; Huang, J.; Huang, K.; Yu, H.; Hong, C.; Guo, L. Different Effects of Interfacial Properties on the Tensile and Compressive Damage Mechanisms of 3D Woven Composites: Multiscale Damage Model and Numerical Comparative Study. Eng. Fract. Mech. 2024, 295, 109741. [Google Scholar] [CrossRef]
- Wang, H.; Zhong, X.-Y.; Jia, H.; Zhang, L.-W.; Liu, H.-S.; Sun, M.-C.; Liu, T.-W.; Bai, J.-B.; Ge, S.-C.; Bao, J.-W. Micromechanical Modeling for Longitudinal Tensile Property of Unidirectional CFRP Considering Dispersion of Fiber Properties. Compos. Struct. 2024, 339, 118081. [Google Scholar] [CrossRef]
- Guo, F.-L.; Huang, P.; Li, Y.-Q.; Hu, N.; Fu, S.-Y. Multiscale Modeling of Mechanical Behaviors of Carbon Fiber Reinforced Epoxy Composites Subjected to Hygrothermal Aging. Compos. Struct. 2021, 256, 113098. [Google Scholar] [CrossRef]
- Guo, F.-L.; Zhou, Z.-L.; Wu, T.; Hu, J.-M.; Li, Y.-Q.; Huang, P.; Hu, N.; Fu, S.-Y.; Hong, Y. Experimental and Multiscale Modeling Investigations of Cryo-Thermal Cycling Effects on the Mechanical Behaviors of Carbon Fiber Reinforced Epoxy Composites. Compos. Part B Eng. 2022, 230, 109534. [Google Scholar] [CrossRef]
- Yang, L.; Wu, Z.; Cao, Y.; Yan, Y. Micromechanical Modelling and Simulation of Unidirectional Fibre-Reinforced Composite under Shear Loading. J. Reinf. Plast. Compos. 2015, 34, 72–83. [Google Scholar] [CrossRef]
- Wu, Q.; Li, M.; Gu, Y.; Li, Y.; Zhang, Z. Nano-Analysis on the Structure and Chemical Composition of the Interphase Region in Carbon Fiber Composite. Compos. Part Appl. Sci. Manuf. 2014, 56, 143–149. [Google Scholar] [CrossRef]
- Arp, J.C.; Nicholson, J.; Geddes, J.; Brown, D.A.; Atamturktur Russcher, S.; Kitchens, C.L. Inferring Effective Interphase Properties in Composites by Inverse Analysis. ACS Appl. Polym. Mater. 2023, 5, 7733–7745. [Google Scholar] [CrossRef]
- Qi, Y.; Jiang, D.; Ju, S.; Zhang, J.; Cui, X. Determining the Interphase Thickness and Properties in Carbon Fiber Reinforced Fast and Conventional Curing Epoxy Matrix Composites Using Peak Force Atomic Force Microscopy. Compos. Sci. Technol. 2019, 184, 107877. [Google Scholar] [CrossRef]
- Sun, Q.; Meng, Z.; Zhou, G.; Lin, S.-P.; Kang, H.; Keten, S.; Guo, H.; Su, X. Multi-Scale Computational Analysis of Unidirectional Carbon Fiber Reinforced Polymer Composites under Various Loading Conditions. Compos. Struct. 2018, 196, 30–43. [Google Scholar] [CrossRef]
- Linde, P.; Pleitner, J.; de Boer, H.; Carmone, C. Modelling and Simulation of Fibre Metal Laminates. In Proceedings of the ABAQUS Users’ Conference, Boston, MA, USA, 25–27 May 2004; pp. 421–439. [Google Scholar]
- Green, B.G.; Wisnom, M.R.; Hallett, S.R. An Experimental Investigation into the Tensile Strength Scaling of Notched Composites. Compos. Part Appl. Sci. Manuf. 2007, 38, 867–878. [Google Scholar] [CrossRef]
- Kaddour, A.; Hinton, M.; Smith, P.; Li, S. Mechanical Properties and Details of Composite Laminates for the Test Cases Used in the Third World-Wide Failure Exercise. J. Compos. Mater. 2013, 47, 2427–2442. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, Z.; Wang, X.; Zhang, B. Analysis and Determination for the Parameters of “Cohesive Element” in the Numerical Model of Single Fiber Composites: The Elastic Parameters. J. Reinf. Plast. Compos. 2012, 31, 1127–1135. [Google Scholar] [CrossRef]
- Li, Z.; Guan, Z.; He, W. Strain invariant failure theory invariant properties of domestic carbon fiber/resin composites. Fuhe Cailiao Xuebao (Acta Mater. Compos. Sin.) 2011, 28, 192–196. [Google Scholar]
- Chowdhury, N.T.; Balasubramani, N.K.; Pearce, G.M.; Tao, C. A Multiscale Modelling Procedure for Predicting Failure in Composite Textiles Using an Enhancement Approach. Eng. Fail. Anal. 2019, 102, 148–159. [Google Scholar] [CrossRef]
- Falzon, B.G.; Apruzzese, P. Numerical Analysis of Intralaminar Failure Mechanisms in Composite Structures. Part I: FE Implementation. Compos. Struct. 2011, 93, 1039–1046. [Google Scholar] [CrossRef]
- Chamis, C.C.; Abdi, F.; Garg, M.; Minnetyan, L.; Baid, H.; Huang, D.; Housner, J.; Talagani, F. Micromechanics-Based Progressive Failure Analysis Prediction for WWFE-III Composite Coupon Test Cases. J. Compos. Mater. 2013, 47, 2695–2712. [Google Scholar] [CrossRef]




| Materials Name | Layers | Length/mm | Width/mm | Hole Diameter/mm |
|---|---|---|---|---|
| T700/5428 | [45/0/−5/90]3s | 54 | 36 | 6 |
| CCF300/5428 | [45/0/−45/90]3s | 54 | 36 | 6 |
| IM7/8552 | [45/90/−45/0]4s | 254 | 64 | 12.7 |
| Materials Name | E11 (GPa) | E22 = E33 (GPa) | G12 = G13 (GPa) | G23 (GPa) | v12 = v13 | v23 | ||
|---|---|---|---|---|---|---|---|---|
| T700 | 230 | 18.2 | 36.2 | 7 | 0.27 | 0.3 | −5.4 × 10−7 | 1.01 × 10−5 |
| CCF300 | 252 | 25.2 | 7 | 6.9 | 0.279 | 0.25 | 1.3 × 10−7 | 1 × 10−5 |
| IM7 | 276 | 19 | 27 | 7 | 0.2 | 0.247 | −4 × 10−7 | 5.6 × 10−6 |
| 5428 | 3.5 | / | 0.35 | 4.41 × 10−5 | ||||
| 8552 | 4.08 | / | 0.38 | 4.67 × 10−5 | ||||
| T700/5428 | 125 | 7.8 | 5.6 | 5.7 | 0.32 | 0.46 | 9.7 × 10−7 | 2.09 × 10−5 |
| CCF300/5428 | 145 | 9.75 | 5.69 | 5.69 | 0.312 | 0.44 | 4 × 10−7 | 2.5 × 10−5 |
| IM7/8552 | 165 | 9 | 5.6 | 2.8 | 0.34 | 0.5 | −1 × 10−6 | 1.8 × 10−5 |
| Material Names | Critical Strain Invariants | Value |
|---|---|---|
| T700/5428 [46] | 0.023 | |
| 0.0313 | ||
| 0.036 | ||
| CCF300/5428 [46] | 0.018 | |
| 0.0319 | ||
| 0.0359 | ||
| IM7/8552 | 0.0177 | |
| 0.0225 | ||
| 0.0345 |
| Materials Name | Method | Ultimate Strength/MPa | Error/% |
|---|---|---|---|
| T700/5428 | Experiment [21] | 517 | / |
| TFAMII | 509.7 | −1.41 | |
| Linde | 496.5 | −3.97 | |
| Hashin | 556.8 | 7.70 | |
| CCF300/5428 | Experiment [21] | 375 | / |
| TFAMII | 350.0 | −6.67 | |
| Linde | 407.5 | 8.67 | |
| Hashin | 422.6 | 12.56 | |
| IM/78552 | Experiment [43] | 374 | / |
| TFAMII | 338.0 | −9.62 | |
| Linde | 418.2 | 11.82 | |
| Hashin | 361.5 | −3.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Peng, F.; Zhao, J.; Guo, S.; Hu, L.; Gong, Y. Trans-Scale Progressive Failure Analysis Methodology for Composite Materials Incorporating Interfacial Phase Effect. Materials 2025, 18, 3667. https://doi.org/10.3390/ma18153667
Li Z, Peng F, Zhao J, Guo S, Hu L, Gong Y. Trans-Scale Progressive Failure Analysis Methodology for Composite Materials Incorporating Interfacial Phase Effect. Materials. 2025; 18(15):3667. https://doi.org/10.3390/ma18153667
Chicago/Turabian StyleLi, Zhijie, Fei Peng, Jian Zhao, Sujuan Guo, Lefei Hu, and Yu Gong. 2025. "Trans-Scale Progressive Failure Analysis Methodology for Composite Materials Incorporating Interfacial Phase Effect" Materials 18, no. 15: 3667. https://doi.org/10.3390/ma18153667
APA StyleLi, Z., Peng, F., Zhao, J., Guo, S., Hu, L., & Gong, Y. (2025). Trans-Scale Progressive Failure Analysis Methodology for Composite Materials Incorporating Interfacial Phase Effect. Materials, 18(15), 3667. https://doi.org/10.3390/ma18153667






