Three-Dimensional Deformation Calculation of Wind Tunnel Flexible Wall Using Orthogonal Beam Function
Abstract
1. Introduction
2. OBF Model Under Small Deflection Deformation
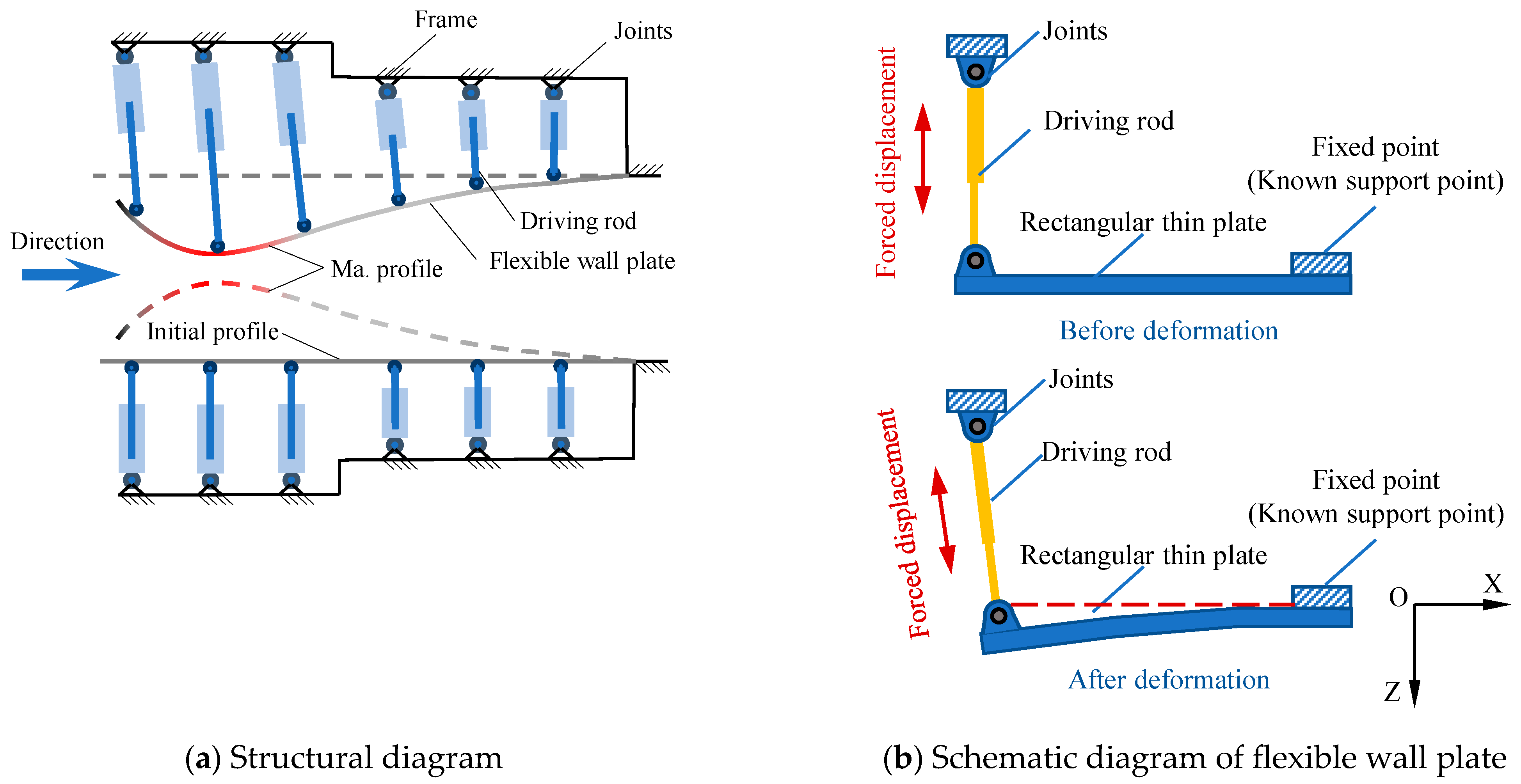
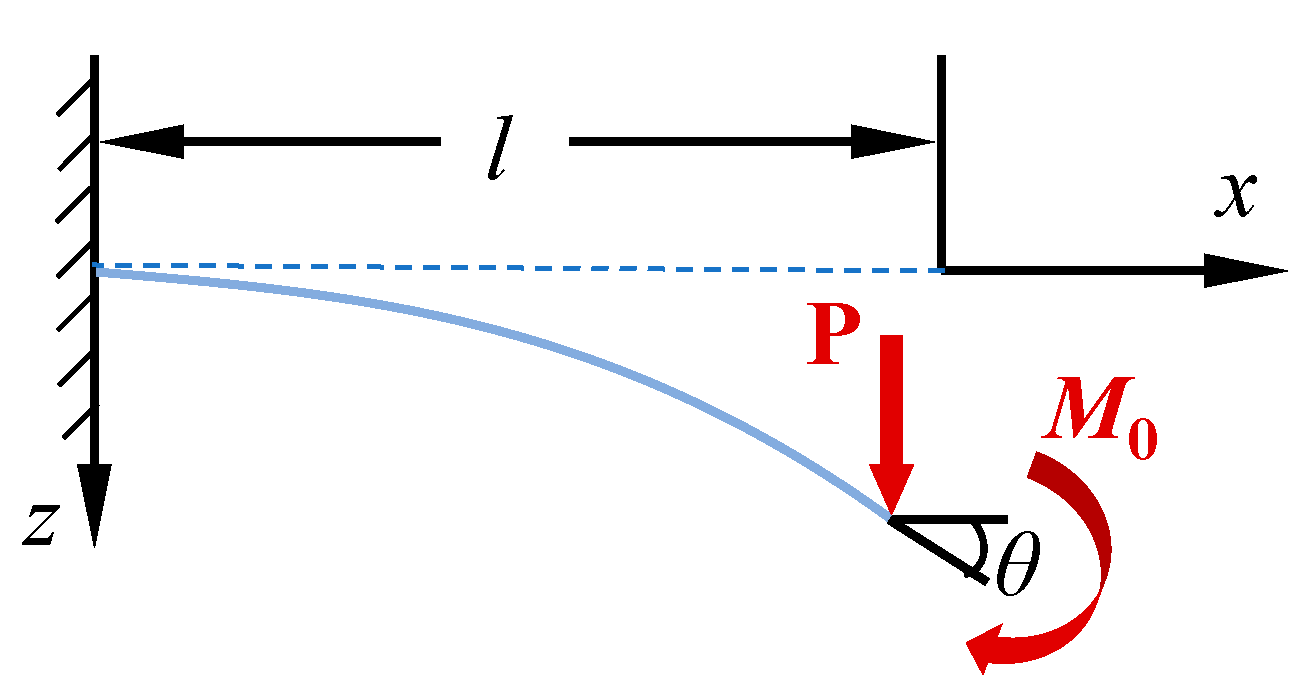
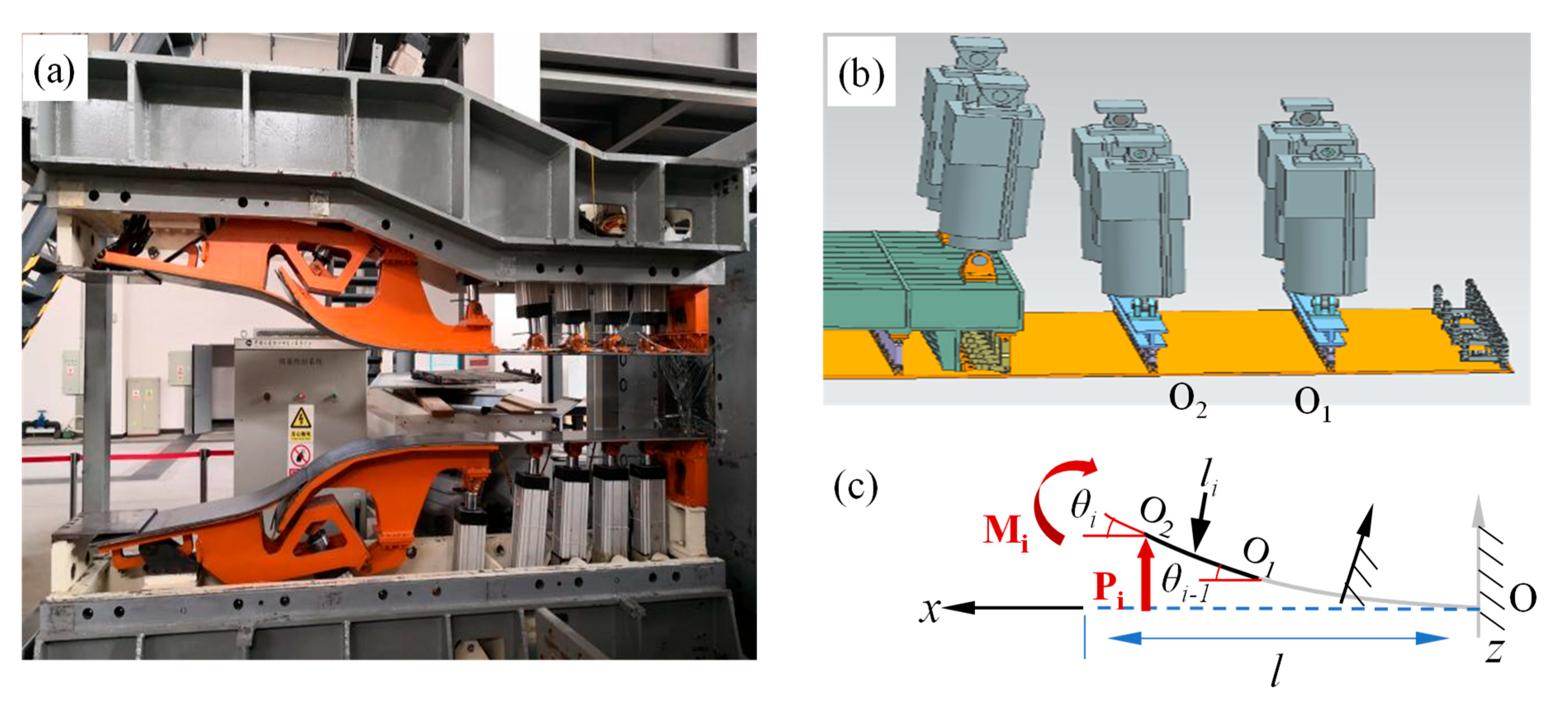
2.1. Flexible Wall Structure and Stress Analysis
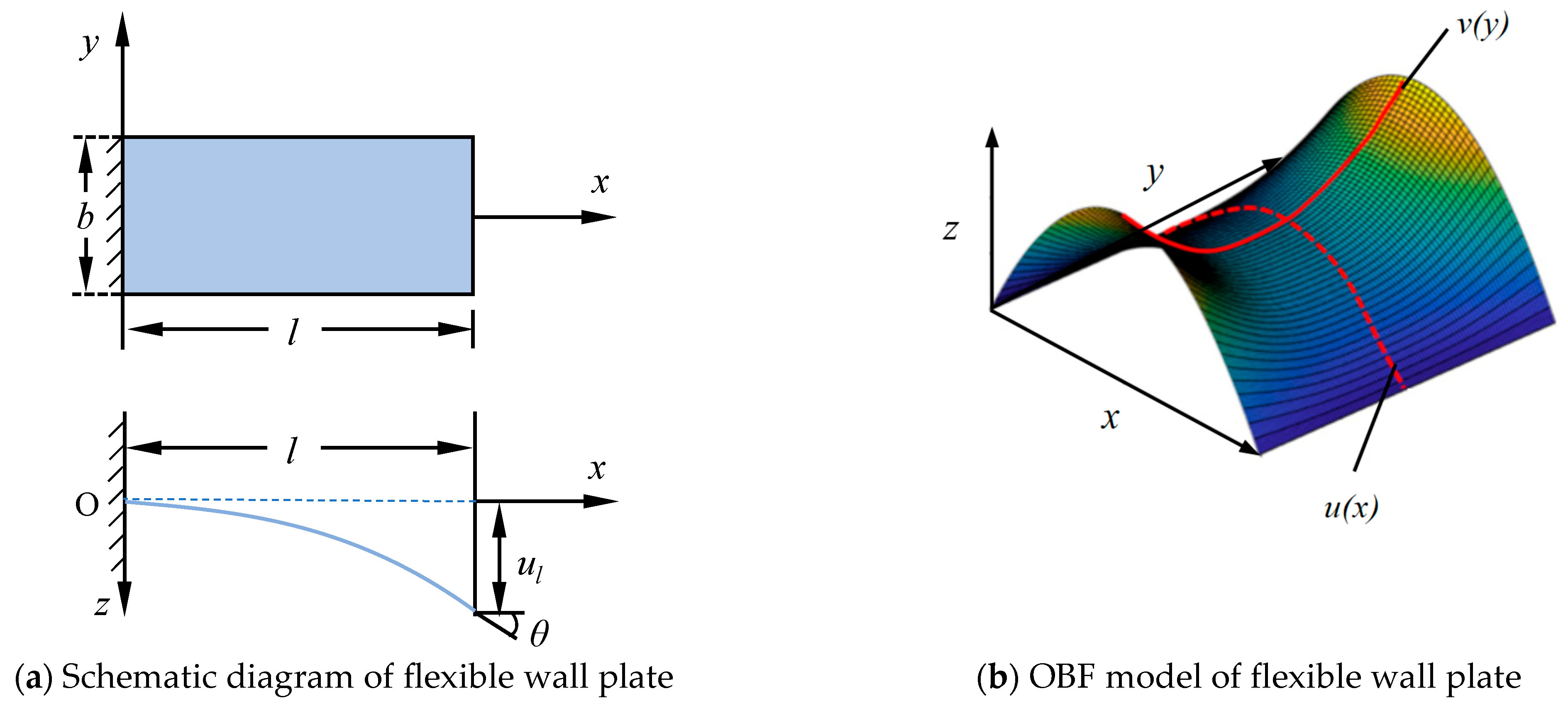
2.2. Establishment of Orthogonal Beam Function of Flexible Wall Plate
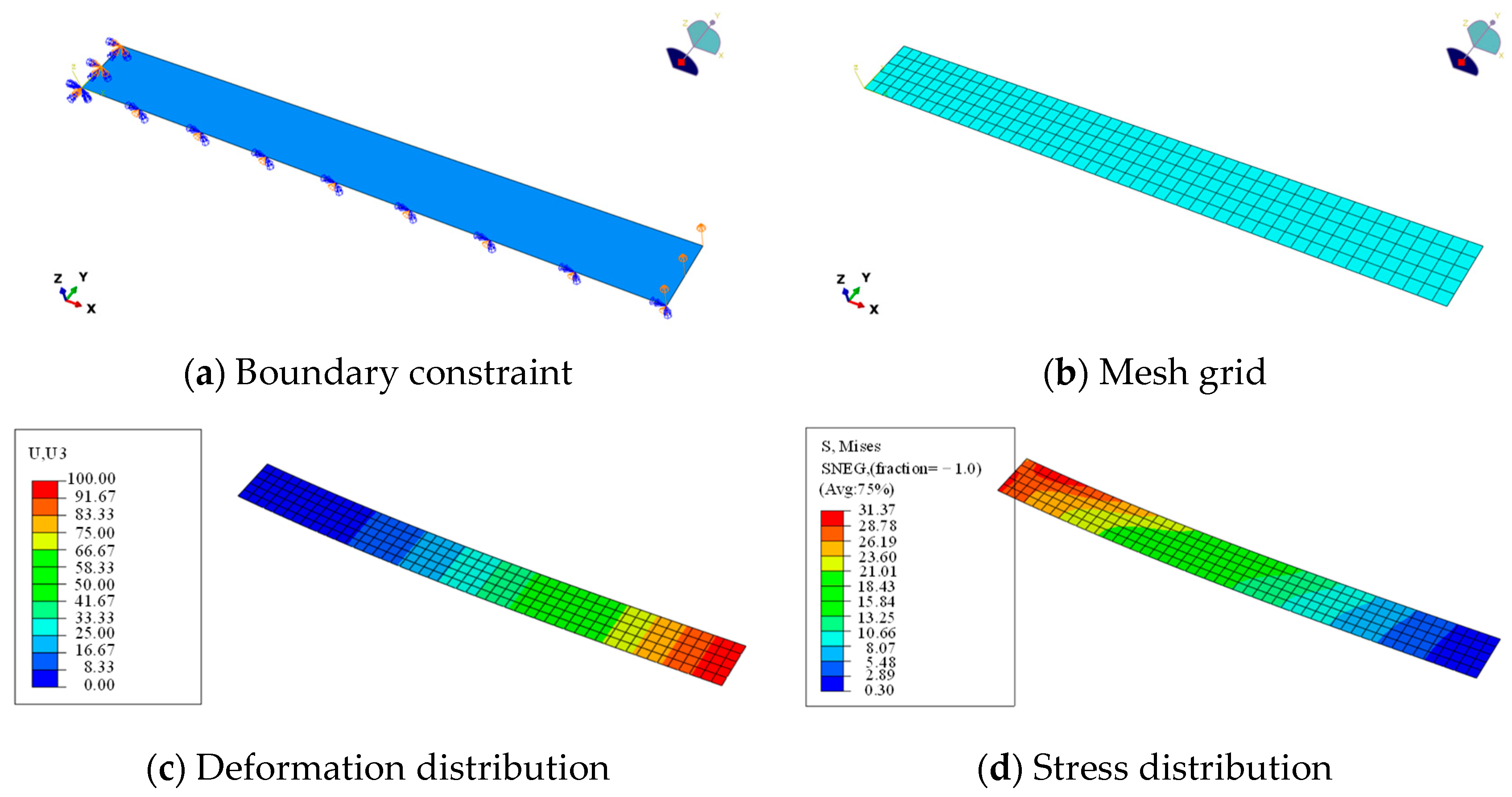
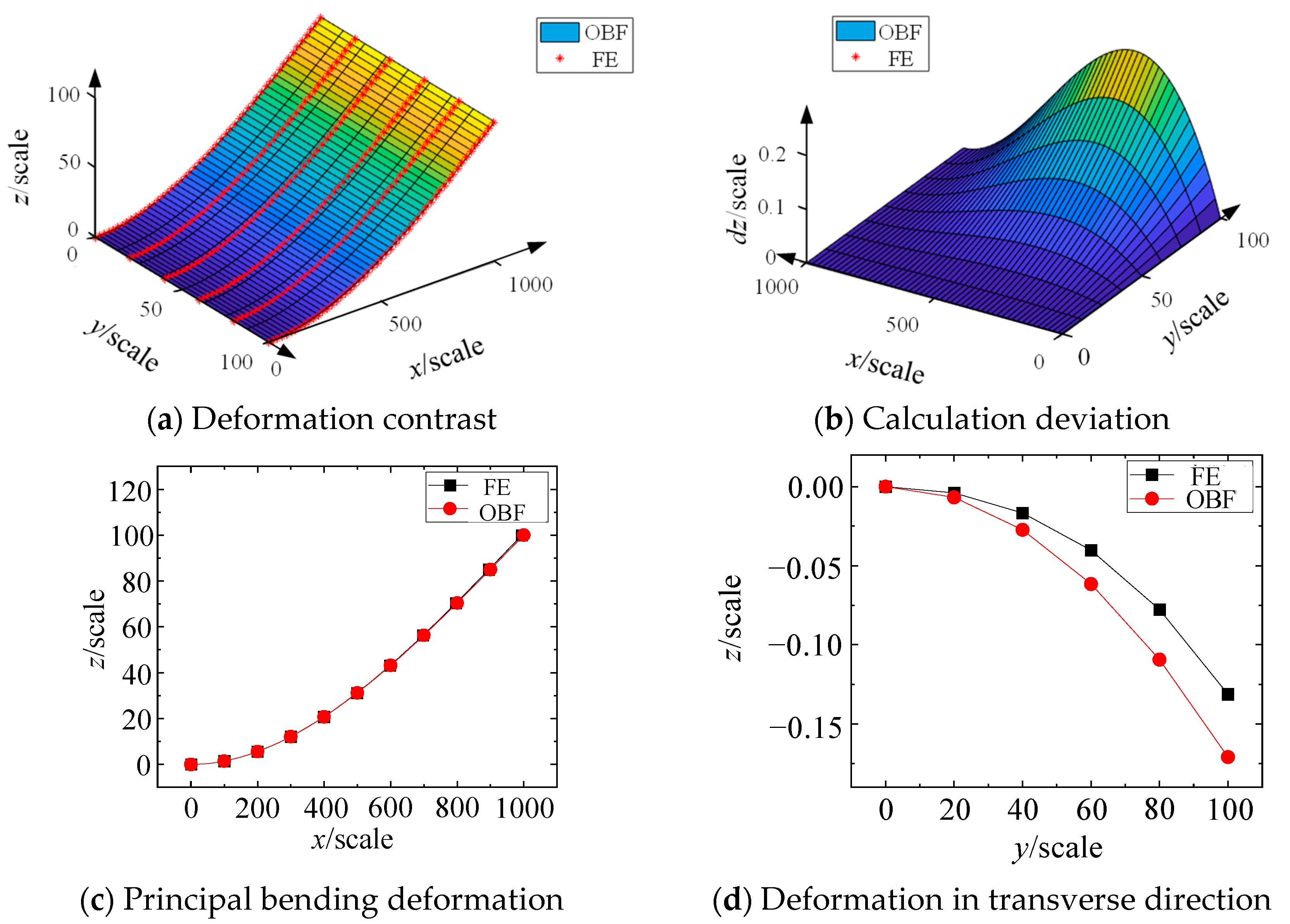
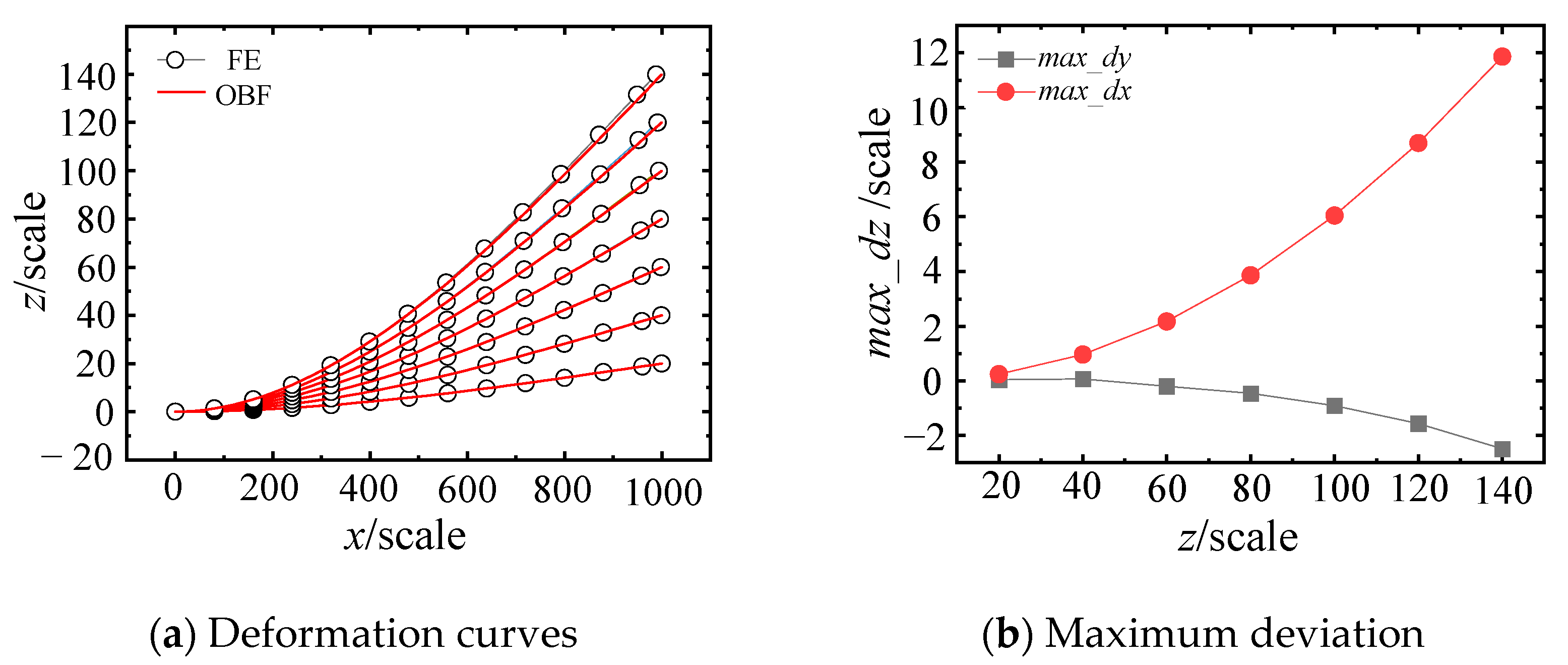
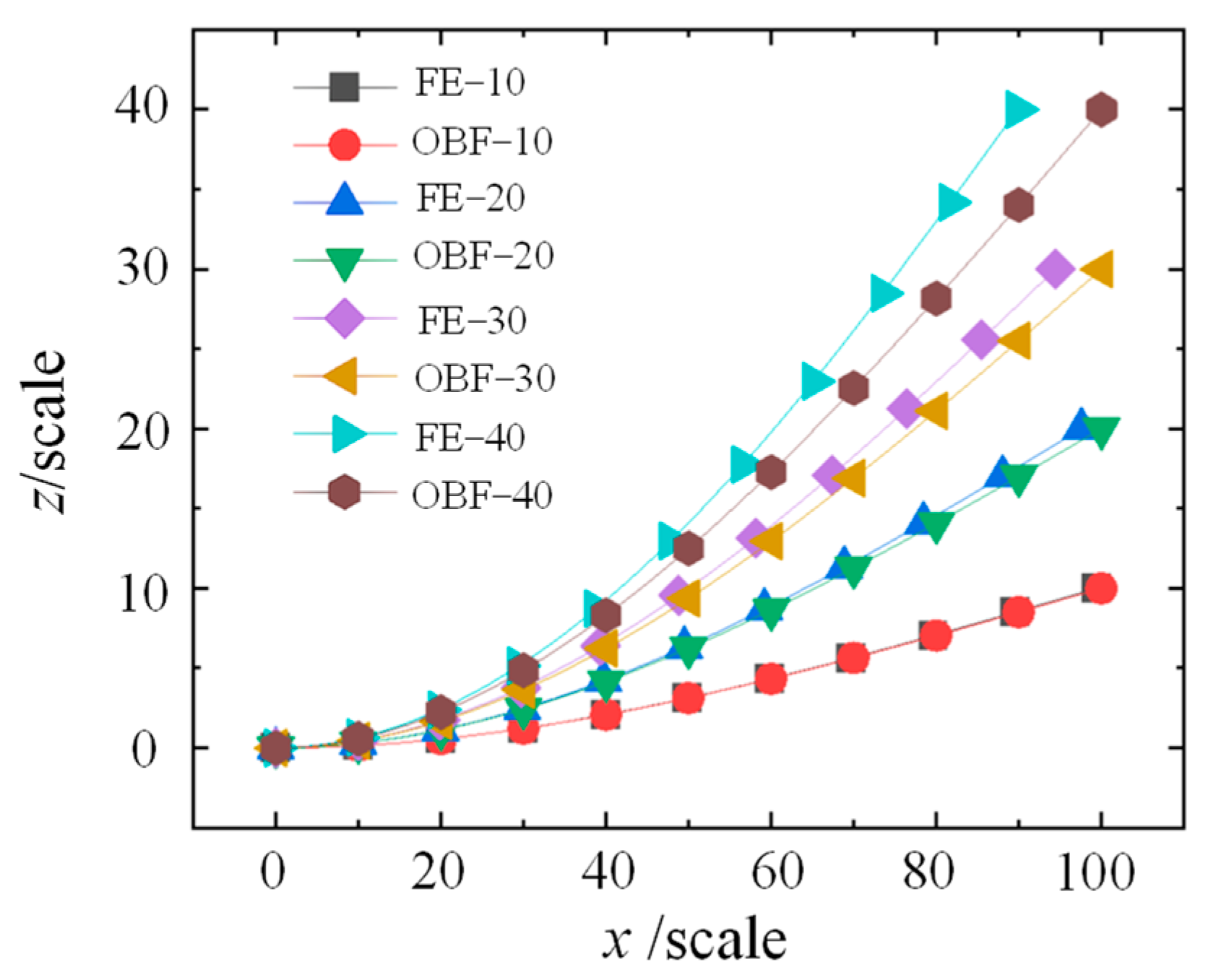
2.3. Deviation Analysis of the OBF Model
3. Solution of Large Deflection Deformation of Flexible Wall Plate
3.1. Elliptic Integral Method for Solving Large Deflection Deformation
3.2. Accuracy Analysis of EI Method
4. Experimental Verification and Discussion
5. Conclusions
- (1)
- Based on the small-deflection deformation of beams, an OBF model for flexible wall plates was established. The deformations of the flexible wall plate in both the principal bending direction and the transverse direction were calculated and compared with FE results. It was found that the OBF model agrees well with the FE results of the flexible wall plate under small deflections. However, the computational deviation gradually increases as the deflection grows.
- (2)
- The large-deflection deformation in the principal bending direction was solved using the EI method, and the OBF model was accordingly modified. The results demonstrate that the modified OBF model significantly improves the accuracy of large-deflection deformation calculations. Under pure force loading, pure moment loading, and combined force-moment loading, the maximum computational deviation was found to be less than 0.2% of the deflection value.
- (3)
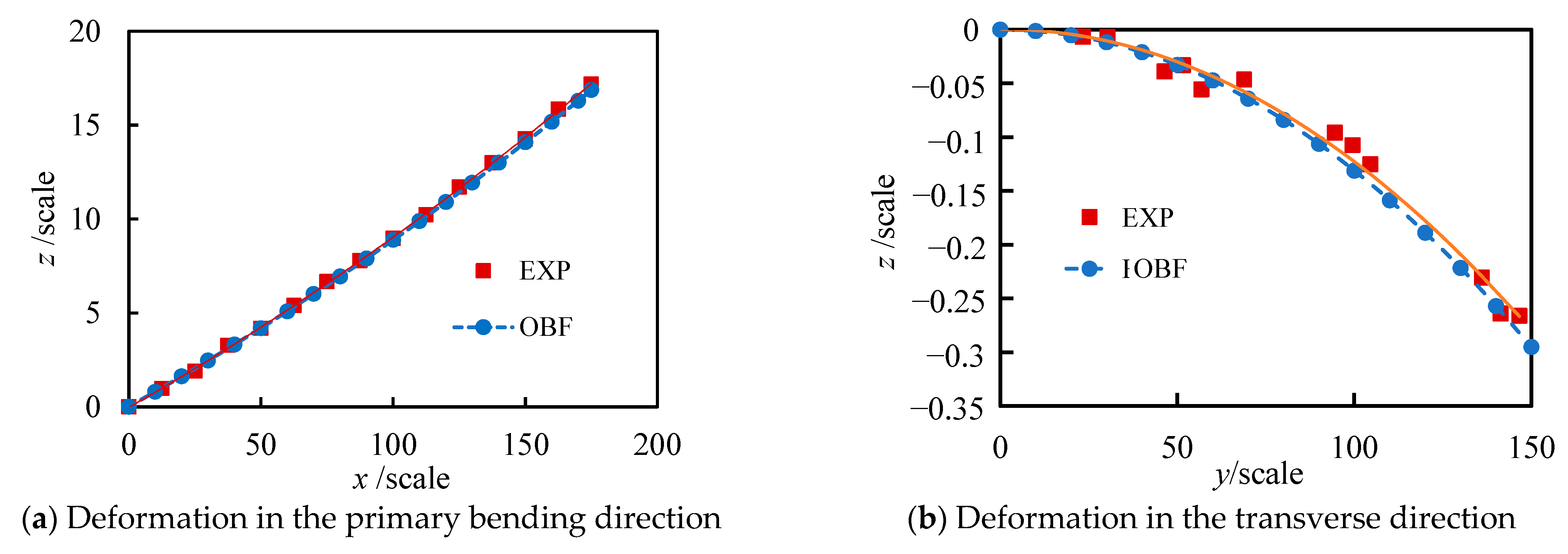
- The modified OBF model was experimentally validated based on the deformation of a flexible wind tunnel nozzle. The results indicate that the modified OBF model exhibits good agreement with experimental data, with a maximum deviation of less than 0.7% in the principal bending direction (x-direction) and less than 5.3% in the transverse direction (y-direction).
- (4)
- This study focuses on the deformation analysis of flexible wind tunnel wall panels. Future investigations will address two key aspects: (a) While the present work adopts prescribed support boundary conditions, subsequent research will explore boundary condition solutions for multi-support configurations in flexible wind tunnel walls; (b) The theoretical design approach presented here shows measurable deviations from actual structural profiles. To bridge this gap, subsequent research will combine online monitoring with the current methodology to reconstruct large-deflection deformations in multi-support flexible wall plates, enabling practical engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vijayakrishnan, V.; Kishore, P.; Muruganandam, T.M. Investigation of Variable Mach Number Wind Tunnel with Symmetric Sliding Block Nozzles. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0716. [Google Scholar]
- Edquist, K.T. Status of Mars Retropropulsion Testing in the Langley Unitary Plan Wind Tunnel. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0911. [Google Scholar]
- Childs, R.; Stremel, P.; Hawke, V.; Garcia, J.; Kleb, W.L.; Hunter, C.; Parikh, P.; Patel, M.; Alter, S.J.; Rhode, M.N.; et al. Flow Characterization of the NASA Langley Unitary Plan Wind Tunnel, Test Section 2: Computational Results. In Proceedings of the AIAA Aviation 2021 Forum, Virtual, 2–6 August 2021; p. 2963. [Google Scholar]
- Nishawala, V.V. A Study of Large Deflection of Beams and Plates. Master’s Thesis, School of Graduate Studies, Rutgers The State University of New Jersey, New Brunswick, NJ, USA, 2011. [Google Scholar]
- Onyeka, F.C.; Okeke, E.T. Analytical solution of thick rectangular plate with clamped and free support boundary condition using polynomial shear deformation theory. Adv. Sci. Technol. Eng. Syst. J. 2021, 6, 1427–1439. [Google Scholar] [CrossRef]
- Nwoji, C.U.; Sopakirite, S.; Oguaghamba, O.A.; Ibeabuchi, V.T. Deflection of simply supported rectangular plates under shear and bending deformations using orthogonal polynomial function. Saudi J. Civ. Eng. 2021, 5, 98–103. [Google Scholar]
- Hu, Z.; Zheng, X.; An, D.; Zhou, C.; Yang, Y.; Li, R. New analytic buckling solutions of side-cracked rectangular thin plates by the symplectic superposition method. Int. J. Mech. Sci. 2021, 191, 106051. [Google Scholar] [CrossRef]
- Hilali, Y.; Bourihane, O. A mixed MLS and Hermite-type MLS method for buckling and postbuckling analysis of thin plates. Structures 2021, 33, 2349–2360. [Google Scholar] [CrossRef]
- Hakim, G.; Abramovich, H. The Behavior of Long Thin Rectangular Plates under Normal Pressure-A Thorough Investigation. Materials 2024, 17, 2902. [Google Scholar] [CrossRef] [PubMed]
- Hakim, G.; Abramovich, H. Innovative Insights on the Thin Square Plate Large Deflection Problem. Materials 2023, 16, 6967. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Wu, F.; Xu, J.; Feng, X.; Yang, Q. Design and implementation of rigid-flexible coupling for a half-flexible single jack nozzle. Chin. J. Aeronaut. 2016, 29, 1477–1483. [Google Scholar] [CrossRef]
- Nie, X.T.; Guo, L.D.; Liu, B.L. Dynamics simulation and analysis of flexible nozzle in wind tunnel based on ADAMS. J. Exp. Fluid Mech. 2011, 25, 73–76. [Google Scholar]
- Nie, X.T.; Lai, H.; Zhang, Y.H. Simulation technique of semi-flexible nozzle machine dynamics. J. Exp. Fluid Mech. 2012, 26, 91–95. [Google Scholar]
- Milam, W.E. Design of Nozzle Contours for the PWT 16-ft Transonic Wind Tunnel. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 1992. [Google Scholar]
- Wu, S.H.; Fang, Y.L.; Chen, J.M.; Chen, Q.; Pei, H.T. Application research on supersonic nozzle performance optimization. J. Aerosp. Power 2017, 32, 2139–2144. [Google Scholar]
- Wu, S.H.; Liao, D.X.; Chen, J.M.; Chen, Q.; Pei, H.T. Supersonic nozzle optimization design with spline curves fitting the nozzle profiles. J. Northwestern Polytech. Univ. 2018, 36, 785–791. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Howell, L.L. Compliant mechanisms. In Encyclopedia of Nanotechnology; Springer: Dordrecht, The Netherlands, 2012; pp. 457–463. [Google Scholar]
- Mattiasson, K. Numerical results from large deflection beam and frame problems analysed by means of elliptic integrals. Int. J. Numer. Methods Eng. 1981, 17, 145–153. [Google Scholar] [CrossRef]
- Kimball, C.; Tsai, L.W. Modeling of flexural beams subjected to arbitrary end loads. J. Mech. Des. 2002, 124, 223–235. [Google Scholar] [CrossRef]
- Holst, G.L.; Teichert, G.H.; Jensen, B.D. Modeling and experiments of buckling modes and deflection of fixed-guided beams in compliant mechanisms. ASME. J. Mech. Des. 2011, 133, 051002. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, P.P.; Cheng, Y.M. The interpolating element-free Galerkin method for elastic large deformation problems. Sci. China Technol. Sci. 2021, 64, 364–374. [Google Scholar] [CrossRef]
- Yuan, W.H.; Wang, H.C.; Zhang, W.; Dai, B.-B.; Liu, K.; Wang, Y. Particle finite element method implementation for large deformation analysis using Abaqus. Acta Geotech. 2021, 16, 2449–2462. [Google Scholar] [CrossRef]
- Chen, L.; Cui, S.; Jing, H.; Zhang, W. Analysis and modeling of a flexible rectangular cantilever plate. Appl. Math. Model. 2020, 78, 117–133. [Google Scholar] [CrossRef]
- Eftekhari, S.A. A simple finite element procedure for free vibration of rectangular thin and thick plates. Appl. Math. Comput. 2021, 401, 126104. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Ilkhani, M.R.; Fadaee, M. Identification of the validity range of Donnell and Sanders shell theories using an exact vibration analysis of functionally graded thick cylindrical shell panel. Acta Mech. 2012, 223, 1101–1118. [Google Scholar] [CrossRef]
- Von Kármán, T. Festigkeitsprobleme im maschinenbau. In Encyklopedie der Mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 1910; Volume 4, pp. 348–351. [Google Scholar]
- Yu, C.; Zhang, Z.; Lai, H.; Chen, W.; Chen, Z.; Nie, X. Semi-analytic solution and verification for large deflection forming of single-jack semi-flexible nozzle based on elliptic integra. J. Aerosp. Power 2022, 37, 383–390. [Google Scholar]
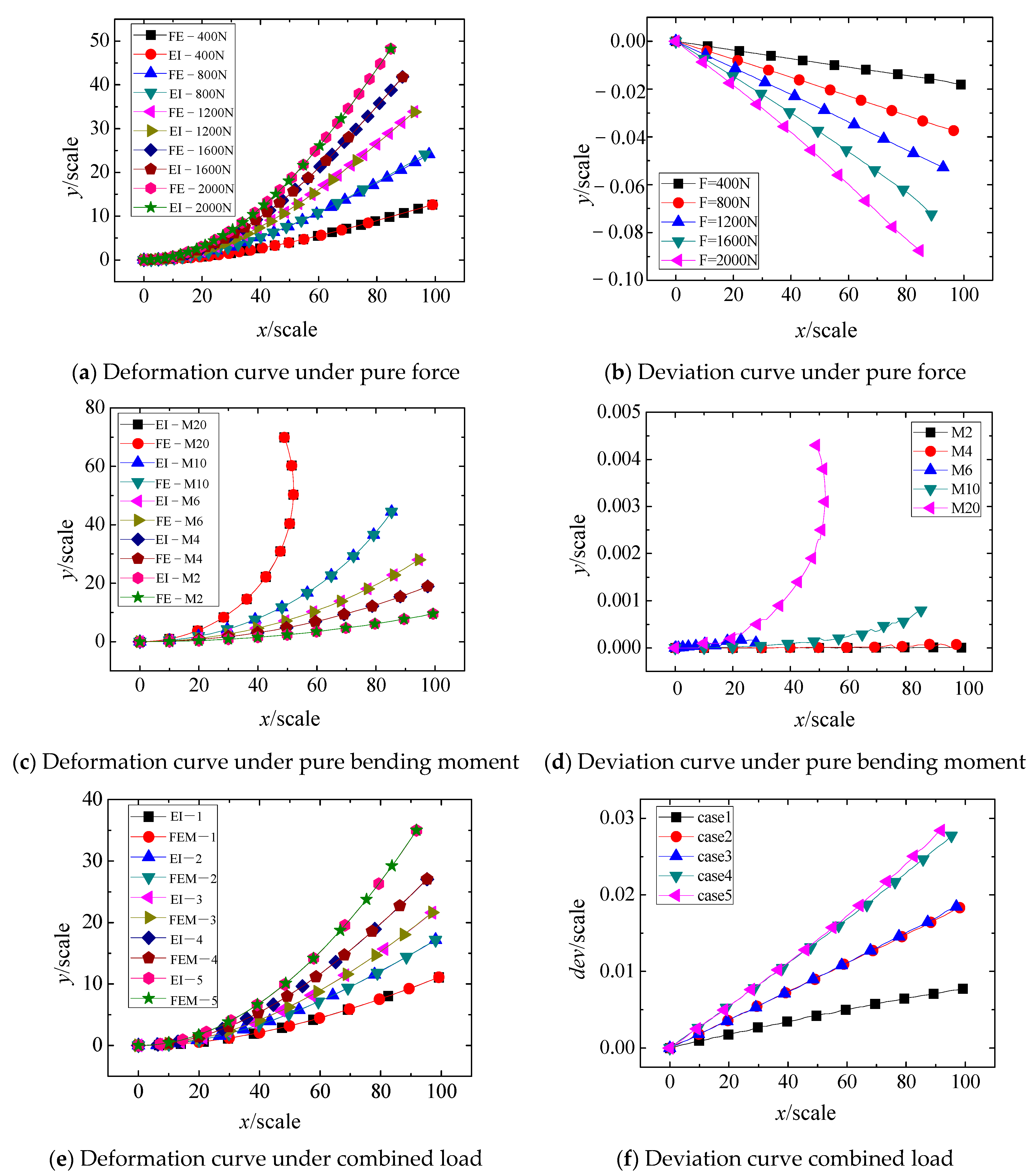
| Conditions | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| F (N) | 200 | 400 | 400 | 600 | 600 |
| M (N·m) | 10 | 10 | 20 | 20 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Ma, Y.; Wang, G.; Yang, C.; Yu, C. Three-Dimensional Deformation Calculation of Wind Tunnel Flexible Wall Using Orthogonal Beam Function. Materials 2025, 18, 3593. https://doi.org/10.3390/ma18153593
Yang X, Ma Y, Wang G, Yang C, Yu C. Three-Dimensional Deformation Calculation of Wind Tunnel Flexible Wall Using Orthogonal Beam Function. Materials. 2025; 18(15):3593. https://doi.org/10.3390/ma18153593
Chicago/Turabian StyleYang, Xiuxuan, Yueyin Ma, Guishan Wang, Can Yang, and Chengguo Yu. 2025. "Three-Dimensional Deformation Calculation of Wind Tunnel Flexible Wall Using Orthogonal Beam Function" Materials 18, no. 15: 3593. https://doi.org/10.3390/ma18153593
APA StyleYang, X., Ma, Y., Wang, G., Yang, C., & Yu, C. (2025). Three-Dimensional Deformation Calculation of Wind Tunnel Flexible Wall Using Orthogonal Beam Function. Materials, 18(15), 3593. https://doi.org/10.3390/ma18153593










