Optimization of the Elastic Modulus of the Filler in High-Rib Thin-Web Grid-Stiffened Panels with Bending Forming Process
Abstract
1. Introduction
2. Theoretical Analysis
2.1. Analysis and Selection of Plate-Bending Machines
2.2. Theoretical Calculation of Elastic Modulus
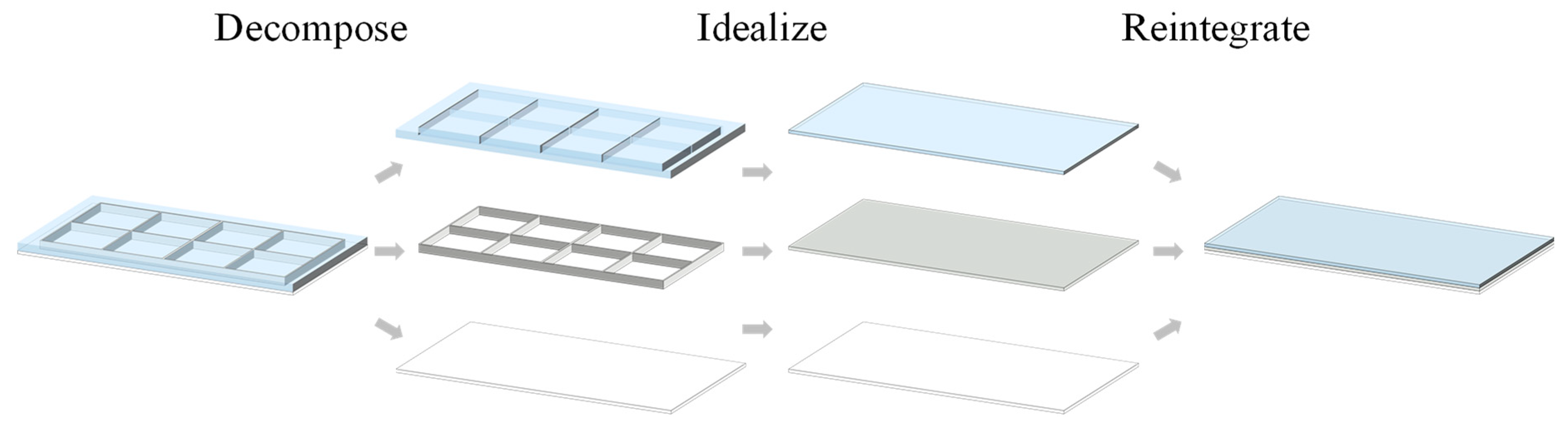
3. Simulation and Experiment
3.1. Simulation
3.2. Experiments
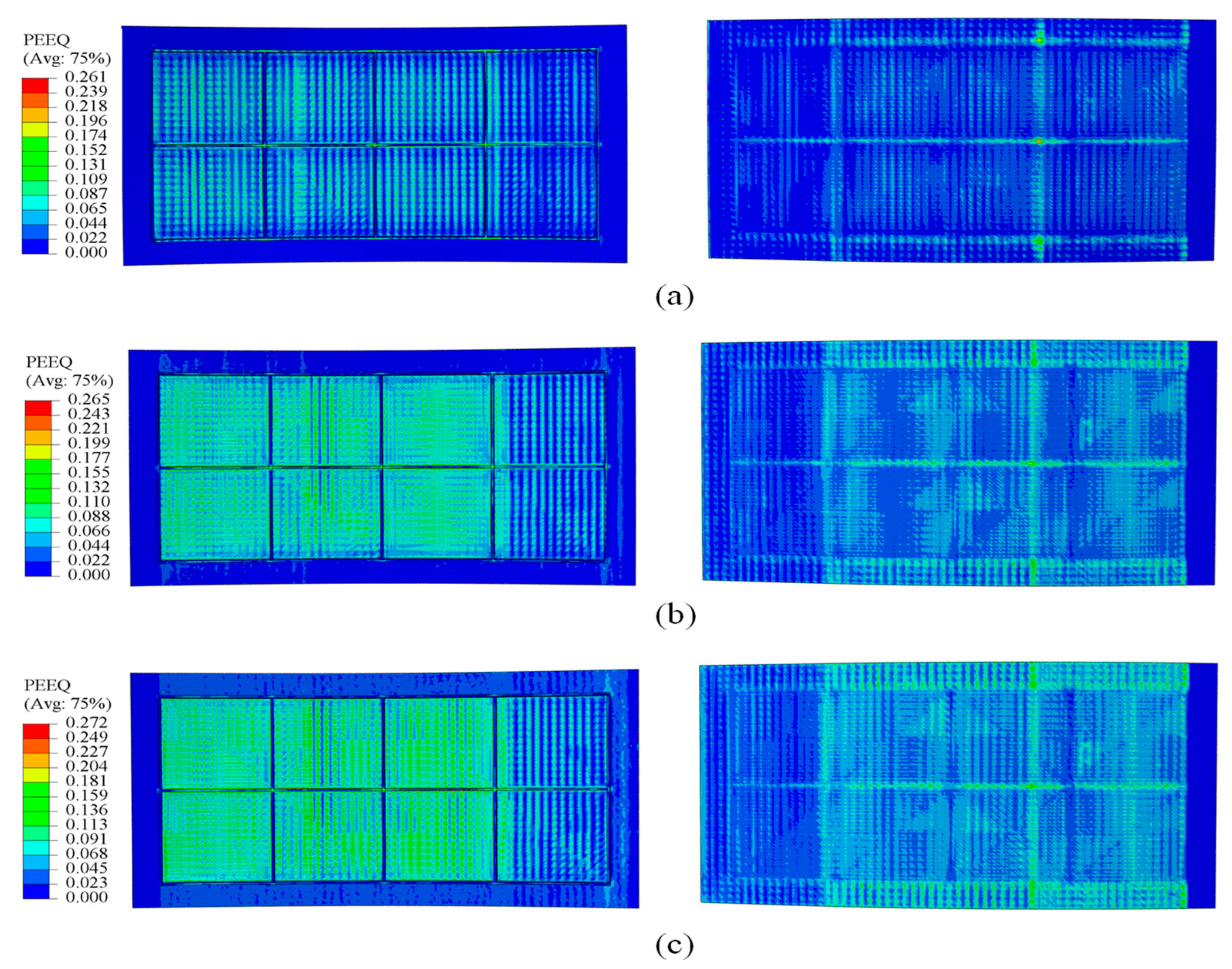
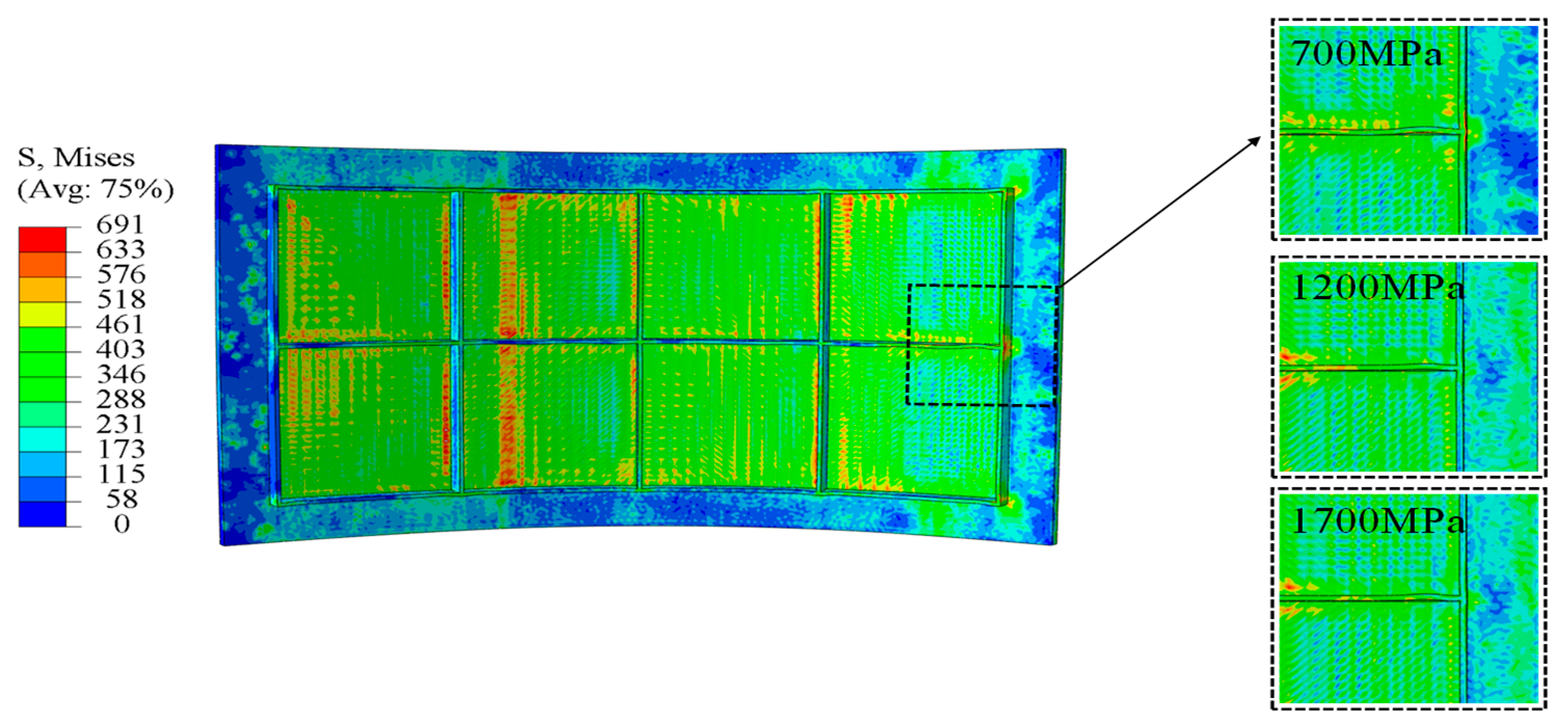
4. Results and Discussion
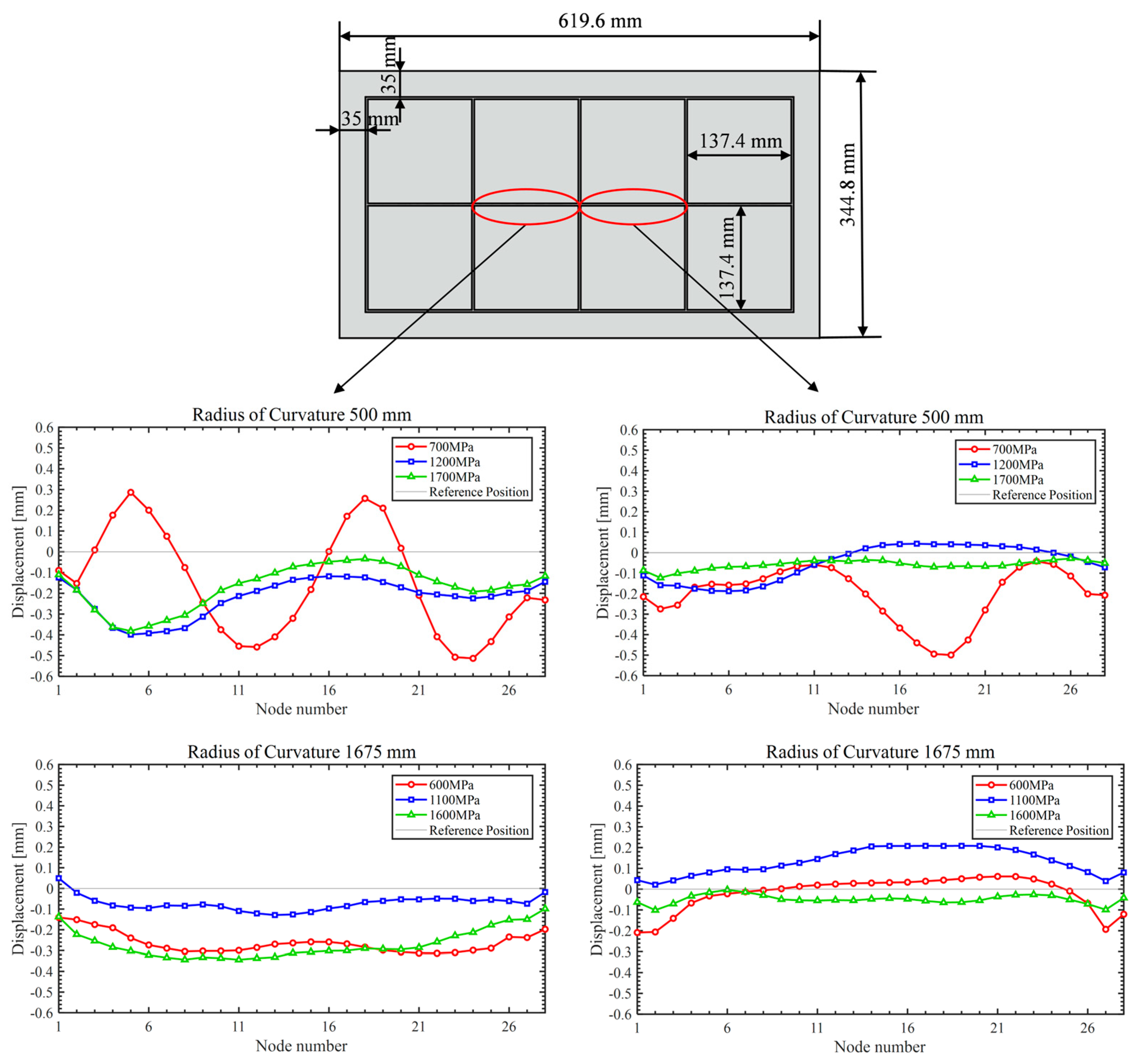
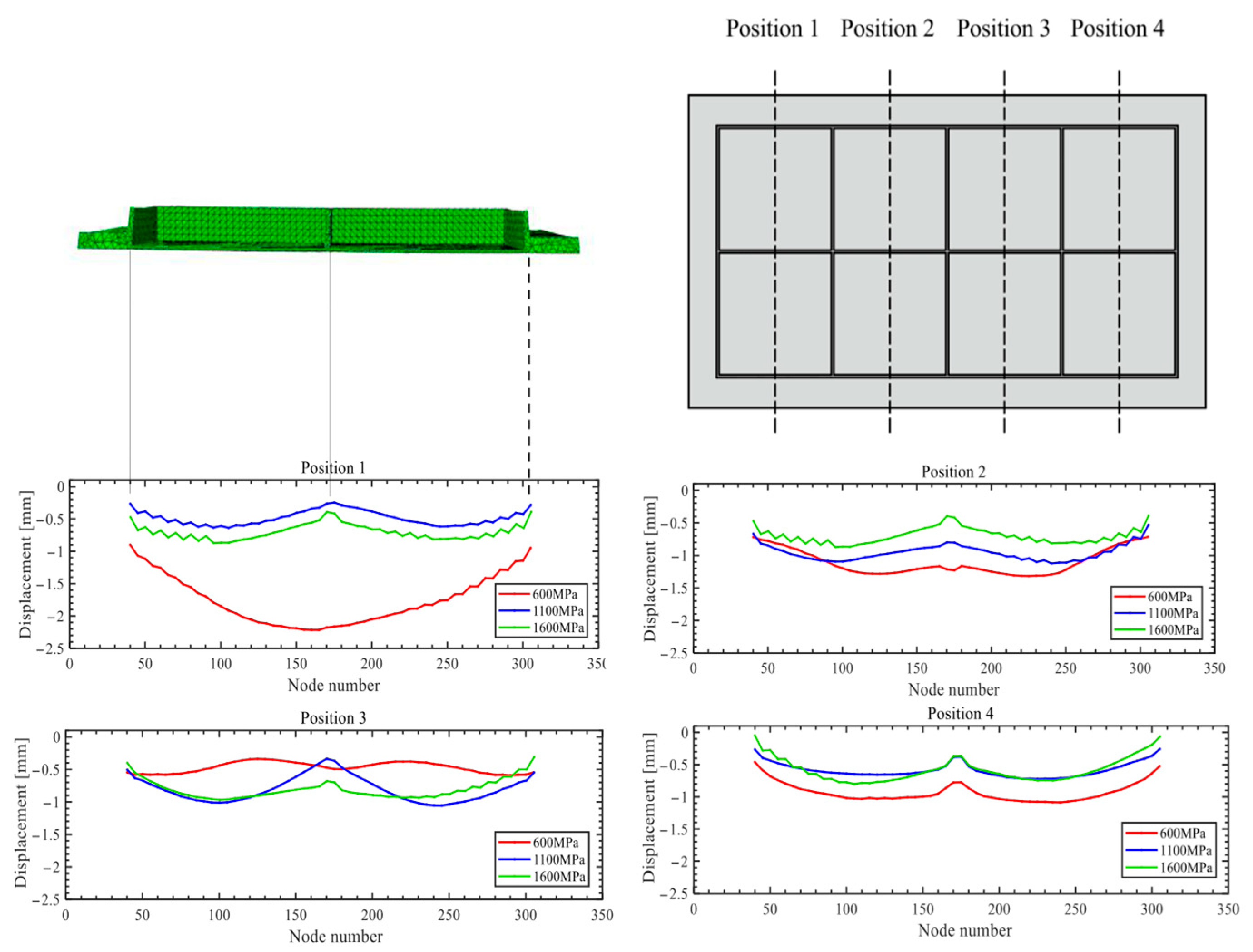
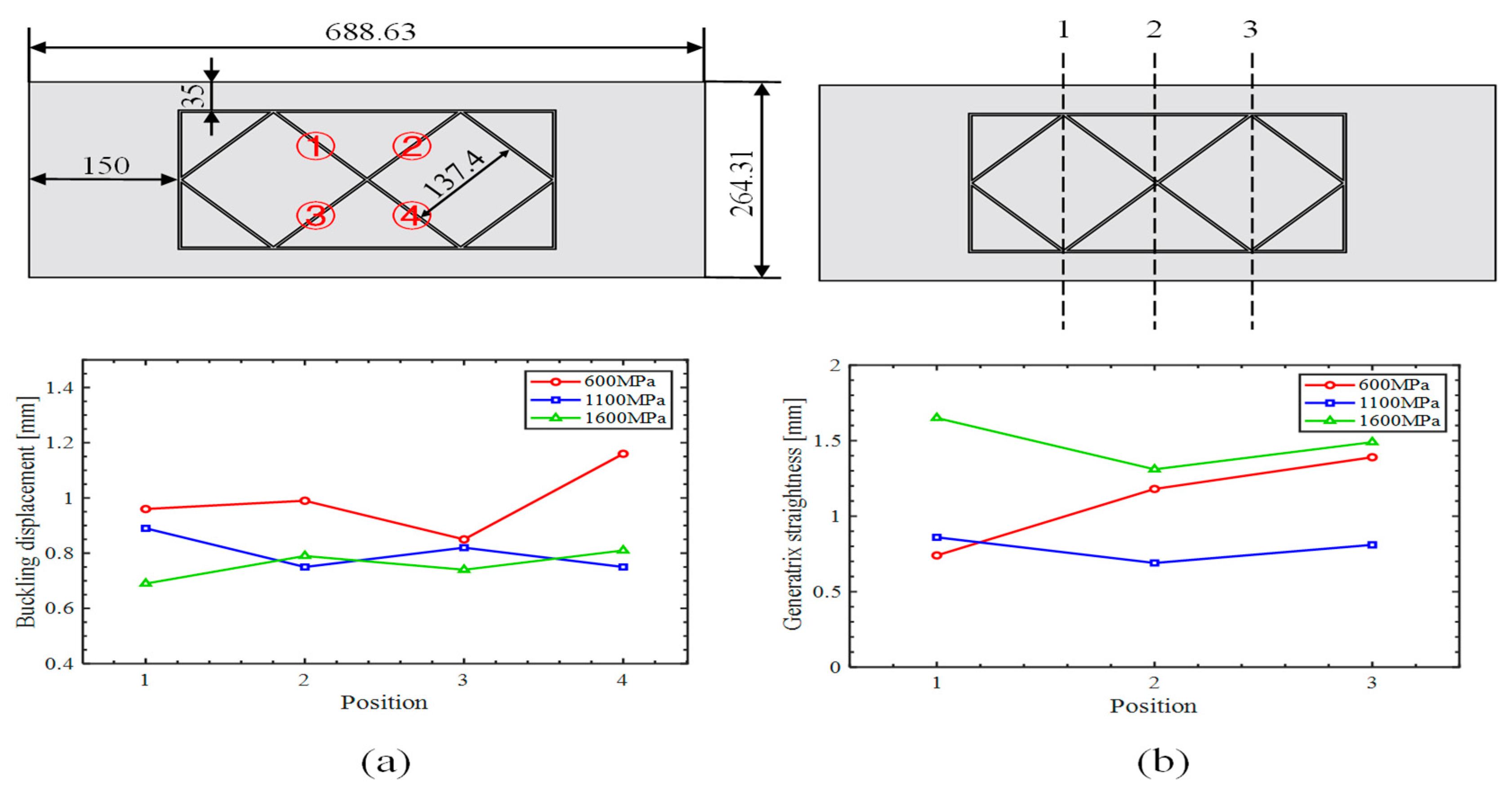
4.1. The Buckling Displacement of the Rib
4.2. Generatrix Straightness
5. Conclusions
- Validated Theoretical Framework
- 2.
- Critical Role of Filler Elastic Modulus
- 3.
- Engineering Application Potential
- 4.
- Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Length of the strut before compression | |
| Length of the strut after compression | |
| Length of the margin area | |
| Spacing between ribs | |
| Width of the plate | |
| Bending stiffness of a single rib | |
| Effective bending stiffness in the direction | |
| Plastic strain energy | |
| Assumed elastic modulus of the filler | |
| Material’s linear hardening modulus | |
| The elastic modulus of the filler | |
| Bending strain energy | |
| Height of the rib | |
| Height of the margin area | |
| Strength coefficient | |
| Relative hardening modulus | |
| Shape factor | |
| Bending moment on the section | |
| Strain-hardening exponent | |
| Normal pressure | |
| Relative curvature radius after springback | |
| Relative curvature radius before springback | |
| Curvature radius after springback | |
| Curvature radius before springback | |
| Deformation area of the filler | |
| Total cross-sectional area of the filler | |
| Equivalent thickness of the total homogeneous panel | |
| Equivalent thickness of the filler | |
| Equivalent thickness of the forming margin area | |
| Equivalent thickness of the grid rib portion | |
| Thickness of the original skin | |
| Thickness of the rib | |
| Total compression | |
| Instability height | |
| Deflection | |
| Section modulus | |
| Maximum stress | |
| Initial yield stress | |
| Ideal compression strain |
References
- Kaufmann, M. Cost optimization of Aircraft Structures. Ph.D. Thesis, KTH, Stockholm, Sweden, 2009. [Google Scholar]
- Kaufmann, M. Cost/Weight Optimization of Aircraft Structures. Licentiate Thesis, KTH, Stockholm, Sweden, 2008. [Google Scholar]
- XU, A.; Zhang, Y.; Li, C.; Jia, Y.; Zhao, C. Research on Incremental Forming Technology for Integral Panels with Flanges. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Brussels, Belgium, 22–25 July 2019; pp. 596–601. [Google Scholar]
- Munroe, J.; Wilkins, K.; Gruber, M.; Domack, M.S. Integral Airframe Structures (IAS): Validated Feasibility Study of Integrally Stiffened Metallic Fuselage Panels for Reducing Manufacturing Costs; NASA: Washington, WA, USA, 2000. [Google Scholar]
- Lam, A.C.; Shi, Z.; Yang, H.; Wan, L.; Davies, C.M.; Lin, J.; Zhou, S. Creep-age forming AA2219 plates with different stiffener designs and pre-form age conditions: Experimental and finite element studies. J. Mater. Process. Technol. 2015, 219, 155–163. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, S.-H.; Liu, J.-S.; Cheng, M.; Liu, H.-X. Experimental and Numerical Investigation on Filling Roll Bending of Aluminum Alloy Integral Panel. J. Manuf. Sci. Eng. 2012, 134, 061011. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Li, J.; Jia, C.-L. Experimental Study on Forming Process of CNC Milling Short-wallboard. J. Aviat. Precis. Manuf. Technol. 2017, 53, 31–33. [Google Scholar]
- Lyu, F.; Li, Y.; Huang, X.; Shi, Z.; Zeng, Y.; Lin, J. An investigation of creep age forming of AA7B04 stiffened plates: Experiment and FE modelling. J. Manuf. Process. 2019, 37, 232–241. [Google Scholar] [CrossRef]
- Yu, Y.; Min, W. Prediction of stiffener buckling in press bend forming of integral panels. Trans. Nonferrous Met. Soc. China 2011, 21, 2459–2465. [Google Scholar] [CrossRef]
- Zhou, W.; Li, Y.; Shi, Z.; Lin, J. An analytical solution for elastic buckling analysis of stiffened panel subjected to pure bending. Int. J. Mech. Sci. 2019, 161, 105024. [Google Scholar] [CrossRef]
- Zhou, W.; Shi, Z.; Li, Y.; Rong, Q.; Zeng, Y.; Lin, J. Elastic-plastic buckling analysis of stiffened panel subjected to global bending in forming process. Aerosp. Sci. Technol. 2021, 115, 106781. [Google Scholar] [CrossRef]
- Zhou, W.; Shi, Z.; Lin, J. Semi-analytical study of buckling response for grid-stiffened panels during creep age forming. Thin-Walled Struct. 2023, 182, 110231. [Google Scholar] [CrossRef]
- Rahbar-Ranji, A. Elastic buckling analysis of longitudinally stiffened plates with flat-bar stiffeners. Ocean Eng. 2013, 58, 48–59. [Google Scholar] [CrossRef]
- Chagraoui, H.; Soula, M. Maximum buckling load design and post-buckling compressive failure of curved grid sub-stiffened composite panels. Eur. J. Mech.-A/Solids. 2024, 107, 105381. [Google Scholar] [CrossRef]
- Liu, J.S.; Guo, Y.; Zhang, S.H.; Xiao, H. Research on Bending Process of Integral Panel Skins. Adv. Mater. Res. 2011, 299, 1048–1051. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, H.; Liu, J. Research on filling roll bending process of integral panel skins. Forg. Stamp. Technol. 2009, 34, 54–56. [Google Scholar]
- Yin, P.; Jin, K.; Zhu, S.Q.; Wang, Y.Q.; Zhen, L.; Zhang, G.W.; Tang, Y.; Sun, C. Research on roll bending process of grid panel by CNC milling. Forg. Stamp. Technol. 2018, 43, 19–23. [Google Scholar] [CrossRef]
- Li, Y.Q.; Liu, J.S.; Liu, T.; Wang, Y.; Du, T.L.; Song, H.W.; Zhang, S.H. Finite element simulation on discrete filling rolling for integral panel skins. Forg. Stamp. Technol. 2020, 45, 106–112. [Google Scholar]
- Li, H.-W.; Song, H.-W.; Zhang, S.-H.; Wan, L.; Jia, C.-L.; Chai, X.-T.; Zhang, G.-W.; LĂZĂRescu, L.; Banabic, D. Operating effect of filler on filling roll bending of integral panel. Trans. Nonferrous Met. Soc. China 2023, 33, 2314–2327. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: Columbus OH, USA, 1959. [Google Scholar]
- Mo, S.N. Theory of Bending Rolls and Straightening Machines; Machine Industry Press: Beijing, China, 1958. [Google Scholar]
- Wang, X.; Cao, J. An analytical prediction of flange wrinkling in sheet metal forming. J. Manuf. Process. 2000, 2, 100–107. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, X.; Zheng, C.; Xiao, J.; Liu, X. Multi-directional hydraulic loading for high-precision calibration of additively manufactured aluminum alloy thin-walled tube. J. Manuf. Process. 2025, 141, 1177–1194. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, G.; Xiao, X.-K. Constitutive relation and fracture criterion of 2A12 aluminum alloy. Acta Armamentarii 2013, 34, 276. [Google Scholar]
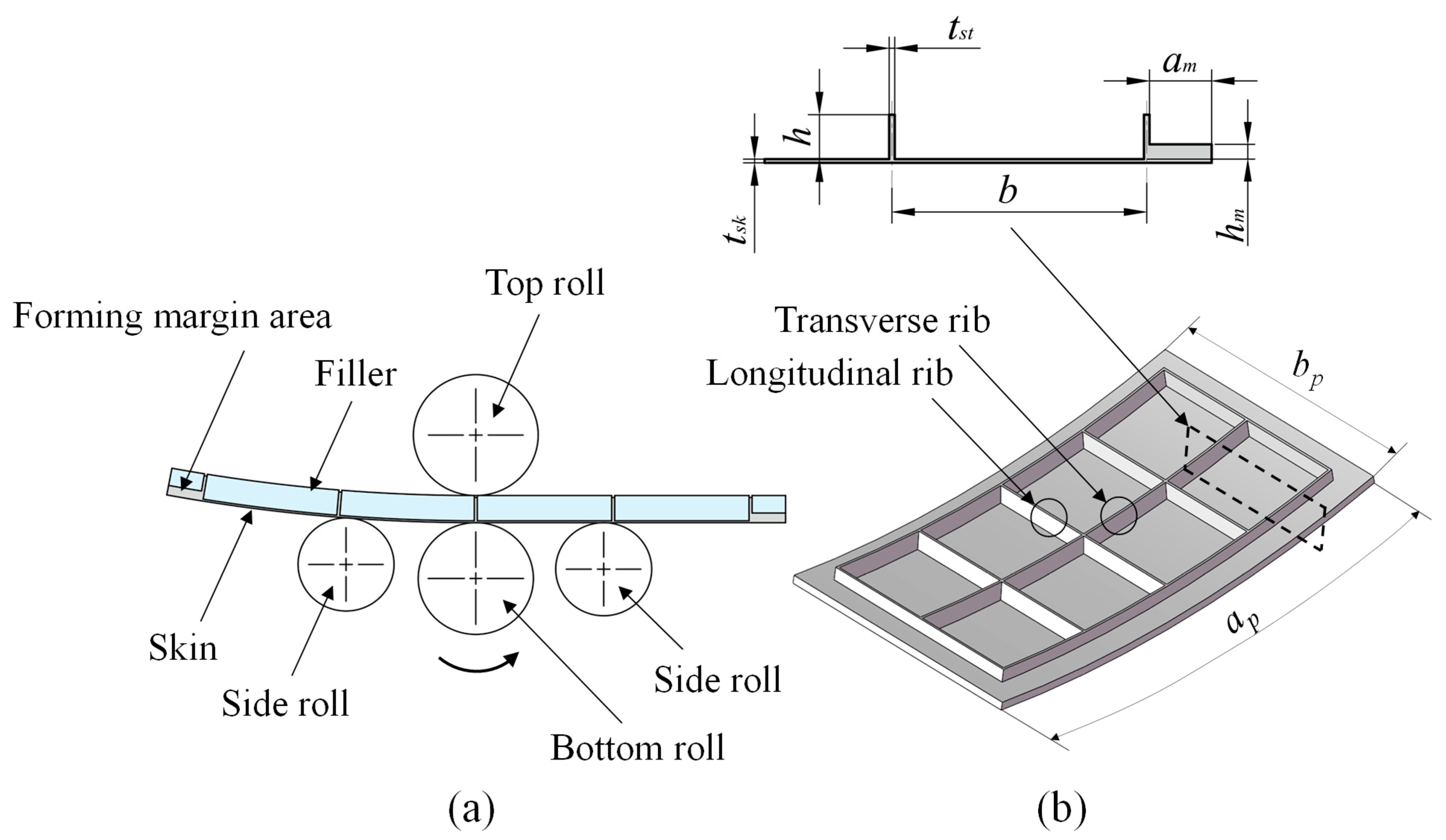
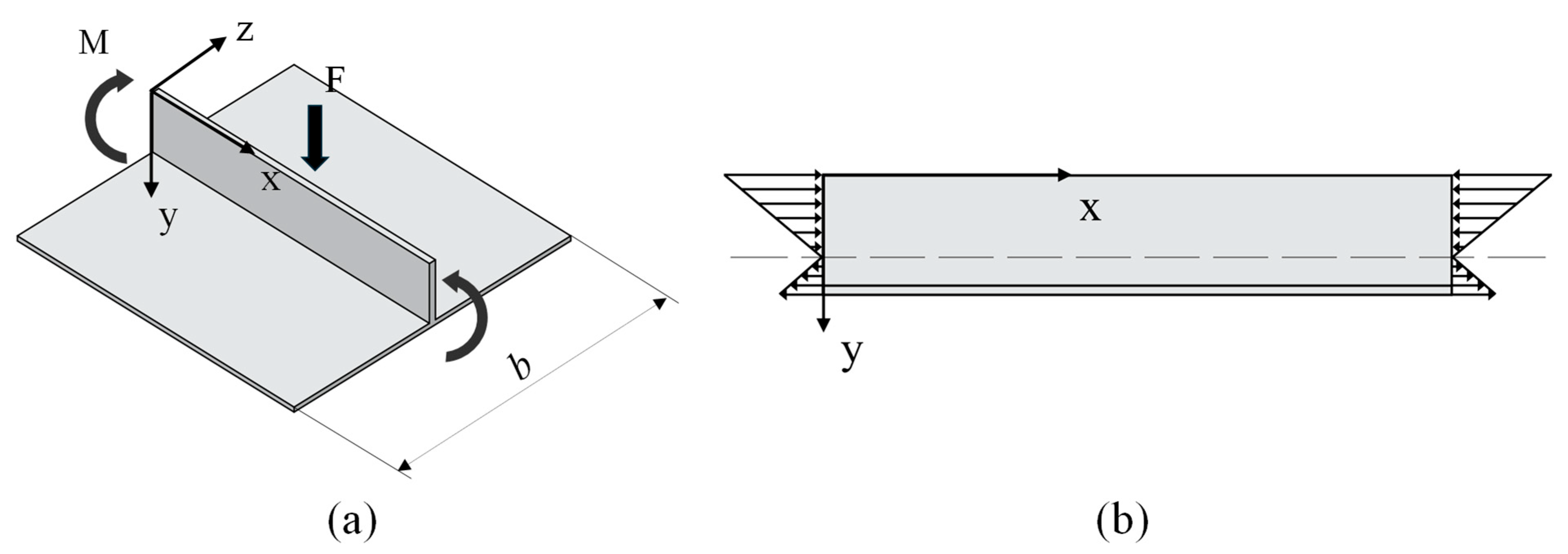
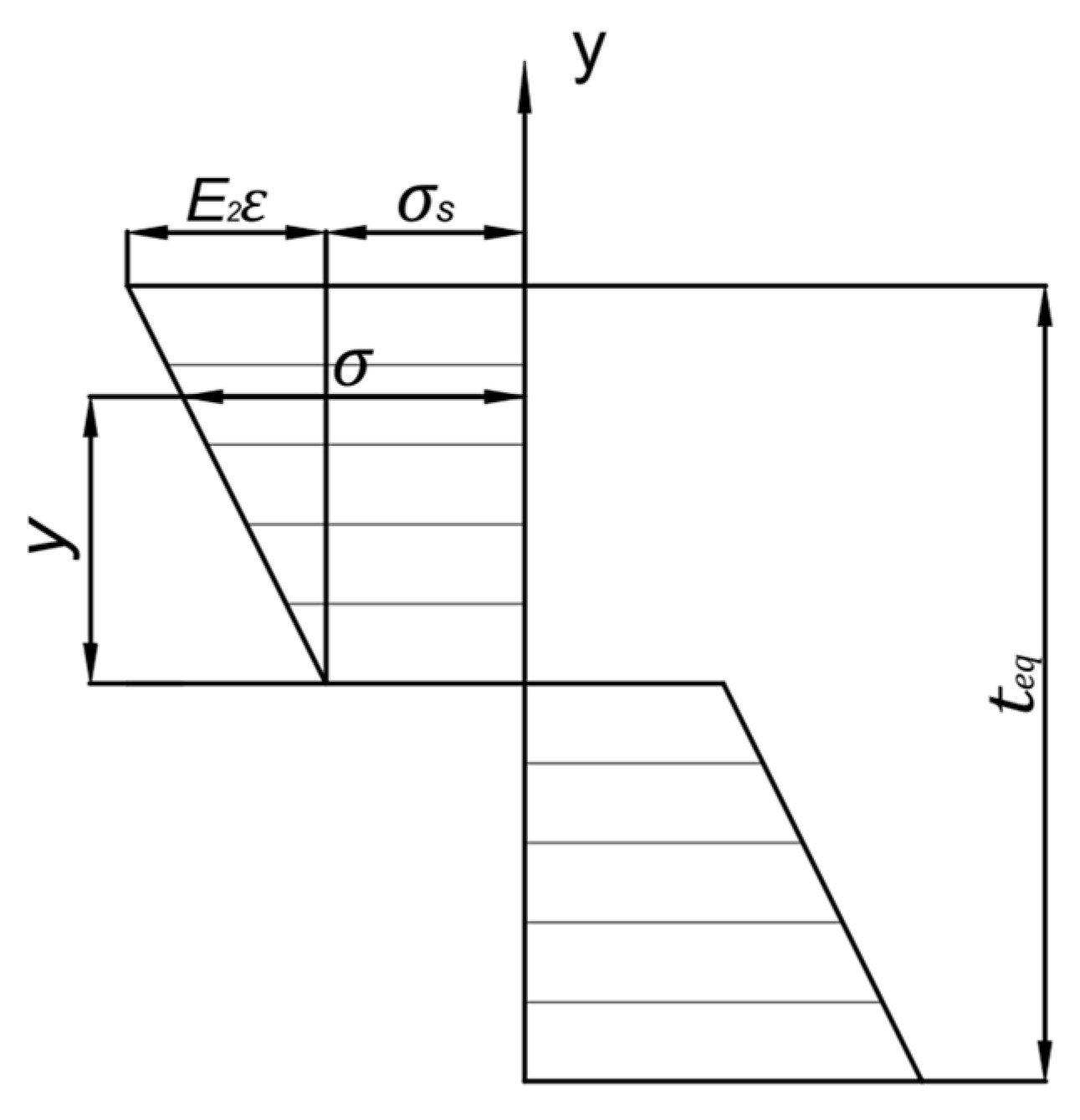
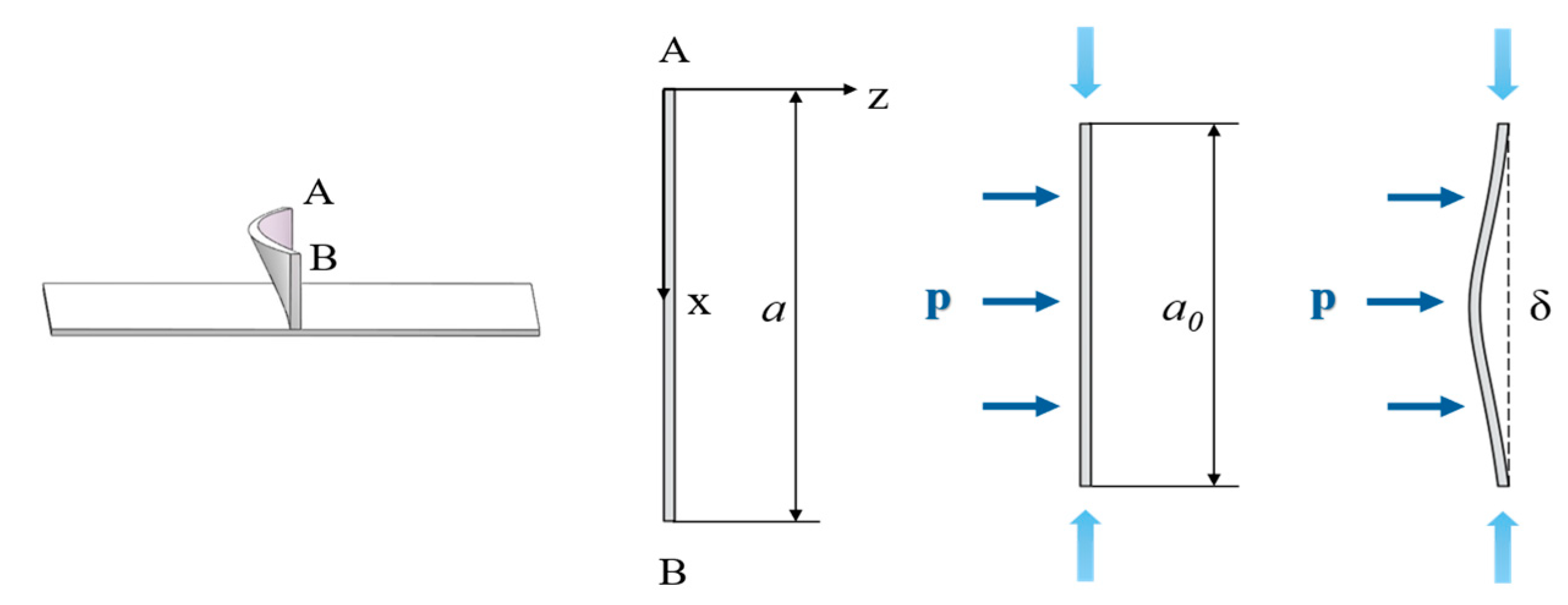
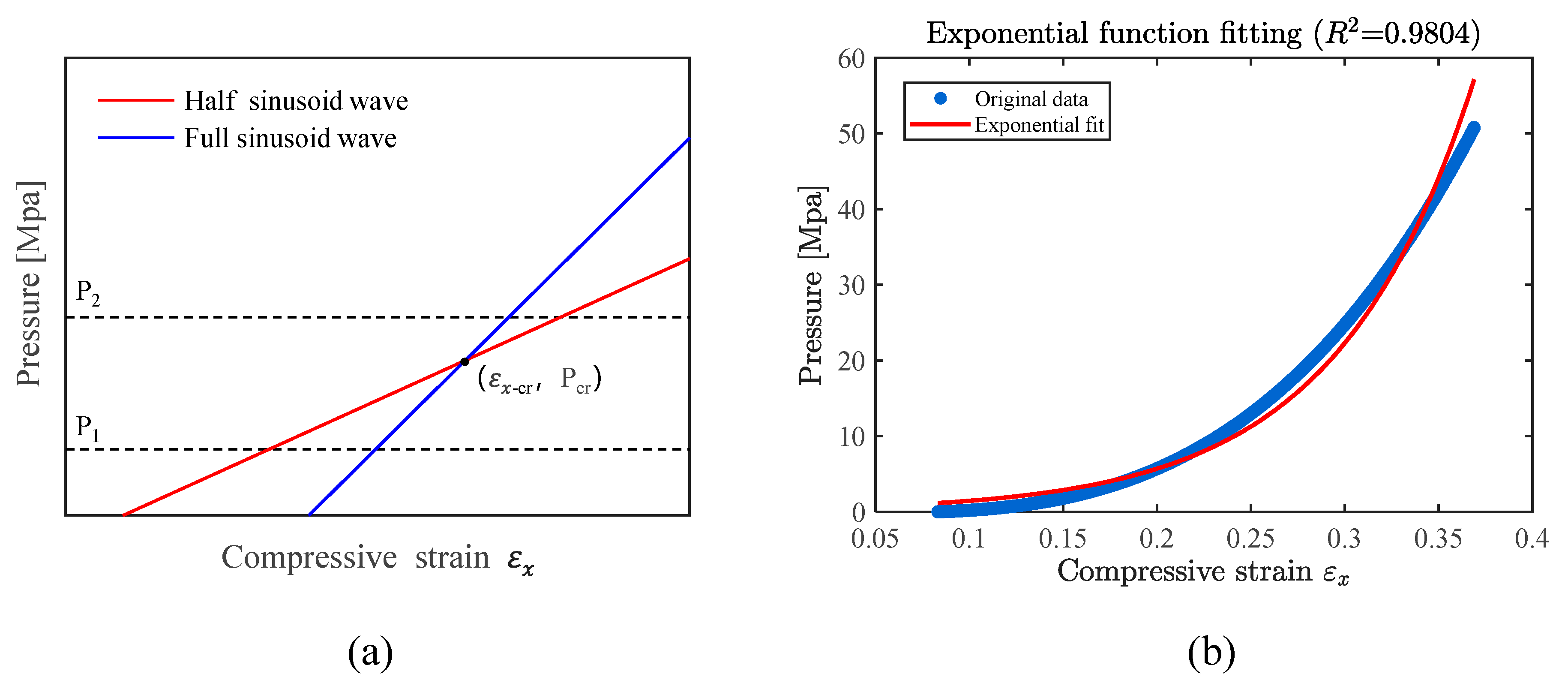

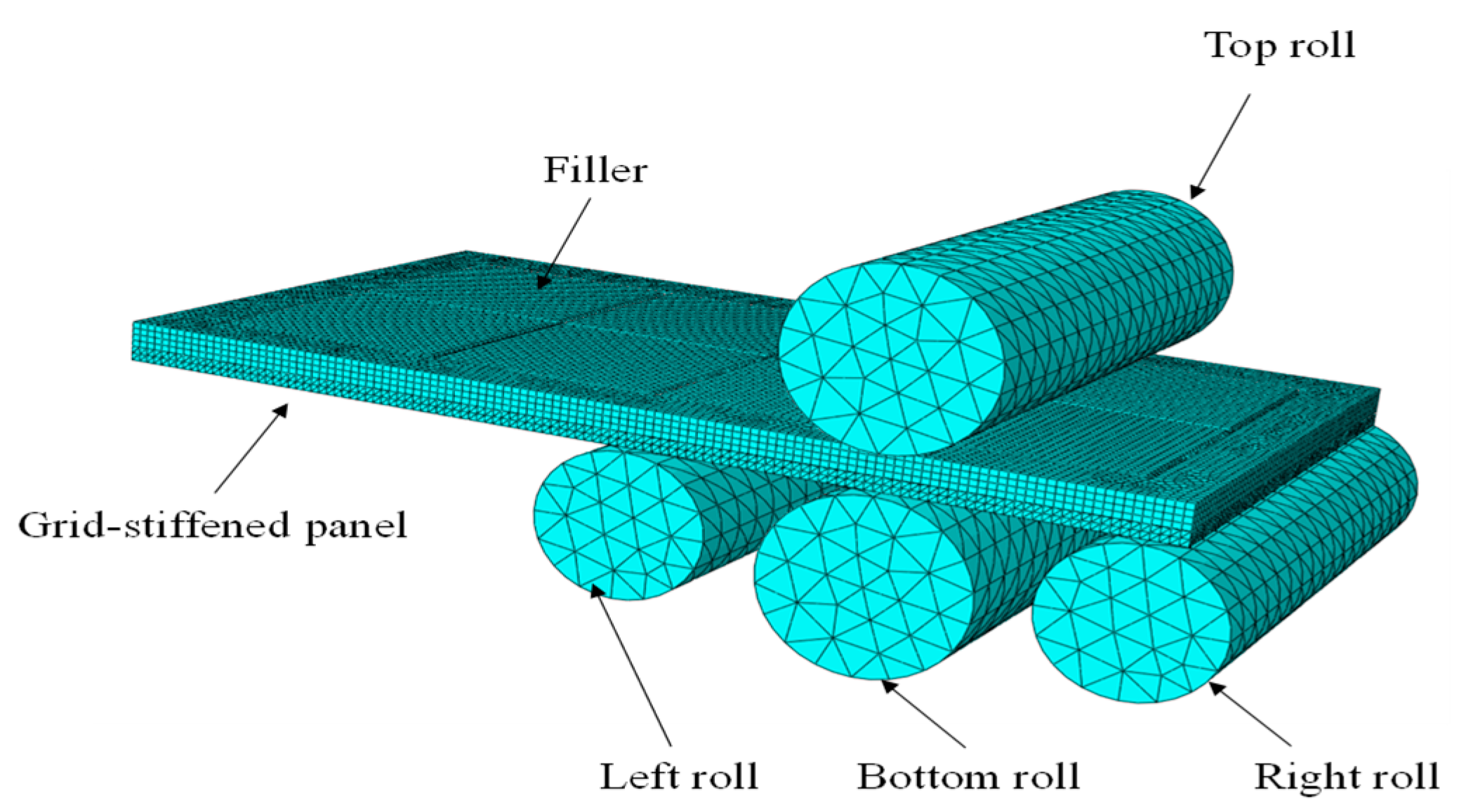



| Material | Elastic Modulus, E/MPa | Initial Yield Stress, /MPa | Poisson Ratio, | Mass Density, kg/m3 | Strengthening Coefficient, K/MPa | Strain-Hardening Exponent, n |
|---|---|---|---|---|---|---|
| aluminum alloy 2A12-T4 | 72,400 | 325 | 0.33 | 2770 | 989 | 0.654 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, S.; Zhang, X. Optimization of the Elastic Modulus of the Filler in High-Rib Thin-Web Grid-Stiffened Panels with Bending Forming Process. Materials 2025, 18, 3782. https://doi.org/10.3390/ma18163782
Nan S, Zhang X. Optimization of the Elastic Modulus of the Filler in High-Rib Thin-Web Grid-Stiffened Panels with Bending Forming Process. Materials. 2025; 18(16):3782. https://doi.org/10.3390/ma18163782
Chicago/Turabian StyleNan, Siyu, and Xinlong Zhang. 2025. "Optimization of the Elastic Modulus of the Filler in High-Rib Thin-Web Grid-Stiffened Panels with Bending Forming Process" Materials 18, no. 16: 3782. https://doi.org/10.3390/ma18163782
APA StyleNan, S., & Zhang, X. (2025). Optimization of the Elastic Modulus of the Filler in High-Rib Thin-Web Grid-Stiffened Panels with Bending Forming Process. Materials, 18(16), 3782. https://doi.org/10.3390/ma18163782









