Optimizing Aortic Arch Stent-Graft Performance Through Material Science: An Exploratory Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometry and Materials
2.2. Mechanical Properties
2.2.1. Bending Test
2.2.2. Crimping Test
2.2.3. Fatigue Loading
3. Results and Discussion
3.1. Flexibility
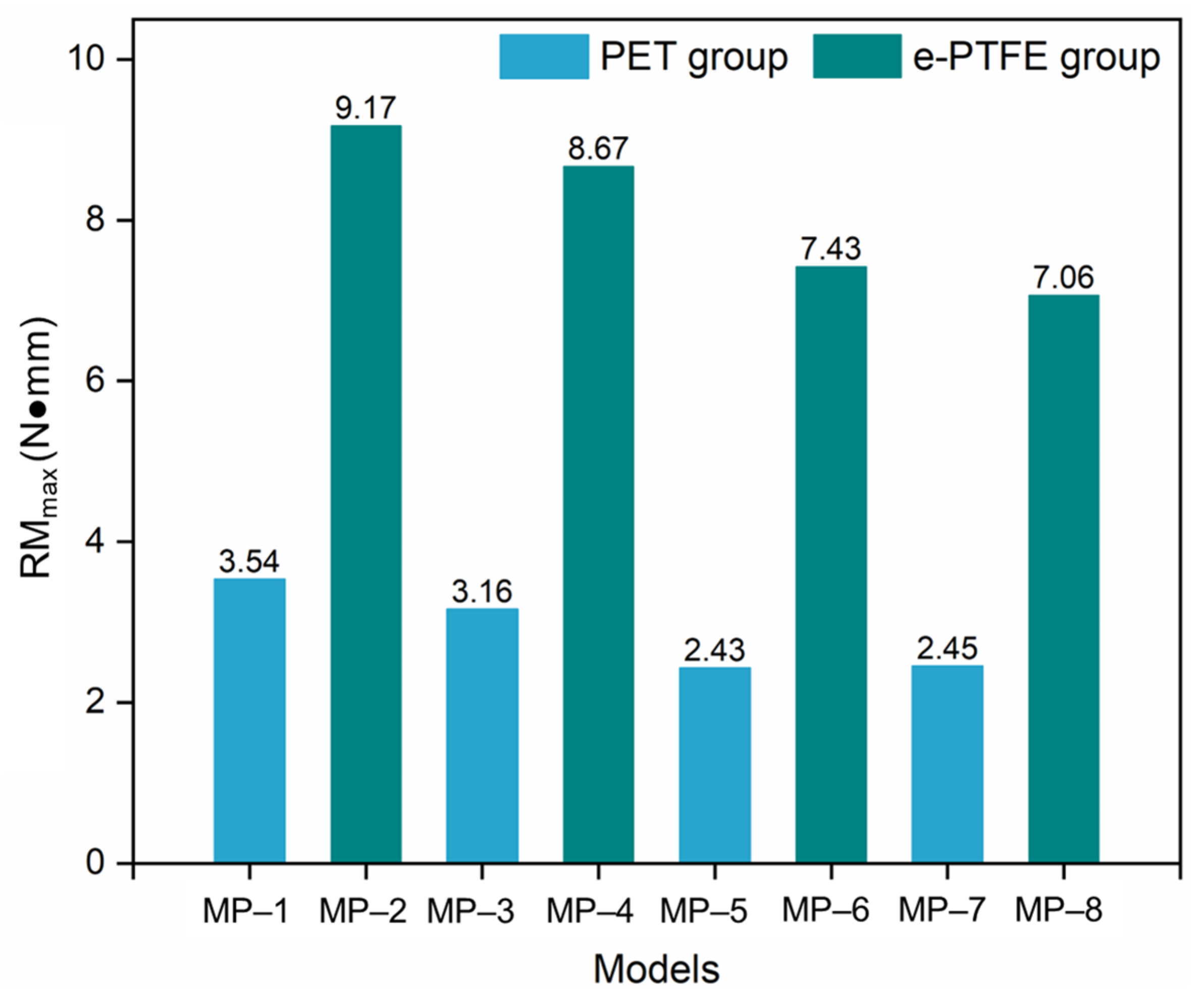
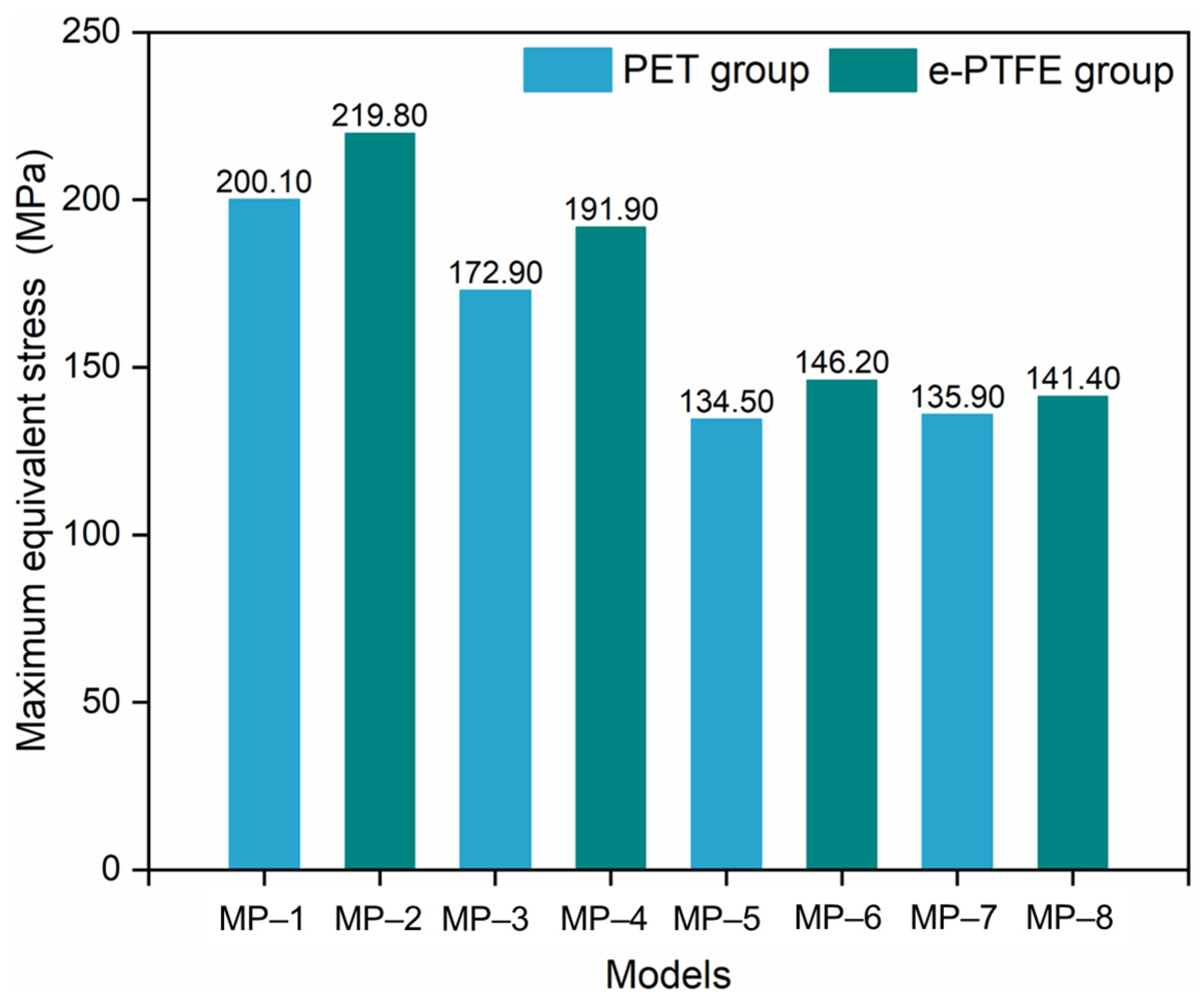
3.2. Radial Force
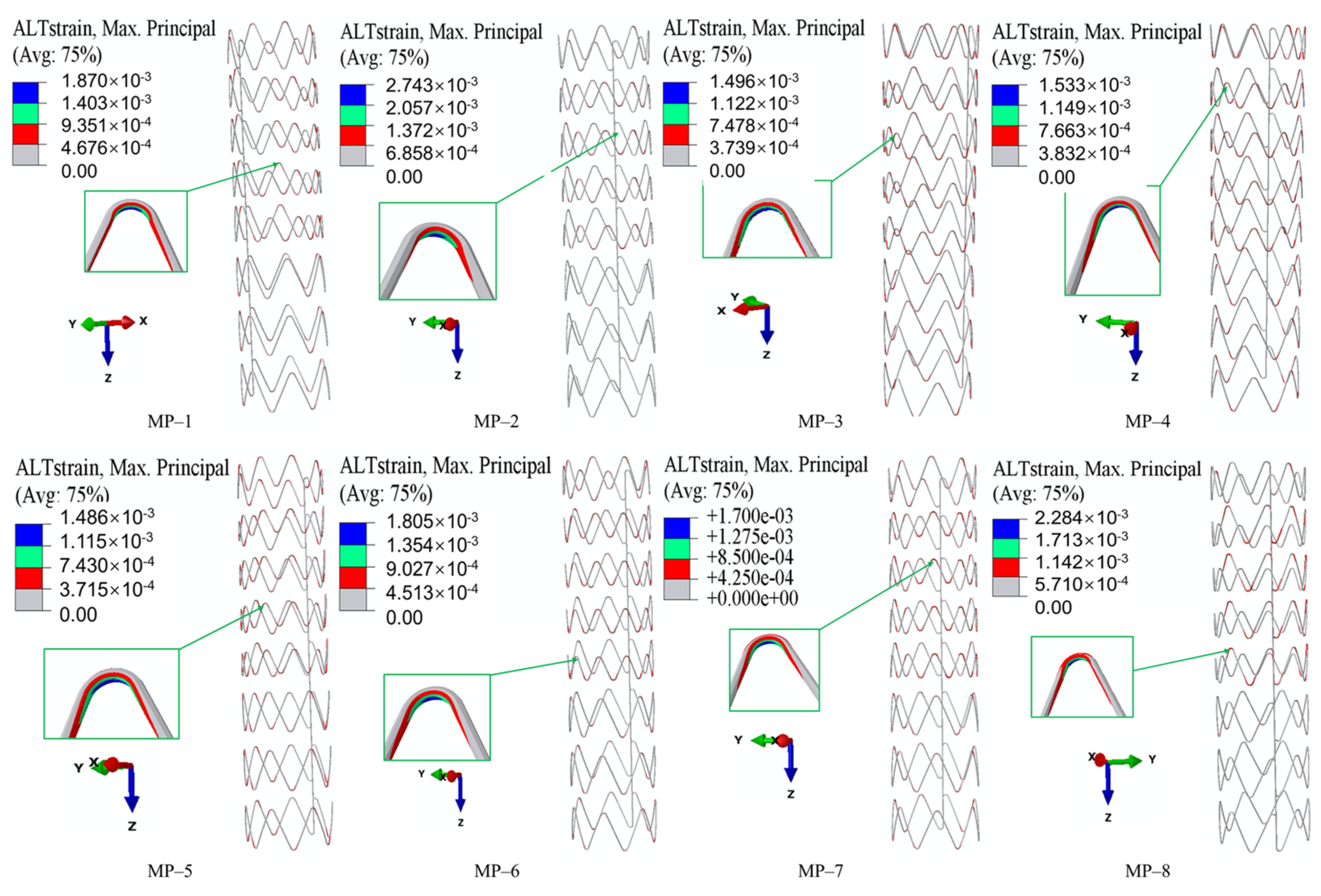
3.3. Fatigue Performance
4. Conclusions
- The material properties of both nitinol and grafts significantly influence SGs’ core mechanical properties. Specifically, PET grafts outperform e-PTFE in enhancing flexibility and fatigue performance.
- The graft material shows a negligible impact on crimpability, as the radial force and equivalent stress during compression are primarily determined by nitinol’s properties.
- Nitinol’s properties dominate all performance metrics. A lower austenitic Young’s modulus (nitinol-3/4) improves flexibility. Nitinol-2 has higher radial force; nitinol-3/4 exhibit lower forces, influenced by phase transformation. Fatigue resistance depends on the nitinol-graft pairing, with nitinol-3 + PET (MP-5) showing optimal durability.
- These results confirm the potential of material science-driven optimization: tailoring nitinol’s composition and manufacturing processes to adjust the initial transformation stress and strain can improve flexibility and crimpability, while selecting PET grafts is preferable for applications prioritizing flexibility and fatigue resistance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiao, Y.; Mao, L.; Wang, Y.; Luan, J.; Chen, Y.; Zhu, T.; Luo, K.; Fan, J. Hemodynamic effects of stent-graft introducer sheath during thoracic endovascular aortic repair. Biomech. Model. Mechanobiol. 2022, 21, 419–431. [Google Scholar] [CrossRef] [PubMed]
- Shahbazian, N.; Doyle, M.G.; Forbes, T.L.; Amon, C.H. A modeling framework for computational simulations of thoracic endovascular aortic repair. Int. J. Numer. Methods Biomed. Eng. 2022, 39, e3578. [Google Scholar] [CrossRef]
- Hynes, N.; Acharya, Y.; Sultan, S. The contemporary design of endovascular aneurysm stent-graft materials: PTFE versus polyester. Front. Surg. 2022, 9, 984727. [Google Scholar] [CrossRef]
- Cao, L.; Ge, Y.; He, Y.; Wang, X.; Rong, D.; Lu, W.; Liu, X.; Guo, W. Association between aortic arch angulation and bird-beak configuration after thoracic aortic stent graft repair of type B aortic dissection. Interact. Cardiovasc. Thorac. Surg. 2020, 31, 688–696. [Google Scholar] [CrossRef]
- Banathy, A.K.; Khaja, M.S.; Williams, D.M. Update on Trials and Devices for Endovascular Management of the Ascending Aorta and Arch. Tech. Vasc. Interv. Radiol. 2021, 24, 100756. [Google Scholar] [CrossRef]
- Kobayashi, K.; Yamashita, A.; Kuroda, Y.; Nakai, S.; Arai, S.; Uchida, T. Unexpected bare metal stent migration associated with aortic remodeling after PETTICOAT technique for aortic dissection. J. Endovasc. Ther. 2022, 30, 35114830. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Zhang, W.; Shu, X.; Wang, E.; Guo, D.; Fu, W. Retrograde Type A Aortic Dissection after Thoracic Endovascular Aortic Repair: Incidence, Time Trends and Risk Factors. Semin. Thorac. Cardiovasc. Surg. 2021, 33, 639–653. [Google Scholar] [CrossRef]
- Bozso, S.J.; Nagendran, J.; Chu, M.W.; Kiaii, B.; El-Hamamsy, I.; Ouzounian, M.; Kempfert, J.; Starck, C.; Moon, M.C. Midterm Outcomes of the Dissected Aorta Repair Through Stent Implantation Trial. Ann. Thorac. Surg. 2021, 111, 463–470. [Google Scholar] [CrossRef] [PubMed]
- Brand, M.; Sharon, N. Analytical Modeling and Validation of Radial Stiffness in Zigzag-Shaped Stents: Experimental and Numerical Approaches. J. Biomed. Mater. Res. Part B Appl. Biomater. 2025, 113, e35574. [Google Scholar] [CrossRef]
- Hemmler, A.; Lutz, B.; Reeps, C.; Gee, M.W. In silico study of vessel and stent-graft parameters on the potential success of endovascular aneurysm repair. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3237. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Chen, J.; He, Z.; Xu, Y.; Liu, Q.; Liang, H.; Yan, H. Machine Learning-Based Rapid Prediction of Torsional Performance of Personalized Peripheral Artery Stent. Int. J. Numer. Methods Biomed. Eng. 2025, 41, e70029. [Google Scholar] [CrossRef]
- Kumar, G.P.; Cui, F.; Danpinid, A.; Su, B.; Hon, J.K.F.; Leo, H.L. Design and finite element-based fatigue prediction of a new self-expandable percutaneous mitral valve stent. Comput. Aided Des. 2013, 45, 1153–1158. [Google Scholar] [CrossRef]
- Singh, C.; Wang, X. A biomimetic approach for designing stent-graft structures: Caterpillar cuticle as design model. J. Mech. Behav. Biomed. Mater. 2014, 30, 16–29. [Google Scholar] [CrossRef]
- Demanget, N.; Avril, S.; Badel, P.; Orgéas, L.; Geindreau, C.; Albertini, J.-N.; Favre, J.-P. Computational comparison of the bending behavior of aortic stent-grafts. J. Mech. Behav. Biomed. Mater. 2012, 5, 272–282. [Google Scholar] [CrossRef] [PubMed]
- Kianpour, G.; Bagheri, R.; Pourjavadi, A.; Ghanbari, H. Synergy of titanium dioxide nanotubes and polyurethane properties for bypass graft application: Excellent flexibility and biocompatibility. Mater. Des. 2022, 215, 10523. [Google Scholar] [CrossRef]
- Hemmler, A.; Lin, A.; Thierfelder, N.; Franz, T.; Gee, M.W.; Bezuidenhout, D. Customized stent-grafts for endovascular aneurysm repair with challenging necks: A numerical proof of concept. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3316. [Google Scholar] [CrossRef]
- Liang, M.; Zhang, R.; Gao, Y.; Shen, L.; You, L.; Feng, W.; Ge, J.; Fan, Y. A multi-objective optimization of degradable polymer vascular stents. Comput. Methods Biomech. Biomed. Eng. 2025, 1–10. [Google Scholar] [CrossRef]
- Ingrund, J.C.; Nasser, F.; De Jesus-Silva, S.G.; Límaco, R.P.; Galastri, F.L.; Burihan, M.C.; Filho, C.E.C.C.; Neser, A. Hybrid procedures for complex thoracic aortic diseases. Braz. J. Cardiovasc. Surg. 2010, 25, 303–310. [Google Scholar] [CrossRef]
- Liu, Z.; Teng, S.; Chen, G.; Wu, L.; Yang, J.; Cui, F.; Ho, P. A systematic approach to further improve stent-graft performance. Mater. Des. 2021, 211, 110144. [Google Scholar] [CrossRef]
- Pelton, A.; Schroeder, V.; Mitchell, M.; Gong, X.; Barney, M.; Robertson, S. Fatigue and durability of Nitinol stents. J. Mech. Behav. Biomed. Mater. 2008, 1, 153–164. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, L.; Yang, J.; Cui, F.; Ho, P.; Wang, L.; Dong, J.; Chen, G. Thoracic aorta stent grafts design in terms of biomechanical investigations into flexibility. Math. Biosci. Eng. 2020, 18, 800–816. [Google Scholar] [CrossRef]
- Wang, H.; Jiao, L.; Sun, J.; Yan, P.; Wang, X.; Qiu, T. Multi-Objective Optimization of Bioresorbable Magnesium Alloy Stent by Kriging Surrogate Model. Cardiovasc. Eng. Technol. 2022, 13, 829–839. [Google Scholar] [CrossRef]
- Shen, X.; Jiang, J.B.; Zhu, H.F.; Deng, Y.Q.; Ji, S. Numerical Investigation of the Flexibility of a New Self-Expandable Tapered Stent. J. Mech. 2020, 36, 577–584. [Google Scholar] [CrossRef]
- Gharleghi, R.; Wright, H.; Luvio, V.; Jepson, N.; Luo, Z.; Senthurnathan, A.; Babaei, B.; Prusty, B.G.; Ray, T.; Beier, S. A multi-objective optimization of stent geometries. J. Biomech. 2021, 125, 110575. [Google Scholar] [CrossRef]
- Vellaparambil, R.; Han, W.S.; Giovanni, P.D.; Avril, S. Potential of auxetic designs in endovascular aortic repair: A computational study of their mechanical performance. J. Mech. Behav. Biomed. Mater. 2023, 138, 105644. [Google Scholar] [CrossRef]
- Demanget, N.; Duprey, A.; Badel, P.; Orgéas, L.; Avril, S.; Geindreau, C.; Albertini, J.-N.; Favre, J.-P. Finite element analysis of the mechanical performances of 8 marketed aortic stent-grafts. J. Endovasc. Ther. 2013, 20, 523–535. [Google Scholar] [CrossRef] [PubMed]
- Gong, X.-Y.; Pelton, A.R.; Duerig, T.W.; Rebelo, N.; Perry, K. Finite element analysis and experimental evaluation of superelastic Nitinol stent. In Proceedings of the International Conference on Shape Memory and Superelastic Technologies 2003, Pacific, CA, USA, 5–8 May 2003. [Google Scholar]
- Nemat-Nasser, S.; Guo, W. Superelastic and cyclic response of NiTi SMA at various strain rates and temperatures. Mech. Mater. 2006, 38, 463–474. [Google Scholar] [CrossRef]
- Kumar, G.P.; Mathew, L. Self-expanding aortic valve stent—Material optimization. Comput. Biol. Med. 2012, 42, 1060–1063. [Google Scholar] [CrossRef] [PubMed]
- Kleinstreuer, C.; Li, Z.; Basciano, C.; Seelecke, S.; Farber, M. Computational mechanics of Nitinol stent grafts. J. Biomech. 2008, 41, 2370–2378. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiong, Y.; Hu, J.; Guo, X.; Xu, X.; Chen, J.; Wang, Y.; Chen, Y. A Finite Element Investigation on Material and Design Parameters of Ventricular Septal Defect Occluder Devices. J. Funct. Biomater. 2022, 13, 182. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, G.; Ong, C.; Yao, Z.; Li, X.; Deng, J.; Cui, F. Multi-objective design optimization of stent-grafts for the aortic arch. Mater. Des. 2023, 227, 111748. [Google Scholar] [CrossRef]
- Azaouzi, M.; Lebaal, N.; Makradi, A.; Belouettar, S. Optimization based simulation of self-expanding Nitinol stent. Mater. Des. 2013, 50, 917–928. [Google Scholar] [CrossRef]
- Santos, I.C.; Rodrigues, A.; Figueiredo, L.; A Rocha, L.; Tavares, J.M.R. Mechanical properties of stent–graft materials. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2012, 226, 330–341. [Google Scholar] [CrossRef]
- Perry, K.E.; Kugler, C. Non-zero mean fatigue testing of NiTi. Exp. Tech. 2002, 26, 37–38. [Google Scholar] [CrossRef]

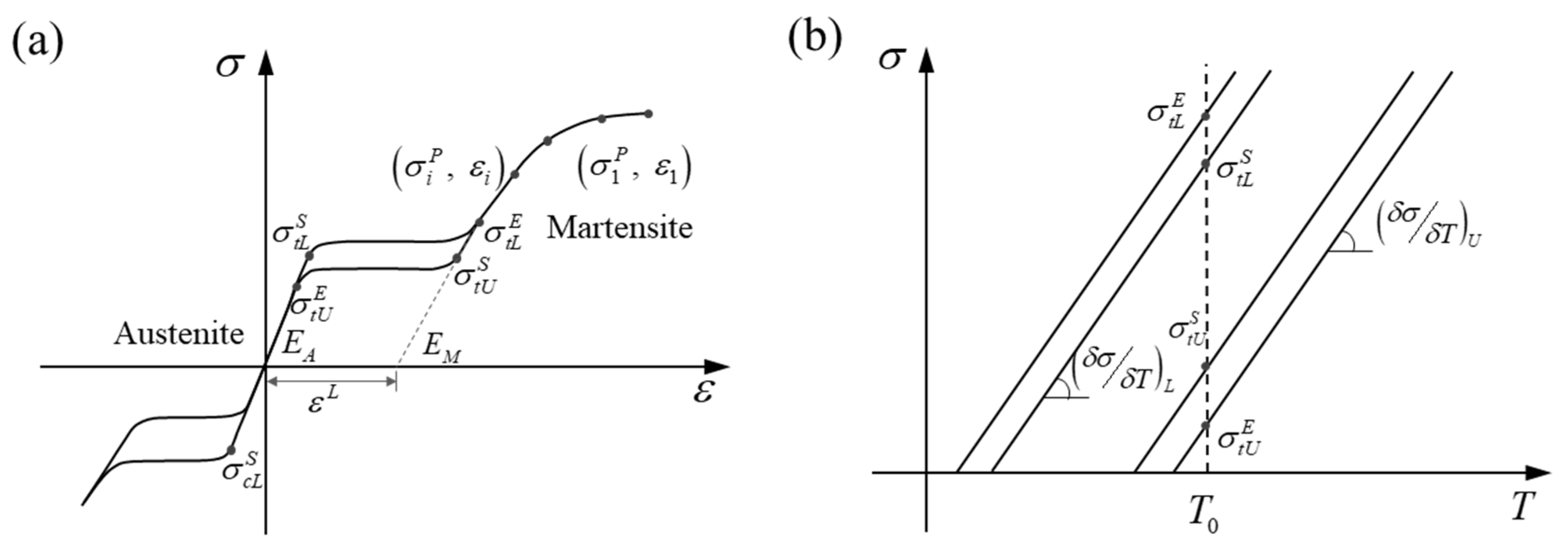

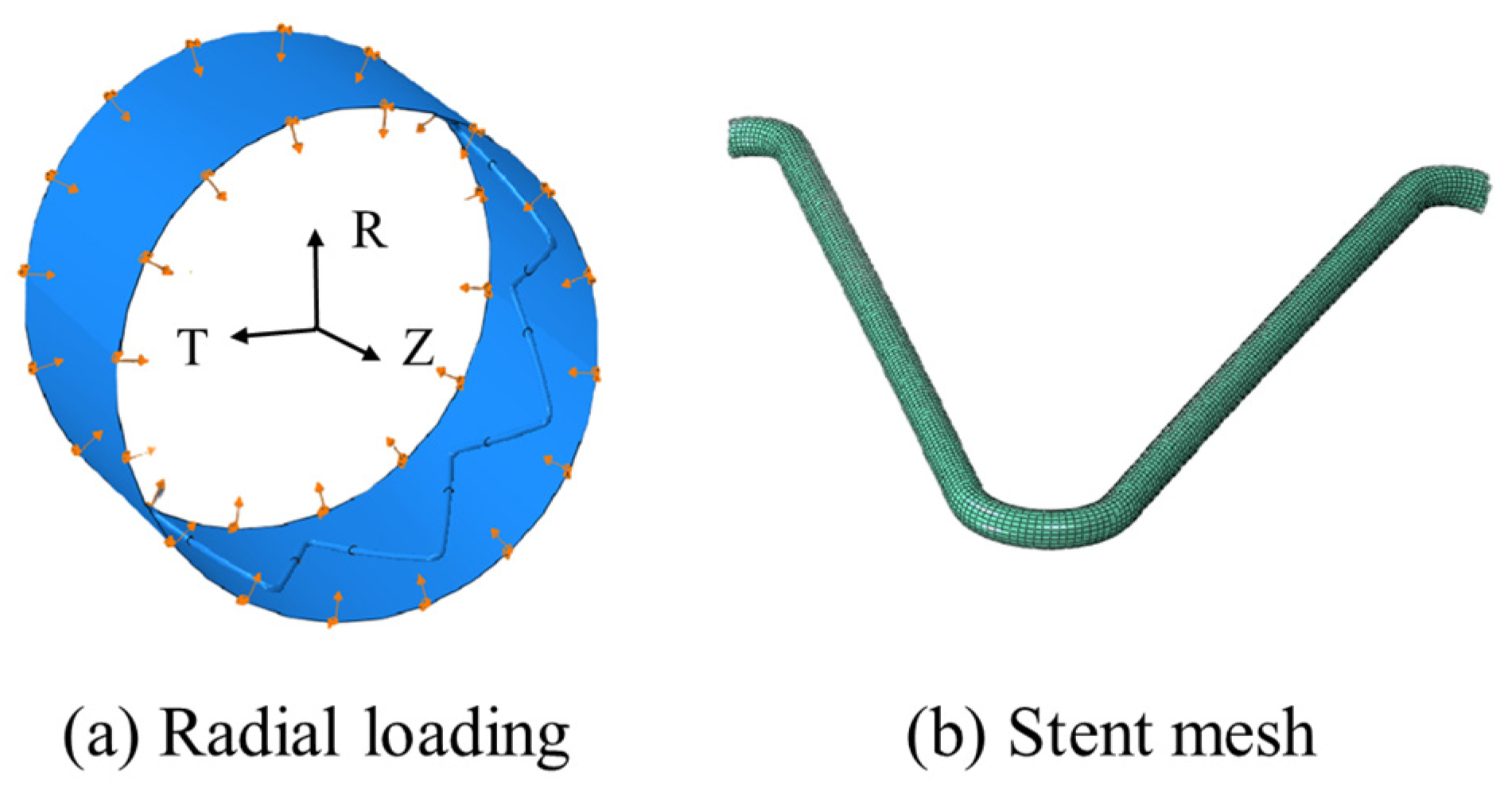




| Nitinol-1 | Nitinol-2 | Nitinol-3 | Nitinol-4 | |
|---|---|---|---|---|
| Austenite Young’s modulus EA (MPa) | 60,000 | 51,700 | 40,000 | 40,000 |
| Austenite Poisson’s ratio | 0.33 | 0.3 | 0.33 | 0.46 |
| Martensite Young’s modulus EM (MPa) | 40,000 | 47,800 | 32,000 | 18,554 |
| Martensite Poisson’s ratio | 0.33 | 0.3 | 0.33 | 0.46 |
| Transformation strain | 0.041 | 0.063 | 0.041 | 0.04 |
| Loading | 6.7 | 6.527 | 6.7 | 6.527 |
| Start of transformation loading | 520 | 600 | 440 | 390 |
| End of transformation loading | 540 | 670 | 540 | 425 |
| Reference temperature T0 (°C) | 22 | 37 | 22 | 37 |
| Unloading | 6.7 | 6.527 | 6.7 | 6.527 |
| Start of transformation loading | 250 | 288 | 250 | 140 |
| End of transformation loading | 140 | 254 | 140 | 135 |
| Strain limit | 12% | 12% | 12% | 12% |
| Elastic Modulus (MPa) | Poisson’s Ratio | Yield Stress (MPa) | Tensile Strength | Graft Thickness (mm) | |
|---|---|---|---|---|---|
| e-PTFE | 55.2 | 0.46 | 6.6 | 8.0 | 0.1 |
| PET | 1.84 | 0.35 | 59.3 | 86 | 0.1 |
| Nitinol-1 | Nitinol-2 | Nitinol-3 | Nitinol-4 | |
|---|---|---|---|---|
| PET | MP-1 | MP-3 | MP-5 | MP-7 |
| e-PTFE | MP-2 | MP-4 | MP-6 | MP-8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, L.; Liu, Z.; Teng, S. Optimizing Aortic Arch Stent-Graft Performance Through Material Science: An Exploratory Study. Materials 2025, 18, 3592. https://doi.org/10.3390/ma18153592
Liu X, Zhang L, Liu Z, Teng S. Optimizing Aortic Arch Stent-Graft Performance Through Material Science: An Exploratory Study. Materials. 2025; 18(15):3592. https://doi.org/10.3390/ma18153592
Chicago/Turabian StyleLiu, Xiaobing, Linxuan Zhang, Zongchao Liu, and Shuai Teng. 2025. "Optimizing Aortic Arch Stent-Graft Performance Through Material Science: An Exploratory Study" Materials 18, no. 15: 3592. https://doi.org/10.3390/ma18153592
APA StyleLiu, X., Zhang, L., Liu, Z., & Teng, S. (2025). Optimizing Aortic Arch Stent-Graft Performance Through Material Science: An Exploratory Study. Materials, 18(15), 3592. https://doi.org/10.3390/ma18153592








