Cutting Force—Vibration Interactions in Precise—and Micromilling Processes: A Critical Review on Prediction Methods
Highlights
- Critical literature review on cutting force and vibration prediction methods.
- Formulation of the generalized cutting forces, displacements/vibrations models.
- Challenges and future directions in cutting force and displacement prediction methods.
Abstract
1. Introduction
- Presentation of the recent analytical cutting force and displacement prediction methods in precise and micromilling processes;
- Indication of a key factors, characteristic for a precise and micromilling processes, which affect the geometric parameters of cut and thus the cutting forces and displacements in the machining system;
- Formulation of the generalized cutting forces, displacements/vibrations models, based on the analysis of the recent and critical literature;
- Identification of challenges and future directions in cutting force and displacement prediction methods dedicated to precise and micromilling processes.
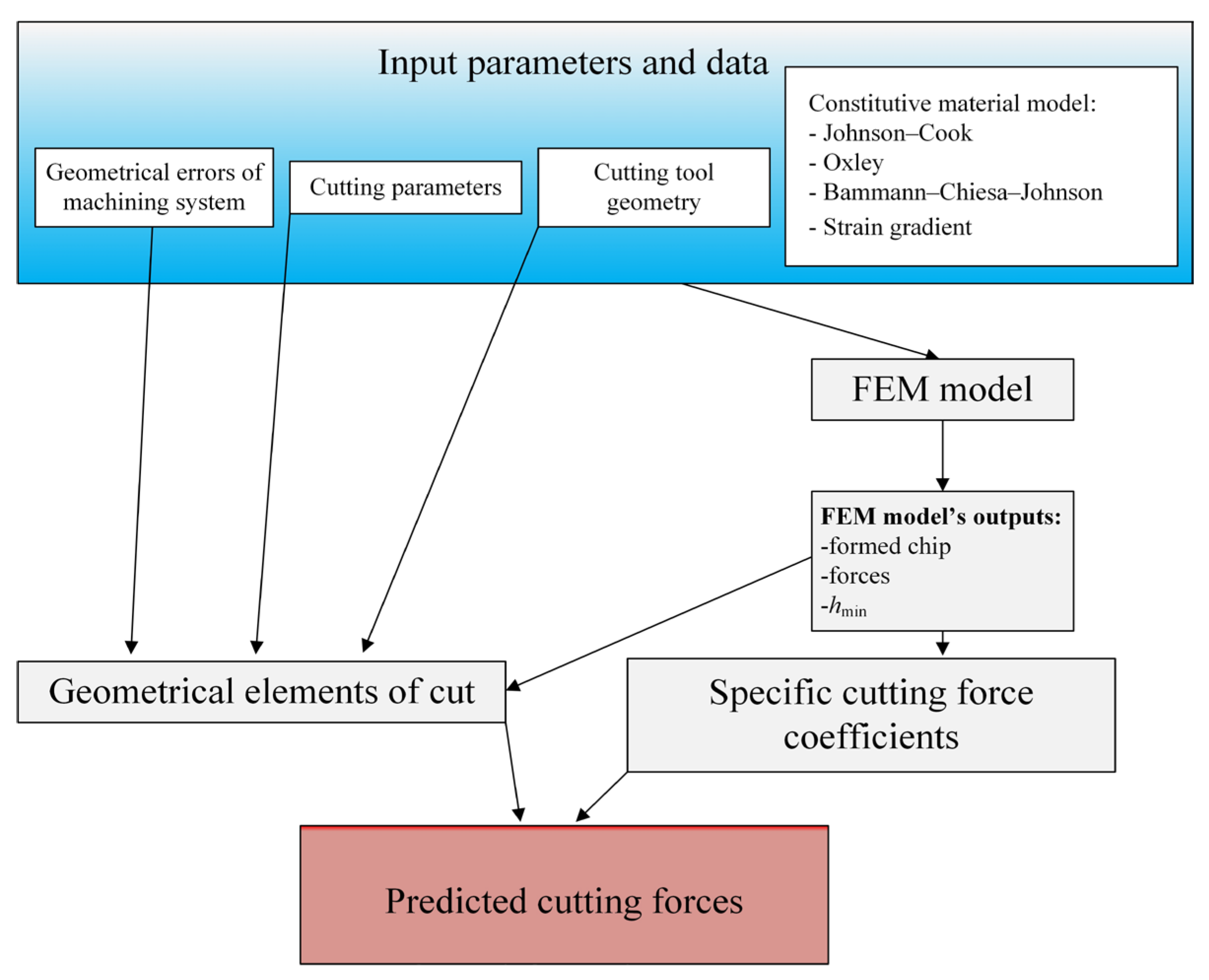
2. Cutting Force Models Applied in Precise Milling and Micromilling
- Ft, Fr, Fa—cutting force components, tangential, radial and binormal components,
- Kte, Kre, Kae—specific edge cutting force coefficients,
- Ktc, Krc, Kac—specific shearing cutting force coefficients,
- Ktp, Krp, Kap—specific ploughing cutting force coefficients,
- hz—uncut chip thickness per 1 tooth,
- dz—elementary length of cutting edge segment,
- Apl—ploughing area.
- by formulating an object function expressed as the difference between the measured and calculated force [87];
- by using a method based on Bayesian inference.
- the workpiece material flowing onto the rounded cutting edge tends to move in the direction determined by the effective rake angle,
- in order to ensure easy material flow, the front section of the dead zone is tangential to the cutting edge.
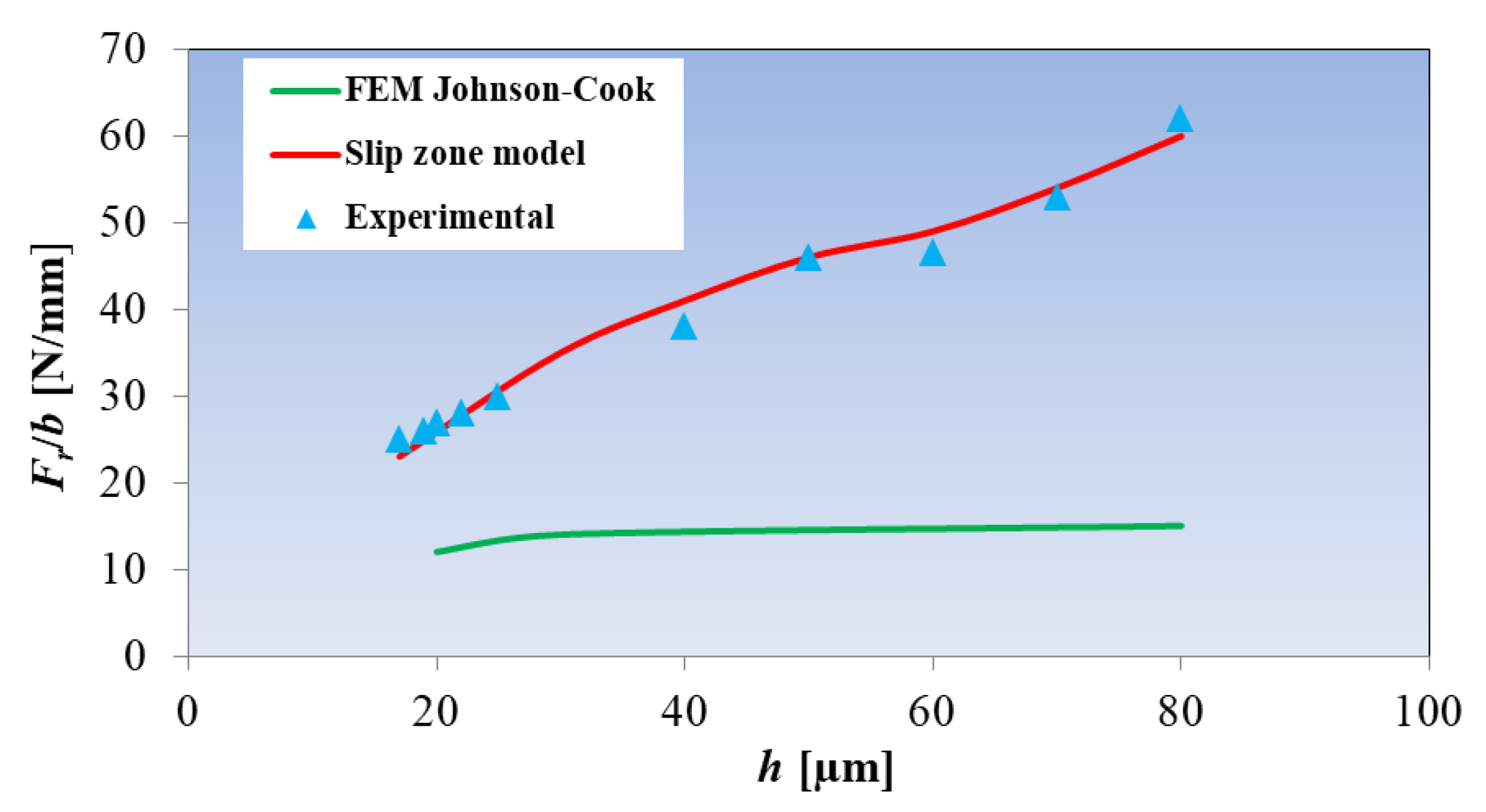
- a1, a2—coefficients taking into account the relationship between the tool and the slip zone,
- lAD—length of the slip zone relative to the frontal section of the dead metal zone.
- at1–at6—proportionality coefficients for the tangential force, determined based on the FEM model,
- ar1–ar6—proportionality coefficients for radial force, determined based on the FEM model.
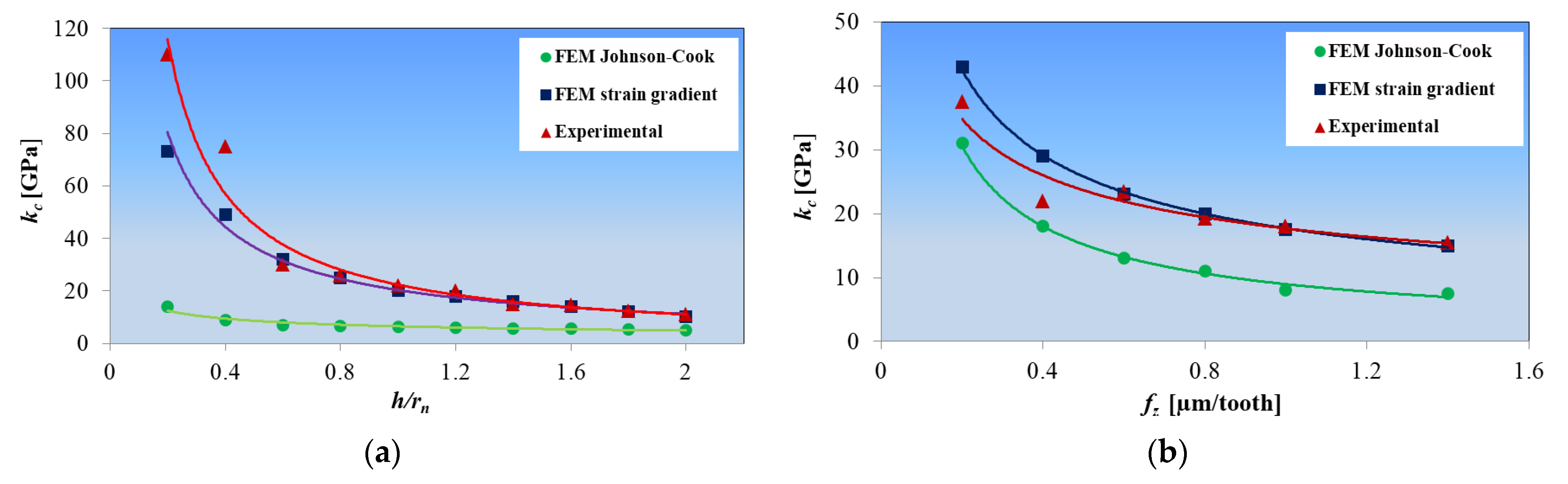
- A decrease in the number of microstructure defects with a decrease in h;
- An increase in the material deformation rate in the main slip zone;
- The effect of material softening caused by the effect of high temperature;
- The effect of the plastic deformation gradient in the deformation zones, in the range of small uncut chip thicknesses.
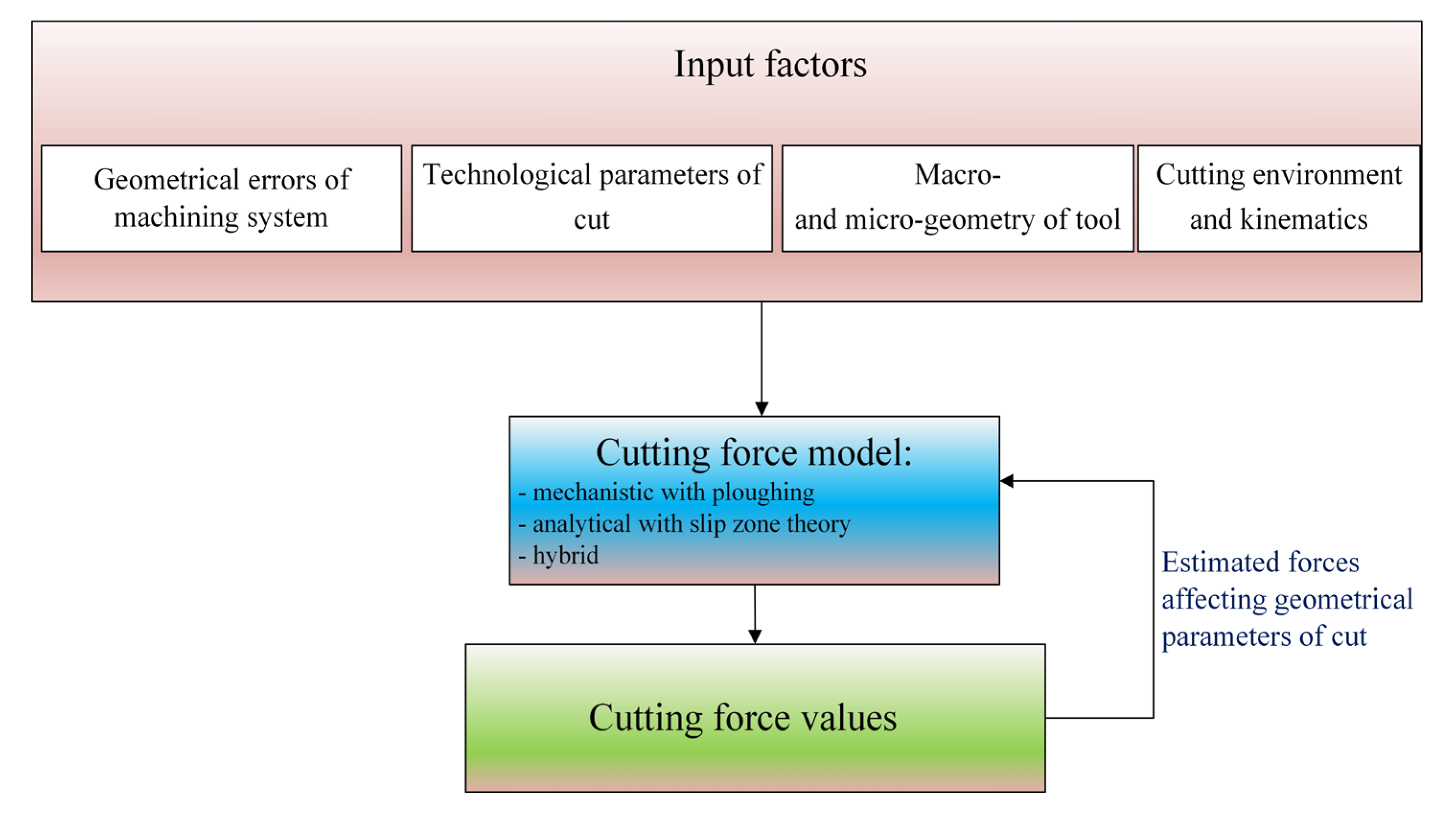
3. Characteristics of Relations Between Geometrical Elements of Cut and Cutting Forces
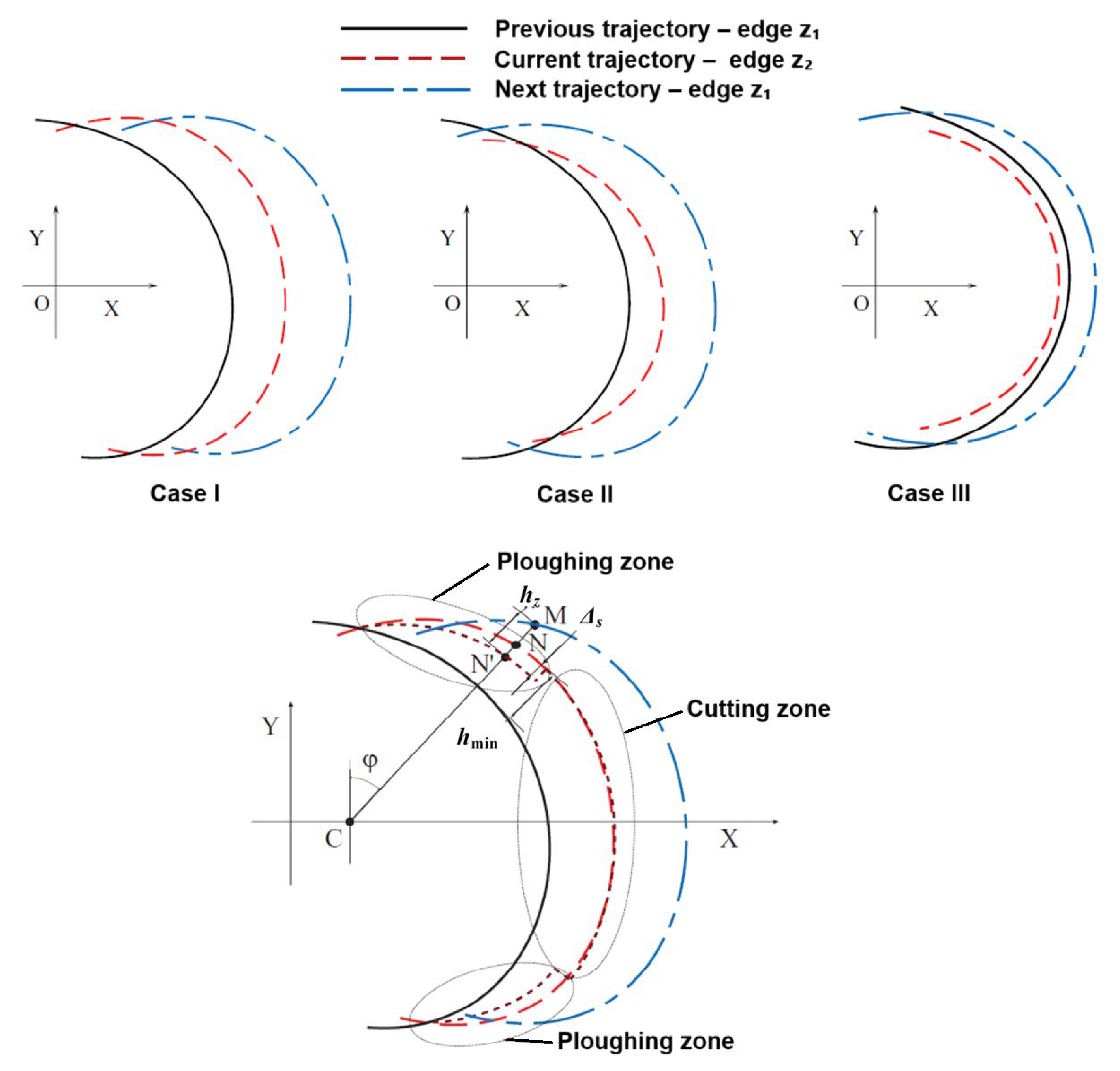
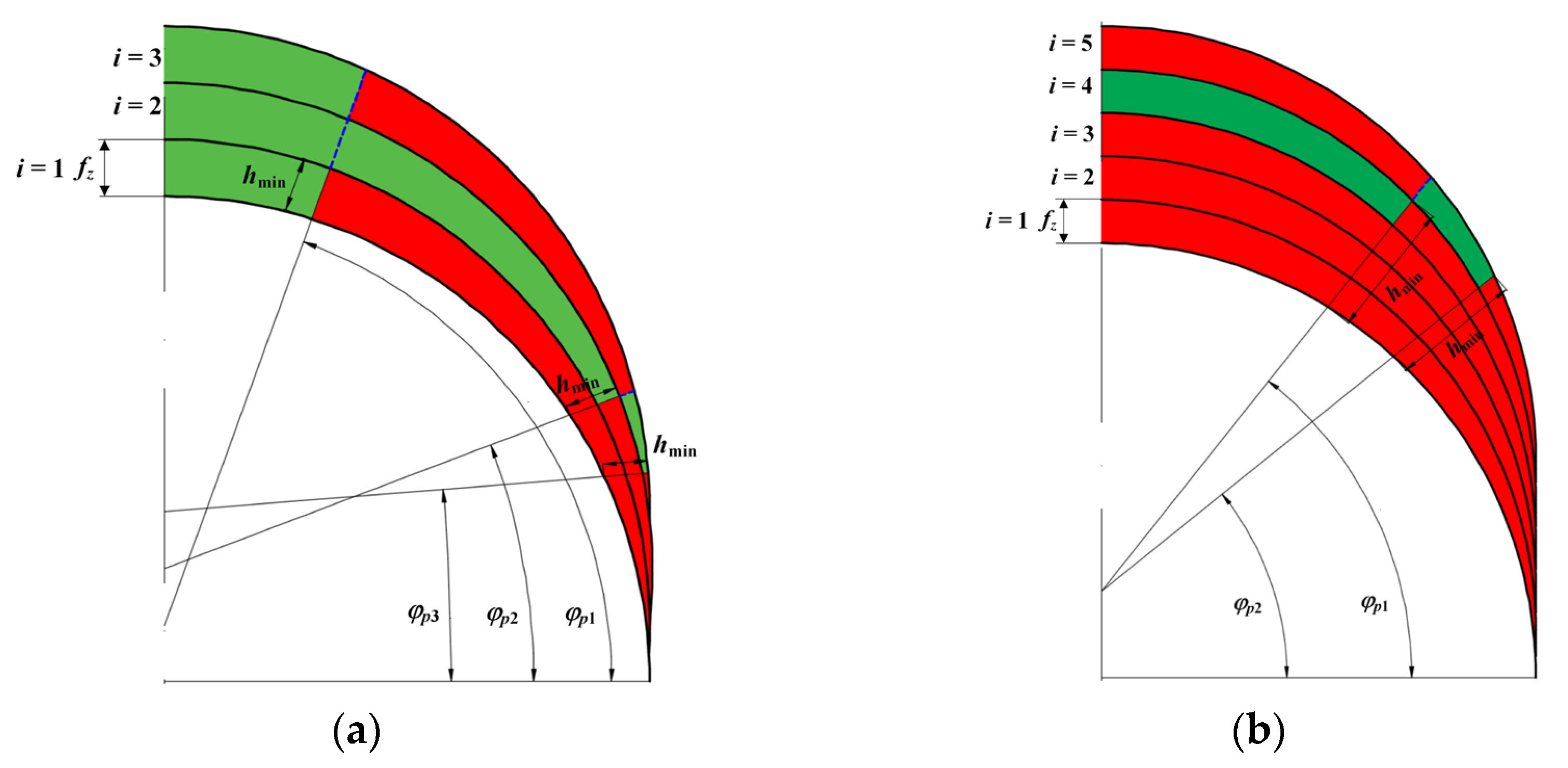
- hz1(φ), hz2(φ)—instant uncut chip thickness per first z1 and second z2 tooth,
- ks—tool static stiffness coefficient,
- Ck—proportionality coefficient of tool deflection,
- Fx(z1), Fx(z2)—maximal feed normal force values per the first z1 and second z2 tooth,
- Fy(z1), Fy(z2)—maximal feed force values per the first z1 and second z2 tooth.
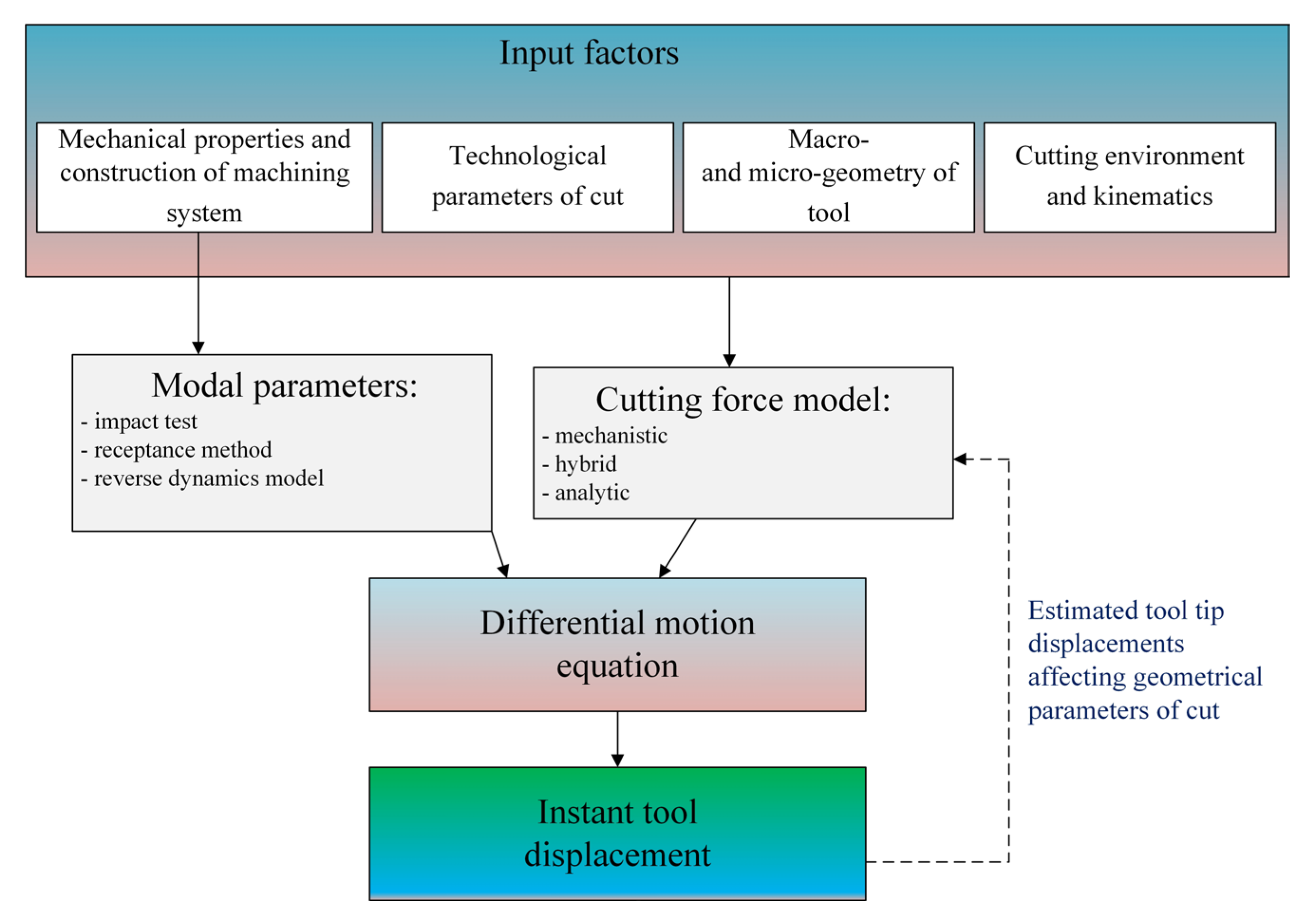
4. Evaluation of Displacements and Vibrations in Machining System
4.1. Static Models
- I—moment of inertia of the tool cross-section,
- L—tool overhang.
- Iu—moment of inertia of the cross-section of the tool shank,
- In—moment of inertia of the cross-section of the tool body,
- Ln—length of tool body,
- ϕu—deflection angle of the tool body.
4.2. Dynamic Models
- yd—instant deflection value,
- m—modal mass,
- c—damping coefficient,
- k—dynamic stiffness coefficient,
- Fy(t)—instant force value in the Y direction.
- yd(t), xd(t)—instant tool tip deflections in Y and X directions
- yd(t − Tz), xd(t − Tz)—instant tool tip deflections in Y and X directions after time t − Tz, where Tz = 60/(n ∙ z).
- Kpd—damping coefficient of machining,
- rd(t)—instant tool deflection in radial direction.
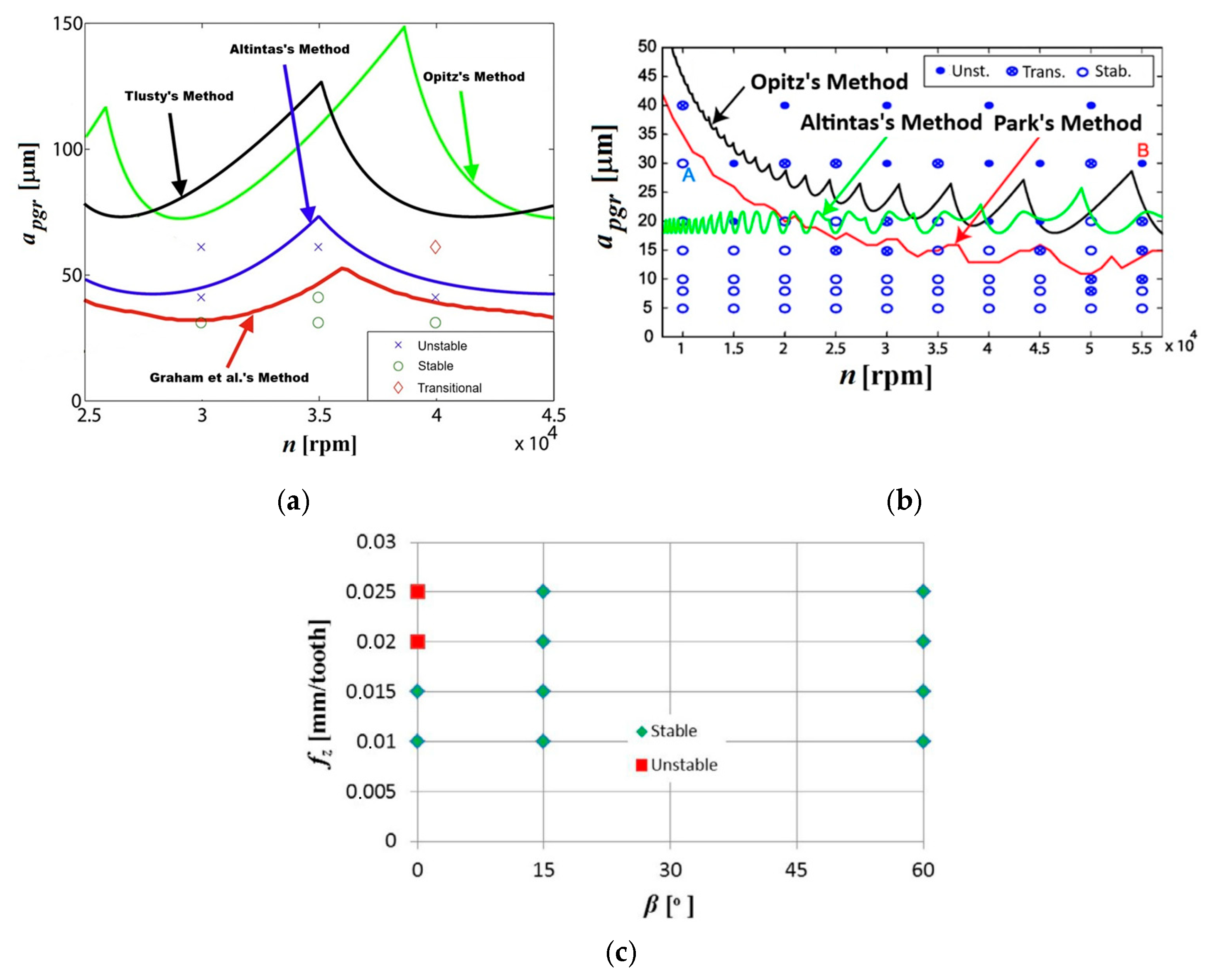
5. Generalized Approaches for Force and Vibrations Prediction
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, Q.; Liu, Z.; Yang, Z.; Jiang, Y.; Sun, Y.; Xu, J.; Zhao, W.; Wang, W.; Wang, W.; Ren, Q.; et al. Development, challenges and future trends on the fabrication of micro-textured surfaces using milling technology. J. Manuf. Process. 2024, 126, 285–331. [Google Scholar] [CrossRef]
- Li, H.; Wu, B. Development of a hybrid cutting force model for micromilling of brass. Int. J. Mech. Sci. 2016, 115–116, 586–595. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, J.; Sun, Q.; Geng, Y.; Yan, Y.; Cui, H. Diffraction characteristics and formation mechanism of nanogratings in tip-based down-milling. Int. J. Mech. Sci. 2024, 266, 108996. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Zhu, K. Generic instantaneous force modeling and comprehensive real engagement identification in micro-milling. Int. J. Mech. Sci. 2020, 176, 105504. [Google Scholar] [CrossRef]
- Wang, D.; Ren, J.; Tian, W. A method for the prediction of cutting force for 5-axis ball-end milling of workpieces with curved surfaces. Int. J. Adv. Manuf. Technol. 2020, 107, 2023–2039. [Google Scholar] [CrossRef]
- Denkena, B.; Krüger, M.; Bachrathy, D.; Stepan, G. Model based reconstruction of milled surface topography from measured cutting forces. Int. J. Mach. Tools Manuf. 2012, 54–55, 25–33. [Google Scholar] [CrossRef]
- Cui, Z.; Liu, H.; Wu, L.; Cao, Z.; Zong, W. Cutting force and surface quality in ultra-precision milling of oxygen-free copper under different cutting strategies. J. Manuf. Process. 2024, 131, 2420–2442. [Google Scholar] [CrossRef]
- Brito, L.C.; Gomes, M.C.; de Oliveira, D.; Bacci da Silva, M.; Viana Duarte, M.A. Vibration features for indirect monitoring of end micromilling process. Precis. Eng. 2023, 79, 7–15. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Li, Y.; Chen, D. Study of different cutting fluids effect on the coupling characteristics of milling noise-vibration and surface roughness of TA2 pure titanium. J. Manuf. Process. 2024, 118, 103–115. [Google Scholar] [CrossRef]
- Sheikhi, M.R.; Gürgen, S.; Li, J. Vibration suppression and surface quality enhancement in milling thin-walled structures using shear thickening fluids. J. Manuf. Process. 2024, 131, 2219–2229. [Google Scholar] [CrossRef]
- Wang, D.; Penter, L.; Hänel, A.; Ihlenfeldt, S.; Wiercigroch, M. Stability enhancement and chatter suppression in continuous radial immersion milling. Int. J. Mech. Sci. 2022, 235, 107711. [Google Scholar] [CrossRef]
- Zhang, S.J.; To, S. The effects of spindle vibration on surface generation in ultra-precision raster milling. Int. J. Mach. Tools Manuf. 2013, 71, 52–56. [Google Scholar] [CrossRef]
- Mann, B.P.; Edes, B.T.; Easley, S.J.; Young, K.A.; Ma, K. Chatter vibration and surface location error prediction for helical end mills. Int. J. Mach. Tools Manuf. 2008, 48, 350–361. [Google Scholar] [CrossRef]
- Deng, D.; Zhang, Z.; Wan, W.; Ma, Q.; Sun, J. Investigation on burr formation characteristics in micro milling of Ω-shaped reentrant microchannels. J. Manuf. Process. 2022, 80, 754–764. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, N.; Bian, R.; He, N.; Li, Z.; Li, L. Investigations on burr formation mechanisms in micro milling of high-aspect-ratio titanium alloy ti-6al-4v structures. Int. J. Mech. Sci. 2020, 185, 105884. [Google Scholar] [CrossRef]
- Yadav, R.; Chakladar, N.D.; Paul, S. Micro-milling of Ti-6Al-4V with controlled burr formation. Int. J. Mech. Sci. 2022, 231, 107582. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Wang, W.; Zhao, J. Improved analytical prediction of burr formation in micro end milling. Int. J. Mech. Sci. 2019, 151, 461–470. [Google Scholar] [CrossRef]
- Becze, C.E.; Clayton, P.; Chen, L.; El-Wardany, T.I.; Elbestawi, M.A. High-speed five-axis milling of hardened tool steel. Int. J. Mach. Tools Manuf. 2000, 40, 869–885. [Google Scholar] [CrossRef]
- Twardowski, P.; Legutko, S.; Krolczyk, G.M.; Hloch, S. Investigation of wear and tool life of coated carbide and cubic boron nitride cutting tools in high speed milling. Adv. Mech. Eng. 2015, 7, 1687814015590216. [Google Scholar] [CrossRef]
- Lopez de Lacalle, L.N.; Lamikiz, A.; Sanchez, J.A.; Salgado, M.A. Toolpath selection based on the minimum deflection cutting forces in the programming of complex surfaces milling. Int. J. Mach. Tools Manuf. 2007, 47, 388–400. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Maruda, R.W.; Krolczyk, G.M.; Nieslony, P. Application of signal to noise ratio and grey relational analysis to minimize forces and vibrations during precise ball end milling. Precis. Eng. 2017, 51, 582–596. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y.; Armarego, E.J.A. Prediction of milling force coefficients from orthogonal cutting data. Trans. ASME J. Manuf. Sci. Eng. 1996, 118, 216–224. [Google Scholar] [CrossRef]
- Dornfeld, D.; Lee, D.E. Precision Manufacturing; Springer: New York, NY, USA, 2008. [Google Scholar]
- Fontaine, M.; Devillez, A.; Moufki, A.; Dudzinski, D. Predictive force model for ball-end milling and experimental validation with a wavelike form machining test. Int. J. Mach. Tools Manuf. 2006, 46, 367–380. [Google Scholar] [CrossRef]
- Fontaine, M.; Moufki, A.; Devillez, A.; Dudzinski, D. Modelling of cutting forces in ball-end milling with tool-surface inclination. Part I: Predictive force model and experimental validation. J. Mater. Process. Technol. 2007, 189, 73–84. [Google Scholar] [CrossRef]
- Chiou, C.H.; Hong, M.S.; Ehmann, K.F. Instantaneous shear plane based cutting force model for end milling. J. Mater. Process. Technol. 2005, 170, 164–180. [Google Scholar] [CrossRef]
- Kienzle, O. Prediction of forces and power in machine tools for metal-cutting. VDI-Z 1952, 94, 299–305. [Google Scholar]
- Kline, W.A.; DeVor, R.E. The effect of runout on cutting geometry and forces in end milling. Int. J. Mach. Tool Des. Res. 1983, 23, 123–140. [Google Scholar] [CrossRef]
- Kline, W.A.; DeVor, R.E. The prediction of cutting forces in end milling with application to cornering cuts. Int. J. Mach. Tool Des. Res. 1982, 22, 7–22. [Google Scholar] [CrossRef]
- Ko, J.H.; Cho, D.-W. 3D ball-end milling force model using instantaneous cutting force coefficients. J. Manuf. Sci. Eng. 2005, 127, 1–12. [Google Scholar] [CrossRef]
- Lee, P.; Altintas, Y. Prediction of ball–end milling forces from orthogonal cutting data. Int. J. Mach. Tools Manuf. 1996, 36, 1059–1072. [Google Scholar] [CrossRef]
- Rao, V.S.; Rao, P.V.M. Effect of workpiece curvature on cutting forces and surface error in machining of curved geometries. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2006, 220, 1399–1407. [Google Scholar] [CrossRef]
- Kim, J.D.; Kim, D.S. Theoretical analysis of micro-cutting characteristics in ultra-precision machining. J. Mater. Process. Technol. 1995, 49, 387–398. [Google Scholar] [CrossRef]
- Kim, C.-J.; Mayor, J.R.; Ni, J. A static model of chip formation in microscale milling. J. Manuf. Sci. Eng. 2004, 126, 710–718. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Wang, W. Prediction of cutting forces and instantaneous tool deflection in micro end milling by considering tool run-out. Int. J. Mech. Sci. 2018, 136, 124–133. [Google Scholar] [CrossRef]
- Biró, I.; Szalay, T. Extension of empirical specific cutting force model for the process of fine chip-removing milling. Int. J. Adv. Manuf. Technol. 2017, 88, 2735–2743. [Google Scholar] [CrossRef]
- Yuan, Y.; Jing, X.; Ehmann, K.F.; Cao, J.; Li, H.; Zhang, D. Modeling of cutting forces in micro end-milling. J. Manuf. Process. 2018, 31, 844–858. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, K.; Wang, G.; Wang, C. Prediction of Nonlinear Micro-milling force with a novel minimum uncut chip thickness model. Micromachines 2021, 12, 1495. [Google Scholar] [CrossRef]
- Wang, P.; Bai, Q.; Cheng, K.; Zhao, L.; Ding, H. The modelling and analysis of micro-milling forces for fabricating thin-walled micro-parts considering machining dynamics. Machines 2022, 10, 217. [Google Scholar] [CrossRef]
- Chen, N.; Li, L.; Wu, J.; Qian, J.; He, N.; Reynaerts, D. Research on the ploughing force in micro milling of soft-brittle crystals. Int. J. Mech. Sci. 2019, 155, 315–322. [Google Scholar] [CrossRef]
- Zhou, L.; Deng, B.; Peng, F.; Yang, M.; Yan, R. Semi-analytic modelling of cutting forces in micro ball-end milling of NAK80 steel with wear-varying cutting edge and associated nonlinear process characteristics. Int. J. Mech. Sci. 2020, 169, 105343. [Google Scholar] [CrossRef]
- Hao, Y.; Liu, Y. Analysis of milling surface roughness prediction for thin-walled parts with curved surface. Int. J. Adv. Manuf. Technol. 2017, 93, 2289–2297. [Google Scholar] [CrossRef]
- Honeycutt, A.; Schmitz, T.L. A Study of Milling Surface Quality during Period-2 Bifurcations. Procedia Manuf. 2017, 10, 183–193. [Google Scholar] [CrossRef]
- Mori, T.; Hiramatsu, T.; Shamoto, E. Simultaneous double-sided milling of flexible plates with high accuracy and high efficiency suppression of forced chatter vibration with synchronized single-tooth cutters. Precis. Eng. 2011, 35, 416–423. [Google Scholar] [CrossRef]
- Shan, C.; Lv, X.; Duan, W. Effect of tool inclination angle on the elastic deformation of thin-walled parts in multi-axis ball-end milling. Procedia CIRP 2016, 56, 311–315. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B.; Yuan, J. Modeling of surface topography based on cutting vibration in ball-end milling of thin-walled parts. Int. J. Adv. Manuf. Technol. 2018, 101, 1837–1854. [Google Scholar] [CrossRef]
- Peng, F.; Wu, J.; Fang, Z.; Yuan, S.; Yan, R.; Bai, Q. Modeling and controlling of surface micro-topography feature in micro-ball-end milling. Int. J. Adv. Manuf. Technol. 2013, 67, 2657–2670. [Google Scholar] [CrossRef]
- Chen, H.-Q.; Wang, Q.-H. Modeling and simulation of the surface topography in ball-end milling based on biharmonic spline interpolation. Int. J. Adv. Manuf. Technol. 2018, 99, 2451–2466. [Google Scholar] [CrossRef]
- Chen, W.; Xie, W.; Huo, D.; Yang, K. A novel 3D surface generation model for micro milling based on homogeneous matrix transformation and dynamic regenerative effect. Int. J. Mech. Sci. 2018, 144, 146–157. [Google Scholar] [CrossRef]
- Miao, H.; Li, C.; Liu, C.; Wang, C.; Zhang, X.; Sun, W. Machined surface prediction and reliability analysis in peripheral milling operations. Int. J. Mech. Sci. 2024, 272, 109193. [Google Scholar] [CrossRef]
- Yuan, X.; Fan, Y.; Liang, Z.; Wang, S.; Mao, X.; Xie, X.; Yang, A.; Liu, H.; Xu, Y. Prediction of measured surface topography with forced vibration effects. Measurement 2024, 229, 114469. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Twardowski, P. The influence of tool wear on the vibrations during ball end milling of hardened steel. Procedia CIRP 2014, 14, 587–592. [Google Scholar] [CrossRef]
- Iglesias, A.; Munoa, J.; Ciurana, J.; Dombovari, Z.; Stepan, G. Analytical expressions for chatter analysis in milling operations with one dominant mode. J. Sound Vib. 2016, 375, 403–421. [Google Scholar] [CrossRef]
- Zheng, C.M.; Junz Wang, J.-J. Stability prediction in radial immersion for milling with symmetric structure. Int. J. Mach. Tools Manuf. 2013, 75, 72–81. [Google Scholar] [CrossRef]
- Zhou, K.; Feng, P.; Xu, C.; Zhang, J.; Wu, Z. High-order full discretization methods for milling stability prediction by interpolating the delay term of time delayed differential equations. Int. J. Adv. Manuf. Technol. 2017, 93, 2201–2214. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.; Ren, Y.; Zhou, Z. 3D chatter stability of high-speed micromilling by considering nonlinear cutting coefficients, and process damping. J. Manuf. Process. 2020, 57, 552–565. [Google Scholar] [CrossRef]
- Singh, K.K.; Kartik, V.; Singh, R. Modeling dynamic stability in high-speed micromilling of Ti-6Al-4V via velocity and chip load dependent cutting coefficients. Int. J. Mach. Tools Manuf. 2015, 96, 56–66. [Google Scholar] [CrossRef]
- Singh, K.K.; Kartik, V.; Singh, R. Stability modeling with dynamic run-out in high speed micromilling of Ti6Al4V. Int. J. Mech. Sci. 2019, 150, 677–690. [Google Scholar] [CrossRef]
- Soori, M.; Arezoo, B.; Habibi, M. Virtual machining considering dimensional, geometrical and tool deflection errors in three-axis CNC milling machines. J. Manuf. Syst. 2014, 33, 498–507. [Google Scholar] [CrossRef]
- Dorgeloh, T.; Beinhauer, A.; Riemer, O.; Brinksmeier, E. Microfluidic balancing concepts for ultraprecision high speed applications. Procedia CIRP 2016, 46, 185–188. [Google Scholar] [CrossRef]
- Peterka, J.; Kováč, M.; Zvončan, M. Influence of tool balancing on machined surface quality in high speed machining. J. Prod. Eng. 2011, 15, 11–14. [Google Scholar][Green Version]
- Saha, S.; Deb, S.; Bandyopadhyay, P.P. Progressive wear based tool failure analysis during dry and MQL assisted sustainable micro-milling. Int. J. Mech. Sci. 2021, 212, 106844. [Google Scholar] [CrossRef]
- Saha, S.; Deb, S.; Bandyopadhyay, P.P. Tool wear induced burr formation and concomitant reduction in MQL wetting capability in micro-milling. Int. J. Mech. Sci. 2023, 245, 108095. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, S.; Zhang, H.; Zhou, L. Modeling and predicting for surface topography considering tool wear in milling process. Int. J. Adv. Manuf. Technol. 2013, 68, 2849–2860. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Li, Y.; Zhou, L. Modeling and on-line simulation of surface topography considering tool wear in multi-axis milling process. Int. J. Adv. Manuf. Technol. 2015, 77, 735–749. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Zhao, J. Surface generation modeling of micro milling process with stochastic tool wear. Precis. Eng. 2020, 61, 170–181. [Google Scholar] [CrossRef]
- Jiang, X.; Ding, J.; Wang, C.; Hong, L.; Yao, W.; Yu, W. Influence of tool wear on geometric surface modeling for TC4 titanium alloy milling. J. Manuf. Process. 2024, 131, 797–814. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Twardowski, P. Tool life and process dynamics in high speed ball end milling of hardened steel. Procedia CIRP 2012, 1, 289–294. [Google Scholar] [CrossRef]
- De Aguiar, M.M.; Diniz, A.E.; Pederiva, R. Correlating surface roughness, tool wear and tool vibration in the milling process of hardened steel using long slender tools. Int. J. Mach. Tools Manuf. 2013, 68, 1–10. [Google Scholar] [CrossRef]
- Klocke, F.; Lung, D.; Puls, H. FEM-Modelling of the thermal workpiece deformation in dry turning. Procedia CIRP 2013, 8, 240–245. [Google Scholar] [CrossRef]
- Creighton, E.; Honegger, A.; Tulsian, A.; Mukhopadhyay, D. Analysis of thermal errors in a high-speed micro-milling spindle. Int. J. Mach. Tools Manuf. 2010, 50, 386–393. [Google Scholar] [CrossRef]
- Chen, W.; Teng, X.; Huo, D.; Wang, Q. An improved cutting force model for micro milling considering machining dynamics. 1006. Int. J. Adv. Manuf. Technol. 2017, 93, 3005–3016. [Google Scholar] [CrossRef]
- Gozu, E.; Karpat, Y. Uncertainty analysis of force coefficients during micromilling of titanium alloy. Int. J. Adv. Manuf. Technol. 2017, 93, 839–855. [Google Scholar] [CrossRef]
- Park, S.S.; Malekian, M. Mechanistic modeling and accurate measurement of micro end milling forces. CIRP Ann.—Manuf. Technol. 2009, 58, 49–52. [Google Scholar] [CrossRef]
- Zhang, X.; Ehmann, K.F.; Yu, T.; Wang, W. Cutting forces in micro end milling processes. Int. J. Mach. Tools Manuf. 2016, 107, 21–40. [Google Scholar] [CrossRef]
- Budak, E. Analytical models for high performance milling, Part I: Cutting forces, structural deformations and tolerance integrity. Int. J. Mach. Tools Manuf. 2006, 46, 1478–1488. [Google Scholar] [CrossRef]
- Denkena, B.; Vehmeyer, J.; Niederwestberg, D.; Maaß, P. Identification of the specific cutting force for geometrically defined cutting edges and varying cutting conditions. Int. J. Mach. Tools Manuf. 2014, 82–83, 42–49. [Google Scholar] [CrossRef]
- Gradisek, J.; Kalveram, M.; Weinert, K. Mechanistic identification of specific force coefficients for a general end mill. Int. J. Mach. Tools Manuf. 2004, 44, 401–414. [Google Scholar] [CrossRef]
- Lamikiz, A.; López de Lacalle, L.N.; Sanchez, J.A.; Salgado, M.A. Cutting force estimation in sculptured surface milling. Int. J. Mach. Tools Manuf. 2004, 44, 1511–1526. [Google Scholar] [CrossRef]
- Ozturk, B.; Lazoglu, I.; Erdim, H. Machining of free-form surfaces. Part II: Calibration and forces. Int. J. Mach. Tools Manuf. 2006, 46, 736–746. [Google Scholar] [CrossRef]
- Wojciechowski, S. The estimation of cutting forces and specific force coefficients during finishing ball end milling of inclined surfaces. Int. J. Mach. Tools Manuf. 2015, 89, 110–123. [Google Scholar] [CrossRef]
- Grossi, N.; Sallese, L.; Scippa, A.; Campatelli, G. Speed-varying cutting force coefficient identification in milling. Precis. Eng. 2015, 42, 321–334. [Google Scholar] [CrossRef]
- Rubeo, M.A.; Schmitz, T.L. Milling Force Modeling: A Comparison of Two Approaches. Procedia Manuf. 2016, 5, 90–105. [Google Scholar] [CrossRef]
- Tsai, M.Y.; Chang, S.Y.; Hung, J.P.; Wang, C.C. Investigation of milling cutting forces and cutting coefficient for aluminum 6060-T6. Comput. Electr. Eng. 2016, 51, 320–330. [Google Scholar] [CrossRef]
- Gonzalo, O.; Beristain, J.; Jauregi, H.; Sanz, C. A method for the identification of the specific force coefficients for mechanistic milling simulation. Int. J. Mach. Tools Manuf. 2010, 50, 765–774. [Google Scholar] [CrossRef]
- Wan, M.; Lu, M.-S.; Zhang, W.-H.; Yang, Y. A new ternary-mechanism model for the prediction of cutting forces in flat end milling. Int. J. Mach. Tools Manuf. 2012, 57, 34–45. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Pang, B.; Zhao, W.-H. An accurate prediction method of cutting forces in 5-axis flank milling of sculptured surface. Int. J. Mach. Tools Manuf. 2016, 104, 26–36. [Google Scholar] [CrossRef]
- Zhou, L.; Peng, F.Y.; Yan, R.; Yao, P.F.; Yang, C.C.; Li, B. Analytical modeling and experimental validation of micro end-milling cutting forces considering edge radius and material strengthening effects. Int. J. Mach. Tools Manuf. 2015, 97, 29–41. [Google Scholar] [CrossRef]
- Srinivasa, Y.V.; Shunmugam, M.S. Mechanistic model for prediction of cutting forces in micro end-milling and experimental comparison. Int. J. Mach. Tools Manuf. 2013, 67, 18–27. [Google Scholar] [CrossRef]
- Bo, L.; Yanlong, C.; Wenhua, C.; Jun, P. Geometry simulation and evaluation of the surface topography in five-axis ball-end milling. Int. J. Adv. Manuf. Technol. 2017, 93, 1651–1667. [Google Scholar] [CrossRef]
- Abdelmoneim, M.E.S.; Scrutton, R.F. Tool edge roundness and stable build up formation in finish machining. Trans. ASME J. Eng. Ind. 1974, 96, 1258–1267. [Google Scholar] [CrossRef]
- Waldorf, D.J.; DeVor, R.E.; Kapoor, S.G. A slip line field for ploughing during orthogonal cutting. Trans. ASME J. Manuf. Sci. Eng. 1998, 120, 693–699. [Google Scholar] [CrossRef]
- Jun, B.G.; Liu, X.; DeVor, R.E.; Kapoor, S.G. Investigation of the Dynamics of Microend Milling. Part I: Model Development. J. Manuf. Sci. Eng. 2006, 128, 893–900. [Google Scholar] [CrossRef]
- Fang, N. Slip-Line Modeling of Machining With a Rounded-Edge Tool. Part I: New Model and Theory. J. Mech. Phys. Solids 2003, 51, 715–742. [Google Scholar] [CrossRef]
- Afazov, S.M.; Ratchev, S.M.; Segal, J.; Popov, A.A. Chatter modelling in micro-milling by considering process nonlinearities. Int. J. Mach. Tools Manuf. 2012, 56, 28–38. [Google Scholar] [CrossRef]
- Afazov, S.M.; Ratchev, S.M.; Segal, J. Modelling and simulation of micro-milling cutting forces. J. Mater. Process. Technol. 2010, 210, 2154–2162. [Google Scholar] [CrossRef]
- Afazov, S.M.; Zdebski, D.; Ratchev, S.M.; Segal, J.; Liu, S. Effects of micro-milling conditions on the cutting forces and process stability. J. Mater. Process. Technol. 2013, 213, 671–684. [Google Scholar] [CrossRef]
- Jin, X.; Altintas, Y. Prediction of micro-milling forces with finite element method. J. Mater. Process. Technol. 2012, 212, 542–552. [Google Scholar] [CrossRef]
- Lai, X.M.; Li, H.T.; Li, C.F.; Lin, Z.Q.; Ni, J. Modeling and analysis of micro scale milling considering size effect, micro cutter edge radius and minimum chip thickness. Int. J. Mach. Tools Manuf. 2008, 48, 1–14. [Google Scholar] [CrossRef]
- Jin, X.; Altintas, Y. Slip-line field model of micro-cutting process with round tool edge effect. J. Mater. Process. Technol. 2011, 211, 339–355. [Google Scholar] [CrossRef]
- Karpat, Y. Investigation of the effect of cutting tool edge radius on material separation due to ductile fracture in machining. Int. J. Mech. Sci. 2009, 51, 541–546. [Google Scholar] [CrossRef]
- Liu, K.; Melkote, S. Finite element analysis of the influence of tool edge radius on size effect in orthogonal micro-cutting process. Int. J. Mech. Sci. 2007, 49, 650–660. [Google Scholar] [CrossRef]
- Liu, K.; Melkote, S. Material strengthening mechanisms and their contribution to size effect in micro-cutting. J. Manuf. Sci. Eng. 2006, 128, 730–738. [Google Scholar] [CrossRef]
- Ding, H.; Shen, N.; Shin, Y.C. Experimental evaluation and modeling analysis of micromilling of hardened H13 tool steels. J. Manuf. Sci. Eng. 2011, 133, 041007. [Google Scholar] [CrossRef]
- Zhou, Y.; Tian, Y.; Jing, X.; Ehmann, K.F. A novel instantaneous uncut chip thickness model for mechanistic cutting force model in micro-end-milling. Int. J. Adv. Manuf. Technol. 2017, 93, 2305–2319. [Google Scholar] [CrossRef]
- Luo, S.; Jun, M.B.G.; Dong, Z. Numerical Simulation of Chip Ploughing Volume and Forces in 5-axis CNC Micro-milling Using Flat-end Mills. Procedia Manuf. 2016, 5, 348–361. [Google Scholar] [CrossRef]
- Bao, W.Y.; Tansel, I.N. Modeling micro-end-milling operations. Part I: Analytical cutting force model. Int. J. Mach. Tools Manuf. 2000, 40, 2155–2173. [Google Scholar] [CrossRef]
- Li, H.Z.; Liu, K.; Li, X.P. A new method for determining the undeformed chip thickness in milling. J. Mater. Process. Technol. 2001, 113, 378–384. [Google Scholar] [CrossRef]
- Perez, H.; Vizan, A.; Hernandez, J.C.; Guzman, M. Estimation of cutting forces in micromilling through the determination of specific cutting pressures. J. Mater. Process. Technol. 2007, 190, 18–22. [Google Scholar] [CrossRef]
- Urbikain, G.; Artetxe, E.; López de Lacalle, L.N. Numerical simulation of milling forces with barrel-shaped tools considering runout and tool inclination angles. Appl. Math. Model. 2017, 47, 619–636. [Google Scholar] [CrossRef]
- Zhu, K.; Zhang, Y. Modeling of the instantaneous milling force per tooth with tool run-out effect in high speed ball-end milling. Int. J. Mach. Tools Manuf. 2017, 118–119, 37–48. [Google Scholar] [CrossRef]
- Zhu, Z.; Yan, R.; Peng, F.; Duan, X.; Zhou, L.; Song, K.; Guo, C. Parametric chip thickness model based cutting forces estimation considering cutter runout of five-axis general end milling. Int. J. Mach. Tools Manuf. 2016, 101, 35–51. [Google Scholar] [CrossRef]
- Omar, O.E.E.K.; El-Wardany, T.; Ng, E.; Elbestawi, M.A. An improved cutting force and surface topography prediction model in end milling. Int. J. Mach. Tools Manuf. 2007, 47, 1263–1275. [Google Scholar] [CrossRef]
- Sastry, S.; Kapoor, S.G.; DeVor, R.E. Compensation of progressive radial run-out in face-milling by spindle speed variation. Int. J. Mach. Tools Manuf. 2000, 40, 1121–1139. [Google Scholar] [CrossRef]
- Desai, K.; Agarwal, P.K.; Rao, P.V.M. Process geometry modelling with cutter runout for milling ofcurved surfaces. Int. J. Mach. Tools Manuf. 2009, 49, 1015–1028. [Google Scholar] [CrossRef]
- Moges, T.M.; Desai, K.A.; Rao, P.V.M. Improved Process Geometry Model with Cutter Runout and Elastic Recovery in Micro-End Milling. Procedia Manuf. 2016, 5, 478–494. [Google Scholar] [CrossRef]
- Rodríguez, P.; Labarga, J.E. A new model for the prediction of cutting forces in micro-end-milling operations. J. Mater. Process. Technol. 2013, 213, 261–268. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Matuszak, M.; Powałka, B.; Madajewski, M.; Maruda, R.W.; Królczyk, G.M. Prediction of cutting forces during micro end milling considering chip thickness accumulation. Int. J. Mach. Tools Manuf. 2019, 147, 103466. [Google Scholar] [CrossRef]
- Sutherland, J.W.; DeVor, R.E. Improved method for cutting force and surface error prediction in flexible end milling systems. J. Eng. Ind. 1986, 108, 269–279. [Google Scholar] [CrossRef]
- Jun, B.G.; DeVor, R.E.; Kapoor, S.G. Investigation of the Dynamics of Micro end Milling. Part II: Model Validation and Interpretation. J. Manuf. Sci. Eng. 2006, 128, 901–912. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y. Modeling and avoidance of static deformations in peripheral milling of plates. Int. J. Mach. Tool Des. Res. 1995, 35, 459–476. [Google Scholar] [CrossRef]
- Kops, L.; Vo, D.T. Determination of the equivalent diameter of an endmill based on its compliance. Ann. CIRP 1990, 39, 93–96. [Google Scholar] [CrossRef]
- Kivanc, E.; Budak, E. Structural modeling of end mills for form error and stability analysis. Int. J. Mach. Tools Manuf. 2004, 44, 1151–1161. [Google Scholar] [CrossRef]
- Kim, G.M.; Kim, B.H.; Chu, C.N. Estimation of cutter deflection and form error in ball-end milling processes. Int. J. Mach. Tools Manuf. 2003, 43, 917–924. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Lamikiz, A.; Sanchez, J.A.; Salgado, M.A. Effects of tool deflection in the high-speed milling of inclined surfaces. Int. J. Adv. Manuf. Technol. 2004, 24, 621–631. [Google Scholar] [CrossRef]
- Graham, E.; Mehrpouya, M.; Park, S.S. Robust prediction of chatter stability in milling based on the analytical chatter stability. J. Manuf. Process. 2013, 15, 508–517. [Google Scholar] [CrossRef]
- Insperger, T.; Gradisek, J.; Kalveram, M.; Stepan, G.; Winert, K.; Govekar, E. Machine Tool Chatter and Surface Location Error in Milling Processes. J. Manuf. Sci. Eng. 2006, 128, 913–920. [Google Scholar] [CrossRef]
- Park, S.S.; Rahnama, R. Robust chatter stability in micro-milling operations. CIRP Ann.—Manuf. Technol. 2010, 59, 391–394. [Google Scholar] [CrossRef]
- Wang, J.J.; Uhlmann, E.; Oberschmidt, D.; Sung, C.F.; Perfilov, I. Critical depth of cut and asymptotic spindle speed for chatter in micro milling with process damping. CIRP Ann.—Manuf. Technol. 2016, 65, 113–116. [Google Scholar] [CrossRef]
- Rahnama, R.; Sajjadi, M.; Park, S.S. Suppression of Chatter in Micro Milling with Process Damping. J. Mater. Process. Technol. 2009, 209, 5766–5776. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Tabaszewski, M.; Krolczyk, G.M.; Maruda, R.W. The study on dynamic properties of monolithic ball end mills with various slenderness. E3S Web Conf. 2017, 19, 03014. [Google Scholar] [CrossRef]
- Graham, E.; Mehrpouya, M.; Nagamune, R.; Park, S.S. Robust prediction of chatter stability in micro milling comparing edge theorem and LMI. CIRP J. Manuf. Sci. Technol. 2014, 7, 29–39. [Google Scholar] [CrossRef]
- Park, S.S.; Altintas, Y.; Movahhedy, M. Receptance coupling for endmills. Int. J. Mach. Tools Manuf. 2003, 43, 889–896. [Google Scholar] [CrossRef]
- Eynian, M. Prediction of vibration frequencies in milling using modified Nyquist method. CIRP J. Manuf. Sci. Technol. 2015, 11, 73–81. [Google Scholar] [CrossRef]
- Yılmaz, E.E.; Budak, E.; Özgüven, H.N. Modeling and Measurement of Micro End Mill Dynamics Using Inverse Stability Approach. Procedia CIRP 2016, 46, 242–245. [Google Scholar] [CrossRef]
- Uhlmann, E.; Mahr, F. A Time Domain Simulation Approach for Micro Milling Processes. Procedia CIRP 2012, 4, 22–28. [Google Scholar] [CrossRef]
- Yuan, M.; Wang, X.; Jiao, L.; Yi, J.; Liu, S. Prediction of dimension error based on the deflection of cutting tool in micro ball-end milling. Int. J. Adv. Manuf. Technol. 2017, 93, 825–837. [Google Scholar] [CrossRef]
- Mamedov, A.; Layegh, K.S.E.; Lazoglu, I. Machining forces and tool deflections in micro milling. Procedia CIRP 2013, 8, 147–151. [Google Scholar] [CrossRef]
- Matuszak, M.; Kochmański, P.; Powałka, B. Workpiece Grain Size Influence on the Vibration in Micro-milling. In Modern Methods of Construction Design; Lecture Notes in Mechanical, Engineering; Ševĉik, L., Lepšík, P., Petrů, M., Mašín, I., Martonka, R., Eds.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Mittal, R.K.; Kulkarni, S.S.; Singh, R.K. Effect of lubrication on machining response and dynamic instability in high-speed micromilling of Ti-6Al-4V. J. Manuf. Process. 2017, 28, 413–421. [Google Scholar] [CrossRef]
- Altintas, Y.; Weck, M. Chatter Stability of Metal Cutting and Grinding. Ann. CIRP 2004, 53, 619–642. [Google Scholar] [CrossRef]
- Opitz, H. Investigation and calculation of the chatter behavior of lathes and milling machines. Ann. CIRP 1970, 18, 335–343. [Google Scholar]
- Tlusty, J. Manufacturing Processes and Equipment; Prentice Hall: New York, NY, USA, 2000. [Google Scholar]
- Jorgensen, B.R.; Shin, Y.C. Dynamics of spindle bearing systems at high speeds including cutting load effects. J. Manuf. Sci. Eng. 1998, 120, 387–394. [Google Scholar] [CrossRef]
- Movahhedy, M.R.; Mosaddegh, P. Prediction of chatter in high speed milling including gyroscopic effects. Int. J. Mach. Tools Manuf. 2006, 46, 996–1001. [Google Scholar] [CrossRef]
- Altintas, Y.; Eynian, M.; Onozuka, H. Identification of Dynamic Cutting Force Coefficients and Chatter Stability with Process Damping. Ann. CIRP 2008, 57, 371–374. [Google Scholar] [CrossRef]
- Haung, C.Y.; Junz Wang, J.J. Mechanistic Modeling of Process damping in peripheral milling. ASME J. Manuf. Sci. Eng. 2007, 129, 12–20. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Mrozek, K. Mechanical and technological aspects of micro ball end milling with various tool inclinations. Int. J. Mech. Sci. 2017, 134, 424–435. [Google Scholar] [CrossRef]
- Cernohlavek, V.; Klimenda, F.; Houska, P.; Suszyński, M. Vibration Measurements on a Six-Axis Collaborative Robotic Arm—Part I. Sensors 2023, 23, 1629. [Google Scholar] [CrossRef] [PubMed]
- Meller, A.; Suszynski, M.; Legutko, S.; Trączyński, M.; Cernohlavek, V. Studies on a Robotised Process for Forging Steel Synchronizer Rings in the Context of Forging Tool Life. Manuf. Technol. 2023, 23, 88–98. [Google Scholar] [CrossRef]
- Klimenda, F.; Cizek, R.; Suszyński, M. Measurement of a Vibration on a Robotic Vehicle. Sensors 2022, 22, 8649. [Google Scholar] [CrossRef]
- Suszyński, M.; Wiśniewski, M.; Wojciechowicz, K.; Trączyński, M.; Butlewski, M.; Cernohlavek, V.; Talar, R. Study of Positioning Accuracy Parameters in Selected Configurations of a Modular Industrial Robot—Part 1. Sensors 2025, 25, 108. [Google Scholar] [CrossRef]
- Cen, L.; Melkote, S.N. Effect of Robot Dynamics on the Machining Forces in Robotic Milling. Procedia Manuf. 2017, 10, 486–496. [Google Scholar] [CrossRef]
- Cvitanic, T.; Nguyen, V.; Melkote, S.N. Pose Optimization in Robotic Machining Using Static and Dynamic Stiffness Models. Robot. Comput.-Integr. Manuf. 2020, 66, 101992. [Google Scholar] [CrossRef]
- Diaz Posada, J.R.; Schneider, U.; Sridhar, A.; Verl, A. Automatic Motion Generation for Robotic Milling Optimizing Stiffness with Sample-Based Planning. Machines 2017, 5, 3. [Google Scholar] [CrossRef]
- Liao, Z.-Y.; Wang, Q.-H.; Xie, H.-L.; Li, J.-R.; Zhou, X.-F.; Pan, T.-H. Optimization of Robot Posture and Workpiece Setup in Robotic Milling with Stiffness Threshold. IEEE/ASME Trans. Mechatron. 2022, 27, 582–593. [Google Scholar] [CrossRef]
- Mun, C.H.; Rezvani, S.; Lee, J.; Park, S.; Park, H.W.; Lee, J. Indirect measurement of cutting forces during robotic milling using multiple sensors and a machine learning-based system identifier. J. Manuf. Process. 2022, 85, 963–976. [Google Scholar] [CrossRef]
- Bisu, C.-F.; Cherif, M.; Gérard, A.; K’Nevez, J.-Y. Dynamic Behavior Analysis for a Six-Axis Industrial Machining Robot. arXiv 2012, arXiv:1201.4443. [Google Scholar] [CrossRef]
- Leonesio, M.; Villagrossi, E.; Beschi, M.; Marini, A.; Bianchi, G.; Pedrocchi, N.; Molinari Tosatti, L.; Grechishnikov, V.; Ilyukhin, Y.; Isaev, A. Vibration analysis of robotic milling tasks. Procedia CIRP 2018, 67, 262–267. [Google Scholar] [CrossRef]
- Raparelli Sahu, G.N.; Otto, A.; Ihlenfeldt, S. Improving Robotic Milling Performance through Active Damping of Low-Frequency Structural Modes. J. Manuf. Mater. Process. 2024, 8, 160. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, H. Analysis and Suppression of Chatter in Robotic Machining Process. In Proceedings of the 2007 International Conference on Control, Automation and Systems (ICCAS), Seoul, Republic of Korea, 17–20 October 2007; pp. 595–600. [Google Scholar]
- Kenan Deng, Dong Gao, Chang Zhao, Yong Lu, Prediction of in-process frequency response function and chatter stability considering pose and feedrate in robotic milling. Robot. Comput.-Integr. Manuf. 2023, 82, 102548. [CrossRef]
- Rainsberger, R.B.; Fong, J.T.; Marcal, P.V. Effect of mesh quality in finite element analysis of crack-tip stresses in a circumferential surface crack of a pipe elbow weldment. In Proceedings of the ICF 2017—14th International Conference on Fracture, Rhodes, Greece, 18–23 June 2017; Volume 2, pp. 425–426. [Google Scholar]
- Zhuang, X.; Heaney, C.; Augarde, C. On error control in the element-free Galerkin method. Eng. Anal. Bound. Elem. 2012, 36, 351–360. [Google Scholar] [CrossRef]
- Dheeravongkit, A.; Shimada, K. Inverse adaptation of a Hex-dominant mesh for large deformation finite element analysis. CAD Comput. Aided Des. 2007, 39, 427–438. [Google Scholar] [CrossRef]
- Kannan, R.; Hendry, S.; Debney, P. What Is Your Structural Model Not Telling You? Finding Hidden Modelling Errors and Inaccuracies in Your Analysis Results. In Structures Congress 2018: Buildings and Disaster Management, Proceedings of the Structures Congress 2018, Fort Worth, TX, USA, 19–21 April 2018; Structural Engineering Institute of ASCE: Reston, VA, USA, 2018; p. 58. [Google Scholar]
- Navarro-Jiménez, J.M.; Nadal, E.; Ródenas, J.J. Recovery-based accuracy assessment of numerical analysis results in linear elasticity. A code for moving least squares recovery based on physics. Adv. Appl. Mech. 2025, 60, 179–200. [Google Scholar]
- Sankararaman, S.; Ling, Y.; Shantz, C.; Mahadevan, S. Fatigue crack growth analysis under uncertainty. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Orlando, FL, USA, 12–15 April 2010; 2010-2517. [Google Scholar]
- Wang, J.D.; Howard, I.M. Error analysis on finite element modeling of involute spur gears. J. Mech. Des. 2006, 128, 90–97. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wojciechowski, S.; Suszyński, M.; Talar, R.; Černohlávek, V.; Štěrba, J. Cutting Force—Vibration Interactions in Precise—and Micromilling Processes: A Critical Review on Prediction Methods. Materials 2025, 18, 3539. https://doi.org/10.3390/ma18153539
Wojciechowski S, Suszyński M, Talar R, Černohlávek V, Štěrba J. Cutting Force—Vibration Interactions in Precise—and Micromilling Processes: A Critical Review on Prediction Methods. Materials. 2025; 18(15):3539. https://doi.org/10.3390/ma18153539
Chicago/Turabian StyleWojciechowski, Szymon, Marcin Suszyński, Rafał Talar, Vit Černohlávek, and Jan Štěrba. 2025. "Cutting Force—Vibration Interactions in Precise—and Micromilling Processes: A Critical Review on Prediction Methods" Materials 18, no. 15: 3539. https://doi.org/10.3390/ma18153539
APA StyleWojciechowski, S., Suszyński, M., Talar, R., Černohlávek, V., & Štěrba, J. (2025). Cutting Force—Vibration Interactions in Precise—and Micromilling Processes: A Critical Review on Prediction Methods. Materials, 18(15), 3539. https://doi.org/10.3390/ma18153539