A New Design Methodology of Asphalt Mixture Dynamic Modulus Based on Pavement Response
Abstract
1. Introduction
2. Test Methods
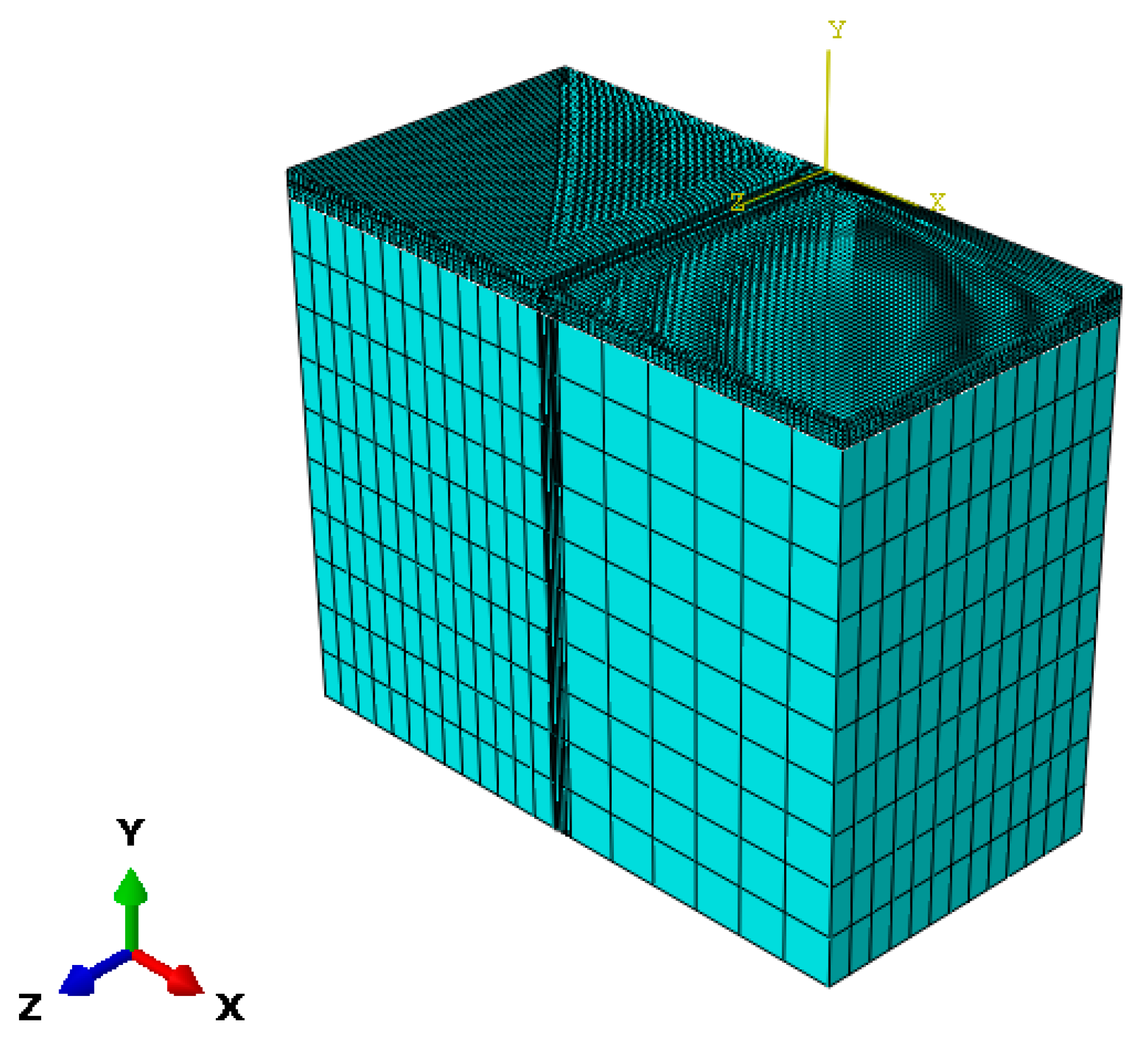
2.1. Establishment and Validation of Finite Element Models
2.1.1. Finite Element Models
2.1.2. Material Parameters of Pavement Structure
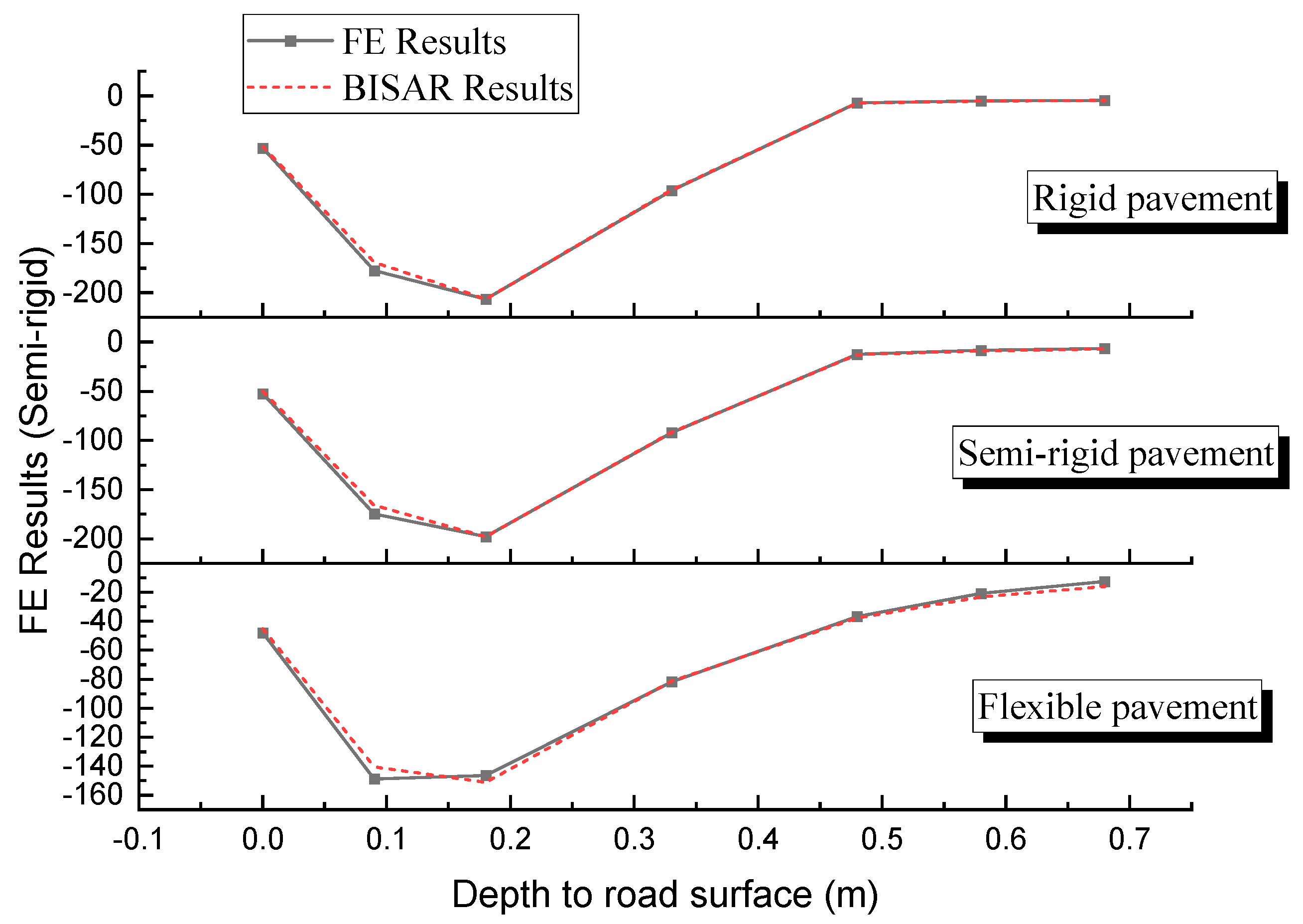
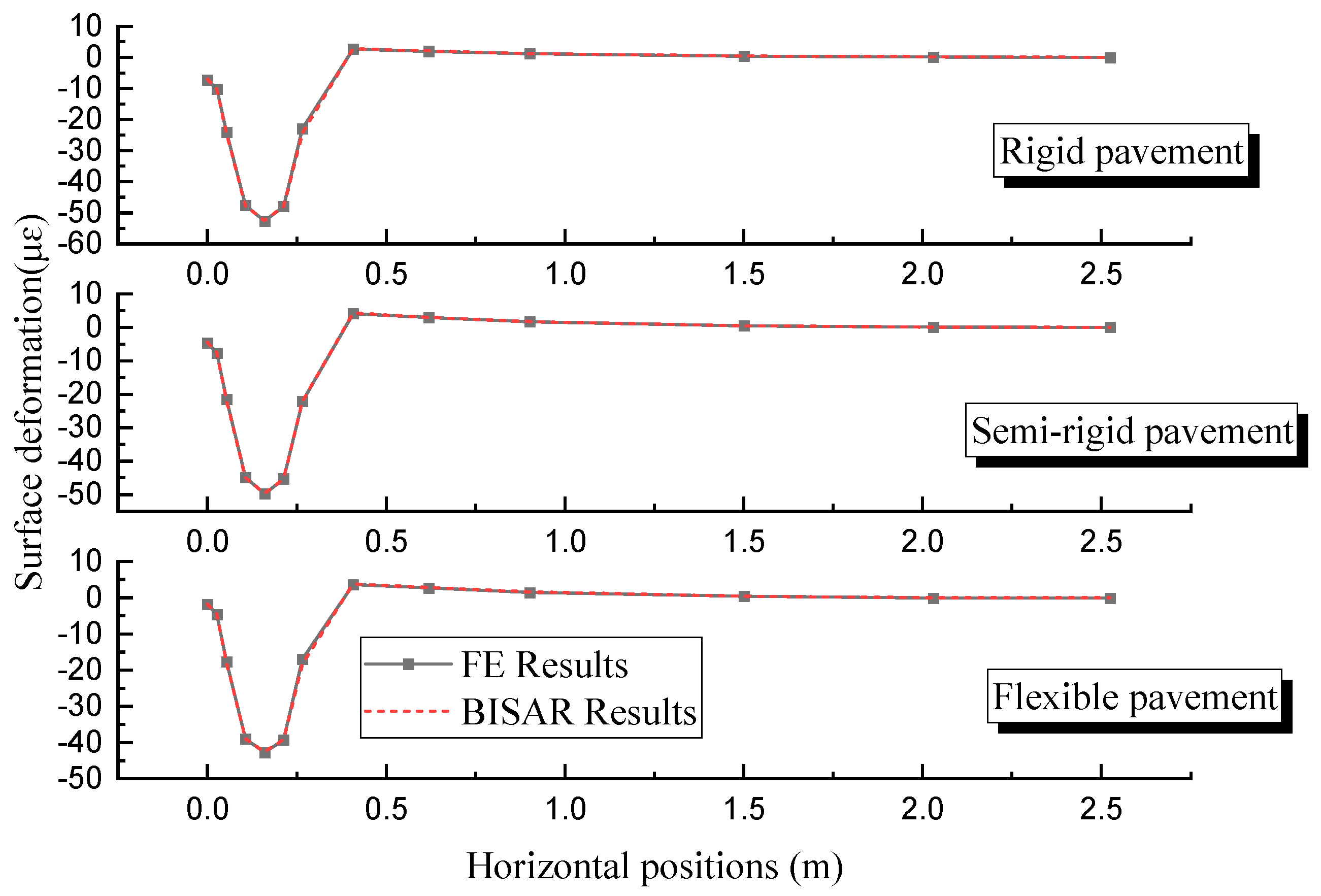
2.1.3. FE Model Verification
2.2. Structural Response of Pavements with Dynamic Modulus Principal Curve Parameters
2.2.1. Response Variables for Response Surface Methodology (RSM)
2.2.2. Statistical Experimental Design
2.3. Prediction of Structural Mechanical Responses Based on WOA-BP Neural Network
2.3.1. Database
2.3.2. Construction of WOA-BP Prediction Model
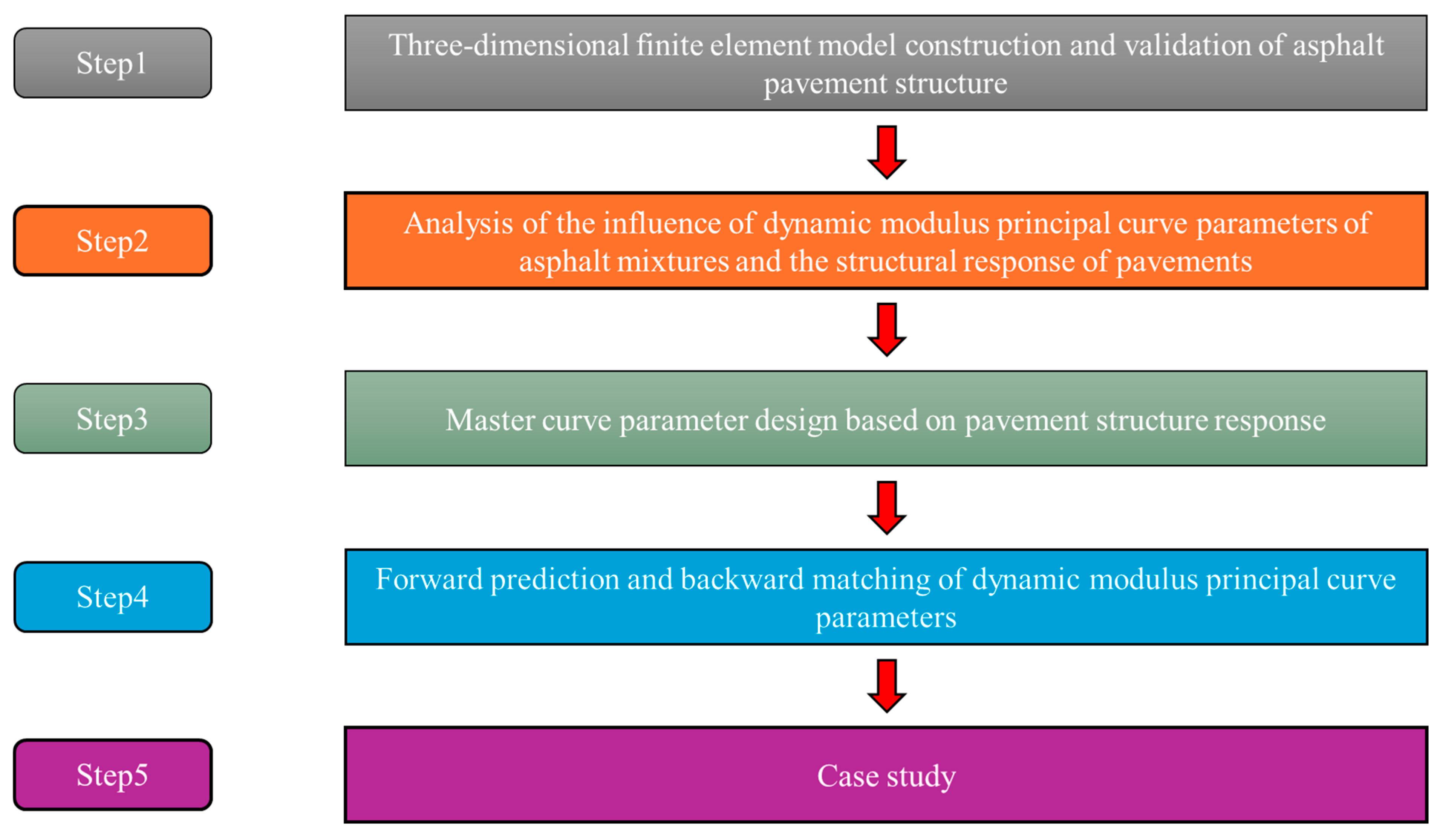
2.4. Design Method and Inverse Matching of Dynamic Modulus Master Curve Parameters
2.4.1. Design Method for Dynamic Modulus Master Curve Parameters
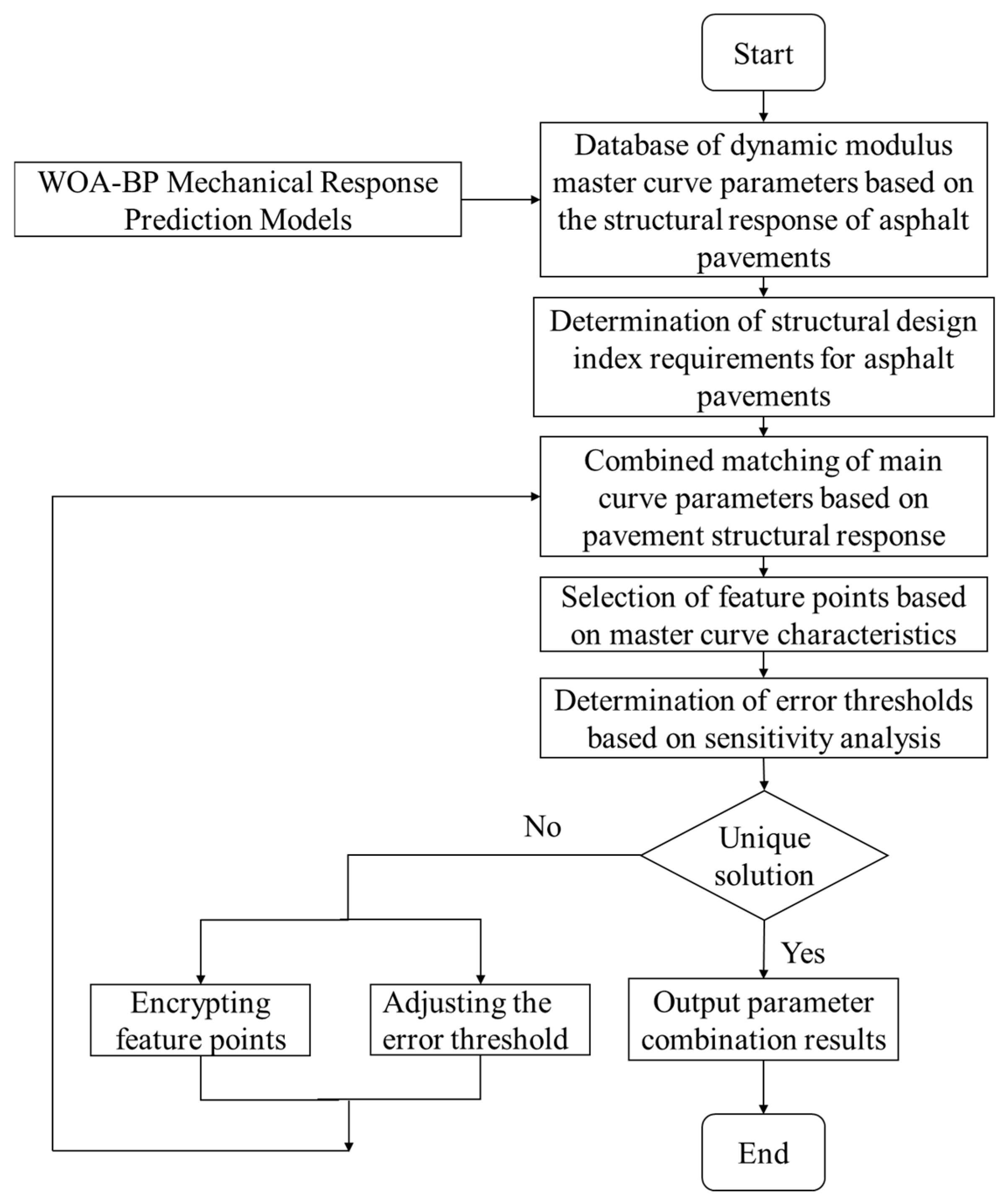
2.4.2. Inverse Matching for Dynamic Modulus Master Curve Parameters
- (1)
- Determine the query target: Based on the above analysis, identify the query target as the main curve parameter combination.
- (2)
- Write and execute the query statement: Based on the query target and SQL syntax, write the query statement. Input the query statement into the SQL database management system and execute the query. The query conditions involve mechanical response values, requiring basic query statements, conditional query statements, and grouping query statements.
- (3)
- Analyze the result set: Examine the result set obtained from the query, ensuring it contains the required data and that there are no duplicates or misinterpretations of the data.
2.5. Case Study
- (1)
- Establish various asphalt pavement structure finite element models, calculate initial data, and use the WOA-BP neural network mechanical response prediction model along with a MySQL database to establish a dynamic modulus master curve parameter database based on the asphalt pavement structure response, comprising a total of 100,000 entries.
- (2)
- Based on the critical pavement responses, strain at the bottom of the asphalt surface layer, tensile stress at the bottom of the base layer, and compressive strain at the top of the subgrade, conduct matching of main curve parameter combinations. Considering the geometric characteristics of the main curve and the results of parameter sensitivity analysis, reasonably select frequency conditions and error thresholds as query criteria. Write SQL query statements to search and match the main curve parameter combinations.
- (3)
- Determine whether step (2) can yield a unique set of dynamic modulus master curve parameters. If the matching result is unique, output the parameter combination result, and the solving process is completed. If the matching result is not unique, optimize the matching strategy using encryption filtering or adjusting error thresholds.
3. Results and Discussions
3.1. FE Model Verification Results and Analysis
3.2. Response Values for RSM
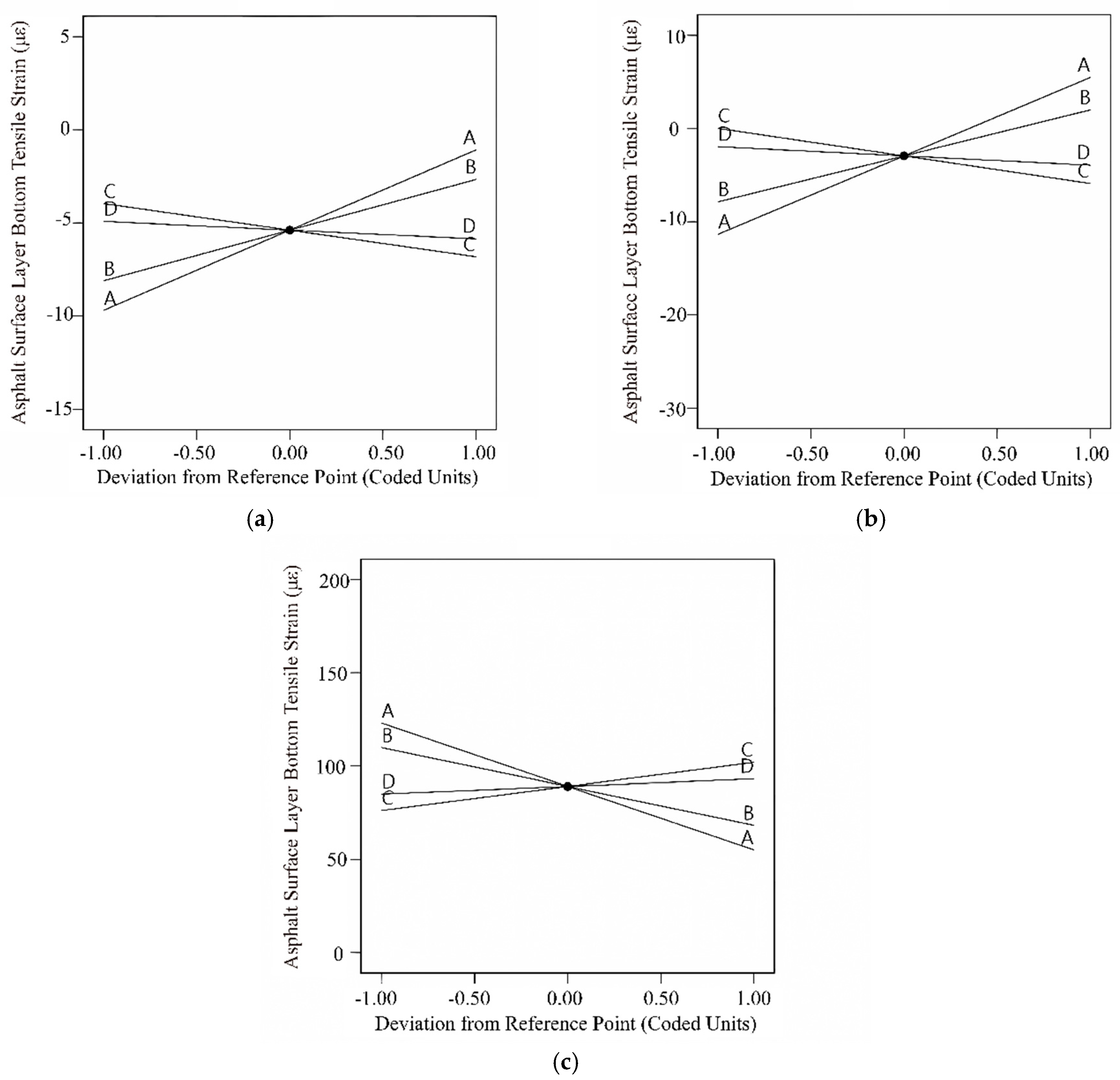
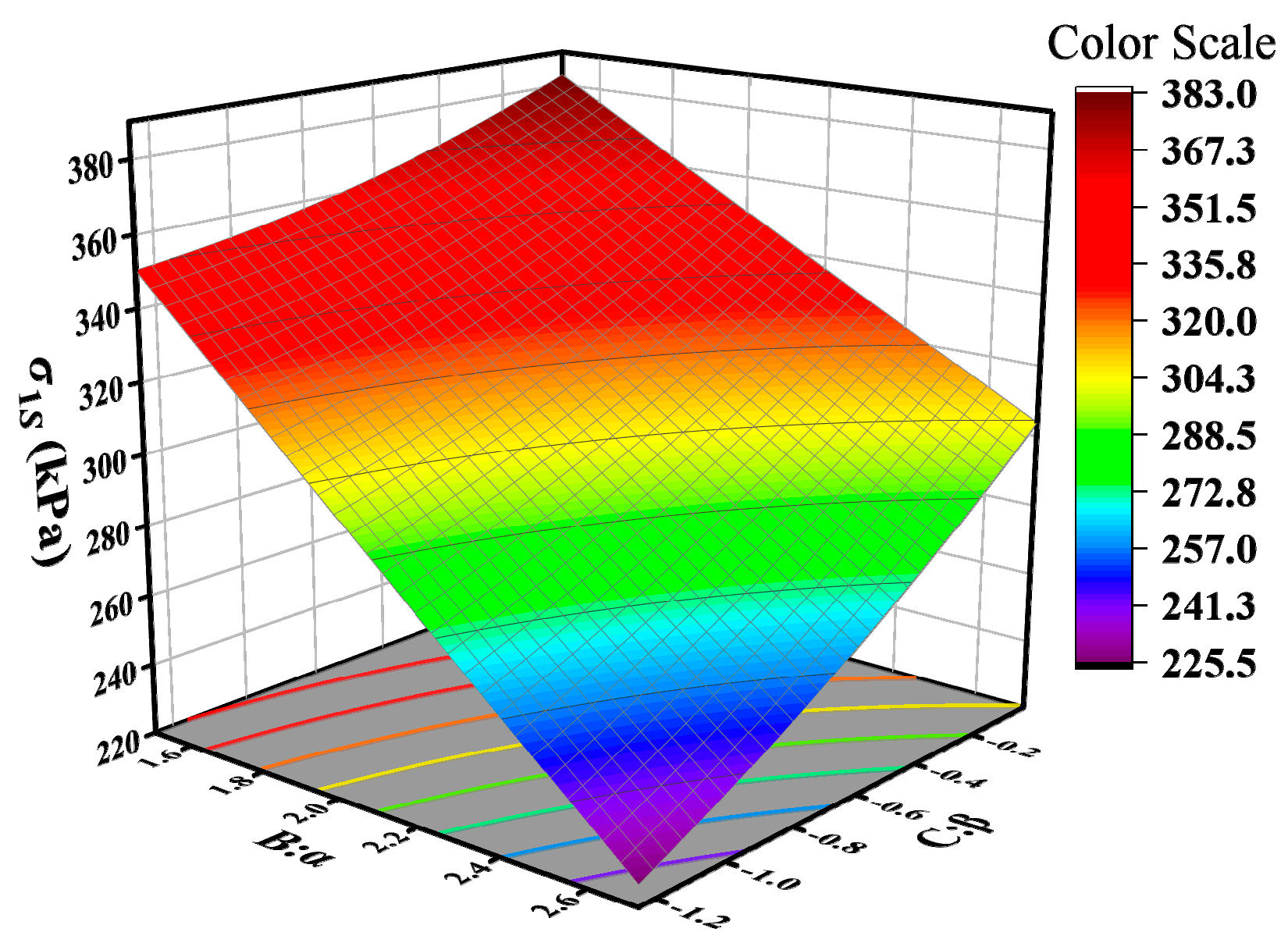
3.2.1. Tensile Strain at the Bottom of the Asphalt Surface Layer
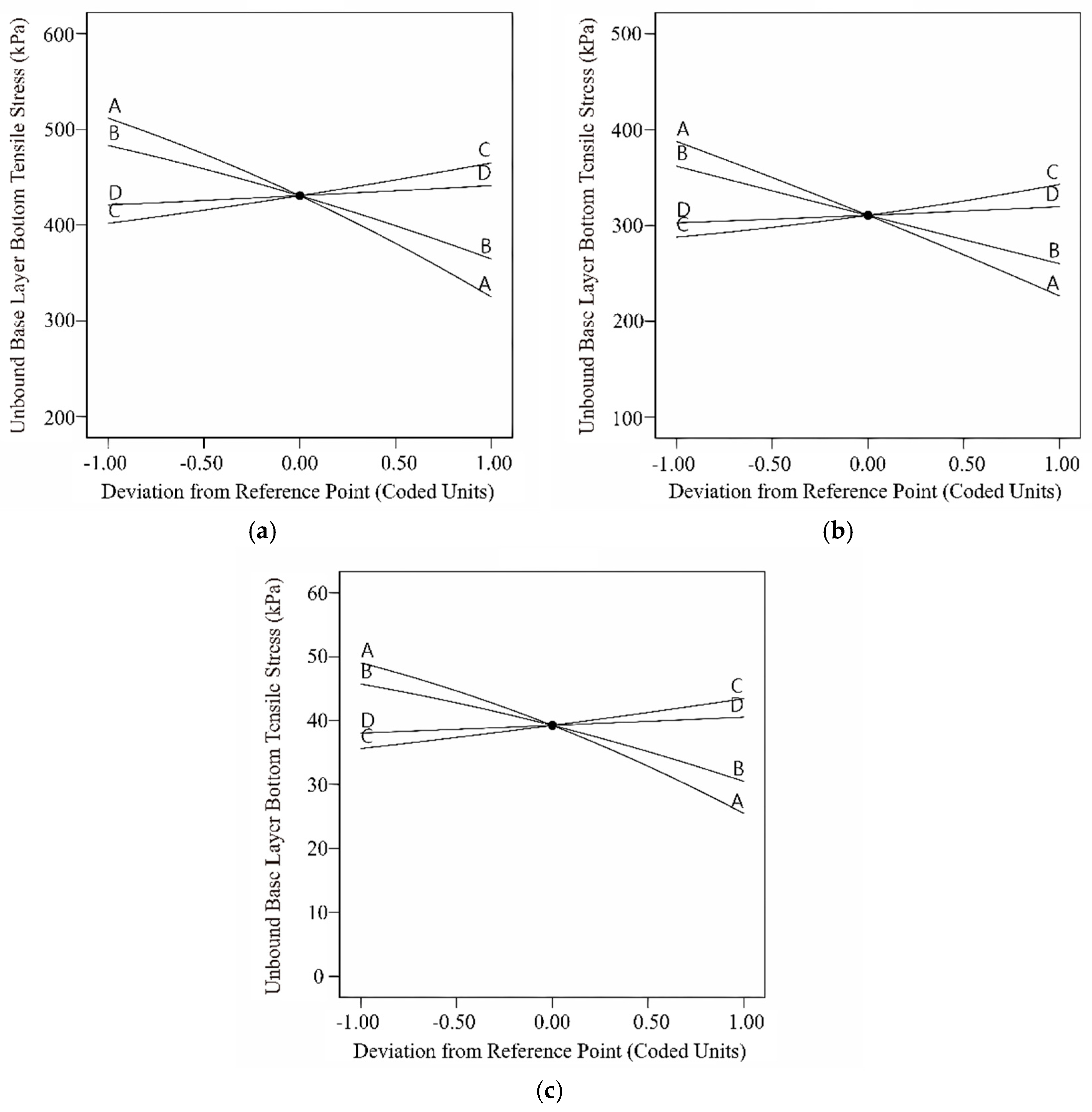
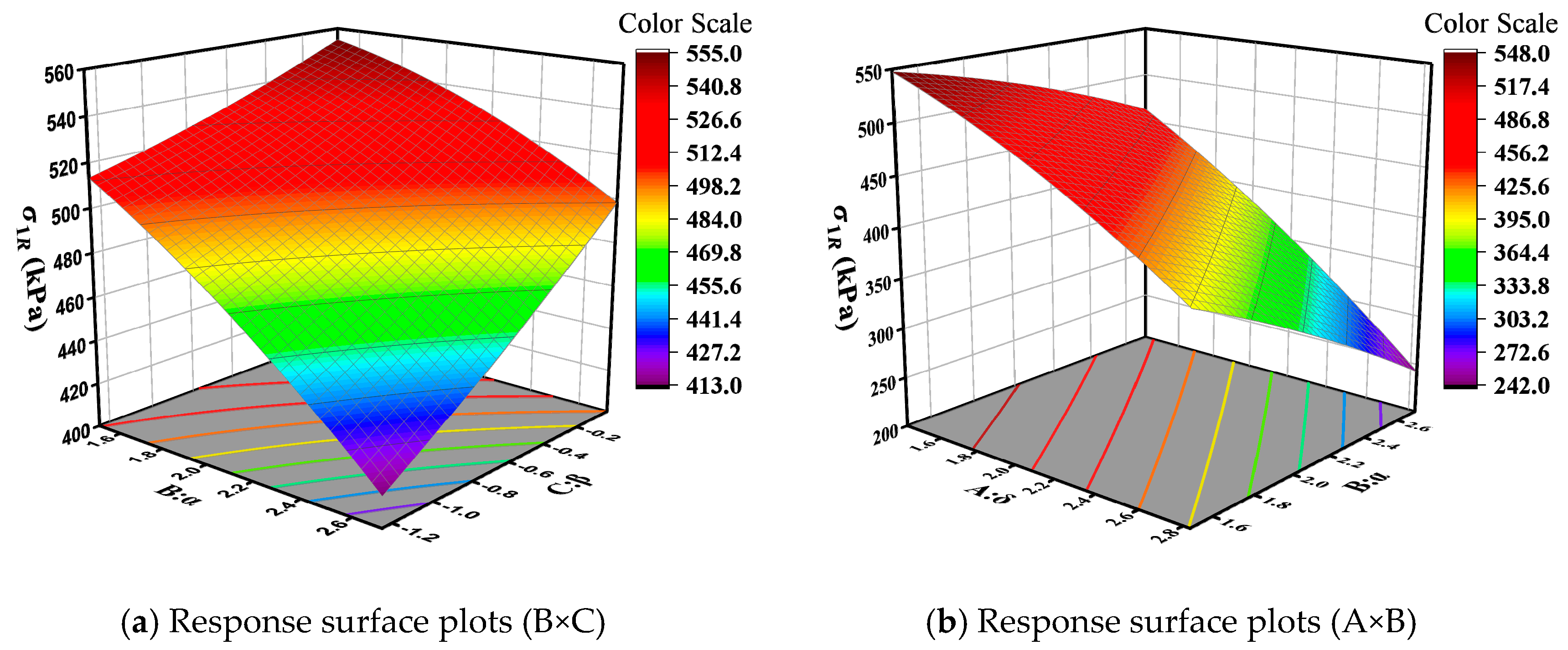
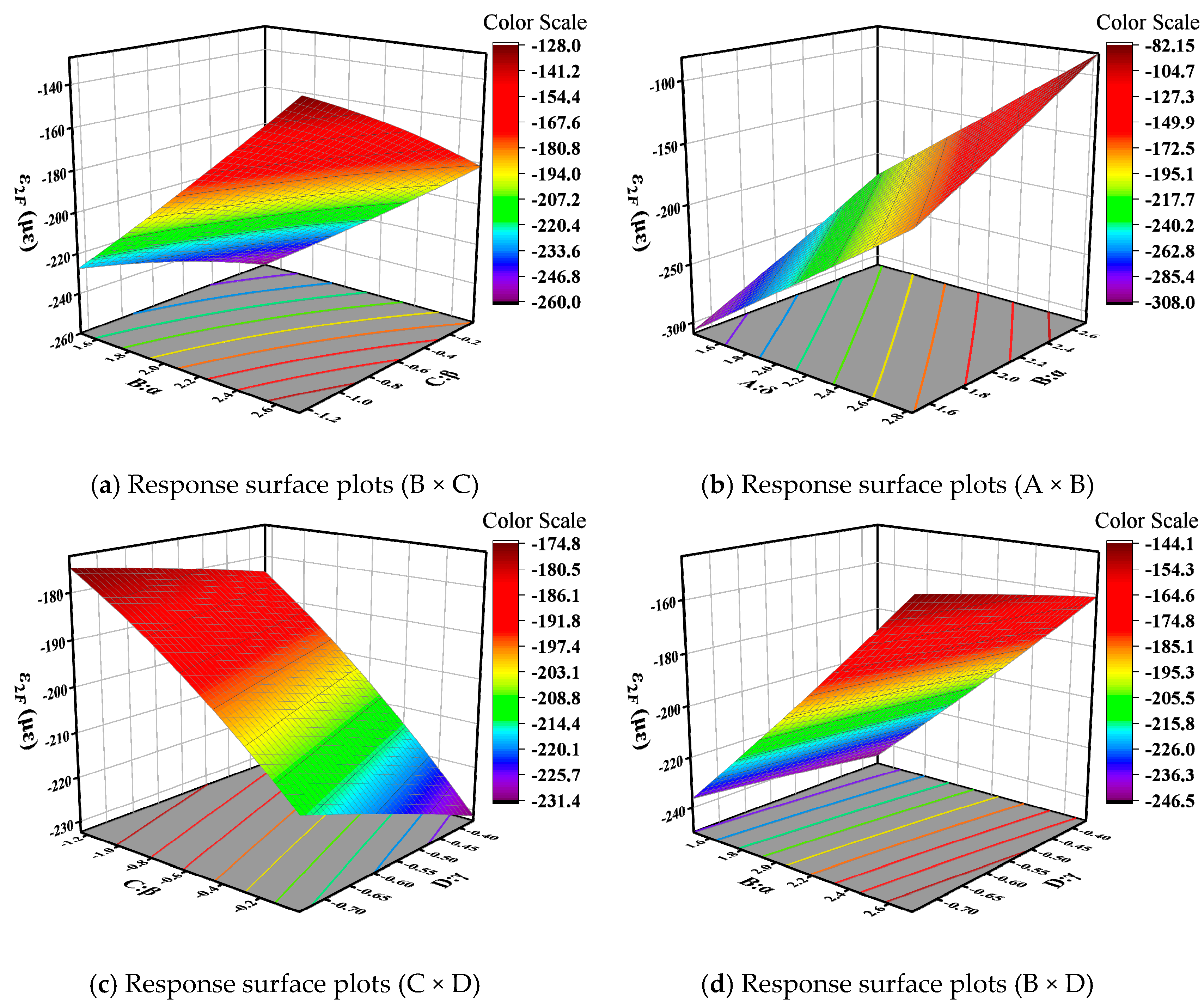
3.2.2. Tensile Stress at the Base of the Subgrade Layer
3.2.3. Vertical Compressive Strain at Top Surface of Roadbed
3.2.4. Sensitivity Analysis
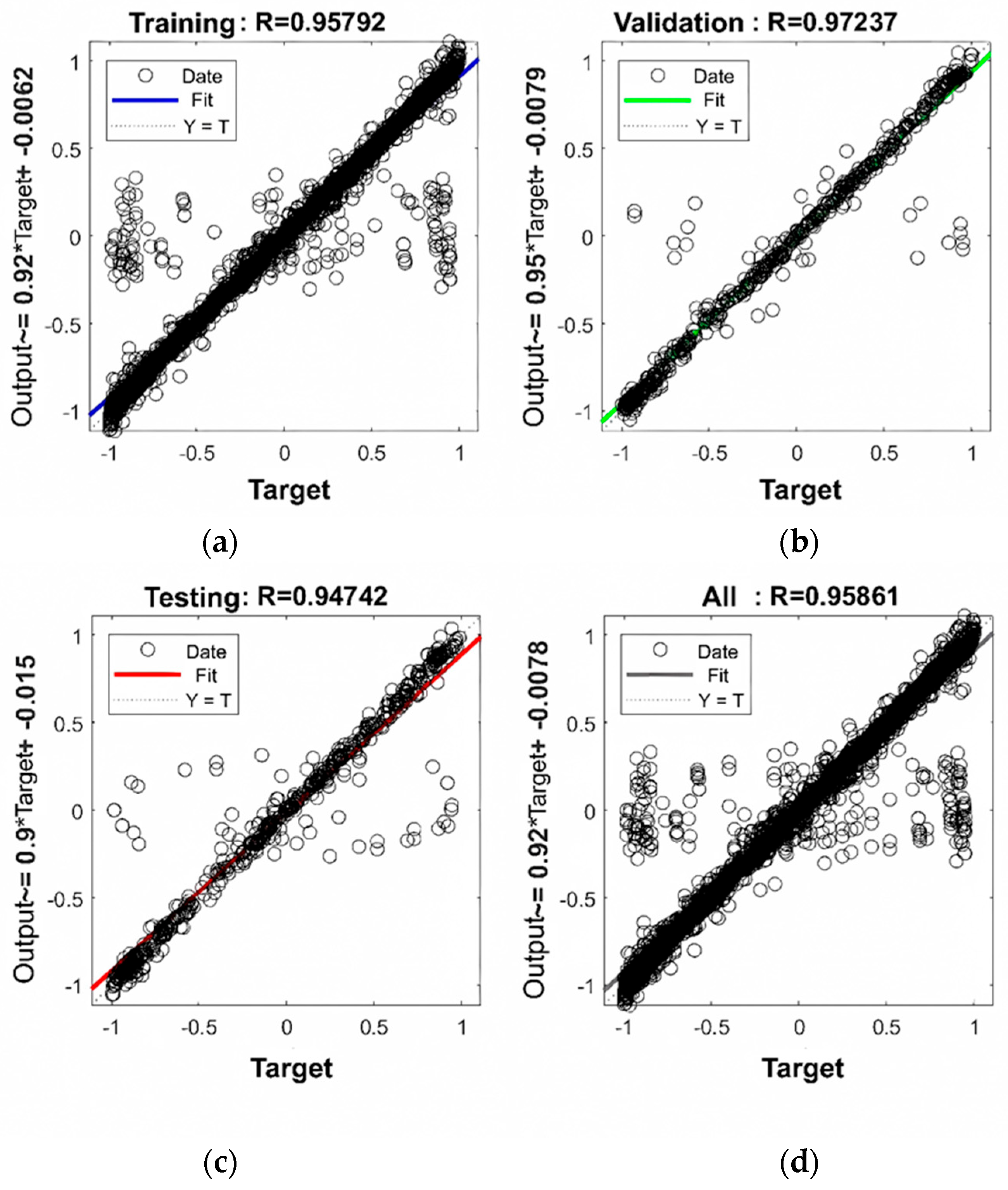
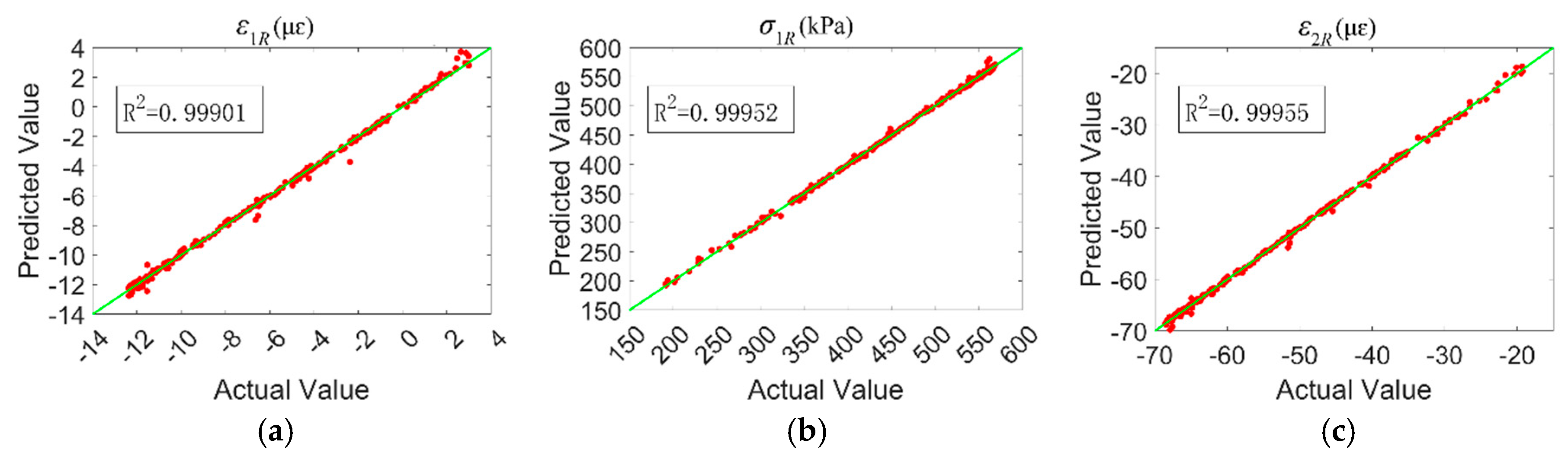
3.3. Results and Analysis of Structural Mechanical Response Prediction Based on WOA-BP Neural Network
3.4. Case Study Results and Analysis
- (1)
- Database establishment
- (2)
- Determine matching criteria and solution objectives
- (3)
- Parameter combination matching based on pavement structure response
4. Conclusions
- (1)
- The effects of individual asphalt mixture main curve parameters and their interactions on critical pavement responses were dependent on pavement structures. In general, parameter δ had the greatest effect on the response of each structure, followed by α, and β and γ had smaller effects. The interaction between the parameters also has a certain effect on the pavement structure response, i.e., tensile stresses at the bottom of the base.
- (2)
- The asphalt pavement structural mechanical response prediction model was successfully established based on the BP neural network, improved by the whale algorithm.
- (3)
- With the help of the WOA-BP neural network mechanical response prediction model, a MySQL mechanical response database was established. The methodology for determining the dynamic modulus master curve parameter based on the critical response of pavement was proposed.
- (4)
- In the future, a larger database with more pavement types will be built in line with long-term performance observations to consistently improve the accuracy of the model. Also, more attention will be paid to building relations between the dynamic modulus master curve parameters and the asphalt mixture characteristics.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, K.-W.; Zhang, H.-W.; Quan, W.-W.; Ma, X.; Dong, Z. Optimization of Design Indicators and Exploration of Reasonable Thickness of Asphalt Pavement Structure. J. Highw. Transp. Res. 2022, 39, 9–16. [Google Scholar]
- Yu, M.; Zhao, X.-N.; Chen, H.-F.; Kong, L.; Wu, C. Study on Viscoelasticity of Crumb Rubber Modified Asphalt Mixture. J. Highw. Transp. Res. 2023, 40, 1–7. [Google Scholar]
- Zhou, Z.-G.; Zhou, Y.; Liu, Z.-R. Analysis of Influencing Factors on Dynamic Modulus of Porous Asphalt. Mater. Rep. 2022, 36, 121–127. [Google Scholar]
- Witczak, M.W.; Fonseca, O.A. Revised Predictive Model for Dynamic (Complex) Modulus of Asphalt Mixtures. Transp. Res. Rec. 1996, 1540, 15–23. [Google Scholar] [CrossRef]
- Liu, F.; Wu, C.-H.; Xu, X.-Q.; Rao, Z.-J. Difference Analysis of Mechanical Properties of Asphalt Pavement Structures under Static Modulus and Dynamic Modulus. Highway 2023, 68, 68–74. [Google Scholar]
- Fan, Z.-H.; Tang, G.-X.; Deng, H.-G.; Chang, M.-F.; Liu, H.-J.; Zhu, L. Research on Dynamic Modulus Master Curve of Gneiss-Modified Asphalt Mixture based on Time-Temperature Equivalence Principle. Highway 2022, 67, 41–46. [Google Scholar]
- JTG D50-2017; Specifications for Highway Design of Asphalt Pavement. People’s Communication Press: Beijing, China, 2017.
- Huang, Y.; Liu, Z.H.; Liu, L.; Zhang, J.; Li, S.; Zhang, Y. Nonlinear behavior of unbound granular layer in asphalt pavement structure. J. Cent. South Univ. (Sci. Technol.) 2022, 53, 665–676. [Google Scholar]
- Huang, Y.; Wang, X.; Liu, Z.; Li, S. Dynamic modulus test and master curve analysis of asphalt mix with trapezoid beam method. Road Mater. Pavement Des. 2017, 18, 281–291. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Z.-H.; Wang, X.-D.; Li, S. Comparison of HMA dynamic modulus between trapezoid beam test and SPT. J. Cent. South Univ. (Sci. Technol.) 2017, 48, 3093–3099. [Google Scholar]
- Liu, H.; Luo, R. Development of master curve models complying with linear viscoelastic theory for complex moduli of asphalt mixtures with improved accuracy. Constr. Build. Mater. 2017, 152, 259–268. [Google Scholar] [CrossRef]
- Vestena, P.M.; Schuster, S.L.; Almeida, P.O.B.D., Jr.; Faccin, C.; Specht, L.P.; da Silva Pereira, D. Dynamic modulus master curve construction of asphalt mixtures: Error analysis in different models and field scenarios. Constr. Build. Mater. 2021, 301, 124343. [Google Scholar] [CrossRef]
- Jiang, Y.-J.; Yi, Y.; Tian, T.; Hang, Y.; Fan, J. Investigation on viscoelastic properties and temperature effects of super large particle size asphalt mixture. J. Build. Mater. 2023, 1–11. [Google Scholar]
- Alghrafy, Y.; El-Badawy, S.; Abd Alla, E.-S.M. A Comparative Study of Different Complex Shear Modulus Master Curve Techniques for Sulfur Extended Asphalt Modified with Recycled Polyethylene Waste. Int. J. Pavement Res. Technol. 2021, 15, 1023–1050. [Google Scholar] [CrossRef]
- Solatifar, N.; Kavussi, A.; Abbasghorbani, M.; Sivilevičius, H. Application of FWD data in developing dynamic modulus master curves of in-service asphalt layers. J. Civ. Eng. Manag. 2017, 23, 661–671. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, L.; Li, C.; Xing, Y. Predict the Phase Angle Master Curve and Study the Viscoelastic Properties of Warm Mix Crumb Rubber-Modified Asphalt Mixture. Materials 2020, 13, 5051. [Google Scholar] [CrossRef]
- Tan, Y.-Q.; Lu, H.-J.; Xu, H.-N. Application Prospect of Material Genetics Idea in Asphalt Pavement Materials. Transp. Res. 2020, 6, 2–12. [Google Scholar]
- Wang, E.-L.; Tian, Y.; Liu, X.-C.; Ren, Z.; Hu, S.; Yu, J.; Liu, C.; Li, Y. Prediction Model of Compressive Strength of Ultra Low Temperature Frozen Soil Based On WOA-BP Neural Network. Chin. J. Theor. Appl. Mech. 2022, 54, 1145–1153. [Google Scholar]
- Zha, X.-D.; Wang, B.-G. Back calculation of pavement layer moduli based on artificial neural networks. J. Traffic Transp. Eng. 2002, 02, 12–15. [Google Scholar]
- Zhang, J.-H.; Fan, H.-S.; Zhang, S.-P.; Jie, L. Analytical Solution for the Dynamic Responses and Parameter Inversion of Pavement Structures Considering the Condition of Interlayer Contact. China J. Highw. Transp. 2021, 34, 11–23. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yang, Y.; Zou, L.; Cao, X.; Yang, X.; Sun, Y. A modified Manson-Halford model based on improved WOA for fatigue life prediction under multi-level loading. Int. J. Damage Mech. 2024, 33, 774–807. [Google Scholar] [CrossRef]
- Huang, M.; Wan, Z.; Cheng, X.; Xu, Z.; Lei, Y.; Pan, D. Two-stage damage identification method based on fractal theory and whale optimization algorithm. Adv. Struct. Eng. 2022, 25, 2364–2381. [Google Scholar] [CrossRef]
- Dehcheshmeh, M.M.; Hosseinzadeh, A.Z.; Amiri, G.G. Feasibility study on model-based damage detection in shear frames using pseudo modal strain energy. Smart Struct. Syst. 2020, 25, 47–56. [Google Scholar]
- Chen, Z.X.; Yu, L. A novel WOA-based structural damage identification using weighted modal data and flexibility assurance criterion. Struct. Eng. Mech. 2020, 75, 445–454. [Google Scholar]
- Chen, H.L.; Yang, C.J.; Heidari, A.A. An efficient double adaptive random spare reinforced whale optimization algorithm. Expert Syst. Appl. 2020, 154, 113018. [Google Scholar] [CrossRef]
- Wang, B.; Gao, D.; Gu, H.; Ding, M.; Wu, Z. Guided Wave Based Composite Structural Fatigue Damage Monitoring Utilizing the WOA-BP Neural Network. Comput. Mater. Contin. 2025, 83, 455–473. [Google Scholar] [CrossRef]
- Zhuo, Y.-C.; Zhang, J.-X.; Zhang, Y.-G. Study on Dynamic Modulus of Different Asphalt Mixtures and its Relation with Pavement Performance. J. China Foreign Highw. 2021, 41, 260–266. [Google Scholar]
- Chen, H.; Hoff, I.; Liu, G.; Zhang, X.; Barbieri, D.M.; Wang, F.; Liu, J. Development of finite element model based on indirect tensile test for various asphalt mixtures. Constr. Build. Mater. 2023, 394, 132085. [Google Scholar] [CrossRef]
- Luo, M.; Chen, C.; Wang, T. The dynamic modulus of three kinds of AC-20 asphalt mixture and its main curve fitting and analysis. J. Chang. Univ. Sci. Technol. (Nat. Sci.) 2018, 15, 30–35+78. [Google Scholar]
- Zhang, X.; Chen, H.; Sara, R.G.; Hannasvik, L.T. Lateral and longitudinal variations in dynamic modulus of asphalt pavement: Surface layer and base layer. Constr. Build. Mater. 2023, 381, 131304. [Google Scholar] [CrossRef]
- Zheng, G.; Zhang, N.; Wang, P.; Lv, S. Study on the characterization method of dynamic modulus for asphalt mixture under multi-factor coupling conditions. Constr. Build. Mater. 2024, 421, 135758. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Tang, J.M.; Liu, H. Construction of triaxial dynamic modulus master curve for asphalt mixtures. Constr. Build. Mater. 2012, 37, 21–26. [Google Scholar] [CrossRef]
- Luo, R.; Liu, H. Improving the accuracy of dynamic modulus master curves of asphalt mixtures constructed using uniaxial compressive creep tests. J. Mater. Civ. Eng. 2017, 29, 04017032. [Google Scholar] [CrossRef]
- Wang, H.; Li, M.; Szary, P.; Hu, X. Structural assessment of asphalt pavement condition using back calculated modulus and field data. Constr. Build. Mater. 2019, 211, 943–951. [Google Scholar] [CrossRef]
- ASTM E2919-22; Standard Test Method for Evaluating the Performance of Systems that Measure Static, Six Degrees of Freedom (6DOF), Pose. ASTM: West Conshohocken, PA, USA, 2022.



| Pavement Structure | Rigid Base | Semi-Rigid Base | Flexible Base |
|---|---|---|---|
| Asphalt Surface Layer | 18 cm | 18 cm | 18 cm |
| Base Layer | 30 cm Cement Concrete | 15 cm + 15 cm Cement-Stabilized Crushed Stone | 15 cm + 15 cm Graded Crushed Stone |
| Subbase Layer | 20 cm | 20 cm | 20 cm |
| Subgrade | 19.5 m | 19.5 m | 19.5 m |
| Materials | Modulus (Mpa) | Poisson’s Ratio |
|---|---|---|
| Cement Concrete (Rigid Base) | 30,000 | 0.15 |
| Cement-Stabilized Crushed Stone (Semi-Rigid Base) | 10,000 | 0.25 |
| Graded Crushed Stone (Flexible Base) | 500 | 0.25 |
| Graded Crushed Stone (Subbase) | 300 | 0.25 |
| Subgrade | 60 | 0.4 |
| Parameter | Min | Max |
|---|---|---|
| δ | 1.405 | 2.83 |
| α | 1.495 | 2.713 |
| β | −1.246 | −0.0044 |
| γ | −0.747 | −0.365 |
| Runs | Parameter | Runs | Parameter | ||||||
|---|---|---|---|---|---|---|---|---|---|
| δ | α | β | γ | δ | α | β | γ | ||
| 1 | 2.83 | 2.713 | −1.246 | −0.365 | 16 | 2.1175 | 2.104 | −0.6252 | −0.556 |
| 2 | 2.1175 | 2.104 | −1.8668 | −0.556 | 17 | 2.1175 | 2.104 | −0.6252 | −0.556 |
| 3 | 1.405 | 1.495 | −1.246 | −0.747 | 18 | 1.405 | 1.495 | −1.246 | −0.365 |
| 4 | 2.83 | 2.713 | −1.246 | −0.747 | 19 | 2.83 | 2.713 | −0.0044 | −0.747 |
| 5 | 2.1175 | 2.104 | −0.6252 | −0.174 | 20 | 1.405 | 2.713 | −1.246 | −0.365 |
| 6 | 2.1175 | 0.886 | −0.6252 | −0.556 | 21 | 2.1175 | 2.104 | −0.6252 | −0.556 |
| 7 | 2.1175 | 2.104 | −0.6252 | −0.556 | 22 | 2.83 | 1.495 | −1.246 | −0.365 |
| 8 | 2.1175 | 2.104 | −0.6252 | −0.938 | 23 | 2.83 | 1.495 | −0.0044 | −0.365 |
| 9 | 2.1175 | 2.104 | 0.6164 | −0.556 | 24 | 2.1175 | 3.322 | −0.6252 | −0.556 |
| 10 | 3.5425 | 2.104 | −0.6252 | −0.556 | 25 | 2.1175 | 2.104 | −0.6252 | −0.556 |
| 11 | 2.83 | 1.495 | −1.246 | −0.747 | 26 | 0.6925 | 2.104 | −0.6252 | −0.556 |
| 12 | 1.405 | 1.495 | −0.0044 | −0.365 | 27 | 1.405 | 2.713 | −0.0044 | −0.365 |
| 13 | 1.405 | 1.495 | −0.0044 | −0.747 | 28 | 2.1175 | 2.104 | −0.6252 | −0.556 |
| 14 | 2.83 | 2.713 | −0.0044 | −0.365 | 29 | 1.405 | 2.713 | −0.0044 | −0.747 |
| 15 | 2.83 | 1.495 | −0.0044 | −0.747 | 30 | 1.405 | 2.713 | −1.246 | −0.747 |
| Pavement Structure | Rigid Base | Semi-Rigid Base | Flexible Base | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Thickness (cm) | Modulus (MPa) | Poisson’s Ratio | Thickness (cm) | Modulus (MPa) | Poisson’s Ratio | Thickness (cm) | Modulus (MPa) | Poisson’s Ratio | |
| Asphalt surface layer | 18 | ― | 0.35 | 18 | ― | 0.35 | 18 | ― | 0.35 |
| Base layer | 30 | 30,000 | 0.15 | 30 | 10,000 | 0.25 | 30 | 500 | 0.25 |
| Subbase layer | 20 | 300 | 0.25 | 20 | 300 | 0.25 | 20 | 300 | 0.25 |
| Subgrade | ― | 60 | 0.4 | ― | 60 | 0.4 | ― | 60 | 0.4 |
| Parameter | Range |
|---|---|
| Parameter δ | 1.405~2.83 |
| Parameter α | 1.495~2.713 |
| Parameter β | −1.246 to −0.0044 |
| Parameter γ | −0.747 to −0.365 |
| Frequency f (Hz) | 10−4~105 |
| Parameter | Value |
|---|---|
| Maximum training iterations (times) | 1000 |
| Learning rate | 0.01 |
| Momentum factor | 0.01 |
| Minimum error | 0.00001 |
| Runs | Rigid Base | Semi-Rigid Base | Flexible Base | Runs | Rigid Base | Semi-Rigid Base | Flexible Base |
|---|---|---|---|---|---|---|---|
| 1 | 2.62398 | 5.90747 | 12.2419 | 16 | −5.61293 | 0.92218 | 96.4388 |
| 2 | −2.38646 | 5.69595 | 65.5259 | 17 | −5.61293 | 0.92218 | 96.4388 |
| 3 | −11.6154 | −18.4151 | 145.404 | 18 | −11.7709 | −19.2908 | 141.762 |
| 4 | 2.54743 | 5.18468 | 9.67211 | 19 | 2.03122 | 7.85097 | 25.5435 |
| 5 | −7.09358 | −3.19617 | 112.576 | 20 | −6.19981 | −1.12327 | 102.669 |
| 6 | −11.4221 | −17.5361 | 148.047 | 21 | −5.61293 | 0.92218 | 96.4388 |
| 7 | −5.61293 | 0.92218 | 96.4388 | 22 | −2.13478 | 5.96394 | 63.2905 |
| 8 | −4.31892 | 3.14004 | 83.4333 | 23 | −5.74334 | 0.674657 | 97.8044 |
| 9 | −10.1113 | −12.3262 | 146.595 | 24 | 1.98584 | 7.88852 | 26.1501 |
| 10 | 2.59773 | 5.55884 | 10.9326 | 25 | −5.61293 | 0.92218 | 96.4388 |
| 11 | −1.48181 | 6.58769 | 57.5551 | 26 | −12.2855 | −21.6816 | 110.885 |
| 12 | −12.2986 | −21.7489 | 109.456 | 27 | −10.7011 | −14.6096 | 150.289 |
| 13 | −12.1516 | −21.1123 | 123.066 | 28 | −5.61293 | 0.92218 | 96.4388 |
| 14 | 0.955492 | 8.03789 | 37.5936 | 29 | −9.49304 | −10.1366 | 140.455 |
| 15 | −4.43294 | 2.96145 | 84.5418 | 30 | −4.96803 | 2.08053 | 89.8375 |
| Runs | Rigid Base | Semi-Rigid Base | Flexible Base | Runs | Rigid Base | Semi-Rigid Base | Flexible Base |
|---|---|---|---|---|---|---|---|
| 1 | 215.167 | 151.045 | 9.75177 | 16 | 430.807 | 310.646 | 39.2467 |
| 2 | 369.26 | 268.218 | 31.8084 | 17 | 430.807 | 310.646 | 39.2467 |
| 3 | 542.864 | 429.719 | 52.1623 | 18 | 545.749 | 434.184 | 52.4877 |
| 4 | 200.104 | 135.639 | 7.99783 | 19 | 266.735 | 199.045 | 17.2534 |
| 5 | 458.451 | 333.166 | 42.4635 | 20 | 441.784 | 319.242 | 40.5281 |
| 6 | 539.279 | 424.32 | 51.7612 | 21 | 430.807 | 310.646 | 39.2467 |
| 7 | 430.807 | 310.646 | 39.2467 | 22 | 364.299 | 265.064 | 31.1786 |
| 8 | 406.442 | 292.883 | 36.3672 | 23 | 433.249 | 312.523 | 39.5324 |
| 9 | 514.636 | 391.057 | 48.9662 | 24 | 268.629 | 200.577 | 17.548 |
| 10 | 207.914 | 143.634 | 8.87429 | 25 | 430.807 | 310.646 | 39.2467 |
| 11 | 351.227 | 256.827 | 29.4886 | 26 | 555.305 | 449.787 | 53.6654 |
| 12 | 555.548 | 450.201 | 53.7006 | 27 | 525.683 | 405.198 | 50.2303 |
| 13 | 552.817 | 445.598 | 53.3287 | 28 | 430.807 | 310.646 | 39.2467 |
| 14 | 301.462 | 224.792 | 22.5577 | 29 | 503.102 | 377.435 | 47.635 |
| 15 | 408.6 | 294.394 | 36.6249 | 30 | 418.698 | 301.614 | 37.823 |
| Runs | Rigid Base | Semi-Rigid Base | Flexible Base | Runs | Rigid Base | Semi-Rigid Base | Flexible Base |
|---|---|---|---|---|---|---|---|
| 1 | −21.3032 | −34.9423 | −62.9223 | 16 | −48.955 | −75.254 | −197.862 |
| 2 | −40.1145 | −61.5215 | −166.258 | 17 | −48.955 | −75.254 | −197.862 |
| 3 | −65.3584 | −116.193 | −289.775 | 18 | −65.7833 | −117.741 | −296.815 |
| 4 | −20.0648 | −32.1984 | −53.4672 | 19 | −26.5122 | −43.8501 | −100.832 |
| 5 | −52.9777 | −82.876 | −212.26 | 20 | −50.5497 | −78.1476 | −203.477 |
| 6 | −64.8306 | −114.321 | −282.297 | 21 | −48.955 | −75.254 | −197.862 |
| 7 | −48.955 | −75.254 | −197.862 | 22 | −39.4128 | −60.5593 | −163.577 |
| 8 | −45.4313 | −69.3655 | −185.547 | 23 | −49.3095 | −75.8837 | −199.104 |
| 9 | −61.2065 | −102.801 | −250.02 | 24 | −26.7334 | −44.1617 | −102.25 |
| 10 | −20.6942 | −33.6243 | −58.2248 | 25 | −48.955 | −75.254 | −197.862 |
| 11 | −37.5756 | −58.1028 | −156.339 | 26 | −67.1911 | −123.152 | −331.368 |
| 12 | −67.2269 | −123.296 | −332.606 | 27 | −62.8302 | −107.696 | −261.731 |
| 13 | −66.8245 | −121.699 | −320.028 | 28 | −48.955 | −75.254 | −197.862 |
| 14 | −30.8173 | −49.5242 | −125.687 | 29 | −59.513 | −98.0916 | −240.236 |
| 15 | −45.7425 | −69.8604 | −186.64 | 30 | −47.2007 | −72.2418 | −191.738 |
| Source | ε1R | ε1S | ε1F | |||
|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Model | 142.89 | <0.0001 | 29.64 | <0.0001 | 23.69 | <0.0001 |
| A-δ | 375.89 | <0.0001 | 80.05 | <0.0001 | 61.84 | <0.0001 |
| B-α | 149.85 | <0.0001 | 27.51 | <0.0001 | 23.15 | <0.0001 |
| C-β | 41.38 | <0.0001 | 9.89 | 0.0042 | 8.87 | 0.0064 |
| D-γ | 4.46 | 0.0449 | 1.12 | 0.3007 | 0.8827 | 0.3565 |
| R2 | 0.9581 | 0.8259 | 0.7912 | |||
| Source | σ1R | σ1S | σ1F | |||
|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Model | 128.63 | <0.0001 | 239.18 | <0.0001 | 220.11 | <0.0001 |
| A-δ | 1131.24 | <0.0001 | 2160.76 | <0.0001 | 1882.99 | <0.0001 |
| B-α | 456.40 | <0.0001 | 860.70 | <0.0001 | 788.17 | <0.0001 |
| C-β | 129.54 | <0.0001 | 252.24 | <0.0001 | 206.55 | <0.0001 |
| D-γ | 13.29 | 0.0024 | 23.65 | 0.0002 | 20.93 | 0.0004 |
| AB | 23.96 | 0.0002 | 3.33 | 0.0879 | 67.62 | <0.0001 |
| AC | 2.81 | 0.1143 | 0.7026 | 0.4151 | 8.64 | 0.0101 |
| AD | 0.4438 | 0.5154 | 0.1475 | 0.7064 | 1.13 | 0.3049 |
| BC | 10.37 | 0.0057 | 28.64 | <0.0001 | 19.81 | 0.0005 |
| BD | 0.9185 | 0.3531 | 2.26 | 0.1536 | 1.76 | 0.2046 |
| CD | 0.3162 | 0.5822 | 0.8046 | 0.3839 | 0.7800 | 0.3911 |
| A2 | 22.93 | 0.0002 | 4.74 | 0.0459 | 61.91 | <0.0001 |
| B2 | 6.95 | 0.0187 | 0.0610 | 0.8083 | 20.62 | 0.0004 |
| C2 | 1.04 | 0.3231 | 8.38 | 0.0111 | 1.20 | 0.2905 |
| D2 | 0.0114 | 0.9164 | 0.1127 | 0.7417 | 0.0196 | 0.8904 |
| R2 | 0.9917 | 0.9955 | 0.9952 | |||
| Source | ε2R | ε2S | ε2F | |||
|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Model | 153.51 | <0.0001 | 239.36 | <0.0001 | 6419.53 | <0.0001 |
| A-δ | 402.36 | <0.0001 | 631.12 | <0.0001 | 58,274.83 | <0.0001 |
| B-α | 161.16 | <0.0001 | 244.77 | <0.0001 | 24,746.77 | <0.0001 |
| C-β | 45.76 | <0.0001 | 74.42 | <0.0001 | 5816.71 | <0.0001 |
| D-γ | 4.78 | 0.0383 | 7.12 | 0.0132 | 560.69 | <0.0001 |
| AB | 14.04 | 0.0019 | ||||
| AC | 0.3272 | 0.5758 | ||||
| AD | 0.0441 | 0.8366 | ||||
| BC | 236.56 | <0.0001 | ||||
| BD | 26.08 | 0.0001 | ||||
| CD | 42.24 | <0.0001 | ||||
| A2 | 6.60 | 0.0214 | ||||
| B2 | 24.59 | 0.0002 | ||||
| C2 | 101.50 | <0.0001 | ||||
| D2 | 1.75 | 0.2055 | ||||
| R2 | 0.9609 | 0.9746 | 0.9998 | |||
| Rigid Base | Semi-Rigid Base | Flexible Base | |||||||
|---|---|---|---|---|---|---|---|---|---|
| P | ε1R | ε2R | σ1R | ε1S | ε2S | σ1S | ε1F | ε2F | σ1F |
| δ | −3.59 | −1.13 | −0.89 | 47.19 | −1.30 | −0.94 | −2.19 | −1.00 | −1.15 |
| α | −2.77 | −0.87 | −0.68 | 37.24 | −1.00 | −0.72 | −1.68 | −0.76 | −0.87 |
| β | 0.41 | 0.13 | 0.10 | −4.71 | 0.15 | 0.09 | 0.11 | 0.11 | 0.13 |
| γ | 0.37 | 0.11 | 0.09 | −4.19 | 0.13 | 0.08 | 0.09 | 0.10 | 0.11 |
| Structure | Rigid Base Pavement | Semi-Rigid Base Pavement | Flexible Base Pavement |
|---|---|---|---|
| Neural Network | WOA-BP | WOA-BP | WOA-BP |
| Training samples R | 0.95792 | 0.96043 | 0.95941 |
| Validation samples R | 0.97237 | 0.96845 | 0.97639 |
| Testing samples R | 0.94742 | 0.96031 | 0.97883 |
| Overall samples R | 0.95861 | 0.96160 | 0.96487 |
| Parameter Combination | δ | α | β | γ |
|---|---|---|---|---|
| 1 | 1.405 | 1.495 | −1.246 | −0.747 |
| 2 | 2.83 | 2.713 | −0.0044 | −0.365 |
| 3 | 2.1175 | 2.104 | −0.6252 | −0.556 |
| Parameter Combination | Frequency (Hz) |
|---|---|
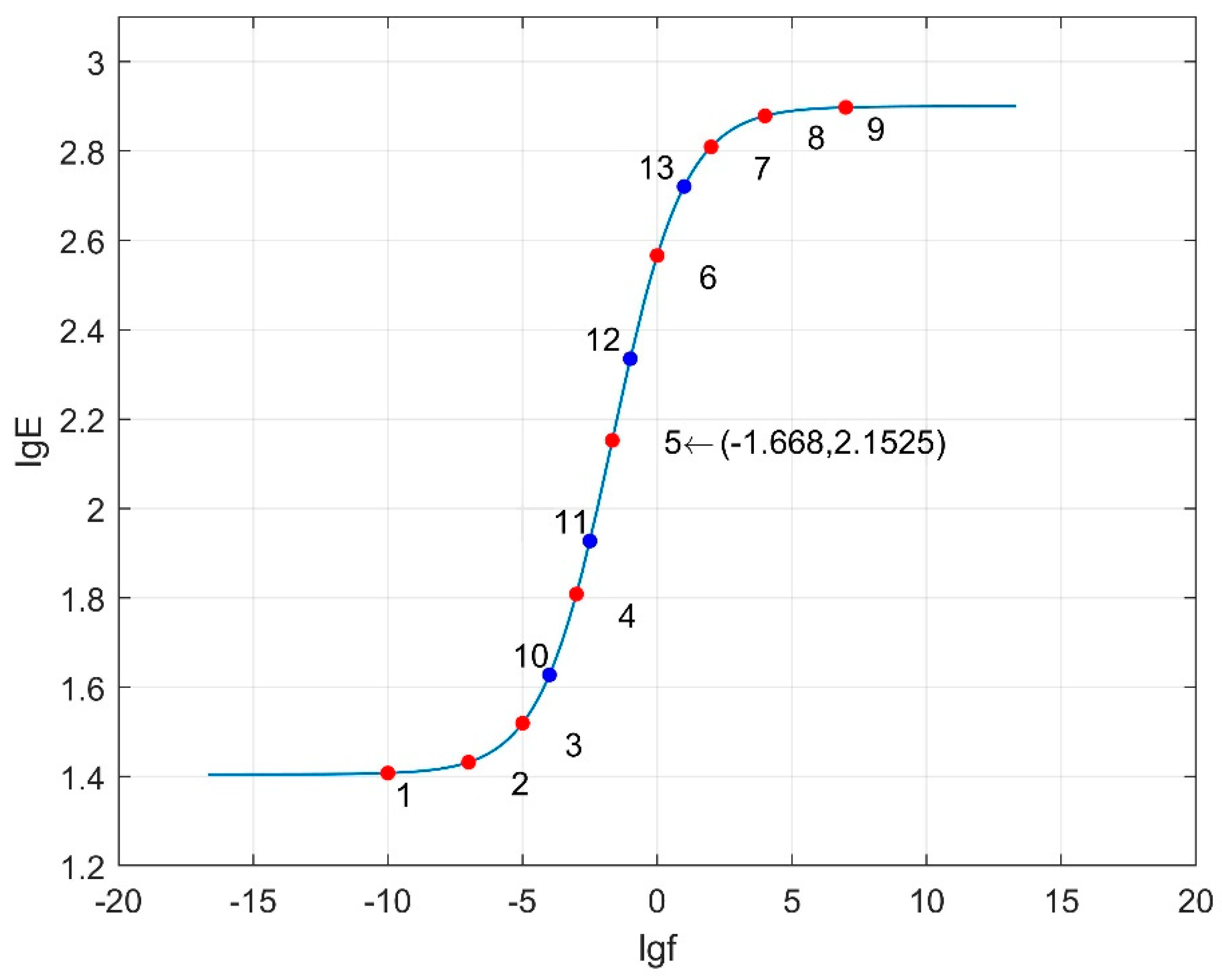
| 1 | 10−10, 10−7, 10−5, 10−4, 10−3, 10−2.5, 10−1.668, 10−1, 1, 10, 102, 104, 107 |
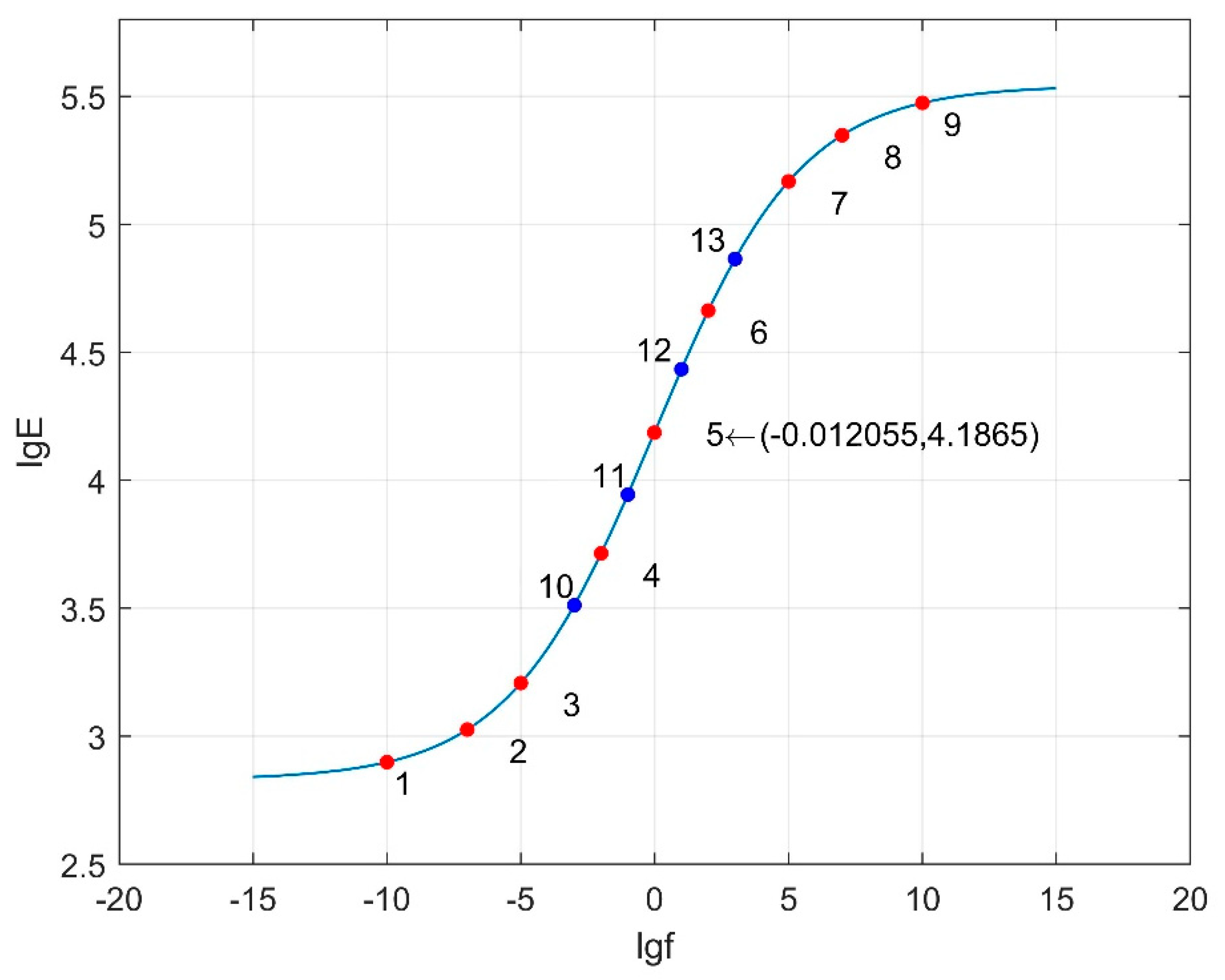
| 2 | 10−10, 10−7, 10−5, 10−3, 10−2, 10−1, 1, 10, 102, 103, 105, 107, 1010 |
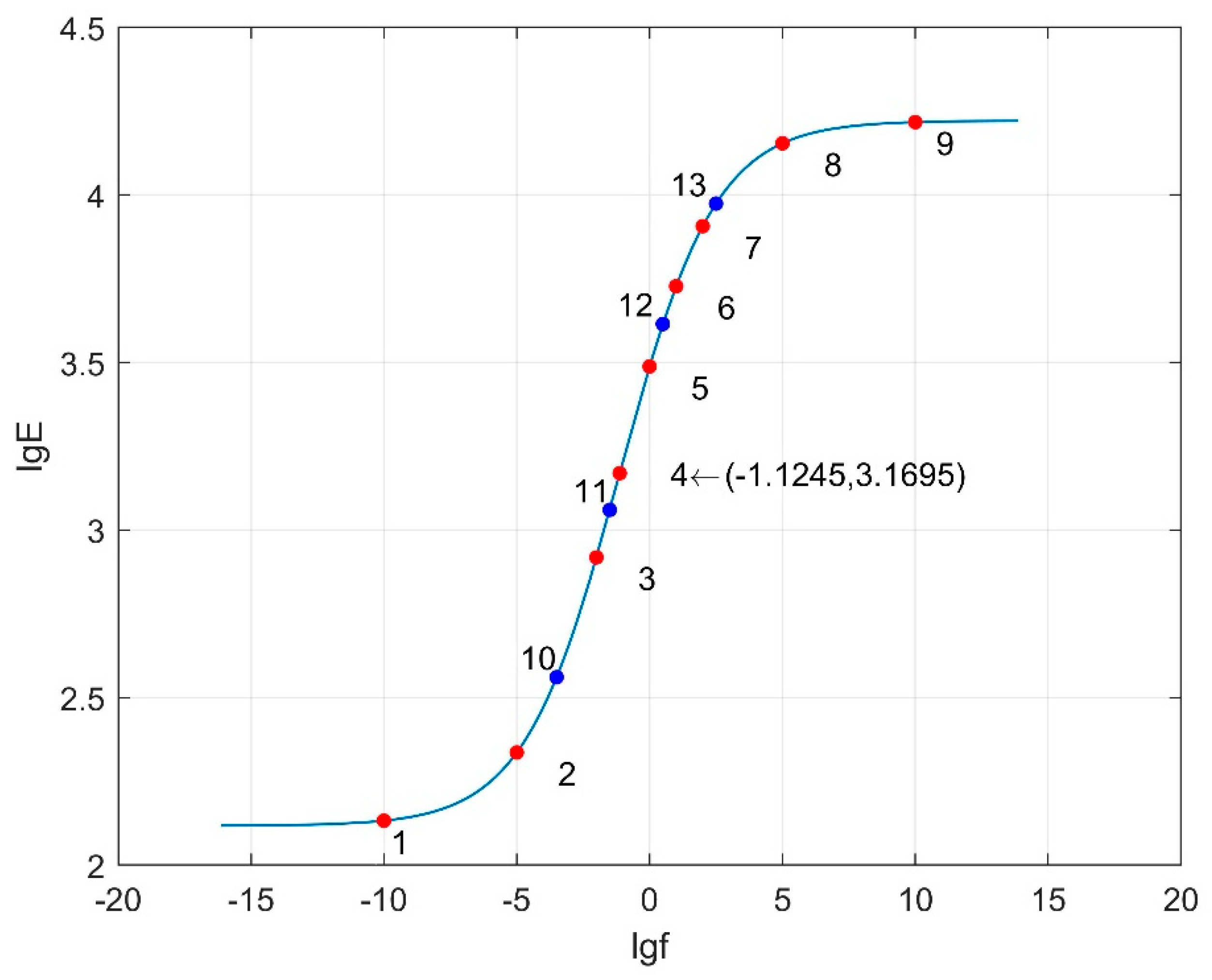
| 3 | 10−10, 10−5, 10−3.5, 10−2, 10−1.5, 10−1.1245, 1, 100.5, 10, 102, 102.5, 105, 1010 |
| Parameter Combination | Rigid Base Pavement Structure | Semi-Rigid Base Pavement Structure | Flexible Base Pavement Structure |
|---|---|---|---|
| 1 | 0.05% | 0.1% | 0.05% |
| 2 | 0.6% | 0.25% | 1% |
| 3 | 0.45% | 0.4% | 0.5% |
| Case | Original Value (Selected from Table 7) | Output (After Structural Response-Based Solving) | ||||||
|---|---|---|---|---|---|---|---|---|
| Parameter Combination | δ | α | β | γ | δ | α | β | γ |
| 1 | 1.405 | 1.495 | −1.246 | −0.747 | 1.405 | 1.495 | −1.246 | −0.747 |
| 2 | 2.83 | 2.713 | −0.0044 | −0.365 | 2.83 | 2.713 | −0.0044 | −0.365 |
| 3 | 2.1175 | 2.104 | −0.6252 | −0.556 | 2.1175 | 2.104 | −0.6252 | −0.556 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Feng, B.; Yang, X.; Cheng, M.; Liu, Z. A New Design Methodology of Asphalt Mixture Dynamic Modulus Based on Pavement Response. Materials 2025, 18, 3184. https://doi.org/10.3390/ma18133184
Huang Y, Feng B, Yang X, Cheng M, Liu Z. A New Design Methodology of Asphalt Mixture Dynamic Modulus Based on Pavement Response. Materials. 2025; 18(13):3184. https://doi.org/10.3390/ma18133184
Chicago/Turabian StyleHuang, You, Boxiong Feng, Xin Yang, Minxiang Cheng, and Zhaohui Liu. 2025. "A New Design Methodology of Asphalt Mixture Dynamic Modulus Based on Pavement Response" Materials 18, no. 13: 3184. https://doi.org/10.3390/ma18133184
APA StyleHuang, Y., Feng, B., Yang, X., Cheng, M., & Liu, Z. (2025). A New Design Methodology of Asphalt Mixture Dynamic Modulus Based on Pavement Response. Materials, 18(13), 3184. https://doi.org/10.3390/ma18133184






