Structural Relaxation, Rejuvenation and Plasticity of Metallic Glasses: Microscopic Details from Anelastic Relaxation Spectra
Abstract
:1. Introduction
- A summary of Argon’s analysis of the mechanics and thermal activation of STZs.
- Our approach, which consists of (i) quasi-static anelastic recovery experiments that span more than ten orders of magnitude of time and (ii) computational determination of relaxation-time spectra by direct spectrum analysis (DSA).
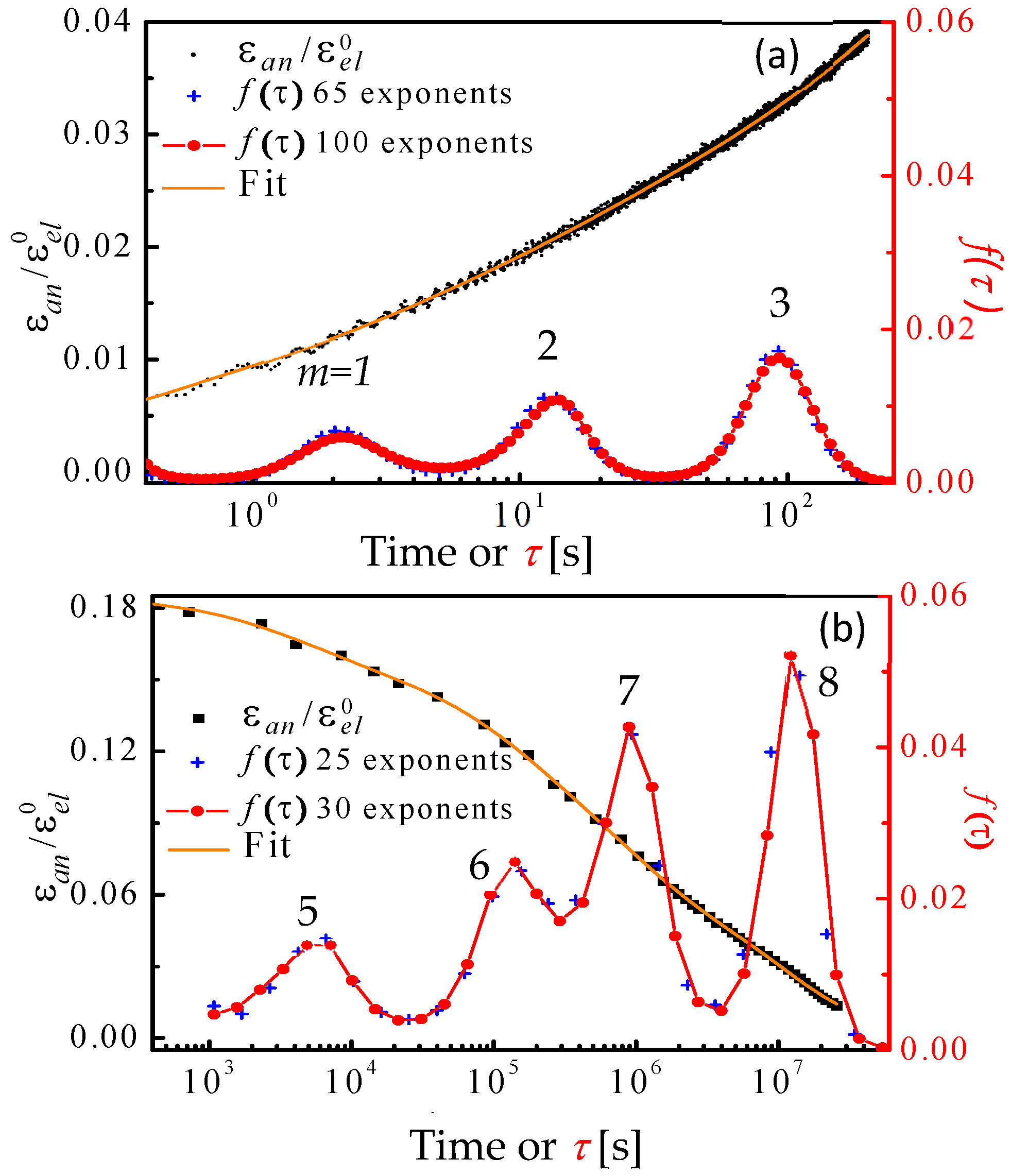
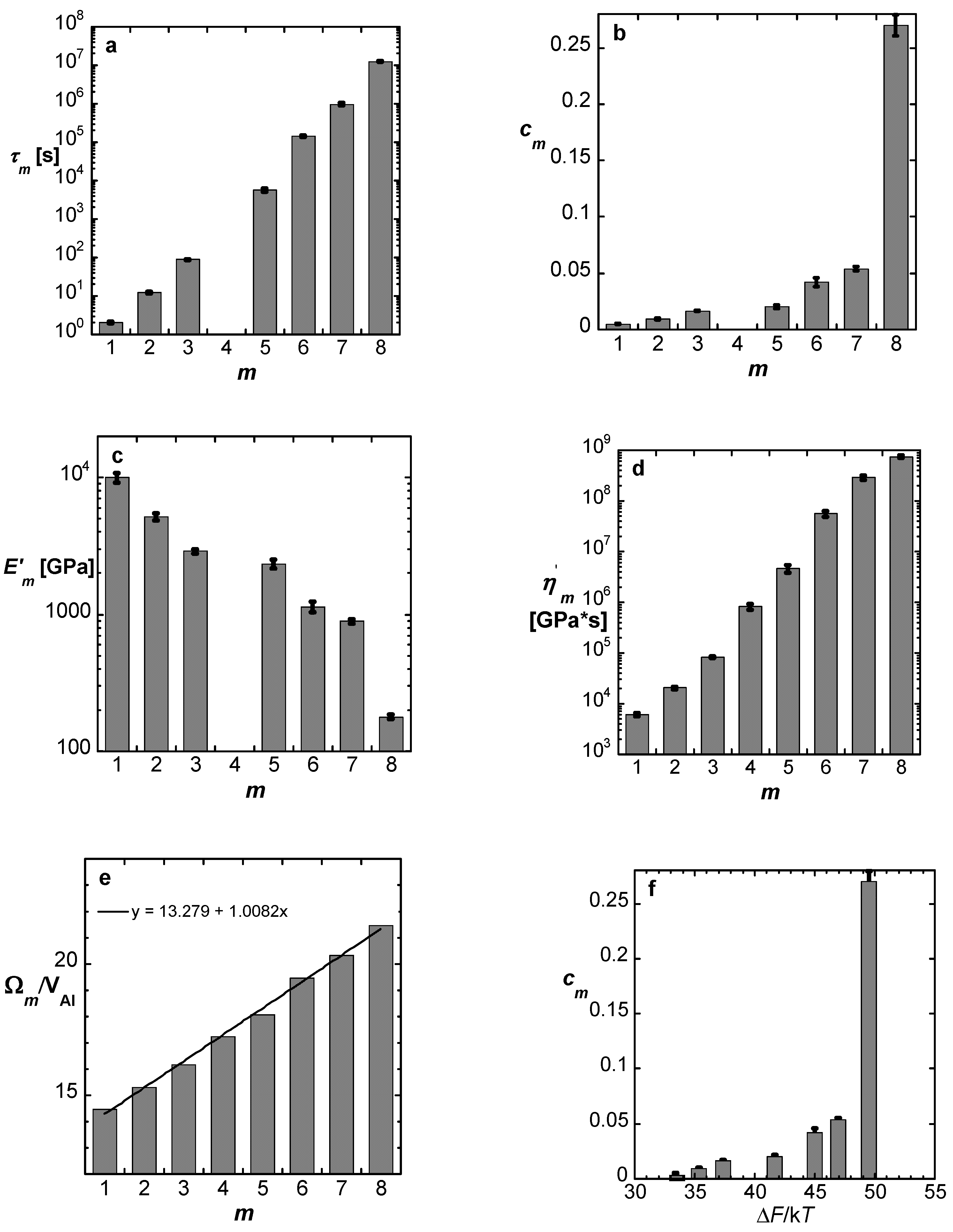
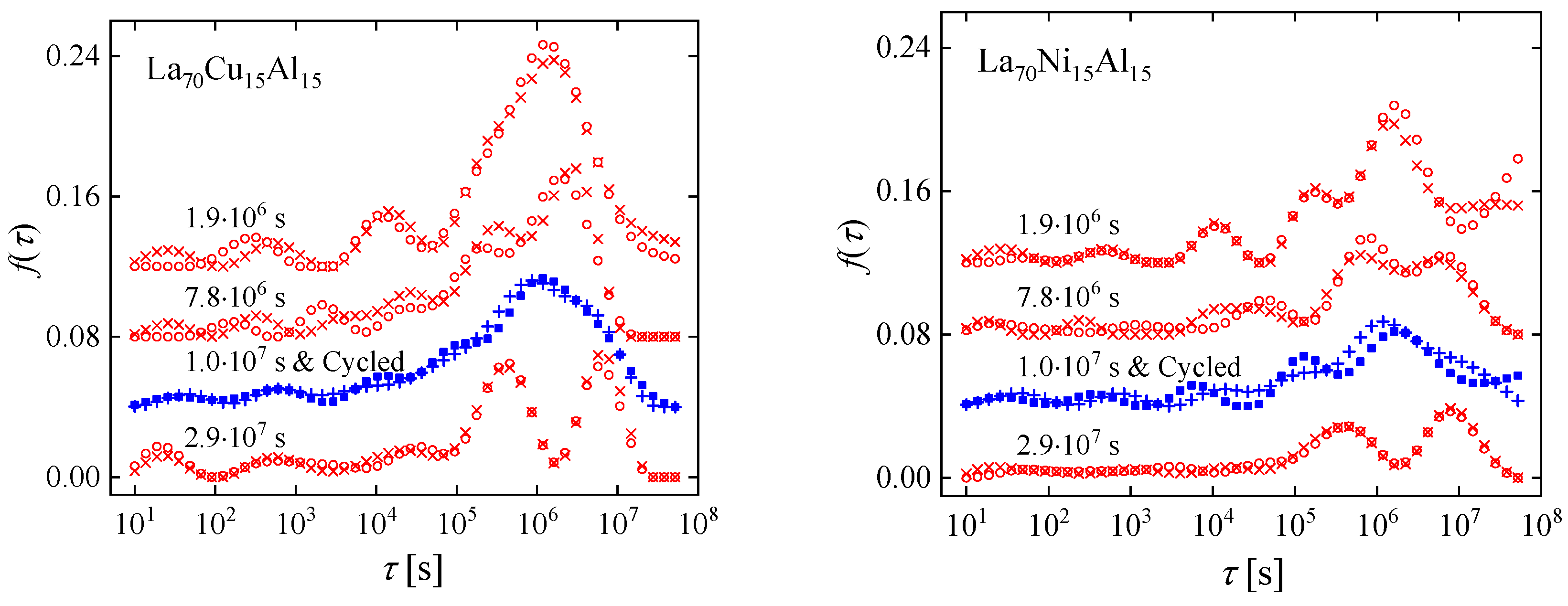
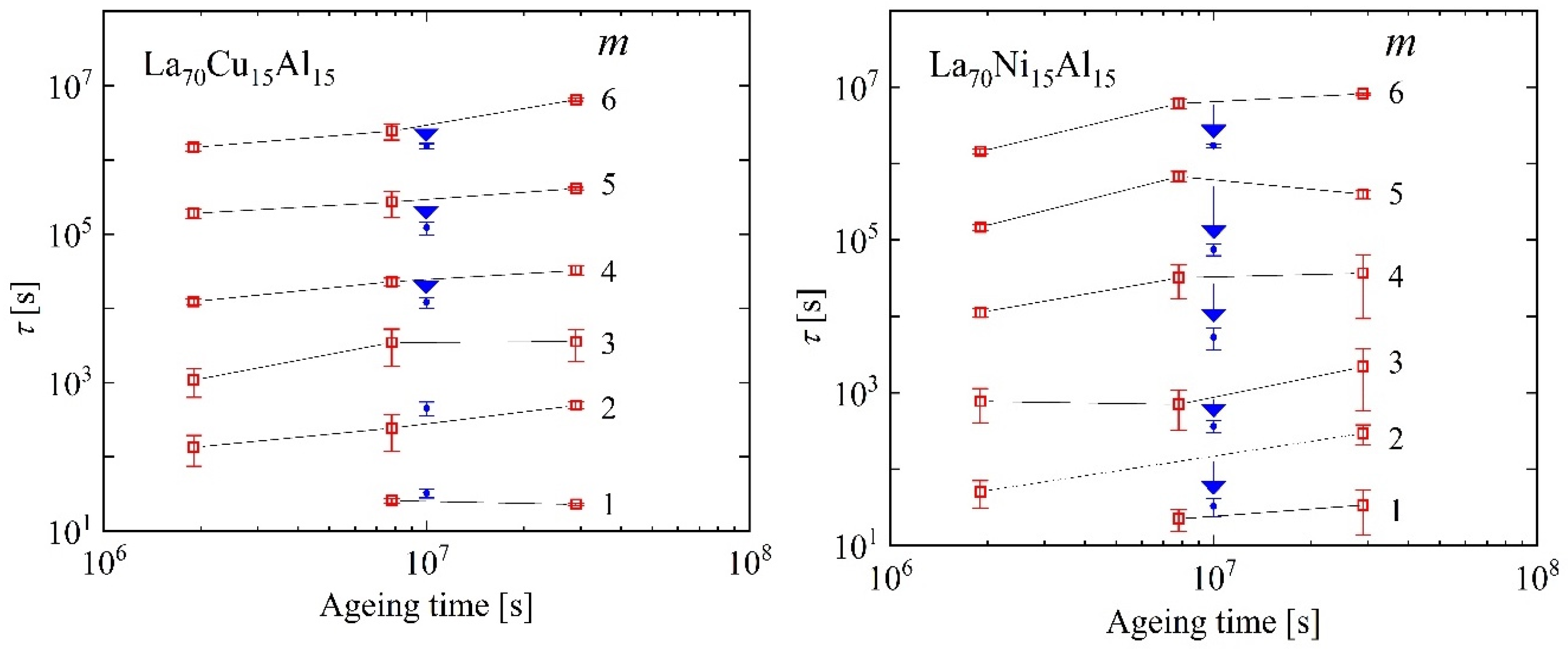
- Relaxation-time spectra were determined numerically from the strain/time data. These provided valuable information on STZ size and property distribution, revealing an atomically-quantized hierarchy of STZs.
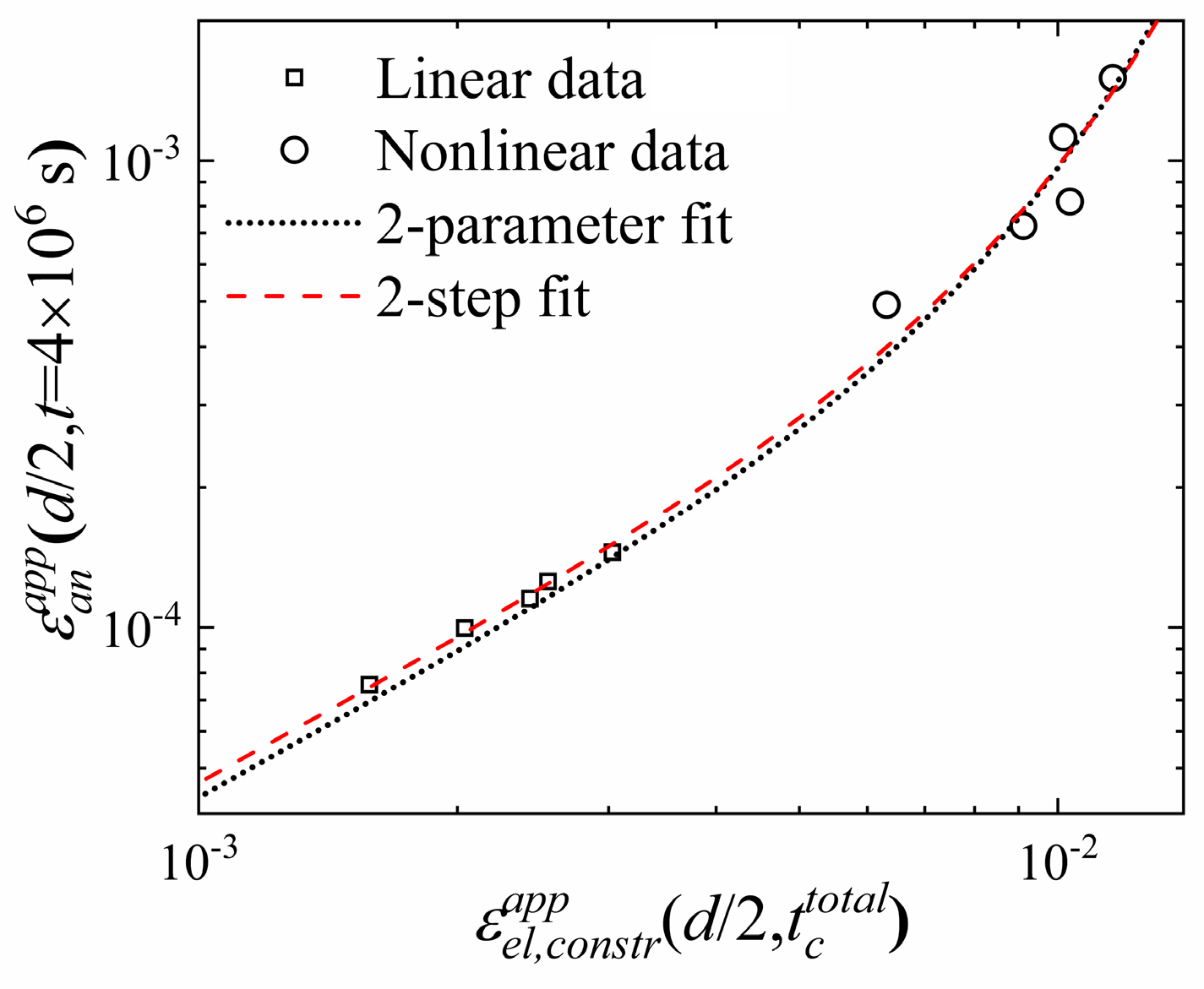
- Analysis of anelastic relaxation in the nonlinear regime, related to that of Argon and Shi’s creep experiments [19], provided an independent determination of the STZ transformation strain. Similar to the dislocation core in crystalline solids, this strain is far larger than the macroscopic yield strain.
- STZ spectra were computed from published dynamic-mechanical data. The results provide further, consistent, confirmation of the prior results and their analysis.
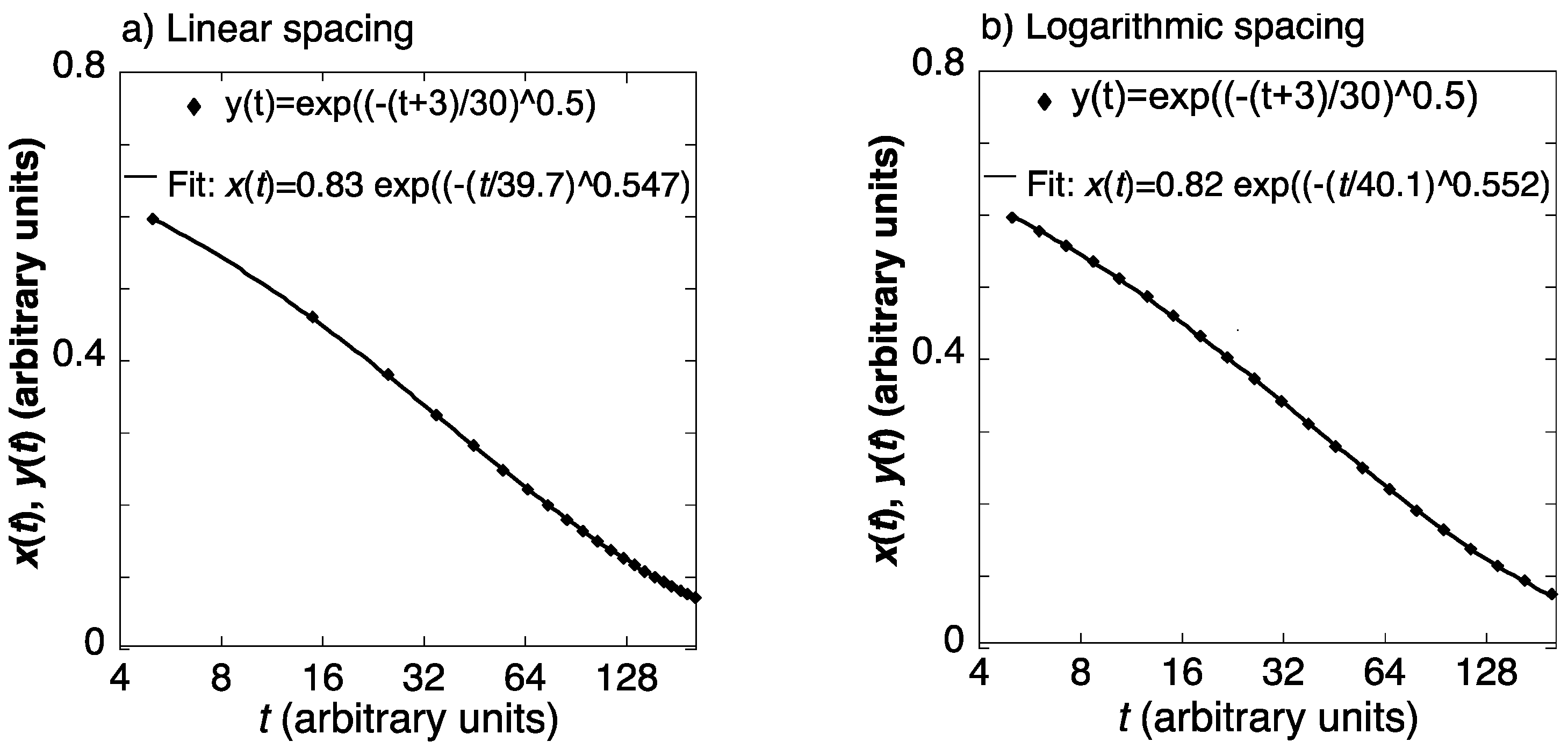
- Simple calculations show that stretched exponent fits, commonly used to fit non-exponential relaxation, are of limited utility. In particular, the time constant is ambiguous, and its apparent activation energy is not expected to reflect a specific physical process.
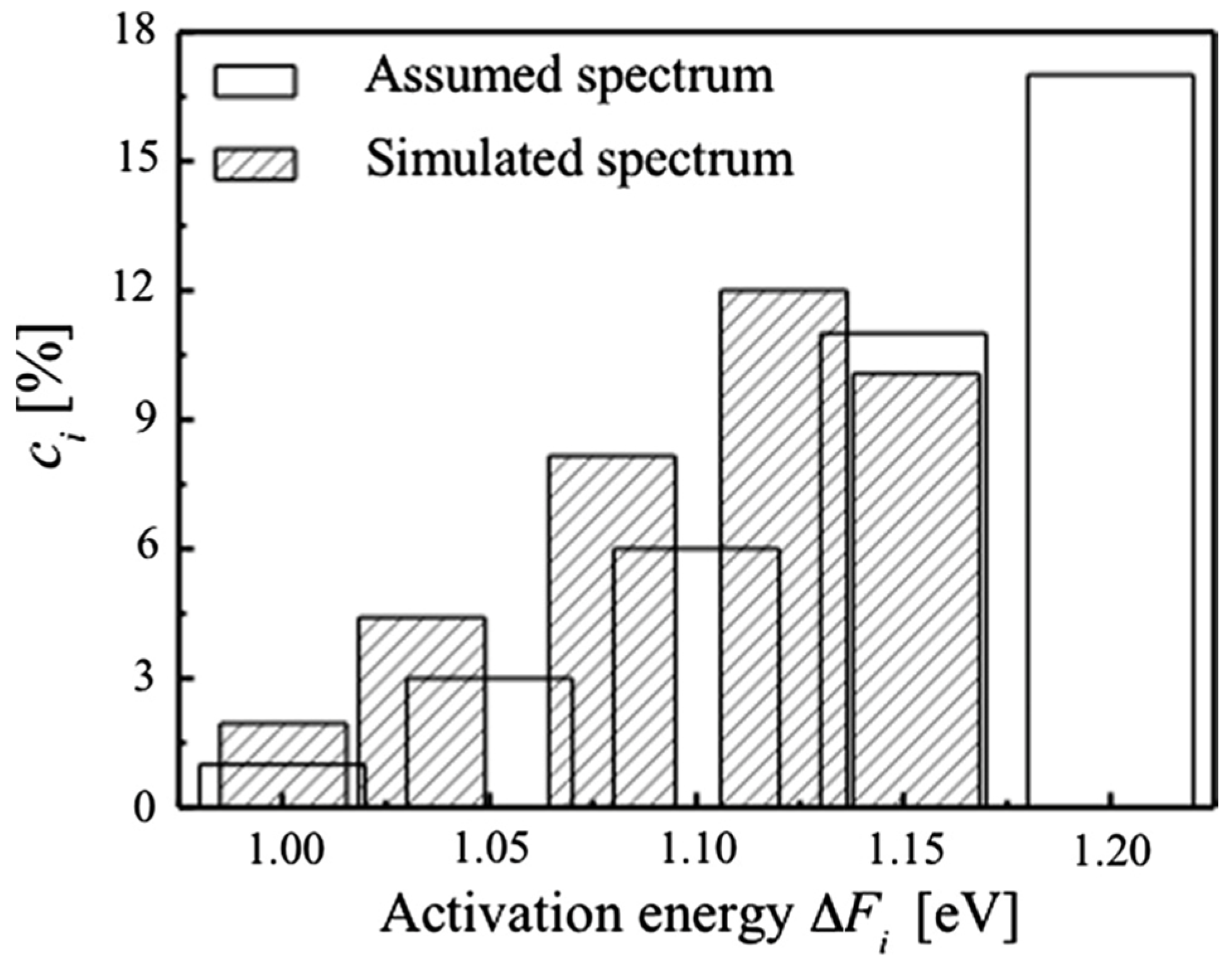
- The systematic error is evaluated for spectrum determination based on measurements conducted at discrete temperature increments and the assumption that the evolution at each temperature is dominated by a single activation free energy.
- Characterization of the details of structural relaxation and induced rejuvenation through their effect on STZ properties shows that these processes cannot be described with the evolution of a single variable.
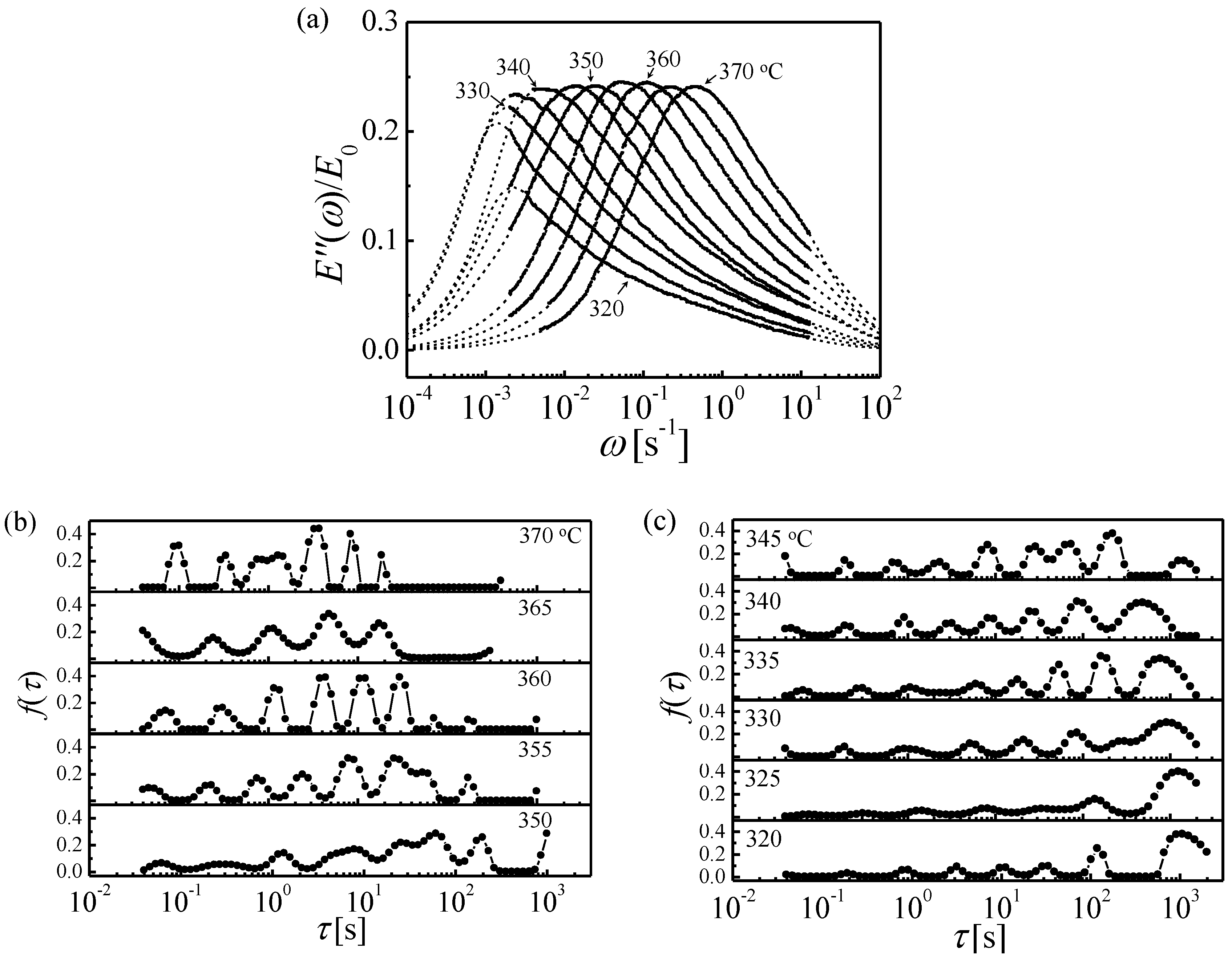
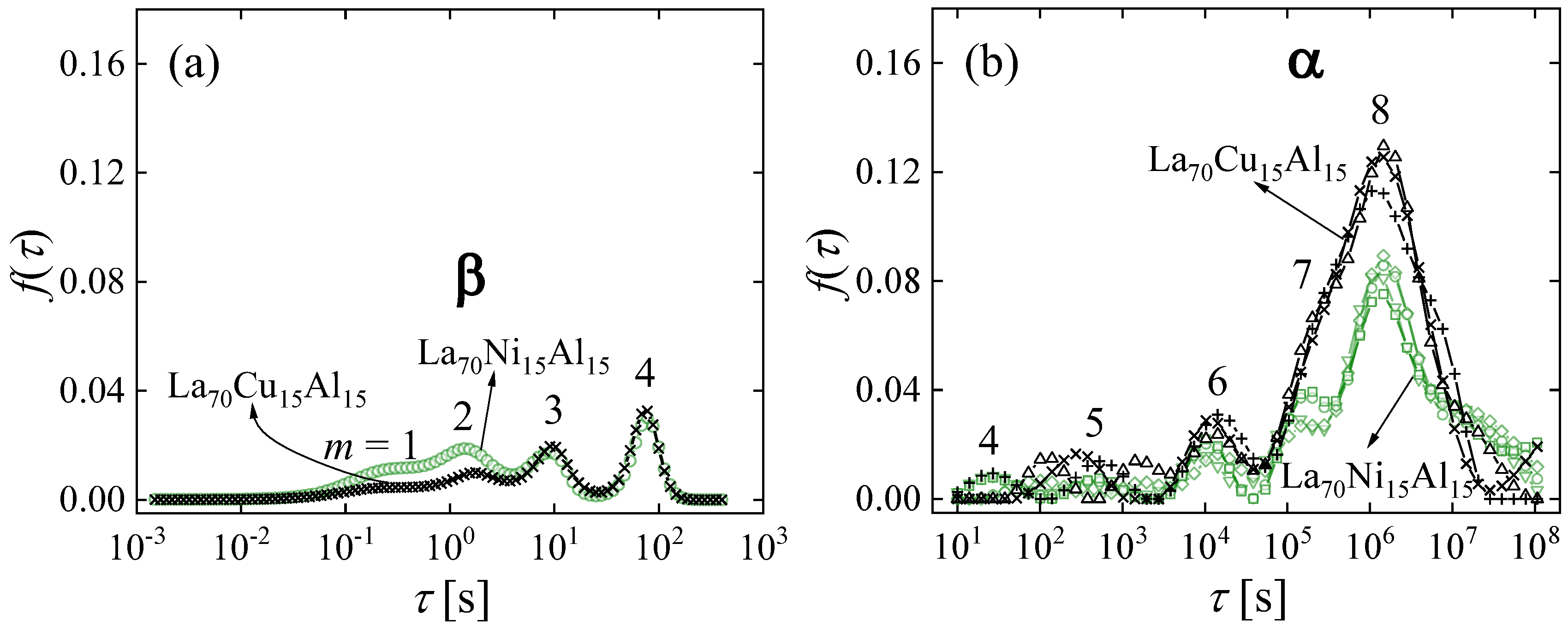
- Anelastic relaxation spectra were obtained for La-based metallic glasses, some of which exhibit a distinct high-frequency/low-temperature (β) relaxation. Among the results, the following was found: contrary to suggestions by many authors, the α and β relaxation correspond to the same mechanism. Both are reversible when the corresponding STZs occupy a small volume fraction. The results also suggest that different elements are involved in slow vs. fast STZs, corresponding to the α and β relaxation, respectively. Simulations of dynamic-mechanical behavior for experimentally obtained STZ spectra further support the notion that the α and β relaxation correspond to the same mechanism. That curves obtained at different temperature can be shifted into a single master curve cannot be seen as proof of a single activation energy.
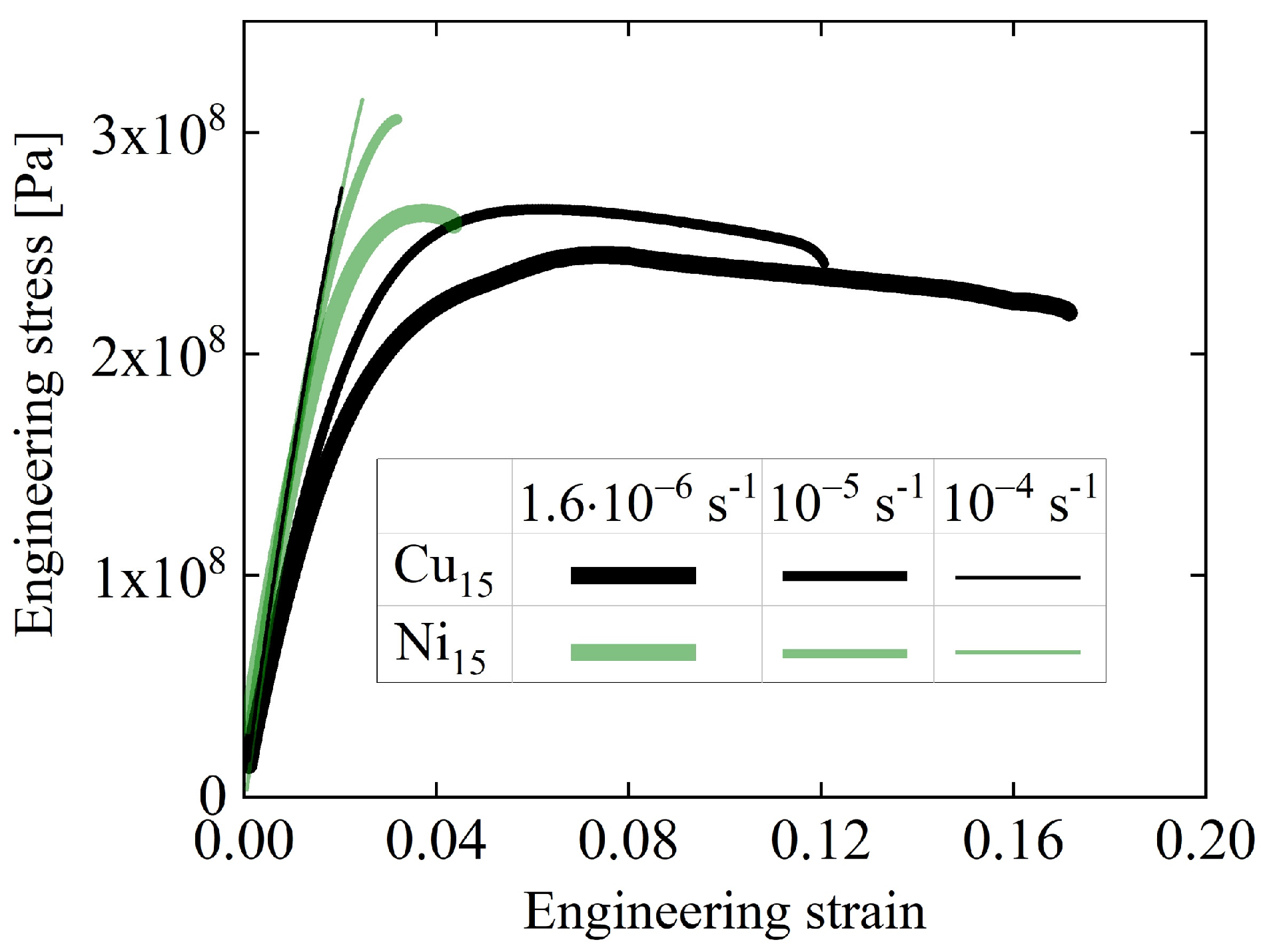
- By comparing metallic glasses that exhibit different degrees of plasticity at similar composition, plasticity is explained in terms of the volume fraction occupied by kinetically active potential STZs.
2. Theory of Thermally-Activated Shear Transformation
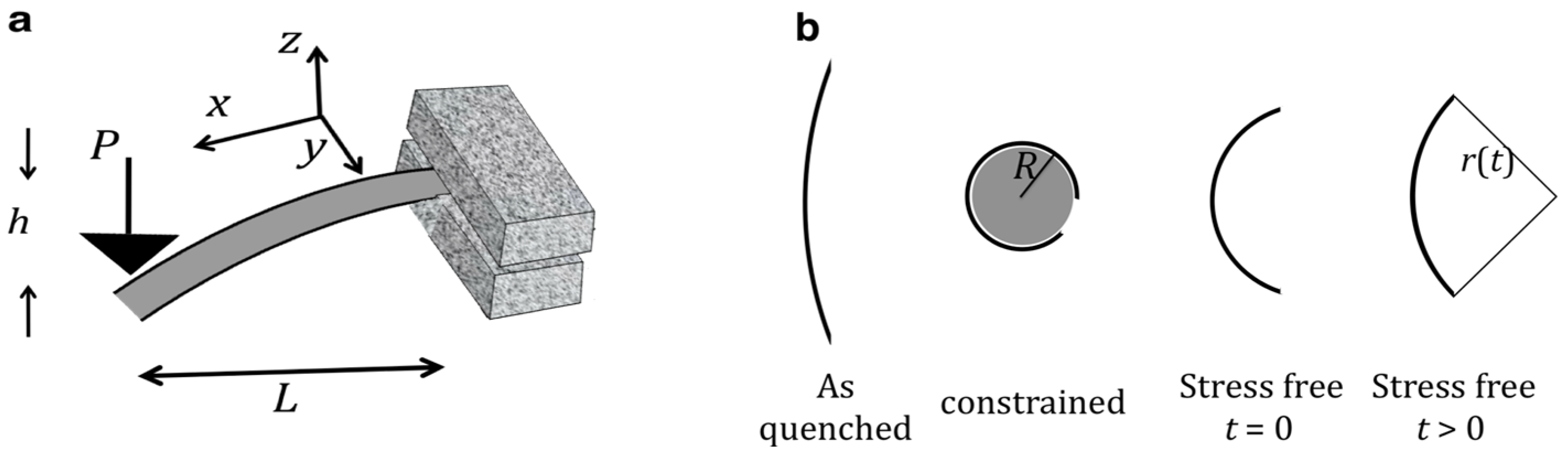
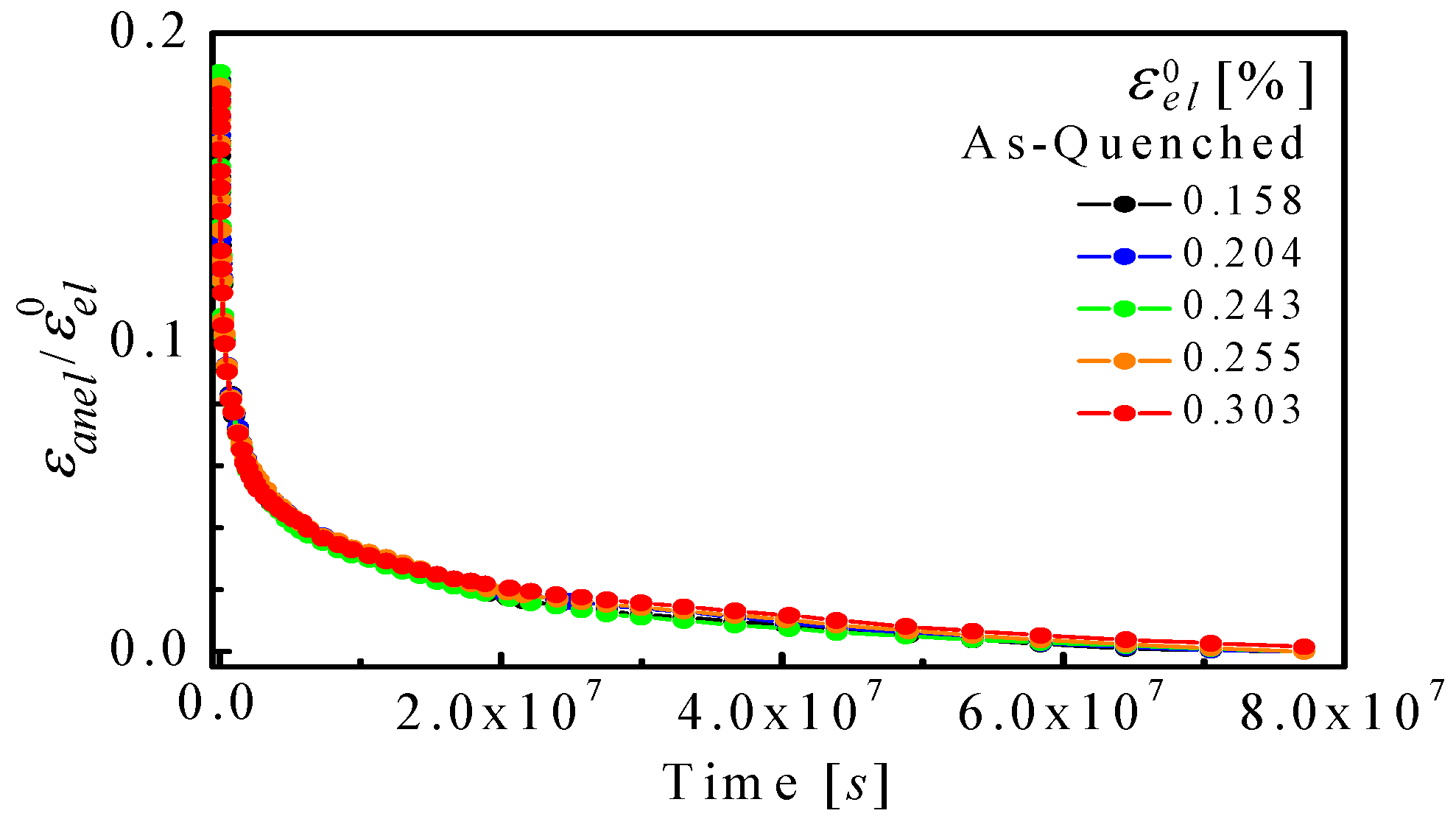
3. Experiments and Spectrum Determination
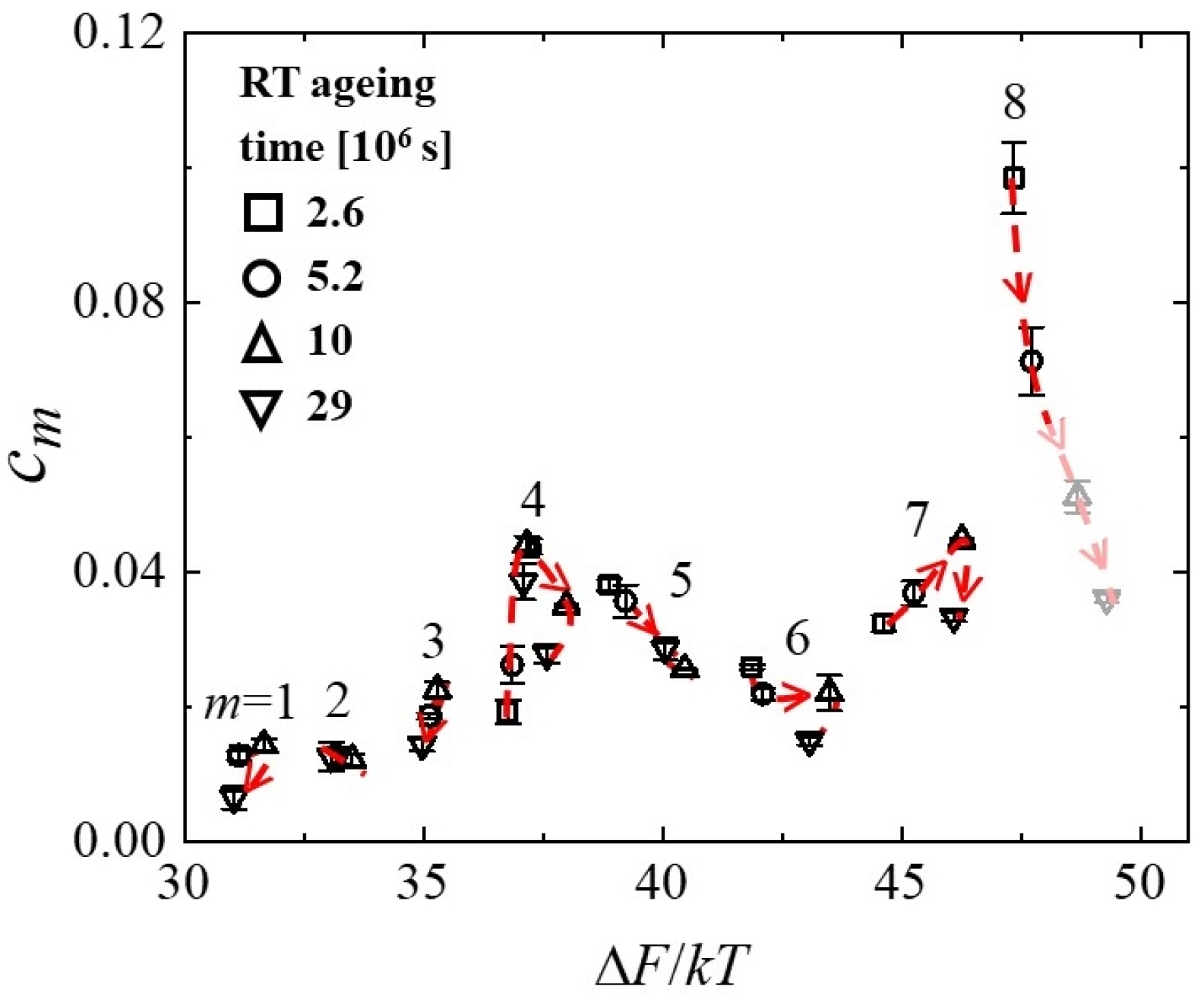
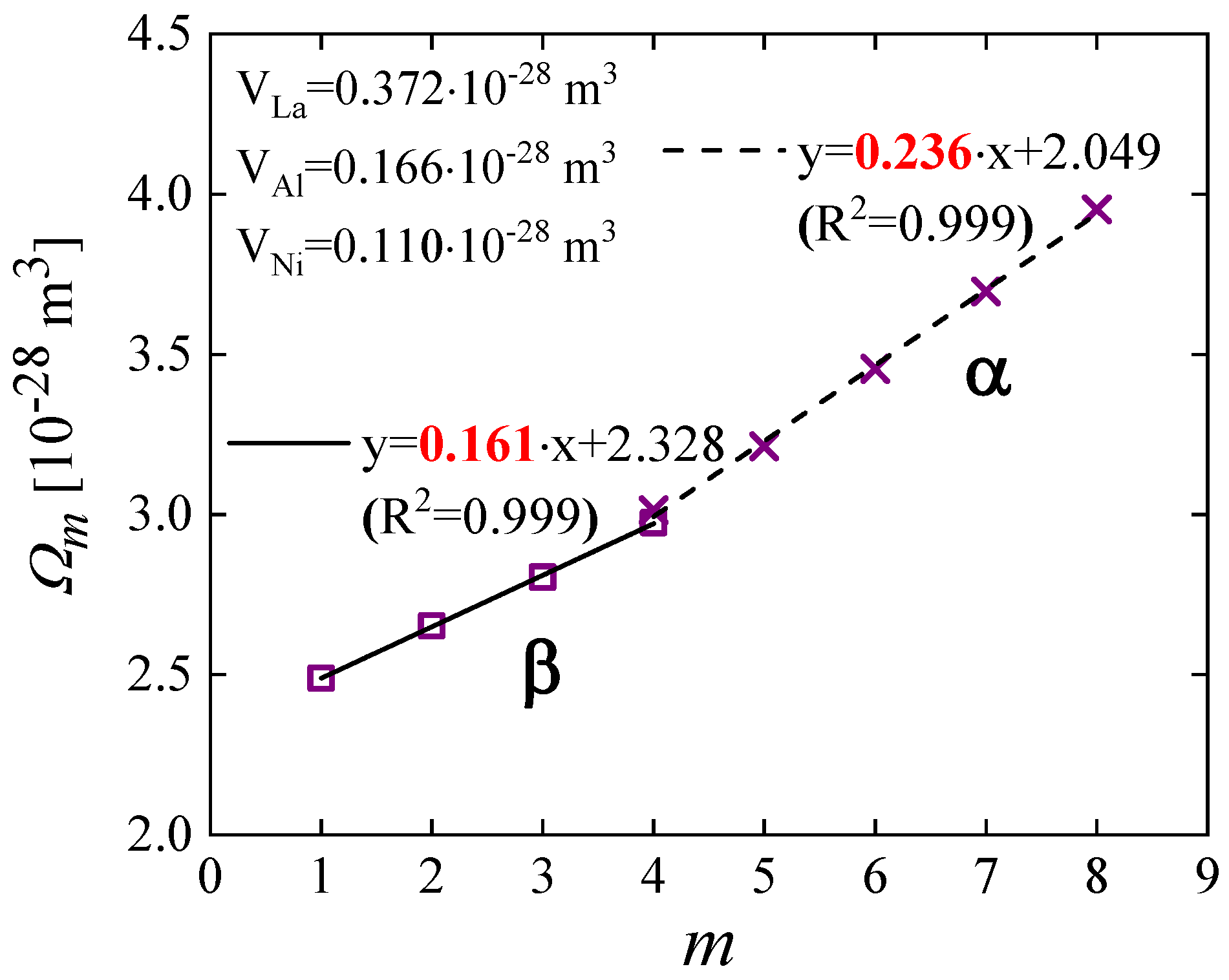
4. An Atomically Quantized Hierarchy of STZs [18]
5. The Transformation Strain [28]
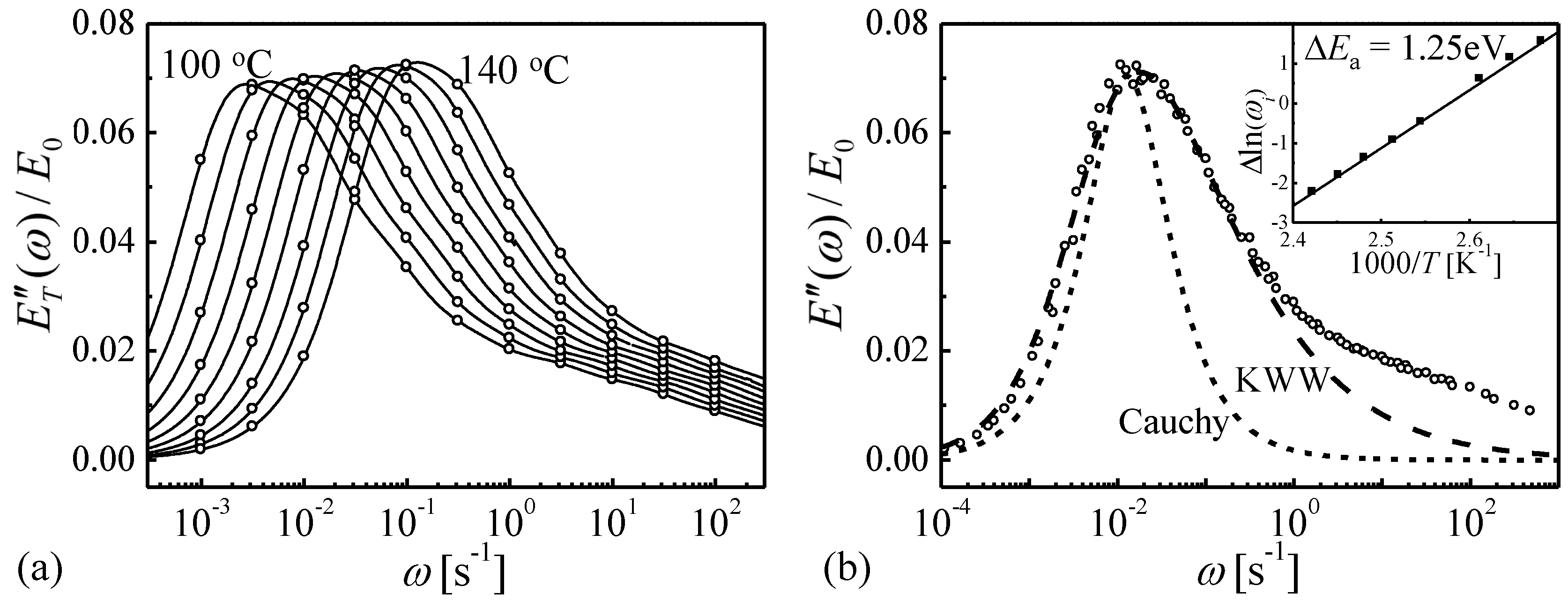
6. Dynamic-Mechanical Analysis [34]
7. The Stretched Exponent [45]
8. Systematic Error in Spectrum Determination by Temperature Stepping [61]
9. Characterization of Structural Evolution [63]
- (1)
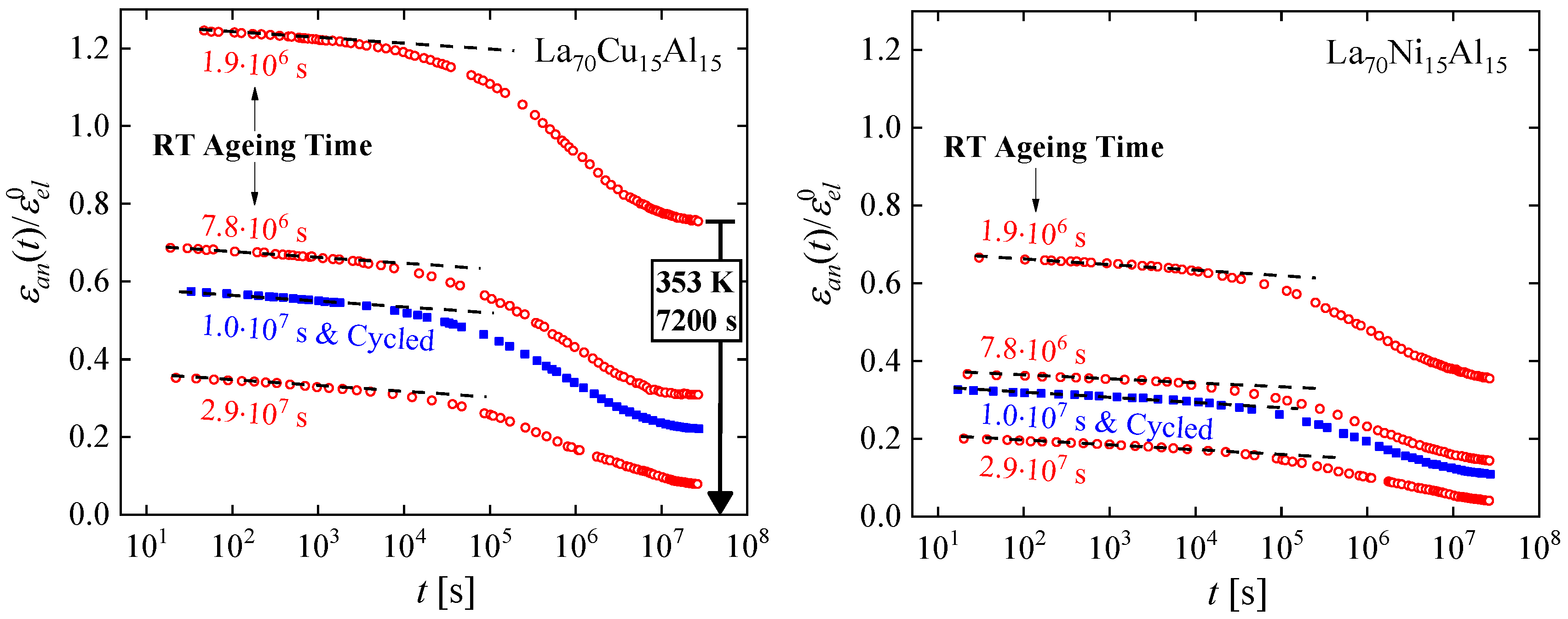
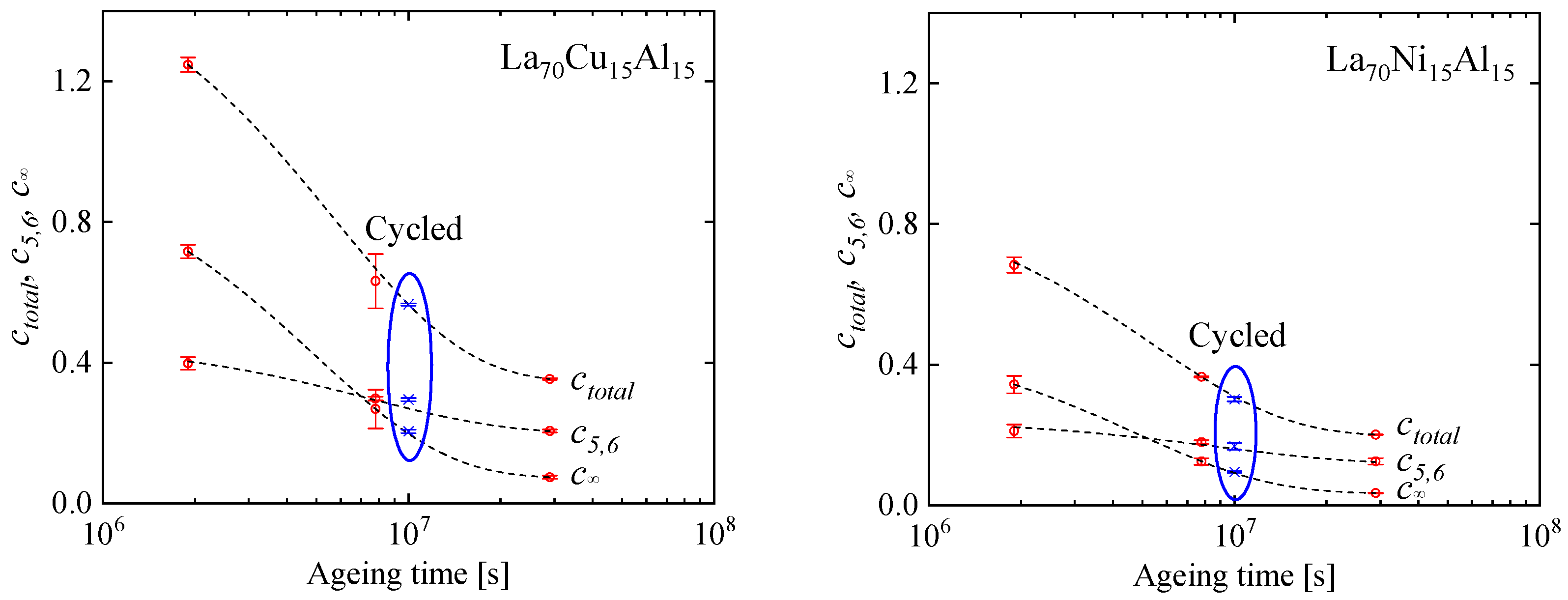
- Although cryogenic rejuvenation does not restore the cm, plasticity is improved by this process because of the increased fraction of potential STZ with a sufficiently short time constant to participate in deformation.
- (2)
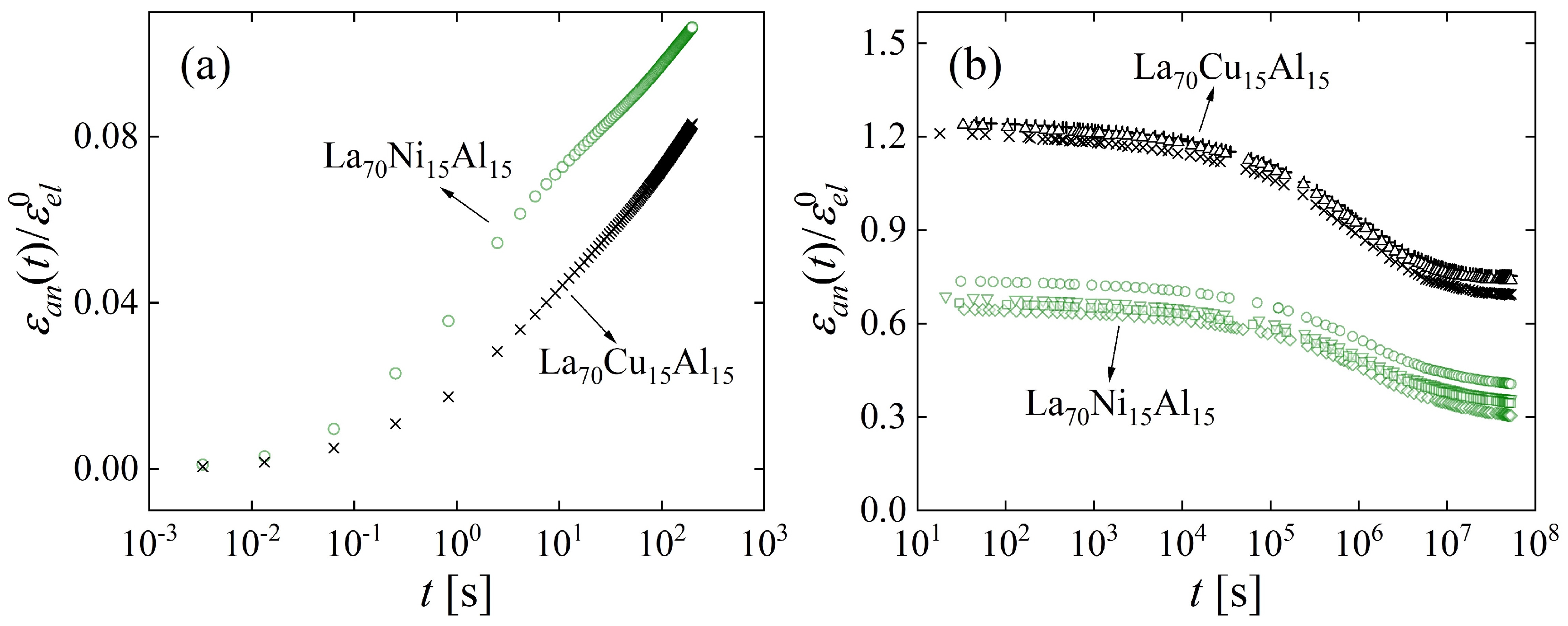
- A comparison of the time scale for structural relaxation, > 106 s, with the shorter times for anelastic relaxation indicates that the mechanisms underlying the two processes cannot be assumed to be the same. The driving force for the former is thermodynamic, whereas for the latter it is mechanical.
- (3)
- While a measurement of a single variable, e.g., stored enthalpy or plasticity, may give the impression that the cryogenic cycling process leads to a reversal of structural relaxation due to aging, these results clearly show that the details are more nuanced. Generally, structural relaxation and rejuvenation cannot be described with a single variable.
10. The Mechanism of the β Relaxation [76]
11. STZ Properties and Plasticity [86]
12. Additional Properties
13. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buckel, W.; Hilsch, R. Einfluß der Kondensation bei tiefen Temperaturen auf den elektrischen Widerstand und die Supraleitung für verschiedene Metalle. Z. Phys. 1954, 138, 109–120. [Google Scholar] [CrossRef]
- Klement, W.; Willens, R.H.; Duwez, P.O. Non-crystalline structure in solidified gold–silicon alloys. Nature 1960, 187, 869–870. [Google Scholar] [CrossRef]
- Drehman, A.J.; Greer, A.L. Kinetics of crystal nucleation and growth in Pd40Ni40P20 glass. Acta Metall. 1984, 32, 323–332. [Google Scholar] [CrossRef]
- Inoue, A.; Zhang, T.; Masumoto, T. Production of amorphous cylinder and sheet of La55Al25Ni20 alloy by a metallic mold casting method. Mater. Trans. JIM 1990, 31, 425–4288. [Google Scholar] [CrossRef]
- Peker, A.; Johnson, W.L. A highly processable metallic glass: Zr41.2Ti13.8Cu12.5Ni10.0Be22.5. Appl. Phys. Lett. 1993, 63, 2342–2344. [Google Scholar] [CrossRef]
- Ashby, M.F.; Greer, A.L. Metallic glasses as structural materials. Scr. Mater. 2006, 54, 321–326. [Google Scholar] [CrossRef]
- Schroers, J.; Nguyen, T.; O’Keeffe, S.; Desai, A. Thermoplastic forming of bulk metallic glass—Applications for MEMS and microstructure fabrication. Mater. Sci. Eng. A 2007, 449, 898–902. [Google Scholar] [CrossRef]
- Hull, D.; Bacon, D.J. Introduction to Dislocations, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Bragg, W.L.; Nye, J.F. A dynamical model of a crystal structure. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1947, 190, 474–481. [Google Scholar]
- Hirsch, P.; Cockayne, D.; Spence, J.; Whelan, M. 50 Years of TEM of dislocations: Past, present and future. Philos. Mag. 2006, 86, 4519–4528. [Google Scholar] [CrossRef]
- Orowan, E. Creep in metallic and nonmetallic materials. In Proceedings of the First U.S. National Congress of Applied Mechanics: Held at Illinois Institute of Technology, Chicago, IL, USA, 11–16 June 1951; pp. 453–472. [Google Scholar]
- Argon, A.S. Plastic deformation in metallic glasses. Acta Metall. 1979, 27, 47–58. [Google Scholar] [CrossRef]
- Harmon, J.S.; Demetriou, M.D.; Johnson, W.L.; Samwer, K. Anelastic to plastic transition in metallic glass-forming liquids. Phys. Rev. Lett. 2007, 99, 135502. [Google Scholar] [CrossRef] [PubMed]
- Demetriou, M.D.; Johnson, W.L.; Samwer, K. Coarse-grained description of localized inelastic deformation in amorphous metals. Appl. Phys. Lett. 2009, 94, 191905. [Google Scholar] [CrossRef]
- Argon, A.S.; Kuo, H.Y. Plastic flow in a disordered bubble raft (an analog of a metallic glass). Mater. Sci. Eng. 1979, 39, 101–109. [Google Scholar] [CrossRef]
- Schall, P.; Weitz, D.A.; Spaepen, F. Structural rearrangements that govern flow in colloidal glasses. Science 2007, 318, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Falk, M.L.; Langer, J.S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 1998, 57, 7192–7205. [Google Scholar] [CrossRef]
- Ju, J.D.; Jang, D.; Nwankpa, A.; Atzmon, M. An atomically quantized hierarchy of shear transformation zones in a metallic glass. J. Appl. Phys. 2011, 109, 053522. [Google Scholar] [CrossRef]
- Argon, A.S.; Shi, L.T. Development of visco-plastic deformation in metallic glasses. Acta Metall. 1983, 31, 499–507. [Google Scholar] [CrossRef]
- Liu, S.T.; Wang, Z.; Peng, H.L.; Yu, H.B.; Wang, W.H. The activation energy and volume of flow units of metallic glasses. Scr. Mater. 2012, 67, 9–12. [Google Scholar] [CrossRef]
- Kato, H.; Igarashi, H.; Inoue, A. Another clue to understand the yield phenomenon at the glassy state in Zr55Al10Ni5Cu30 metallic glass. Mater. Lett. 2008, 62, 1592–1594. [Google Scholar]
- Cost, J.R. Nonlinear regression least-squares method for determining relaxation time spectra for processes with first-order kinetics. J. Appl. Phys. 1983, 54, 2137–2146. [Google Scholar] [CrossRef]
- Available online: http://s-provencher.com/contin.shtml (accessed on 14 November 2023).
- Provencher, S.W. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comput. Phys. Commun. 1982, 27, 213–227. [Google Scholar] [CrossRef]
- Provencher, S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229–242. [Google Scholar] [CrossRef]
- Lakes, R.S. Viscoelastic Solids; CRC Press: Boca Baton, FL, USA, 1999. [Google Scholar]
- Atzmon, M.; Ju, J.D. Microscopic description of flow defects and relaxation in metallic glasses. Phys. Rev. E 2014, 90, 042313. [Google Scholar] [CrossRef] [PubMed]
- Lei, T.J.; Atzmon, M. Activation volume details from nonlinear anelastic deformation of a metallic glass. J. Appl. Phys. 2019, 126, 185104. [Google Scholar] [CrossRef]
- Delogu, F. Identification and characterization of potential shear transformation zones in metallic glasses F. Phys. Rev. Lett. 2008, 100, 255901. [Google Scholar] [CrossRef] [PubMed]
- Neudecker, M.; Mayr, S.G. Dynamics of shear localization and stress relaxation in amorphous Cu50Ti50. Acta Mater. 2009, 57, 1437–1441. [Google Scholar] [CrossRef]
- Johnson, W.L.; Samwer, K. A universal criterion for plastic yielding of metallic glasses with a (T/Tg)2/3 temperature dependence. Phys. Rev. Lett. 2005, 95, 195501. [Google Scholar] [CrossRef]
- Pan, D.; Inoue, A.; Sakurai, T.; Chen, M.W. Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses. Proc. Nat. Acad. Sci. USA 2008, 105, 14769. [Google Scholar] [CrossRef]
- Krausser, J.; Samwer, K.; Zaccone, A. Interatomic repulsion softness directly controls the fragility of supercooled metallic melts. Proc. Natl. Acad. Sci. USA 2015, 112, 13762. [Google Scholar] [CrossRef]
- Ju, J.D.; Atzmon, M. A comprehensive atomistic analysis of the experimental dynamic-mechanical response of a metallic glass. Acta Mater. 2014, 74, 183–188. [Google Scholar] [CrossRef]
- Pelletier, J.M. Dynamic mechanical properties in a Zr46.8Ti13.8Cu12.5 Ni10Be27.5 bulk metallic glass. J. Alloys Compd. 2005, 393, 223–230. [Google Scholar] [CrossRef]
- Keryvin, V.; Vaillant, M.-L.; Rouxel, T.; Huger, M.; Gloriant, T.; Kawamura, Y. Thermal stability and crystallisation of a Zr55Cu30Al10Ni5 bulk metallic glass studied by in situ ultrasonic echography. Intermetallics 2002, 10, 1289–1296. [Google Scholar] [CrossRef]
- Rouxel, T. Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 2007, 90, 3019–3039. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wang, W.H.; Bai, H.Y. Extended elastic model for flow in metallic glasses. J. Non-Cryst. Solids 2011, 357, 223–226. [Google Scholar] [CrossRef]
- Wang, W.H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 2012, 57, 487–656. [Google Scholar] [CrossRef]
- Ngai, K.L.; Plazek, D.J.; Rendell, R.W. Some examples of possible descriptions of dynamic properties of polymers by means of the coupling model. Rheol. Acta 1997, 36, 307–319. [Google Scholar] [CrossRef]
- Salmén, L. Viscoelastic properties of in situ lignin under water-saturated conditions. J. Mater. Sci. 1984, 19, 3090–3096. [Google Scholar] [CrossRef]
- Qiao, J.C.; Pelletier, J.M. Mechanical relaxation in a Zr-based bulk metallic glass: Analysis based on physical models. J. Appl. Phys. 2012, 112, 033518. [Google Scholar] [CrossRef]
- Jeong, H.T.; Fleury, E.; Kim, W.T.; Kim, D.H.; Hono, K. Study on the mechanical relaxations of a Zr36Ti24Be40 amorphous alloy by time–temperature superposition principle. J. Phys. Soc. Jpn. 2004, 11, 3192. [Google Scholar] [CrossRef]
- Ju, J.D.; Atzmon, M. Atomistic interpretation of the dynamic response of glasses. MRS Comm. 2014, 4, 63–66. [Google Scholar] [CrossRef]
- Atzmon, M. The pitfalls of empirical fitting of glass relaxation data with stretched exponents. J. Appl. Phys. 2018, 123, 065103. [Google Scholar] [CrossRef]
- Kohlrausch, V.R. Theory of the electric residue in the Leyden jar. Ann. Phys. Chem. (Poggendorff) 1854, 91, 179–214. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C. Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.; Dev, S.B.; North, A.M. Further considerations of non symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1971, 67, 1323–1335. [Google Scholar] [CrossRef]
- Phillips, J.C. Stretched exponential relaxation in molecular and electronic glasses. Rep. Prog. Phys. 1996, 59, 1133. [Google Scholar] [CrossRef]
- MacDonald, J.R. Linear relaxation: Distributions, thermal activation, structure, and ambiguity. J. Appl. Phys. 1987, 62, R51–R62. [Google Scholar] [CrossRef]
- Svare, I.; Martin, S.W.; Borsa, F. Stretched exponentials with T-dependent exponents from fixed distributions of energy barriers for relaxation times in fast-ion conductors. Phys. Rev. B 2000, 61, 228–233. [Google Scholar] [CrossRef]
- Hodge, I.M. Enthalpy relaxation and recovery in amorphous materials. J. Non-Cryst. Solids 1994, 169, 211–266, and references therein. [Google Scholar] [CrossRef]
- Qiao, J.C.; Pelletier, J.M. Enthalpy relaxation in Cu46Zr45Al7Y2 and Zr55Cu30Ni5Al10 bulk metallic glasses by differential scanning calorimetry (DSC). Intermetallics 2011, 19, 9–18. [Google Scholar] [CrossRef]
- Raghavan, R.; Murali, P.; Ramamurty, U. Influence of cooling rate on the enthalpy relaxation and fragility of a metallic glass. Metall. Mater. Trans. A 2008, 39, 1573–1577. [Google Scholar] [CrossRef]
- Kawai, K.; Hagiwara, T.; Takai, R.; Suzuki, T. Comparative investigation by two analytical approaches of enthalpy relaxation for glassy glucose, sucrose, maltose, and trehalose. Pharm. Res. 2005, 22, 490–495, and references therein. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Yue, Y. Secondary relaxation in metallic glass formers: Its correlation with the genuine Johari− Goldstein relaxation. J. Phys. Chem. C. 2009, 113, 15001–15006. [Google Scholar] [CrossRef]
- Qiao, J.C.; Casalini, R.; Pelletier, J.M. Main (α) relaxation and excess wing in Zr50Cu40Al10 bulk metallic glass investigated by mechanical spectroscopy. J. Non-Cryst. Solids 2015, 407, 106–109. [Google Scholar] [CrossRef]
- Zhao, Z.F.; Wen, P.; Shek, C.H.; Wang, W.H. Measurements of slow β-relaxations in metallic glasses and supercooled liquids. Phys. Rev. B 2007, 75, 174201. [Google Scholar] [CrossRef]
- Rösner, P.; Samwer, K.; Lunkenheimer, P. Indications for an "excess wing" in metallic glasses from the mechanical loss modulus in Zr65Al7.5Cu27.5. Europhys. Lett. 2004, 68, 226. [Google Scholar] [CrossRef]
- Brand, R.; Lunkenheimer, P.; Schneider, U.; Loidl, A. Is there an excess wing in the dielectric loss of plastic crystals? Phys. Rev. Lett. 1999, 82, 1951. [Google Scholar] [CrossRef]
- Ju, J.D.; Atzmon, M. Evaluation of approximate measurements of activation-free-energy spectra of shear transformation zones in metallic glasses. J. Alloys Comp. 2015, 643, S8–S10. [Google Scholar] [CrossRef]
- Argon, A.S.; Kuo, H.Y. Free energy spectra for inelastic deformation of five metallic glass alloys. J. Non-Cryst. Solids 1980, 37, 241–266. [Google Scholar] [CrossRef]
- Lei, T.J.; DaCosta, L.R.; Liu, M.; Wang, W.H.; Sun, Y.H.; Greer, A.L.; Atzmon, M. Microscopic characterization of structural relaxation and cryogenic rejuvenation in metallic glasses. Acta Mater. 2019, 164, 165–170. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, M.; Ma, M.; Cao, X.; He, Y.; Wang, W.; Luo, J. Influence of annealing on the tribological properties of Zr-based bulk metallic glass. J. Non-Cryst. Solids 2018, 481, 94–97. [Google Scholar] [CrossRef]
- Kumar, G.; Rector, D.; Conner, R.D.; Schroers, J. Embrittlement of Zr-based bulk metallic glasses. Acta Mater. 2009, 57, 3572–3583. [Google Scholar] [CrossRef]
- Concustell, A.; Méar, F.O.; Surinach, S.; Baró, M.D.; Greer, A.L. Structural relaxation and rejuvenation in a metallic glass induced by shot-peening. Phil. Mag. Lett. 2009, 89, 831. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D.V.; Zadorozhnyy, V.Y.; Ketov, S.V.; Wang, Z.; Tsarkov, A.A.; Greer, A.L. On room-temperature quasi-elastic mechanical behaviour of bulk metallic glasses. Acta Mater. 2017, 129, 343–351. [Google Scholar] [CrossRef]
- Pan, J.; Wang, Y.X.; Guo, Q.; Zhang, D.; Greer, A.L.; Li, Y. Extreme rejuvenation and softening in a bulk metallic glass. Nat. Commun. 2018, 9, 560. [Google Scholar] [CrossRef] [PubMed]
- Magagnosc, D.J.; Kumar, G.; Schroers, J.; Felfer, P.; Cairney, J.M.; Gianola, D.S. Effect of ion irradiation on tensile ductility, strength and fictive temperature in metallic glass nanowires. Acta Mater. 2014, 74, 165–182. [Google Scholar] [CrossRef]
- Heo, J.; Kim, S.; Ryu, S.; Jang, D. Delocalized Plastic Flow in Proton-Irradiated Monolithic Metallic Glasses. Sci. Rep. 2016, 6, 23244. [Google Scholar] [CrossRef]
- Ketov, S.V.; Sun, Y.H.; Nachum, S.; Lu, Z.; Checchi, A.; Beraldin, A.R.; Bai, H.Y.; Wang, W.H.; Louzguine-Luzgin, D.V.; Carpenter, M.A.; et al. Rejuvenation of metallic glasses by non-affine thermal strain. Nature 2015, 524, 200–203. [Google Scholar] [CrossRef]
- Miyazaki, N.; Wakeda, M.; Wang, Y.-J.; Ogata, S. Prediction of pressure-promoted thermal rejuvenation in metallic glasses. npj Comput. Mater. 2016, 2, 1–9. [Google Scholar] [CrossRef]
- Madge, S.V.; Louzguine-Luzgin, D.V.; Kawashima, A.; Greer, A.L.; Inoue, A. Compressive plasticity of a La-based glass-crystal composite at cryogenic temperatures. Mater. Des. 2016, 101, 146–151. [Google Scholar] [CrossRef]
- Grell, D.; Dabrock, F.; Kerscher, E. Cyclic cryogenic pretreatments influencing the mechanical properties of a bulk glassy Zr-based alloy. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1330–1343. [Google Scholar] [CrossRef]
- Costa, M.B.; Londoño, J.J.; Blatter, A.; Hariharan, A.; Gebert, A.; Carpenter, M.A.; Greer, A.L. Anelastic-like nature of the rejuvenation of metallic glasses by cryogenic thermal cycling. Acta Mater. 2023, 244, 118551. [Google Scholar] [CrossRef]
- Lei, T.J.; Liu, M.; Wang, W.H.; Sun, Y.H.; Greer, A.L.; Atzmon, M. Shear transformation zone analysis of anelastic relaxation of a metallic glass reveals distinct properties of α and β relaxations. Phys. Rev. E 2019, 100, 033001. [Google Scholar] [CrossRef]
- Gallino, I.; Cangialosi, D.; Evenson, Z.; Schmitt, L.; Hechler, S.; Stolpe, M.; Beatrice Ruta, B. Hierarchical aging pathways and reversible fragile-to-strong transition upon annealing of a metallic glass former. Acta Mater. 2018, 144, 400–410. [Google Scholar] [CrossRef]
- Monnier, X.; Cangialosi, D.; Ruta, B.; Busch, R.; Gallino, I. Vitrification decoupling from α-relaxation in a metallic glass. Sci. Adv. 2020, 6, eaay1454. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P.; Goldstein, M. Molecular mobility in simple glasses. J. Phys. Chem. 1970, 74, 2034–2035. [Google Scholar] [CrossRef]
- Schneider, U.; Brand, R.; Lunkenheimer, P.; Loidl, A. Excess wing in the dielectric loss of glass formers: A Johari-Goldstein β relaxation? Phys. Rev. Lett. 2000, 84, 5560. [Google Scholar] [CrossRef]
- Cohen, Y.; Karmakar, S.; Procaccia, I.; Samwer, K. The nature of the β-peak in the loss modulus of amorphous solids. Europhys. Lett. 2012, 100, 36003. [Google Scholar] [CrossRef]
- Johari, G.P.; Goldstein, M. Viscous liquids and the glass transition. II. Secondary relaxations in glasses of rigid molecules. J. Chem. Phys. 1970, 53, 2372–2388. [Google Scholar] [CrossRef]
- Yu, H.B.; Shen, X.; Wang, Z.; Gu, L.; Wang, W.H.; Bai, H.Y. Tensile Plasticity in Metallic Glasses with Pronounced β relaxations. Phys. Rev. Lett. 2012, 108, 015504. [Google Scholar] [CrossRef]
- Yu, H.B.; Wang, W.H.; Bai, H.Y.; Wu, Y.; Chen, M.W. Relating activation of shear transformation zones to β relaxations in metallic glasses. Phys. Rev. B 2010, 81, 220201. [Google Scholar] [CrossRef]
- Küchemann, S.; Maaß, R. Gamma relaxation in bulk metallic glasses. Scr. Mater. 2017, 137, 5–8. [Google Scholar] [CrossRef]
- Lei, T.J.; DaCosta, L.R.; Liu, M.; Shen, J.; Sun, Y.H.; Wang, W.H.; Atzmon, M. Composition dependence of metallic glass plasticity and its prediction from anelastic relaxation–A shear transformation zone analysis. Acta Mater. 2020, 195, 81–86. [Google Scholar] [CrossRef]
- Qiao, J.C.; Pelletier, J.M. Dynamic Mechanical Relaxation in Bulk Metallic Glasses: A Review. J. Mater. Sci. Tech. 2014, 30, 523–545. [Google Scholar] [CrossRef]
- Hao, Q.; Pineda, E.; Wang, Y.-J.; Yang, Y.; Qiao, J.C. Reversible anelastic deformation mediated by β relaxation and resulting two-step deformation in a La60Ni15Al25 metallic glass. Phys. Rev. B 2023, 108, 024101. [Google Scholar] [CrossRef]
- Zhao, R.; Jiang, H.Y.; Luo, P.; Shen, L.Q.; Wen, P.; Sun, Y.H.; Bai, H.Y.; Wang, W.H. Reversible and irreversible β-relaxations in metallic glasses. Phys. Rev. B 2020, 101, 094203. [Google Scholar] [CrossRef]
- Wang, X.D.; Ruta, B.; Xiong, L.H.; Zhang, D.W.; Chushkin, Y.; Sheng, H.W.; Lou, H.B.; Cao, Q.P.; Jiang, J.Z. Free-volume dependent atomic dynamics in beta relaxation pronounced La-based metallic glasses. Acta Mater. 2015, 99, 290–296. [Google Scholar] [CrossRef]
- Atzmon, M.; Spaepen, F. Study of Interdiffusion in Amorphous Compositionally Modulated Ni-Zr Thin Films. In Science and Technology of Rapidly Quenched Alloys; Tenhover, M., Johnson, W.L., Tanner, L.E., Eds.; Materials Research Society: Pittsburgh, PA, USA, 1987; pp. 55–59. [Google Scholar]
- Fan, Y.; Iwashita, T.; Egami, T. Energy landscape-driven non-equilibrium evolution of inherent structure in disordered material. Nat. Comm. 2017, 8, 15417. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atzmon, M.; Ju, J.D.; Lei, T. Structural Relaxation, Rejuvenation and Plasticity of Metallic Glasses: Microscopic Details from Anelastic Relaxation Spectra. Materials 2023, 16, 7444. https://doi.org/10.3390/ma16237444
Atzmon M, Ju JD, Lei T. Structural Relaxation, Rejuvenation and Plasticity of Metallic Glasses: Microscopic Details from Anelastic Relaxation Spectra. Materials. 2023; 16(23):7444. https://doi.org/10.3390/ma16237444
Chicago/Turabian StyleAtzmon, Michael, Jong Doo Ju, and Tianjiao Lei. 2023. "Structural Relaxation, Rejuvenation and Plasticity of Metallic Glasses: Microscopic Details from Anelastic Relaxation Spectra" Materials 16, no. 23: 7444. https://doi.org/10.3390/ma16237444
APA StyleAtzmon, M., Ju, J. D., & Lei, T. (2023). Structural Relaxation, Rejuvenation and Plasticity of Metallic Glasses: Microscopic Details from Anelastic Relaxation Spectra. Materials, 16(23), 7444. https://doi.org/10.3390/ma16237444





