Effect of Zr and Er Addition on the Microstructural Evolution of a Novel Al−Mg−Zn−Er−Zr Alloy during Hot Compression
Abstract
:1. Introduction
2. Materials and Methods
3. Results
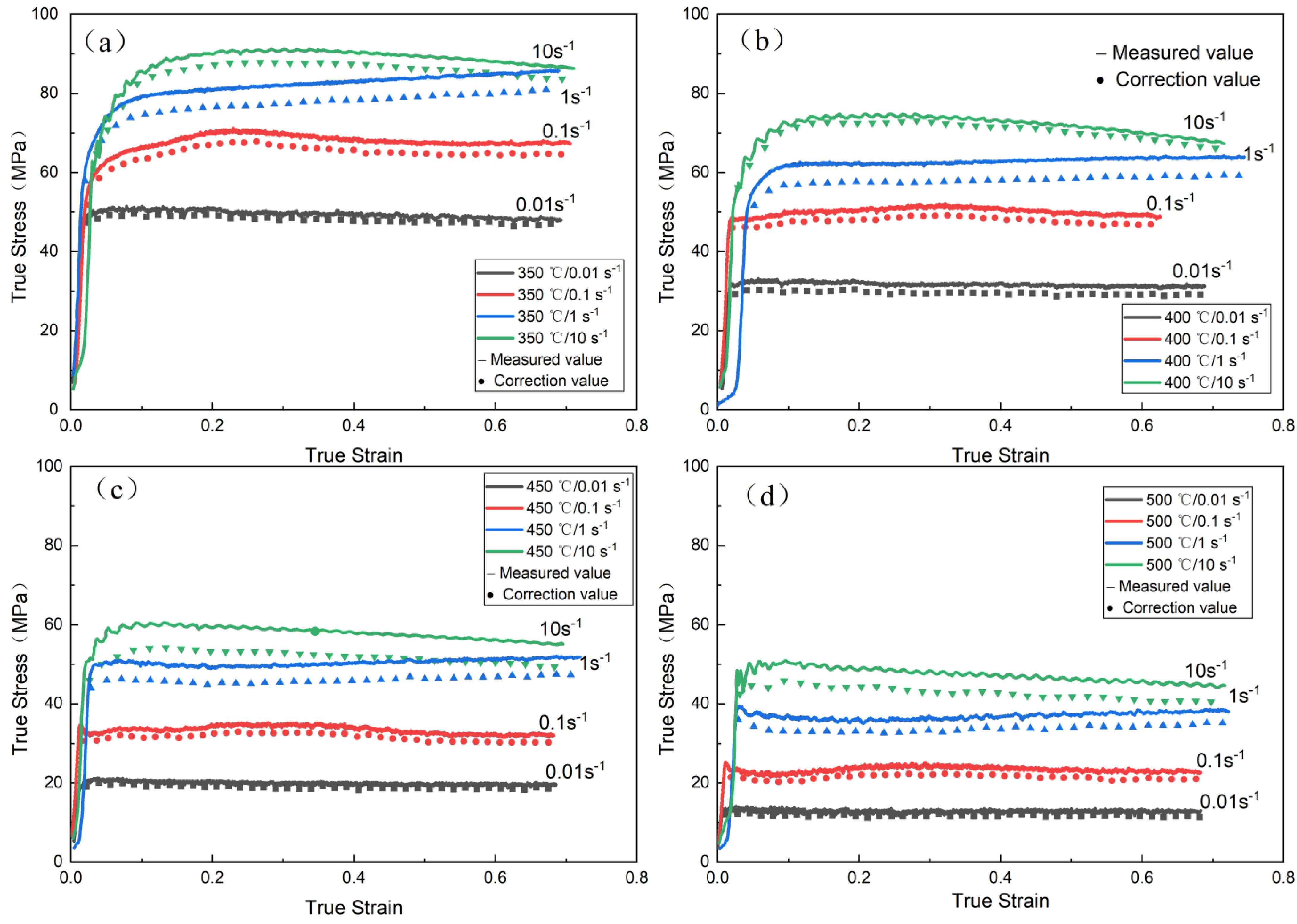
3.1. Flow Behavior
3.2. Constitutive Analyses
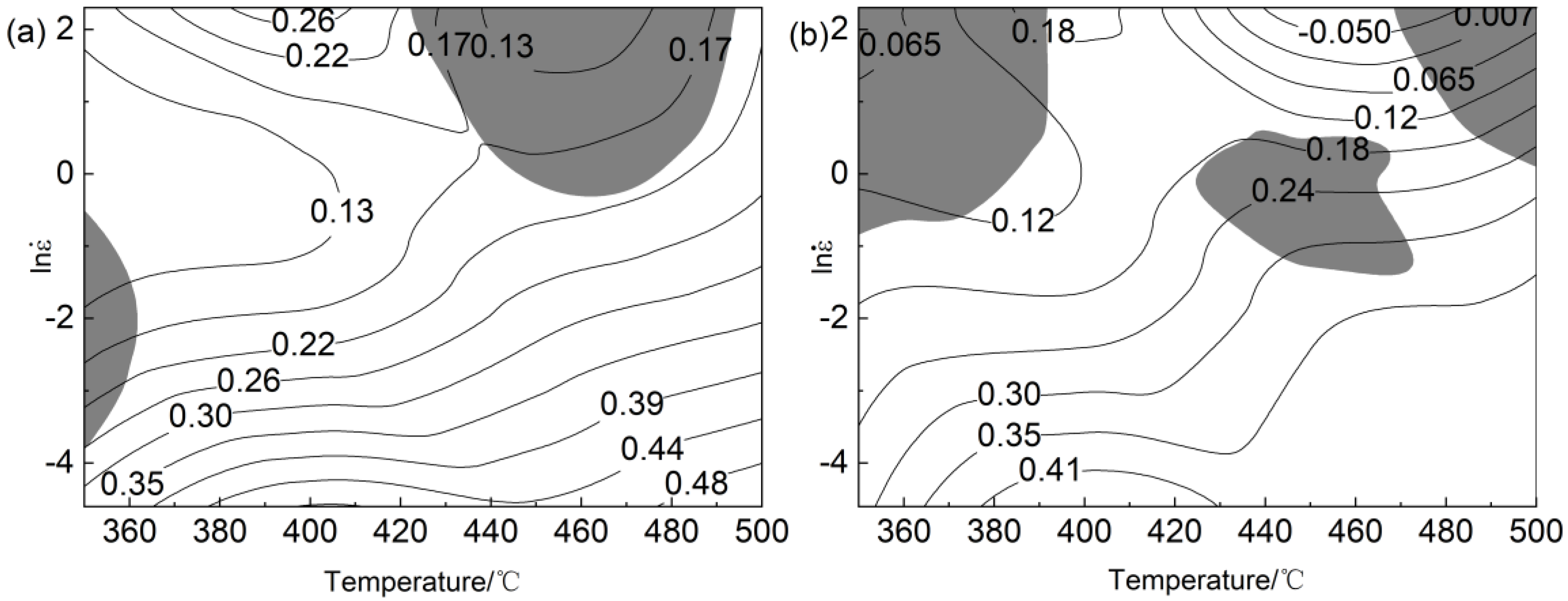
3.3. Establishment of Processing Maps
4. Discussion
4.1. Effect of Al3(Er, Zr) on the Deformation Behavior
4.2. Effect of Strain Rates on Microstructure Evolution
4.3. Effect of Deformation Temperatures on Microstructure Evolution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, M.P.; Roven, H.J.; Murashkin, M.Y.; Valiev, R.Z.; Kilmametov, A.; Zhang, Z.; Yu, Y. Structure and mechanical properties of nanostructured Al–Mg alloys processed by severe plastic deformation. J. Mater. Sci. 2013, 48, 4681–4688. [Google Scholar] [CrossRef]
- Xue, D.; Wei, W.; Shi, W.; Guo, Y.; Wen, S.P.; Wu, X.L.; Huang, H.; Nie, Z.R. Effect of cold rolling on mechanical and corrosion properties of stabilized Al–Mg–Mn–Er–Zr alloy. J. Mater. Res. Technol. 2021, 15, 6329–6339. [Google Scholar] [CrossRef]
- Wen, S.P.; Xing, Z.B.; Huang, H.; Li, B.L.; Wang, W.; Nie, Z.R. The effect of erbium on the microstructure and mechanical properties of Al–Mg–Mn–Zr alloy. Mater. Sci. Eng. A 2009, 516, 42–49. [Google Scholar] [CrossRef]
- Meng, C.; Zhang, D.; Cui, H.; Zhuang, L.; Zhang, J. Mechanical properties, intergranular corrosion behavior and microstructure of Zn modified Al–Mg alloys. J. Alloys Compd. 2014, 617, 925–932. [Google Scholar] [CrossRef]
- Wei, W.; Gonzalez, S.; Hashimoto, T.; Babu, R.; Thompson, G.E.; Zhou, X. Effect of low temperature sensitization on the susceptibility to intergranular corrosion in AA5083 aluminum alloy. Mater. Corros. 2016, 67, 331–339. [Google Scholar] [CrossRef]
- Wei, W.; González, S.; Hashimoto, T.; Abuaisha, R.R.; Thompson, G.E.; Zhou, X. In-service sensitization of a microstructurally heterogeneous AA5083 alloy. Mater. Corros. 2016, 67, 378–386. [Google Scholar] [CrossRef]
- Zhao, L.; Yan, H.; Chen, J.; Xia, W.; Su, B.; Song, M.; Li, Z.; Li, X.; Liao, Y. High ductility and strong work-hardening behavior of Zn modified as-hot-rolled Al–Mg sheets. J. Alloys Compd. 2021, 854, 157079. [Google Scholar] [CrossRef]
- Malopheyev, S.; Kulitskiy, V.; Kaibyshev, R. Deformation structures and strengthening mechanisms in an Al Mg Sc Zr alloy. J. Alloys Compd. 2017, 698, 957–966. [Google Scholar] [CrossRef]
- Xu, P.; Jiang, F.; Tang, Z.; Yan, N.; Jiang, J.; Xu, X.; Peng, Y. Coarsening of Al3Sc precipitates in Al-Mg-Sc alloys. J. Alloys Compd. 2019, 781, 209–215. [Google Scholar] [CrossRef]
- Meng, C.; Zhang, D.; Zhuang, L.; Zhang, J. Correlations between stress corrosion cracking, grain boundary precipitates and Zn content of Al–Mg–Zn alloys. J. Alloys Compd. 2016, 655, 178–187. [Google Scholar] [CrossRef]
- Wen, S.; Gao, K.; Li, Y.; Huang, H.; Nie, Z. Synergetic effect of Er and Zr on the precipitation hardening of Al–Er–Zr alloy. Scr. Mater. 2011, 65, 592–595. [Google Scholar] [CrossRef]
- Zhou, H.; Qian, Z.; Zhou, M.; Liu, X.; Li, Y. Synergistic Balance of Strength and Corrosion Resistance in Al-Mg-Er Alloys. Acta Metall. Sin. Engl. Lett. 2020, 33, 659–670. [Google Scholar] [CrossRef]
- Fu, L.; Li, Y.; Jiang, F.; Huang, J.; Xu, G.; Yin, Z. On the role of Sc or Er micro-alloying in the microstructure evolution of Al-Mg alloy sheets during annealing. Mater. Charact. 2019, 157, 109918. [Google Scholar] [CrossRef]
- Wen, S.; Wang, W.; Zhao, W.; Wu, X.; Gao, K.; Huang, H.; Nie, Z. Precipitation hardening and recrystallization behavior of Al Mg Er Zr alloys. J. Alloys Compd. 2016, 687, 143–151. [Google Scholar] [CrossRef]
- Jiang, J.; Jiang, F.; Huang, H.; Zhang, M.; Tang, Z.; Tong, M. Hot deformation analysis and microstructure evolution of Al–Mg–Mn-Sc-Zr alloy by isothermal compression. J. Alloys Compd. 2021, 858, 157655. [Google Scholar] [CrossRef]
- Huang, H.; Jiang, F.; Zhou, J.; Wei, L.; Zhong, M.; Liu, X. Hot deformation behavior and microstructural evolution of as-homogenized Al–6Mg–0.4Mn–0.25Sc–0.1Zr alloy during compression at elevated temperature. J. Alloys Compd. 2015, 644, 862–872. [Google Scholar] [CrossRef]
- Gang, M. Hot deformation behavior of an Al–5.7wt.%Mg alloy with erbium. Mater. Sci. Eng. A 2009, 516, 131–137. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, B.; Gao, M.; Guan, R. Deformation behavior and dynamic recrystallization during hot compression in ho-mogenized Al–6Mg–0.8Mn alloys. Mater. Sci. Eng. A 2022, 840, 142953. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, Y.; Tang, J.; Zhang, J. Influence of strain rate on hot deformation behavior and recrystallization behavior under isothermal compression of Al-Zn-Mg-Cu alloy. J. Alloys Compd. 2019, 809, 151788. [Google Scholar] [CrossRef]
- Lin, X.; Huang, H.; Yuan, X.; Wang, Y.; Zheng, B.; Zuo, X.; Zhou, G. Study on hot deformation behavior and processing map of a Ti-47.5Al-2.5V-1.0Cr-0.2Zr alloy with a fully lamellar microstructure. J. Alloys Compd. 2022, 901, 163648. [Google Scholar] [CrossRef]
- Wu, H.; Wen, S.; Huang, H.; Gao, K.; Wu, X.; Wang, W.; Nie, Z. Hot deformation behavior and processing map of a new type Al-Zn-Mg-Er-Zr alloy. J. Alloys Compd. 2016, 685, 869–880. [Google Scholar] [CrossRef]
- Mostafaei, M.A.; Kazeminezhad, M. Hot deformation behavior of hot extruded Al–6Mg alloy. Mater. Sci. Eng. A 2012, 535, 216–221. [Google Scholar] [CrossRef]
- Lin, Y.C.; Li, L.T.; Xia, Y.C.; Jiang, Y.Q. Hot deformation and processing map of a typical Al-Zn-Mg-Cu alloy. J. Alloys Compd. 2013, 550, 438–445. [Google Scholar] [CrossRef]
- Wu, H.; Wen, S.P.; Huang, H.; Wu, X.L.; Gao, K.Y.; Wang, W.; Nie, Z.R. Hot deformation behavior and constitutive equation of a new type Al-Zn-Mg-Er-Zr alloy during isothermal compression. Mater. Sci. Eng. A 2016, 651, 415–424. [Google Scholar] [CrossRef]
- Rudra, A.; Ashiq, M.; Tiwari, J.K.; Das, S.; Dasgupta, R. Study of Processing Map and Effect of Hot Rolling on Mechanical Properties of Aluminum 5083 Alloy. Trans. Indian Inst. Met. 2020, 73, 1809–1826. [Google Scholar] [CrossRef]
- Dai, Q.; Deng, Y.; Wang, Y.; Huang, W. Dynamic Recrystallization Critical Conditions and a Physically-Based Constitutive Model of Al-4.8Mg Alloy Under Hot Working Conditions. Materials 2020, 13, 4982. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Yang, X.; Li, J.; Xiang, S.; Shi, J.; Xu, J.; Sanders, R.E. The influence of Sc and Zr additions on microstructure and corrosion behavior of AA5182 alloy sheet. Corros. Sci. 2022, 199, 110181. [Google Scholar] [CrossRef]






| Mg | Mn | Zn | Er | Zr | Si | Fe | Al |
|---|---|---|---|---|---|---|---|
| 5.20 | 0.60 | 0.29 | 0.16 | 0.12 | 0.03 | 0.01 | Bal. |
| Composition of Alloy | Value of Hot Deformation Activation Energy | References |
|---|---|---|
| Al−5.2Mg−0.6Mn−0.29Zn−0.16Er−0.12Zr | 203.70 kJ·mol−1 | Present study |
| Al−5.7Mg−0.33Er [17] | 172.00 kJ·mol−1 | [17] |
| Al−6Mg−0.3Mn [22] | 193.88 kJ·mol−1 | [22] |
| Al−5083 [25] | 199.31 kJ·mol−1 | [25] |
| Al−4.8Mg [26] | 174.70 kJ·mol−1 | [26] |
| Pure aluminum [17] | 165.00 kJ·mol−1 | [17] |
| Deformation Condition | Composition | Recrystallized (%) | References |
|---|---|---|---|
| 450 °C/1 s−1 | Al−5.2Mg−0.6Mn−0.29Zn−0.16Er−0.12Zr | 0.97 | Present study |
| 450 °C/1 s−1 | Al−6Mg−0.8Mn | 31.19 | [17] |
| Cold-rolled | Al−5082 | 98.50 | [27] |
| Cold-rolled | Al−5082–0.05Sc−0.1Zr | 22.60 | [27] |
| Cold-rolled | Al−5082−0.1Sc−0.1Zr | 7.60 | [27] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Wei, W.; Zuo, R.; Wen, S.; Shi, W.; Zhou, X.; Wu, X.; Gao, K.; Huang, H.; Nie, Z. Effect of Zr and Er Addition on the Microstructural Evolution of a Novel Al−Mg−Zn−Er−Zr Alloy during Hot Compression. Materials 2023, 16, 858. https://doi.org/10.3390/ma16020858
Wu M, Wei W, Zuo R, Wen S, Shi W, Zhou X, Wu X, Gao K, Huang H, Nie Z. Effect of Zr and Er Addition on the Microstructural Evolution of a Novel Al−Mg−Zn−Er−Zr Alloy during Hot Compression. Materials. 2023; 16(2):858. https://doi.org/10.3390/ma16020858
Chicago/Turabian StyleWu, Minbao, Wu Wei, Rui Zuo, Shengping Wen, Wei Shi, Xiaorong Zhou, Xiaolan Wu, Kunyuan Gao, Hui Huang, and Zuoren Nie. 2023. "Effect of Zr and Er Addition on the Microstructural Evolution of a Novel Al−Mg−Zn−Er−Zr Alloy during Hot Compression" Materials 16, no. 2: 858. https://doi.org/10.3390/ma16020858
APA StyleWu, M., Wei, W., Zuo, R., Wen, S., Shi, W., Zhou, X., Wu, X., Gao, K., Huang, H., & Nie, Z. (2023). Effect of Zr and Er Addition on the Microstructural Evolution of a Novel Al−Mg−Zn−Er−Zr Alloy during Hot Compression. Materials, 16(2), 858. https://doi.org/10.3390/ma16020858








