Grain Size-Dependent Thermal Expansion of Nanocrystalline Metals
Abstract
1. Introduction
2. Methods
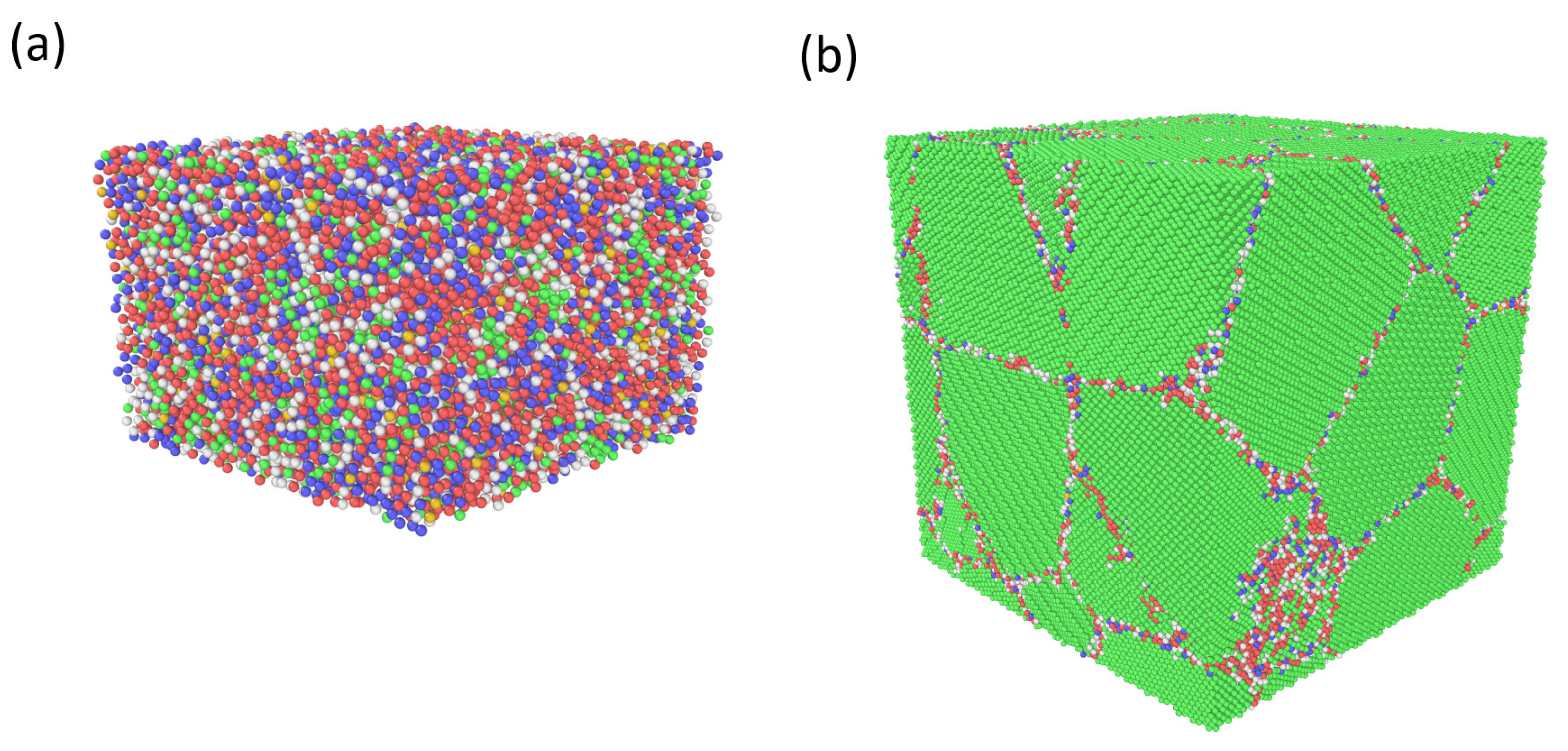
2.1. Classical Molecular Dynamics Modelling
2.2. Ab Initio Modelling
3. Results
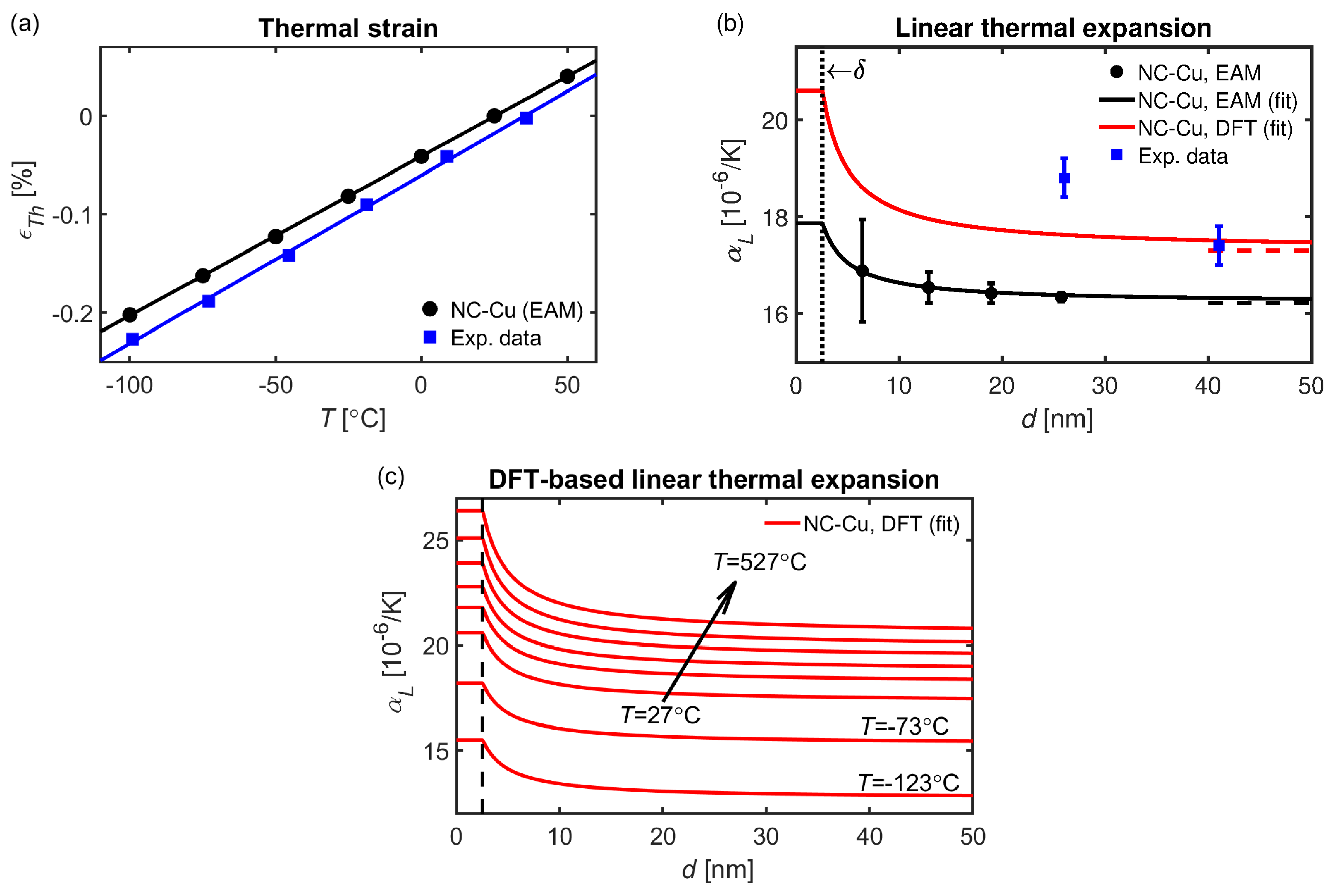
3.1. Thermal Expansion of Amorphous and Crystalline Morphologies
3.2. Thermal Expansion of Nanocrystalline Microstructures
3.3. Electronic Scale Analysis
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Linear Thermal Expansion
References
- Kolahalam, L.A.; Viswanath, I.V.K.; Diwakar, B.S.; Govindh, B.; Reddy, V.; Murthy, Y.L.N. Review on nanomaterials: Synthesis and applications. Mater. Today Proc. 2019, 18, 2182. [Google Scholar] [CrossRef]
- Petford-Long, A.K.; Chiaramonti, A.N. Transmission Electron Microscopy of Multilayer Thin Films. Annu. Rev. Mater. Res. 2008, 38, 559. [Google Scholar] [CrossRef]
- Piraux, L.; George, J.M.; Despres, J.F.; Leroy, C.; Ferain, E.; Legras, R.; Ounadjela, K.; Fert, A. Giant magnetoresistance in magnetic multilayered nanowires. Appl. Phys. Lett. 1994, 65, 2484. [Google Scholar] [CrossRef]
- Mikhaylova, M.; Kim, D.K.; Bobrysheva, N.; Osmolowsky, M.; Semenov, V.; Tsakalakos, T.; Muhammed, M. Superparamagnetism of magnetite nanoparticles: Dependence on surface modification. Langmuir 2004, 20, 2472. [Google Scholar] [CrossRef] [PubMed]
- Cuenot, S.; Frétigny, C.; Demoustier-Champagne, S.; Nysten, B. Surface tension effect on the mechanical properties of nanomaterials measured by atomic force microscopy. Phys. Rev. B 2004, 69, 165410. [Google Scholar] [CrossRef]
- Zhou, L.G.; Huang, H. Are surfaces elastically softer or stiffer? Appl. Phys. Lett. 2004, 84, 1940–1942. [Google Scholar] [CrossRef]
- Dingreville, R.; Qu, J.; Cherkaoui, M. Surface free energy and its effect on the elastic behavior of nano-sized particles, wires and films. J. Mech. Phys. Solids 2005, 53, 1827–1854. [Google Scholar] [CrossRef]
- Petrova, H.; Perez-Juste, J.; Zhang, Z.Y.; Zhang, J.; Kosel, T.; Hartland, G.V. Crystal structure dependence of the elastic constants of gold nanorods. J. Mater. Chem. 2006, 16, 3957–3963. [Google Scholar] [CrossRef]
- Olsson, P.A.T.; Melin, S.; Persson, C. Atomistic simulations of tensile and bending properties of single-crystal bcc iron nanobeams. Phys. Rev. B 2007, 76, 224112. [Google Scholar] [CrossRef]
- Richter, G.; Hillerich, K.; Gianola, D.S.; Mönig, R.; Kraft, O.; Volkert, C.A. Ultrahigh Strength Single Crystalline Nanowhiskers Grown by Physical Vapor Deposition. Nano Lett. 2009, 9, 3048–3052. [Google Scholar] [CrossRef]
- Olsson, P.A.T. Transverse resonant properties of strained gold nanowires. J. Appl. Phys. 2010, 108, 034318. [Google Scholar] [CrossRef]
- Olsson, P.A.T.; Park, H.S.; Lidström, P.C. The Influence of shearing and rotary inertia on the resonant properties of gold nanowires. J. Appl. Phys. 2010, 108, 104312. [Google Scholar] [CrossRef]
- Olsson, P.A.T.; Park, H.S. Atomistic study of the buckling of gold nanowires. Acta Mater. 2011, 59, 3883–3894. [Google Scholar] [CrossRef]
- Olsson, P.A.T.; Park, H.S. On the importance of surface elastic contributions to the flexural rigidity of nanowires. J. Mech. Phys. Solids 2012, 60, 2064–2083. [Google Scholar] [CrossRef]
- Schiøtz, J.; Di Tolla, F.; Jacobsen, K. Softening of nanocrystalline metals at very small grain sizes. Nature 1998, 391, 561–563. [Google Scholar] [CrossRef]
- Schiøtz, J.; Jacobsen, K.W. A Maximum in the Strength of Nanocrystalline Copper. Science 2003, 301, 1357. [Google Scholar] [CrossRef]
- Gupta, A.; Gruber, J.; Rajaram, S.S.; Thompson, G.B.; McDowell, D.L.; Tucker, G.J. On the mechanistic origins of maximum strength in nanocrystalline metals. npj Comput. Mater. 2020, 6, 153. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Han, Z.; Zhao, Y. Grain-size-dependent thermal conductivity of nanocrystalline materials. J. Nanopart. Res. 2016, 18, 296. [Google Scholar] [CrossRef]
- Daniel, R.; Holec, D.; Bartosik, M.; Keckes, J.; Mitterer, C. Size effect of thermal expansion and thermal/intrinsic stresses in nanostructured thin films: Experiment and model. Acta Mater. 2011, 59, 6631. [Google Scholar] [CrossRef]
- Klam, H.J.; Hahn, H.; Gleiter, H. The thermal expansion of grain boundaries. Acta Metall. 1987, 35, 2101–2104. [Google Scholar] [CrossRef]
- Lu, T.J.; Fleck, N.A. The thermal shock resistance of solids. Acta Mater. 1998, 46, 4755. [Google Scholar] [CrossRef]
- Janssen, G.C.A.M. Stress and strain in polycrystalline thin films. Thin Solid Films 2007, 515, 6654. [Google Scholar] [CrossRef]
- Kuru, Y.; Wohlschlögel, M.; Welzel, U.; Mittemeijer, E.J. Crystallite size dependence of the coefficient of thermal expansion of metals. Appl. Phys. Lett. 2007, 90, 243113. [Google Scholar] [CrossRef]
- Kuru, Y.; Wohlschlögel, M.; Welzel, U.; Mittemeijer, E.J. Coefficients of thermal expansion of thin metal films investigated by non-ambient X-ray diffraction stress analysis. Surf. Coat. Technol. 2008, 202, 2306–2309. [Google Scholar] [CrossRef]
- Bogatyrenko, S.; Kryshtal, A. Thermal expansion coefficients of Ag, Cu and diamond nanoparticles: In situ TEM diffraction and EELS measurements. Mater. Charact. 2021, 178, 111296. [Google Scholar] [CrossRef]
- Birringer, R.; Gleiter, H. Nanocrystalline Materials. In Encyclopedia of Materials Science and Engineering: Supplementary, Vol. 1 (Advances in Materials Science and and Engineering); Cahn, R.W., Ed.; Pergamon Press: Oxford, UK, 1988; pp. 339–349. [Google Scholar]
- Qin, X.Y. Thermal expansion behavior of nanocrystalline silver at high temperatures. Acta Phys. Sin. 1995, 44, 244–250. [Google Scholar]
- Lu, K.; Sui, M.L. Thermal expansion behaviors in nanocrystalline materials with a wide grain size range. Acta Mater. 1995, 43, 3325–3332. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Lu, K. Grain-size dependence of thermal properties of nanocrystalline elemental selenium studied by x-ray diffraction. Phys. Rev. B 1997, 56, 14330–14337. [Google Scholar] [CrossRef]
- Yang, C.C.; Xiao, M.X.; Li, W.; Jiang, Q. Size effects on Debye temperature, Einstein temperature, and volume thermal expansion coefficient of nanocrystals. Solid State Commun. 2006, 139, 148. [Google Scholar] [CrossRef]
- Yang, L.; Ge, T.; Guo, G.Q.; Huang, C.L.; Meng, X.F.; Wei, S.H.; Chen, D.; Chen, L.Y. Atomic and cluster level dense packing contributes to the high glass-forming ability in metallic glasses. Intermetallics 2013, 34, 106. [Google Scholar] [CrossRef]
- Eastman, J.A.; Fitzsimmons, M.R.; Thompson, L.J. The thermal properties of nanocrystalline Pd from 16 to 300 K. Philos. Mag. B 1992, 66, 667–696. [Google Scholar] [CrossRef]
- Eastman, J.A.; Fitzsimmons, M.R.; Thompson, L.J.; Lawson, A.C.; Robinson, R.A. Diffraction studies of the thermal properties of nanocrystalline Pd and Cr. Nanostruct. Mater. 1992, 1, 465–470. [Google Scholar] [CrossRef]
- Turi, T.; Erb, U. Thermal expansion and heat capacity of porosity-free nanocrystalline materials. Mater. Sci. Eng. A 1995, 204, 34–38. [Google Scholar] [CrossRef]
- Panigrahi, B.B.; Dabhade, V.V.; Godkhindi, M.M. Thermal expansion behaviour of nanocrystalline titanium powder compacts. Mater. Lett. 2005, 59, 2539–2541. [Google Scholar] [CrossRef]
- Fang, W.; Lo, C.-Y. On the thermal expansion coefficients of thin films. Sens. Actuator A Phys. 2000, 84, 310–314. [Google Scholar] [CrossRef]
- Chang, I.-L.; Chang, F.-R. The atomistic study on the thermal expansion behaviors of nanowires. Comput. Mater. Sci. 2012, 54, 266. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Huang, B.-L.; Zhang, T.-Y. Size- and temperature-dependent Young’s modulus and size-dependent thermal expansion coefficient of thin films. Phys. Chem. Chem. Phys. 2016, 18, 21508. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast parallel algorithms for short-range molecular dynamics. J. Chem. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Comm. 2002, 271, 108171. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper: ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef]
- Hallberg, H.; Olsson, P.A.T. Investigation of microstructure evolution during self-annealing in thin Cu films by combining mesoscale level set and ab initio modeling. J. Mech. Phys. Solids 2016, 90, 160–178. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The Nosé–Hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Foley, D.; Coleman, S.P.; Tucker, G.; Tschopp, M.A. Voronoi Based Nanocrystalline Generation Algorithm for Atomistic Simulations; ARL Technical Note. ARL-TN-0806; US Army Research Laboratory: Adelphi, MD, USA, 2016. [Google Scholar]
- Fortunato, M.E.; Mattson, J.; Taylor, D.E.; Larentzos, J.P.; Brennan, J.K. Pre- and Post-Processing Tools to Create and Characterize Particle-Based Composite Model Structures; ARL Technical Report, ARL-TR-8213; US Army Research Laboratory: Adelphi, MD, USA, 2017. [Google Scholar]
- Ackland, G.J.; Jones, A.P. Applications of local crystal structure measures in experiment and simulation. Phys. Rev. B 2006, 73, 054104. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mat. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Efficient projector expansion for the ab initio LCAO method. Phys. Rev. B 2005, 72, 045121. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Music, D.; Geyer, R.W.; Schneider, J.M. Recent progress and new directions in density functional theory based design of hard coatings. Surf. Coat. Technol. 2016, 286, 178–190. [Google Scholar] [CrossRef]
- Söderlind, P.; Nordström, L.; Yongming, L.; Johansson, B. Relativistic effects on the thermal expansion of the actinide elements. Phys. Rev. B 1990, 42, 4544. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Dronskowski, R.; Blöchl, P.E. Crystal Orbital Hamilton Populations (COHP). Energy-Resolved Visualization of Chemical Bonding in Solids based on Density-Functional Calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougreeff, A.L.; Dronskowski, R. Crystal Orbital Hamilton Population (COHP) Analysis as Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef]
- Maintz, S.; Deringer, V.L.; Tchougreeff, A.L.; Dronskowski, R. Analytic Projection from Plane-Wave and PAW Wavefunctions and Application to Chemical-Bonding Analysis in Solids. J. Comput. Chem. 2013, 34, 2557–2567. [Google Scholar] [CrossRef]
- Nelson, R.; Ertural, C.; George, J.; Deringer, V.L.; Hautier, G.; Dronskowski, R. LOBSTER: Local orbital projections, atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory. J. Comput. Chem. 2020, 41, 1931–1940. [Google Scholar] [CrossRef] [PubMed]
- Manz, T.A. Introducing DDEC6 atomic population analysis: Part 3. Comprehensive method to compute bond orders. RSC Adv. 2017, 7, 45552–45581. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Pearson, W.B. A Handbook of Lattice Spacings and Structures of Metals and Alloys, 1st ed.; Pergamon: Oxford, UK, 1958; pp. 123–130. [Google Scholar]
- Carvill, J. Mechanical Engineer’s Data Handbook, 1st ed.; Butterworth-Heinemann: Oxford, UK, 1993; pp. 218–266. [Google Scholar]
- Wang, L.; Teng, J.; Liu, P.; Hirata, A.; Ma, E.; Zhang, Z.; Chen, M.; Han, X. Grain rotation mediated by grain boundary dislocations in nanocrystalline platinum. Nat. Commun. 2014, 5, 4402. [Google Scholar] [CrossRef]
- Music, D.; Schmidt, P.; Czigány, Z.; Greczynski, G.; Geyer, R.W.; Hans, M. Electrical resistivity modulation of thermoelectric iron based nanocomposites. Vacuum 2018, 157, 384–390. [Google Scholar] [CrossRef]
- O’Connell, K.; Regalbuto, J.R. High Sensitivity Silicon Slit Detectors for 1 nm Powder XRD Size Detection Limit. Catal. Lett. 2015, 145, 777–783. [Google Scholar] [CrossRef]
- Munro, J.M.; Latimer, K.; Horton, M.K.; Dwaraknath, S.; Persson, K.A. An improved symmetry-based approach to reciprocal space path selection in band structure calculations. npj Comput. Mater. 2020, 6, 112. [Google Scholar] [CrossRef]
- Mavračić, J.; Mocanu, F.C.; Deringer, V.L.; Csányi, G.; Elliott, S.R. Similarity Between Amorphous and Crystalline Phases: The Case of TiO2. J. Phys. Chem. Lett. 2018, 9, 2985–2990. [Google Scholar] [CrossRef]
- Jaiswal, R.L.; Pandey, B.K.; Mishra, D.; Fatma, H. Thermo-physical Behavior of Nanomaterials with the Change in Size and Shape. Int. J. Thermodyn. 2021, 24, 1–7. [Google Scholar] [CrossRef]
- Goyal, M.; Gupta, B.R.K. Shape, size and temperature dependency of thermal expansion, lattice parameter and bulk modulus in nanomaterials. Pramana J. Phys. 2018, 90, 80. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olsson, P.A.T.; Awala, I.; Holmberg-Kasa, J.; Krause, A.M.; Tidefelt, M.; Vigstrand, O.; Music, D. Grain Size-Dependent Thermal Expansion of Nanocrystalline Metals. Materials 2023, 16, 5032. https://doi.org/10.3390/ma16145032
Olsson PAT, Awala I, Holmberg-Kasa J, Krause AM, Tidefelt M, Vigstrand O, Music D. Grain Size-Dependent Thermal Expansion of Nanocrystalline Metals. Materials. 2023; 16(14):5032. https://doi.org/10.3390/ma16145032
Chicago/Turabian StyleOlsson, Pär A. T., Ibrahim Awala, Jacob Holmberg-Kasa, Andreas M. Krause, Mattias Tidefelt, Oscar Vigstrand, and Denis Music. 2023. "Grain Size-Dependent Thermal Expansion of Nanocrystalline Metals" Materials 16, no. 14: 5032. https://doi.org/10.3390/ma16145032
APA StyleOlsson, P. A. T., Awala, I., Holmberg-Kasa, J., Krause, A. M., Tidefelt, M., Vigstrand, O., & Music, D. (2023). Grain Size-Dependent Thermal Expansion of Nanocrystalline Metals. Materials, 16(14), 5032. https://doi.org/10.3390/ma16145032






