Parametric Random Vibration Analysis of an Axially Moving Laminated Shape Memory Alloy Beam Based on Monte Carlo Simulation
Abstract
:1. Introduction
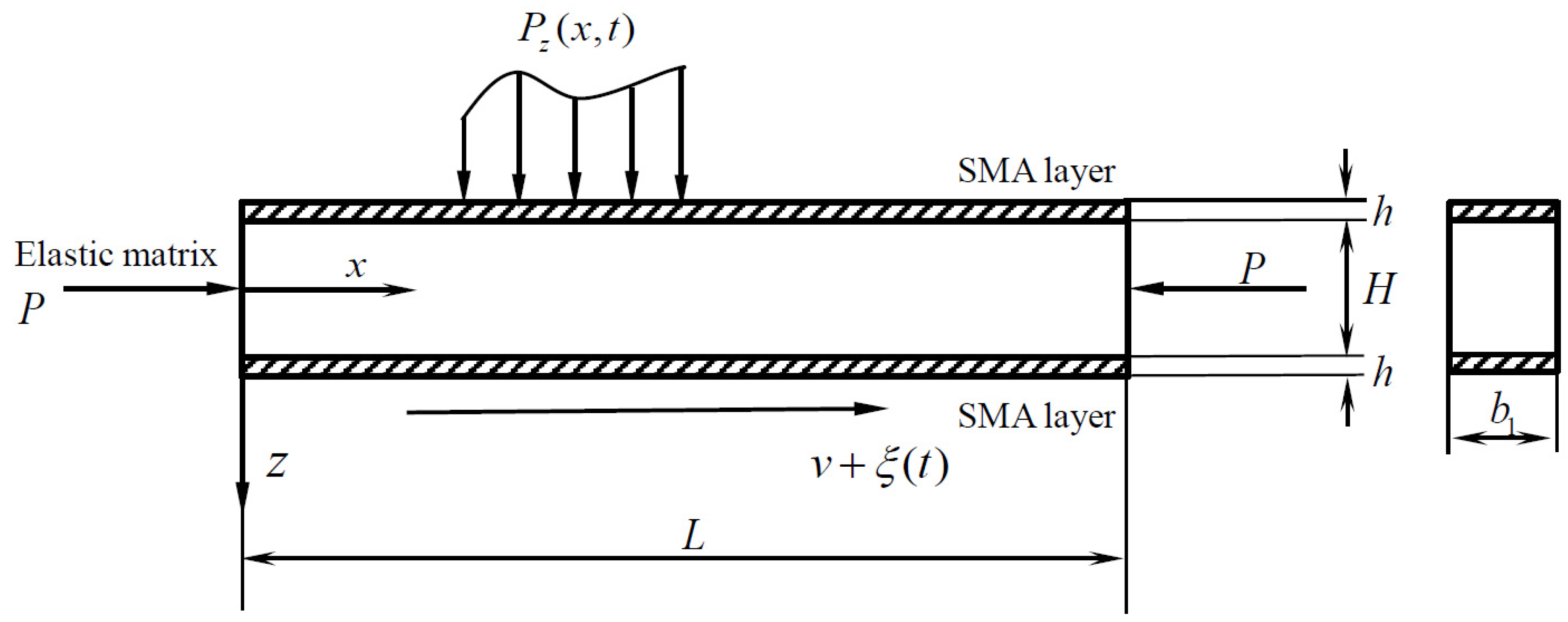
2. Random Vibration Equation of Laminated SMA Beams Moving Axially with Variable Velocity
2.1. Polynomial Constitutive Relation of SMA
2.2. Dynamics Equation of Laminated SMA Beams
3. Numerical Example and Parametric Effects
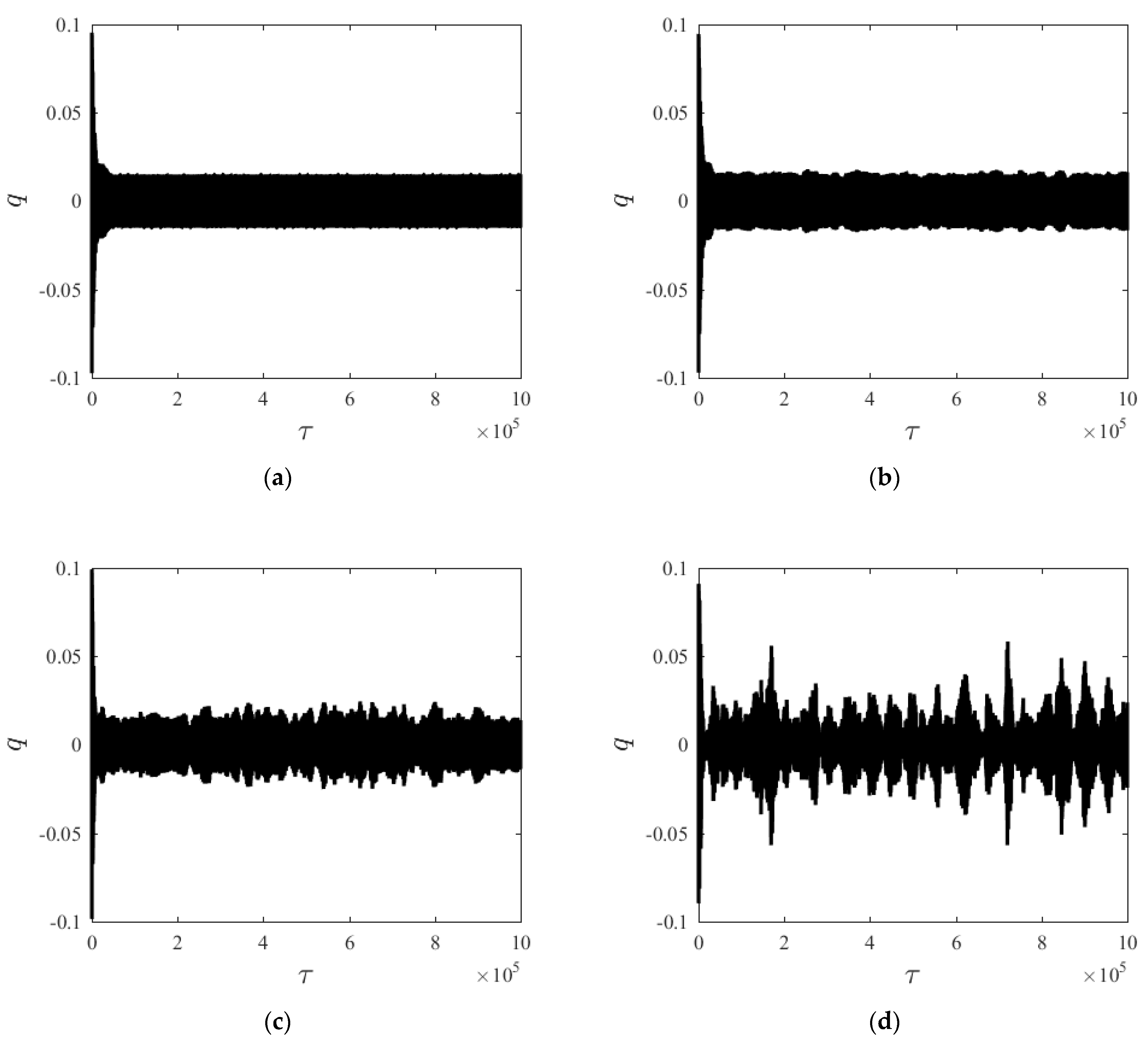
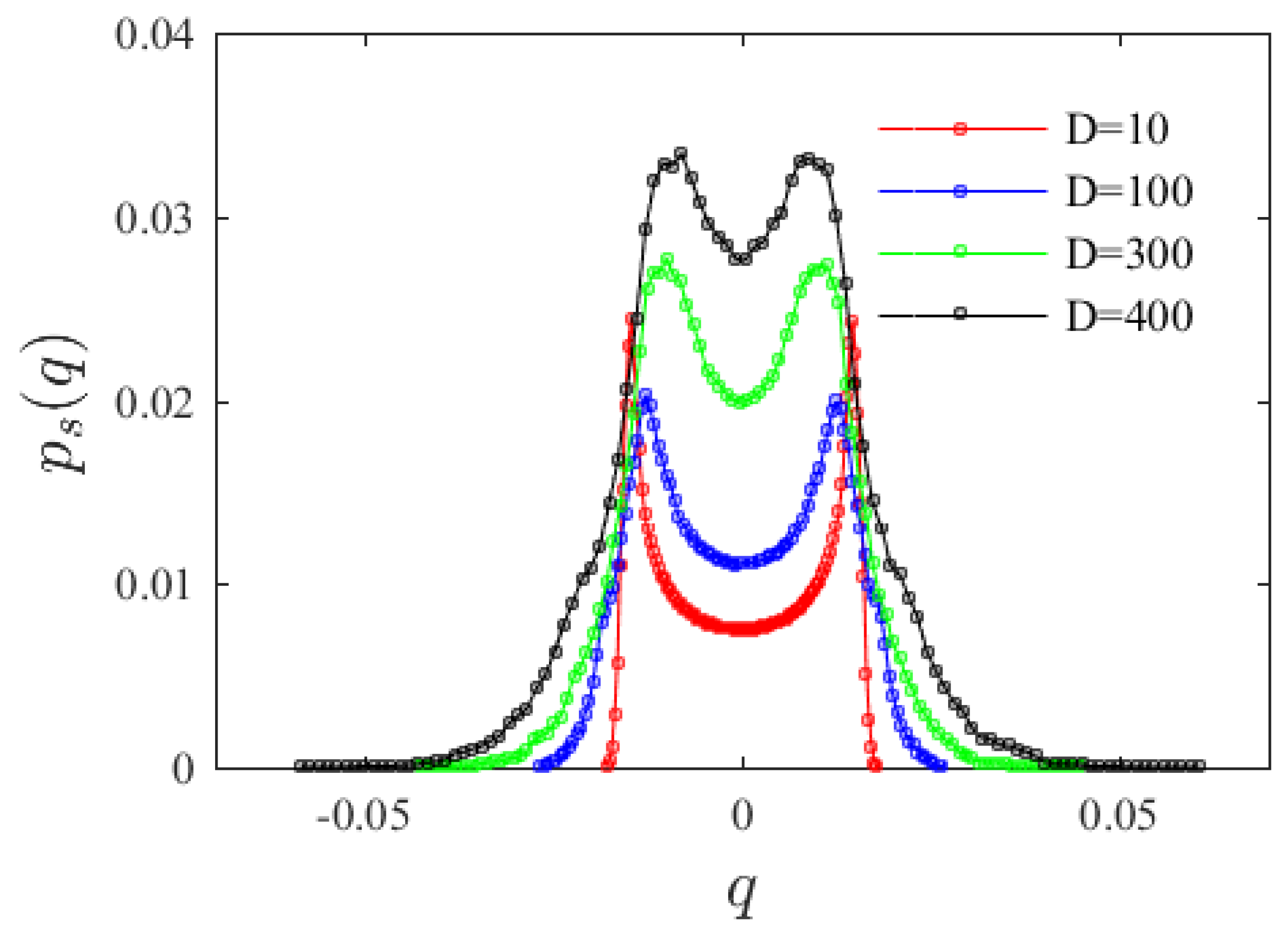
3.1. Effect of Random Intensity
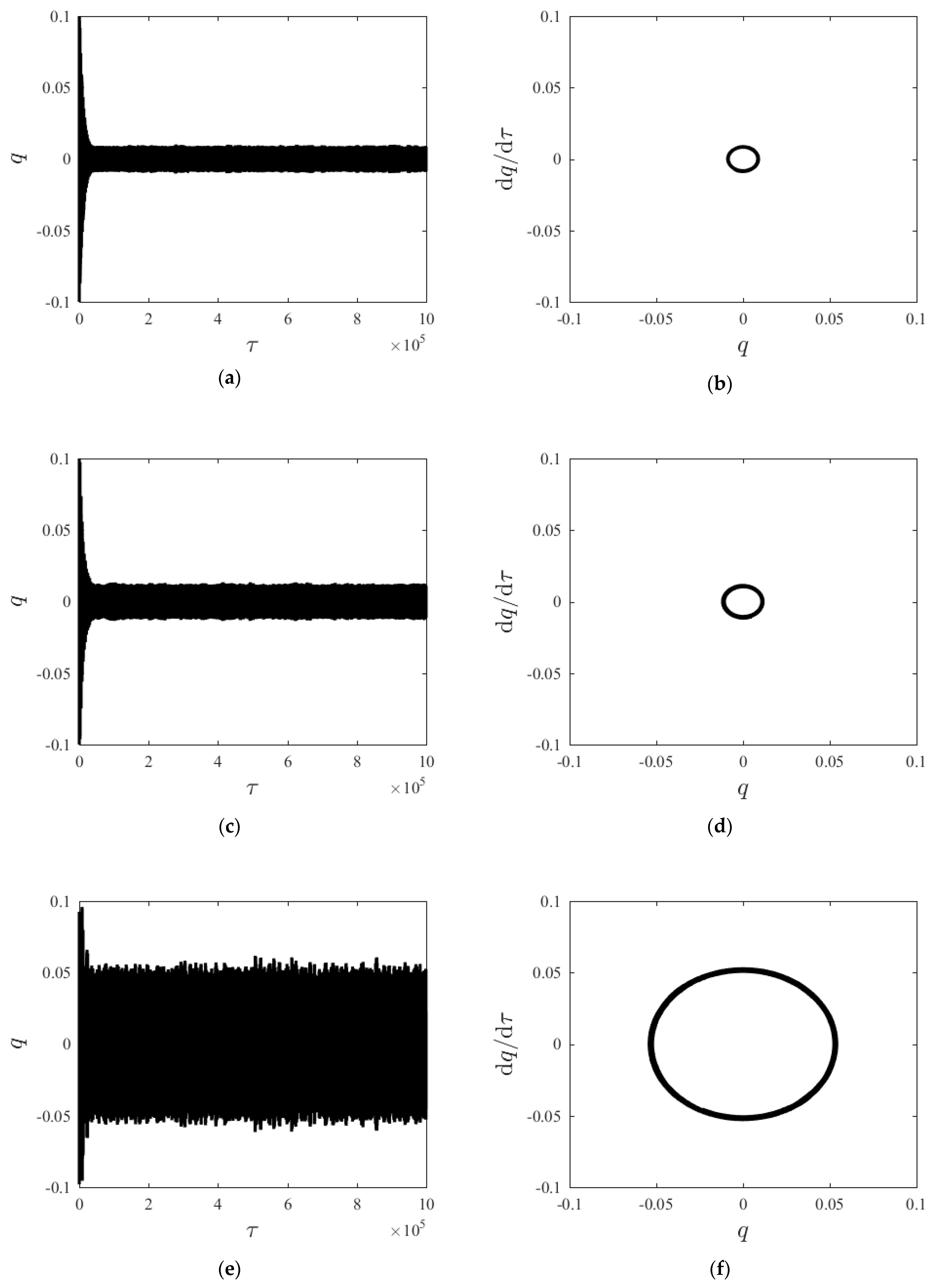
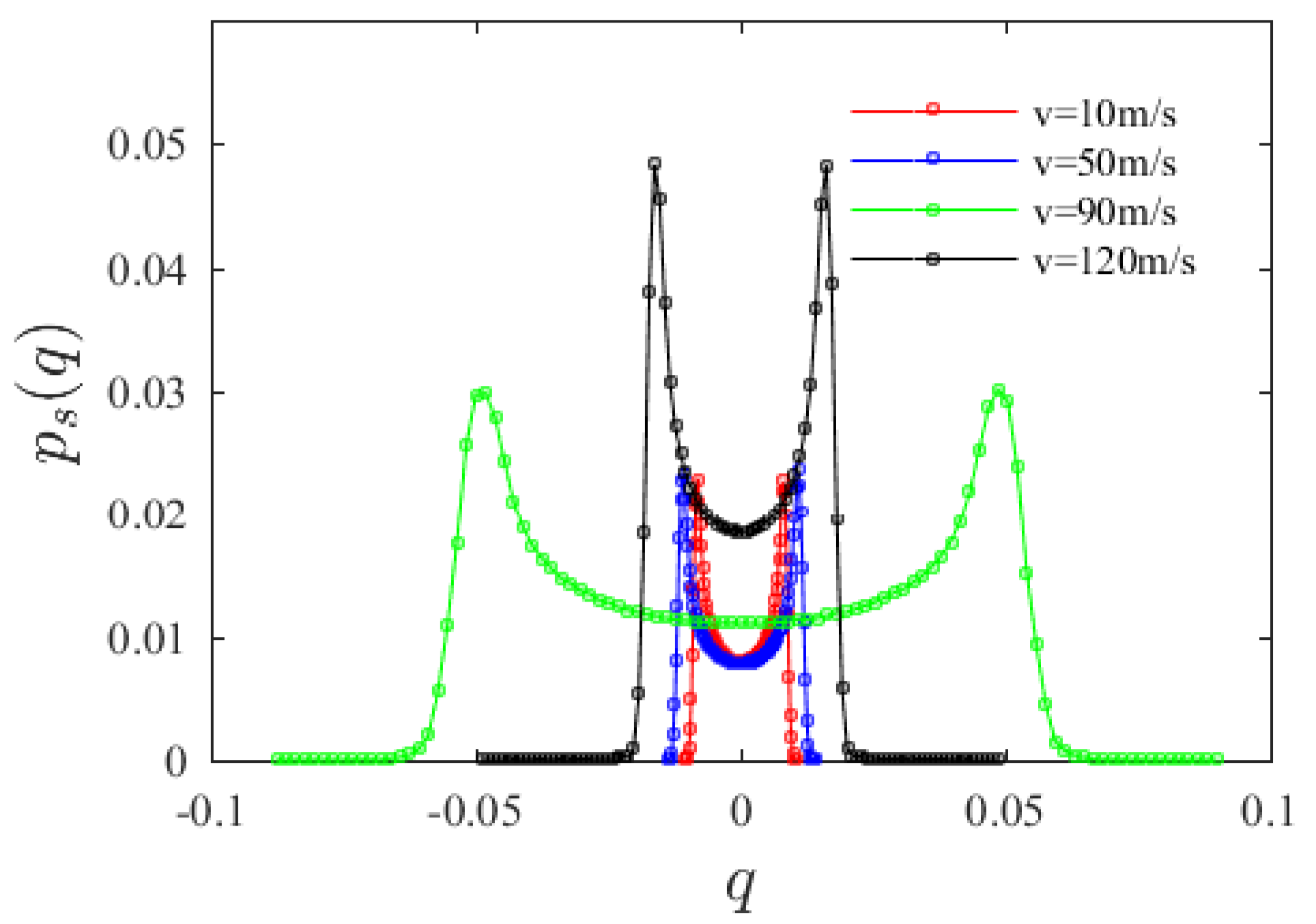
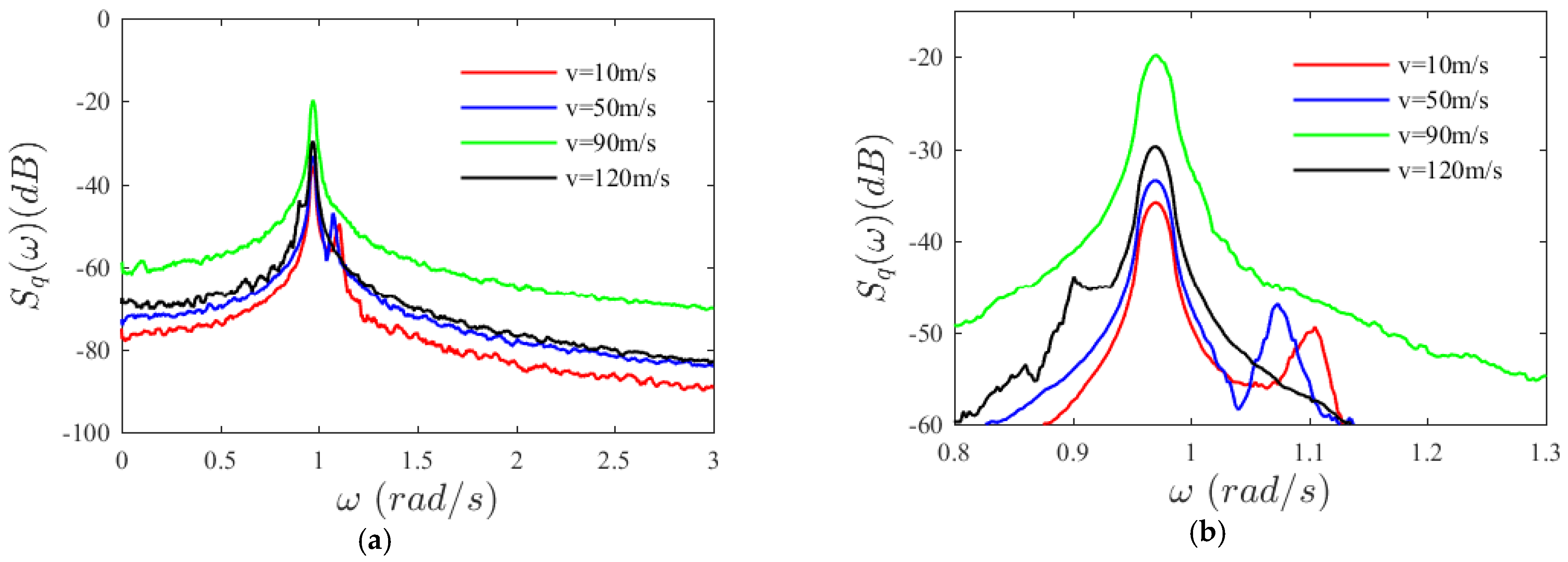
3.2. Effect of Axial Velocity
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, S.H.; Huang, J.L. On internal resonance of nonlinear vibration of axially moving beams. Acta Mech. Sin. 2005, 37, 57–63. [Google Scholar]
- Ding, H.; Chen, L.Q.; Zhang, G.C. Advances in Nonlinear Models for Transverse Vibration of Axially Moving Beams. J. Dyn. Control 2013, 11, 20–30. [Google Scholar]
- Yang, X.D. Dynamical Analysis of Transverse Vibrations of Axially Moving Viscoelastic Beams. Ph.D. Thesis, Shang Hai University, Shanghai, China, 2004. [Google Scholar]
- Liu, X.G.; Tang, Y.Q.; Zhou, Y. Comparison of Vibration Characteristics of Three Typical Axially Moving Structures. Chin. J. Theor. Appl. Mech. 2020, 52, 522–532. [Google Scholar]
- Ding, H.; Chen, L.Q. Transverse Non Linear Forced Vibration of Axially Moving Iscoelastic Beam. J. Vib. Shock 2009, 28, 128–131. [Google Scholar]
- Al-Bedoor, B.O.; Khulief, Y.A. An Approximate Analytical Solution of Beam Vibrations During Axlal Motion. J. Sound Vib. 1996, 192, 159–171. [Google Scholar] [CrossRef]
- Sze, K.Y.; Chen, S.H.; Huang, J.L. The Incremental Harmonic Balance Method for Nonlinear Vibration of Axially Moving Beams. J. Sound Vib. 2005, 281, 611–626. [Google Scholar] [CrossRef] [Green Version]
- Özhan, B.B. Vibration and Stability Analysis of Axially Moving Beams with Variable Speed and Axial Force. Int. J. Struct. Stab. Dyn. 2014, 14, 1450015. [Google Scholar] [CrossRef]
- Lenci, S.; Rega, G. Axial-transversal Coupling in The Free Nonlinear Vibrations of Timoshenko Beams with Arbitrary Slenderness and Axial Boundary Conditions. Proc. Math. Phys. Eng. Sci. 2016, 472, 20160057. [Google Scholar] [CrossRef] [Green Version]
- Xiao, G.; Chen, B.; Li, S.; Zhuo, X. Fatigue life analysis of aero-engine blades for abrasive belt grinding considering residual stress. Eng. Faire Anal. 2022, 131, 105846. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, Y.; Wang, Y.; Zhang, T.; Jia, H. Hybrid Dynamic Modeling and Analysis of High-Speed Thin-Rimmed Gears. J. Mech. Des. 2021, 143, 123401. [Google Scholar] [CrossRef]
- Jin, X.; Chen, Y.; Wang, L.; Han, H.; Chen, P. Failure prediction, monitoring and diagnosis methods for slewing bearingsof large-scale wind turbine: A review. Measurement 2021, 172, 10855. [Google Scholar] [CrossRef]
- Mirzaeifar, R.; DesRoches, R.A.; Yavari, A. Combined Analytical, Numerical, and Experimental Study of Shape-memory-alloy Helical Springs. Int. J. Solids Struct. 2011, 48, 611–624. [Google Scholar] [CrossRef]
- Shao, B.; Ren, Y.S. Analysis of Free Vibrations of Shape Memory Alloy Hybrid Composite Beams. Eng. Mech. 2003, 20, 183–187. [Google Scholar]
- Shao, B.; Ren, Y.S. The Semi-Active Control of Shape Memory Alloy Composite Beam. Mech. Eng. 2004, 26, 16–19. [Google Scholar]
- Ren, Y.S.; Liu, T.R.; Yang, S.L.; Wang, X.H. Active Deformation Models of Sma Fiber Hybrid Thin-Wall-ed Laminated Beams. Chin. J. Solid Mech. 2010, 31, 228–236. [Google Scholar]
- Collet, M.; Foltête, E.; Lexcellent, C. Analysis of The Behavior of a Shape Memory Alloy Beam under Dynamical Loading. Eur. J. Mech. A/Solids 2001, 20, 615–630. [Google Scholar] [CrossRef]
- de Matos Junior, O.D.; Donadon, M.V.; Castro, S.G.P. Aeroelastic Behavior of Stiffened Composite Laminated Panel with Embedded SMA Wire Using the Hierarchical Rayleigh–Ritz Method. Compos. Struct. 2017, 181, 26–45. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhou, S.; Meng, W.Q.; Piao, X.D. Expermental Study on Random Vibration of Avaiation Conduit with Memory Alloy Joint. Chin. J. Constr. Mach. 2018, 16, 95–100. [Google Scholar]
- Razavilar, R.; Fathi, A.; Dardel, M.; Hadi, J.A. Dynamic analysis of a shape memory alloy beam with pseudoelastic behavior. J. Intell. Mater. Syst. Struct. 2018, 29, 1835–1849. [Google Scholar] [CrossRef]
- Nassiri-monfared, A.; Baghani, M.; Zakerzadeh, M.R.; Fahimi, P. Developing a Semi-analytical Model for Thermomechanical Response of SMA Laminated Beams, Considering SMA Asymmetric Behavior. Meccanica 2018, 53, 957–971. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, M.; Hao, Y. The 1/3rd Subharmonic and 3rd Superharmonic Resonance of a Shape Memory Alloy (SMA) Laminated Beam. J. Theor. Appl. Mech. 2020, 59, 27–41. [Google Scholar] [CrossRef]
- Nejati, M.; Ghasemi-Ghalebahman, A.; Soltanimaleki, A.; Dimitri, R.; Tornabene, F. Thermal Vibration Analysis of SMA Hybrid Composite Double Curved Sandwich Panels. Compos. Struct. 2019, 224, 111035. [Google Scholar] [CrossRef]
- Samadpour, M.; Asadi, H.; Wang, Q. Nonlinear Aero-thermal Flutter Postponement of Supersonic Laminated Composite Beams with Shape Memory Alloys. Eur. J. Mech.-A/Solids 2016, 57, 18–28. [Google Scholar] [CrossRef]
- Li, B.; Tang, Y.Q.; Ding, H.; Chen, L.Q. Nonlinear Vibrations of Axially Moving Viscoelastic Timoshenko Beams under Strong External Excitation. J. Vib. Shock 2012, 31, 142–146. [Google Scholar]
- Ding, H.; Yan, Q.Y.; Chen, L.Q. Chaotic Dynamics in The Forced Nonlinear Vibration of an Axially Accelerating Viscoelastic Beam. Acta Phys. Sin 2013, 62, 1–7. [Google Scholar] [CrossRef]
- Ding, H.; Tan, X.; Zhang, G.C.; Chen, L.Q. Equilibrium Bifurcation of High-speed Axially Moving Timoshenko Beams. Acta Mech. 2016, 227, 3001–3014. [Google Scholar] [CrossRef]
- Wang, J.; Hu, Y.D. Magneto-elastic Primary Resonance of Axially Moving Current-carrying Beams in Magnetic Fieid. J. Vib. Shock 2016, 35, 65–73. [Google Scholar]
- Wang, J.; Hu, Y.D.; Su, Y.; Gong, L.F.; Zhang, Q.N. Magneto-elastic internal resonance of an axially moving conductive beam in the magnetic field. J. Theor. Appl. Mech. 2019, 57, 179–191. [Google Scholar] [CrossRef]
- Tang, Y.; Ma, Z. Nonlinear Vibration of Axially Moving Beams with Internal Resonance, Speed-dependent Tension, and Tension-dependent Speed. Nonlinear Dyn. 2019, 98, 2475–2490. [Google Scholar] [CrossRef]
- Shao, M.; Wu, J.M.; Wang, Y.; Wu, Q.M. Nonlinear Parametric Vibration and Chaotic Behaviors of an Axially Accelerating Moving Membrane. Shock Vib. 2019, 2019, 6294814. [Google Scholar] [CrossRef]
- Sahoo, B.; Panda, L.N.; Pohit, G. Two-frequency Parametric Excitation and Internal Resonance of a Moving Viscoelastic Beam. Nonlinear Dyn. 2015, 82, 1721–1742. [Google Scholar] [CrossRef]
- Yan, T.; Yang, T.Z.; Ding, H.; Chen, L.Q. Direct Multiscale Analysis of The Stability of an Axially Moving Compressible Sandwich Beam with Time-dependent Velocity. J. Vib. Shock. 2019, 38, 40–44. [Google Scholar]
- Hu, R.C.; Zhang, D.X.; Huan, R.H.; Deng, Z.C. Response and reliability analysis of random time-delay controlled systems undergo wide-band random excitations. Probabilistic Eng. Mech. 2021, 67, 103191. [Google Scholar] [CrossRef]
- Hu, R.C.; Gu, X.D.; Deng, Z.C. Stochastic response analysis of multi-degree-of-freedom vibro-impact system undergoing Markovian jump. Nonlinear Dyn. 2020, 101, 823–834. [Google Scholar] [CrossRef]
- Hu, R.C.; Lü, Q.F. Optimal Time-Delay Control for Multi-Degree-of-Freedom Nonlinear Systems Excited by Harmonic and Wide-Band Noises. Int. J. Struct. Stab. Dyn. 2021, 21, 2150053. [Google Scholar] [CrossRef]
- Paiva, A.; Savi, M.A. An Overview of Constitutive Models for Shape Memory Alloys. Math. Probl. Eng. 2005, 2006, 056876. [Google Scholar] [CrossRef]
- Hao, Y.; Gao, M.L. Traverse Vibration of Axially Moving Laminated SMA Beam considering Random Perturbation. Shock. Vib. 2019, 2019, 6341289. [Google Scholar]
- Hao, Y.; Gao, M.; Hu, Y.; Li, Y. Nonlinear Dynamic Analysis of Axially Moving Laminated Shape Memory Alloy Beam with 1:3 Internal Resonance. Materials 2021, 14, 4022. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Gao, M.; Gong, J. Parametric Random Vibration Analysis of an Axially Moving Laminated Shape Memory Alloy Beam Based on Monte Carlo Simulation. Materials 2022, 15, 562. https://doi.org/10.3390/ma15020562
Hao Y, Gao M, Gong J. Parametric Random Vibration Analysis of an Axially Moving Laminated Shape Memory Alloy Beam Based on Monte Carlo Simulation. Materials. 2022; 15(2):562. https://doi.org/10.3390/ma15020562
Chicago/Turabian StyleHao, Ying, Ming Gao, and Jiajie Gong. 2022. "Parametric Random Vibration Analysis of an Axially Moving Laminated Shape Memory Alloy Beam Based on Monte Carlo Simulation" Materials 15, no. 2: 562. https://doi.org/10.3390/ma15020562
APA StyleHao, Y., Gao, M., & Gong, J. (2022). Parametric Random Vibration Analysis of an Axially Moving Laminated Shape Memory Alloy Beam Based on Monte Carlo Simulation. Materials, 15(2), 562. https://doi.org/10.3390/ma15020562





