Nonlinear Dynamic Analysis of Axially Moving Laminated Shape Memory Alloy Beam with 1:3 Internal Resonance
Abstract
:1. Introduction
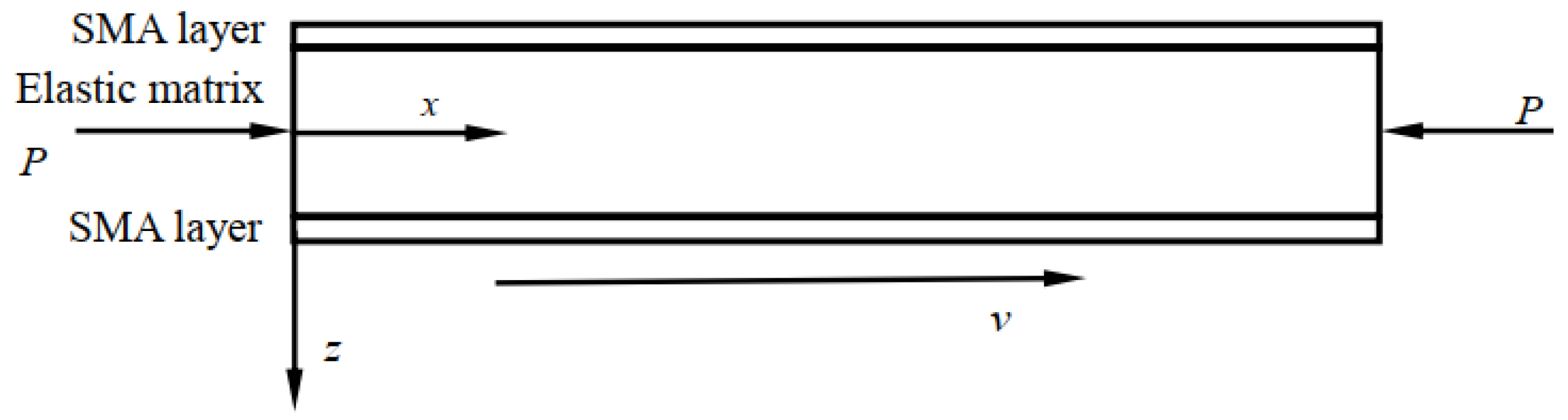
2. Dynamic Modelling of SMA Laminated Beam in Axial Movement
2.1. Polynomial Constitutive Relationship of SMA
2.2. Vibration Equation of SMA Laminated Beam
3. Internal Resonance
3.1. Differential Equation of Vibration
3.2. Application of Multi-Scale Method
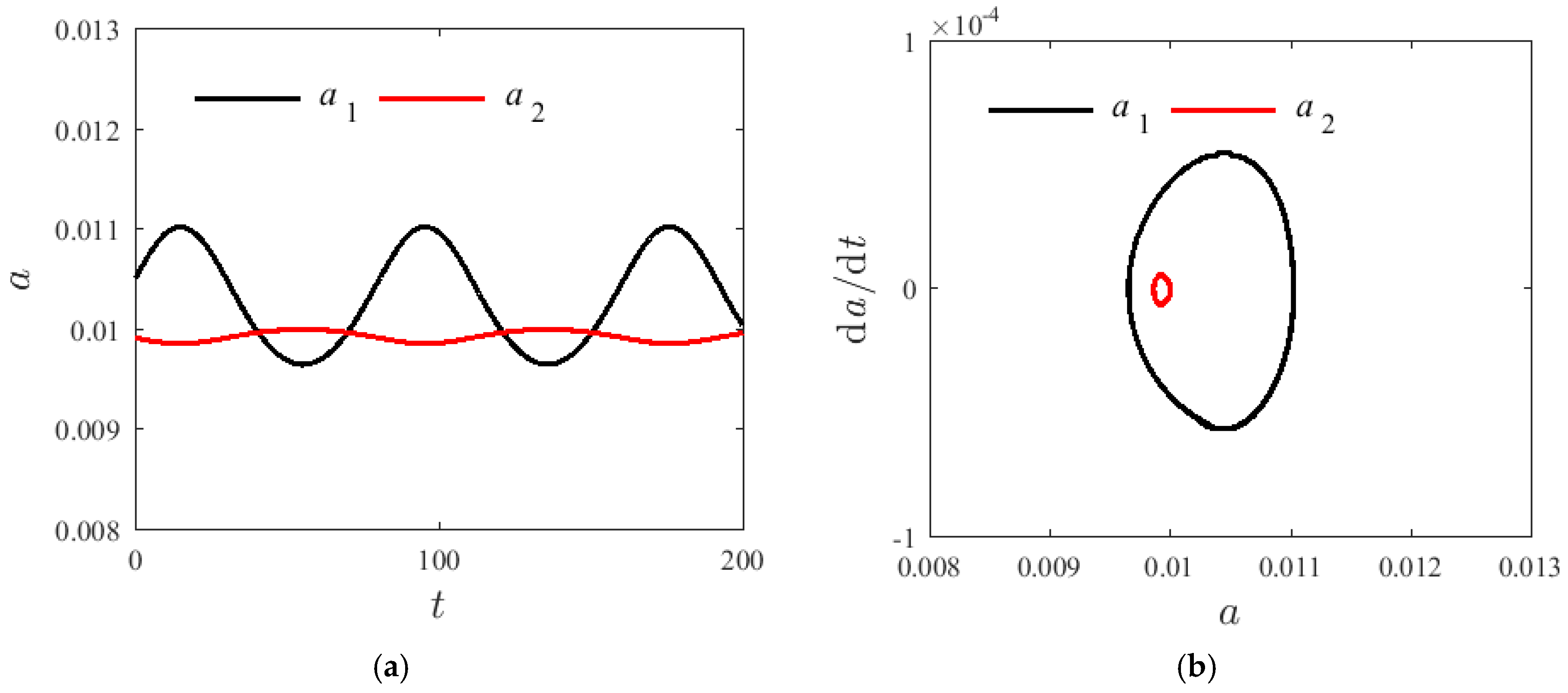
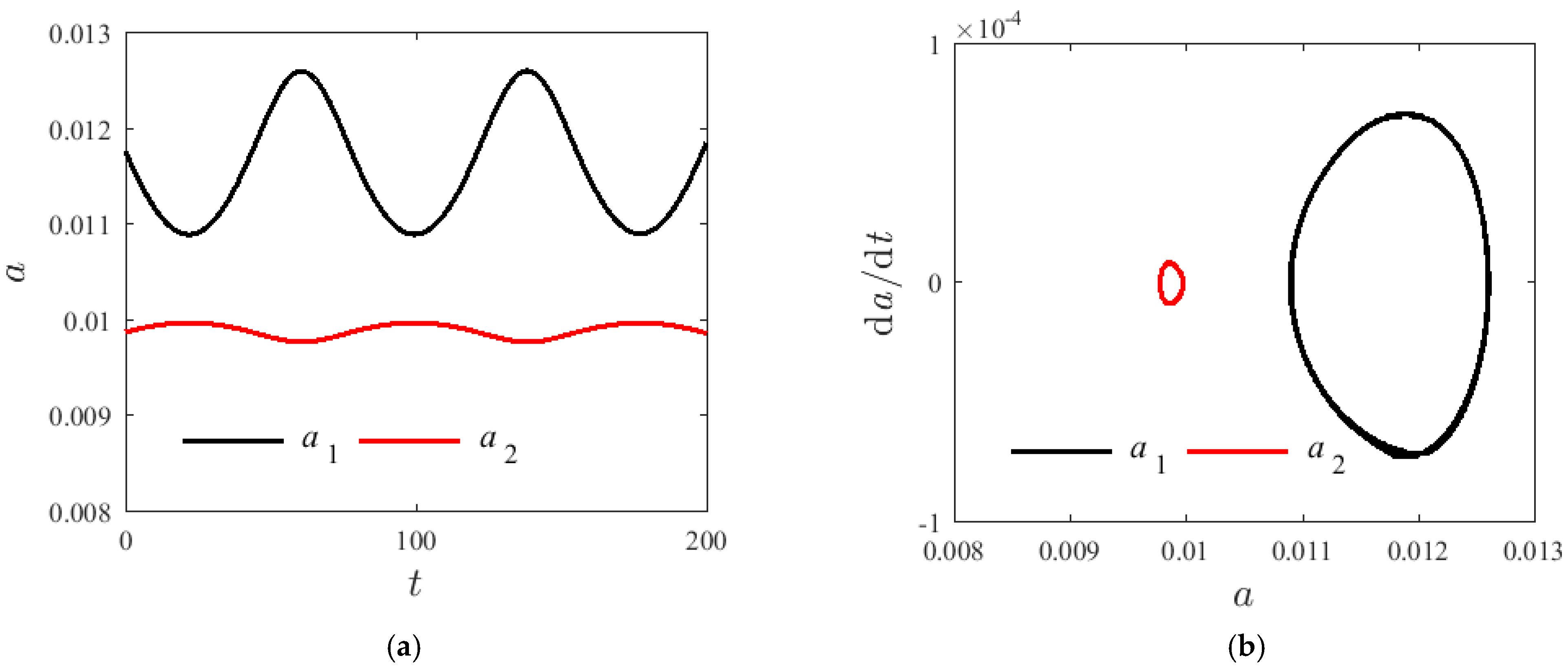
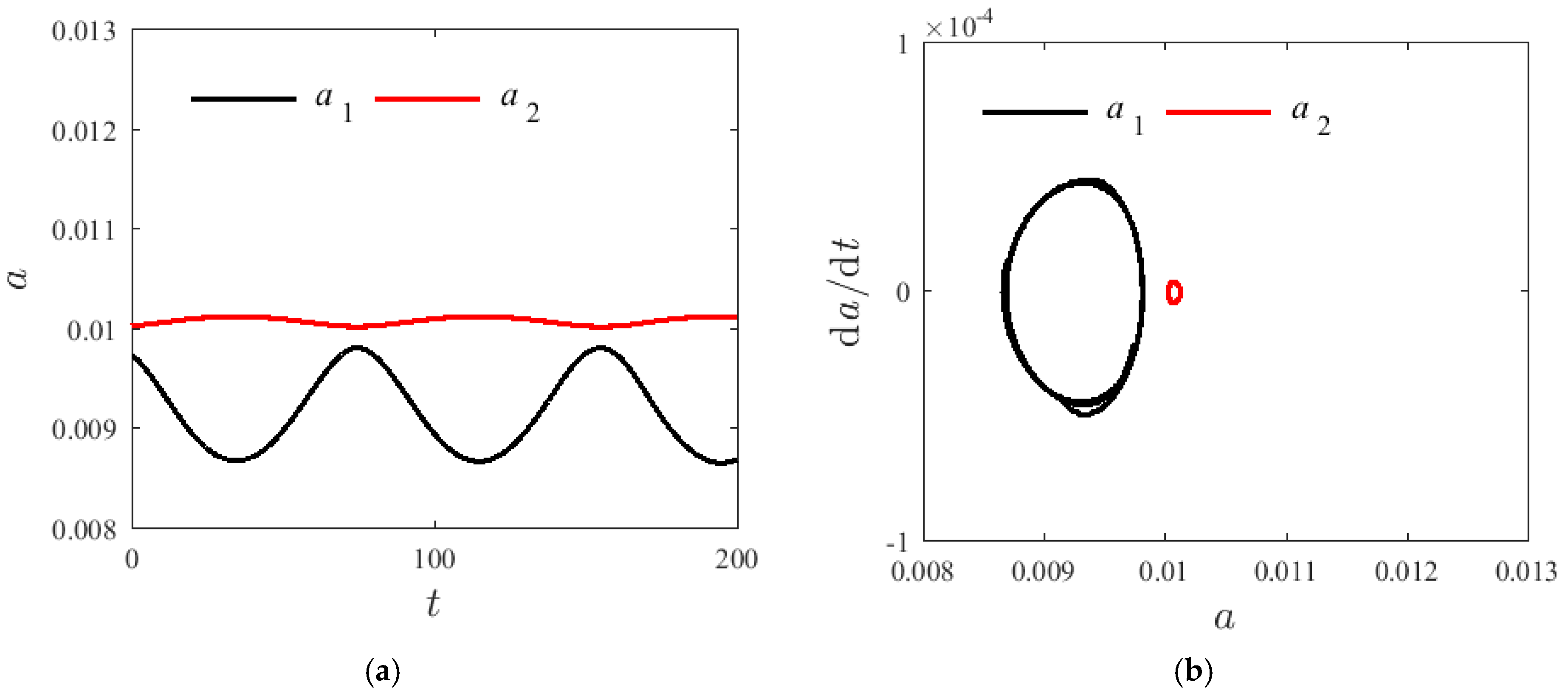
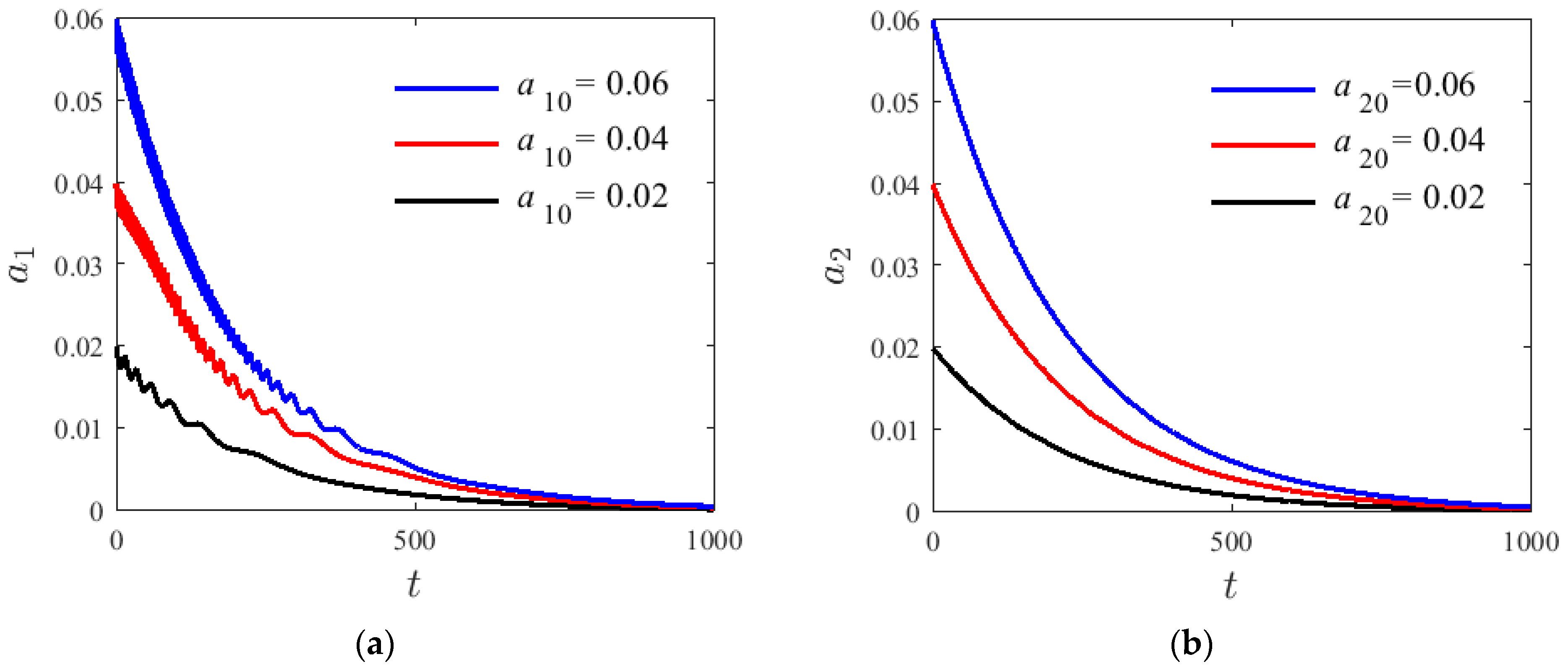
4. Influence of Parameters for the Internal Resonances of Laminated SMA Beam
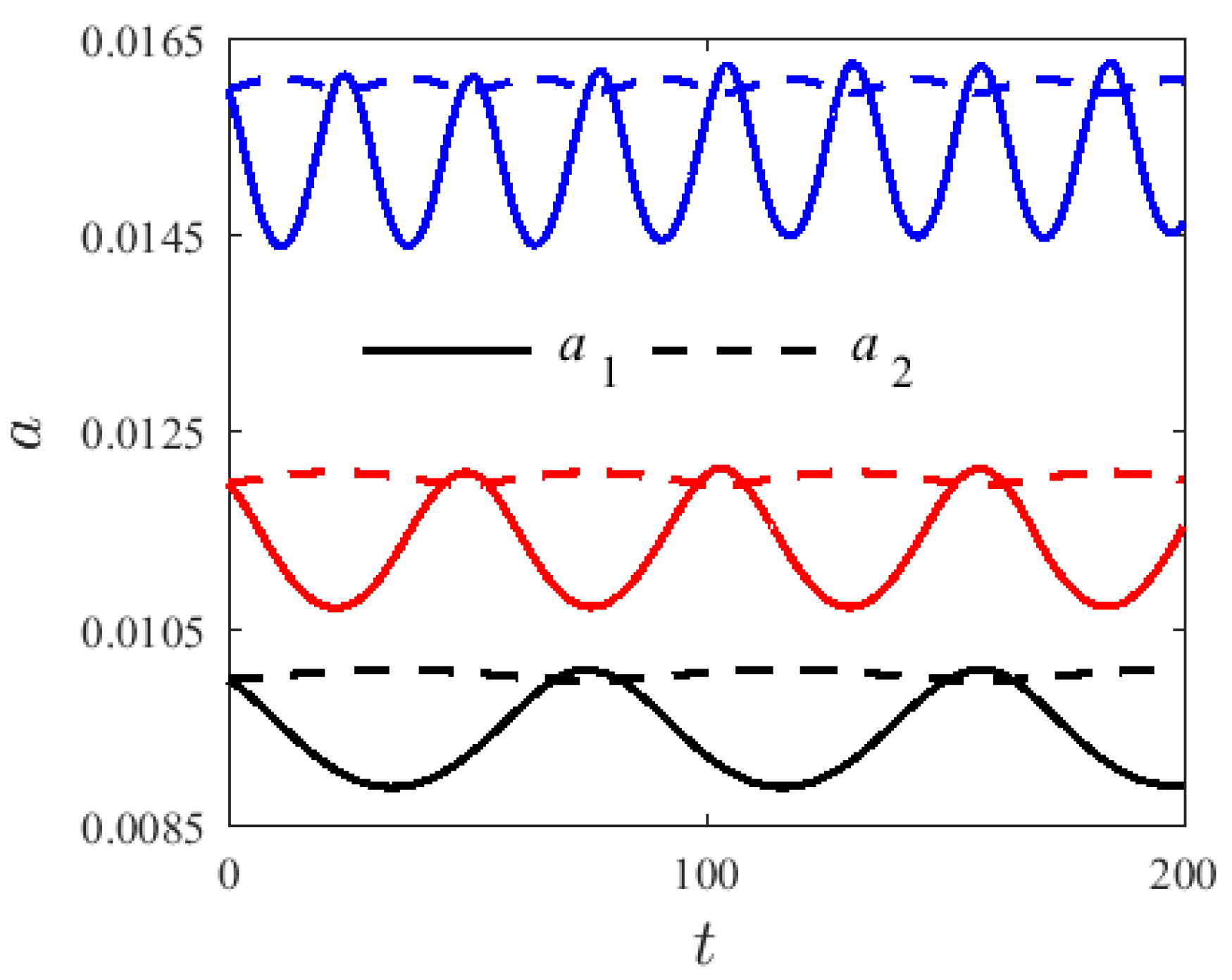
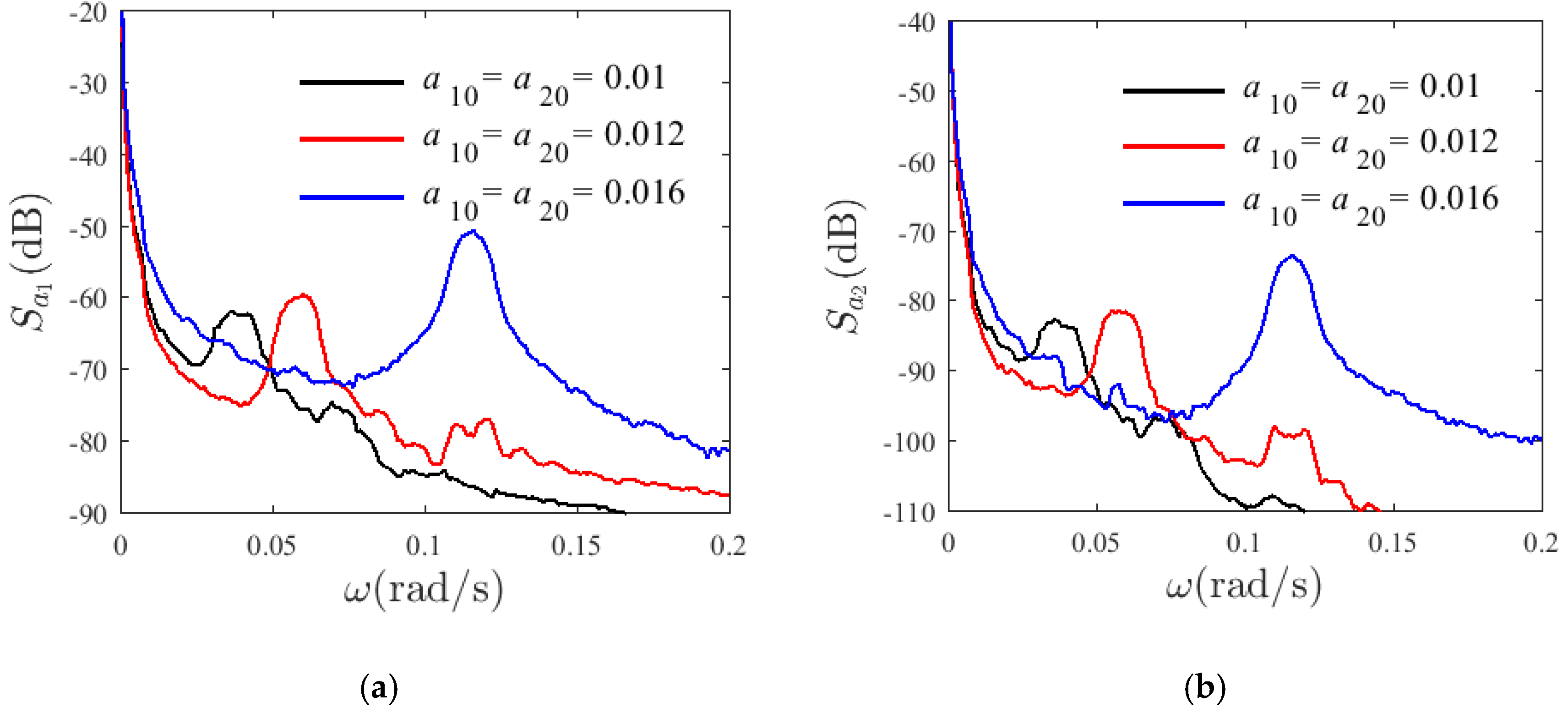
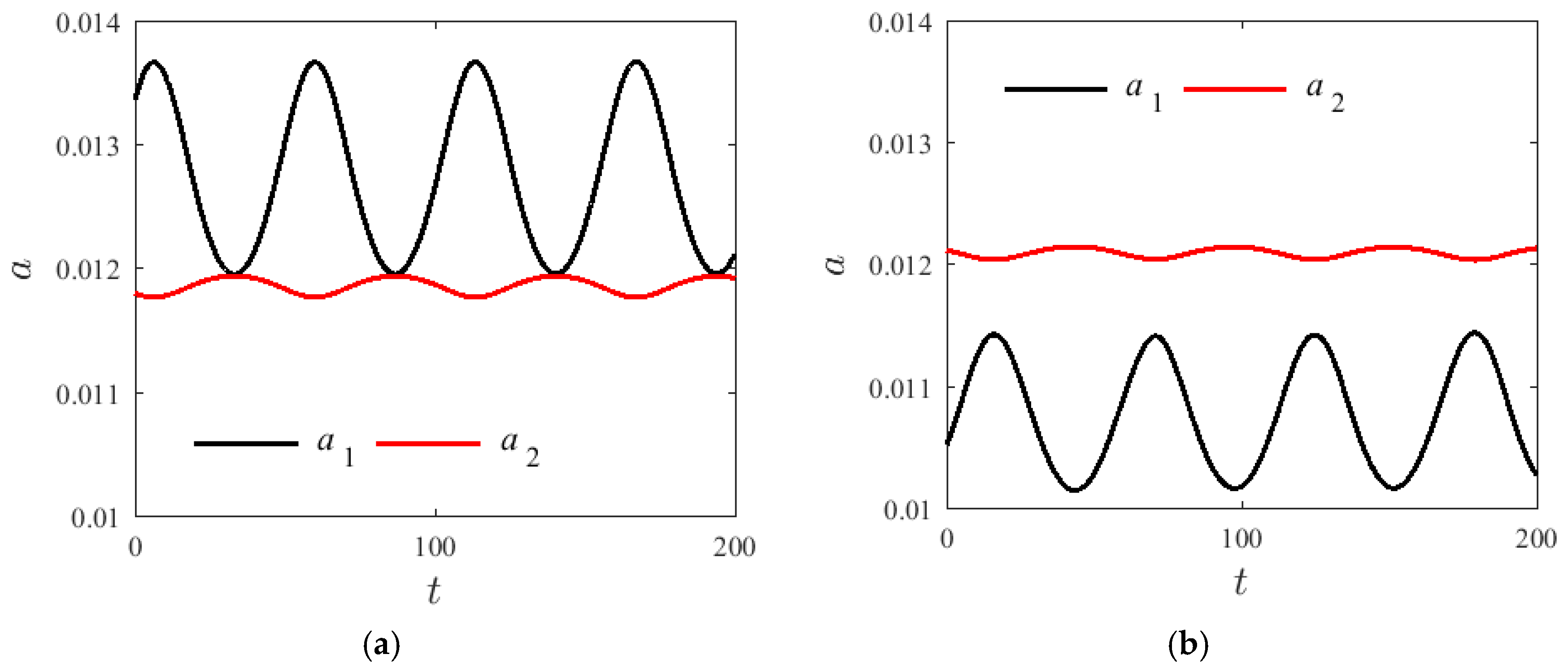
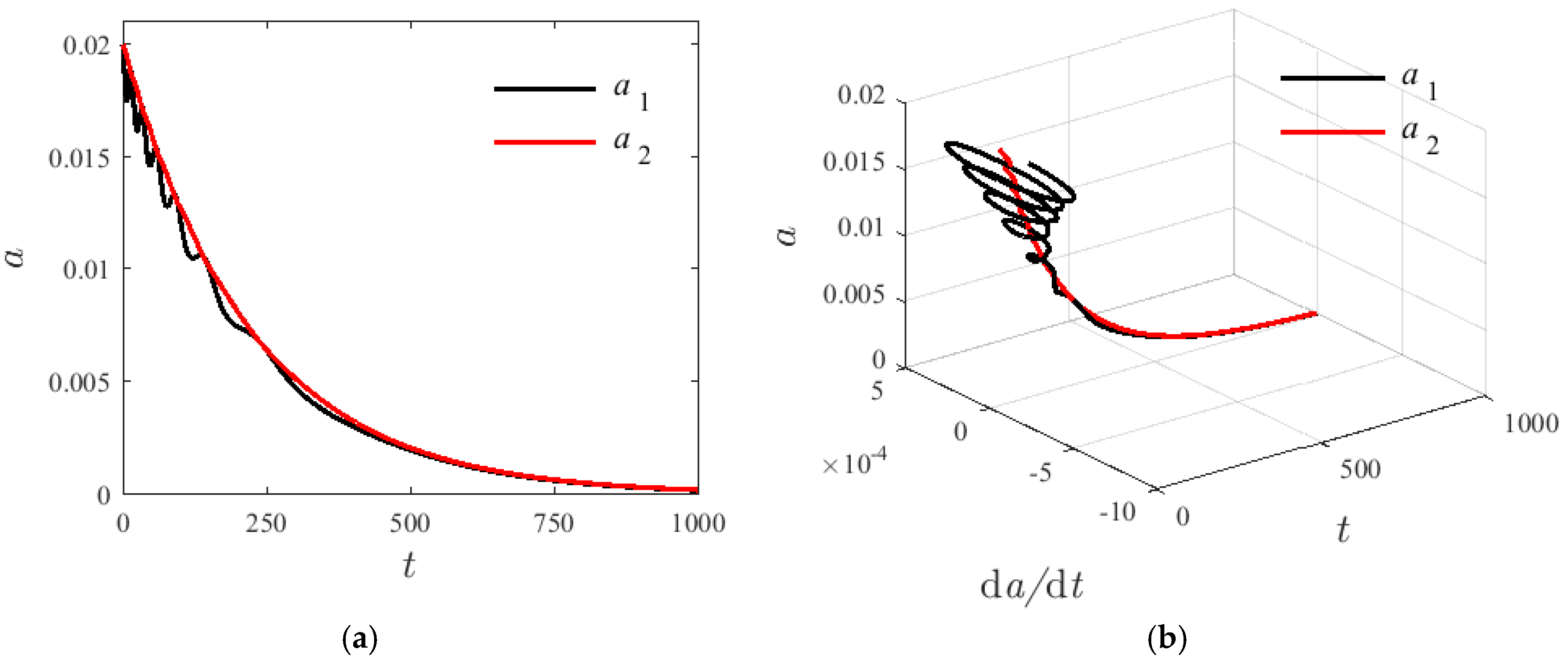
4.1. System without Damping
4.2. Damped System
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Mirzaeifar, R.; Desroches, R.; Yavari, A. A combined analytical, numerical, and experimental study of shape-memory-alloy helical springs. Int. J. Solids Struct. 2011, 48, 611–624. [Google Scholar] [CrossRef]
- Pacheco, P.M.C.L.; Machado, L.G.; Savi, M.A. Nonlinear dynamics and chaos in coupled shape memory oscillators. Int. J. Solids Struct. 2003, 40, 5139–5156. [Google Scholar]
- Savi, M.A.; Pacheco, P.M.C.L.; Braga, A.M.B. Chaos in a shape memory two-bar truss. Int. J. Non Linear Mech. 2002, 37, 1387–1395. [Google Scholar] [CrossRef]
- Ren, Y.; Shao, B. Analysis of free vibrations of shape memory alloy hybrid composite beams. Eng. Mech. 2003, 20, 183–187. [Google Scholar]
- Shao, B.; Ren, Y.S. The semi-active control of shape memory alloy composite beam. Mech. Eng. 2004, 20, 16–19. [Google Scholar]
- Ren, Y.S.; Liu, Y.R.; Yang, S.; Wang, X. Active deformation models of SMA fiber hybrid thin-walled laminated beams. Chin. J. Solid Mech. 2010, 31, 228–236. [Google Scholar]
- Collet, M.; Foltête, E.; Lexcellent, C. Analysis of the behavior of a Shape Memory Alloy beam under dynamical loading. Eur. J. Mech. Solids 2001, 20, 615–630. [Google Scholar] [CrossRef]
- de Matos Junior, O.D.; Donadon, M.V.; Castro, S.G.P. Aeroelastic behavior of stiffened composite laminated panel with embedded SMA wire using the hierarchical Rayleigh–Ritz method. Compos. Struct. 2017, 181, 26–45. [Google Scholar] [CrossRef]
- Akhavan-Rad, B.; Kheirikhah, M.M. Static analysis of sandwich plates embedded with shape memory alloy wires using active strain energy tuning method. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–17. [Google Scholar] [CrossRef]
- Razavilar, R.; Fathi, A.; Dardel, M.; Hadi, J.A. Dynamic analysis of a shape memory alloy beam with pseudoelastic behavior. J. Intell. Mater. Syst. Struct. 2018, 29, 1835–1849. [Google Scholar] [CrossRef]
- Lu, P.; Cui, F.S.; Tan, M.J. A theoretical model for the bending of a laminated beam with SMA fiber embedded layer. Compos. Struct. 2009, 90, 458–464. [Google Scholar] [CrossRef]
- Zhang, Z. Dynamic Bifurcation and Control of the Structures with Shape Memory Alloy (SMA). Ph.D. Thesis, Tianjin University, Tianjin, China, 2012. [Google Scholar]
- Fu, S.; Lu, Q. Nonlinear dynamics and vibration reduction of a dry friction oscillator with SMA restraints. Nonlinear Dyn. 2012, 69, 1365–1381. [Google Scholar] [CrossRef]
- Asadi, H.; Bodaghi, M.; Shakeri, M.; Aghdam, M. On the free vibration of thermally pre/post-buckled shear deformable SMA hybrid composite beams. Aerosp. Sci. Technol. 2013, 31, 73–86. [Google Scholar] [CrossRef]
- Samadpour, M.; Asadi, H.; Wang, Q. Nonlinear aero-thermal flutter postponement of supersonic laminated composite beams with shape memory alloys. Eur. J. Mech. Solids 2016, 57, 18–28. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, M.; Hao, Y. The 1/3rd subharmonic and 3rd superharmonic resonance of a shape memory alloy (SMA) laminated beam. J. Theor. Appl. Mech. 2021, 59, 27–41. [Google Scholar]
- Wang, J.; Hu, Y.; Su, Y.; Gong, L. Magneto-elastic internal resonance of an axially moving conductive beam in the magnetic field. J. Theor. Appl. Mech. 2019, 57, 179–191. [Google Scholar] [CrossRef]
- Zhang, K.; Tan, X.; Ding, H.; Chen, L. Parametric Vibration Responses of Supercritical Fluid-Conveying Pipes in 3:1 Internal Resonance. Appl. Math. Mech. 2018, 39, 1227–1235. [Google Scholar]
- Yang, J.; Zhang, W.; Xi, A. Nonlinear Dynamics Analysis of a Composite Cantilever Piezoelectric Plate with One-To-Three Internal Resonance. J. Dyn. Control 2018, 16, 183–187. [Google Scholar]
- Zhang, D.B.; Tang, Y.Q.; Liang, R.Q.; Yang, L.; Chen, L.Q. Dynamic stability of an axially transporting beam with two-frequency parametric excitation and internal resonance. Eur. J. Mech. Solids 2021, 85, 104084. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Y.; Zhang, B.; Shen, H.; Liu, J. Nonlocal and strain gradient effects on nonlinear forced vibration of axially moving nanobeams under internal resonance conditions. Appl. Math. Mech. 2020, 41, 261–278. [Google Scholar] [CrossRef]
- Zhang, D.-B.; Tang, Y.-Q.; Chen, L.-Q. Internal resonance in parametric vibrations of axially accelerating viscoelastic plates. Eur. J. Mech. Solids 2019, 75, 142–155. [Google Scholar] [CrossRef]
- Mao, X.-Y.; Ding, H.; Chen, L.-Q. Internal resonance of a supercritically axially moving beam subjected to the pulsating speed. Nonlinear Dyn. 2019, 95, 631–651. [Google Scholar] [CrossRef]
- Ding, H.; Huang, L.; Chen, L. Primary resonance of traveling viscoelastic beam under internal resonance. Appl. Math. Mech. 2017, 38, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Dong, Y.; Li, Y. Nonlinear dynamics of a viscoelastic sandwich beam with parametric excitations and internal resonance. Nonlinear Dyn. 2018, 94, 2575–2612. [Google Scholar] [CrossRef]
- Sahoo, B.; Panda, L.N.; Pohit, G. Stability, Bifurcation and Chaos of a Traveling Viscoelastic Beam Tuned to 3:1 Internal Resonance and Subjected to Parametric Excitation. Int. J. Bifurc. Chaos 2017, 27, 1750017. [Google Scholar] [CrossRef]
- Paiva, A.; Savi, M.A. An overview of constitutive models for shape memory alloys. Math. Probl. Eng. 2006, 4, 1–30. [Google Scholar] [CrossRef]
- Ying, H.; Minglei, G. Traverse Vibration of Axially Moving Laminated SMA Beam considering Random Perturbation. Shock Vib. 2019, 2019, 6341289. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J. Principal-internal resonance of an axially moving current-carrying beam in magnetic field. Nonlinear Dyn. 2017, 90, 683–695. [Google Scholar] [CrossRef]
| 0.35 | 0.5546 | 1.6630 | |
| 0.32 | 0.5503 | 1.6502 | |
| 0.22 | 0.5372 | 1.6112 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Gao, M.; Hu, Y.; Li, Y. Nonlinear Dynamic Analysis of Axially Moving Laminated Shape Memory Alloy Beam with 1:3 Internal Resonance. Materials 2021, 14, 4022. https://doi.org/10.3390/ma14144022
Hao Y, Gao M, Hu Y, Li Y. Nonlinear Dynamic Analysis of Axially Moving Laminated Shape Memory Alloy Beam with 1:3 Internal Resonance. Materials. 2021; 14(14):4022. https://doi.org/10.3390/ma14144022
Chicago/Turabian StyleHao, Ying, Ming Gao, Yuda Hu, and Yuehua Li. 2021. "Nonlinear Dynamic Analysis of Axially Moving Laminated Shape Memory Alloy Beam with 1:3 Internal Resonance" Materials 14, no. 14: 4022. https://doi.org/10.3390/ma14144022
APA StyleHao, Y., Gao, M., Hu, Y., & Li, Y. (2021). Nonlinear Dynamic Analysis of Axially Moving Laminated Shape Memory Alloy Beam with 1:3 Internal Resonance. Materials, 14(14), 4022. https://doi.org/10.3390/ma14144022






