A Modified Three-Dimensional Negative-Poisson-Ratio Metal Metamaterial Lattice Structure
Abstract
:1. Introduction
2. Design and Manufacture of a Modified 3D NPR Structure
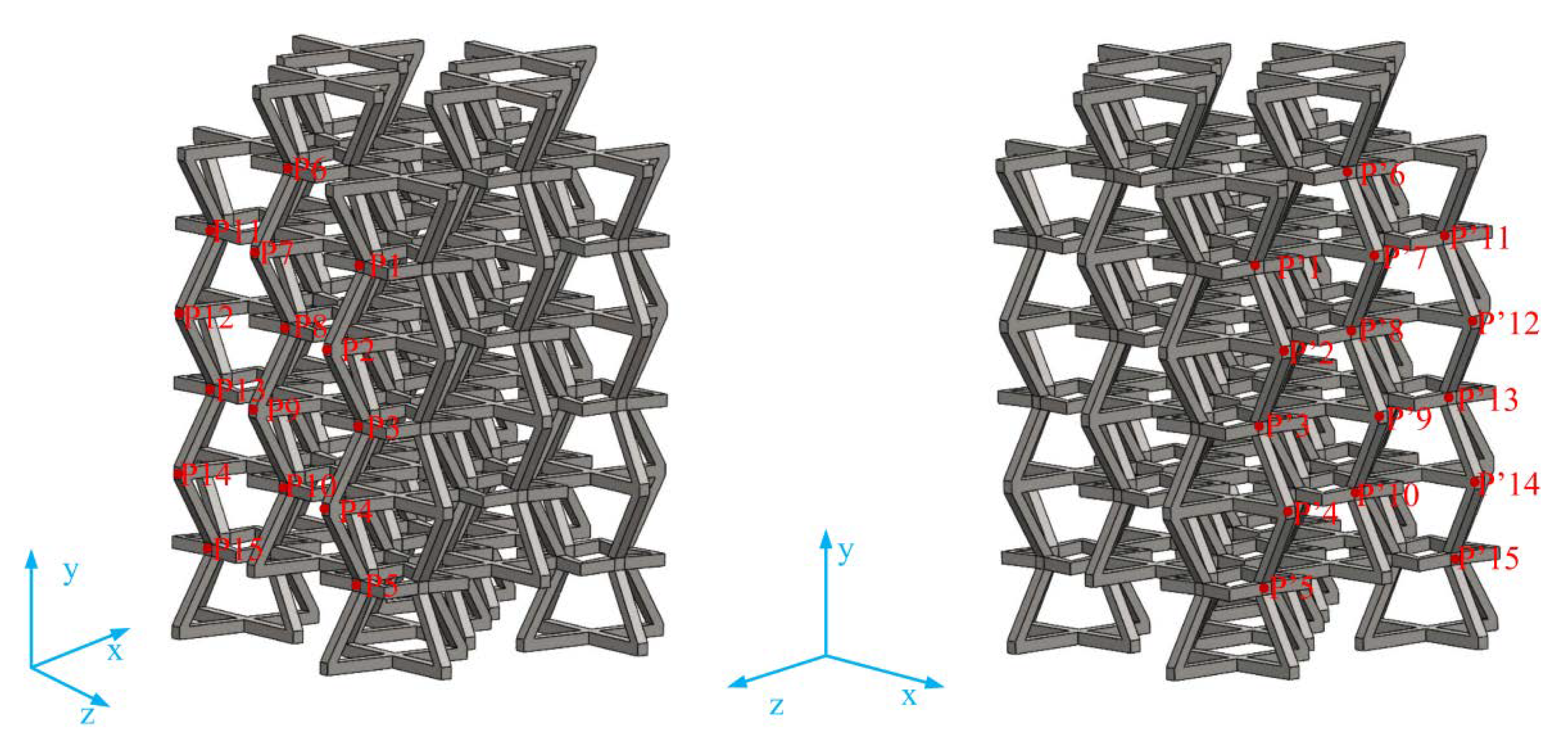
2.1. Modified 3D NPR Structural Design
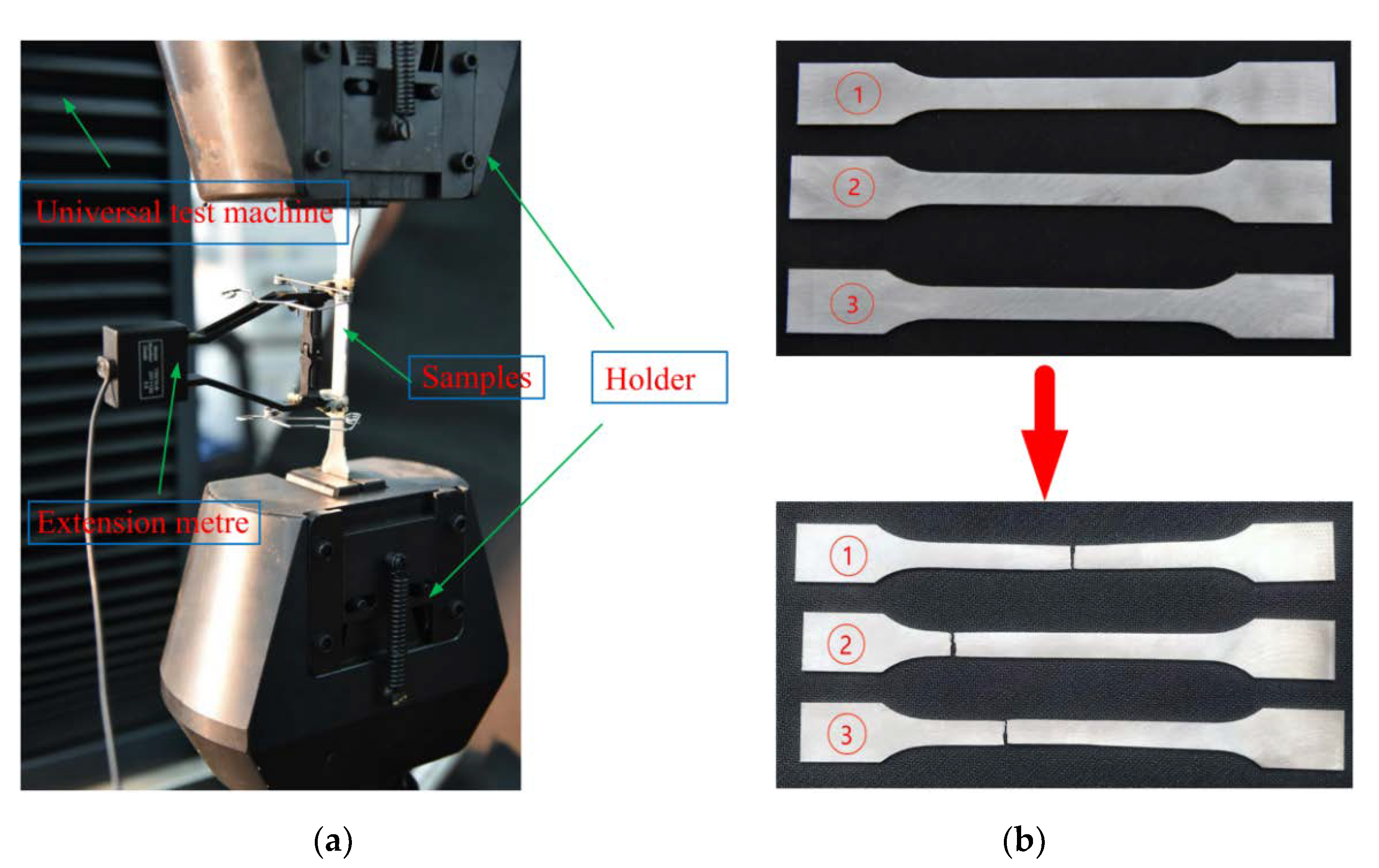
2.2. Manufacture of a Modified 3D NPR Structure
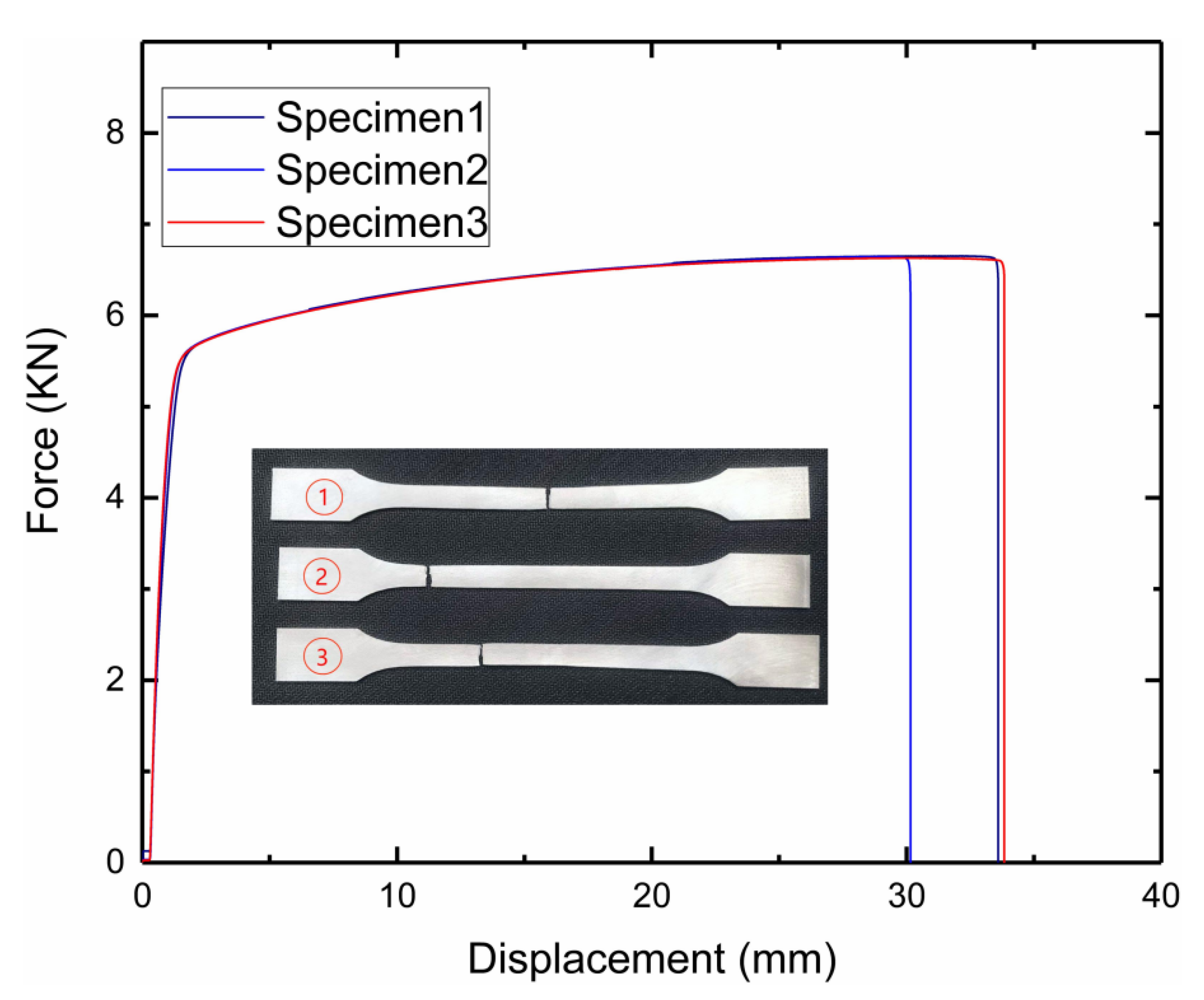
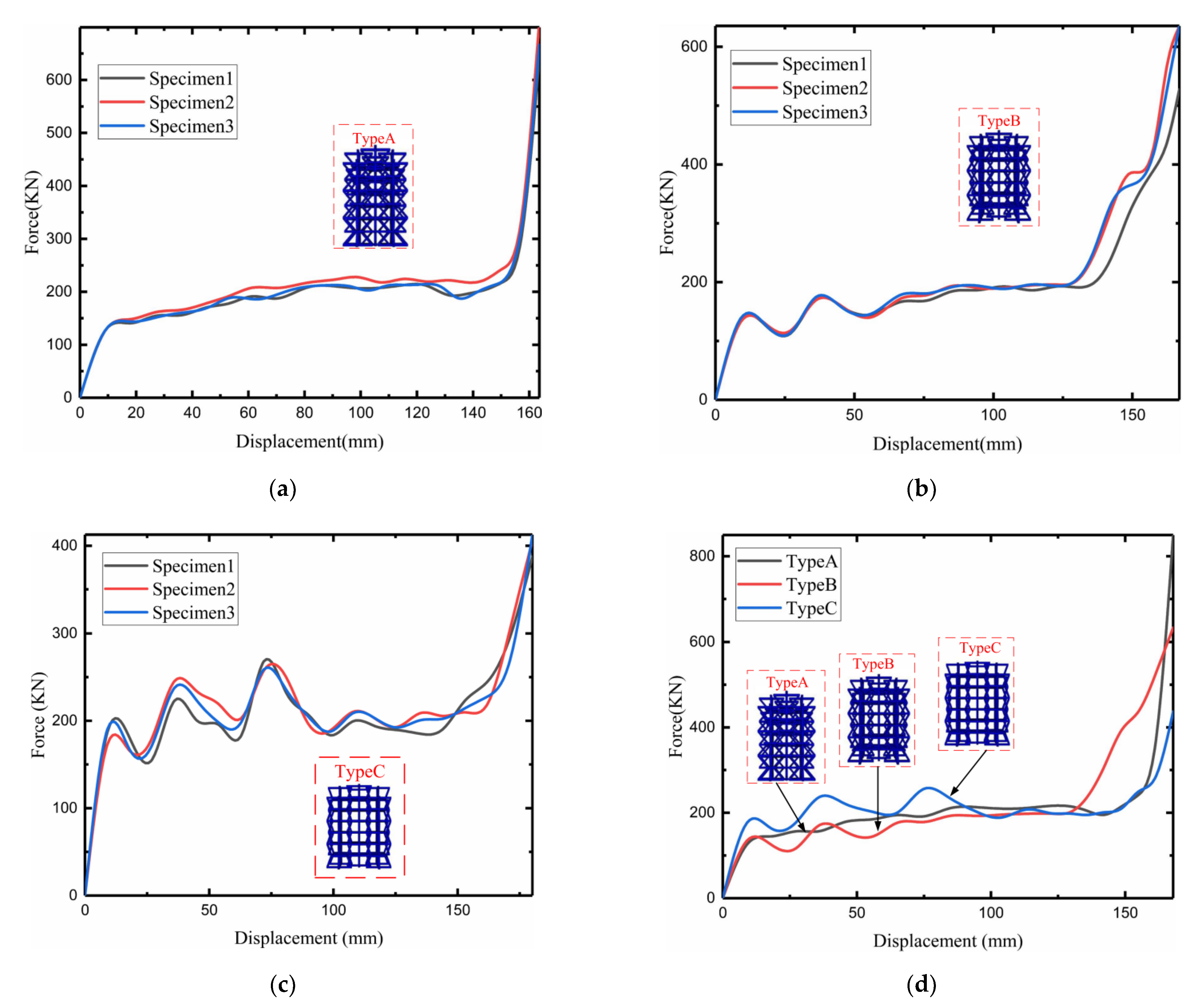
3. Modified 3D Negative-Poisson-Specific Lattice Test
4. Finite Element Numerical Simulation Analysis
4.1. Performance of 316 L Stainless Steel
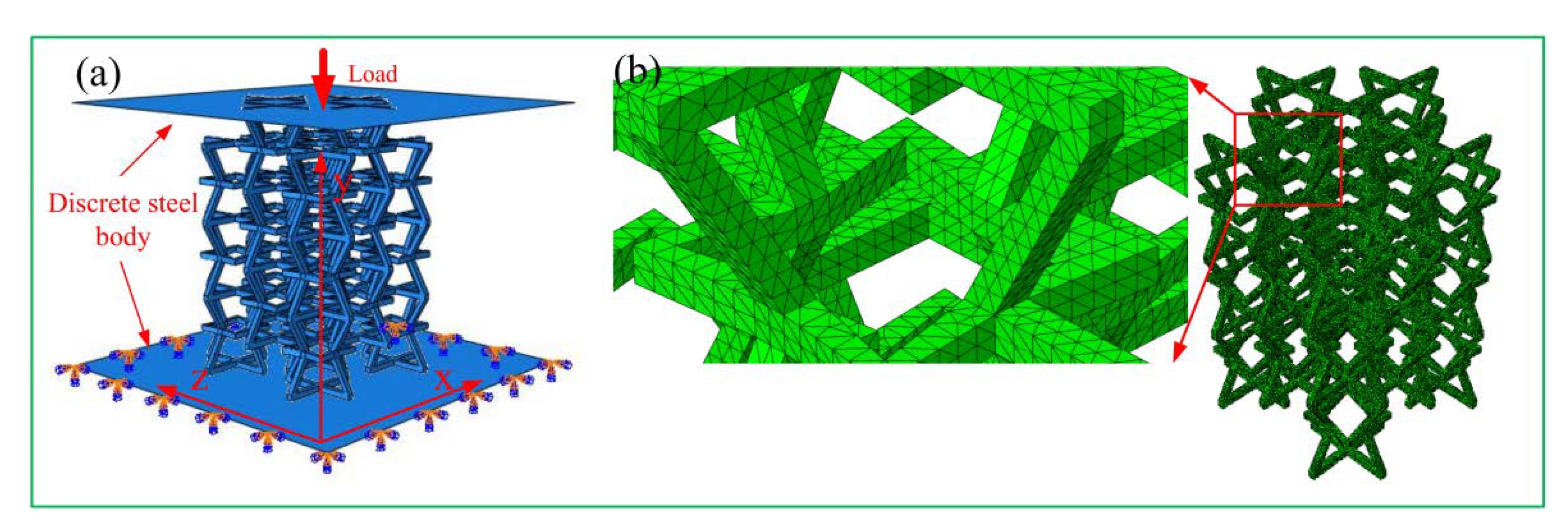
4.2. Finite Element Model Establishment
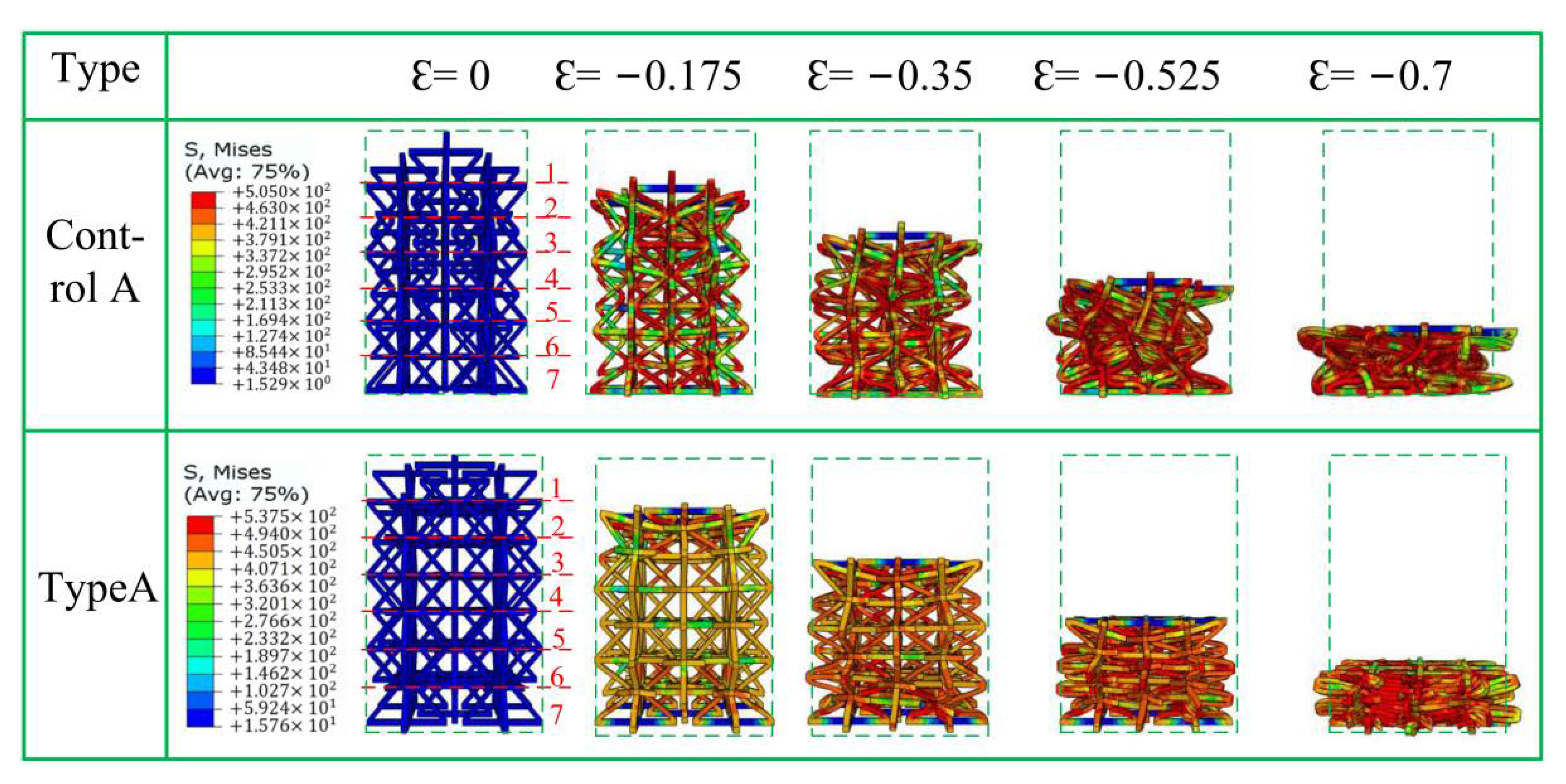
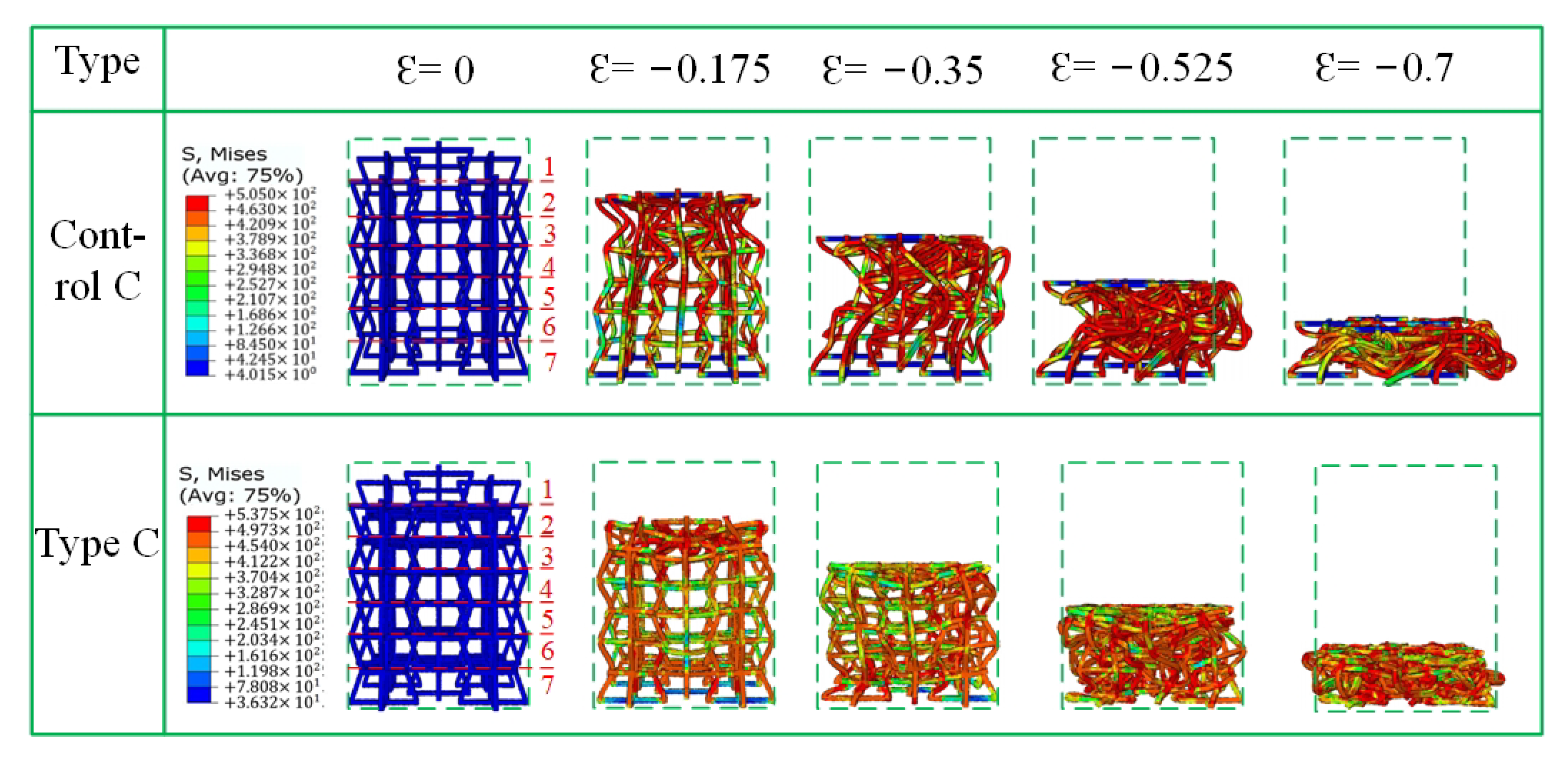
4.3. Analysis and Discussion of Mechanical Responses of Finite Element Models
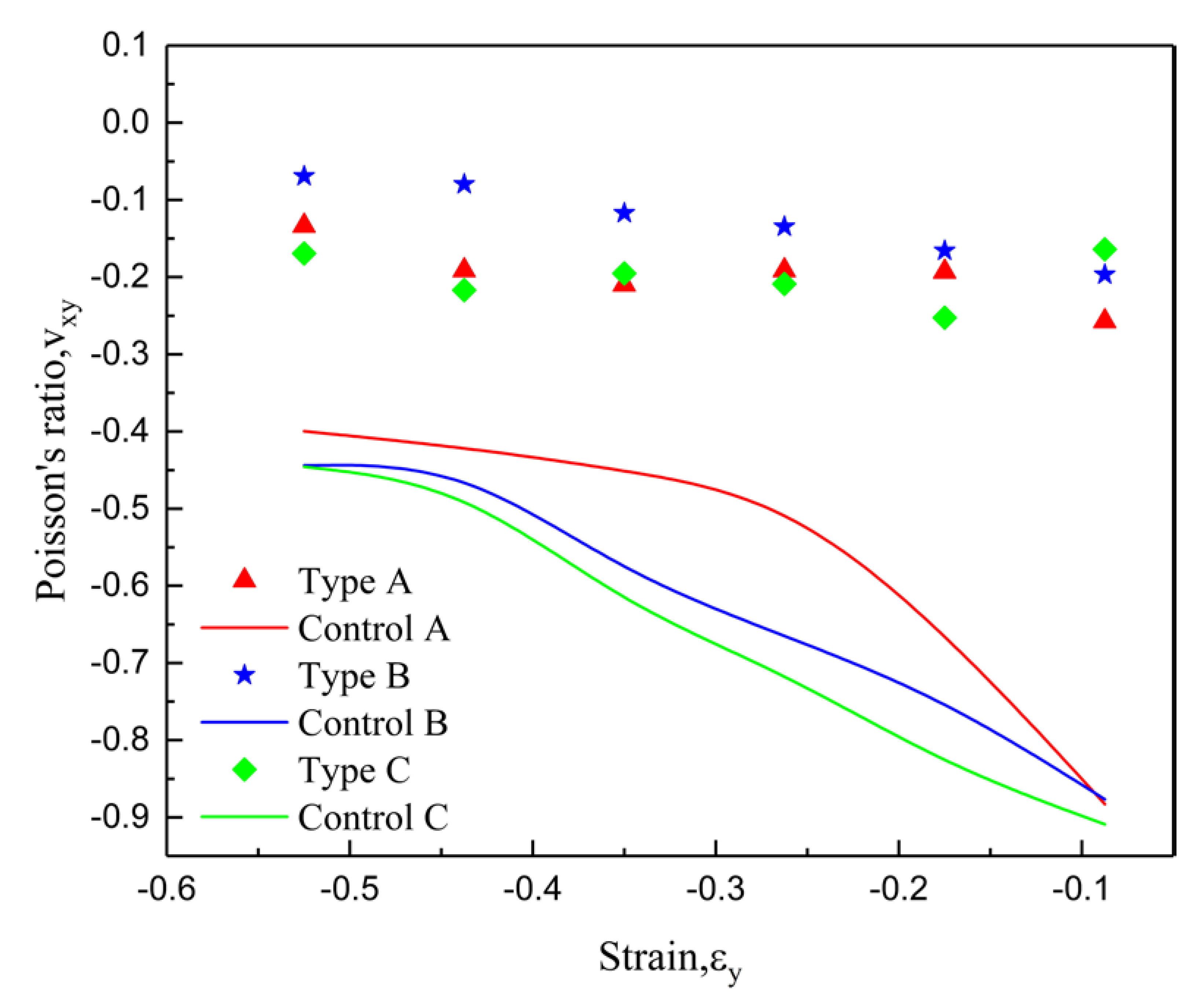
4.4. Finite Element Poisson’s Ratio Analysis and Discussion
4.5. Energy Absorption
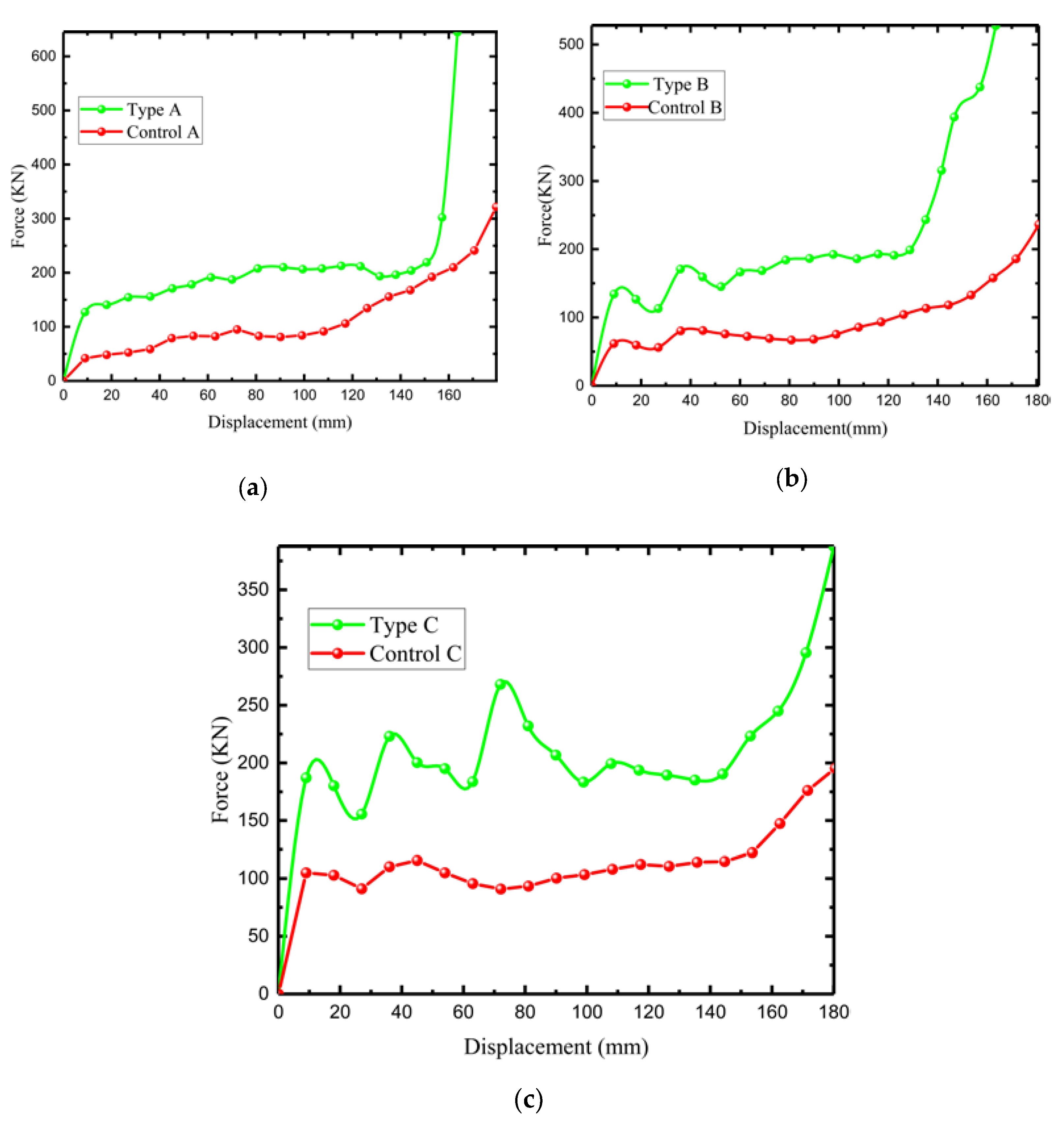
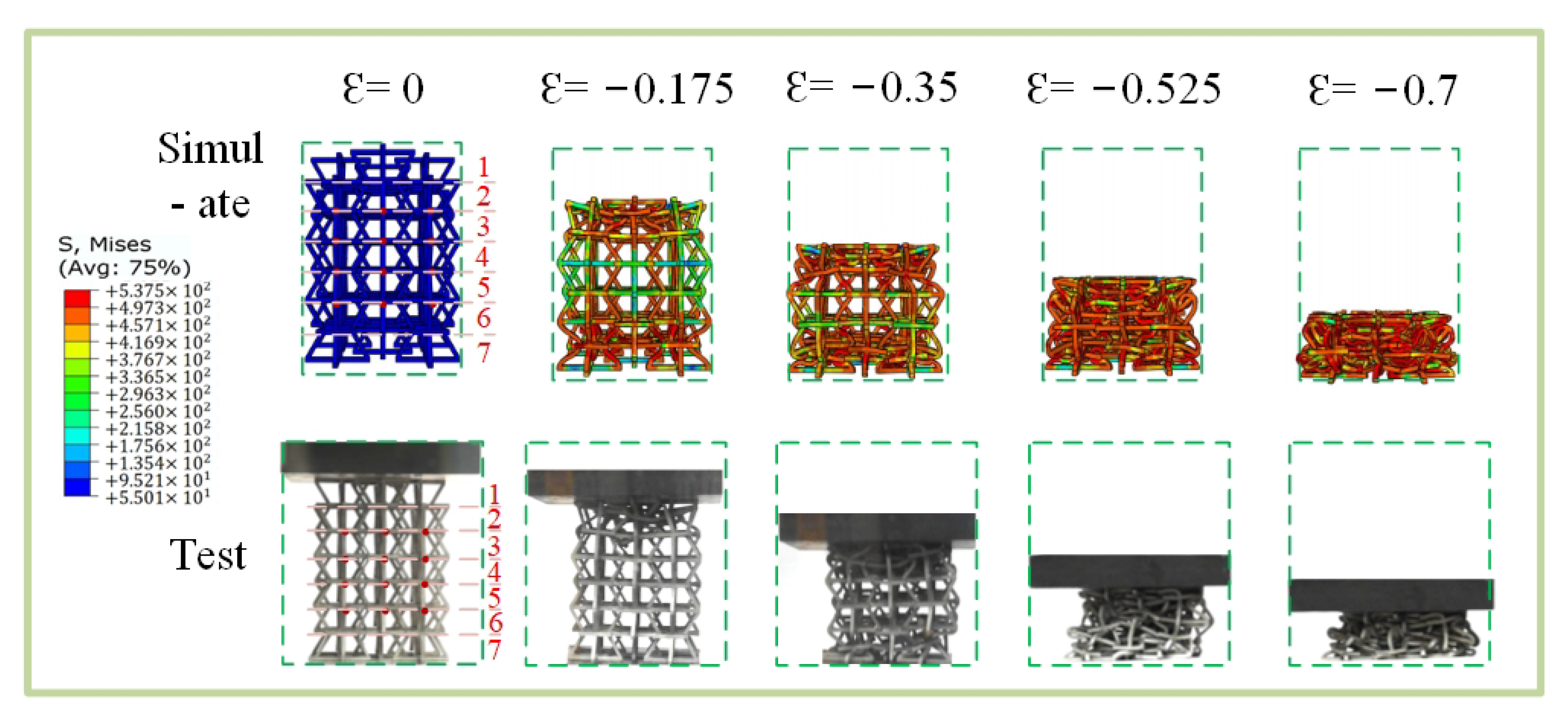
5. Finite Element Model Comparison between Experiments
6. Conclusions
- The modified NPR structure designed here can effectively improve the stiffness of the structure and make up for the low stiffness of the negative Poisson relative to the metamaterial model;
- Increasing the modified NPR structure of the star can effectively improve the stability of the structure and can avoid the phenomenon of “convexity” during destruction. The macroscopic stability of the structure is worse with increasing the ∅ angle of the star structure;
- The energy absorption effect of the modified structure depends on the ∅ angle of the star structure rather than the concave angle . The energy absorption effect of the modified NPR structure is the best when ∅ = 70.9°.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.Y.; Ren, X.; Wang, X.Y.; Zhang, Y.; Xie, Y.M. A novel combined auxetic tubular structure with enhanced tunable stiffness. Compos. Part B Eng. 2021, 226, 109303. [Google Scholar] [CrossRef]
- Imbalzano, G.; Phuong, T.; Tuan, D.N.; Lee, P.V.S. A numerical study of auxetic composite panels under blast loadings. Compos. Struct. 2016, 135, 339–352. [Google Scholar] [CrossRef]
- Wang, T.; An, J.; He, H.; Wen, X.; Xi, X. A novel 3D impact energy absorption structure with negative Poisson? s ratio and its application in aircraft crashworthiness. Compos. Struct. 2021, 262, 113663. [Google Scholar] [CrossRef]
- Wang, D.; Xu, H.; Wang, J.; Jiang, C.; Zhu, X.; Ge, Q.; Gu, G. Design of 3D Printed Programmable Horseshoe Lattice Structures Based on a Phase-Evolution Model. ACS Appl. Mater. Interfaces 2020, 12, 22146–22156. [Google Scholar] [CrossRef]
- John, C.S.M.; Enrique, C.-U. Curved-Layered Additive Manufacturing of Non-Planar, Parametric Lattice Structures. Mater. Des. 2018, 160, 949–963. [Google Scholar]
- Tiantian, L.; Fan, L.; Lifeng, W. Enhancing indentation and impact resistance in auxetic composite materials. Compos. Part B Eng. 2020, 198, 108229. [Google Scholar]
- Jie, L.; Tingting, C.; Yonghui, Z.; Guilin, W.; Qixiang, Q.; Hongxin, W.; Ramin, S.; Yi Min, X. On sound insulation of pyramidal lattice sandwich structure. Compos. Struct. 2019, 208, 385–394. [Google Scholar]
- Guilin, W.; Gaoxi, C.; Kai, L.; Xuan, W.; Jie, L.; Yi Min, X. Stacked-origami mechanical metamaterial with tailored multistage stiffness. Mater. Des. 2021, 212, 110203. [Google Scholar]
- Fangyi, L.; Jie, L.; Yufei, Y.; Jianhua, R.; Jijun, Y.; Guilin, W. A time-variant reliability analysis method for non-linear limit-state functions with the mixture of random and interval variables. Eng. Struct. 2020, 213, 110588. [Google Scholar]
- Bohara, R.P.; Linforth, S.; Nguyen, T.; Ghazlan, A.; Ngo, T. Novel lightweight high-energy absorbing auxetic structures guided by topology optimisation. Int. J. Mech. Sci. 2021, 211, 106793. [Google Scholar] [CrossRef]
- Mizzi, L.; Spaggiari, A. Lightweight mechanical metamaterials designed using hierarchical truss elements. Smart Mater. Struct. 2020, 29, 105036. [Google Scholar] [CrossRef]
- Li, Z.-H.; Nie, Y.-F.; Liu, B.; Kuai, Z.-Z.; Zhao, M.; Liu, F. Mechanical properties of AlSi10Mg lattice structures fabricated by selective laser melting. Mater. Des. 2020, 192, 108709. [Google Scholar] [CrossRef]
- Saurav, V.; Cheng-Kang, Y.; Chao-Hsun, L.; Jeng Ywam, J. Additive manufacturing of lattice structures for high strength mechanical interlocking of metal and resin during injection molding. Addit. Manuf. 2021, 49, 102463. [Google Scholar]
- Carneiro, V.H.; Meireles, J.; Puga, H. Auxetic materials—A review. Mater. Sci. Pol. 2013, 31, 561–571. [Google Scholar] [CrossRef]
- Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Phuong, T.; Tuan Duc, N.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Yang, S.; Qi, C.; Wang, D.; Gao, R.; Hu, H.; Shu, J. A Comparative Study of Ballistic Resistance of Sandwich Panels with Aluminum Foam and Auxetic Honeycomb Cores. Adv. Mech. Eng. 2013, 5, 589216. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Fracture toughness of re-entrant foam materials with a negative Poisson’s ratio: Experiment and analysis. Int. J. Fract. 1996, 80, 73–83. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Chirima, G.; Ravirala, N.; Zied, K.M. The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs. Compos. Sci. Technol. 2010, 70, 1034–1041. [Google Scholar] [CrossRef] [Green Version]
- Schaedler, T.A.; Jacobsen, A.J.; Torrents, A.; Sorensen, A.E.; Lian, J.; Greer, J.R.; Valdevit, L.; Carter, W.B. Ultralight Metallic Microlattices. Science 2011, 334, 962–965. [Google Scholar] [CrossRef] [PubMed]
- Ai, L.; Gao, X.L. Metamaterials with negative Poisson’s ratio and non-positive thermal expansion. Compos. Struct. 2017, 162, 70–84. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.-S.; Huang, Y.-J.; Chien, I.T. Flexural wave propagation in metamaterial beams containing membrane-mass structures. Int. J. Mech. Sci. 2017, 131, 500–506. [Google Scholar] [CrossRef]
- Dudek, K.K.; Attard, D.; Caruana-Gauci, R.; Wojciechowski, K.W.; Grima, J.N. Unimode metamaterials exhibiting negative linear compressibility and negative thermal expansion. Smart Mater. Struct. 2016, 25, 025009. [Google Scholar] [CrossRef]
- Shen, L.; Wang, Z.; Wang, X.; Wei, K. Negative Poisson’s ratio and effective Young’s modulus of a vertex-based hierarchical re-entrant honeycomb structure. Int. J. Mech. Sci. 2021, 206, 106611. [Google Scholar] [CrossRef]
- Mizzi, L.; Mahdi, E.M.; Titov, K.; Gatt, R.; Attard, D.; Evans, K.E.; Grima, J.N.; Tan, J.-C. Mechanical metamaterials with star-shaped pores exhibiting negative and zero Poisson’s ratio. Mater. Des. 2018, 146, 28–37. [Google Scholar] [CrossRef]
- Ai, L.; Gao, X.L. An analytical model for star-shaped re-entrant lattice structures with the orthotropic symmetry and negative Poisson’s ratios. Int. J. Mech. Sci. 2018, 145, 158–170. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the potential of connected stars as auxetic systems. Mol. Simul. 2005, 31, 925–935. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.-P.; Poh, L.H.; Dirrenberger, J.; Zhu, Y.; Forest, S. Isogeometric shape optimization of smoothed petal auxetic structures via computational periodic homogenization. Comput. Methods Appl. Mech. Eng. 2017, 323, 250–271. [Google Scholar] [CrossRef] [Green Version]
- Farrugia, P.-S.; Gatt, R.; Attard, D.; Attenborough, F.R.; Evans, K.E.; Grima, J.N. The Auxetic Behavior of a General Star-4 Structure. Phys. Status Solidi B Basic Solid State Phys. 2021, 258, 2100158. [Google Scholar] [CrossRef]
- Sharon, L. Unidirectional waves on rings: Models for chiral preference of circumnutating plants. Bull. Math. Biol. 1994, 56, 795–810. [Google Scholar]
- Davood, M.; Babak, H.; Ranajay, G.; Abdel Magid, H.; Hamid, N.-H.; Ashkan, V. Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: A simple energy-based approach. Theor. Appl. Mech. Lett. 2016, 6, 81–96. [Google Scholar]
- Masters, I.G.; Evans, K.E. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al Ba’ba’a, H.B.; Nouh, M. Mechanics of longitudinal and flexural locally resonant elastic metamaterials using a structural power flow approach. Int. J. Mech. Sci. 2017, 122, 341–354. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Hu, X.; Chen, Y.; Wang, L. Harnessing out-of-plane deformation to design 3D architected lattice metamaterials with tunable Poisson’s ratio. Sci. Rep. 2017, 7, 8949. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Shen, J.; Ghaedizadeh, A.; Tian, H.; Xie, Y.M. Experiments and parametric studies on 3D metallic auxetic metamaterials with tuneable mechanical properties. Smart Mater. Struct. 2015, 24. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. Rsc Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Guo, X.; Watanabe, I. A mathematically defined 3D auxetic metamaterial with tunable mechanical and conduction properties. Mater. Des. 2021, 198, 109313. [Google Scholar] [CrossRef]
- Mozafar Shokri, R.; Zaini, A.; Amran, A. Computational Approach in Formulating Mechanical Characteristics of 3D Star Honeycomb Auxetic Structure. Adv. Mater. Sci. Eng. 2015, 2015, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Rad, M.S.; Hatami, H.; Ahmad, Z.; Yasuri, A.K. Analytical solution and finite element approach to the dense re-entrant unit cells of auxetic structures. Acta Mech. 2019, 230, 2171–2185. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Ghaedizadeh, A.; Tian, H.; Xie, Y.M. A simple auxetic tubular structure with tuneable mechanical properties. Smart Mater. Struct. 2016, 25. [Google Scholar] [CrossRef]
- Sun, Y.; Pugno, N. Hierarchical Fibers with a Negative Poisson’s Ratio for Tougher Composites. Materials 2013, 6, 699–712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duan, S.; Xi, L.; Wen, W.; Fang, D. A novel design method for 3D positive and negative Poisson’s ratio material based on tension-twist coupling effects. Compos. Struct. 2020, 236, 111899. [Google Scholar] [CrossRef]
- Frenzel, T.; Kadic, M.; Wegener, M. Three-dimensional mechanical metamaterials with a twist. Science 2017, 358, 1072–1074. [Google Scholar] [CrossRef] [Green Version]
- Gao, Q.; Wang, L.; Zhou, Z.; Ma, Z.D.; Wang, C.; Wang, Y. Theoretical, numerical and experimental analysis of three-dimensional double-V honeycomb. Mater. Des. 2018, 139, 380–391. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Zhou, S.; Shao, J.; Wu, X. Novel Negative Poisson’s Ratio Lattice Structures with Enhanced Stiffness and Energy Absorption Capacity. Materials 2018, 11, 1095. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, H.; Mousanezhad, D.; Nayeb-Hashemi, H.; Norato, J.; Vaziri, A. 3D cellular metamaterials with planar anti-chiral topology. Mater. Des. 2018, 145, 226–231. [Google Scholar] [CrossRef]
- Schilthuizen, M.; Davison, A. The convoluted evolution of snail chirality. Naturwissenschaften 2005, 92, 504–515. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, X.; Xie, Y.M.; Wang, Z.; Zhou, S. Re-entrant auxetic lattices with enhanced stiffness: A numerical study. Int. J. Mech. Sci. 2020, 178, 105619. [Google Scholar] [CrossRef]
- Fu, M.; Chen, Y.; Zhang, W.; Zheng, B. Experimental and numerical analysis of a novel three-dimensional auxetic metamaterial. Phys. Status Solidi B Basic Solid State Phys. 2016, 253, 1565–1575. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing. Int. J. Solids Struct. 2015, 69–70, 475–490. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Modeling of uniaxial compression in a 3D periodic re-entrant lattice structure. J. Mater. Sci. 2013, 48, 1413–1422. [Google Scholar] [CrossRef]
- Li, Y.; Ola, H.; Harvey, W.; Denis, C. Compressive properties of Ti–6Al–4V auxetic mesh structures made by electron beam melting. Acta Mater. 2012, 60, 3370–3379. [Google Scholar] [CrossRef]
- Li, X.; Lu, Z.; Yang, Z.; Yang, C. Directions dependence of the elastic properties of a 3D augmented re-entrant cellular structure. Mater. Des. 2017, 134, 151–162. [Google Scholar] [CrossRef]
- Wang, X.-T.; Wang, B.; Li, X.-W.; Ma, L. Mechanical properties of 3D re-entrant auxetic cellular structures. Int. J. Mech. Sci. 2017, 131–132, 396–407. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, X.; Wang, W.; Zhong, X.; Han, F. Compressive property of Al-based auxetic lattice structures fabricated by 3-D printing combined with investment casting. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2018, 722, 255–262. [Google Scholar] [CrossRef]
- Shen, J.; Liu, K.; Zeng, Q.; Ge, J.; Dong, Z.; Liang, J. Design and mechanical property studies of 3D re-entrant lattice auxetic structure. Aerosp. Sci. Technol. 2021, 118, 106998. [Google Scholar] [CrossRef]
- Li, Q.M.; Magkiriadis, I.; Harrigan, J.J. Compressive strain at the onset of densification of cellular solids. J. Cell. Plast. 2006, 42, 371–392. [Google Scholar] [CrossRef]
- Li, F.; Wang, R.; Zheng, Z.; Liu, J. A time variant reliability analysis framework for selective laser melting fabricated lattice structures with probability and convex hybrid models. Virtual Phys. Prototyp. 2022. [Google Scholar] [CrossRef]
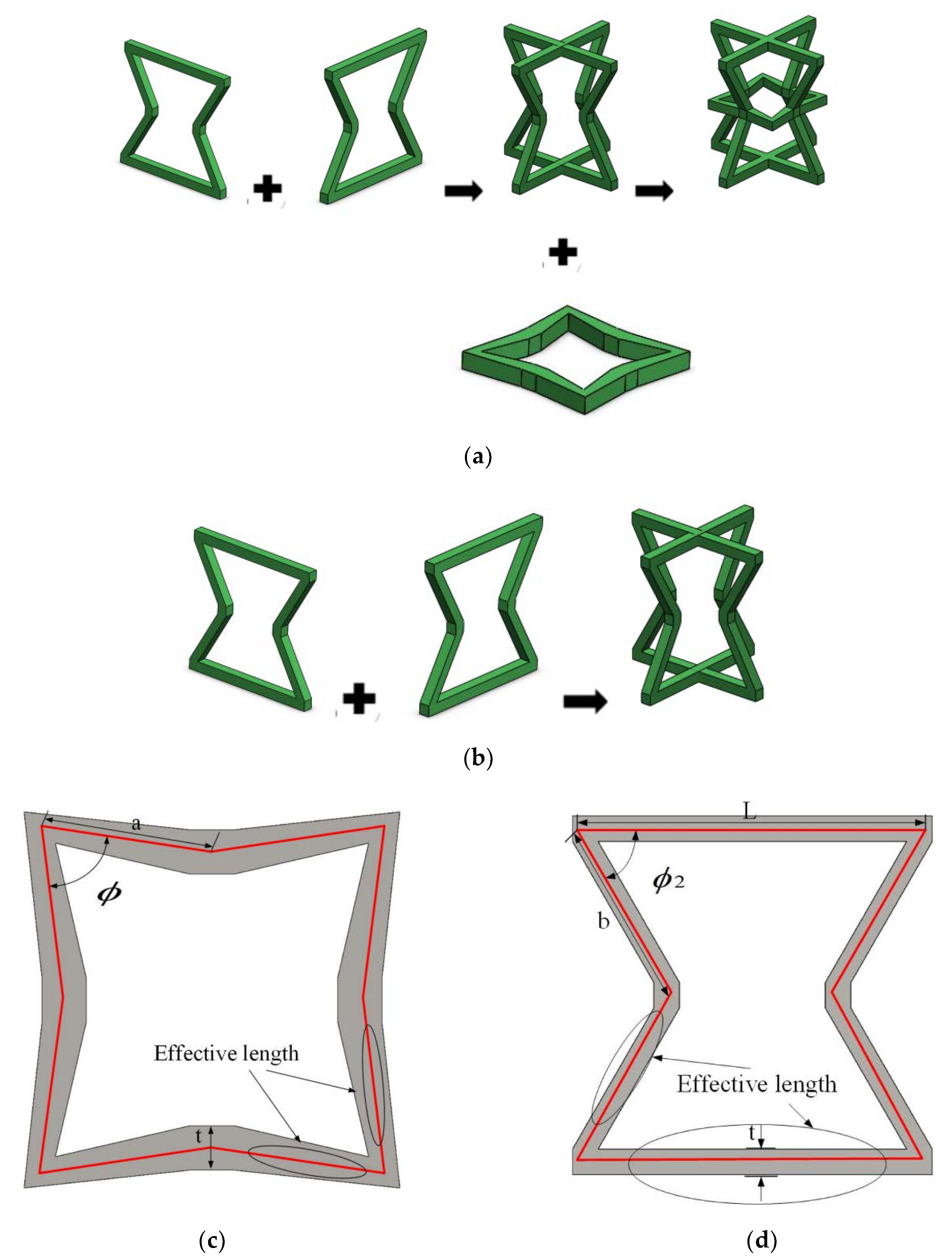

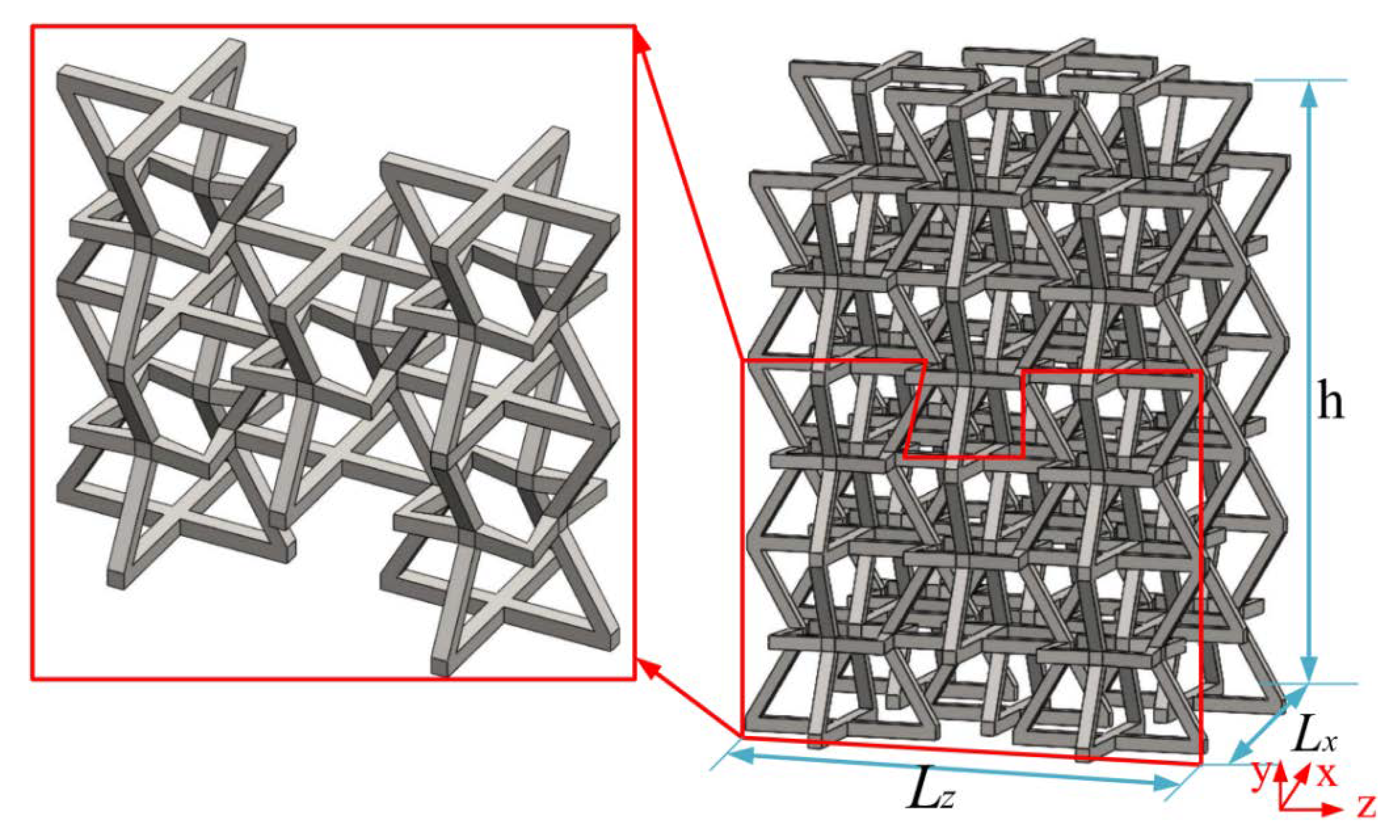
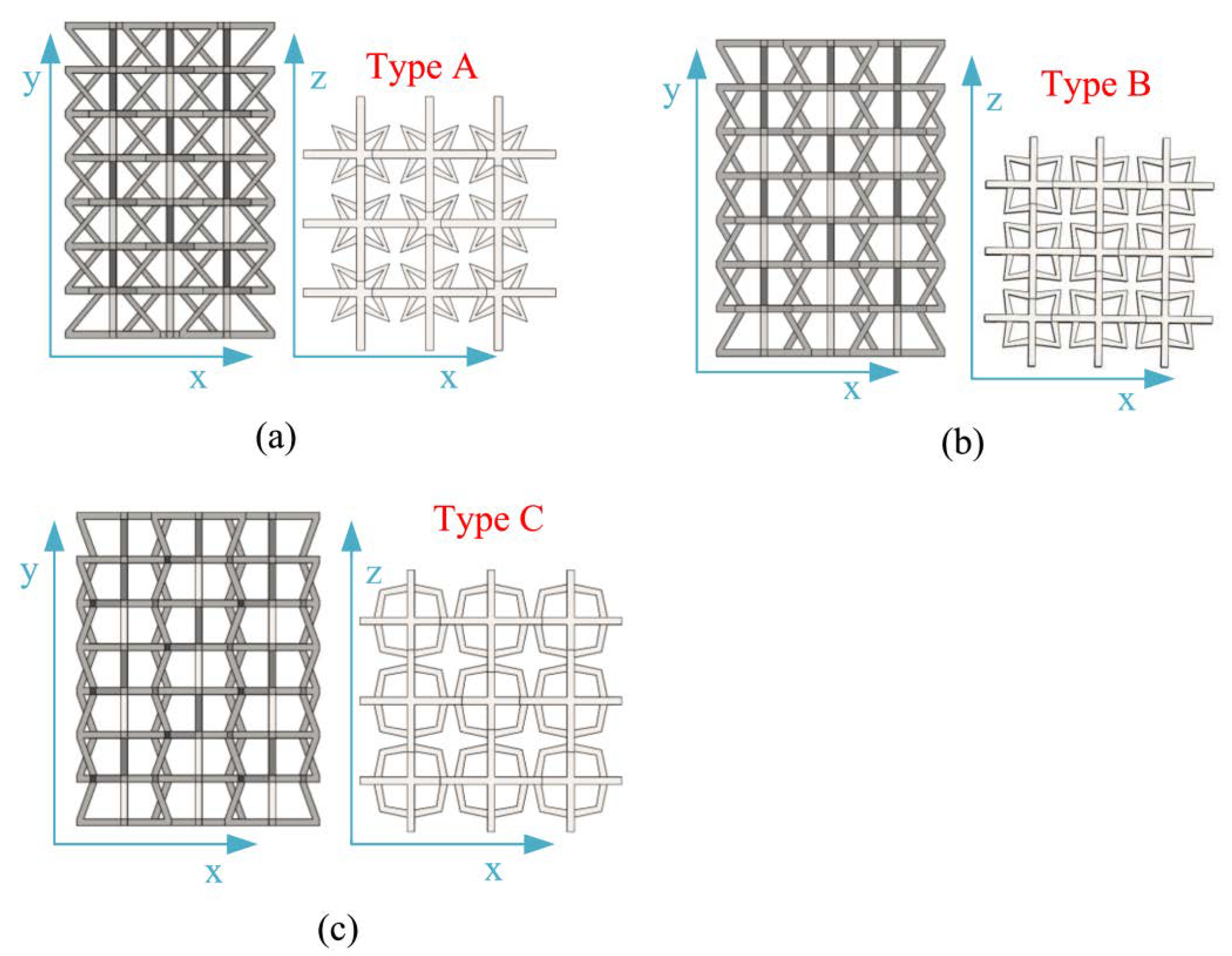



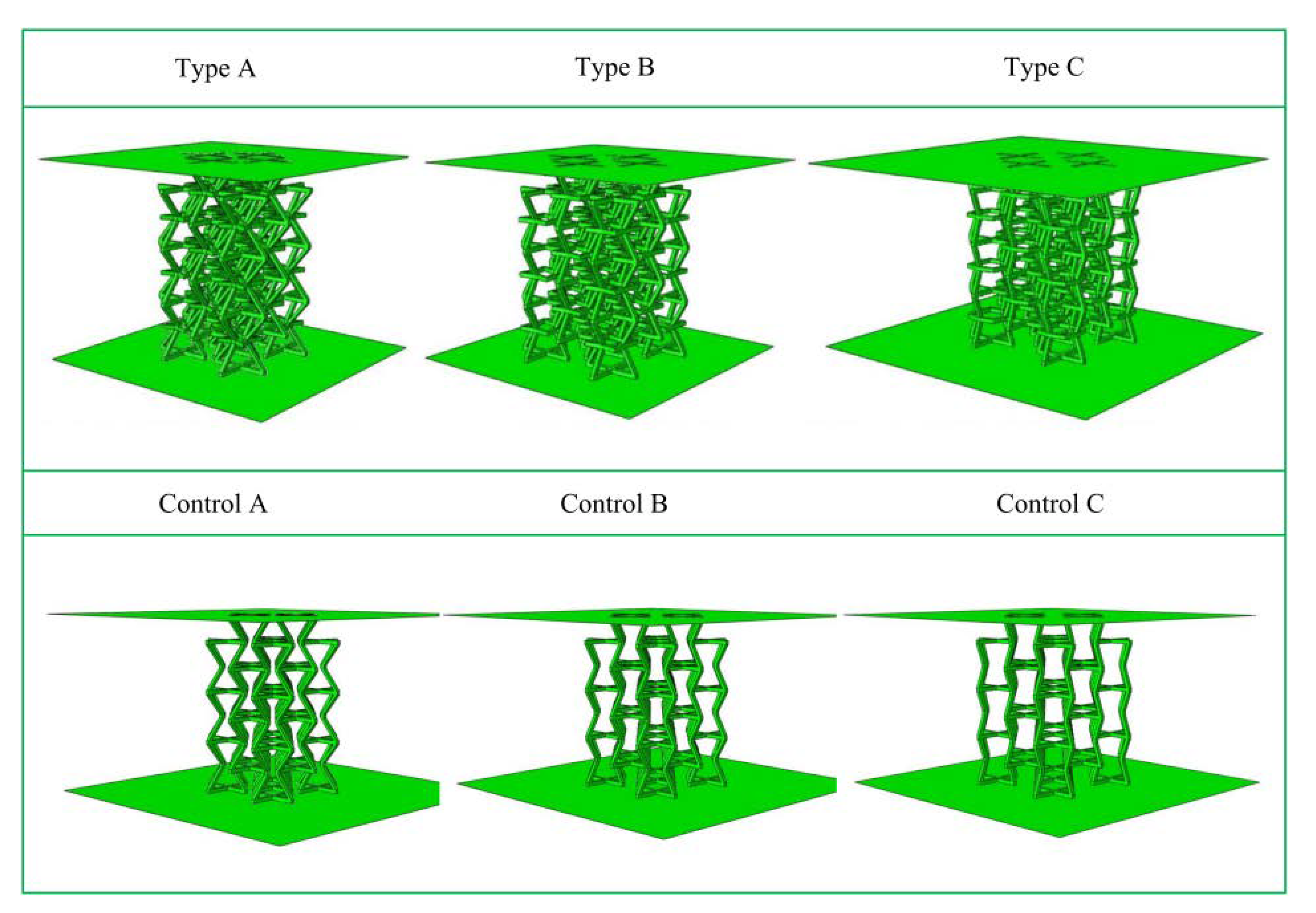




| Type | A (mm) | B (mm) | ∅ (°) | ∅2 (°) | L (mm) |
|---|---|---|---|---|---|
| A | 18.82 | 39.70 | 38.14 | 50 | 70 |
| B | 18.82 | 36.03 | 70.90 | 60 | 70 |
| C | 18.82 | 33.88 | 105.77 | 70 | 70 |
| Type | ∅2 | H (mm) | Lx | Lz | T (mm) |
|---|---|---|---|---|---|
| A | 50 | 231.66 | 154.05 | 154.05 | 5 |
| B | 60 | 231.66 | 168.38 | 168.38 | 5 |
| C | 70 | 231.66 | 180.37 | 180.37 | 5 |
| Classification | Elastic Modulus (GPa) | Yield Limit (MPa) | Tensile Strength (MPa) | Poisson Ratio | |
|---|---|---|---|---|---|
| SLM Specimen1 | 183.99 | 505 | 665 | 8.737 | 0.317 |
| SLM Specimen2 | 197.51 | 500 | 665 | 8.791 | 0.316 |
| SLM Specimen3 | 200.74 | 510 | 665 | 8.816 | 0.318 |
| Ordinary 316 L | 206 | 269.17 | 603.50 | 8.027 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zhang, Q.; Shi, H.; Liu, Z. A Modified Three-Dimensional Negative-Poisson-Ratio Metal Metamaterial Lattice Structure. Materials 2022, 15, 3752. https://doi.org/10.3390/ma15113752
Li F, Zhang Q, Shi H, Liu Z. A Modified Three-Dimensional Negative-Poisson-Ratio Metal Metamaterial Lattice Structure. Materials. 2022; 15(11):3752. https://doi.org/10.3390/ma15113752
Chicago/Turabian StyleLi, Fangyi, Qiang Zhang, Huimin Shi, and Zheng Liu. 2022. "A Modified Three-Dimensional Negative-Poisson-Ratio Metal Metamaterial Lattice Structure" Materials 15, no. 11: 3752. https://doi.org/10.3390/ma15113752
APA StyleLi, F., Zhang, Q., Shi, H., & Liu, Z. (2022). A Modified Three-Dimensional Negative-Poisson-Ratio Metal Metamaterial Lattice Structure. Materials, 15(11), 3752. https://doi.org/10.3390/ma15113752





