Non-Contact Multiscale Analysis of a DPP 3D-Printed Injection Die for Investment Casting
Abstract
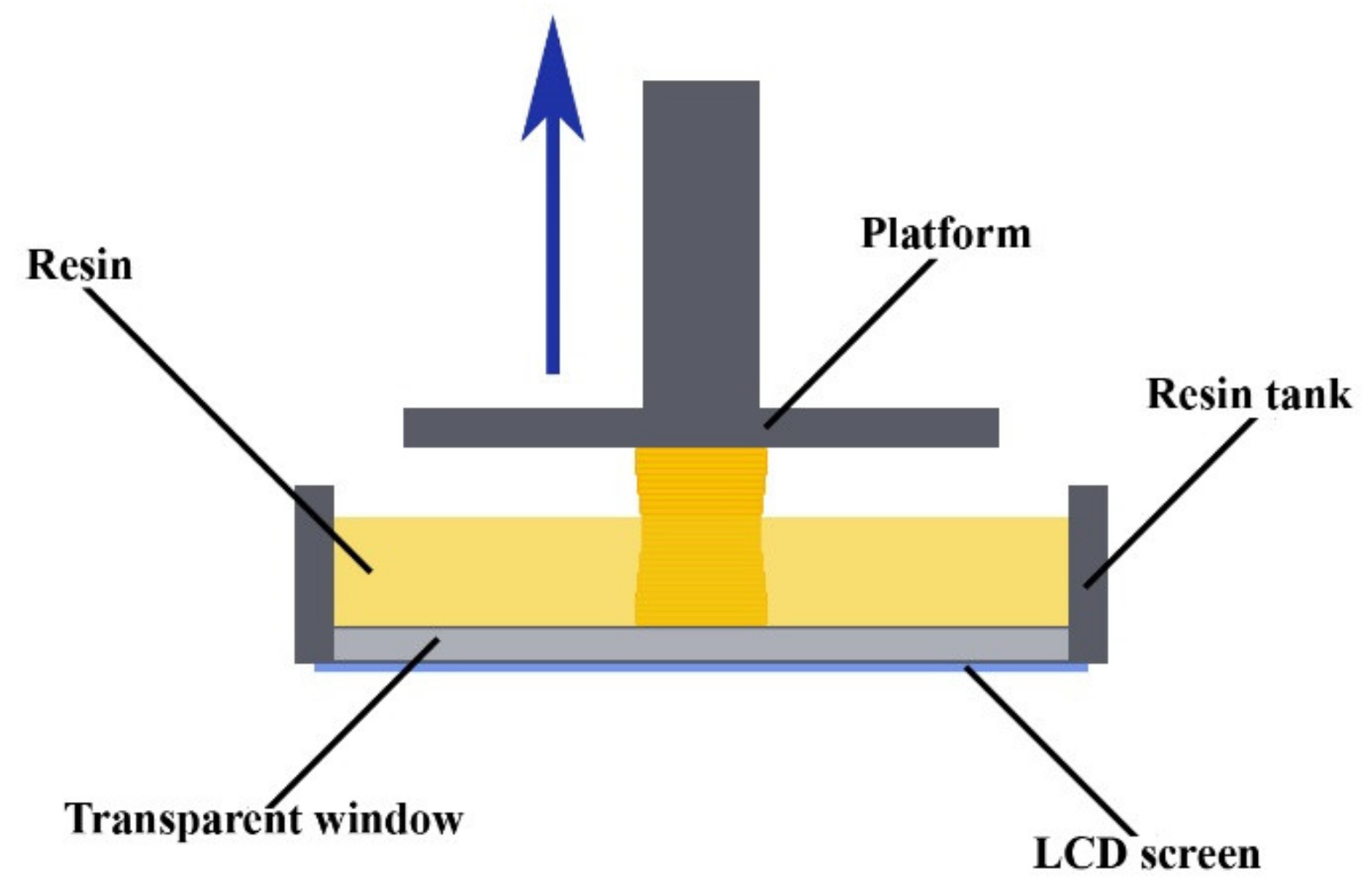
:1. Introduction
- Indirect—geometric analysis of the wax models formed in the injection die;
- Direct—geometric analysis of the 3D-printed injection die.
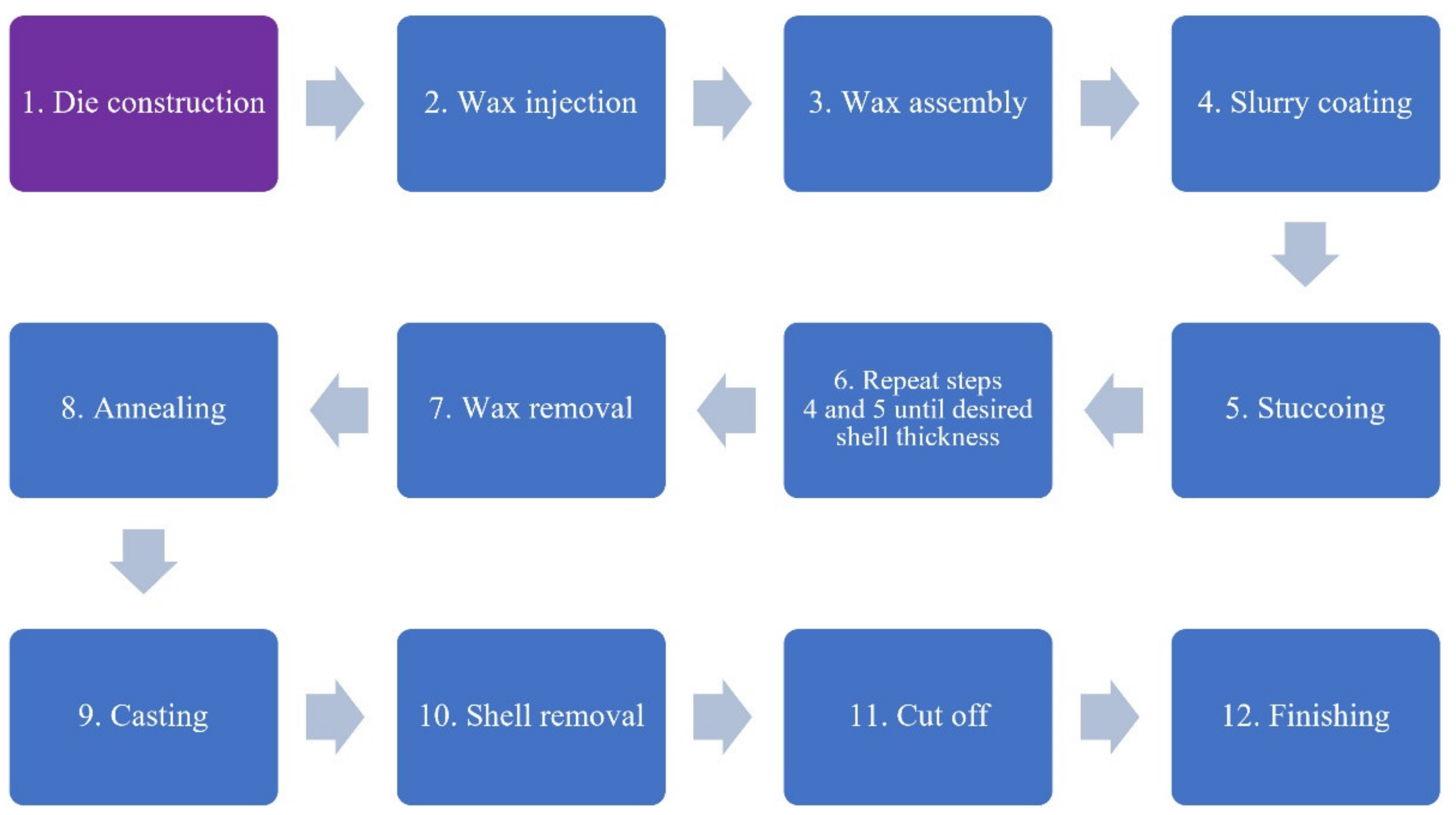
2. Materials and Methods
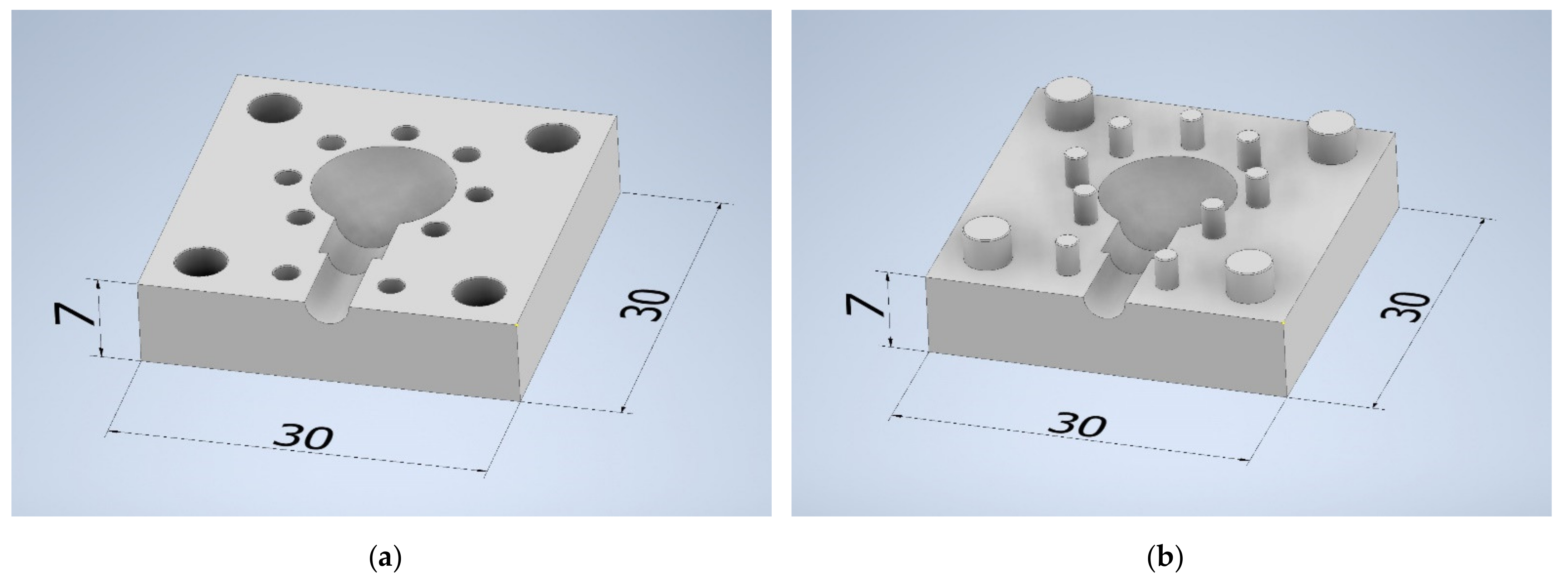
2.1. Model and Injection Die
2.2. Measurement Technologies and Measurement Strategy
- Material’s toughness and pliability—characteristics essential when considering tactile measurement. To some extent, a contact stylus may scratch and deform the surface, rendering the results unreliable;
- Transparency and light dispersion—a limiting factor when using optical technologies. Transparency limits the use of focus- or contrast-based methods (such as Focus Variation, focus stacking, etc.), and light dispersion decreases either contrast (in image-based measurement) or signal strength;
- Varying surface reflectivity—this factor is especially present in powder-based technologies. However, complex shapes, that are possible to achieve in additive manufacturing, can render an adequate exposure adjustment problematic.
2.2.1. X-ray CT
2.2.2. Structured Blue-Light Scanner
2.2.3. Focus Variation Microscope
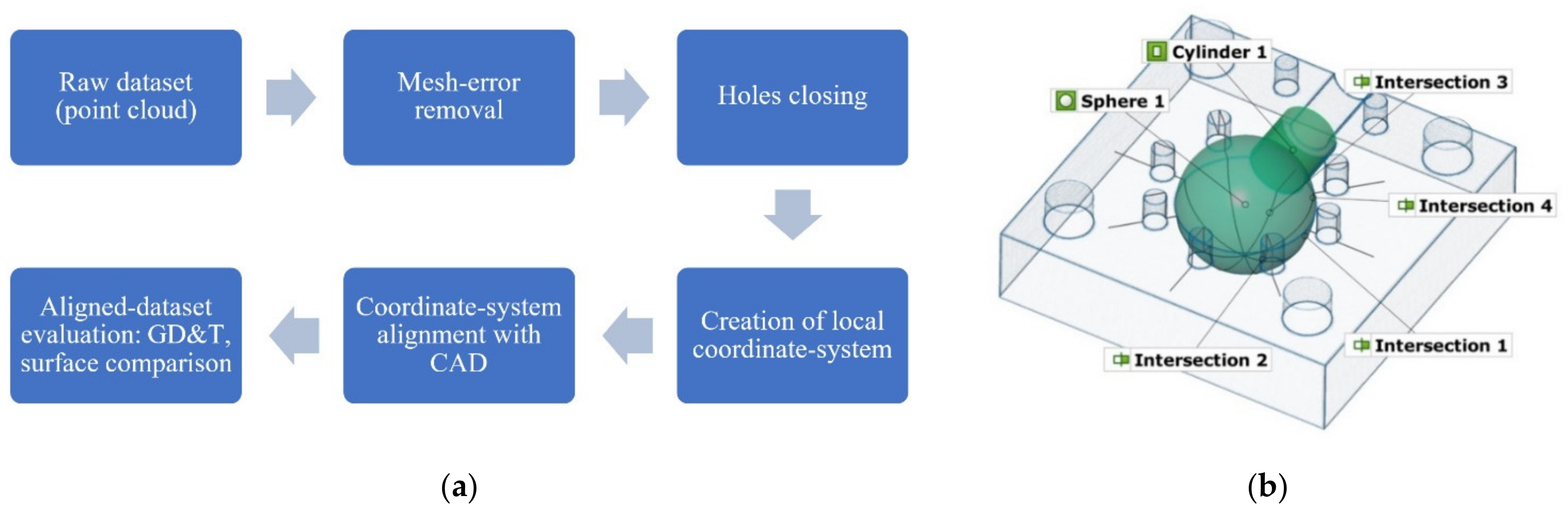
2.3. Dataset Evaluation
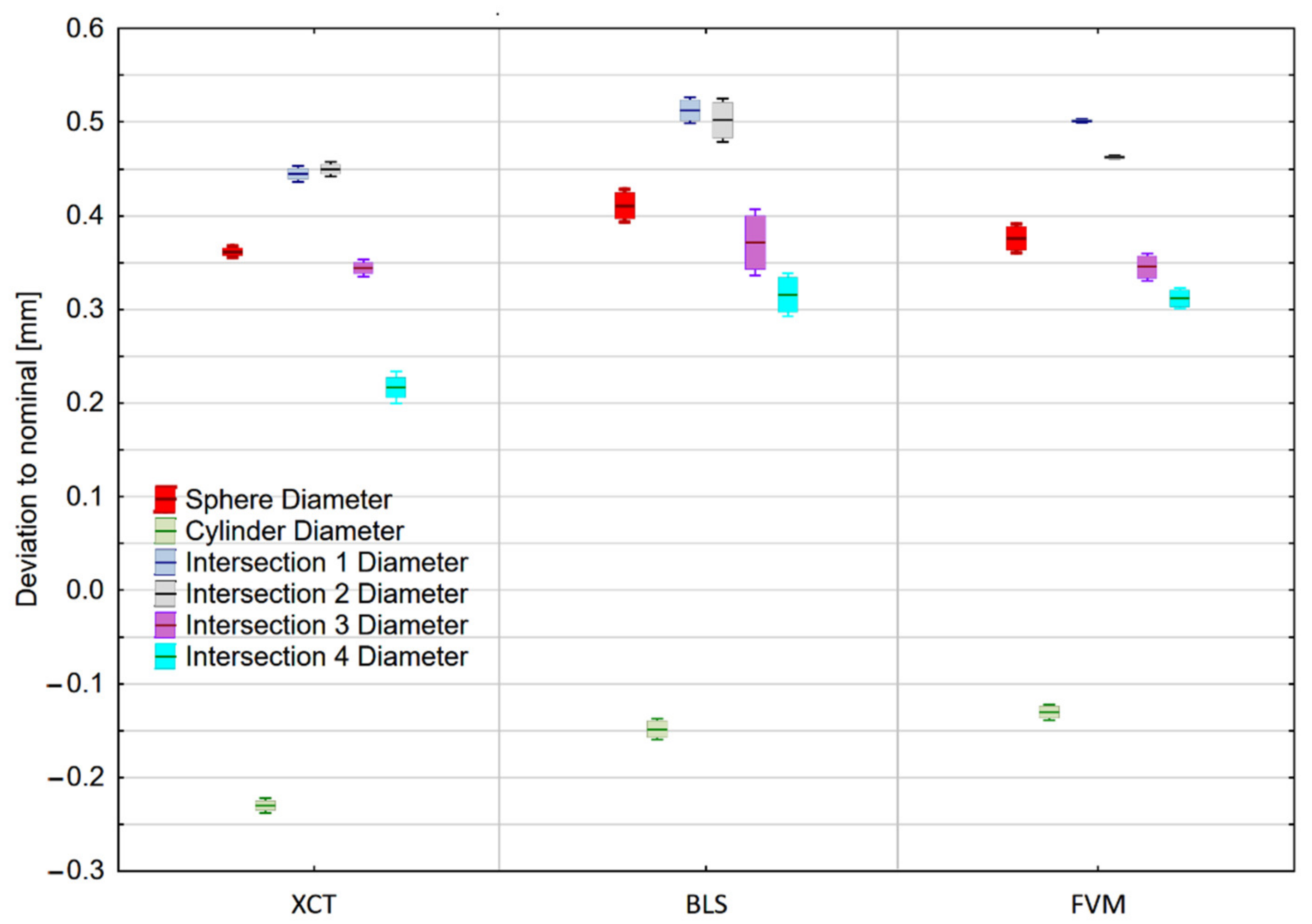
2.3.1. Dimensional Accuracy
- Sphere’s diameter;
- Cylinder’s diameter;
- Circles’ diameter on each of the four, evenly distributed cross-sections.
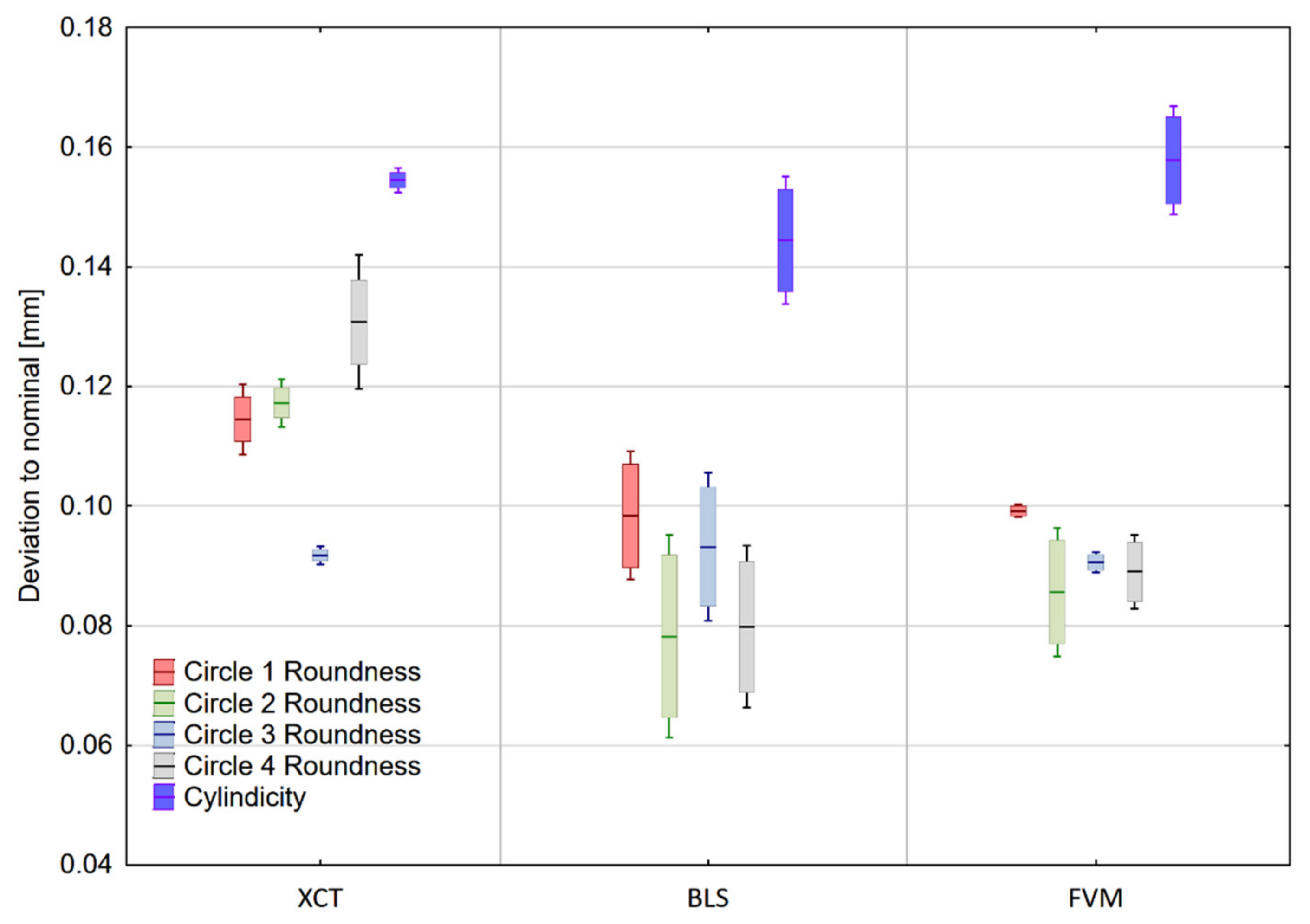
2.3.2. Form and Position Deviations
- Cylindricity;
- Roundness deviation of each cross-section to the fitted circles;
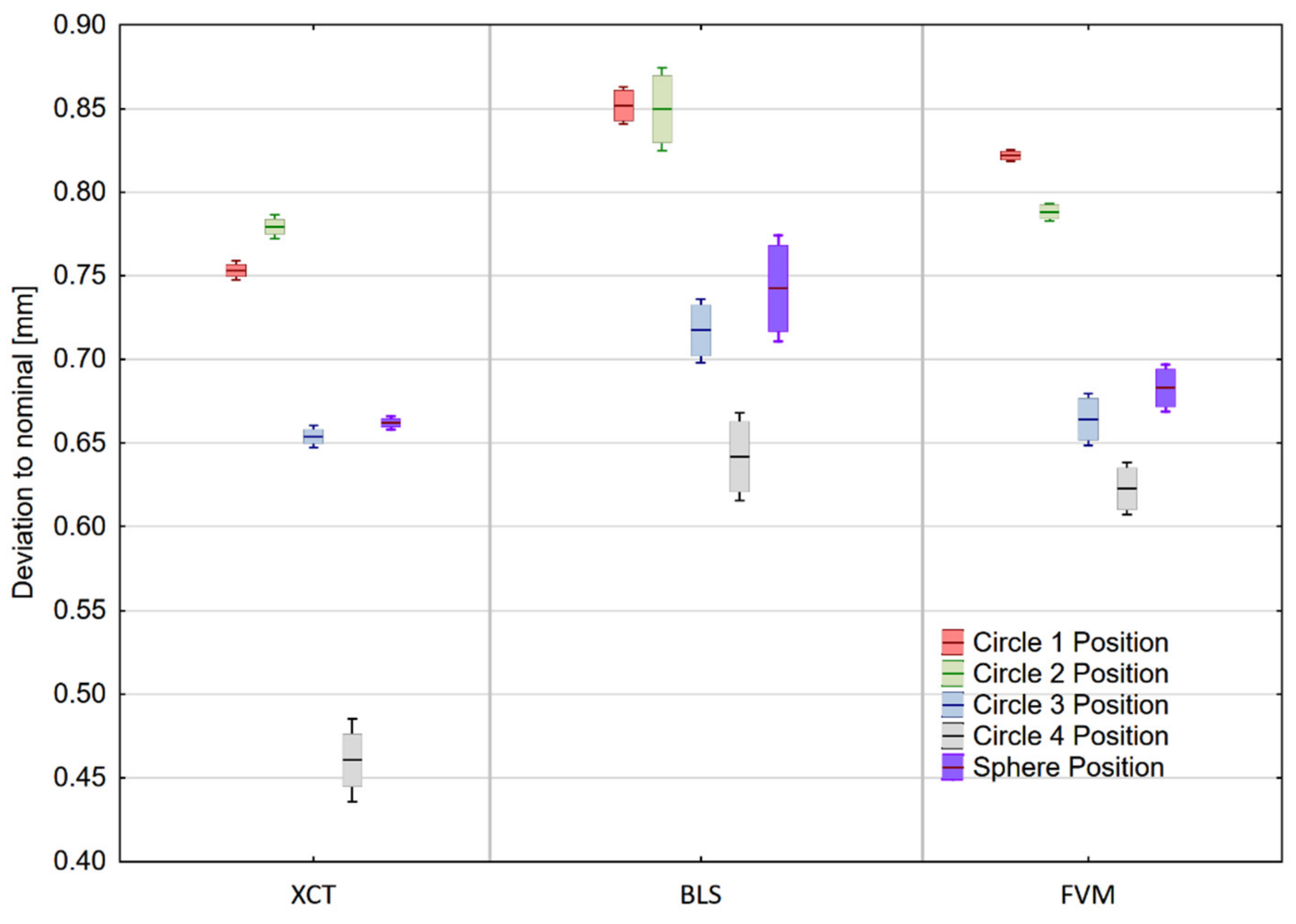
- Each fitted circle’s center-point position in relation to Plane Z (XY) in accordance with ISO 1101;
- Sphere’s center-point position in relation to Plane Z (XY) in accordance with ISO 1101.
2.3.3. Defect Detection
- Defect’s visibility on the dataset;
- System’s ability to measure both width and depth of the fractures;
- Visual quality of the defect’s representation.
2.3.4. Comparison with CAD Model
3. Results and Discussion
3.1. Dimensional Accuracy
3.2. Form and Position Deviations
3.3. Comparison with CAD Model
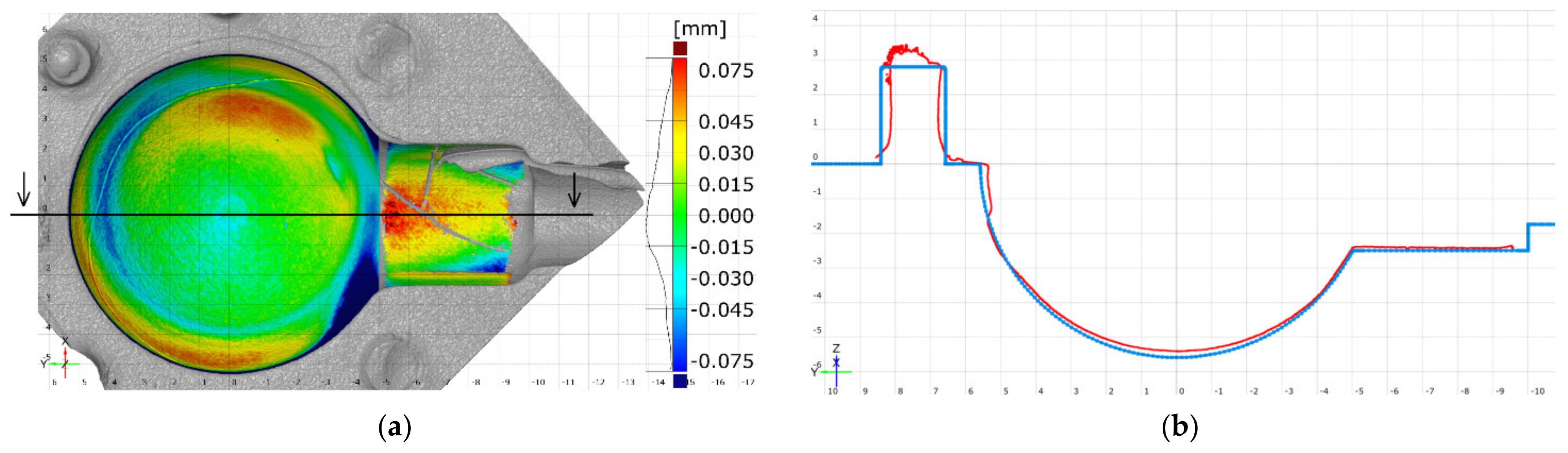
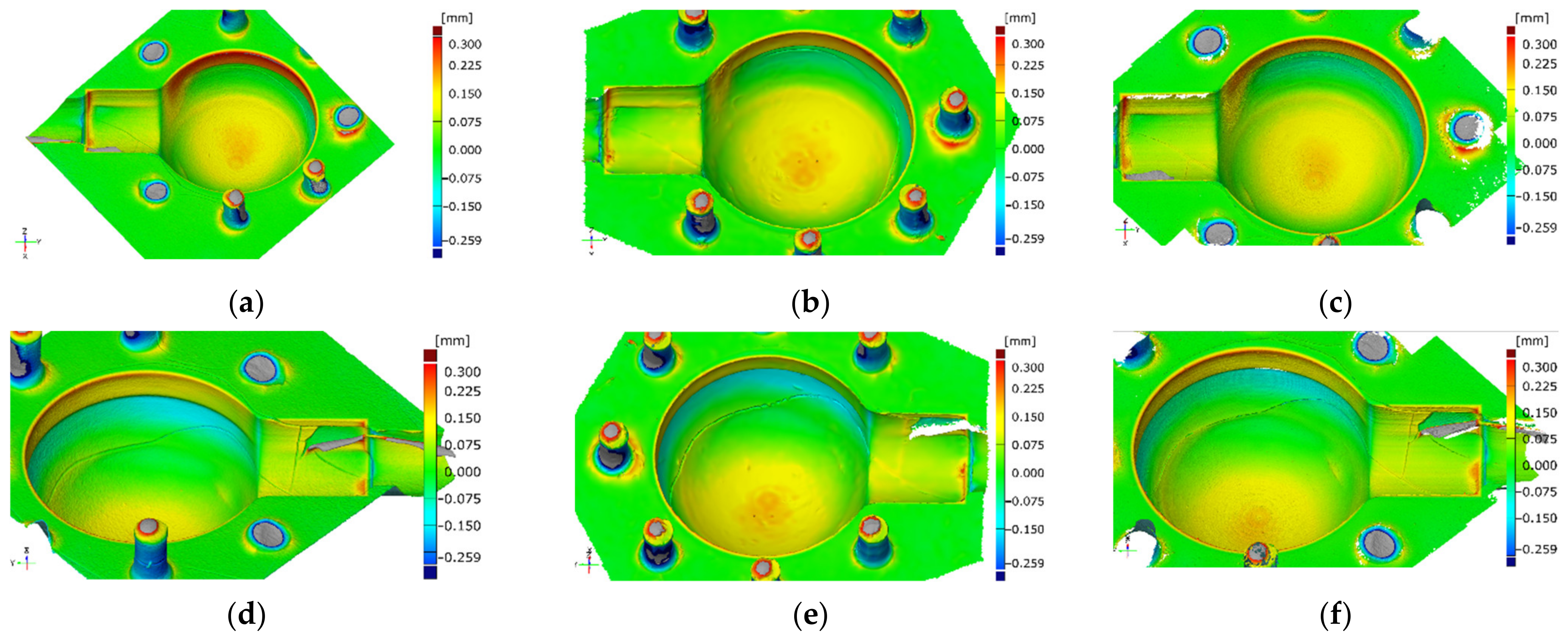
3.4. Defects Detection and Dataset Quality
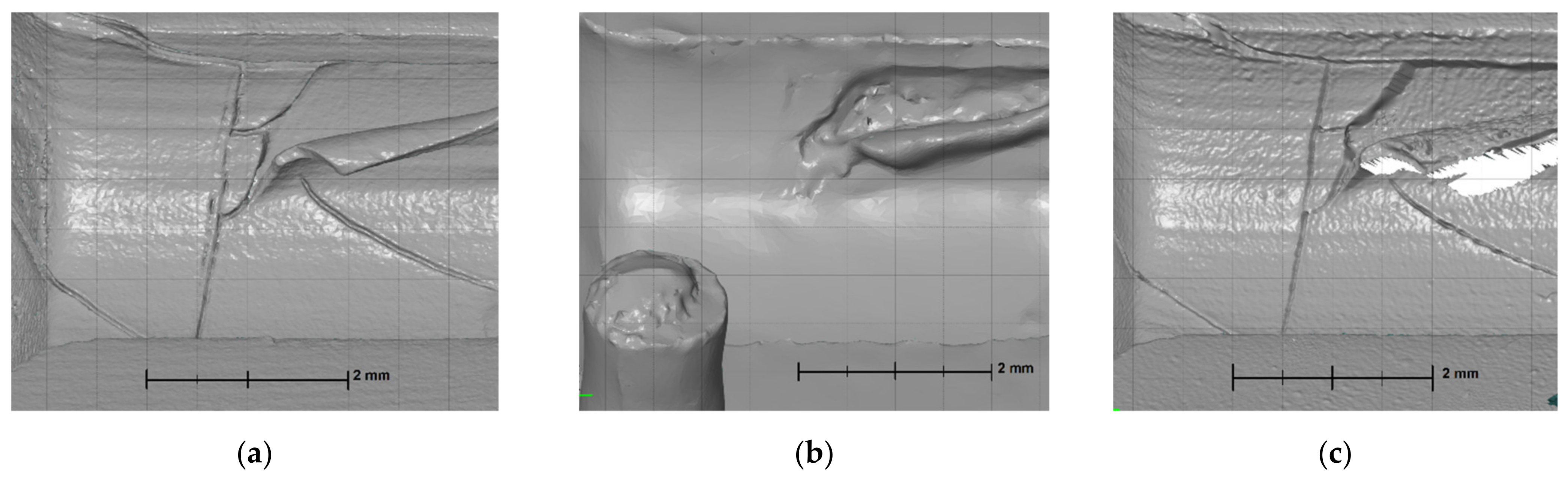
3.4.1. Cracks
3.4.2. Top-Layer Flaking
3.5. Results Summary
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dudek, P.; Rapacz-Kmita, A. Rapid Prototyping: Technologies, Materials and Advances. Arch. Met. Mater. 2016, 61, 891–896. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies, 3rd ed.; Springer: Cham, Switzerland, 2021; pp. 1–12. [Google Scholar]
- Campbell, J. Complete Casting Handbook, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2015; pp. 871–878. [Google Scholar]
- Macku, M.; Horacek, M. Applying RP-FDM Technology to Produce Prototype Castings Using the Investment Casting Method. Arch. Foundry Eng. 2012, 12, 75–82. [Google Scholar] [CrossRef] [Green Version]
- Singh, D.; Singh, R.; Boparai, K.S. Investigations on hardness of investment-casted implants fabricated after vapour smoothing of FDM replicas. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 178. [Google Scholar] [CrossRef]
- Simnofske, D.; Mollenhauer, K. Effect of wax crystallization on complex modulus of modified bitumen after varied temperature conditioning rates. IOP Conf. Ser. Mater. Sci. Eng. 2017, 236, 012003. [Google Scholar] [CrossRef]
- Wang, D.; Dong, A.; Zhu, G.; Shu, D.; Sun, J.; Li, F.; Sun, B. Rapid casting of complex impeller based on 3D printing wax pattern and simulation optimization. Int. J. Adv. Manuf. Technol. 2018, 100, 2629–2635. [Google Scholar] [CrossRef]
- Surace, R.; Basile, V.; Bellantone, V.; Modica, F.; Fassi, I. Micro Injection Molding of Thin Cavities Using Stereolithography for Mold Fabrication. Polymers 2021, 13, 1848. [Google Scholar] [CrossRef]
- Krizsma, S.; Kovács, N.; Kovács, J.; Suplicz, A. In-situ monitoring of deformation in rapid prototyped injection molds. Addit. Manuf. 2021, 42, 102001. [Google Scholar] [CrossRef]
- Udroiu, R.; Braga, I.C. Polyjet technology applications for rapid tooling. MATEC Web Conf. 2017, 112, 03011. [Google Scholar] [CrossRef] [Green Version]
- Technical Application Guide—PolyJet for Injection Molding. Available online: http://www.alphacam.ch/fileadmin/user_upload/Applikationen/PDFs/Technical_Application_Guide_-_Injection_Molding_-_PolyJet_For_Injection_Molding_-_English_A4_Web.pdf (accessed on 10 May 2021).
- Kumar, P.; Singh, R.; Ahuja, I. Investigations for Mechanical Properties of Hybrid Investment Casting: A Case Study. Mater. Sci. Forum 2014, 808, 89–95. [Google Scholar] [CrossRef]
- Using Castable Wax Resin. Available online: https://support.formlabs.com/s/article/Using-Castable-Wax-Resin?language=en_US (accessed on 5 May 2021).
- Chhabra, M.; Singh, R. Rapid casting solutions: A review. Rapid Prototyp. J. 2011, 17, 328–350. [Google Scholar] [CrossRef]
- Kroma, A.; Adamczak, O.; Sika, R.; Górski, F.; Kuczko, W.; Grześkowiak, K. Modern Reverse Engineering Methods Used to Modification of Jewelry. Adv. Sci. Technol. Res. J. 2020, 14, 298–306. [Google Scholar] [CrossRef]
- DLP Materials. Available online: https://cpspolymers.com/dlp (accessed on 5 May 2021).
- A New Method for Preparing 3D Acrylic Photopolymer Patterns for Investment Casting. Available online: https://www.assayofficelondon.co.uk/media/2552/a-new-method-for-preparing-3d-acyrlic-james-binnion.pdf (accessed on 31 May 2021).
- Freeman Flakes Injection Waxes. Available online: https://www.freemanwax.com/products/jewelry-injection-waxes/freeman-flakes-injection-waxes (accessed on 10 May 2021).
- Budzik, G.; Turek, P.; Jozwik, J.; Oleksy, M.; Paszkiewicz, A.; Damian, Z.; Wozniak, J. Analysis of Wear of the Polymer Mold in the Production of Wax Casting Models of Aircraft Engine Blades. In Proceedings of the 2020 IEEE 7th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 22–24 June 2020; pp. 265–269. [Google Scholar]
- Turek, P.; Budzik, G.; Sęp, J.; Oleksy, M.; Józwik, J.; Przeszłowski, Ł.; Paszkiewicz, A.; Kochmański, Ł.; Żelechowski, D. An Analysis of the Casting Polymer Mold Wear Manufactured Using PolyJet Method Based on the Measurement of the Surface Topography. Polymers 2020, 12, 3029. [Google Scholar] [CrossRef]
- Saini, J.; Dowling, L.; Kennedy, J.; Trimble, D. Investigations of the mechanical properties on different print orientations in SLA 3D printed resin. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 2279–2293. [Google Scholar] [CrossRef]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of Layer Thickness and Raster Angle on the Mechanical Properties of 3D-Printed PEEK and a Comparative Mechanical Study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef]
- Szykiedans, K.; Credo, W. Mechanical Properties of FDM and SLA Low-cost 3-D Prints. Procedia Eng. 2016, 136, 257–262. [Google Scholar] [CrossRef] [Green Version]
- Galeja, M.; Hejna, A.; Kosmela, P.; Kulawik, A. Static and Dynamic Mechanical Properties of 3D Printed ABS as a Function of Raster Angle. Materials 2020, 13, 297. [Google Scholar] [CrossRef] [Green Version]
- Czarnecka-Komorowska, D.; Grześkowiak, K.; Popielarski, P.; Barczewski, M.; Gawdzińska, K.; Popławski, M. Polyethylene Wax Modified by Organoclay Bentonite Used in the Lost-Wax Casting Process: Processing−Structure−Property Relationships. Materials 2020, 13, 2255. [Google Scholar] [CrossRef]
- Grzeskowiak, K.; Czarnecka-Komorowska, D.; Sytek, K.; Wojciechowski, M. Influence of waxes remelting used in investment casting on their thermal properties and linear shrinkage. Metalurgija 2015, 54, 350–352. [Google Scholar]
- Wieczorowski, M.; Gapiński, B.; Grzelka, M.; Szostak, M.; Szymański, M. The use of photogrammetry in improving quality of workpieces after an injection molding process. Polymery 2018, 63, 134–144. [Google Scholar] [CrossRef]
- Gapinski, B.; Janicki, P.; Marciniak-Podsadna, L.; Jakubowicz, M. Application of the computed tomography to control parts made on additive manufacturing process. Procedia Eng. 2016, 149, 105–121. [Google Scholar] [CrossRef] [Green Version]
- Luongo, A.; Falster, V.; Doest, M.B.; Ribo, M.M.; Eiriksson, E.R.; Pedersen, D.B.; Frisvad, J.R. Microstructure Control in 3D Printing with Digital Light Processing. Comput. Graph. Forum 2020, 39, 347–359. [Google Scholar] [CrossRef]
- Technical Data. Available online: https://photocentricgroup.com/wp-content/uploads/2020/08/TDS-Daylight-Flexible.pdf (accessed on 20 October 2021).
- Lou, S.; Jiang, X.; Sun, W.; Zeng, W.; Pagani, L.; Scott, P. Characterisation methods for powder bed fusion processed surface topography. Precis. Eng. 2019, 57, 1–15. [Google Scholar] [CrossRef]
- Senin, N.; Leach, R. Information-rich surface metrology. Procedia CIRP 2018, 75, 19–26. [Google Scholar] [CrossRef]
- Hermanek, P.; Carmignato, S. Porosity measurements by X-ray computed tomography: Accuracy evaluation using a calibrated object. Precis. Eng. 2017, 49, 377–387. [Google Scholar] [CrossRef]
- Launhardt, M.; Wörz, A.; Loderer, A.; Laumer, T.; Drummer, D.; Hausotte, T.; Schmidt, M. Detecting surface roughness on SLS parts with various measuring techniques. Polym. Test. 2016, 53, 217–226. [Google Scholar] [CrossRef]
- Thompson, A.; Senin, N.; Maskery, I.; Leach, R. Effects of magnification and sampling resolution in X-ray computed tomography for the measurement of additively manufactured metal surfaces. Precis. Eng. 2018, 53, 54–64. [Google Scholar] [CrossRef]
- Gapinski, B.; Wieczorowski, M.; Marciniak-Podsadna, L.; Dybala, B.; Ziolkowski, G. Comparison of Different Method of Measurement Geometry Using CMM, Optical Scanner and Computed Tomography 3D. Procedia Eng. 2014, 69, 255–262. [Google Scholar] [CrossRef] [Green Version]
- Lou, S.; Brown, S.; Sun, W.; Zeng, W.; Jiang, X.; Scott, P. An investigation of the mechanical filtering effect of tactile CMM in the measurement of additively manufactured parts. Measurement 2019, 144, 173–182. [Google Scholar] [CrossRef]
- Villarraga-Gómez, H.; Lee, C.; Smith, S.T. Dimensional metrology with X-ray CT: A comparison with CMM measurements on internal features and compliant structures. Precis. Eng. 2018, 51, 291–307. [Google Scholar] [CrossRef]
- Michalski, R.; Wieczorowski, M.; Glazowski, P.J.; Gapiński, B. Analysis of the Influence of Support During Measurement Using Coordinate Measuring Techniques. Adv. Sci. Technol. Res. J. 2019, 13, 22–29. [Google Scholar] [CrossRef]
- Mueller, T.; Jordan, M.; Schneider, T.; Poesch, A.; Reithmeier, E. Measurement of steep edges and undercuts in confocal microscopy. Micron 2016, 84, 79–95. [Google Scholar] [CrossRef]
- Grochalski, K.; Wieczorowski, M.; H’Roura, J.; Le Goic, G. The Optical Aspect of Errors in Measurements of Surface Asperities Using the Optical Profilometry Method. Front. Mech. Eng. 2020, 6, 12. [Google Scholar] [CrossRef]
- Villarraga-Gómez, H.; Körner, L.; Leach, R.; Smith, S.T. Amplitude-wavelength maps for X-ray computed tomography systems. Precis. Eng. 2020, 64, 228–242. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M. Problem of Non-Measured Points in Surface Texture Measurements. Metrol. Meas. Syst. 2017, 24, 525–536. [Google Scholar] [CrossRef]
- Senin, N.; Thompson, A.; Leach, R. Characterisation of the topography of metal additive surface features with different measurement technologies. Meas. Sci. Technol. 2017, 28, 095003. [Google Scholar] [CrossRef]
- Tato, W.; Blunt, L.; Llavori, I.; Aginagalde, A.; Townsend, A.; Zabala, A. Surface integrity of additive manufacturing parts: A comparison between optical topography measuring techniques. Procedia CIRP 2020, 87, 403–408. [Google Scholar] [CrossRef]
- Villarraga-Gómez, H.; Smith, S.T. Effect of the number of projections on dimensional measurements with X-ray computed tomography. Precis. Eng. 2020, 66, 445–456. [Google Scholar] [CrossRef]
- Du Plessis, A.; Broeckhoven, C.; Guelpa, A.; le Roux, S. Laboratory X-ray micro-computed tomography: A user guideline for biological samples. GigaScience 2017, 6, 1–11. [Google Scholar] [CrossRef]
- Hiller, J.; Hornberger, P. Measurement accuracy in X-ray computed tomography metrology: Toward a systematic analysis of interference effects in tomographic imaging. Precis. Eng. 2016, 45, 18–32. [Google Scholar] [CrossRef]
- Townsend, A.; Racasan, R.; Leach, R.; Senin, N.; Thompson, A.; Ramsey, A.; Bate, D.; Woolliams, P.; Brown, S.; Blunt, L. An interlaboratory comparison of X-ray computed tomography measurement for texture and dimensional characterisation of additively manufactured parts. Addit. Manuf. 2018, 23, 422–432. [Google Scholar] [CrossRef]
- Koteras, R.; Wieczorowski, M.; Znaniecki, P.; Swojak, N. Measurement strategy as a determinant of the measurement uncertainty of an optical scanner. Arch. Mech. Technol. Mater. 2019, 39, 26–31. [Google Scholar] [CrossRef] [Green Version]
- Helmli, F. Optical Measurement of Surface Topography. Leach, R., Ed.; Springer: Berlin, Germany, 2011; pp. 131–166. [Google Scholar]
- Pagani, L.; Townsend, A.; Zeng, W.; Lou, S.; Blunt, L.; Jiang, X.Q.; Scott, P. Towards a new definition of areal surface texture parameters on freeform surface: Re-entrant features and functional parameters. Measurement 2019, 141, 442–459. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M. Comparison of Results of Surface Texture Measurement Obtained with Stylus Methods and Optical Methods. Metrol. Meas. Syst. 2018, 25, 589–602. [Google Scholar]






| Sensor Resolution/Voxel Size | X-ray Tube | No. of Projections | Exposure Time | Voltage | Current | Material Filter |
|---|---|---|---|---|---|---|
| 1000 × 1000/15 μm | Transmission | 1500 | 350 ms | 120 kV | 140 mA | none |
| Vertical Resolution | Lateral Resolution | Lens | Tilt | Illumination | Total Time |
|---|---|---|---|---|---|
| 0.350 µm | 8 µm | 5× | 45 degrees | Coaxial, polarized | 28 min per single measurement |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kroma, A.; Mendak, M.; Jakubowicz, M.; Gapiński, B.; Popielarski, P. Non-Contact Multiscale Analysis of a DPP 3D-Printed Injection Die for Investment Casting. Materials 2021, 14, 6758. https://doi.org/10.3390/ma14226758
Kroma A, Mendak M, Jakubowicz M, Gapiński B, Popielarski P. Non-Contact Multiscale Analysis of a DPP 3D-Printed Injection Die for Investment Casting. Materials. 2021; 14(22):6758. https://doi.org/10.3390/ma14226758
Chicago/Turabian StyleKroma, Arkadiusz, Michał Mendak, Michał Jakubowicz, Bartosz Gapiński, and Paweł Popielarski. 2021. "Non-Contact Multiscale Analysis of a DPP 3D-Printed Injection Die for Investment Casting" Materials 14, no. 22: 6758. https://doi.org/10.3390/ma14226758
APA StyleKroma, A., Mendak, M., Jakubowicz, M., Gapiński, B., & Popielarski, P. (2021). Non-Contact Multiscale Analysis of a DPP 3D-Printed Injection Die for Investment Casting. Materials, 14(22), 6758. https://doi.org/10.3390/ma14226758








