Analytical Solution of the Non-Stationary Heat Conduction Problem in Thin-Walled Products during the Additive Manufacturing Process
Abstract
:1. Introduction
2. Model and Methods Description
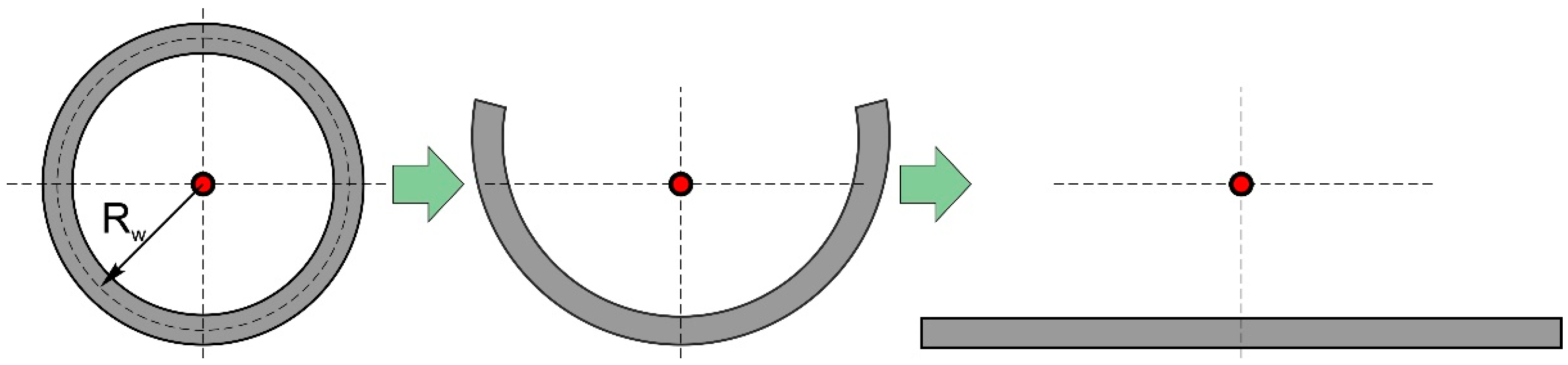
2.1. Problem Statement
- The physical properties of the substrate and the filler material (specific heat capacity c, density ρ, thermal conductivity λ, thermal diffusivity a) are temperature-independent.
- The effect of convection of liquid metal is not considered.
- Heat flux distribution of the heat source qh is presented as a surface normally distributed heat source.
- Heat transfer occurs according to Newton’s law.
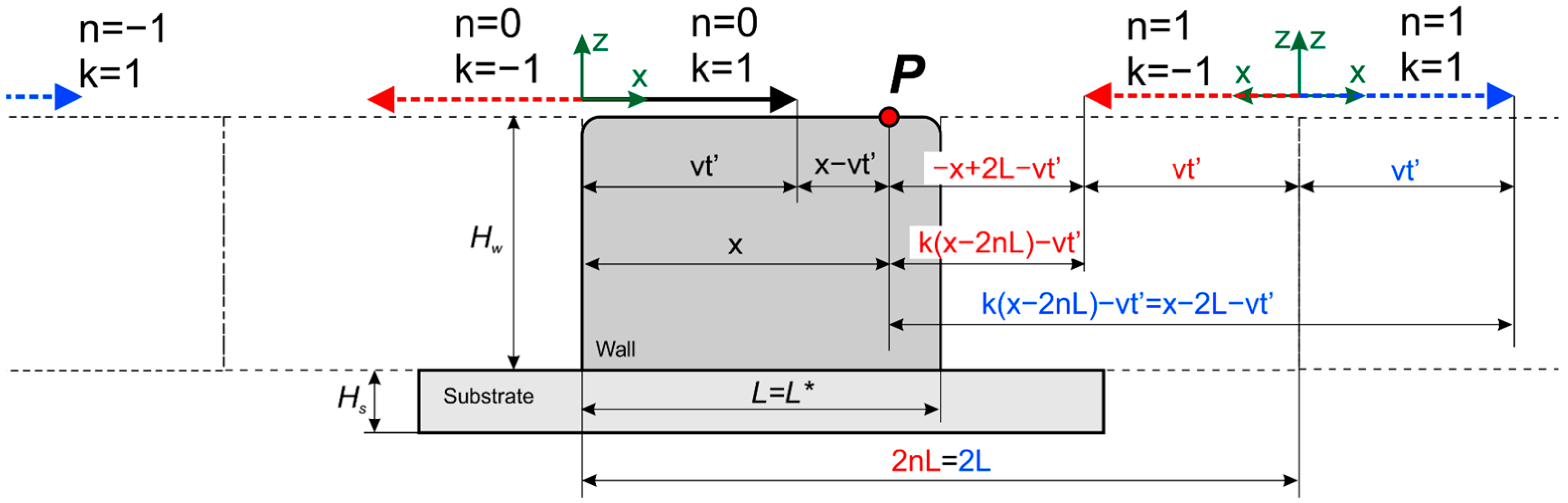
2.2. Analytical Model of Non-Stationary Heat Transfer
2.3. Influence of the Substrate on the Temperature Field
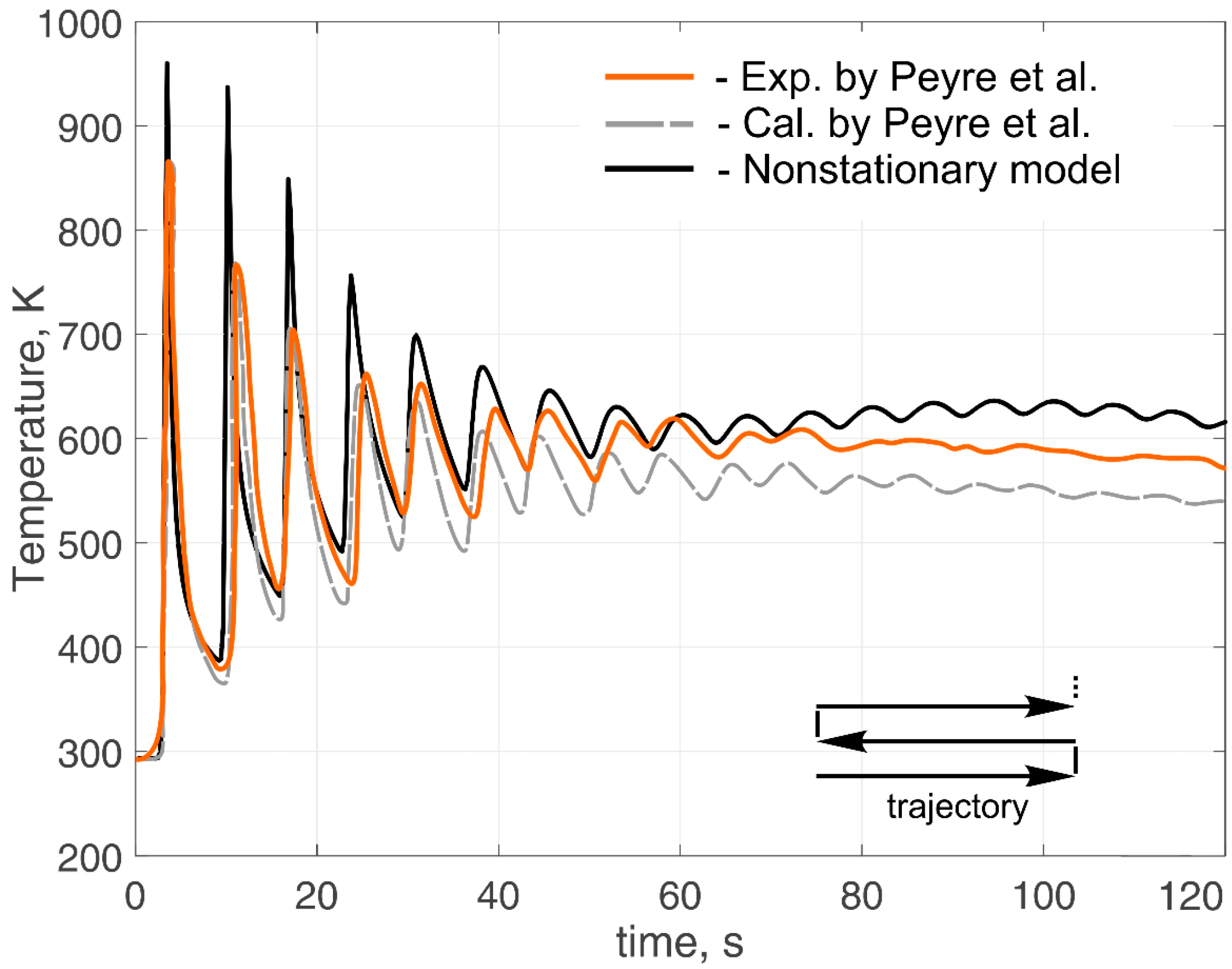
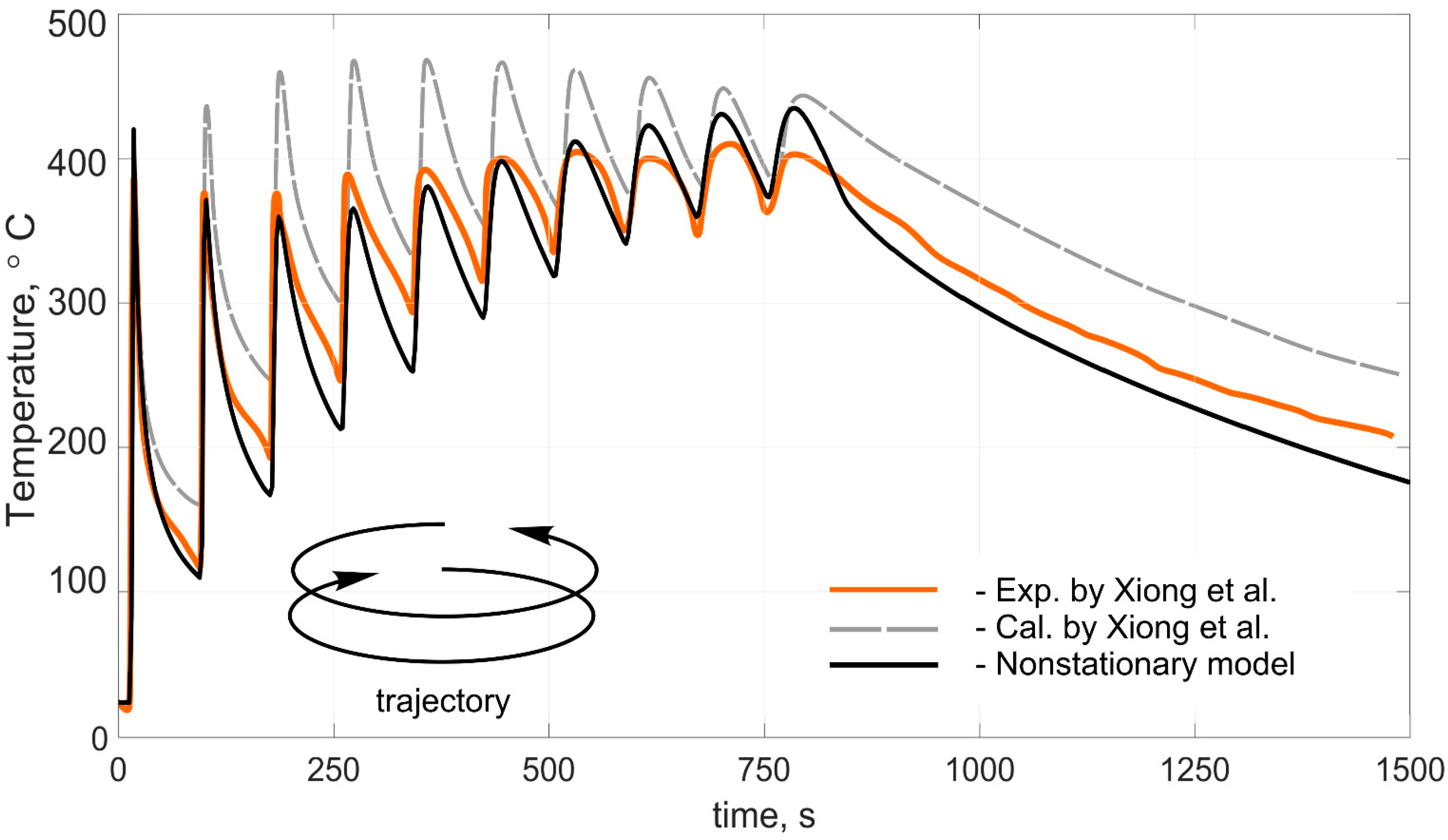
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uriondo, A.; Esperon-Miguez, M.; Perinpanayagam, S. The present and future of additive manufacturing in the aerospace sector: A review of important aspects. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 2132–2147. [Google Scholar] [CrossRef]
- Gisario, A.; Kazarian, M.; Martina, F.; Mehrpouya, M. Metal additive manufacturing in the commercial aviation industry: A review. J. Manuf. Syst. 2019, 53, 124–149. [Google Scholar] [CrossRef]
- Ahn, D.-G. Direct metal additive manufacturing processes and their sustainable applications for green technology: A review. Int. J. Precis. Eng. Manuf. Technol. 2016, 3, 381–395. [Google Scholar] [CrossRef]
- Busachi, A.; Erkoyuncu, J.A.; Colegrove, P.; Martina, F.; Watts, C.; Drake, R. A review of Additive Manufacturing technology and Cost Estimation techniques for the defence sector. CIRP J. Manuf. Sci. Technol. 2017, 19, 117–128. [Google Scholar] [CrossRef] [Green Version]
- Korsmik, R.; Tsybulskiy, I.; Rodionov, A.; Klimova-Korsmik, O.; Gogolukhina, M.; Ivanov, S.; Zadykyan, G.; Mendagaliev, R. The approaches to design and manufacturing of large-sized marine machinery parts by direct laser deposition. Procedia CIRP 2020, 94, 298–303. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Babkin, K.D.; Cheverikin, V.V.; Klimova-Korsmik, O.G.; Sklyar, M.O.; Stankevich, S.; Turichin, G.A.; Travyanov, A.Y.; Valdaytseva, E.A.; Zemlyakov, E.V. High-Speed Laser Direct Deposition Technology: Theoretical Aspects, Experimental Researches, Analysis of Structure, and Properties of Metallic Products. In Proceedings of the Scientific-Practical Conference “Research and Development—2016”, Moscow, Russia, 14–15 December 2016; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2017; pp. 501–509. [Google Scholar]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Klimova-Korsmik, O.; Turichin, G.; Zemlyakov, E.; Babkin, K.; Petrovskiy, P.; Travyanov, A. Technology of High-speed Direct Laser Deposition from Ni-based Superalloys. Phys. Procedia 2016, 83, 716–722. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Cong, W. A review on laser deposition-additive manufacturing of ceramics and ceramic reinforced metal matrix composites. Ceram. Int. 2018, 44, 20599–20612. [Google Scholar] [CrossRef]
- Promakhov, V.; Zhukov, A.; Ziatdinov, M.; Zhukov, I.; Schulz, N.; Kovalchuk, S.; Dubkova, Y.; Korsmik, R.; Klimova-Korsmik, O.; Turichin, G.; et al. Inconel 625/TiB2 Metal Matrix Composites by Direct Laser Deposition. Metals 2019, 9, 141. [Google Scholar] [CrossRef] [Green Version]
- Heigel, J.; Michaleris, P.; Reutzel, E. Thermo-mechanical model development and validation of directed energy deposition additive manufacturing of Ti–6Al–4V. Addit. Manuf. 2015, 5, 9–19. [Google Scholar] [CrossRef]
- Kiran, A.; Hodek, J.; Vavřík, J.; Urbánek, M.; Džugan, J. Numerical Simulation Development and Computational Optimization for Directed Energy Deposition Additive Manufacturing Process. Materials 2020, 13, 2666. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Hu, Y.; Ji, X.; Ma, L.; Huang, W. In situ measurements and thermo-mechanical simulation of Ti–6Al–4V laser solid forming processes. Int. J. Mech. Sci. 2019, 153–154, 119–130. [Google Scholar] [CrossRef]
- Rodriguez, E.; Mireles, J.; Terrazas, C.A.; Espalin, D.; Perez, M.A.; Wicker, R.B. Approximation of absolute surface temperature measurements of powder bed fusion additive manufacturing technology using in situ infrared thermography. Addit. Manuf. 2015, 5, 31–39. [Google Scholar] [CrossRef]
- Tang, Z.-J.; Liu, W.-W.; Wang, Y.-W.; Saleheen, K.M.; Liu, Z.-C.; Peng, S.-T.; Zhang, Z.; Zhang, H.-C. A review on in situ monitoring technology for directed energy deposition of metals. Int. J. Adv. Manuf. Technol. 2020, 108, 1–27. [Google Scholar] [CrossRef]
- Schöpp, H.; Sperl, A.; Kozakov, R.; Gött, G.; Uhrlandt, D.; Wilhelm, G. Temperature and emissivity determination of liquid steel S235. J. Phys. D Appl. Phys. 2012, 45. [Google Scholar] [CrossRef]
- Altenburg, S.J.; Straße, A.; Gumenyuk, A.; Maierhofer, C. In-situ monitoring of a laser metal deposition (LMD) process: Comparison of MWIR, SWIR and high-speed NIR thermography. Quant. Infrared Thermogr. J. 2020, 1–18. [Google Scholar] [CrossRef]
- Peyre, P.; Dal, M.; Pouzet, S.E.; Castelnau, O. Simplified numerical model for the laser metal deposition additive manufacturing process. J. Laser Appl. 2017, 29, 022304. [Google Scholar] [CrossRef]
- Ge, J.; Ma, T.; Han, W.; Yuan, T.; Jinguo, G.; Fu, H.; Xiao, R.; Lei, Y.; Lin, J. Thermal-induced microstructural evolution and defect distribution of wire-arc additive manufacturing 2Cr13 part: Numerical simulation and experimental characterization. Appl. Therm. Eng. 2019, 163, 114335. [Google Scholar] [CrossRef]
- Chiumenti, M.; Lin, X.; Cervera, M.; Lei, W.; Zheng, Y.; Huang, W. Numerical simulation and experimental calibration of additive manufacturing by blown powder technology. Part I: Thermal analysis. Rapid Prototyp. J. 2017, 23, 448–463. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Ma, N.; Chen, J.; Feng, Z.; Murakawa, H. Toward large-scale simulation of residual stress and distortion in wire and arc additive manufacturing. Addit. Manuf. 2020, 34, 101248. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Irwin, J.; Michaleris, P. Thermomechanical Modeling of Additive Manufacturing Large Parts. J. Manuf. Sci. Eng. 2014, 136, 061007. [Google Scholar] [CrossRef]
- Malmelöv, A.; Lundbäck, A.; Lindgren, L.-E. History Reduction by Lumping for Time-Efficient Simulation of Additive Manufacturing. Metal 2019, 10, 58. [Google Scholar] [CrossRef] [Green Version]
- Gan, Z.; Liu, H.; Li, S.; He, X.; Yu, G. Modeling of thermal behavior and mass transport in multi-layer laser additive manufacturing of Ni-based alloy on cast iron. Int. J. Heat Mass Transf. 2017, 111, 709–722. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, T.; Zhang, W.; DebRoy, T. An improved prediction of residual stresses and distortion in additive manufacturing. Comput. Mater. Sci. 2017, 126, 360–372. [Google Scholar] [CrossRef] [Green Version]
- Ou, W.; Knapp, G.; Mukherjee, T.; Wei, Y.; DebRoy, T. An improved heat transfer and fluid flow model of wire-arc additive manufacturing. Int. J. Heat Mass Transf. 2021, 167, 120835. [Google Scholar] [CrossRef]
- Rykalin, N.N. Calculations of Thermal Processes in Welding; Mashgiz Publ.: Moscow, Russia, 1951. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series. Vol.1. Elementary Functions; Gordon and Breach: New York, NY, USA, 1986. [Google Scholar]
- Howlett, J. Handbook of Mathematical Functions. Edited by Milton Abramowitz and Irene A. Stegun. Constable (Dover Publications Inc.) Paperback edition 1965. Math. Gaz. 1966, 50, 358–359. [Google Scholar] [CrossRef]
- Peyre, P.; Aubry, P.; Fabbro, R.; Neveu, R.; Longuet, A. Analytical and numerical modelling of the direct metal deposition laser process. J. Phys. D Appl. Phys. 2008, 41. [Google Scholar] [CrossRef]
- Xiong, J.; Lei, Y.; Li, R. Finite element analysis and experimental validation of thermal behavior for thin-walled parts in GMAW-based additive manufacturing with various substrate preheating temperatures. Appl. Therm. Eng. 2017, 126, 43–52. [Google Scholar] [CrossRef]



| Process | Heat Source | Power (W) | Cladding Speed (mm·s−1) | Heat Convection (W·K−1·m−2) | Heat Efficiency | Pause Time(s) |
|---|---|---|---|---|---|---|
| DLD | laser | 600 | 6 | 20 | 0.35 | 0 |
| WAAM | arc | 2850 | 5 | 5.7 | 0.85 | 33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukin, D.; Valdaytseva, E.; Turichin, G. Analytical Solution of the Non-Stationary Heat Conduction Problem in Thin-Walled Products during the Additive Manufacturing Process. Materials 2021, 14, 4049. https://doi.org/10.3390/ma14144049
Mukin D, Valdaytseva E, Turichin G. Analytical Solution of the Non-Stationary Heat Conduction Problem in Thin-Walled Products during the Additive Manufacturing Process. Materials. 2021; 14(14):4049. https://doi.org/10.3390/ma14144049
Chicago/Turabian StyleMukin, Dmitrii, Ekaterina Valdaytseva, and Gleb Turichin. 2021. "Analytical Solution of the Non-Stationary Heat Conduction Problem in Thin-Walled Products during the Additive Manufacturing Process" Materials 14, no. 14: 4049. https://doi.org/10.3390/ma14144049





