Reduced Order Multiscale Simulation of Diffuse Damage in Concrete
Abstract
:1. Introduction
Goals and Structure of the Paper
2. Experimental Program
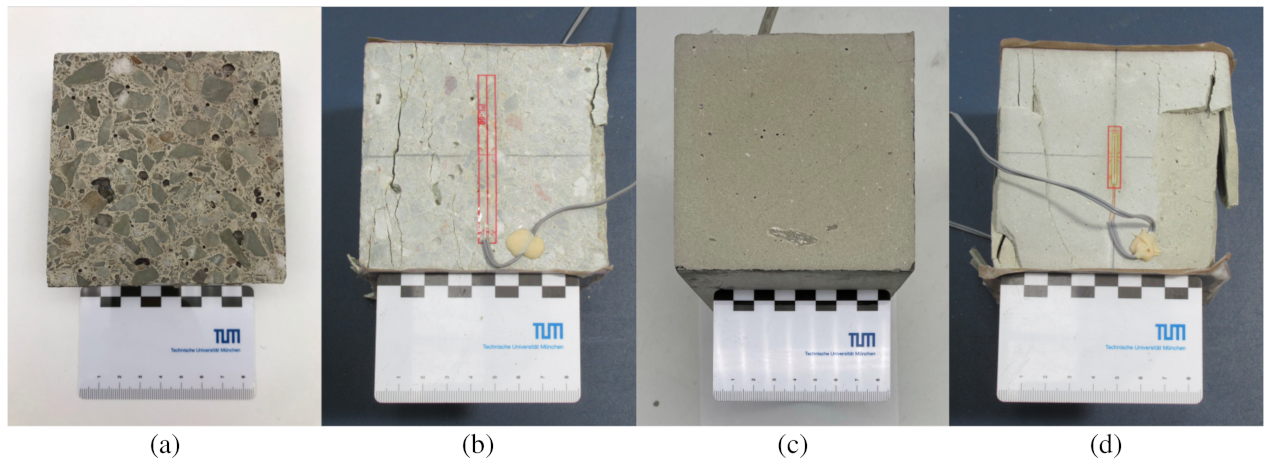
2.1. Material and Specimen Preparation
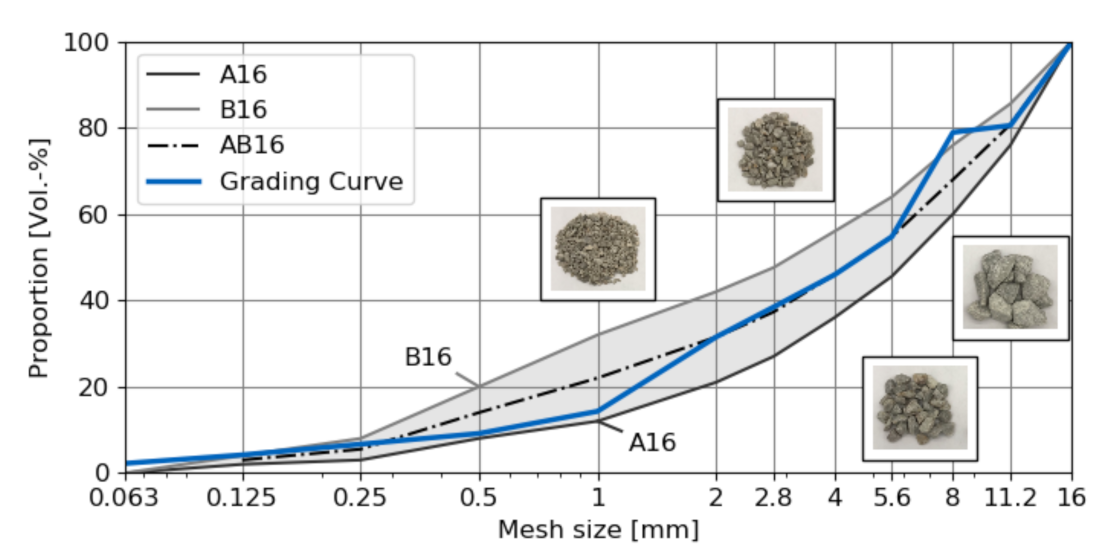
2.2. Characterisation of the Mesostructure of Concrete
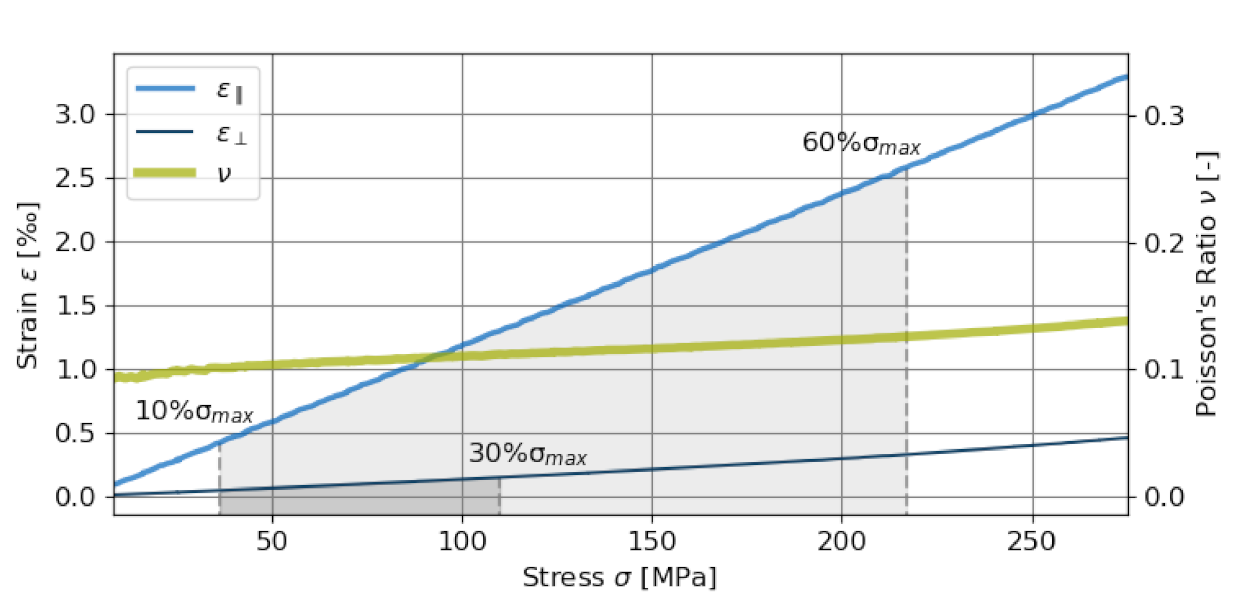
2.3. Determination of Elastic Properties of Concrete and Its Constituents
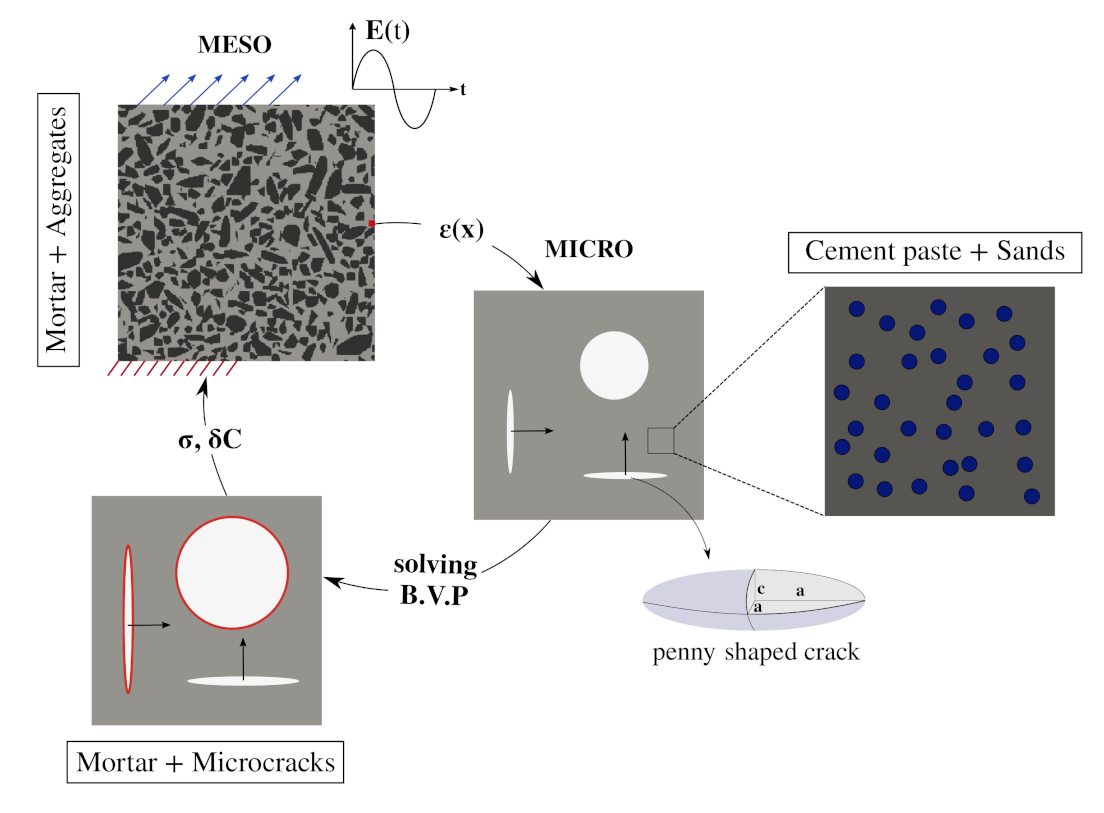
3. Scale-Bridging Modelling of Cementitious Materials
3.1. The Scale-Bridging Modelling Concept
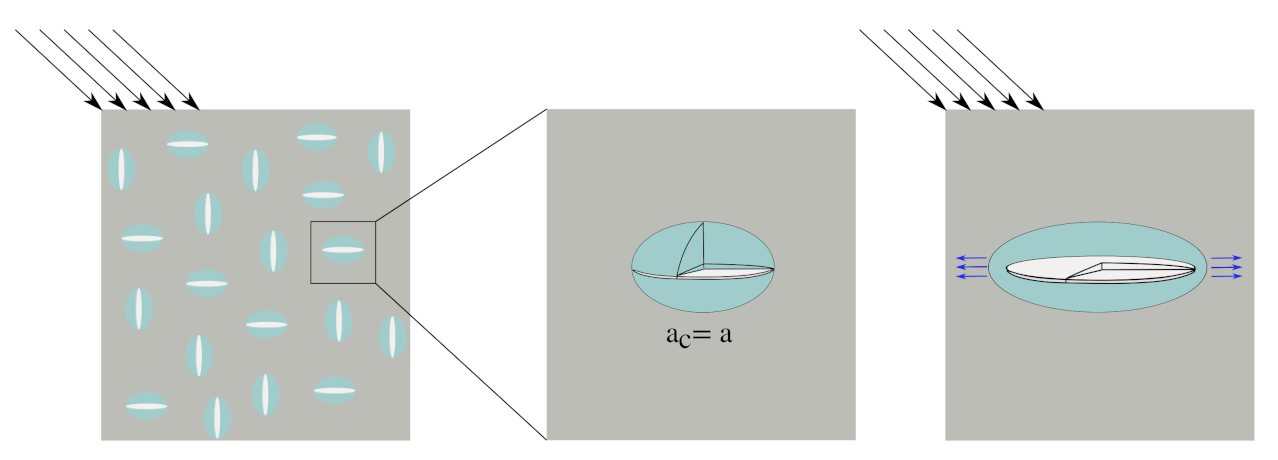
3.2. Microscale Model: Microcracking in the Mortar Material
3.2.1. Model Description
3.2.2. Microcrack Growth
3.2.3. Analysis of a Micro-Cracked Mortar REV under Uniaxial Loading Tests Using the Mori–Tanaka Homogenisation Scheme
3.3. Computational Model of Concrete on the Mesoscopic Scale
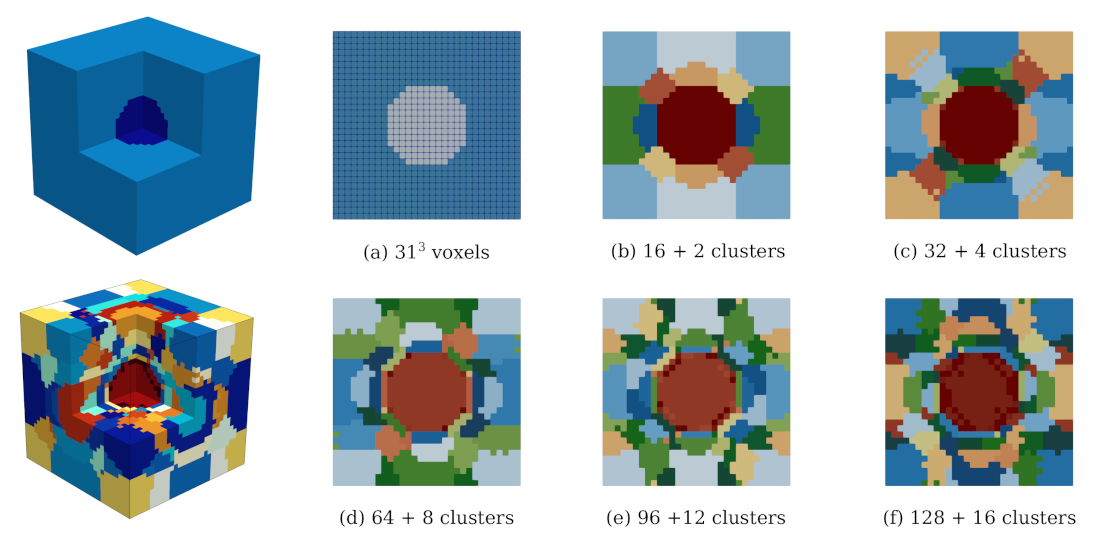
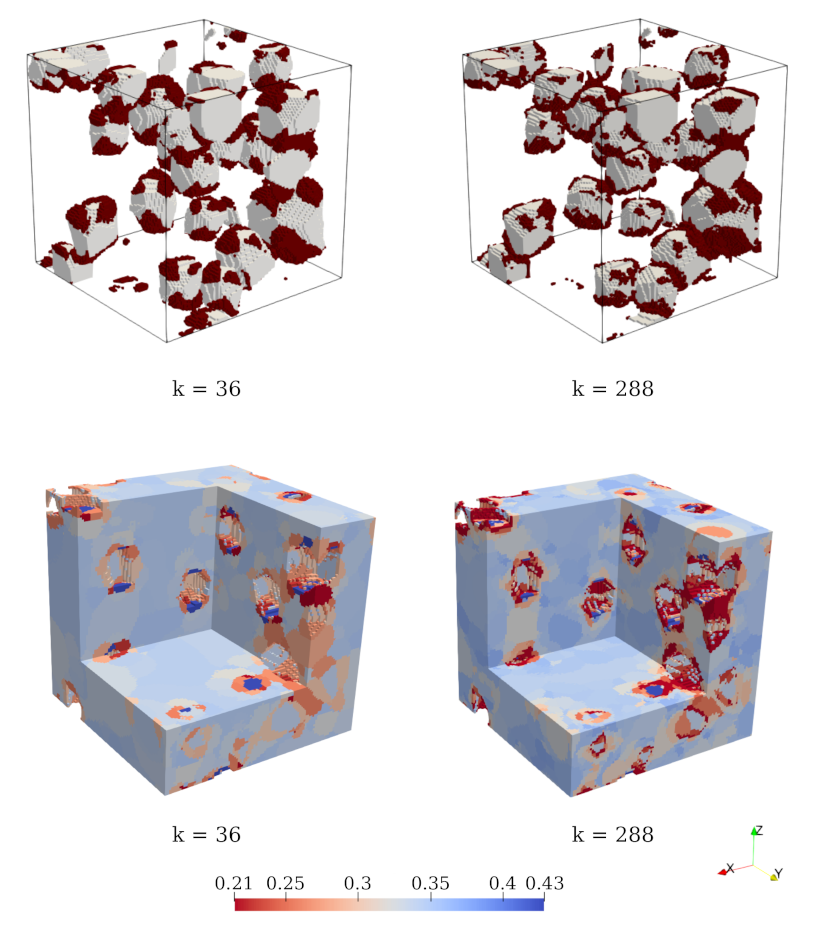
4. Model Reduction Using K-Means Clustering
- Offline stage Pre-computation of a reduced-order dataset characterising the behaviour of a given REV by decomposing the entire domain of the high fidelity REV into a set of sub-domains (often denoted as clusters) and computing the so-called interaction tensors for all cluster pairs.
- Online stage Actual computation of the response of the REV for various loading conditions using the reduced-order dataset obtained from the offline stage.
4.1. K-Means Model Reduction Procedure
4.1.1. Offline Stage
4.1.2. Online Stage
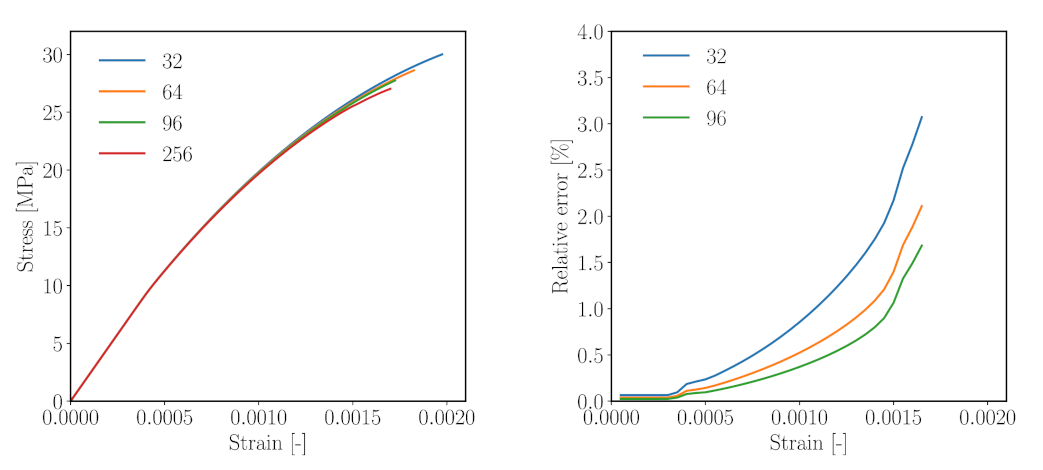
4.2. Numerical Assessment of the Convergence Behaviour of the Reduced Order Simulation (ROS)
- The convergence behaviour of the ROS in comparison to Direct Numerical Simulations (DNS) on a simple microstructure.
- The convergence behaviour with respect to the number of clusters on a simplified concrete microstructure.
4.2.1. Study 1—Comparison with DNS
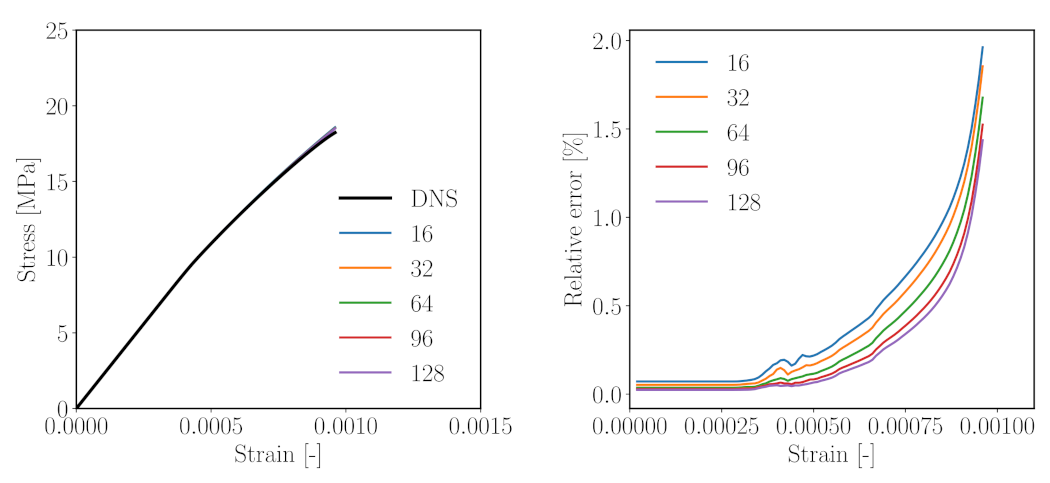
- in comparison with DNS, the ROSs capture the overall response in the elastic regime (up to a strain level of 0.03%) well. In this range, an error of only 0.03–0.08% is observed (Figure 8, right).
- The ROSs generally tend to overestimate the computed effective stress as compared to the DNS.
- When microcracking starts in the nonlinear regime, the error increases with increasing loading strain (Figure 8). At the loading strain of 0.1%, up to a 2% error is reported.
- As the number of clusters is increased, the reduced order simulation converges to the result of the high fidelity simulation.
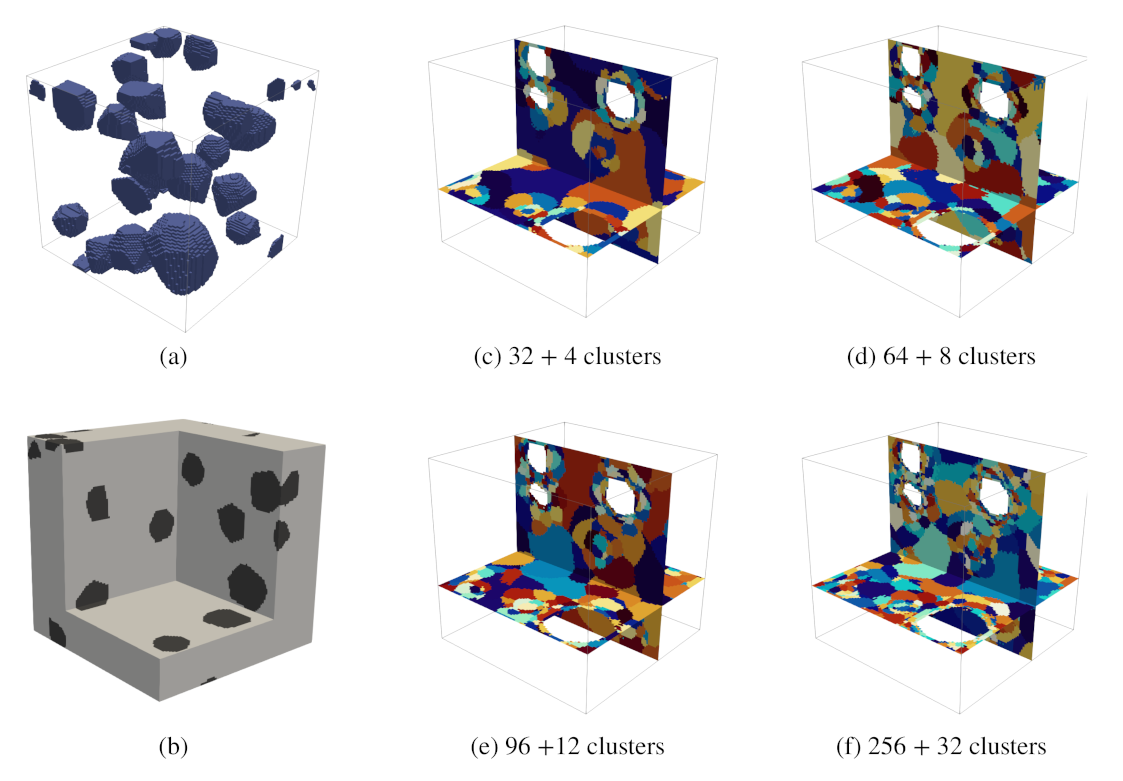
4.2.2. Study 2—Convergence Analysis on a Concrete-Like Meso-Structure
- Simulations with a higher number of clusters entered the inelastic stage earlier and failed earlier as well. Subsequently, the maximum compressive stress reduces with increasing cluster count.
- A maximum 3.07% of error with respect to the reference result () at ’failure strain’ is recorded.
- In comparison with the previous analysis, the effective stress–strain curves obtained from the different analysis show a slightly larger spread. However, the discrepancy is still within a tolerable range.
4.2.3. Computational Aspects
5. Model Validation: Simulation of a Realistic Concrete Mesoscale Model Subjected to Uniaxial Compression
5.1. Simulated Concrete Sample
5.2. Calibration of the Parameters of Mortar Constituents
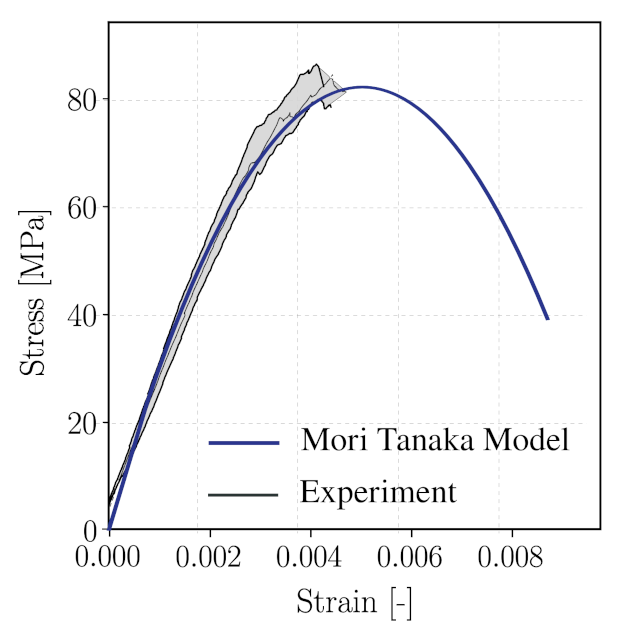
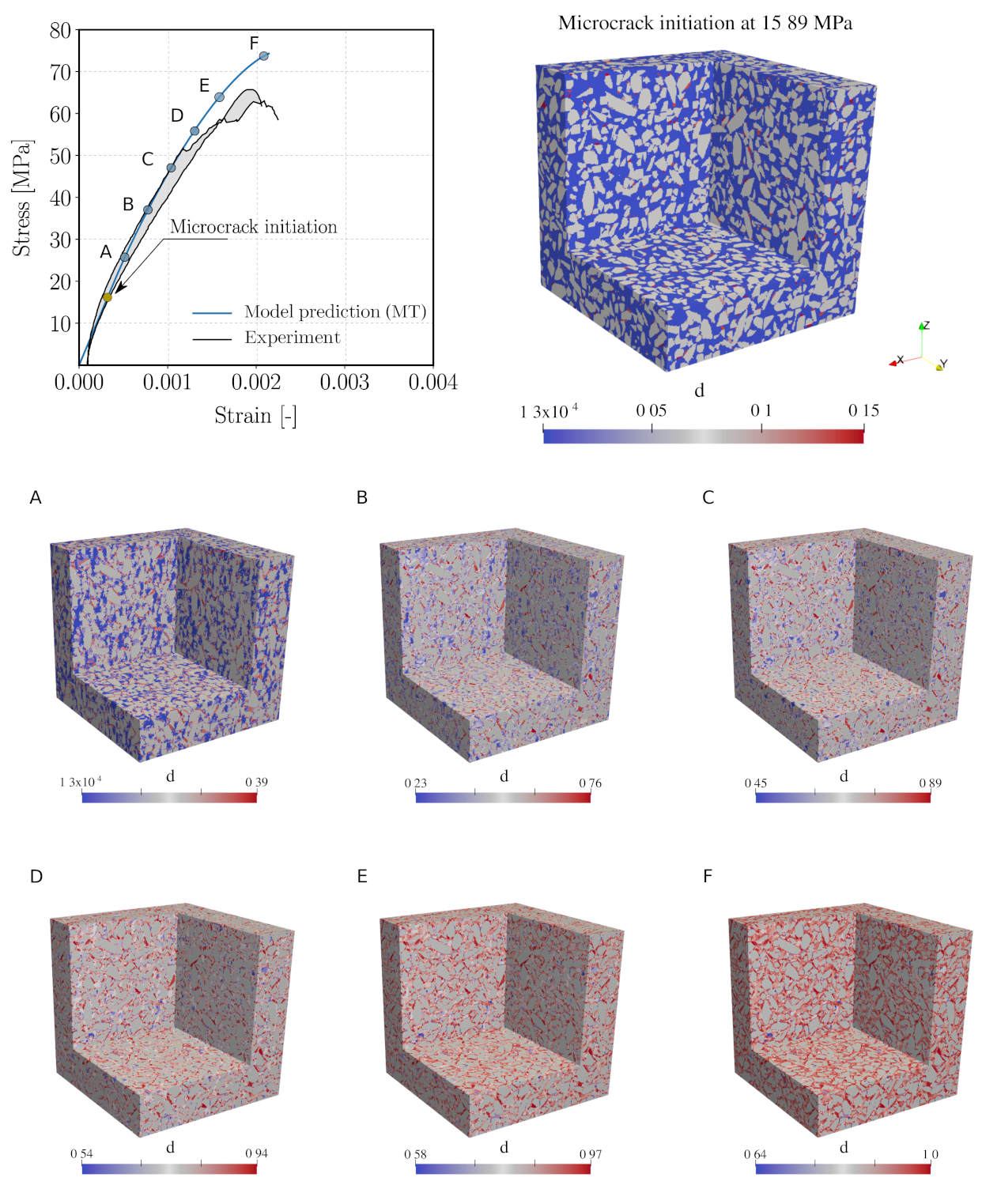
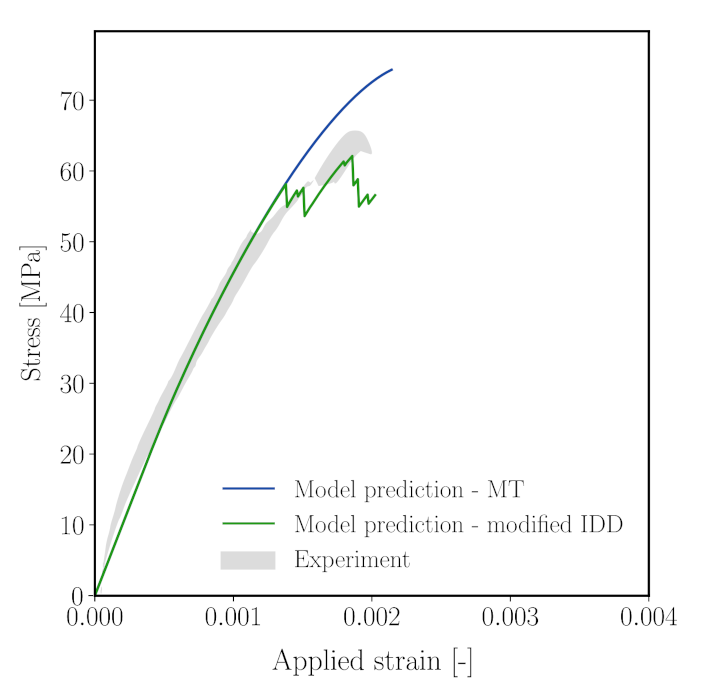
- We use experimental data from the mortar samples () to calibrate the microscopic constituents parameters such that the Young’s modulus and compressive strength of the mortar REV match the experimental stress–strain curve. The parameters to be calibrated include the Young’s modulus of the cement paste solid , the microcrack volume fraction and their aspect ratio X, and the microscopic fracture energy . Figure 12 shows the calibrated (homogenised) stress–strain curve of the mortar REV in comparison with the experimental stress–strain curve.
- In the numerical concrete sample (Figure 11a), the mortar matrix contains cement paste and fine aggregates with the relative proportion of between the two material phases. Thus, in mortar matrix equals 43.95% and differs from the actual mortar sample. We assume the content of microcracks is identical for the same cement mixture. The effective Young’s modulus of mortar matrix is obtained, by setting instead of , while the other parameters are kept unchanged. As a result, the mortar matrix of the simulated concrete has a Young’s modulus of GPa. At this scale, the fine sand grain inclusions are assumed to have a spherical geometry. A summary of the parameters is contained in Table 5.
5.3. Offline Training Stage
5.4. Simulation of a Uniaxial Compression Test on the Virtual Concrete Sample
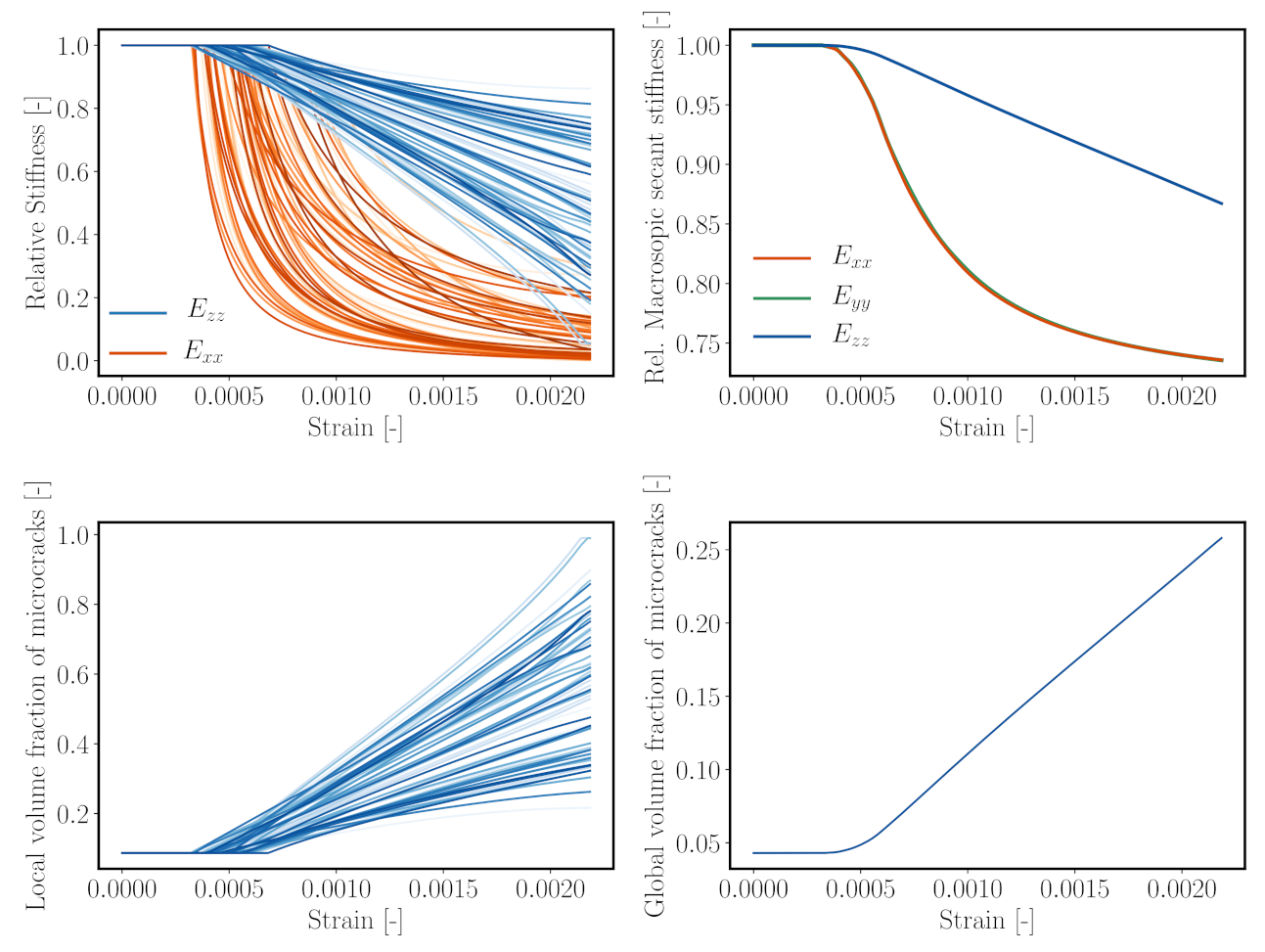
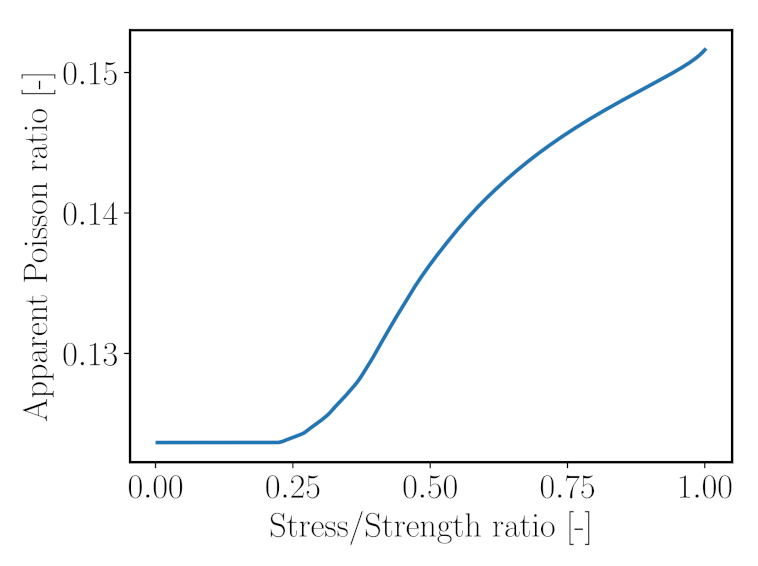
5.5. Interpretation of Numerical Results
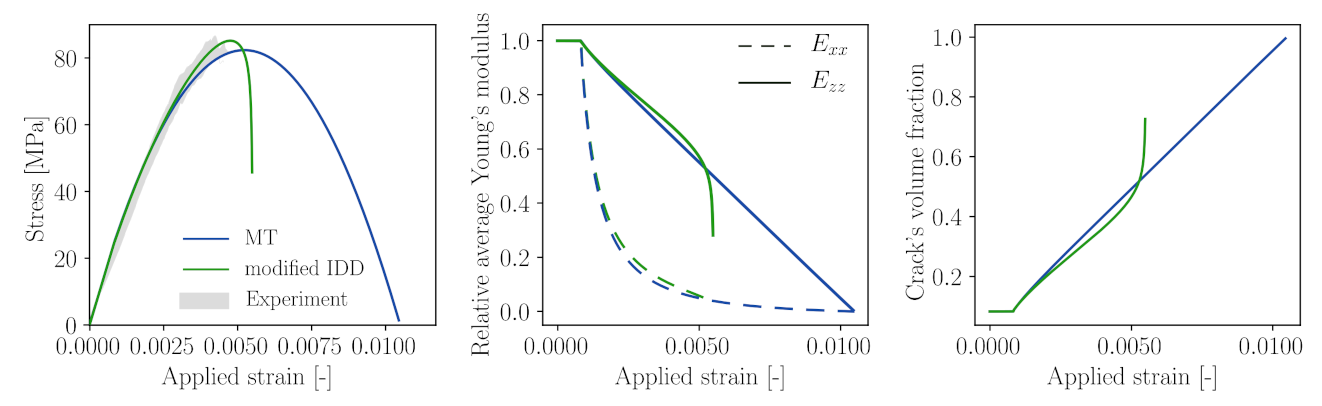
5.6. Improvement of the Model by Means of the Modified Interaction Direct Derivative Scheme (MIDD)
6. Conclusions
- It was observed that the Mori–Tanaka scheme, which has been used in the initial model design at the micro-level, overestimates the compressive strength of concrete.
- In order to improve the model predictions, the Mori–Tanaka scheme governing microcracking at the microscale has been replaced by an improved interaction direct derivative scheme [79]. This model is able to incorporate information on the microcrack distribution, which, however, needs additional calibration effort.
- After calibration of the additional distribution-related parameters, model predictions of the improved model for the uniaxial compression test have substantially improved, with a deviation of only 3.2%.
- The proposed model has been proven to be capable of simulating anisotropic microcrack evolution, leading to anisotropic stiffness degradation on the macroscopic level. In addition, the evolution of the Poisson’s ratio during loading could be predicted.
- Due to the multiscale nature of the proposed model, it can be used to simulate a wide variety of concrete compositions by simply altering the predominantly physically measurable microscale and mesoscale parameters governing the topology and material properties of the required concrete composition. Thus, the proposed modelling framework can be the basis of a Virtual Material Testing Environment and can collaboratively aid in the development of concrete with a better performance.
- From a structural health monitoring view point, the outcome of the model can serve as a high-fidelity input for an ultrasonic-wave propagation numerical investigation of damaged concrete (see, e.g., [81,82,83]). This, in turn, can support the development of an ultrasonic wave based technology (the so-called coda wave) on early detection of (diffuse) damage in concrete.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CWI | Coda Wave Interferometry |
| FFT | Fast Fourier Transform |
| REV | Representative Elementary Volume |
| LEFM | Linear Elastic Fracture Mechanics |
| CMG | Concrete Mesostructure Generator |
| DNS | Direct Numerical Simulation |
| ROS | Reduced Order Simulation |
| SCA | Self-consistent Clustering Analysis |
| ITZ | Interfacial Transition zone |
| IDD | Interaction Direct Derivative |
| MIDD | Modified Interaction Direct Derivative |
Appendix A. Structure of Hierarchical Numerical Simulation of the Multiscale Model
| Algorithm 1: Structure of hierarchical numerical simulation of the multiscale model (High-fidelity model). |
 |
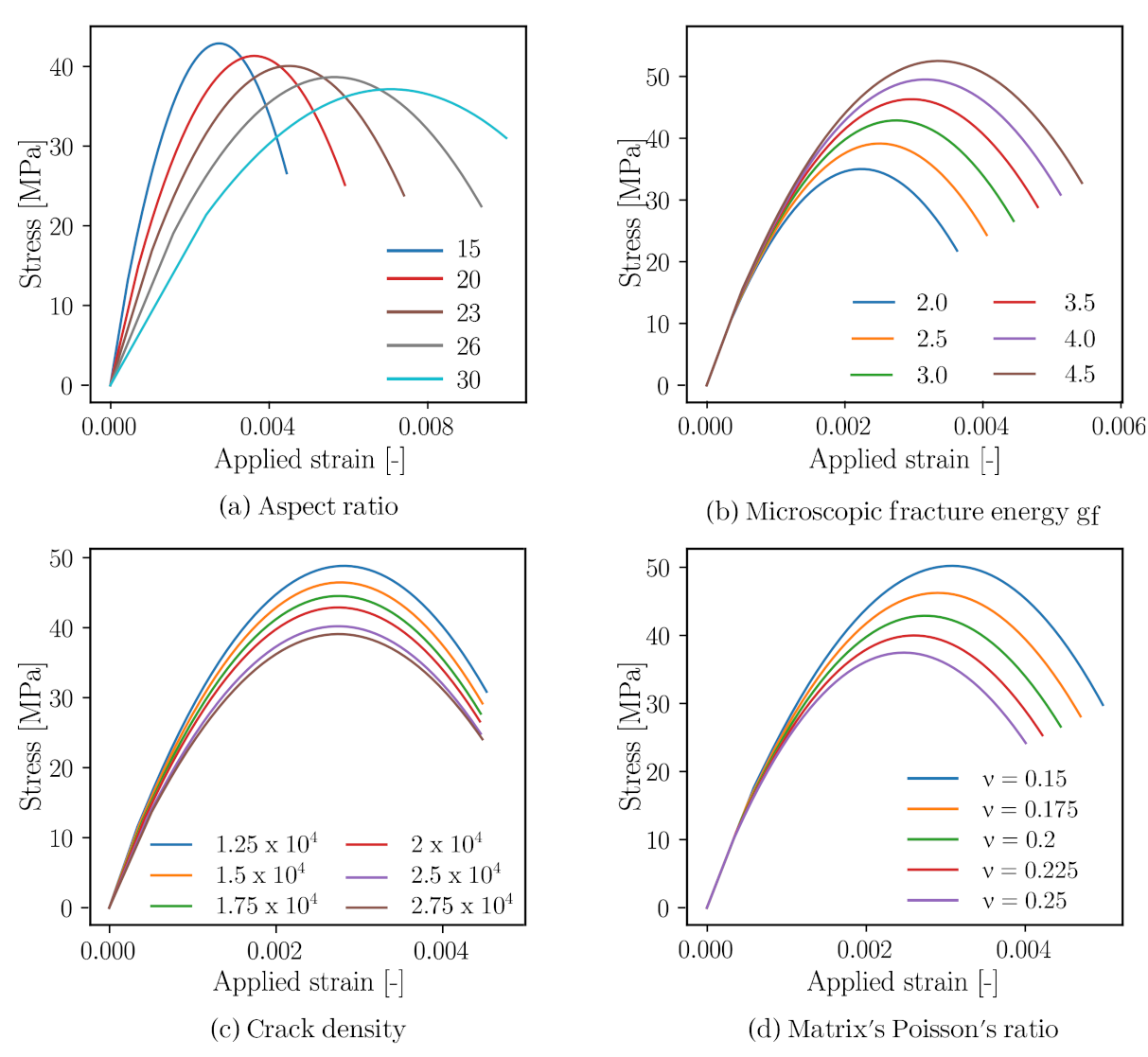
Appendix B. Parametric Study of Mori–Tanaka Based Damage Model of Cementitious Composite
| Model Parameters | ||
|---|---|---|
| m | ||
| 1 | m | |
| N/mm | ||
| 43 | GPa | |
| 0.3 | ||
References
- Ulm, F.J.; Constantinides, G.; Heukamp, F.H. Is concrete a poromechanics materials?—A multiscale investigation of poroelastic properties. Mater. Struct. 2004, 37, 43–58. [Google Scholar] [CrossRef]
- Hoagland, R.G.; Hahn, G.T.; Rosenfield, A.R. Influence of microstructure on fracture propagation in rock. Rock Mech. 1973, 5, 77–106. [Google Scholar] [CrossRef]
- Van Mier, J.G. Fracture Processes of Concrete; CRC Press: Boca Raton, FL, USA, 2017; Volume 12. [Google Scholar]
- Kobayashi, T.; Shockey, D.A. Fracture surface topography analysis (FRASTA)—Development, accomplishments, and future applications. Eng. Fract. Mech. 2010, 77, 2370–2384. [Google Scholar] [CrossRef]
- Macek, W.; Marciniak, Z.; Branco, R.; Rozumek, D.; Królczyk, G. A fractographic study exploring the fracture surface topography of S355J2 steel after pseudo-random bending-torsion fatigue tests. Measurement 2021, 178, 109443. [Google Scholar] [CrossRef]
- Hsu, T.T.; Slate, F.O.; Sturman, G.M.; Winter, G. Microcracking of plain concrete and the shape of the stress–strain curve. Proceedings 1963, 60, 209–224. [Google Scholar]
- Hsu, T.T. Fatigue and microcracking of concrete. Mater. Constr. 1984, 17, 51–54. [Google Scholar] [CrossRef]
- Shah, S.P.; Chandra, S. Critical stress, volume change, and microcracking of concrete. Proceedings 1968, 65, 770–780. [Google Scholar]
- Shah, S.; Sankar, R. Internal cracking and strain softening response of concrete under uniaxial compression. Mater. J. 1987, 84, 200–212. [Google Scholar]
- Ravindrarajah, R.S.; Swamy, R. Load effects on fracture of concrete. Mater. Struct. 1989, 22, 15–22. [Google Scholar] [CrossRef]
- Nemati, K.M.; Monteiro, P.J.; Scrivener, K.L. Analysis of compressive stress-induced cracks in concrete. ACI Mater. J. 1998, 95, 617–630. [Google Scholar]
- Hall, A.J.; Brennan, I.; Raymond, E.; Ghoshal, A.; Liu, K.C.; Coatney, M.; Haynes, R.; Bradley, N.; Weiss, V.; Tzeng, J. Damage Precursor Investigation of Fiber-Reinforced Composite Materials under Fatigue Loads; Technical Report; Army Research Lab Aberdeen Proving Ground MD Vehicle Technology Directorate: Aberdeen, MD, USA, 2013. [Google Scholar]
- Reifsnider, K.L.; Case, S.W. Damage Tolerance and Durability of Material Systems; Willey: Hoboken, NJ, USA, 2002. [Google Scholar]
- Selleck, S.F.; Landis, E.N.; Peterson, M.L.; Shah, S.; Achenbach, J.D. Ultrasonic investigation of concrete with distributed damage. ACI Mater. J. 1998, 95, 27–36. [Google Scholar]
- Anugonda, P.; Wiehn, J.S.; Turner, J.A. Diffusion of ultrasound in concrete. Ultrasonics 2001, 39, 429–435. [Google Scholar] [CrossRef]
- Schurr, D.P.; Kim, J.Y.; Sabra, K.G.; Jacobs, L.J. Damage detection in concrete using coda wave interferometry. Ndt E Int. 2011, 44, 728–735. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Matér. Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef] [Green Version]
- Oñate, E.; Oller, S.; Oliver, J.; Lubliner, J. A constitutive model for cracking of concrete based on the incremental theory of plasticity. Eng. Comput. 1988, 5, 309–319. [Google Scholar] [CrossRef]
- Meschke, G.; Lackner, R.; Mang, H.A. An anisotropic elastoplastic-damage model for plain concrete. Int. J. Numer. Methods Eng. 1998, 42, 703–727. [Google Scholar] [CrossRef]
- Jirasek, M. Nonlocal models for damage and fracture: Comparison of approaches. Int. J. Solids Struct. 1998, 35, 4133–4145. [Google Scholar] [CrossRef]
- Peerlings, R.H.; de Borst, R.; Brekelmans, W.M.; De Vree, J. Gradient enhanced damage for quasi-brittle materials. Int. J. Numer. Methods Eng. 1996, 39, 3391–3403. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Caner, F.C.; Bažant, Z.P. Microplane model M7 for plain concrete. I: Formulation. J. Eng. Mech. 2013, 139, 1714–1723. [Google Scholar] [CrossRef]
- Pichler, B.; Hellmich, C. Upscaling quasi-brittle strength of cement paste and mortar: A multi-scale engineering mechanics model. Cem. Concr. Res. 2011, 41, 467–476. [Google Scholar] [CrossRef]
- Iskhakov, T.; Timothy, J.; Meschke, G. Expansion and deterioration of concrete due to ASR: Micromechanical modeling and analysis. Cem. Concr. Res. 2019, 11, 407–418. [Google Scholar] [CrossRef]
- Horii, H.; Nemat-Nasser, S. Overall moduli of solids with microcracks: Load-induced anisotropy. J. Mech. Phys. Solids 1983, 31, 155–171. [Google Scholar] [CrossRef]
- Zimmerman, R.W. The effect of microcracks on the elastic moduli of brittle materials. J. Mater. Sci. Lett. 1985, 4, 1457–1460. [Google Scholar] [CrossRef]
- Kachanov, M. Elastic solids with many cracks and related problems. Adv. Appl. Mech. 1993, 30, 259–445. [Google Scholar]
- Castañeda, P.P.; Willis, J.R. The effect of spatial distribution on the effective behavior of composite materials and cracked media. J. Mech. Phys. Solids 1995, 43, 1919–1951. [Google Scholar] [CrossRef]
- Pichler, B.; Hellmich, C.; Mang, H. A combined fracture-micromechanics model for tensile strain-softening in brittle materials, based on propagation of interacting microcracks. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 111–132. [Google Scholar] [CrossRef]
- Pensée, V.; Kondo, D.; Dormieux, L. Micromechanical analysis of anisotropic damage in brittle materials. J. Eng. Mech. 2002, 128, 889–897. [Google Scholar] [CrossRef]
- Zhu, Q.Z.; Kondo, D.; Shao, J.F. Homogenization-based analysis of anisotropic damage in brittle materials with unilateral effect and interactions between microcracks. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 749–772. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S.O. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Benkemoun, N.; Hautefeuille, M.; Colliat, J.B.; Ibrahimbegovic, A. Failure of heterogeneous materials: 3D meso-scale FE models with embedded discontinuities. Int. J. Numer. Methods Eng. 2010, 82, 1671–1688. [Google Scholar] [CrossRef] [Green Version]
- La Borderie, C.; Lawrence, C.; N’Guyen, T.; Nahas, G. A mesoscopic approach for a better understanding of the transition from diffuse damage to localized damage. In Proceedings of the FraMCoS’7, Jeju, Korea, 23–28 May 2010. [Google Scholar]
- Zhang, H.; Sheng, P.; Zhang, J.; Ji, Z. Realistic 3D modeling of concrete composites with randomly distributed aggregates by using aggregate expansion method. Constr. Build. Mater. 2019, 225, 927–940. [Google Scholar] [CrossRef]
- Kim, S.M.; Al-Rub, R.K.A. Meso-scale computational modeling of the plastic-damage response of cementitious composites. Cem. Concr. Res. 2011, 41, 339–358. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, Z.; Ren, W.; Liu, G.; Zhang, C. 3D meso-scale fracture modelling and validation of concrete based on in-situ X-ray Computed Tomography images using damage plasticity model. Int. J. Solids Struct. 2015, 67, 340–352. [Google Scholar] [CrossRef]
- Roubin, E.; Vallade, A.; Benkemoun, N.; Colliat, J.B. Multi-scale failure of heterogeneous materials: A double kinematics enhancement for Embedded Finite Element Method. Int. J. Solids Struct. 2015, 52, 180–196. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yvonnet, J.; Bornert, M.; Chateau, C. Initiation and propagation of complex 3D networks of cracks in heterogeneous quasi-brittle materials: Direct comparison between in situ testing-microCT experiments and phase field simulations. J. Mech. Phys. Solids 2016, 95, 320–350. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yvonnet, J.; Bornert, M.; Chateau, C.; Bilteryst, F.; Steib, E. Large-scale simulations of quasi-brittle microcracking in realistic highly heterogeneous microstructures obtained from micro CT imaging. Extrem. Mech. Lett. 2017, 17, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Yılmaz, O.; Molinari, J.F. A mesoscale fracture model for concrete. Cem. Concr. Res. 2017, 97, 84–94. [Google Scholar] [CrossRef]
- Ren, W.; Yang, Z.; Sharma, R.; Zhang, C.; Withers, P.J. Two-dimensional X-ray CT image based meso-scale fracture modelling of concrete. Eng. Fract. Mech. 2015, 133, 24–39. [Google Scholar] [CrossRef]
- Qiu, Q.; Dai, J.G. Meso-scale modeling of chloride diffusivity in mortar subjected to corrosion-induced cracking. Comput. Aided Civ. Infrastruct. Eng. 2021, 36, 602–619. [Google Scholar] [CrossRef]
- Suchorzewski, J.; Tejchman, J.; Nitka, M. Discrete element method simulations of fracture in concrete under uniaxial compression based on its real internal structure. Int. J. Damage Mech. 2018, 27, 578–607. [Google Scholar] [CrossRef]
- Moulinec, H.; Suquet, P. A fast numerical method for computing the linear and nonlinear mechanical properties of composites. Comptes Rendus De L’Académie Des Sciences. Série II, Mécanique, Phys. Chim. Astron. 1994, 318, 1417–1423. [Google Scholar]
- Escoda, J.; Willot, F.; Jeulin, D.; Sanahuja, J.; Toulemonde, C. Estimation of local stresses and elastic properties of a mortar sample by FFT computation of fields on a 3D image. Cem. Concr. Res. 2011, 41, 542–556. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Tian, X.X.; Abdelmoula, R. A damage model for crack prediction in brittle and quasi-brittle materials solved by the FFT method. Int. J. Fract. 2012, 173, 135–146. [Google Scholar] [CrossRef]
- Yvonnet, J.; He, Q.C. The reduced model multiscale method (R3M) for the nonlinear homogenization of hyperelastic media at finite strains. J. Comput. Phys. 2007, 223, 341–368. [Google Scholar] [CrossRef] [Green Version]
- Goury, O.; Amsallem, D.; Bordas, S.P.A.; Liu, W.K.; Kerfriden, P. Automatised selection of load paths to construct reduced-order models in computational damage micromechanics: From dissipation-driven random selection to Bayesian optimization. Comput. Mech. 2016, 58, 213–234. [Google Scholar] [CrossRef] [Green Version]
- Ladevèze, P.; Passieux, J.C.; Néron, D. The latin multiscale computational method and the proper generalized decomposition. Comput. Methods Appl. Mech. Eng. 2010, 199, 1287–1296. [Google Scholar] [CrossRef] [Green Version]
- Kalidindi, S.R. A Bayesian framework for materials knowledge systems. MRS Commun. 2019, 9, 518–531. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Bessa, M.; Liu, W.K. Self-consistent clustering analysis: An efficient multi-scale scheme for inelastic heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2016, 306, 319–341. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Liu, W.K. From virtual clustering analysis to self-consistent clustering analysis: A mathematical study. Comput. Mech. 2018, 62, 1443–1460. [Google Scholar] [CrossRef]
- Liu, Z.; Fleming, M.; Liu, W.K. Microstructural material database for self-consistent clustering analysis of elastoplastic strain softening materials. Comput. Methods Appl. Mech. Eng. 2018, 330, 547–577. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and testing of a generalized reduced gradient code for nonlinear programming. ACM Trans. Math. Softw. (TOMS) 1978, 4, 34–50. [Google Scholar] [CrossRef]
- ISO. 3310-1: Test Sieves—Technical Requirements and Testing—Part 1: Test Sieves of Metal wire Cloth; ISO: Geneva, Switzerland, 2016. [Google Scholar]
- 1045-2 D. Concrete, Reinforced and Prestressed Concrete Structures—Part 2: Concrete—Specification, Properties, Production and Conformity—Application Rules for DIN EN 206-1; Beuth: Berlin, Germany, 2015. [Google Scholar]
- Wesche, K.; Manns, W. Results of an international survey on the determination of the modulus of elasticity of the beton in compression. Mater. Constr. 1970, 3, 179–196. [Google Scholar] [CrossRef]
- Ross, B.E.; Hamilton, H.T., III. Evaluation of strain gage lengths for testing limestone and granite aggregate concretes. Constr. Build. Mater. 2011, 25, 406–408. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Schön, J. Physical Properties of Rocks: Fundamentals and Principles of Petrophysics; Developments in Petroleum Science Series; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Mazars, J. A description of micro-macroscale damage of concrete structures. Eng. Fract. Mech. 1986, 25, 729–737. [Google Scholar] [CrossRef]
- Haecker, C.J.; Garboczi, E.; Bullard, J.; Bohn, R.; Sun, Z.; Shah, S.; Voigt, T. Modeling the linear elastic properties of Portland cement paste. Cem. Concr. Res. 2005, 35, 1948–1960. [Google Scholar] [CrossRef]
- Concrete Mesostructure Generation Using Python. Available online: https://pycmg.readthedocs.io/en/latest/ (accessed on 8 June 2021).
- Bessa, M.A.; Bostanabad, R.; Liu, Z.; Hu, A.; Apley, D.W.; Brinson, C.; Chen, W.; Liu, W.K. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 2017, 320, 633–667. [Google Scholar] [CrossRef]
- Bessa, M.A.; Glowacki, P.; Houlder, M. Bayesian machine learning in metamaterial design: Fragile becomes supercompressible. Adv. Mater. 2019, 31, 1904845. [Google Scholar] [CrossRef] [Green Version]
- Holla, V.; Vu, G.; Timothy, J.J.; Diewald, F.; Gehlen, C.; Meschke, G. Computational Generation of Virtual Concrete Mesostructures. Materials 2021, 14, 3782. [Google Scholar] [CrossRef]
- Soroushian, P.; Elzafraney, M.; Nossoni, A. Specimen preparation and image processing and analysis techniques for automated quantification of concrete microcracks and voids. Cem. Concr. Res. 2003, 33, 1949–1962. [Google Scholar] [CrossRef]
- Constantinides, G.; Ulm, F.J. The effect of two types of CSH on the elasticity of cement-based materials: Results from nanoindentation and micromechanical modeling. Cem. Concr. Res. 2004, 34, 67–80. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Hori, H. Micromechanics: Overall Properties of Heterogeneous Materials, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Belytschko, T.; Loehnert, S.; Song, J.H. Multiscale aggregating discontinuities: A method for circumventing loss of material stability. Int. J. Numer. Methods Eng. 2008, 73, 869–894. [Google Scholar] [CrossRef]
- Coenen, E.; Kouznetsova, V.; Bosco, E.; Geers, M. A multi-scale approach to bridge microscale damage and macroscale failure: A nested computational homogenization-localization framework. Int. J. Fract. 2012, 178, 157–178. [Google Scholar] [CrossRef]
- Linder, C.; Raina, A. A strong discontinuity approach on multiple levels to model solids at failure. Comput. Methods Appl. Mech. Eng. 2013, 253, 558–583. [Google Scholar] [CrossRef]
- Jones, R. A method of studying the formation of cracks in a material subjected to stress. Br. J. Appl. Phys. 1952, 3, 229. [Google Scholar] [CrossRef]
- Loo, Y. A new method for microcrack evaluation in concrete under compression. Mater. Struct. 1992, 25, 573–578. [Google Scholar] [CrossRef]
- Osorio, E.; Bairán, J.M.; Marí, A.R. Lateral behavior of concrete under uniaxial compressive cyclic loading. Mater. Struct. 2013, 46, 709–724. [Google Scholar] [CrossRef]
- Hu, G.K.; Weng, J. The connection between the double-inclusion model and the Ponte Casteneda-Willis, Mori–Tanaka and the Kuster-Toksoz models. Mech. Mater. 2000, 32, 495–503. [Google Scholar] [CrossRef]
- Zheng, Q.S.; Du, D.X. An explicit and universally applicable estimate for the effective properties of multiphase composites which accounts for inclusion distribution. J. Mech. Phys. Solids 2001, 49, 2765–2788. [Google Scholar] [CrossRef]
- Charpin, L.; Ehrlacher, A. Estimating the poroelastic properties of cracked materials. Acta Mech. 2014, 225, 2501–2519. [Google Scholar] [CrossRef] [Green Version]
- Saenger, E.H.; Gold, N.; Shapiro, S.A. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion 2000, 31, 77–92. [Google Scholar] [CrossRef]
- Kocur, G.K.; Saenger, E.H.; Vogel, T. Elastic wave propagation in a segmented X-ray computed tomography model of a concrete specimen. Constr. Build. Mater. 2010, 24, 2393–2400. [Google Scholar] [CrossRef]
- Saenger, E.H.; Kocur, G.K.; Jud, R.; Torrilhon, M. Application of time reverse modeling on ultrasonic non-destructive testing of concrete. Appl. Math. Model. 2011, 35, 807–816. [Google Scholar] [CrossRef]

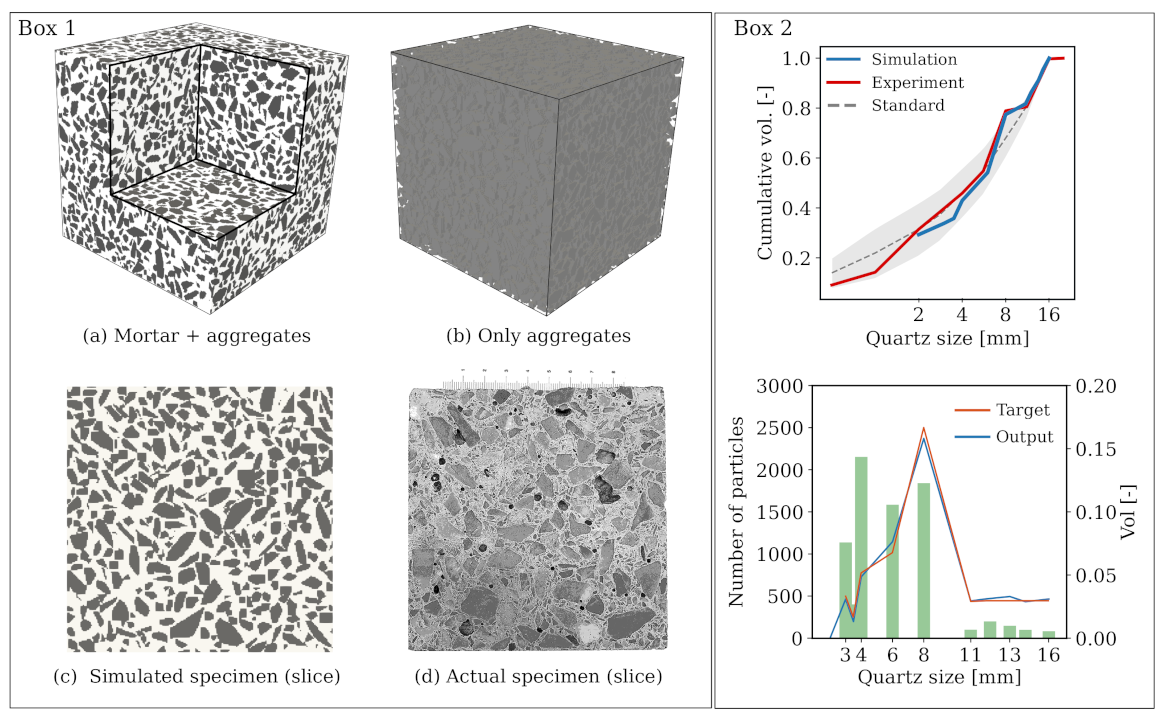
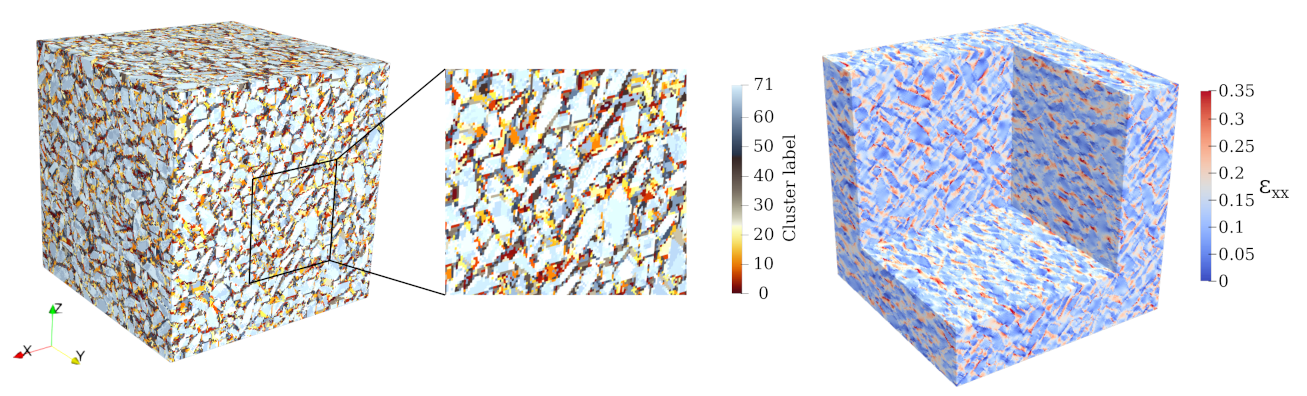
| Type | Description | Amount | Density | Volume |
|---|---|---|---|---|
| [-] | [-] | [kg/dm] | [dm/m] | |
| w/c | 0.45 | |||
| Cement | CEM I 52.5 R | 350 [kg/m] | 310 | 112.9 |
| Plasticizer | 1.0 [m-%] | |||
| Air voids | 2.00 % | 0 | 20 | |
| Water | 157.5 [kg/m] | 1 | 157.5 | |
| Aggregate 0/2 | Quartz | 39.46 [%] | 2.67 | 280.02 |
| Aggregate 2/5 | Quartz | 12.18 [%] | 2.64 | 86.44 |
| Aggregate 5/8 | Quartz | 28.91 [%] | 2.64 | 205.13 |
| Aggregate 8/16 | Quartz | 19.45 [%] | 2.65 | 138.01 |
| Cement Matrix | Fine Aggregates | Coarse Aggregates | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size [mm] | - | 0.063 | 0.125 | 0.25 | 0.5 | 1 | 2 | 2.8 | 4 | 5.6 | 8 | 11.2 | 16 |
| Volume fraction [%] | 29.259 | 1.504 | 1.619 | 1.758 | 1.758 | 3.634 | 12.174 | 5.0626 | 5.146 | 6.743 | 16.606 | 2.904 | 11.832 |
| Total [%] | 29.259 | 22.448 | 48.292 | ||||||||||
| Total [%] | 29.259 | 70.741 | |||||||||||
| Material Parameter | Quartzitic Aggregate | Mortar | AB16 Concrete |
|---|---|---|---|
| Young’s Modulus E [GPa ] | 84.6 | 27.1 | 48.03 |
| Poisson’s ratio [-] | 0.12 | 0.19 | 0.15 |
| Compressive strength [MPa] | 368 | 80.3 | 64.4 |
| Material parameters | |||
| Young’s modulus of aggregates | 84.6 | GPa | |
| Poisson ratio of aggregates | 0.2 | ||
| Aggregates’ volume fraction | 0.35 | ||
| Model parameters | |||
| Microcrack’s initial radius (i = 1, 2, 3) | 0.017 | mm | |
| Microcrack’s initial half thickness | 0.001 | mm | |
| Microcrack’s density | 1/mm | ||
| Young’s modulus of cement paste solid | 44 | GPa | |
| Poisson ratio of cement paste solid | 0.25 | ||
| Mortar solid microscopic fracture energy | 6.88 | N/mm | |
| Numerical output | |||
| Young’s modulus of mortar REV | 26.9 | GPa | |
| Compressive strength of mortar REV | GPa | ||
| Tensile strength of mortar REV | MPa | ||
| Ratio between Compressive and Tensile strength | 14.86 | ||
| Material parameters (from laboratory tests) | |||
| Young’s modulus of aggregates | 86.4 | GPa | |
| Poisson ratio of aggregates | 0.12 | ||
| Volume fraction of aggregates | 0.3034 | ||
| Model parameters | |||
| Microcrack initial radius (i = 1, 2, 3) | 0.023 | mm | |
| Microcrack initial half thickness | 0.001 | mm | |
| Microcrack’s density | 1/mm | ||
| Mortar solid microscopic fracture energy | 6.61 | N/mm | |
| Young’s modulus of cement paste solid | 49 | GPa | |
| Poisson ratio of cement paste solid | 0.23 | ||
| Homogenised parameters | |||
| Young’s modulus of mortar | 29.8 | GPa | |
| Poisson ratio of mortar | 0.124 | ||
| Compressive strength of mortar | MPa | ||
| Volume Fraction [%] | Average Modulus of Elasticity [GPa] | Poisson’s Ratio [-] | Anisotropy [-] | ||
|---|---|---|---|---|---|
| Model | Exp. | Model | Exp. | ||
| 47.74 | 50.311 | 48.03 | 0.124 | 0.152 | 1.003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, G.; Diewald, F.; Timothy, J.J.; Gehlen, C.; Meschke, G. Reduced Order Multiscale Simulation of Diffuse Damage in Concrete. Materials 2021, 14, 3830. https://doi.org/10.3390/ma14143830
Vu G, Diewald F, Timothy JJ, Gehlen C, Meschke G. Reduced Order Multiscale Simulation of Diffuse Damage in Concrete. Materials. 2021; 14(14):3830. https://doi.org/10.3390/ma14143830
Chicago/Turabian StyleVu, Giao, Fabian Diewald, Jithender J. Timothy, Christoph Gehlen, and Günther Meschke. 2021. "Reduced Order Multiscale Simulation of Diffuse Damage in Concrete" Materials 14, no. 14: 3830. https://doi.org/10.3390/ma14143830
APA StyleVu, G., Diewald, F., Timothy, J. J., Gehlen, C., & Meschke, G. (2021). Reduced Order Multiscale Simulation of Diffuse Damage in Concrete. Materials, 14(14), 3830. https://doi.org/10.3390/ma14143830









