1. Introduction
In many industrial processes that involve diffusion, e.g., alloy solidification, heat treatment, coating and electric packaging, the characterization of composition-dependent interdiffusion coefficients is a crucial task, as it quantifies a diffusion process clearly. The classic approach is based on Boltzmann–Matano analysis [
1,
2] which transforms the diffusion system into a linear system of equations. However, the Boltzmann–Matano analysis is only applicable to a binary system and becomes problematic for a system with more than three components, as it generates an under-determined system of equations that mathematically does not yield a unique solution. To address such a challenge, a number of methods have been developed over the years. Kirkaldy et al. [
3] introduced the Kirkaldy–Matano method and provided extra equations to the linear system by adding additional
M diffusion paths with intersection points. Although the results have been shown to be accurate, this method cannot generalize well to a multi-component system because the difficulty in experimentally generating intersection points grows drastically with the number of components
[
4]. Alternatively, methods based on one diffusion couple were proposed. Dayananda and Sohn [
5] suggested integrating over certain composition ranges along the diffusion path to evaluate an average interdiffusion coefficient. Cermak and Rothova [
6] later extended this method by choosing an infinitely small integration interval. Nevertheless, as is pointed out by Cheng et al. [
7], the integration approach can lead to ill-conditional problems. A pseudobinary approach is introduced by considering only two components diffused into the diffusion zone. This method takes advantage of its time independence in the first-order linear equations and thus is very efficient when the pseudobinary condition is strictly satisfied in experiments. In practice, such experimental conditions may be difficult to meet, and in addition, for a multi-component system with a limited number of experimental samples, the linear equations are not capable of eliminating the extra solutions [
8,
9]. Separately, Zhang and Zhao [
10] suggested a forward-simulation approach by iteratively optimizing the interdiffusion coefficients with repeated forward-simulations, similar to the classic inference approach for inverse problems. Although such a method is shown to be accurate and stable, it incurs an overwhelming computational cost because each iteration requires a complete diffusion simulation with a fine spatial-temporal grid.
Another branch of the one-diffusion-couple method lies in assuming a polynomial functional form for the interdiffusivities. Ideally, with a proper design of the polynomial function, one can compute the coefficients of the polynomial functions to estimate the interdiffusion using a numerical inverse method [
11]. This numerical inverse approach is adopted by Chen et al. [
4] to include the atomic mobility [
12] to study the diffusion in the solution phase of a multicomponent system. To improve the efficiency of the numerical inverse method, Cheng et al. [
13] recast the original parabolic inverse problem [
11] as a linear multi-objective optimization to improve computation efficiency while maintaining similar accuracy. The optimization algorithm places weak limits on the experimental samples and is applied to interdiffusivities of solid solution as well as various alloy systems [
14,
15]. This approach was recently improved by Qin et al. [
16], who suggest solving an underdetermined linear system using compress sensing, a popular regularization technique, to increases stability against high order polynomial functions. However, the
penalty imposed by compress sensing may introduce inappropriate prior assumptions, leading to inferior overall performance. We will see this issue in detail in the later experiment section.
Despite the notable performance and the popularity of the polynomial functional interdiffusion coefficient approaches, they share a fatal issue—how does one design the polynomial functions? Considering a quadternary system (), we have polynomial functions requiring careful designs; modifying one function will affect the results of the other two. The challenge grows quadratically with the number M. Without proper design and repeated validations, the polynomial approach will lead to overfitting or underfitting, making this approach infeasible in practice.
One way to resolve this challenge is to use a complicated enough model with many polynomial terms and utilize classic Bayesian inference techniques [
17] to estimate the posterior of the polynomial coefficients. In particular, Girolami [
18] proposed an interesting Markov chain Monte Carlo (MCMC) for nonlinear and complex differential equations where the fully analytic expressions for the posterior distribution do not exist, which is similar to our problem. Despite its elegance and great accuracy, an MCMC approach often suffers from slow convergence and poor mixing, making it less practical for complex applications. To improve inference efficiency, the approximate Bayesian computation (ABC) and their variations, e.g., MCMC ABC and sequential Monte Carlo ABC (SMC ABC) are put forth by Alahmadi et al. [
19]. However, despite being accurate and easy to implement, these types of sampling methods do not scale well with the number of parameters to be inferred. With unknown polynomials, the large number of parameters makes such methods impractical even with the latest accelerated variations [
20,
21].
Recently, the Gaussian process (GP) [
22] has been utilized in dealing with data that are generated from a system of differential equations. As a back-box regression model, GP is proposed for fast parameter posterior estimations with the derivative information of the differential equations even with partially observed data [
23]. The explicit derivative information is further utilized to improve a general GP’s performance for data that are generated from differential equations [
24]. The derivative in a given system of differential equations is further harnessed through a constraint manifold such that the derivatives of the Gaussian process must match an ordinary differential Equation (ODE) [
25]. Despite their success, these works generally require explicitly known differential equations to work. Thus, they cannot directly be implemented for our problem.
A closely related work is [
26], where GP is used as a generalization for a parametric function for binary images. However, their work cannot be directly implemented in our problem because our systems of equations will lead to a mixture of GPs that are augmented by the derivative of concentrations, whereas there is normally only one GP to estimate in most of the previous works [
23,
24,
25,
26,
27].
To address the challenge of stable characterization of the interdiffusion coefficients, we introduce InfPolyn (Infinite Polynomial), a nonparametric Bayesian framework for the characterization of composition-dependent interdiffusion coefficients.
In particular, we first extend the general polynomial fitting method with an infinite number of polynomial terms. We then integrate out the polynomial coefficients with a Gaussian prior to derive a nonparametric functional form for the interdiffusion coefficients. To further improve our model with prior assumptions of an interdiffusion system, we introduce a diagonal-dominant prior for the functions of the interdiffusion coefficients. Unlike most Bayesian fitting problems, the interdiffusion coefficients are not known/observable to us. Thus, we introduce latent variables, the virtual ghost interdiffusion coefficients to address this issue. Finally, we derive a tractable joint likelihood function for model training. We compare InfPolyn with the state-of-the-art Matano-based numerically inverse methods and their variations. In ternary and quaternary systems with polynomial, exponential, and sinusoidal interdiffusion coefficients, InfPolyn shows a significant improvement over the competitors in terms of relative errors. In most of the experiments, our model shows an excellent performance with only 40 EPMA measurements, which is very desirable in practical interdiffusion coefficient estimations.
Essentially, InfPolyn is a functional estimation method tailored for the characterization of interdiffusion coefficients by imposing a mixture of the SOTA nonparametric models, GPs, and particular prior knowledge. Unlike the classic Bayesian inference approaches [
18,
19], InfPolyn does not require a time-consuming sampling process and is thus much more efficient. The highlights of this work for interdiffusion coefficient characterizations are as follows:
InfPolyn does not require assumptions for the particular functional form of the interdiffusion coefficient; it is robust against overfitting and underfitting.
InfPolyn does not require a significant number of training data.
Prior knowledge of the interdiffusion system can be added easily in the framework of InfPolyn.
We hope the success of the nonparametric Bayesian framework can inspire more interesting applications in other interdiffusion coefficient estimation methods, e.g., the forward-simulation approach [
10], in the material community. Thus, we publish our code and will maintain it as an open source toolbox on Github (
https://github.com/wayXing/InfPolyn, accessed on 26 June 2021).
The rest of this paper is organized as follows. The interdiffusion coefficient estimation problem is introduced in
Section 2, followed by a brief summary of the Matano–Boltzmann numerical inverse method with polynomial functions in
Section 3. Our method is presented in
Section 4, including the derivation, prior knowledge assumptions, and model training. The comparisons to the other SOTA methods through ternary and quandary systems are demonstrated in
Section 5. Finally,
Section 6 summarizes our work.
2. Statement of the Problem
We firstly formulate our problem mathematically as a foundation of this work. Consider a general one-dimensional diffusion system with
components. According to Fick’s second law [
28], the diffusion process is fully characterized by
where
is the partial derivative operator,
is the concentration of
i component (note that the concentration is a function of space and time
);
is the interdiffusion coefficient w.r.t. the concentration gradient of component
j. In many textbook examples,
is assumed constant, but in practice,
depends on the concentrations of all components
. Our goal is to find
for all
with, ideally, a concentrations profile
at some terminal time
and spatial locations
, where
N is the number of sampling points at different locations. To avoid clutter, we denote
. One may notice that an important factor, temperature, is not considered in the formulation. This is due to the general process of the experiment. To conduct the experiment and obtain the concentration profile, one first bonds two blocks of materials together and holds them at certain temperatures to activate interdiffusion at the initial interface. The annealing procedure may last from hours to days, depending on the speed of forming an interdiffusion zone wide enough for analysis. The temperature remains constant during the long-lasting annealing process except for the beginning and ending stages, which take short time. Thus, the temperature is considered constant for the interdiffusion coefficient characterizations. To fabricate just one diffusion couple, around 50–100 sample points are often selected in a line parallel to the direction of element diffusion within the interdiffusion zone. Each sample point is analyzed through electron probe micro-analysis (EPMA), which requires several minutes for the equipment to detect the concentrations. As a result, the experiment is time-consuming, and only a small amount of samples, i.e., small
N, can be provided.
3. Boltzmann–Matano Polynomial Interdiffusion Coefficients
We follow the original work of the Boltzmann–Matano method [
2], which is widely used to extract concentration-dependent interdiffusion coefficient
from experimental concentration profiles. The Boltzmann–Matano method first integrates Fick’s law of diffusion (
1) in time to obtain the following system,
where
denotes the terminal concentration of i components,
is the concentration gradient, and
is the known Matano plane, defined by
For a binary system, i.e.,
, there is only one composition-dependent interdiffusion coefficient
to determine with one diffusion couple. Based on Equation (
2), we can can directly compute
for
and then use any curve-fitting method to characterize the function of
. For a ternary system, i.e.,
, we need to determine
for
and
. For each sample
, we can write only two equations whereas there are four unknown parameters. This is an underdetermined system of equations to solve and will lead to multiple solutions. An effective and efficient solution is to assume a continuous function of interdiffusivity in a polynomial form, e.g., an independent quadratic form,
where
w is the weight coefficient in the polynomial function. Denote the flux of the L.H.S. of Equation (
2) as
u: we have
, where
. Estimation of
for
can then be computed by solving the system of equation
where
is the polynomial function fully determined by its weight coefficients given a particular functional form and
. All weight coefficients
in the polynomial functions can be computed by solving the optimization problem,
where
denotes the
norm, which can be replaced with other norms.
Remark 1. Since the estimation of for each only depends on and is computed independently, we omit the index i and reformulate the Matano–Boltzmann method with polynomial interdiffusion coefficients to avoid clutter,whereis the flux for any arbitrary component, andis the concentration gradient for j component, both of which are computed from the profile;is the j column of any arbitrary row ofthat matches the chosen flux at concentration;is the collection. We aim to revealfor. Optimization for Polynomial Fitting
Equation (
7) is a convex optimization problem provided that we have
EPMA samples and we use a
K-order polynomial function of Equation (
4) for all
; the closed-form solution is presented in the
Appendix A. This is certainly impractical for large
M and/or
K. In this case, regularization techniques, e.g.,
-norm minimization or compress sensing, can be implemented to solve such an underdetermined system. The polynomial fitting approach with regularization is efficient in terms of computational time, space complexity, and implementation simplicity, thanks to many excellent software solutions, e.g.,
-magic,
SPGL1, and
SeDuMi [
29,
30,
31].
5. Results
In practical experiments, the interdiffusion coefficients are unknown and uncontrollable, leading to difficulties for unbiased evaluations. Thus, we first assess InfPolyn on numerical examples of ternary (
) and quaternary (
) systems. To imitate a real system but not to lose generality, we use polynomial and exponential functions to construct the interdiffusion coefficient functions. To give an example, the fourth-order polynomial function in a two-component system is represented as
where for each coefficient in the polynomial
, the superscript
r represents the degree of polynomial and the value of them are generated independently from uniform distributions
. We put constraints on the high order terms to prevent the diffusion coefficients from increasing/decreasing drastically with the concentrations
; the diffusion matrix is considered symmetric to ensure numerical stability for the diffusion simulations. Note that this symmetric structure prior information is not injected into InfPolyn or other competing models. For the ternary system, the initial conditions for the forward simulation are
where
denotes the Heaviside step function, which equals to 0 when
and equals to 1 when
. Similarly, for the quaternary system, we defined the initial condition as
With the defined initial condition and the interdiffusion coefficient functions, we use a finite difference (DF) diffusion forward solver to simulate a diffusion process until the terminal time and obtain the terminal concentration profile . To remain numerically stable and accurate, we use a second-order central difference for space and a fourth-order Runge–Kutta for time. The forward simulation solver uses a spatial step , which suggests 1601 grinds points on the space domain , the terminal time is set to .
We then take equally spaced samples from the terminal concentration profile to mimic the EPMA process to provide the terminal concentration profile
. Unless stated otherwise, the terminal concentration profile consists of 40 samples. Since we are concerned with the center areas where the diffusion process is significant, the EPMA samples are limited in the range of
in order to avoid numerical error closed to the boundaries for all Boltzmann–Matano method. All variables are considered dimensionless in the experiments. To evaluate the performance for different methods, we follow Cheng et al. [
13] and use the relative error (RE),
where
and
are the predicted and truth interdiffusion coefficients for concentration
, respectively. As a Boltzmann–Matano numerical inversion-based method, InfPolyn are compared with the other SOTA Boltzmann–Matano numerical inversion-based methods, i.e., the polynomial interdiffusion methods [
13] with 3rd and 4th orders of the polynomial, the compress sensing approach [
16] combined with 4th-order polynomial (high order model enough to capture the subtle changes), and the
regularization approach, which replaces the
penalty term in the work of Qin et al. [
16] with an
penalty term, combined with a 4th-order polynomial function.
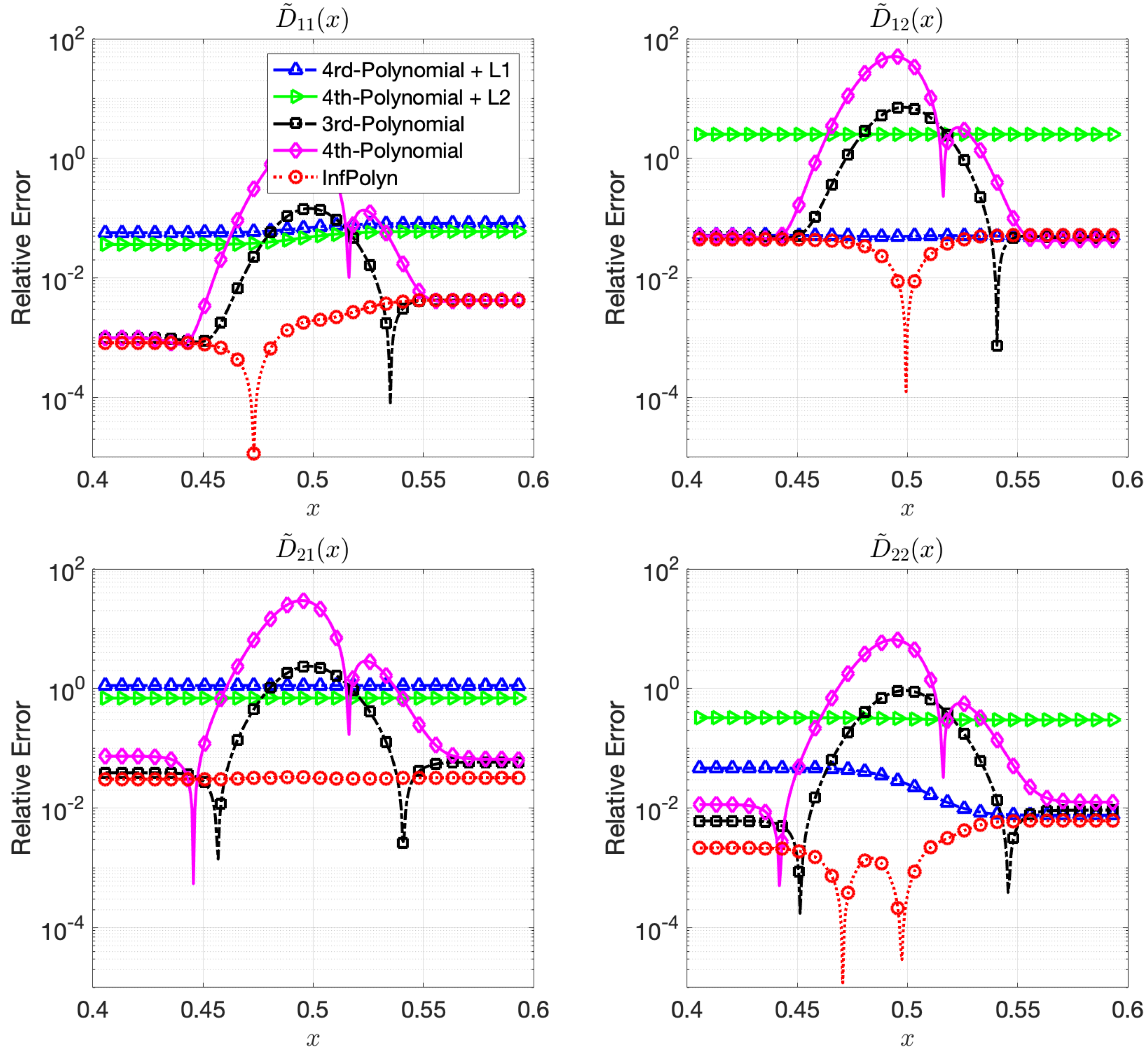
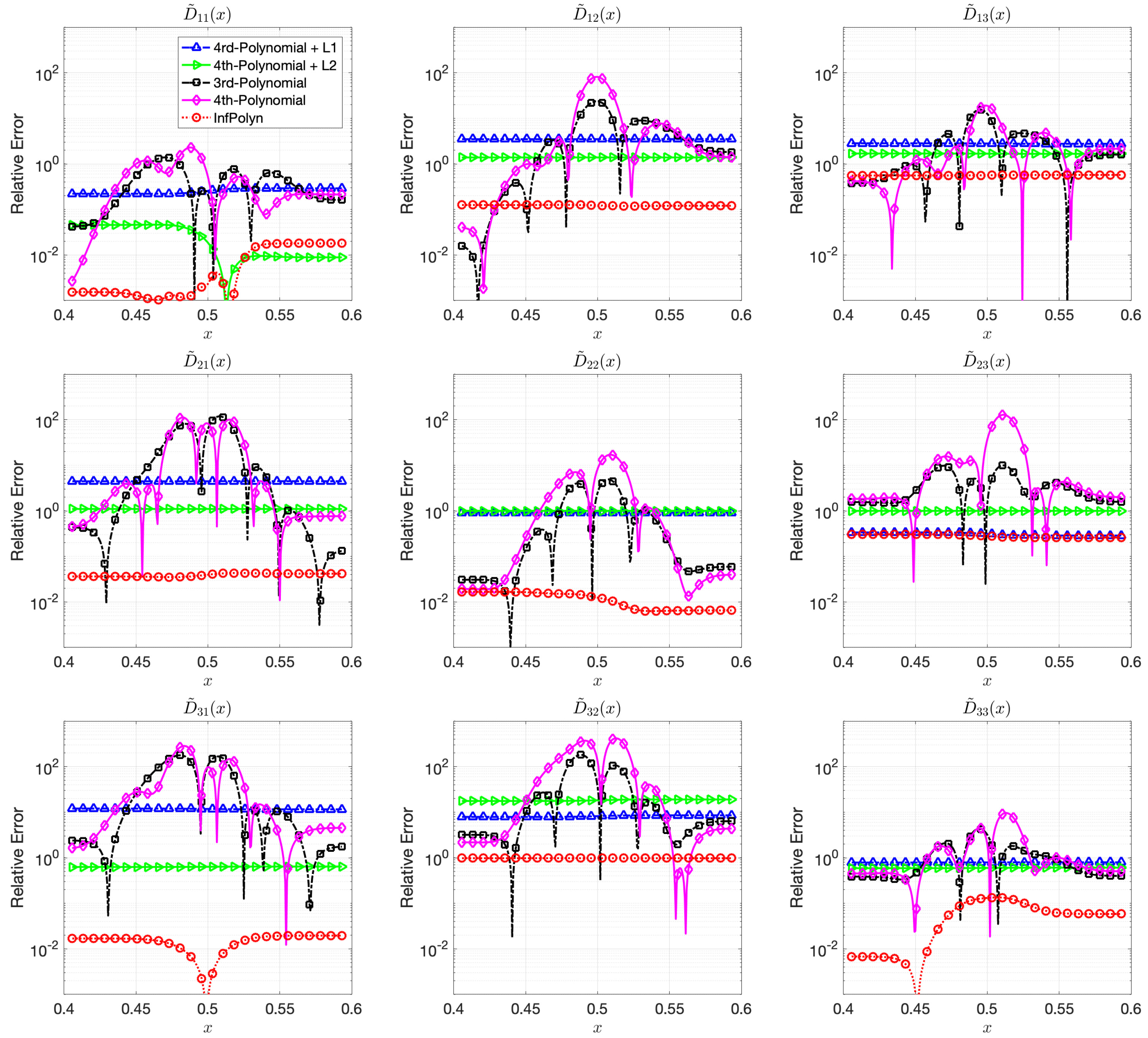
5.1. Case Study 1: Polynomial Diffusion Coefficients
In this case study, we assess InfPolyn in a ternary system and a quaternary with 4th-order polynomial interdiffusion coefficients:
where each coefficients
are randomly generated using independent uniform distributions. To ensure the symmetrical structure of matrix
, we force
by taking their average. In a general interdiffusion process, the interdiffusion coefficients are supposed to be smooth and close to constants, which also prevents instability in the numerical forward solver. To ensure this prior knowledge, we constrain the polynomial coefficients by
. The particularly used values are shown in the
Appendix A. The REs for
for the ternary and the quaternary system are shown in
Figure 1 and
Figure 2. We omit areas outside
because the REs are just extended flat lines without interesting information. As expected, the 4th order polynomial method has a strong model capacity and it can thus achieve few lowest REs at as is shown in some figures within
Figure 1 and
Figure 2. However, if we look at the whole area of interest, the overall performance is the worst among all methods. In particular, due to the overfitting issue, the 4th order polynomial method shows a highly fluctuational performance, which is highly depreciated for real applications. It is not surprising to learn that the 3rd-order polynomial approach shows slightly fewer fluctuations but also fewer lowest REs. This is indeed the aforementioned dilemma of model selection for the polynomial based methods. Similar to results shown in [
16], adding a regularization term of
can ease the overfitting issue and greatly overcome the performance fluctuation issue in both
Figure 1 and
Figure 2. Unfortunately, the improvement comes with the price of low model capacity, leading to a rather flat-fitting RE. The 4th-order polynomial method combined with a
regularization term shows a similar improvement. It is, however, difficult to tell which regularization terms are better. The
regularization works better with the ternary system in
Figure 1, whereas the
approach outperforms the
with a large margin in most cases of
Figure 2. The inconsistency of performance for the
and
regularization approaches certainly hinders their applications for practical problems. In contrast, guided by the correct priors and benefited from the nonparametric nature, InfPolyn shows a consistent and accurate fitting and outperforms the competitors by a significant margin. Thanks to the model flexibility of InfPolyn, it can capture the dramatic changes in the center while maintaining a good fitting in the other flat areas. In all cases, InfPolyn can not only remain stable (indicated by a smooth RE curve) but also achieve the lowest REs in most areas. Furthermore, note that the diagonal interdiffusion coefficients in general show a lower relative error. This is because, in the simulation setting, the diagonal interdiffusion coefficients play a dominant role in the diffusion process. For the non-diagonal interdiffusion coefficients, the REs are amplified by being divided by smaller true interdiffusion coefficients.
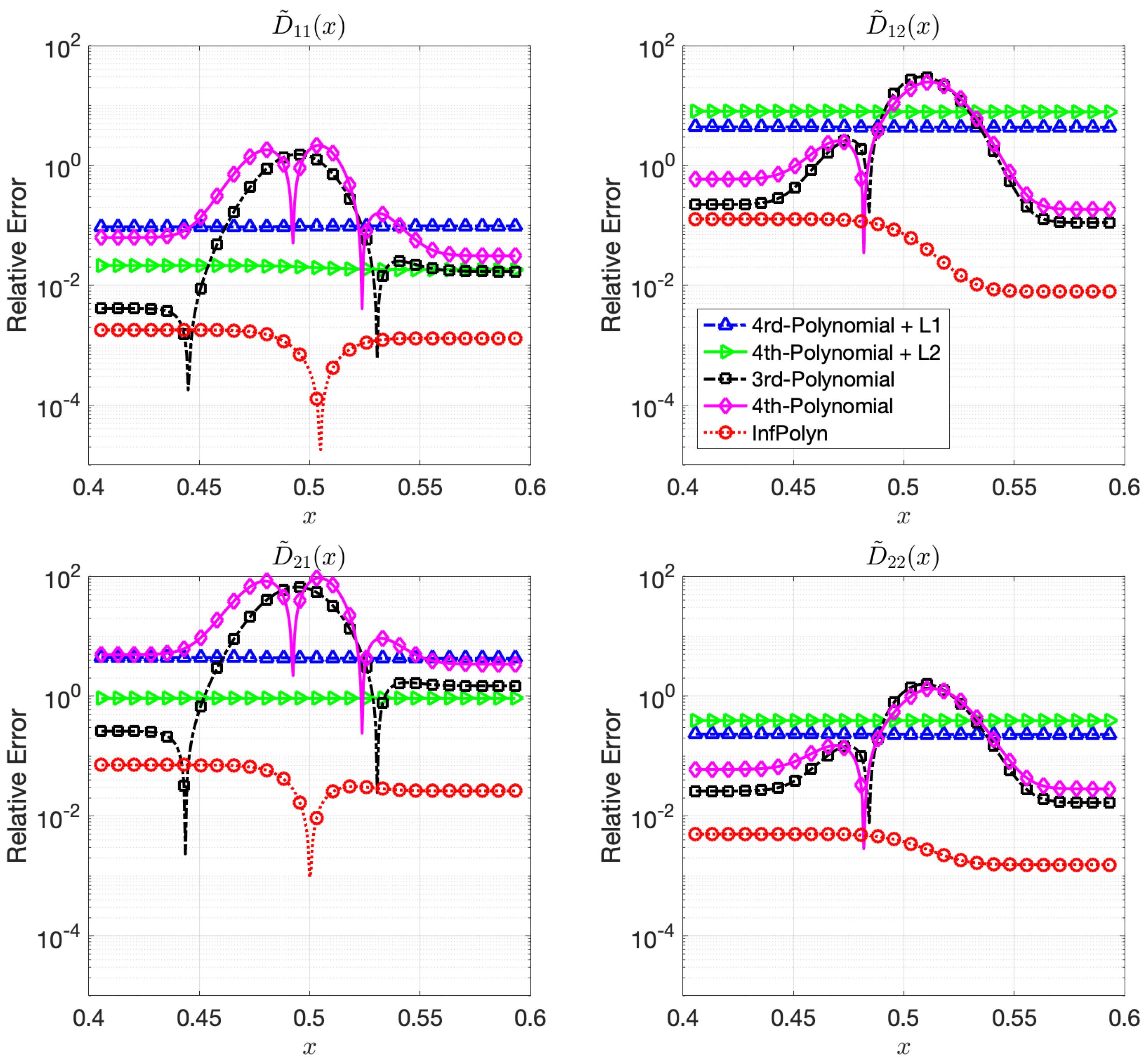
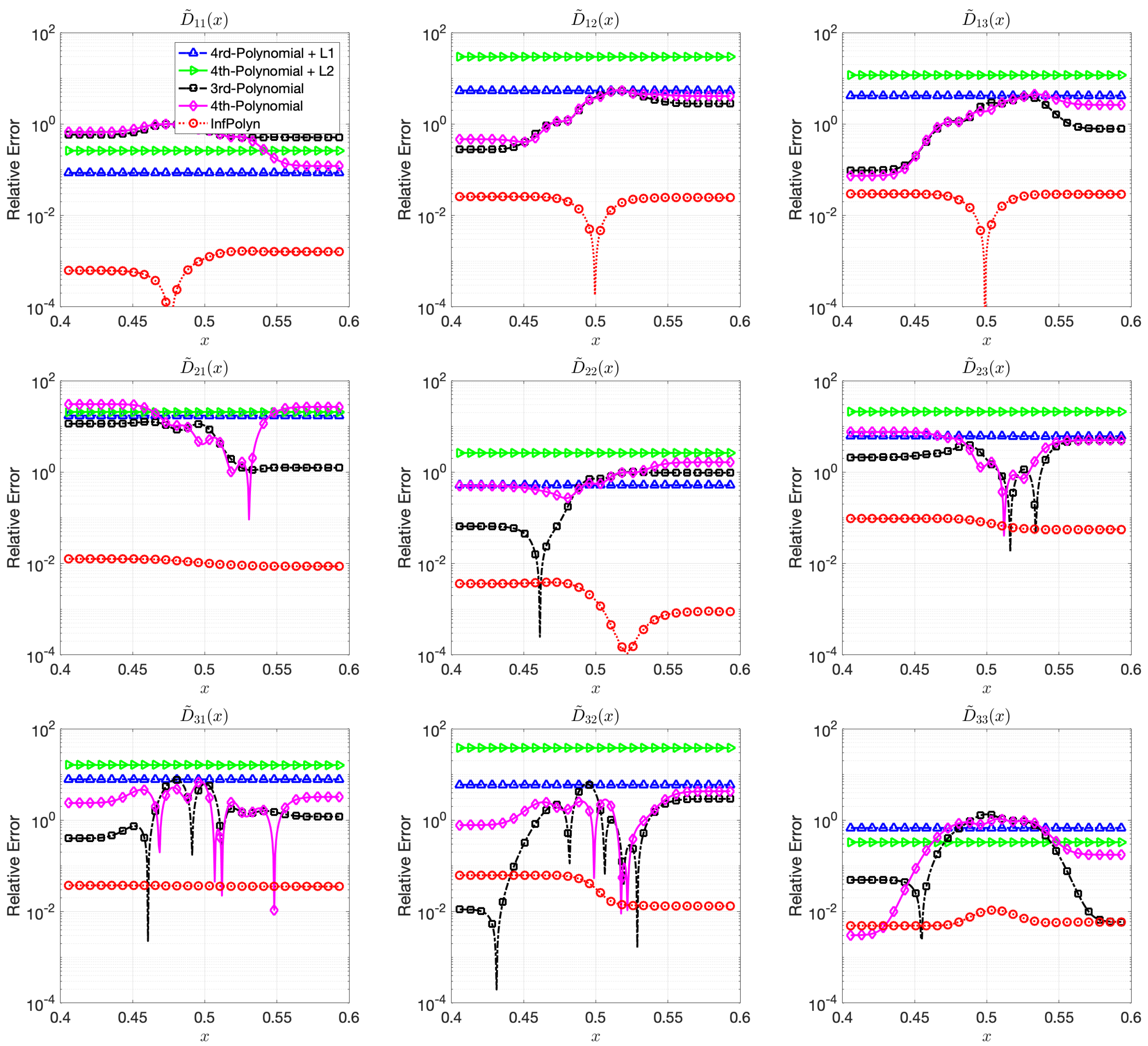
5.2. Case Study 2: Exponential Diffusion Coefficients
In general, the diffusion coefficients can be highly complex that they are not in polynomial forms. To imitate such challenging situations, in this case study, we assess InfPolyn in ternary and quaternary systems with the following interdiffusion coefficient that combines an exponential term and a sinusoidal term,
where the functional coefficients
are similarly sampled from different uniform distributions, i.e.,
,
, and
. Similarly, to ensure the forward diffusion stability, we use the previous approach to ensure the symmetrical structure of matrices
,
, and
. The used exact values of the functional coefficients are shown in
Appendix A. The model performances measured by REs are shown in
Figure 3 and
Figure 4.
In this case study, the 3rd-order polynomial slightly outperforms the 4th-order polynomial approaches in most cases in both
Figure 3 and
Figure 4. Nevertheless, the performance of both 3rd-order and 4th-order polynomial approaches are depreciated due to the fluctuation across the domain. Furthermore, note that REs for the polynomial approaches in
Figure 4 are flat and smooth, indicating that a rich model capacity does not necessarily lead to performance fluctuations in all cases. The
and
regularization combined with 4th-order polynomial degenerate the model performance rather than improving them in many cases in
Figure 4. This shows evidence that inappropriate implicit prior assumptions caused by the
and
regularization terms can hurt model performance. It might be possible to circumvent this issue by adjusting the penalty weight. However, this will create a new issue of how to properly decide the value of the penalty weight, taking us back to the dilemma of model selections. In contrast, InfPolyn shows a consistent and accurate performance; it outperforms the competitors by a large margin for all cases except for
of the quaternary system in the left area in
Figure 4. We would also like to point out that many methods actually fail the quaternary system in
Figure 4 as their REs are larger than 1, meaning a total prediction failure.
5.3. Case Study 3: Uncertainty Quantification Analysis
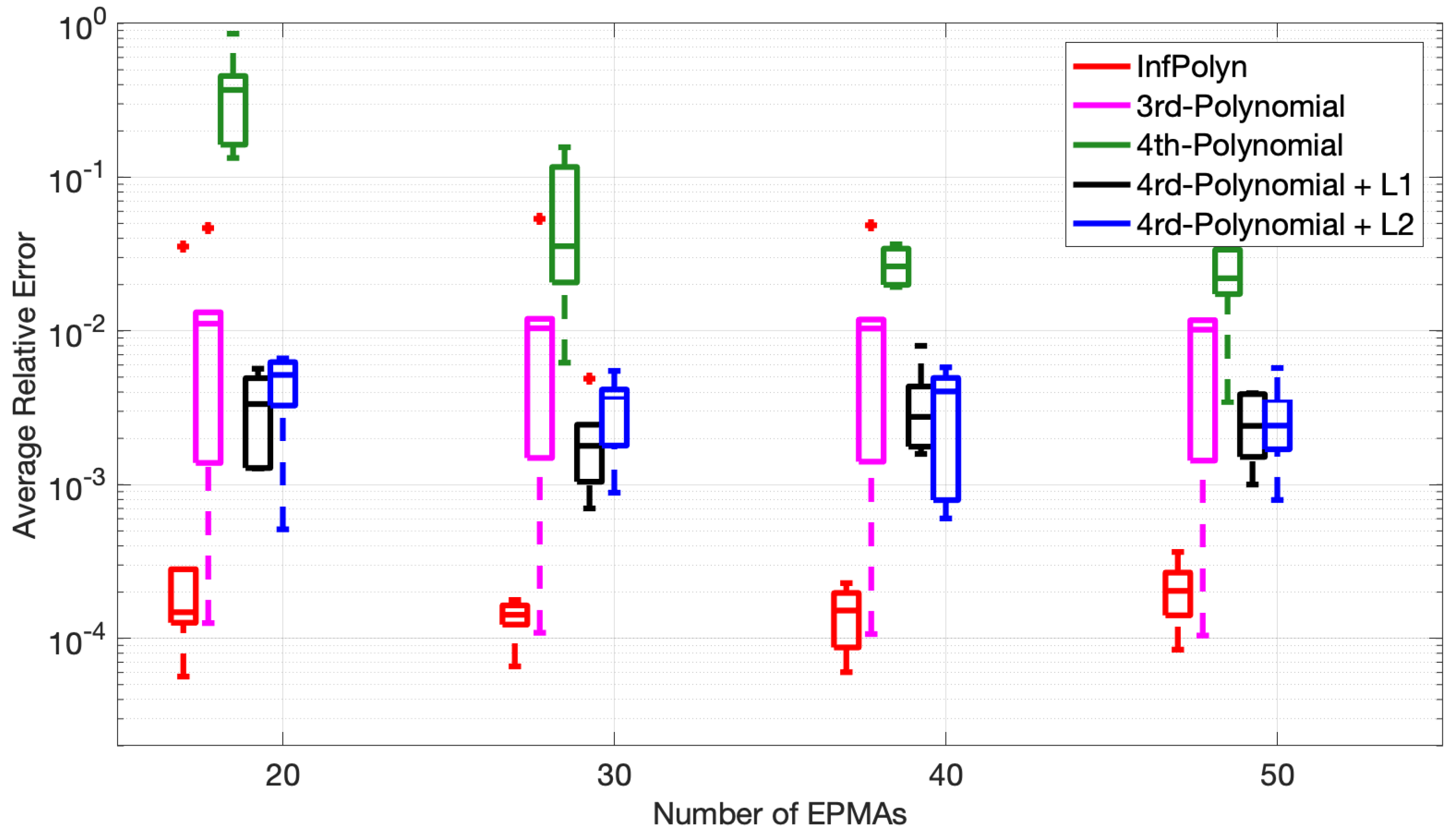
Finally, to assess the consistency of InfPolyn, we conducted a ternary system experiment in Case Study 1 based on five distinct random polynomial coefficient sets, which assemble five different diffusion coefficients, and show the performance statistics. To also investigate the influence of the number of the EPMA samples, we ran each experiment with
EPMA samples. The minimum number of the EPMA samples was 20 because the 4th-order polynomial has 18 coefficients and thus requires at least 18 EPMA samples to work. For each experiment with the given EPMA samples, the model performance was evaluated by average relative error (ARE),
where
indicates the whole spatial domain. We show the statistics of
and
over the five different diffusion coefficients in
Figure 5 using the Tukey box plot. The distinct fact we immediately see is the superiority of InfPolyn compared to the competitors in terms of accuracy and consistency. We then notice that the performance does not improve gradually with the increasing number of EPMA samples for all methods except for the 4th-order polynomial. We believe that each method can already approach reasonable diffusion coefficients (by minimizing the loss function) with only 20 EPMA samples. In this case, more samples will not bring improvement, whereas the performance can fluctuate with different EPMA concentration profiles. Comparing the fluctuations, InfPolyn shows a modest level of changes, whereas the most unstable one is the 4th-order polynomial with
regularization. The most stable method for both
and
is the 3rd order polynomial, which can indicate a lack of model capacity or an underfitting issue. The only exception of performance improvement is the 4th order polynomial, which improves with more EPMA samples. This is a clear sign of overfitting, which can be addressed by introducing more training data. This explains the overfitting phenomena we previously encountered in Case Studies 1 and 2. Will the performance keep improving and outperform InfPolyn with the trend shown in
Figure 5? It may happen with more than 200 EPMA samples, which becomes infeasible in practice. Furthermore, the decreasing trend should slowly disappear at some point, which is already happening for
.
It is also noticeable that the
and
regularization techniques indeed can improve the performance of a 4th-order polynomial by a large margin for all cases with a different number of EPMA samples, which is consistent with the finding in [
16].
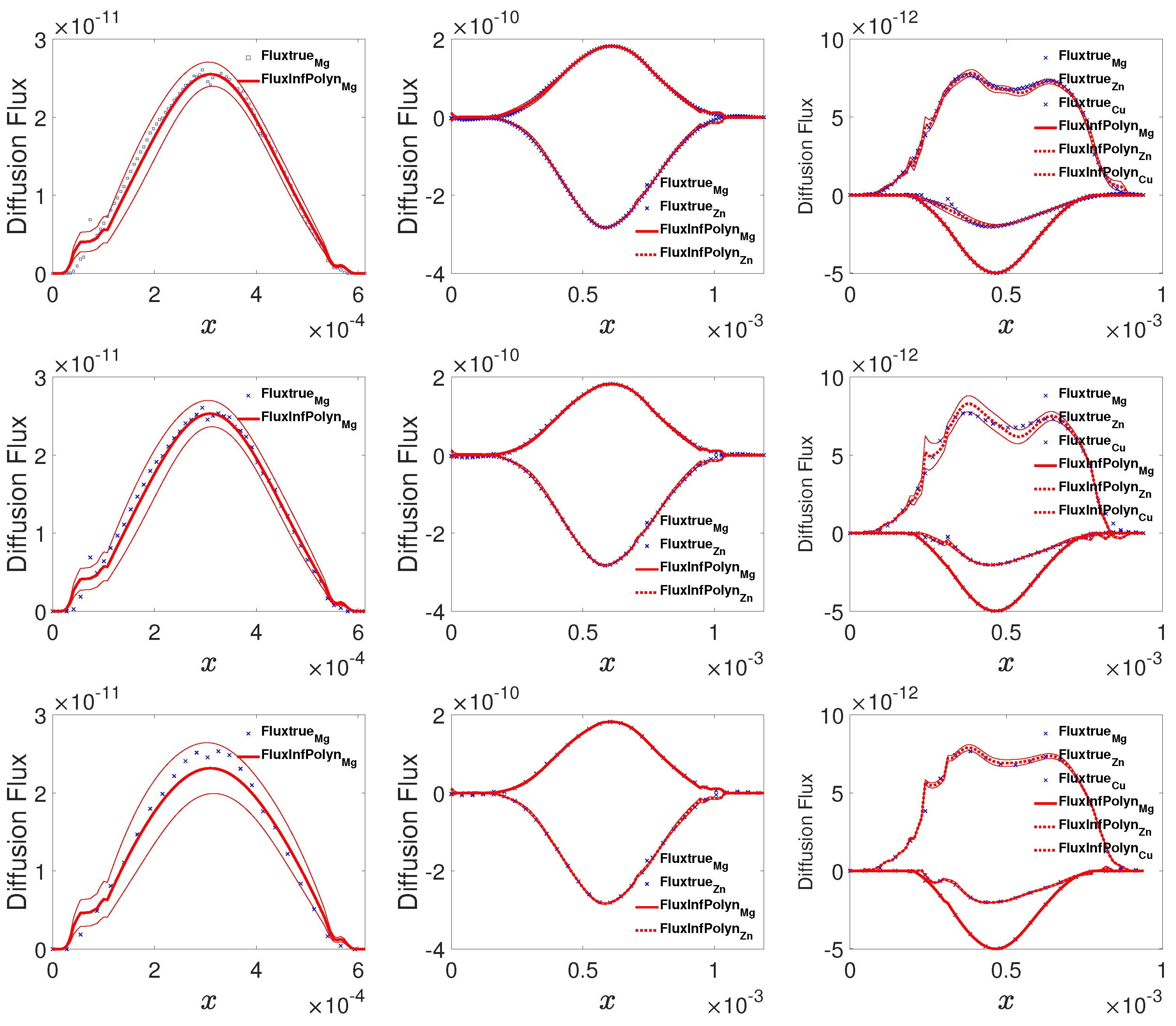
5.4. Case Study 4: Experiment Verification
To present the practical applicability of InfPolyn, we then apply it to the reproduction of the interdiffusion flux from experiment data of the Mg-Al, Mg-Al-Zn, and Mg-Al-Zn-Cu systems collected from the previous literature [
13]. These experimental data include composition profiles of the annealed diffusion couples of Mg-Al at 781 K for 36,960 s, Mg-Al-Zn at 868 K for 5400 s, and Mg-Al-Zn-Cu at 755 K for 75,530 s. Since the experimental measurements are taken non-uniformly on the spatial domain for all of the components, they are reprocessed with local polynomials interpolation techniques to provide values on a uniform grid, which is the common preprocessing for the Matano-based approaches. The derivative and integral terms in the Matano equation are then obtained. Given all the preprocessed data as inputs, we then randomly take all of the samples, half of the samples, and a quarter of the samples from the diffusion systems to test the robustness of the testing methods. As shown in
Figure 6, the curves for all three cases computed by InfPolyn fit well with the experimental data, which lie in the 95% confident areas, indicating a good uncertainty quantification for the predictions. As for the half size and the quarter size training data, the left areas induce oscillations in some intervals. However, InfPolyn still captures the major tendency of the fluxes with slightly increasing uncertainty.