Porous Alumina Ceramics with Multimodal Pore Size Distributions
Abstract
1. Introduction
2. Materials and Methods
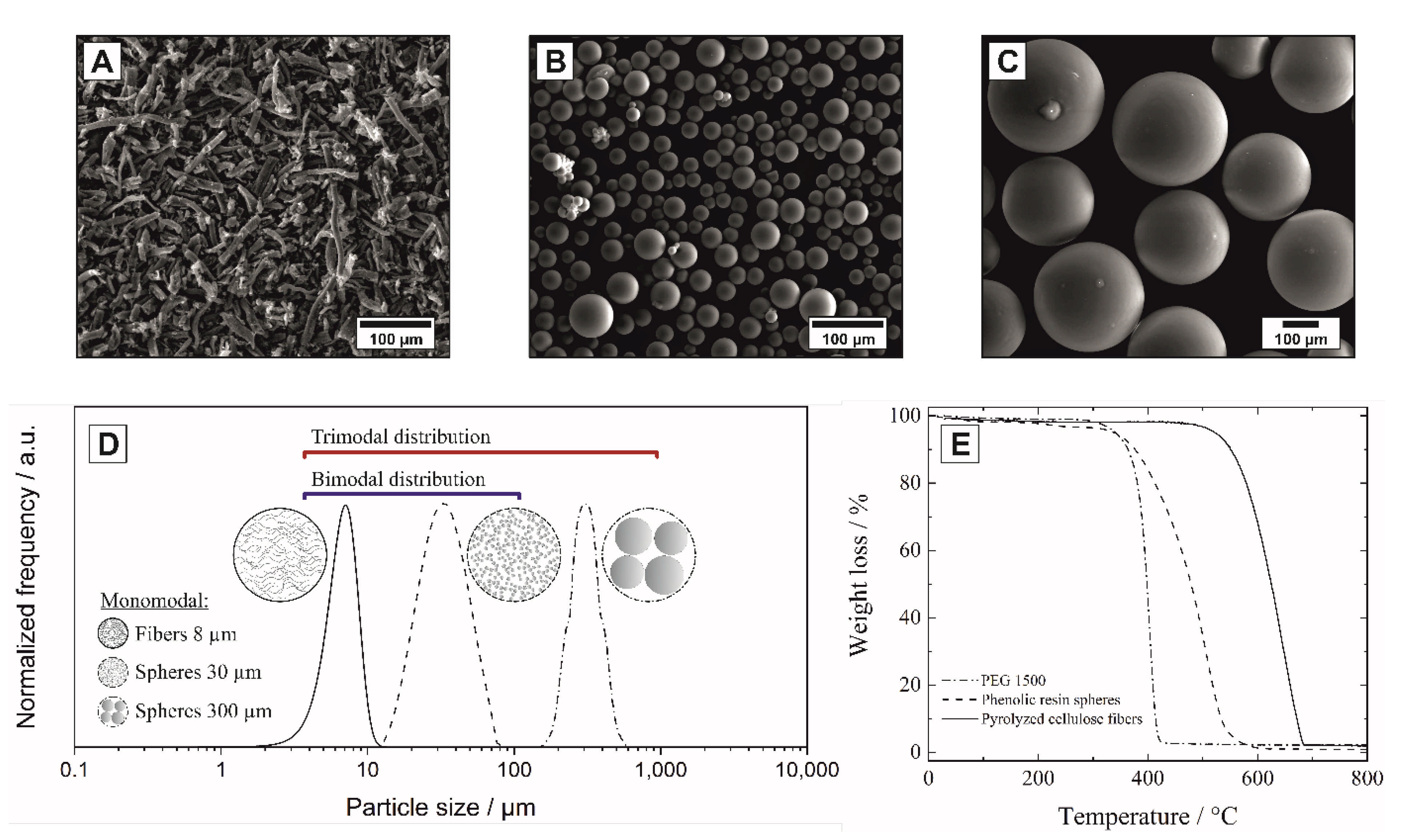
2.1. Fabrication of Alumina with Multimodal Pore Size Distribution
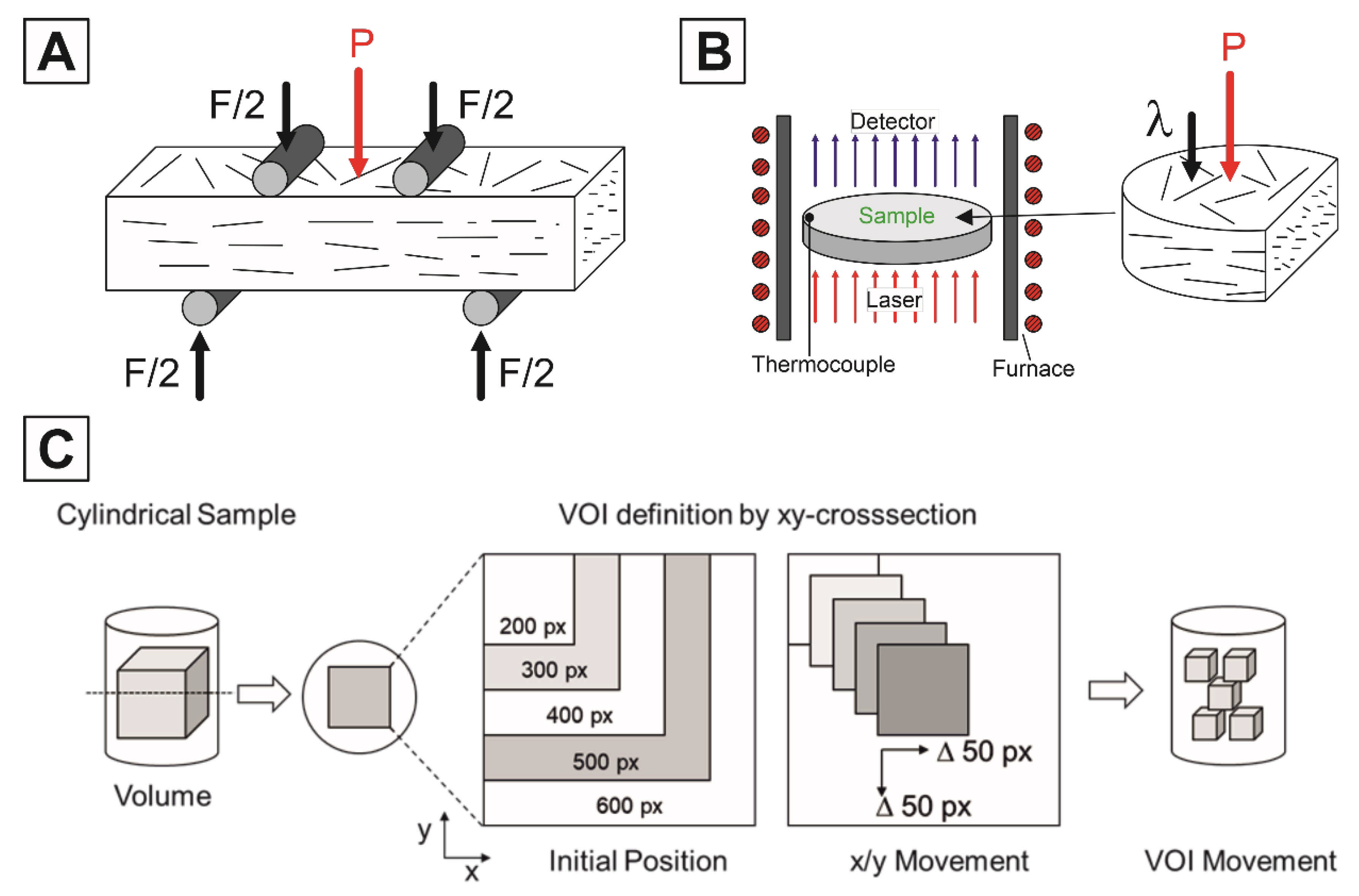
2.2. Mechanical and Thermal Properties Characterization
2.3. Microstructural Characterization and Digital Twin
3. Results and Discussion
3.1. Microstructural Characterization—SEM and µCT
3.2. Mechanical Properties
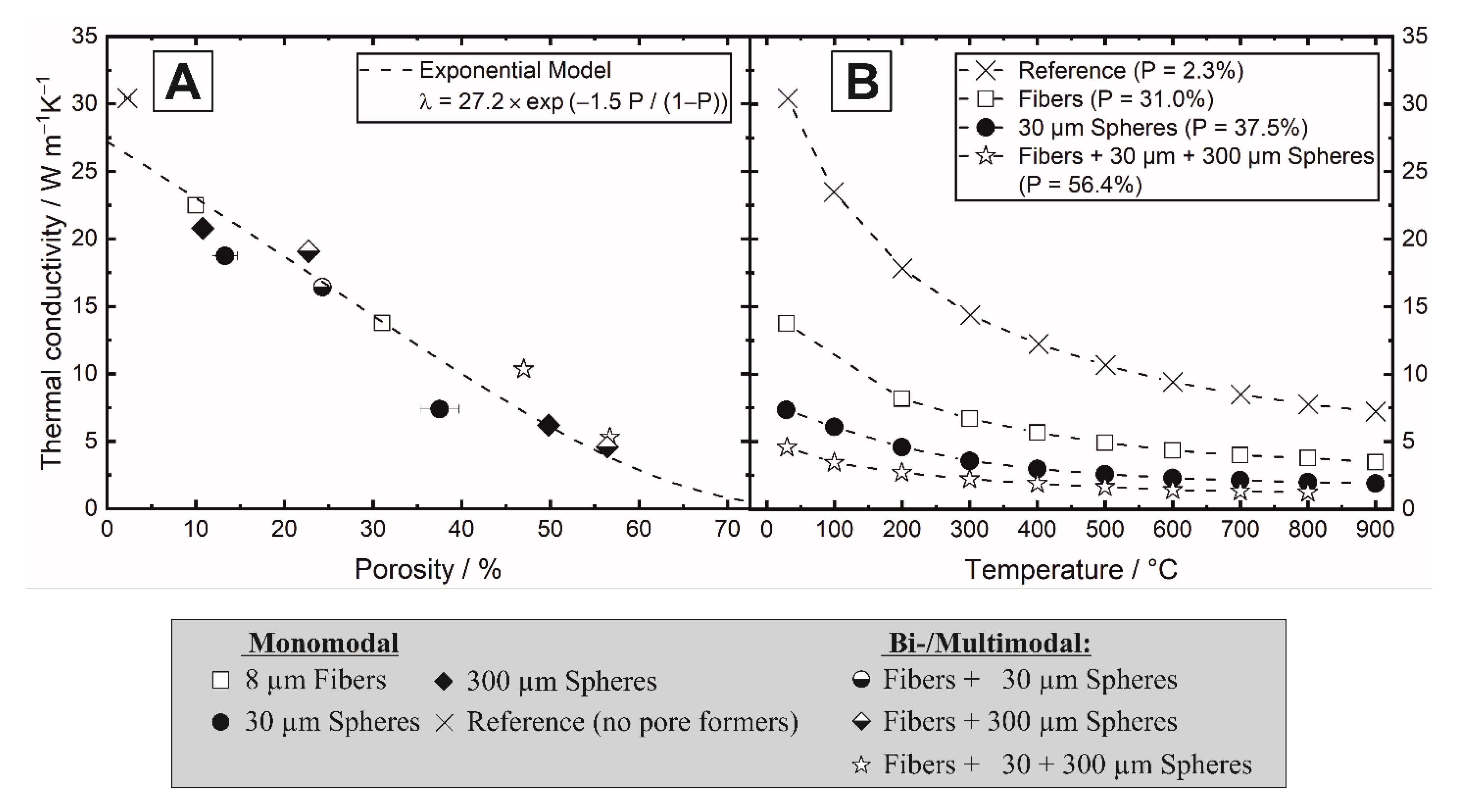
3.3. Thermal Properties
4. Conclusions
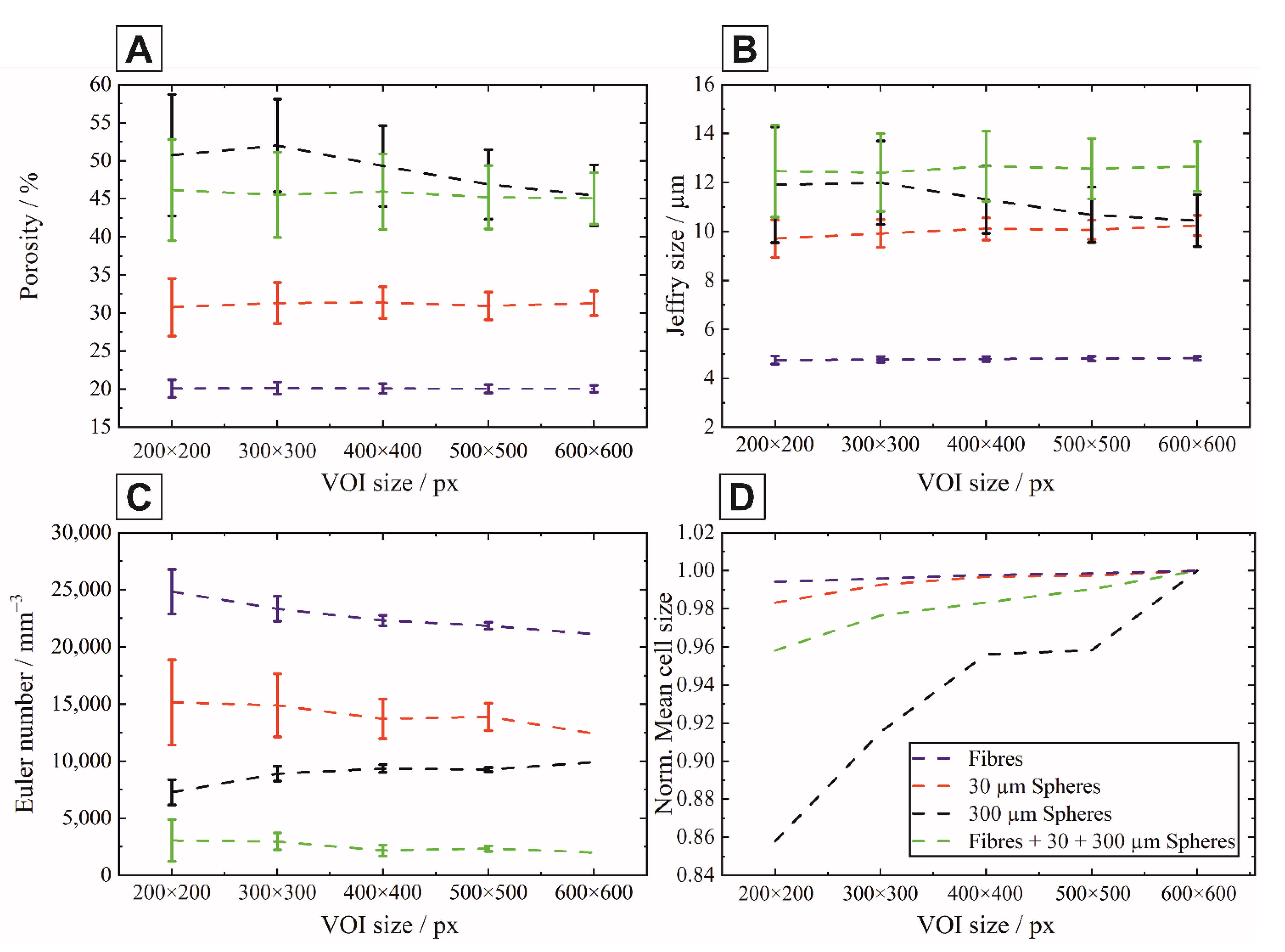
- The application of the three Minkowski functionals (M1, M2, M3) to the µCT images of the heterogeneous structures with different sample formers in terms of shape and size was successfully applied. Thus, the representative volume-of-interest could be set to a size of 400 400 400 px3 or 896 896 896 µm3 at the available resolution of 2.24 µm and thus the digital twin could be defined. The digital twin of each structure enabled the visualization and evaluation of the pore network of the structures and the determination of their connectivity.
- The pyrolyzed cellulose fibers show a perpendicular alignment to the pressing direction induced by the uniaxial pressing. The combination of fibrous templates and spherical templates did not interfere with the alignment of the fibers in the samples with multimodal distributions of sacrificial templates. The volumetric evaluation using the digital twin for the orientation of the fibers has confirmed and complemented the 2D analysis.
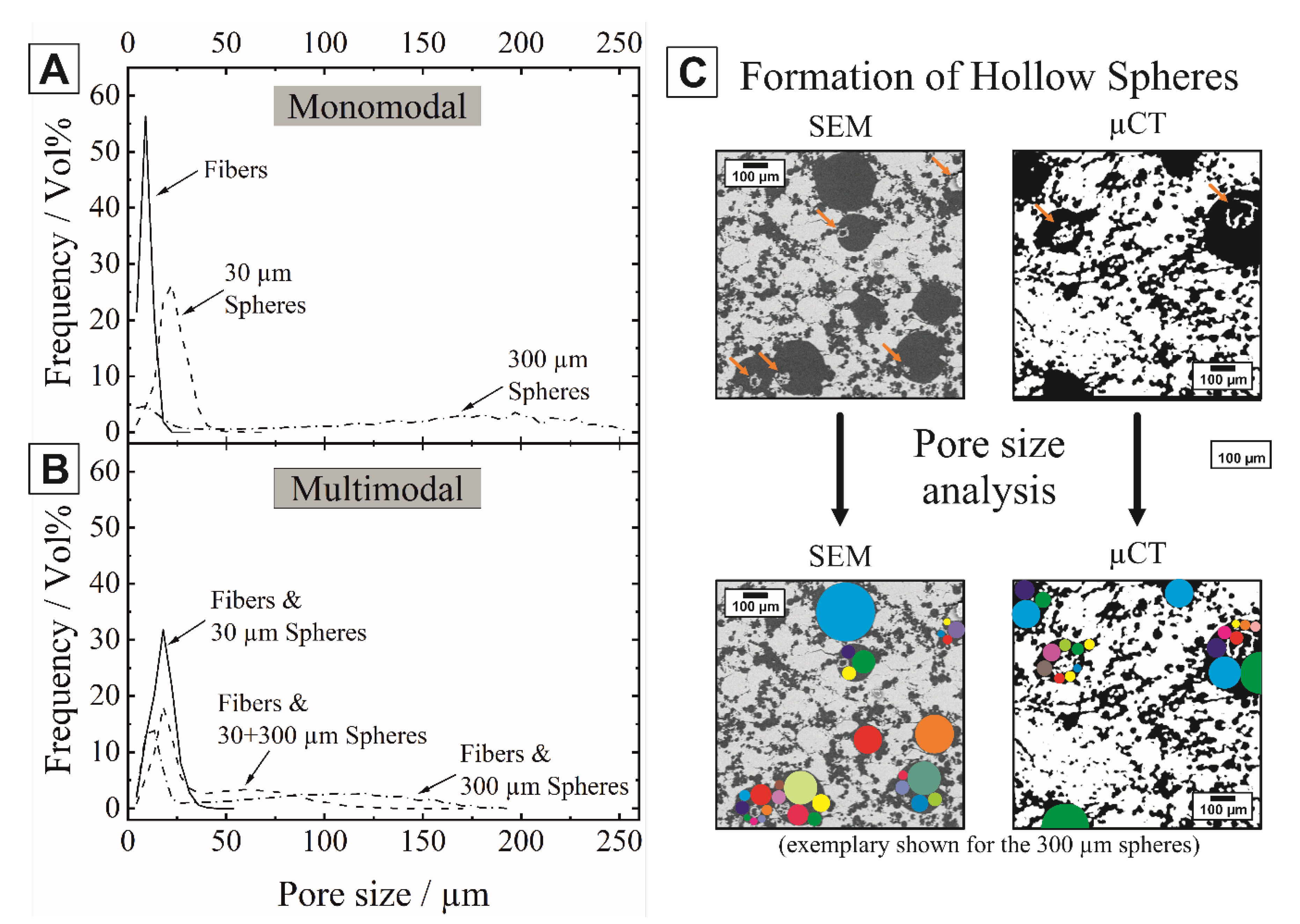
- The permeability is mainly dependent on the pore size of the spherical pore formers as long as the porous matrix provides an interconnected pore network. The 300 µm phenolic resin spheres provided larger pore channels and thus a higher permeability in comparison to the 30 µm phenolic resin spheres. The tubular pores are essential to connect isolated spherical pores. The identified pore networks and their quantification by segment lengths and connectivity at the branch nodes are consistent with the results of the Euler number.
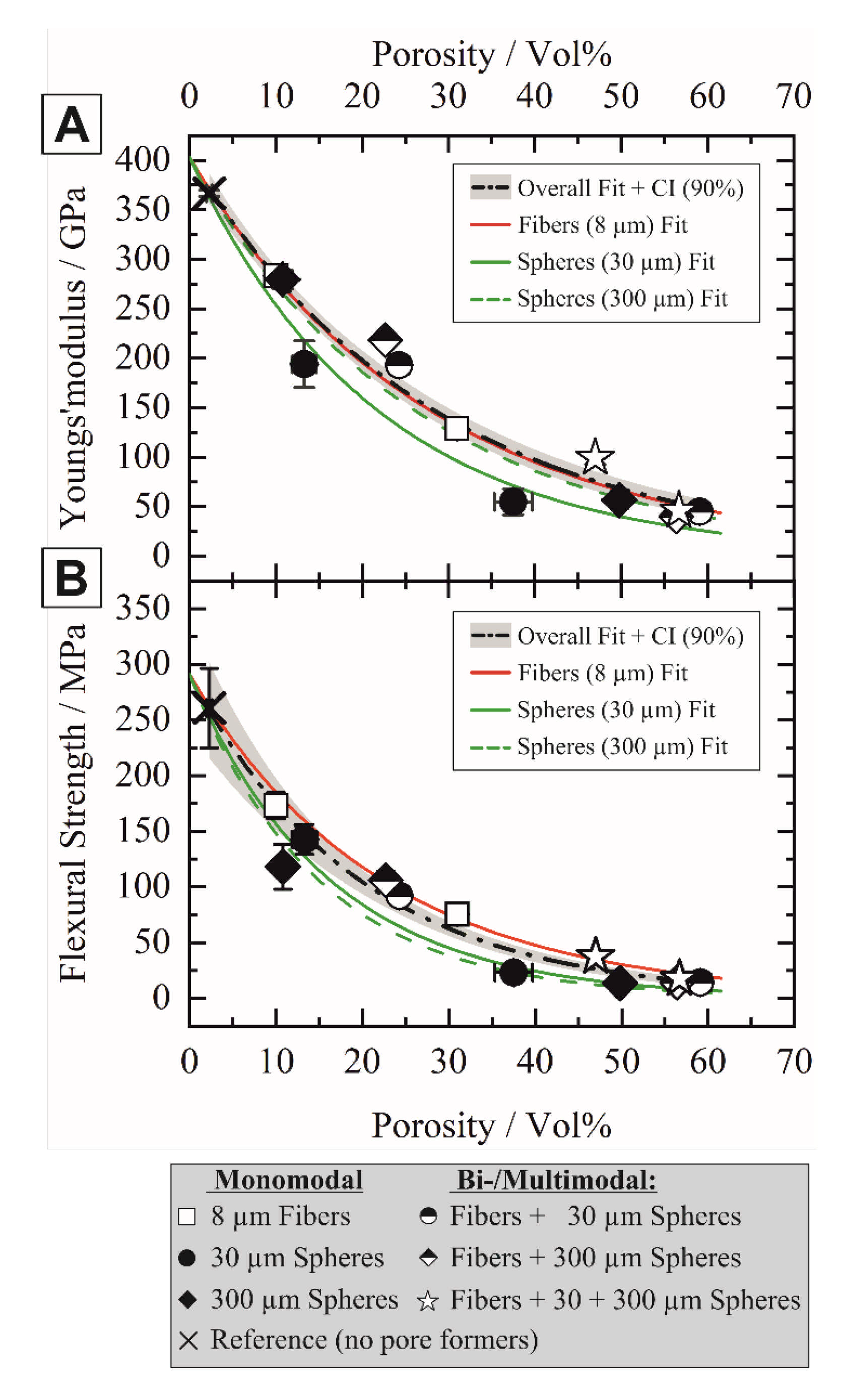
- The type of the sacrificial templates predominantly influenced the mechanical properties. Small tubular pores lead to a higher stiffness and strength compared to spherical pores, based on the smaller defect size and anisotropic microstructure. Low elastic moduli with higher specific strength were obtained for the samples with a monomodal distribution of 30 µm phenolic resin spheres. The FEM simulations performed on the digital twins agree with the experimental results with respect to the distribution of the stresses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scheffler, M.; Colombo, P. Cellular Ceramics: Structure, Manufacturing, Properties and Applications; Wiley-VCH: Weinheim, UK, 2010; ISBN 978-3-527-31320-4. [Google Scholar]
- Green, D.J.; Colombo, P. Cellular Ceramics: Intriguing Structures, Novel Properties, and Innovative Applica-tions. MRS Bull. 2003, 28, 296–300. [Google Scholar] [CrossRef]
- Greil, P. Advanced Engineering Ceramics. Adv. Mater. 2002, 14, 709. [Google Scholar] [CrossRef]
- Hammel, E.C.; Ighodaro, O.-R.; Okoli, O.I. Processing and properties of advanced porous ceramics: An applica-tion based review. Ceram. Int. 2014, 40, 15351–15370. [Google Scholar] [CrossRef]
- Ohji, T.; Fukushima, M. Macro-porous ceramics: Processing and properties. Int. Mater. Rev. 2012, 57, 115–131. [Google Scholar] [CrossRef]
- Studart, A.R.; Gonzenbach, U.T.; Tervoort, E.; Gauckler, L.J. Processing Routes to Macroporous Ceramics: A Review. J. Am. Ceram. Soc. 2006, 89, 1771–1789. [Google Scholar] [CrossRef]
- Shigegaki, Y.; Brito, M.E.; Hirao, K.; Toriyama, M.; Kanzaki, S. Strain Tolerant Porous Silicon Nitride. J. Am. Ceram. Soc. 1997, 80, 495–498. [Google Scholar] [CrossRef]
- Shi, L.; Wang, L.; Duan, Y.; Lei, W.; Wang, Z.; Li, J.; Fan, X.; Li, X.; Li, S.; Guo, Z. The improved biological per-formance of a novel low elastic modulus implant. PLoS ONE 2013, 8, e55015. [Google Scholar] [CrossRef]
- Ridzwan, M.; Shuib, S.; Hassan, A.Y.; Shokri, A.A.; Mohamad Ib, M.N. Problem of Stress Shielding and Im-provement to the Hip Implant Designs: A Review. J. Med. Sci. 2007, 7, 460–467. [Google Scholar] [CrossRef]
- Ha, J.-H.; Oh, E.; Song, I.-H. The effect of sacrificial templates on the pore characteristics of sintered diatomite membranes. J. Ceram. Soc. Jpn. 2013, 121, 940–945. [Google Scholar] [CrossRef][Green Version]
- Colombo, P.; Bernardo, E.; Biasetto, L. Novel Microcellular Ceramics from a Silicone Resin. J. Am. Ceram. Soc. 2004, 87, 152–154. [Google Scholar] [CrossRef]
- Eom, J.-H.; Kim, Y.-W. Effect of template size on microstructure and strength of porous silicon carbide ceram-ics. J. Ceram. Soc. Jpn. 2008, 116, 1159–1163. [Google Scholar] [CrossRef]
- Lopes, R.A.; Segadaĕs, A.M. Microstructure, permeability and mechanical behaviour of ceramic foams. Mater. Sci. Eng. A 1996, 209, 149–155. [Google Scholar] [CrossRef]
- Schlichting, K.W.; Padture, N.P.; Klemens, P.G. Thermal conductivity of dense and porous yttria-stabilized zirconia. J. Mater. Sci. 2001, 36, 3003–3010. [Google Scholar] [CrossRef]
- Petit, C.; Meille, S.; Maire, E.; Tadier, S.; Adrien, J. Mechanical behaviour of a β-TCP ceramic with a random porosity: Study of the fracture path with X-ray tomography. J. Eur. Ceram. Soc. 2016, 36, 3225–3233. [Google Scholar] [CrossRef]
- Lyckfeldt, O.; Ferreira, J. Processing of porous ceramics by ‘starch consolidation’. J. Eur. Ceram. Soc. 1998, 18, 131–140. [Google Scholar] [CrossRef]
- Zhang, G.-J.; Yang, J.-F.; Ohji, T. Fabrication of Porous Ceramics with Unidirectionally Aligned Continuous Pores. J. Am. Ceram. Soc. 2001, 84, 1395–1397. [Google Scholar] [CrossRef]
- Isobe, T.; Kameshima, Y.; Nakajima, A.; Okada, K.; Hotta, Y. Gas permeability and mechanical properties of porous alumina ceramics with unidirectionally aligned pores. J. Eur. Ceram. Soc. 2007, 27, 53–59. [Google Scholar] [CrossRef]
- Okada, K.; Shimizu, M.; Isobe, T.; Kameshima, Y.; Sakai, M.; Nakajima, A.; Kurata, T. Characteristics of mi-crobubbles generated by porous mullite ceramics prepared by an extrusion method using organic fibers as the pore former. J. Eur. Ceram. Soc. 2010, 30, 1245–1251. [Google Scholar] [CrossRef]
- Okada, K.; Uchiyama, S.; Isobe, T.; Kameshima, Y.; Nakajima, A.; Kurata, T. Capillary rise properties of porous mullite ceramics prepared by an extrusion method using organic fibers as the pore former. J. Eur. Ceram. Soc. 2009, 29, 2491–2497. [Google Scholar] [CrossRef]
- Eom, J.-H.; Kim, Y.-W.; Jeong, D.-H.; Lee, S.-S. Thermal conductivity and compressive strength anisotropy in vermiculite–ceramic composites with layered structure. J. Ceram. Soc. Jpn. 2011, 119, 319–321. [Google Scholar] [CrossRef]
- Eom, J.-H.; Kim, Y.-W.; Lee, S.-S.; Jeong, D.-H. Processing of Vermiculite-Silica Composites with Prefer-Oriented Rod-Like Pores. J. Korean Ceram. Soc. 2012, 49, 347–351. [Google Scholar] [CrossRef]
- Suvaci, E.; Seabaugh, M.M.; Messing, G.L. Reaction-based Processing of Textured Alumina by Templated Grain Growth. J. Eur. Ceram. Soc. 1999, 19, 2465–2474. [Google Scholar] [CrossRef]
- Ciurans Oset, M.; Nordin, J.; Akhtar, F. Processing of Macroporous Alumina Ceramics Using Pre-Expanded Polymer Microspheres as Sacrificial Template. Ceramics 2018, 1, 329–342. [Google Scholar] [CrossRef]
- Andersson, L.; Jones, A.C.; Knackstedt, M.A.; Bergström, L. Permeability, pore connectivity and critical pore throat control of expandable polymeric sphere templated macroporous alumina. Acta Mater. 2011, 59, 1239–1248. [Google Scholar] [CrossRef]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef]
- Akolkar, A.; Petrasch, J. Tomography-Based Characterization and Optimization of Fluid Flow through Porous Media. Transp. Porous Med. 2012, 95, 535–550. [Google Scholar] [CrossRef]
- DeHoff, R.T. Use of the disector to estimate the Euler characteristic of three dimensional microstructures. Acta Stereol. 1987, 6, 133–140. [Google Scholar]
- Hadwiger, H. Vorlesungen Über Inhalt, Oberfläche und Isoperimetrie; Springer: Berlin/Heidelberg, Germany, 1957; ISBN 978-3-642-94702-5. [Google Scholar]
- DeHoff, R.T. Stereological Characterization of Anisotropy in the Statistical Description of the Spatial Distribu-tion of Scalar Properties of Microstructures. Microsc Microanal 2004, 10, 724–725. [Google Scholar] [CrossRef]
- Ohser, J.; Nagel, W. The estimation of the Euler-Poincare characteristic from observations on parallel sections. J. Microsc. 1996, 184, 117–126. [Google Scholar] [CrossRef]
- Gregorová, E.; Uhlířová, T.; Pabst, W.; Diblíková, P.; Sedlářová, I. Microstructure characterization of mullite foam by image analysis, mercury porosimetry and X-ray computed microtomography. Ceram. Int. 2018, 44, 12315–12328. [Google Scholar] [CrossRef]
- Uhlířová, T.; Gregorová, E.; Pabst, W. Application of Stereological Relations for the Characterization of Porous Materials via Microscopic Image Analysis. KEM 2015, 647, 180–187. [Google Scholar] [CrossRef]
- Odgaard, A. Three-dimensional methods for quantification of cancellous bone architecture. Bone 1997, 20, 315–328. [Google Scholar] [CrossRef]
- Hildebrand, T.; Rüegsegger, P. A new method for the model-independent assessment of thickness in three-dimensional images. J. Microsc. 1997, 185, 67–75. [Google Scholar] [CrossRef]
- Hildebrand, T.; Laib, A.; Müller, R.; Dequeker, J.; Rüegsegger, P. Direct three-dimensional morphometric analy-sis of human cancellous bone: Microstructural data from spine, femur, iliac crest, and calcaneus. J. Bone Miner. Res. 1999, 14, 1167–1174. [Google Scholar] [CrossRef]
- Fouard, C.; Malandain, G.; Prohaska, S.; Westerhoff, M. Blockwise processing applied to brain microvascular network study. IEEE Trans. Med. Imaging 2006, 25, 1319–1328. [Google Scholar] [CrossRef]
- Kohjiya, S.; Katoh, A.; Suda, T.; Shimanuki, J.; Ikeda, Y. Visualisation of carbon black networks in rubbery ma-trix by skeletonisation of 3D-TEM image. Polymer 2006, 47, 3298–3301. [Google Scholar] [CrossRef]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. MeshLab: An Open-Source Mesh Processing Tool. In Proceedings of the The Eurographics Association, Eurographics Italian Chapter Conference, Salerno, Italy, 2–4 July 2008; pp. 129–136. [Google Scholar]
- Biggemann, J.; Hoffmann, P.; Hristov, I.; Simon, S.; Müller, P.; Fey, T. Injection Molding of 3-3 Hydroxyapatite Composites. Materials 2020, 13, 1907. [Google Scholar] [CrossRef]
- El Seoud, O.A.; Fidale, L.C.; Ruiz, N.; D’Almeida, M.L.O.; Frollini, E. Cellulose swelling by protic solvents: Which properties of the biopolymer and the solvent matter? Cellulose 2008, 15, 371–392. [Google Scholar] [CrossRef]
- Mantanis, G.I.; Young, R.A.; Rowell, R.M. Swelling of compressed cellulose fiber webs in organic liquids. Cellulose 1995, 2, 1–22. [Google Scholar]
- Heunisch, A.; Dellert, A.; Roosen, A. Effect of powder, binder and process parameters on anisotropic shrinkage in tape cast ceramic products. J. Eur. Ceram. Soc. 2010, 30, 3397–3406. [Google Scholar] [CrossRef]
- Rutkowski, P.; Klimczyk, P.; Jaworska, L.; Stobierski, L.; Dubiel, A. Thermal properties of pressure sintered alumina–graphene composites. J. Anal. Calorim 2015, 122, 105–114. [Google Scholar] [CrossRef]
- Itatani, K.; Tanaka, T.; Davies, I.J. Thermal properties of silicon carbide composites fabricated with chopped Tyranno® SiAlC fibres. J. Eur. Ceram. Soc. 2006, 26, 703–710. [Google Scholar] [CrossRef]
- Bradt, R.C.; Evans, A.G.; Hasselman, D.P.H.; Lange, F.F. Fracture Mechanics of Ceramics; Springer: Boston, MA, USA, 1986; ISBN 978-1-4615-7025-7. [Google Scholar]
- Giesche, H. Mercury Porosimetry: A General (Practical) Overview. Part. Part. Syst. Charact. 2006, 23, 9–19. [Google Scholar] [CrossRef]
- Innocentini, M.D.; Salvini, V.R.; Pandolfelli Victor, C. The Permeability of Ceramic Foams. Am. Ceram. Soc. Bull. 1999, 78, 78–84. [Google Scholar]
- Gauckler, L.J.; Waeber, M.M. Light Metals. In Proceedings of the 114th Annual Meeting of the Metallurgical Society of AIME, New York, NY, USA, 24–28 February 1985; pp. 1261–1283. [Google Scholar]
- Rice, R.W. Proposity of Ceramics; M. Dekker: New York, NY, USA; Basel, Switzerland; Hong Kong, China, 1998; ISBN 0-8247-0151-8. [Google Scholar]
- Duckworth, W. Discussion of Ryshkewitch Paper by Winston Duckworth. J. Am. Ceram. Soc. 1953, 36, 68. [Google Scholar] [CrossRef]
- Spriggs, R.M. Expression for Effect of Porosity on Elastic Modulus of Polycrystalline Refractory Materials, Particularly Aluminum Oxide. J. Am. Ceram. Soc. 1961, 44, 628–629. [Google Scholar] [CrossRef]
- Andersson, C.A. Derivation of the Exponential Relation for the Effect of Ellipsoidal Porosity on Elastic Modulus. J. Am. Ceram. Soc. 1996, 79, 2181–2184. [Google Scholar] [CrossRef]
- Travitzky, N.; Windsheimer, H.; Fey, T.; Greil, P. Preceramic Paper-Derived Ceramics. J. Am. Ceram. Soc. 2008, 91, 3477–3492. [Google Scholar] [CrossRef]
- Yoshida, K.; Tsukidate, H.; Murakami, A.; Miyata, H. Influence of Pore Size on Fracture Strength of Porous Ceramics. JMMP 2008, 2, 1060–1069. [Google Scholar] [CrossRef]
- Liu, D.-M. Influence of porosity and pore size on the compressive strength of porous hydroxyapatite ceramic. Ceram. Int. 1997, 23, 135–139. [Google Scholar] [CrossRef]
- Hu, L.; Wang, C.-A. Effect of sintering temperature on compressive strength of porous yttria-stabilized zirconia ceramics. Ceram. Int. 2010, 36, 1697–1701. [Google Scholar] [CrossRef]
- Tancret, F.; Bouler, J.-M.; Chamousset, J.; Minois, L.-M. Modelling the mechanical properties of microporous and macroporous biphasic calcium phosphate bioceramics. J. Eur. Ceram. Soc. 2006, 26, 3647–3656. [Google Scholar] [CrossRef]
- Živcová, Z.; Gregorová, E.; Pabst, W.; Smith, D.S.; Michot, A.; Poulier, C. Thermal conductivity of porous alumina ceramics prepared using starch as a pore-forming agent. J. Eur. Ceram. Soc. 2009, 29, 347–353. [Google Scholar] [CrossRef]

| Batch No. | Distribution Type | Fibers /Vol% | 30 µm Spheres /Vol% | 300 µm Spheres /Vol% | Target Porosity /Vol% | Total Porosity /Vol% |
|---|---|---|---|---|---|---|
| 1 | Reference | 0 | 2.3 | |||
| 2 | Monomodal | 10 | 10 | 10.0 | ||
| 3 | 15 | 15 | 13.3 | |||
| 4 | 15 | 15 | 10.8 | |||
| 5 | 34 | 34 | 31.0 | |||
| 6 | 37 * | 37 | 37.5 | |||
| 7 | 52 * | 52 | 49.8 | |||
| 8 | Bimodal | 8 | 16 | 25 | 22.2 | |
| 9 | 8 | 16 | 25 | 24.3 | ||
| 10 | 22 | 35 * | 57 | 59.1 | ||
| 11 | 17 | 50 * | 67 | 56.4 | ||
| 12 | Trimodal | 28 | 8 | 8 | 44 | 47.0 |
| 13 | 5 | 27 | 27 | 58 | 56.7 |
| Sample Type | Ratio of Sacrificial Templates/Vol% | Mean Pore Size ** (d50)/µm | Porosity * /Vol% | Permeability ** /D | |||
|---|---|---|---|---|---|---|---|
| Fibers | 35 µm Spheres | 300 µm Spheres | Peak I (dI50) | Peak II (dII50) | (9.87·10−13 m2) | ||
| Initial pore formers * | 100 | 8 | - | - | - | ||
| 100 | 31 | - | - | - | |||
| 100 | 303 | - | - | - | |||
| Monomodal ** | 34 | 9 | - | 31.0 | 0 | ||
| 37 | 22 | - | 37.5 | 4.1 | |||
| 52 | 181 | - | 49.8 | 9.0 | |||
| Bimodal ** | 22 | 35 | 18 | - | 59.1 | 34.9 | |
| 17 | 50 | 18 | 62 | 56.4 | 136.0 | ||
| Trimodal ** | 5 | 27 | 27 | 18 | 53 | 47.0 | 33.4 |
| 28 | 8 | 8 | 11 | 69 | 56.7 | 4.6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biggemann, J.; Stumpf, M.; Fey, T. Porous Alumina Ceramics with Multimodal Pore Size Distributions. Materials 2021, 14, 3294. https://doi.org/10.3390/ma14123294
Biggemann J, Stumpf M, Fey T. Porous Alumina Ceramics with Multimodal Pore Size Distributions. Materials. 2021; 14(12):3294. https://doi.org/10.3390/ma14123294
Chicago/Turabian StyleBiggemann, Jonas, Martin Stumpf, and Tobias Fey. 2021. "Porous Alumina Ceramics with Multimodal Pore Size Distributions" Materials 14, no. 12: 3294. https://doi.org/10.3390/ma14123294
APA StyleBiggemann, J., Stumpf, M., & Fey, T. (2021). Porous Alumina Ceramics with Multimodal Pore Size Distributions. Materials, 14(12), 3294. https://doi.org/10.3390/ma14123294







