Finite Element Modeling of the Dynamic Properties of Composite Steel–Polymer Concrete Beams
Abstract
1. Introduction
2. Materials and Methods
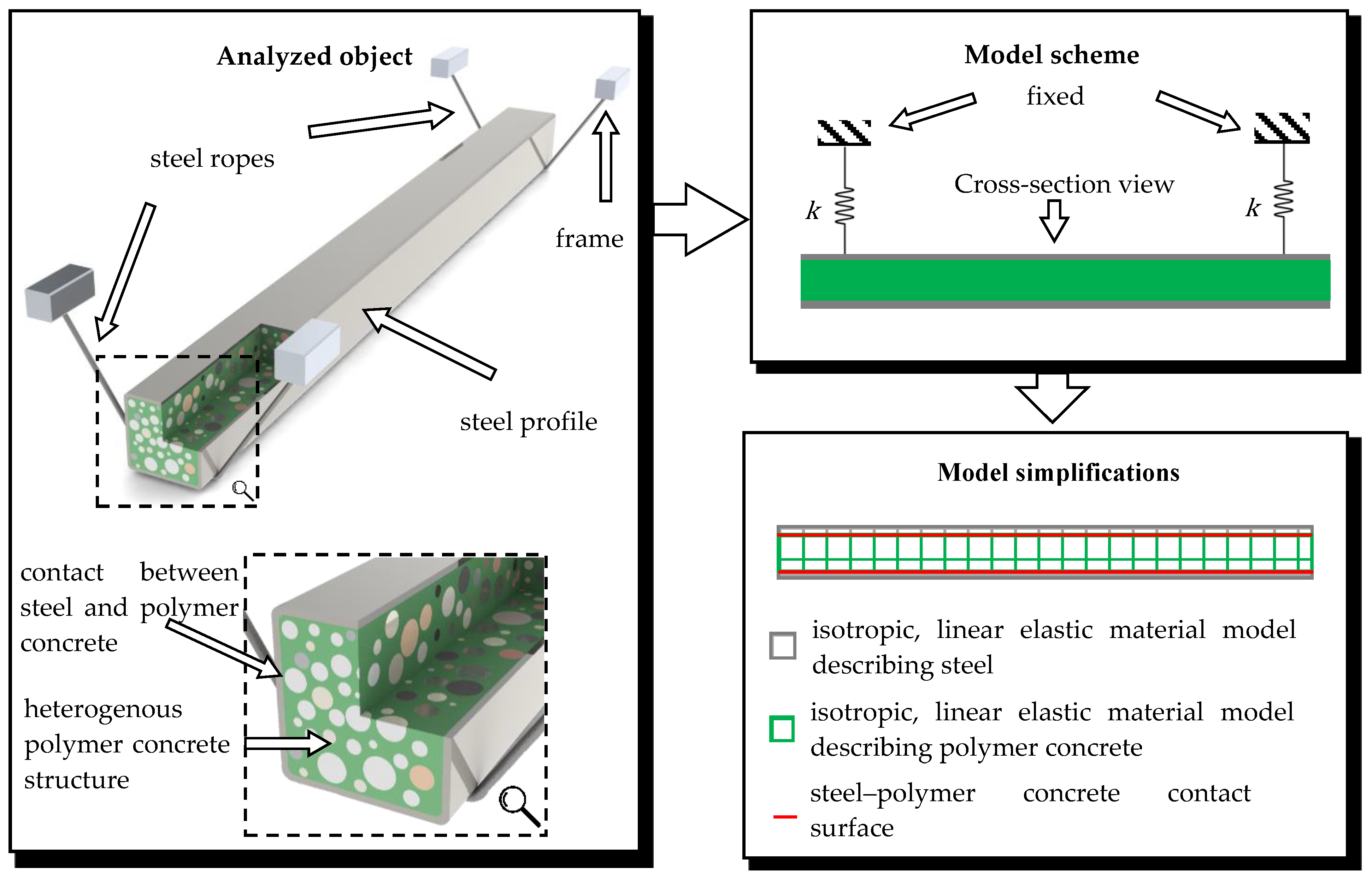
2.1. Steel–Polymer Concrete Beam Concept
2.2. Static Tests
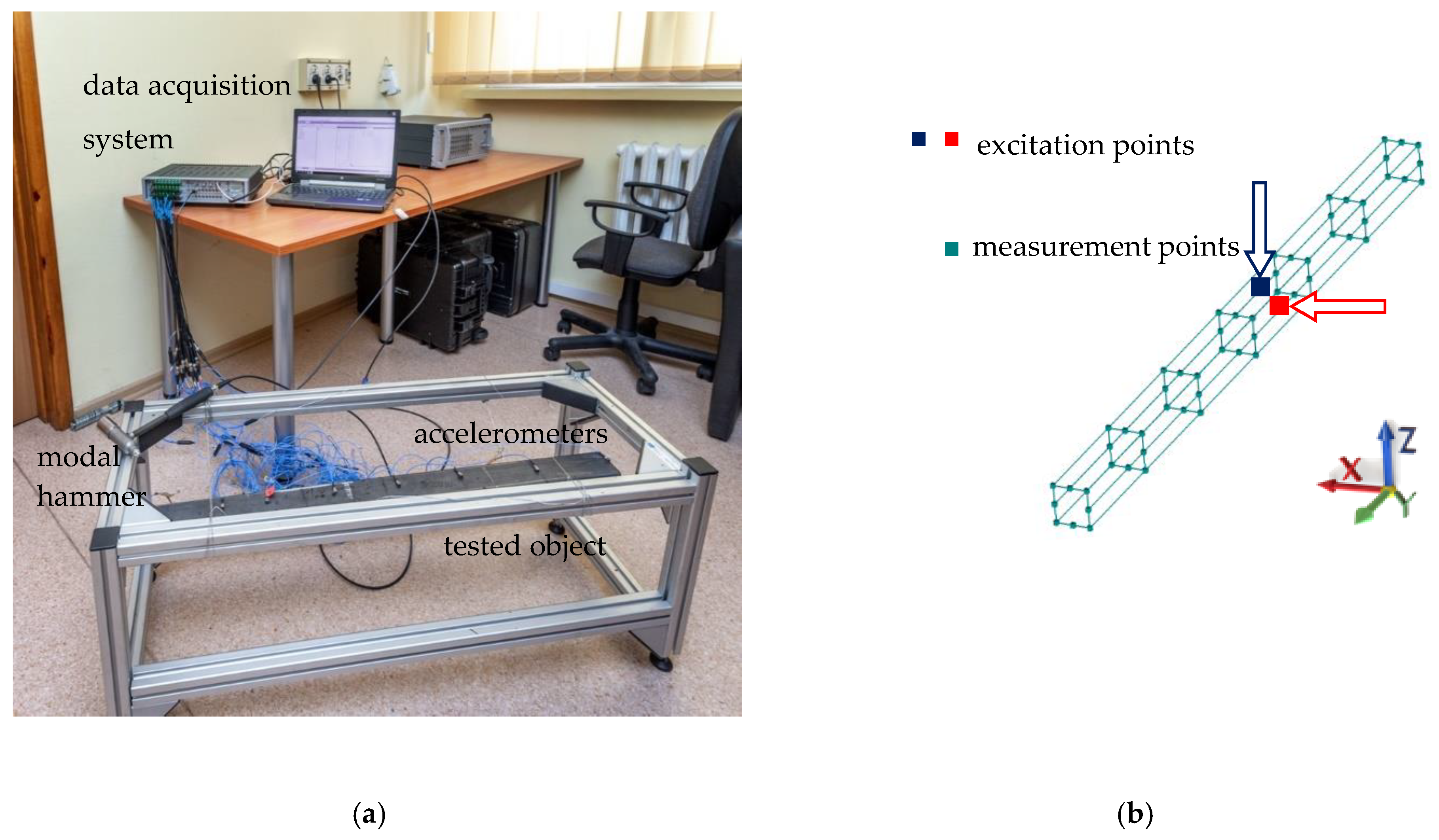
2.3. Dynamic Tests
2.4. Experimental Test Results
- The steel–polymer concrete beam fulfilled the basic assumptions of the modal analysis, which validates its use in the assessment of its dynamic properties;
- The steel–polymer concrete beam is characterized by the close identity between the complex and real mode shapes, which indicates the proportional damping of the beam;
- Despite the fact that the steel–polymer concrete beam was made of materials with significantly different properties, the experimental mode shapes were similar to those of a beam made of homogeneous material, which indicates a lack of mutual displacements between the steel profile and polymer concrete filling.
3. Modeling of the Steel–Polymer Concrete Beams
3.1. Model Assumptions
3.2. Finite Element Model of A Steel–Polymer Concrete Beam
3.3. Timoshenko Beam Model of a Steel–Polymer Concrete Beam
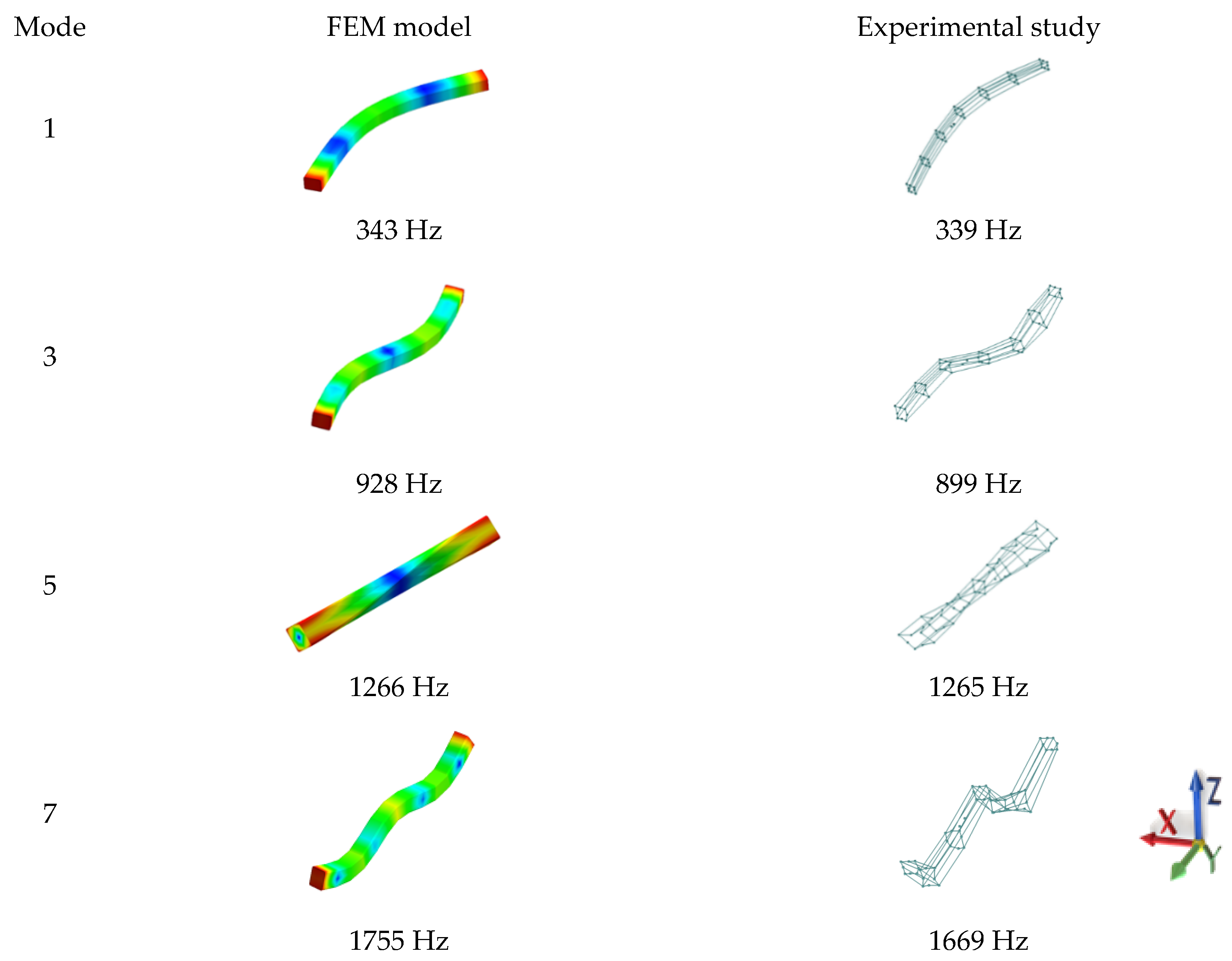
3.4. Results Comparison
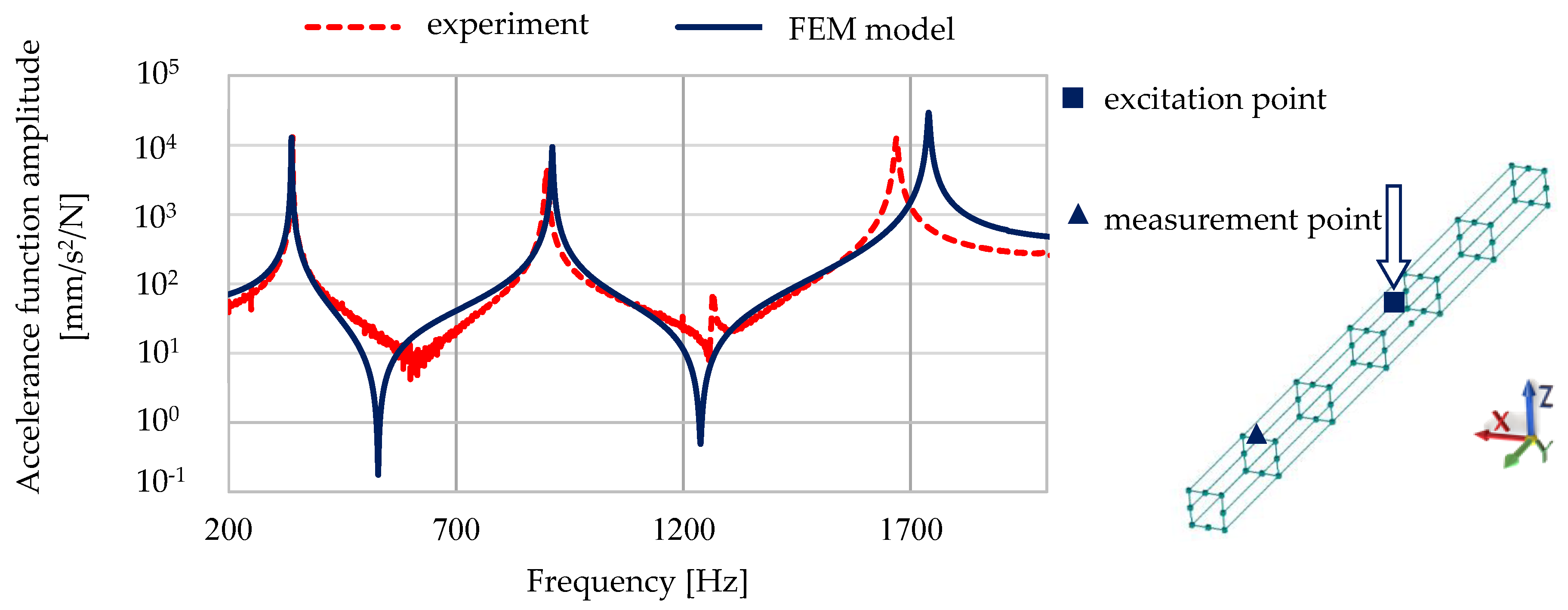
3.5. Model Validation
3.6. An Example of Using A Steel–Polymer Concrete Beam Model
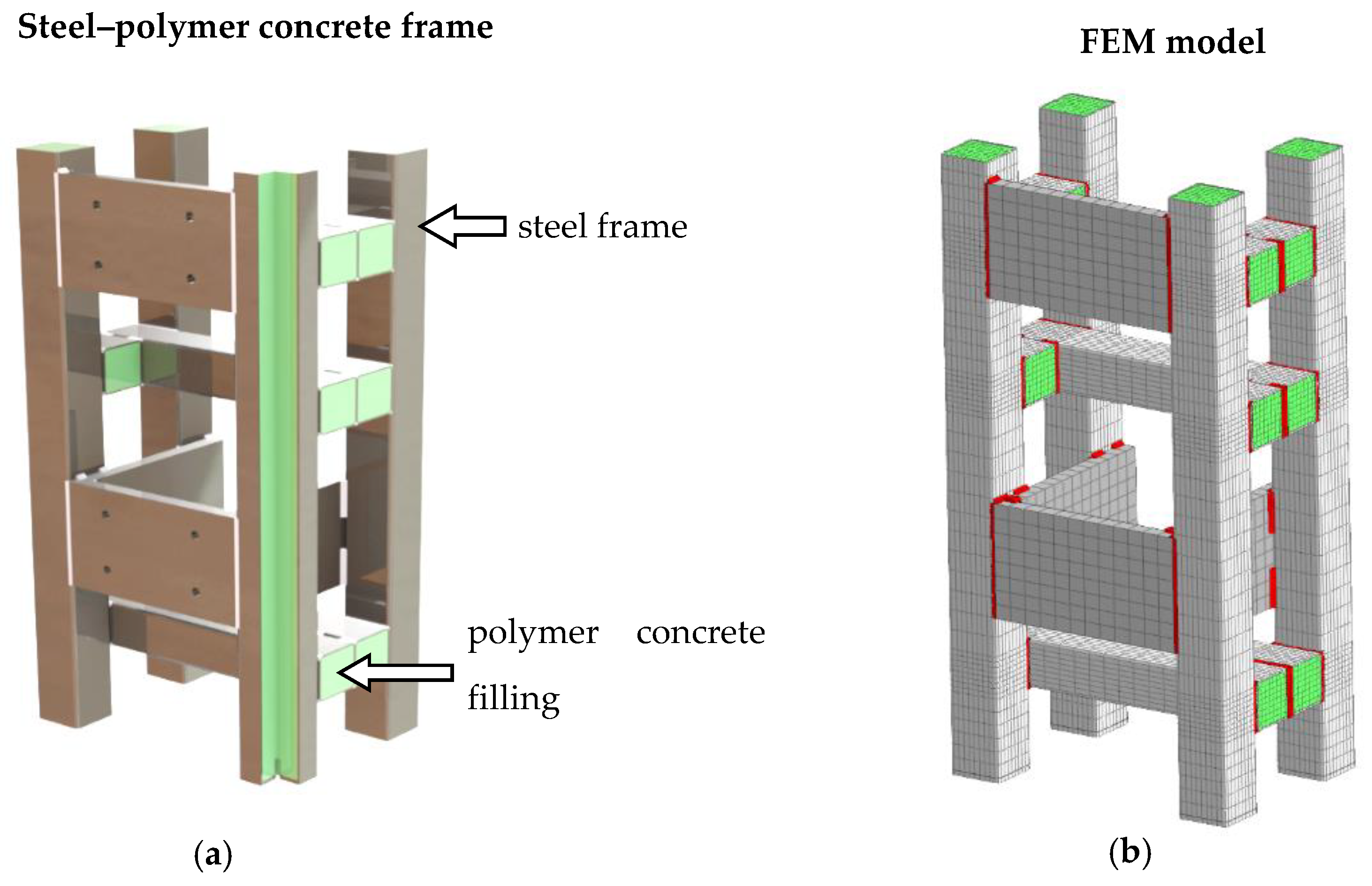
3.6.1. Finite Element Model of Steel–Polymer Concrete Frame
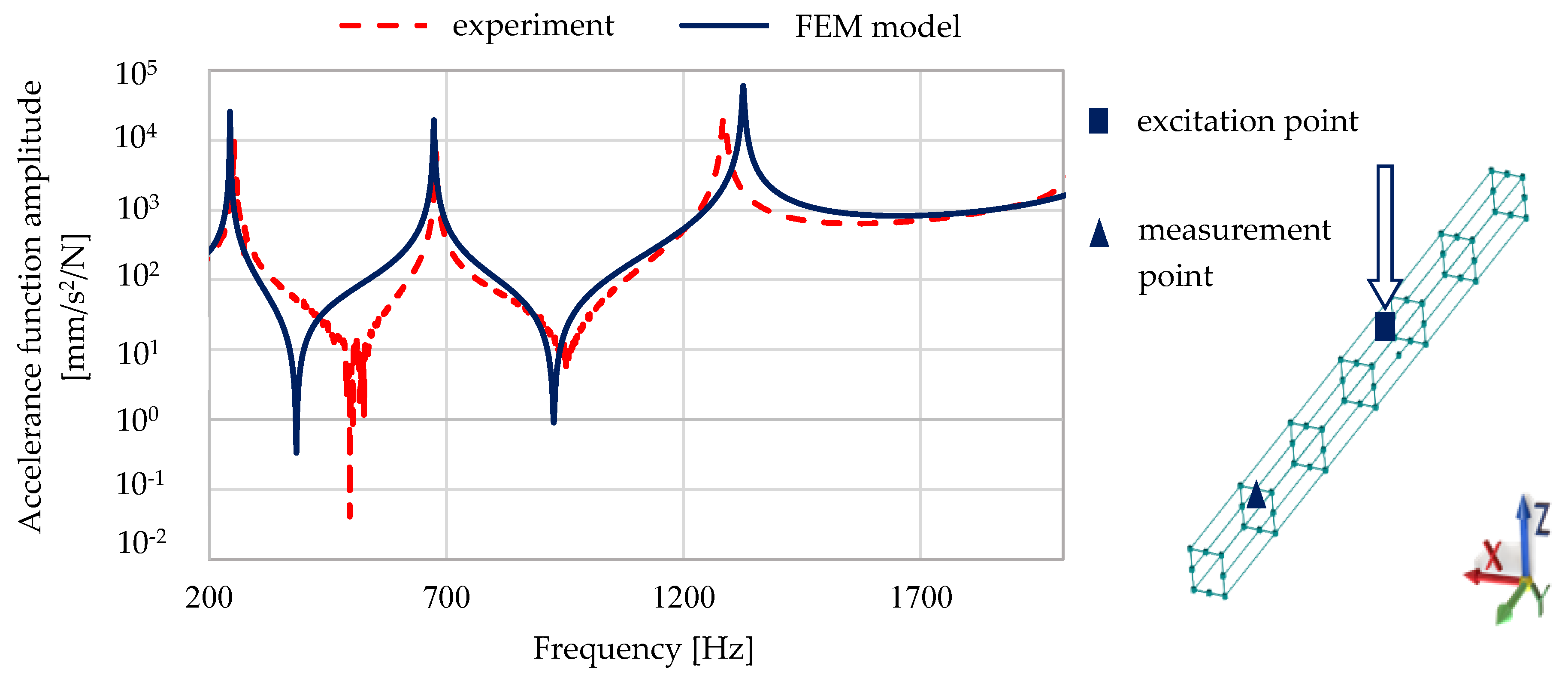
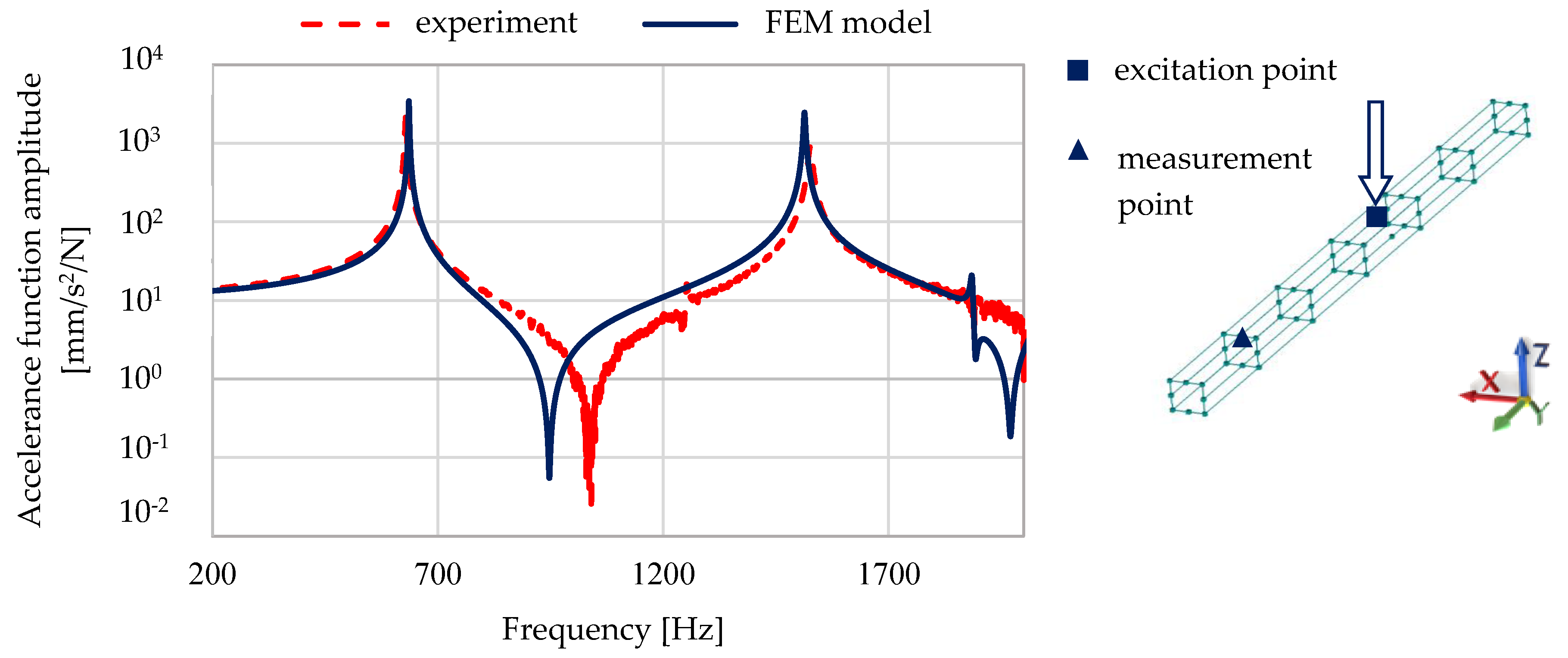
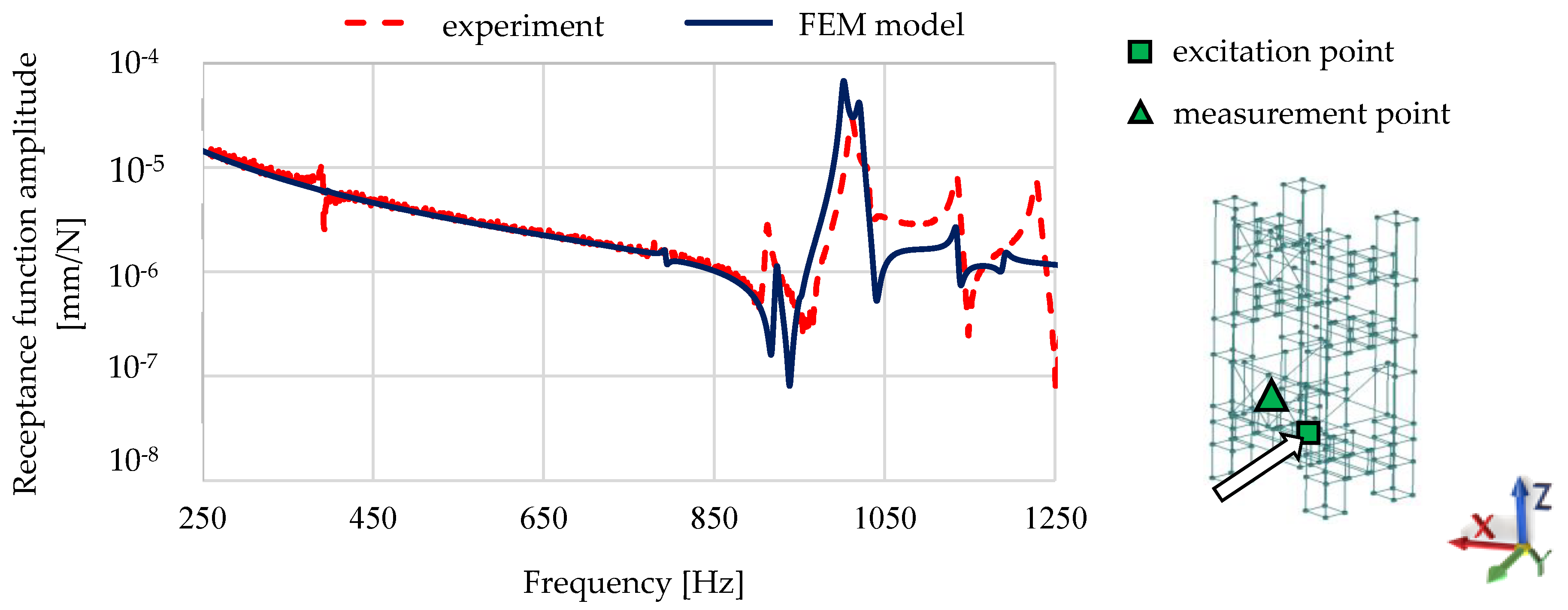
3.6.2. Experimental Verification of the Finite Element Model
4. Discussion
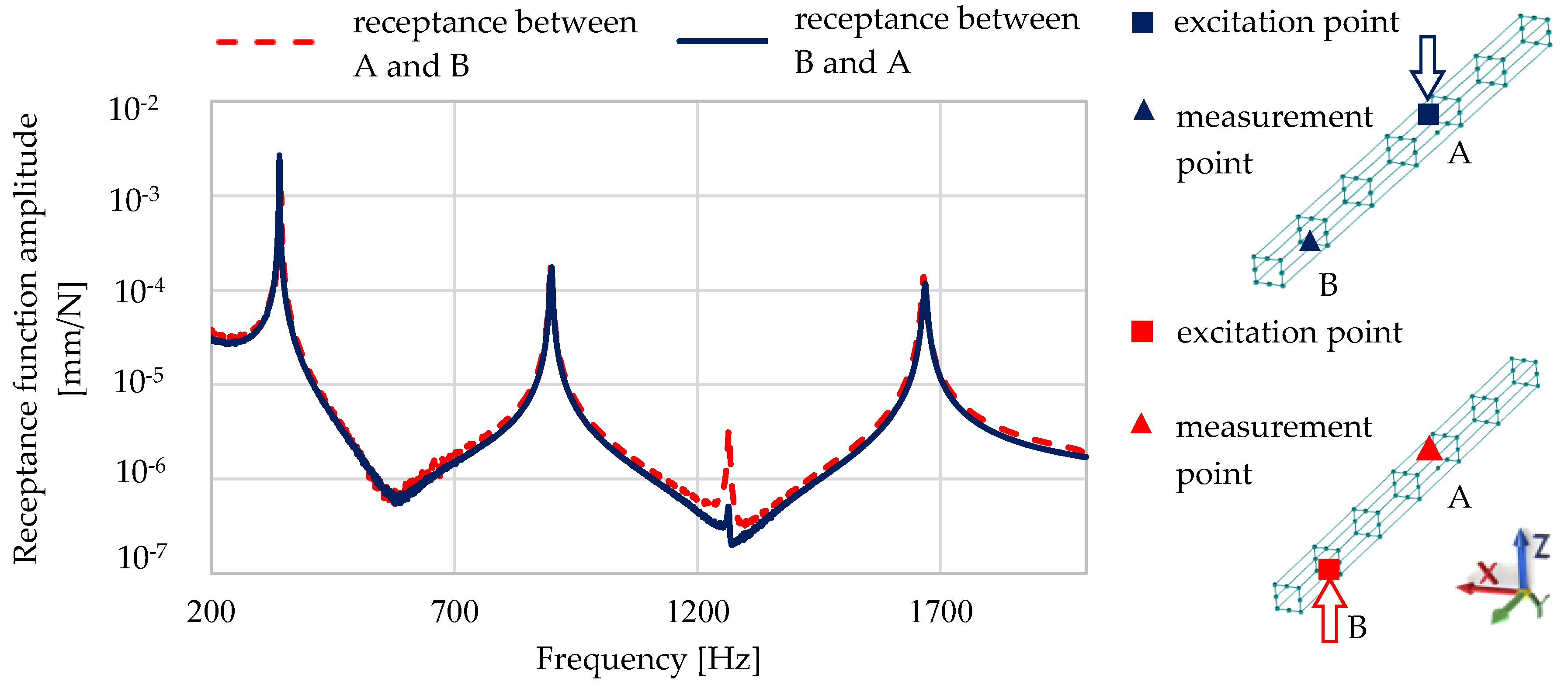
- The analysed beam meets the Maxwell’s Reciprocal Theorem, which indicates its linearity;
- The identity of the complex and real mode shapes were close, which indicates the proportional damping of the beam;
- The similar values of natural frequencies for forms 1 and 2, 3 and 4, and 6 and 7 may indicate the isotropicity of the polymer concrete;
- That, despite the highly heterogenous character of the polymer concrete used, the experimental mode shapes were similar to those of an isotropic homogenous beam, which may indicate the lack of mutual displacements between the steel profile and polymer concrete filling and that it can be modeled using a linear isotropic model of the material that is present in the composite structure.
- The derived Hamiltonian Equation (3) indicates that it is possible to build a reliable analytical model of a composite steel–polymer concrete beam using an homogeneous beam model with equivalent bending stiffness and equivalent mass per unit length of the beam ;
- The analytical model could accurately represent mode shapes and natural frequencies of the analyzed beams: 50 mm × 50 mm (relative error below 4%, mean 3.1%), 70 mm × 70 mm (relative error below 2%, mean 0.47%) and 140 mm × 140 mm (relative error below 0.9%, mean 0.6%).
- The proposed FEM model of a steel–polymer concrete beam ensured agreement of the mode shapes with the experimentally determined mode shapes;
- The agreement of the mode shapes for torsional and flexural vibrations show the correctness of adopting the linear elastic isotropic model for polymer concrete; it confirms conclusions (i), (iii) and (iv);
- The application of the structural damping model, expressed as a complex stiffness model, enables a good representation of the damping properties of steel–polymer concrete beams, which is shown in the high compliance of frequency response functions (FRFs) calculated and experimentally determined; this also confirms conclusion (ii);
- The developed procedure and the determined model parameters allow for the development of reliable models for steel–polymer concrete beams with sizes: 50 mm × 50 mm (relative error below 3%, mean 1.4%), 70 mm × 70 mm (relative error below 5%, mean 2.6%) and 140 mm × 140 mm (relative error below 3%, mean 2.6%) for natural frequencies;
- The developed FEM model is a good alternative to continuous models, showing only slightly larger discrepancies compared to the results of experimental tests.
- The presented results of tests and analyses indicate that the proposed methodology of modeling the dynamic properties of steel–polymer concrete beams facilitates obtaining the results of calculations with high reliability, both in terms of quality and quantity, also for complex structures.
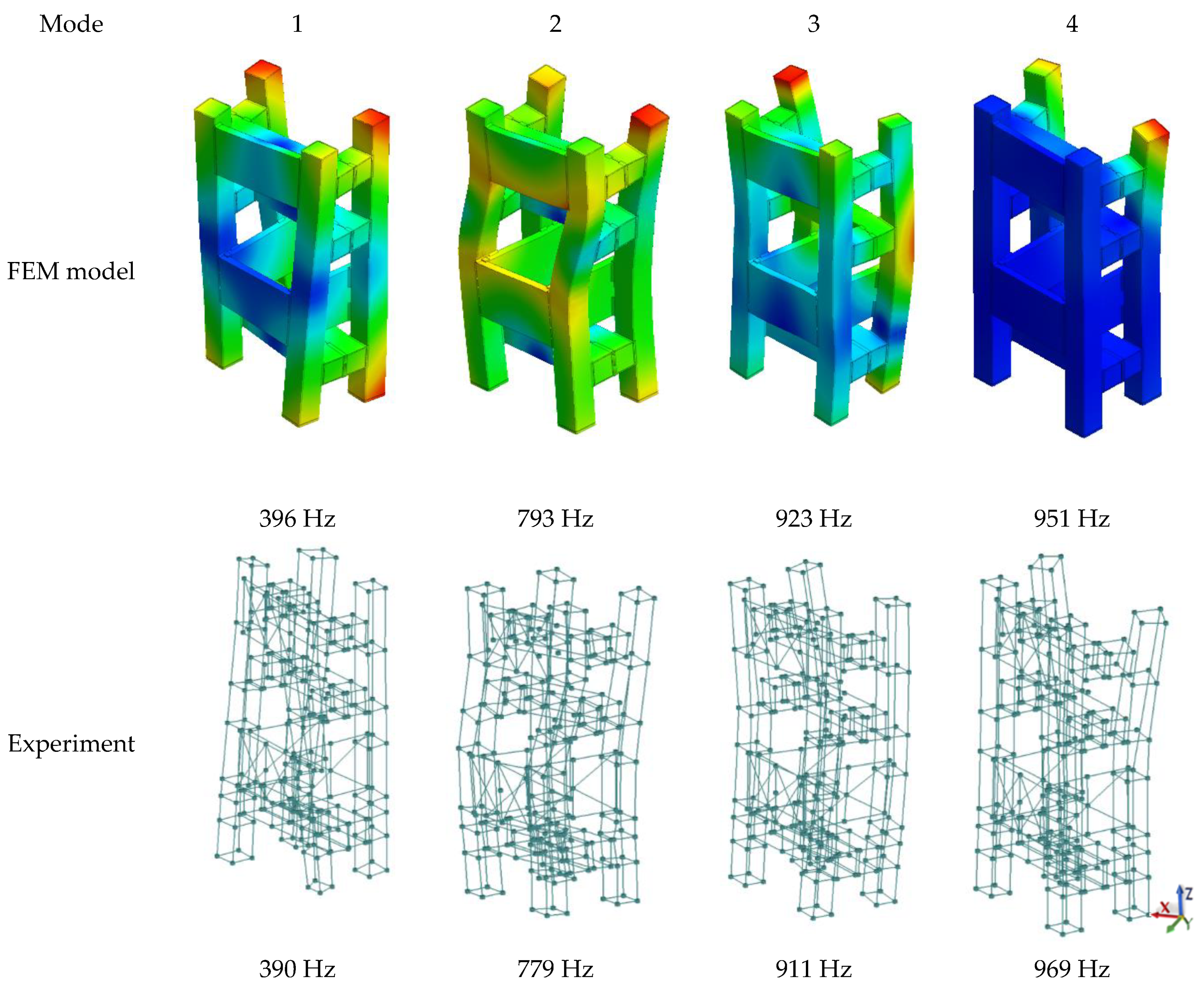
- Agreement of the mode shape was obtained for the model of a complex steel–polymer concrete structure;
- Relative errors obtained by comparing the calculated and experimentally determined values did not exceed 3%, on average they were 1.7%, which proves good quantitative agreement of the model with the real structure;
- The calculated frequency response functions obtained for the complex model of a structure consisting of steel–polymer concrete beams showed good agreement with experimental data, which showed that the model reliably reproduced the dynamic properties of the structure in the studied frequency range;
- A reliable description of the dynamic properties of a complex steel–polymer concrete structure was obtained without additional (global) model updating.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Used Symbols
| Cross-section area () | |
| Young’s modulus (Pa) | |
| Shear modulus (Pa) | |
| Outer height of the beam cross-section | |
| Inner height of the beam cross-section | |
| Area moment of inertia () | |
| Polar moment of inertia () | |
| Material: steel (1), polymer concrete (2) | |
| Imaginary unit | |
| Shear correction factor | |
| Torsional parameter () | |
| Length of a beam | |
| Transverse deflection () | |
| Mass density |
References
- Pokhrel, M.; Bandelt, M.J. Material properties and structural characteristics influencing deformation capacity and plasticity in reinforced ductile cement-based composite structural components. Compos. Struct. 2019, 224, 111013. [Google Scholar] [CrossRef]
- Katwal, U.; Tao, Z.; Hassan, M.K. Finite element modelling of steel-concrete composite beams with profiled steel sheeting. J. Constr. Steel Res. 2018, 146, 1–15. [Google Scholar] [CrossRef]
- Idris, Y.; Ozbakkaloglu, T. Behavior of square fiber reinforced polymer–high-strength concrete–steel double-skin tubular columns under combined axial compression and reversed-cyclic lateral loading. Eng. Struct. 2016, 118, 307–319. [Google Scholar] [CrossRef]
- Henriques, D.; Gonçalves, R.; Camotim, D. A visco-elastic GBT-based finite element for steel-concrete composite beams. Thin Walled Struct. 2019, 145, 106440. [Google Scholar] [CrossRef]
- Di, J.; Cao, L.; Han, J. Experimental Study on the Shear Behavior of GFRP–Concrete Composite Beam Connections. Materials 2020, 13, 1067. [Google Scholar] [CrossRef] [PubMed]
- Śledziewski, K.; Górecki, M. Finite Element Analysis of the Stability of a Sinusoidal Web in Steel and Composite Steel-Concrete Girders. Materials 2020, 13, 1041. [Google Scholar] [CrossRef]
- Górecki, M.; Śledziewski, K. Experimental Investigation of Impact Concrete Slab on the Bending Behavior of Composite Bridge Girders with Sinusoidal Steel Web. Materials 2020, 13, 273. [Google Scholar] [CrossRef]
- Lyu, X.; Xu, Y.; Xu, Q.; Yu, Y. Axial compression performance of square thin walled concrete-Filled steel tube stub columns with reinforcement stiffener under constant high-Temperature. Materials 2019, 12, 1098. [Google Scholar] [CrossRef]
- Li, R.; Yu, Y.; Samali, B.; Li, C. Parametric analysis on the circular CFST column and RBS steel beam joints. Materials 2019, 12, 1535. [Google Scholar] [CrossRef]
- Berczyński, S.; Wróblewski, T. Vibration of steel–concrete composite beams using the Timoshenko beam model. J. Vib. Control 2005, 11, 829–848. [Google Scholar] [CrossRef]
- Dilena, M.; Morassi, A. Vibrations of steel–concrete composite beams with partially degraded connection and applications to damage detection. J. Sound Vib. 2009, 320, 101–124. [Google Scholar] [CrossRef]
- Nijgh, M.P.; Veljkovic, M. A static and free vibration analysis method for non-prismatic composite beams with a non-uniform flexible shear connection. Int. J. Mech. Sci. 2019, 159, 398–405. [Google Scholar] [CrossRef]
- Liu, Q.; Thompson, D.J.; Xu, P.; Feng, Q.; Li, X. Investigation of train-induced vibration and noise from a steel-concrete composite railway bridge using a hybrid finite element-statistical energy analysis method. J. Sound Vib. 2020, 471, 115197. [Google Scholar] [CrossRef]
- Sonawane, H.; Subramanian, T. Improved Dynamic Characteristics for Machine Tools Structure Using Filler Materials. Procedia CIRP 2017, 58, 399–404. [Google Scholar] [CrossRef]
- Dunaj, P.; Okulik, T.; Powałka, B.; Berczyński, S.; Chodźko, M. Experimental Investigations of Steel Welded Machine Tool Bodies Filled with Composite Material. In Proceedings of the International Scientific-Technical Conference Manufacturing, Poznan, Poland, 19–22 May 2019; Lecture Notes in Mechanical Engineering. Springer: Cham, Switzerland, 2019; pp. 61–69. [Google Scholar]
- Powałka, B.; Dolata, M. Development of a computational model of a lightweight vertical lathe with the use of superelements. Arch. Mech. Technol. Mater. 2019, 39, 1–6. [Google Scholar] [CrossRef]
- Dunaj, P.; Chodźko, M.; Okulik, T.; Berczyński, S.; Powałka, B. Assessment of the time-varying load influence on damping abilities of steel beams filled with composite material. In Mechanisms and Machine Science, Proceedings of the Advances in Mechanism and Machine Science, Krakow, Poland, 15–18 July 2019; Springer: Cham, Switzerland, 2019; pp. 3309–3317. [Google Scholar]
- Okulik, T.; Dunaj, P.; Chodźko, M.; Marchelek, K.; Powałka, B. Determination of Dynamic Properties of a Steel Hollow Section Filled with Composite Mineral Casting. In Proceedings of the International Scientific-Technical Conference Manufacturing, Poznan, Poland, 19–22 May 2019; Lecture Notes in Mechanical Engineering. Springer: Cham, Switzerland, 2019; pp. 561–571. [Google Scholar]
- Dunaj, P.; Berczyński, S.; Chodźko, M. Method of modeling steel-polymer concrete frames for machine tools. Compos. Struct. 2020, 242, 112197. [Google Scholar] [CrossRef]
- Peeters, B.; Van der Auweraer, H.; Guillaume, P.; Leuridan, J. The PolyMAX frequency-domain method: A new standard for modal parameter estimation? Shock Vib. 2004, 11, 395–409. [Google Scholar] [CrossRef]
- Peeters, B.; Van der Auweraer, H. PolyMAX: A revolution in operational modal analysis. In Proceedings of the 1st International Operational Modal Analysis Conference, Copenhagen, Denmark, 26–27 April 2005; pp. 26–27. [Google Scholar]
- Allemang, R.J. The modal assurance criterion–twenty years of use and abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Allemang, R.J.; Brown, D.L. A correlation coefficient for modal vector analysis. In Proceedings of the 1st International Modal Analysis Conference &Exhibit, Orlando, FL, USA, 8–10 November 1982; Volume 1, pp. 110–116. [Google Scholar]
- Chodźko, M. The search for weak elements affecting the vibrostability of the system consisting of the machine tool and the cutting process, based on symptoms observed during operation. Probl. Eksploat. 2015, 1, 5–23. [Google Scholar]
- Chodźko, M.; Marchelek, K. Doświadczalne badania właściwości dynamicznych układów korpusowych obrabiarek. Wybrane zagadnienia. Inż. Masz. 2011, 16, 67–81. [Google Scholar]
- Chowdhury, I.; Dasgupta, S.P. Computation of Rayleigh damping coefficients for large systems. Electron. J. Geotech. Eng. 2003, 8, 1–11. [Google Scholar]
- Liu, M.; Gorman, D.G. Formulation of Rayleigh damping and its extensions. Comput. Struct. 1995, 57, 277–285. [Google Scholar] [CrossRef]
- Holanda, S.A.; Silva, A.A.; de Araújo, C.J.; de Aquino, A.S. Study of the complex stiffness of a vibratory mechanical system with shape memory alloy coil spring actuator. Shock Vib. 2014, 2014, 162781. [Google Scholar] [CrossRef]
- Neumark, S. Concept of Complex Stiffness Applied to Problems of Oscillations with Viscous and Hysteretic Damping; HM Stationery Office: London, UK, 1962.
- Dunaj, P.; Powałka, B.; Okulik, T.; Berczyński, S.; Chodźko, M. Modelling steel beams filled with a composite material. J. Mach. Constr. Maint. Probl. Eksploat. 2018, 100, 71–78. [Google Scholar]
- Dai, X.H.; Lam, D.; Jamaluddin, N.; Ye, J. Numerical analysis of slender elliptical concrete filled columns under axial compression. Thin Walled Struct. 2014, 77, 26–35. [Google Scholar] [CrossRef]
- Duarte, A.P.C.; Silva, B.A.; Silvestre, N.; De Brito, J.; Júlio, E.; Castro, J.M. Finite element modelling of short steel tubes filled with rubberized concrete. Compos. Struct. 2016, 150, 28–40. [Google Scholar] [CrossRef]
- Hu, H.-T.; Huang, C.-S.; Chen, Z.-L. Finite element analysis of CFT columns subjected to an axial compressive force and bending moment in combination. J. Constr. Steel Res. 2005, 61, 1692–1712. [Google Scholar] [CrossRef]
- Li, S.; Han, L.-H.; Hou, C. Concrete-encased CFST columns under combined compression and torsion: Analytical behaviour. J. Constr. Steel Res. 2018, 144, 236–252. [Google Scholar] [CrossRef]
- Ren, Q.-X.; Han, L.-H.; Hou, C.; Tao, Z.; Li, S. Concrete-encased CFST columns under combined compression and torsion: Experimental investigation. J. Constr. Steel Res. 2017, 138, 729–741. [Google Scholar] [CrossRef]
- Alatshan, F.; Osman, S.A.; Mashiri, F.; Hamid, R. Explicit Simulation of Circular CFST Stub Columns with External Steel Confinement under Axial Compression. Materials 2020, 13, 23. [Google Scholar] [CrossRef]
- Xie, F.; Chen, J.; Yu, Q.-Q.; Dong, X. Behavior of Cross Arms Inserted in Concrete-Filled Circular GFRP Tubular Columns. Materials 2019, 12, 2280. [Google Scholar] [CrossRef] [PubMed]
- Szopa, L. Współpraca Betonu i Stali na Różnych Poziomach Obciążenia w Osiowo Ściskanych Elementach Zespolonych Stalowo-Betonowych; Politechnika Krakowska: Kraków, Poland, 2007. [Google Scholar]
- Midas, I.T. User’s Manual of Midas NFX; MIDAS IT: Seongnam, Korea, 2011. [Google Scholar]
- Haddad, H.; Al Kobaisi, M. Optimization of the polymer concrete used for manufacturing bases for precision tool machines. Compos. Part B Eng. 2012, 43, 3061–3068. [Google Scholar] [CrossRef]


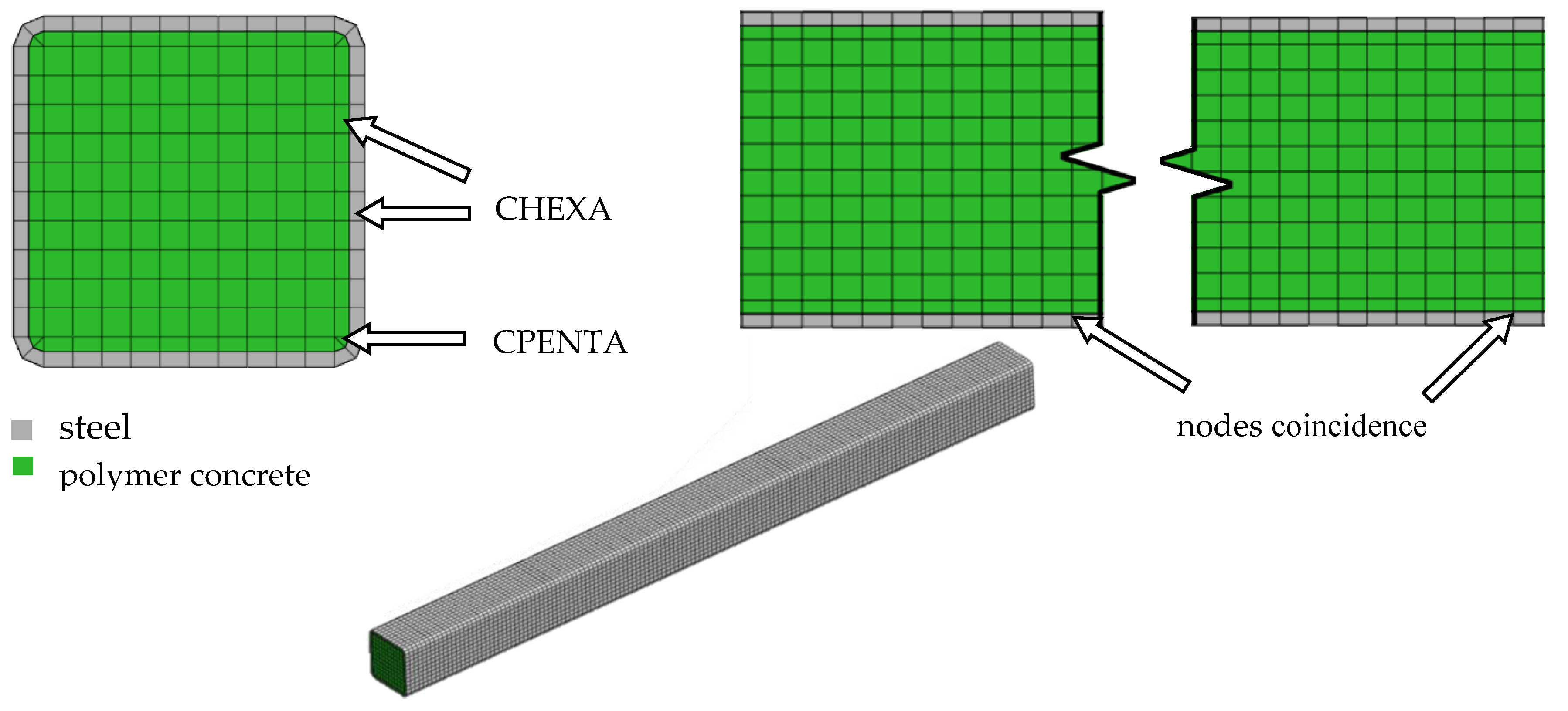
| Component | Epoxy Resin | Ash | Fine Fraction (0.25–2 mm) | Medium Fraction (2–10 mm) | Coarse Fraction (8–16 mm) |
|---|---|---|---|---|---|
| Mass percentage | 15% | 1% | 19% | 15% | 50% |
| Parameter | Value |
|---|---|
| Sampling rate | 4096 Hz |
| Frequency resolution | 0.5 Hz |
| Signal acquisition time | 2 s |
| Frequency response function estimator | H1 |
| Number of averages | 10 |
| Scaling of the frequency response function | global |
| Property | Steel | Polymer Concrete |
|---|---|---|
| Modulus of elasticity | 210 ± 5 GPa | 17.2 ± 0.2 GPa |
| Poisson’s ratio | 0.28 ± 0.03 | 0.20 ± 0.05 |
| Density | 7812 ± 35 kg/m3 | 2200 ± 6 kg/m3 |
| Loss factor | 0.00220 ± 0.00005 | |
| Equivalent loss factor | 0.00480 ± 0.00024 | |
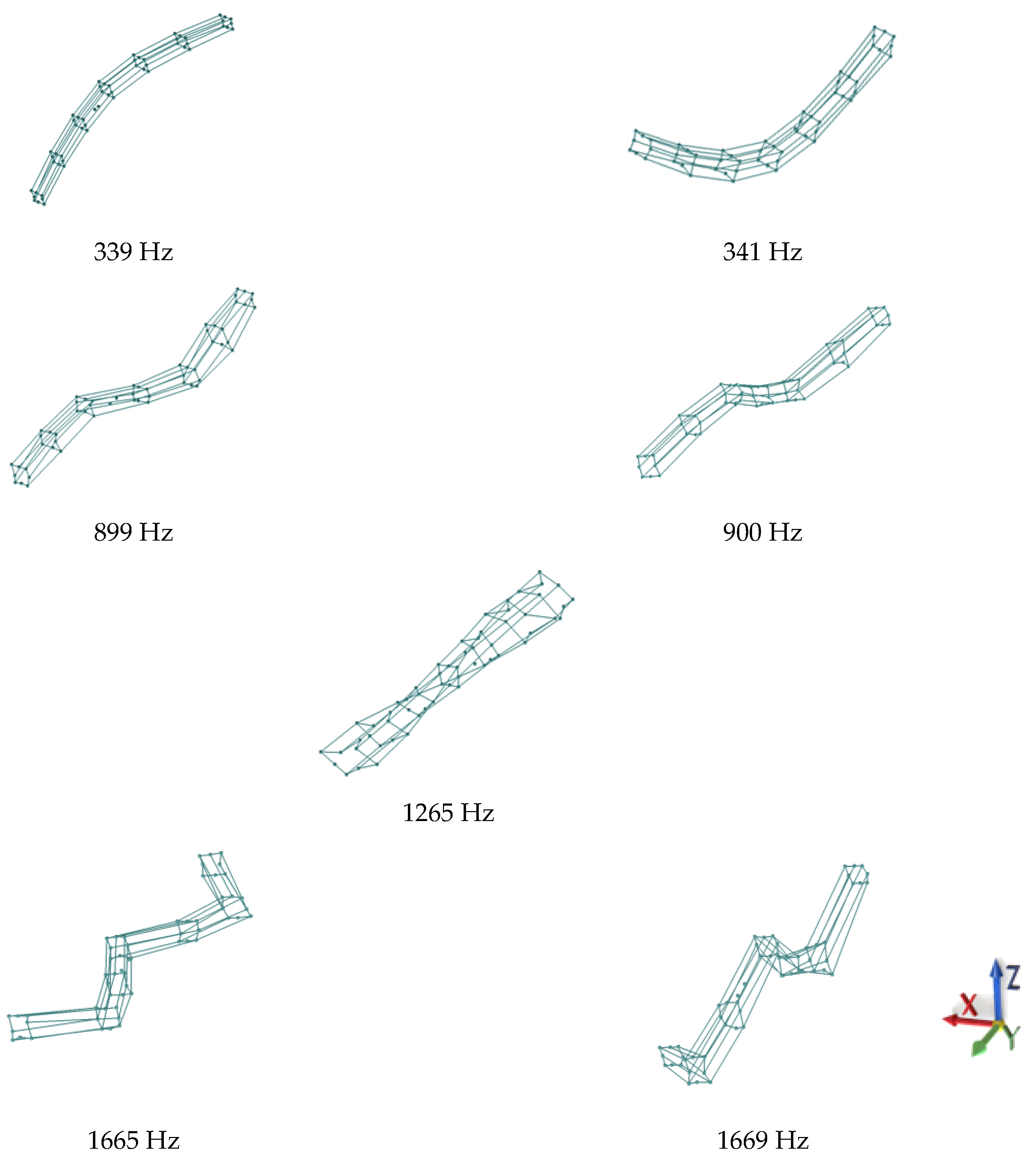
| Mode Shape | Natural Frequency | Modal Damping |
|---|---|---|
| 1. | 339 Hz | 0.16% |
| 2. | 341 Hz | 0.25% |
| 3. | 899 Hz | 0.16% |
| 4. | 900 Hz | 0.13% |
| 5. | 1265 Hz | 0.17% |
| 6. | 1665 Hz | 0.16% |
| 7. | 1669 Hz | 0.17% |
| Model | Experiment | FEM Model | Relative Error δFEM | Continuous Model | Relative Error δC |
|---|---|---|---|---|---|
| 1. | 339 Hz | 343 Hz | ~1.2% | 338 Hz | <0.3% |
| 2. | 341 Hz | 343 Hz | <0.6% | 338 Hz | <0.9% |
| 3. | 899 Hz | 928 Hz | ~3.2% | 899 Hz | ~0% |
| 4. | 900 Hz | 928 Hz | ~3.1% | 899 Hz | <0.1% |
| 5. | 1265 Hz | 1266 Hz | ~0% | 1242 Hz | <2% |
| 6. | 1665 Hz | 1755 Hz | ~6.0% | 1665 Hz | ~0% |
| 7. | 1669 Hz | 1755 Hz | ~5.2% | 1665 Hz | ~0% |
| Mode Shape | Experiment | FEM Model | Continuous Model | Relative Error δC | |
|---|---|---|---|---|---|
| 50 mm × 50 mm beam | |||||
| 1. | 247 Hz | 248 Hz | <0.1% | 241 Hz | ~2.4% |
| 2. | 251 Hz | 248 Hz | ~1.2% | 241 Hz | <4.0% |
| 3. | 676 Hz | 685 Hz | ~1.3% | 655 Hz | ~3.1% |
| 4. | 678 Hz | 685 Hz | ~1.0% | 655 Hz | ~3.4% |
| 5. | 1276 Hz | 1241 Hz | ~2.7% | 1243 Hz | ~2.6% |
| 140 mm × 140 mm beam | |||||
| 1. | 628 Hz | 648 Hz | ~3.2% | 630 Hz | ~0.3% |
| 2. | 629 Hz | 648 Hz | ~3.0% | 630 Hz | ~0.2% |
| 3. | 1252 Hz | 1265 Hz | ~1.0% | 1242 Hz | ~0.8% |
| 4. | 1526 Hz | 1567 Hz | <2.7% | 1539 Hz | ~0.9% |
| 5. | 1527 Hz | 1567 Hz | <2.6% | 1539 Hz | ~0.8% |
| Mode Shape | FEM Model | Experiment | |
|---|---|---|---|
| 1. | 396 Hz | 390 Hz | <2% |
| 2. | 793 Hz | 779 Hz | <2% |
| 3. | 923 Hz | 911 Hz | ~1% |
| 4. | 951 Hz | 969 Hz | <2% |
| 5. | 1002 Hz | 1012 Hz | <1% |
| 6. | 1021 Hz | 1031 Hz | <1% |
| 7. | 1135 Hz | 1135 Hz | <1% |
| 8. | 1190 Hz | 1228 Hz | ~3% |
| 9. | 1314 Hz | 1284 Hz | ~2% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunaj, P.; Berczyński, S.; Chodźko, M.; Niesterowicz, B. Finite Element Modeling of the Dynamic Properties of Composite Steel–Polymer Concrete Beams. Materials 2020, 13, 1630. https://doi.org/10.3390/ma13071630
Dunaj P, Berczyński S, Chodźko M, Niesterowicz B. Finite Element Modeling of the Dynamic Properties of Composite Steel–Polymer Concrete Beams. Materials. 2020; 13(7):1630. https://doi.org/10.3390/ma13071630
Chicago/Turabian StyleDunaj, Paweł, Stefan Berczyński, Marcin Chodźko, and Beata Niesterowicz. 2020. "Finite Element Modeling of the Dynamic Properties of Composite Steel–Polymer Concrete Beams" Materials 13, no. 7: 1630. https://doi.org/10.3390/ma13071630
APA StyleDunaj, P., Berczyński, S., Chodźko, M., & Niesterowicz, B. (2020). Finite Element Modeling of the Dynamic Properties of Composite Steel–Polymer Concrete Beams. Materials, 13(7), 1630. https://doi.org/10.3390/ma13071630






