A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites
Abstract
1. Introduction
2. Assumptions for Modeling the Graphene Structure
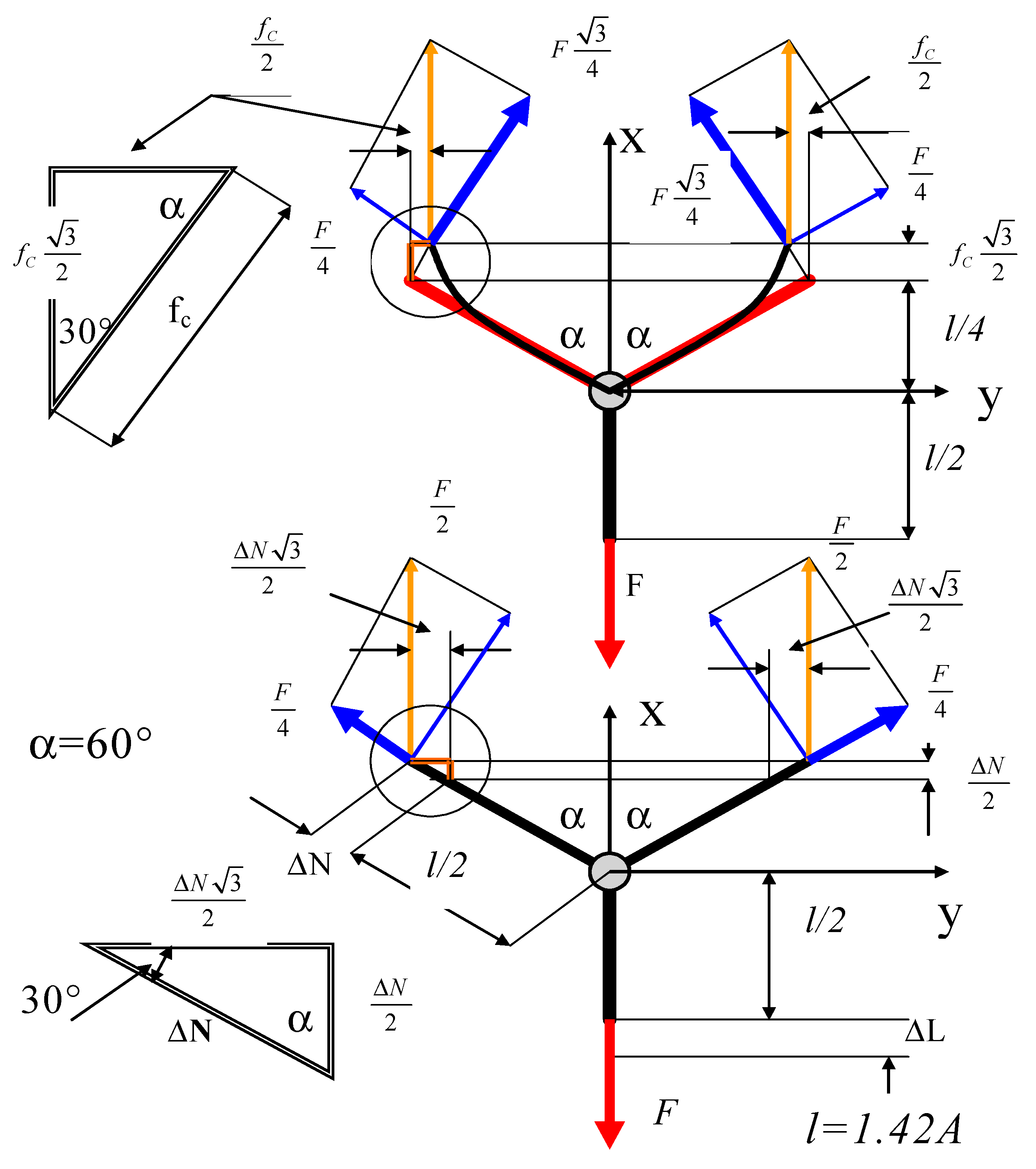
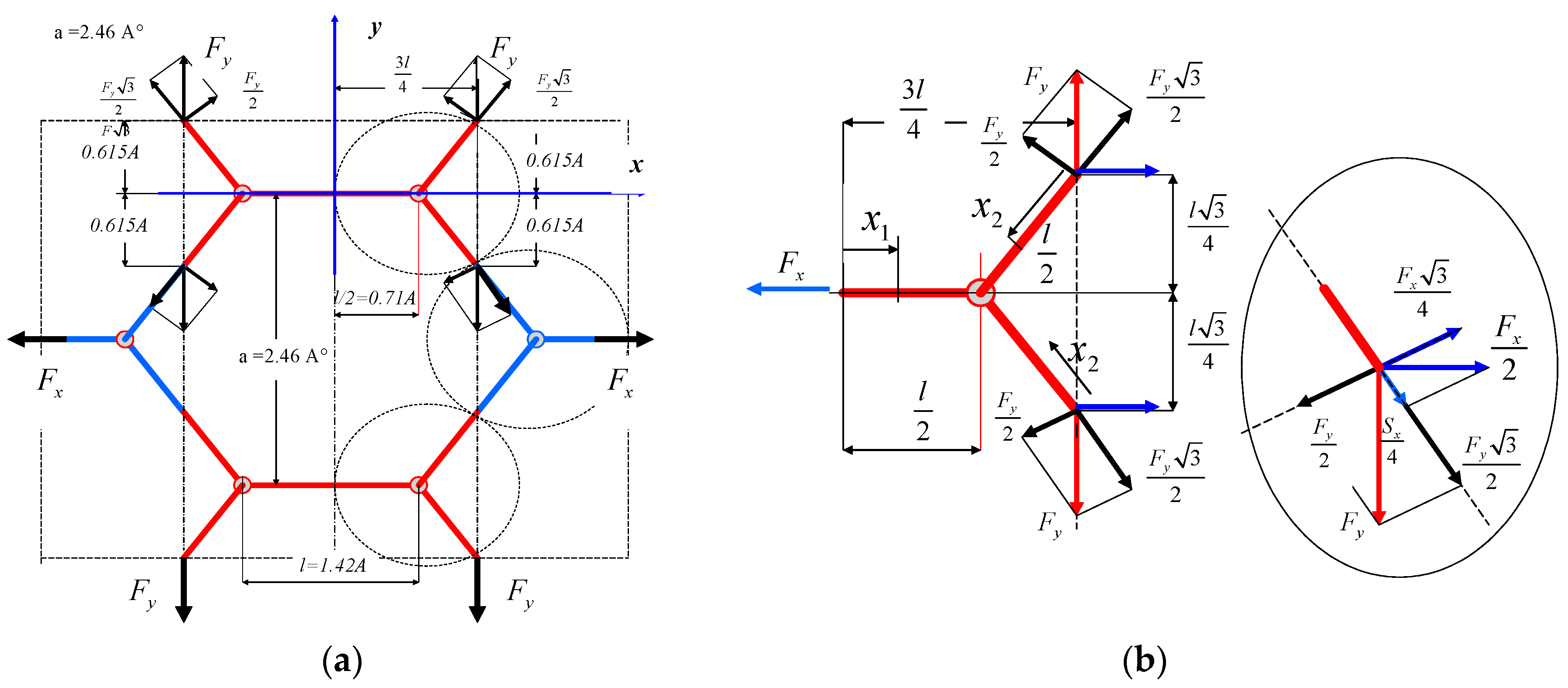
3. Basic Model of Graphene Cell (Calculations of Strains)
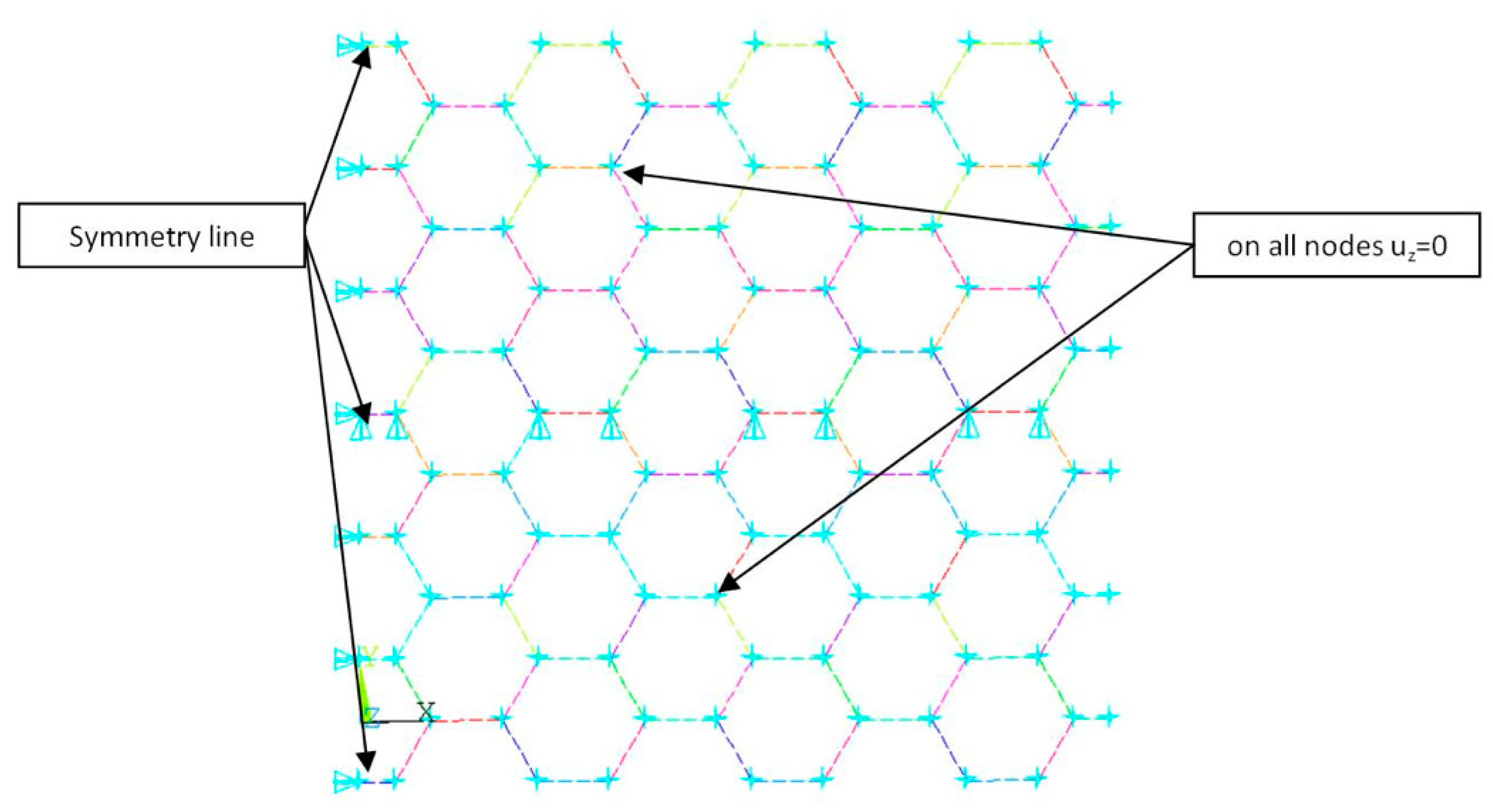
4. Numerical Model of Graphene Band
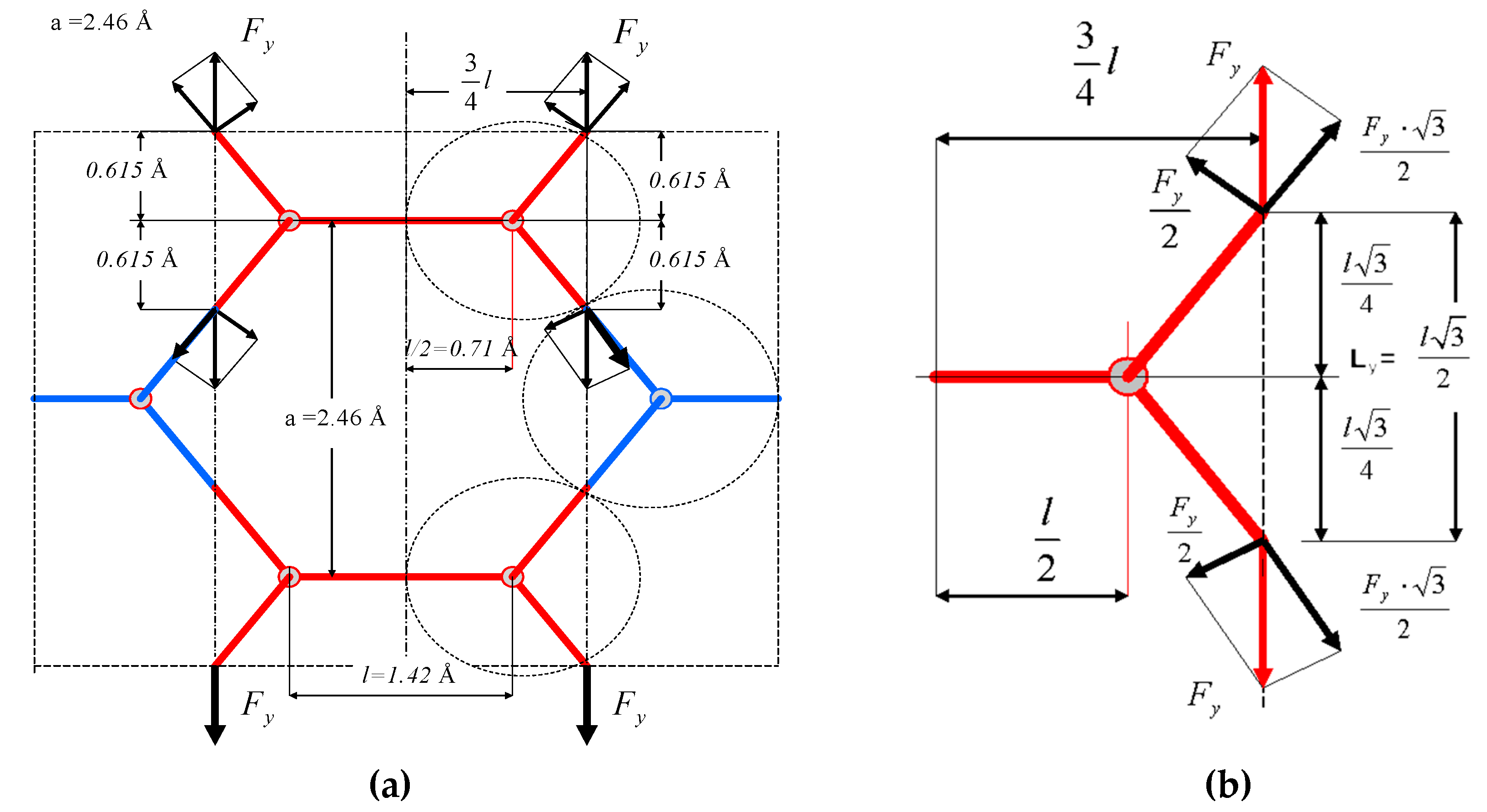
5. The Strain in y-Direction
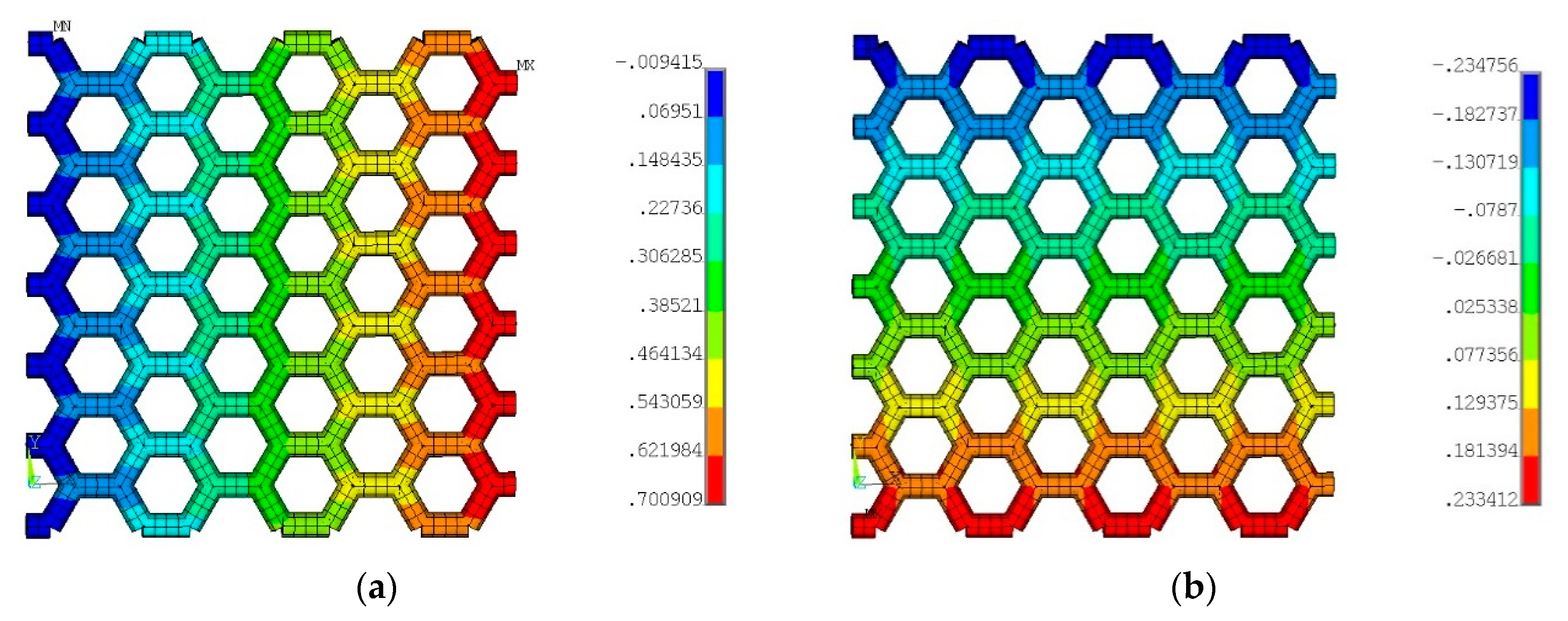
6. Results
7. Strains in Both Directions
8. Summary
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Dimension between atoms bond | |
| Length of graphene bar | |
| Diameter of graphene bar | |
| Thickness of single graphene sheet for one layer | |
| Length of segment | |
| Tension force for armchair edge (x-direction) | |
| Tension force for zigzag edge (y-direction) | |
| Angle between graphene bar | |
| Increment of elongation of segment caused by tension | |
| Increment of elongation of bar | |
| Total elongation caused by bending | |
| Young’s modulus of segment of graphene sheet | |
| Young’s modulus of graphene bar | |
| Moment of inertia of graphene bar | |
| Cross-section area | |
| Total increment of elongation due to bending and tension | |
| Length of graphene segment | |
| Poisson’s ratio for graphene bar | |
| Poisson’s ratio for graphene cut-out for x-direction | |
| Poisson’s ratio for graphene cut-out for y-direction | |
| Strain of segment in x-direction caused by tension and bending in x-direction | |
| Strain of segment in y-direction caused by tension and bending in x-direction | |
| Strain in x-direction of alternative segment in x-direction | |
| Strain of segment in y-direction caused by tension and bending in y-direction | |
| Strain of segment in x-direction caused by tension and bending in y-direction | |
| Strain in y-direction of alternative segment in y-direction | |
| νxy | Poisson’s ratio of graphene calculated for two perpendicular forces |
| kxy | Ratio of forces |
References
- Zhou, B.L.; Zhou, B.H.; Chen, X.W.; Zhou, G.H.; Zhou, G. Electronic transport for impurity-doped armchair-edge graphene nanoribbons. Eur. Phys. J. B 2012, 85, 85–121. [Google Scholar] [CrossRef]
- Shin, S.; Kim, J.; Kim, J.H.; Kim, S.I. Enhanced performance of organic light-emitting diodes by using hybrid anodes composed of graphene and conducting polimer. Curr. Appl. Phys. 2013, 13, 144–147. [Google Scholar] [CrossRef]
- Atabaki, M.M.; Kovacevic, R. Graphene composites as anode materials in lithium-ion batteries. Electron. Mater. Lett. 2013, 9, 133–153. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Yan, X.; Chen, Y.; Tian, J. Nonlinear optical properties of graphene-based materials. Chin. Sci. Bull. 2012, 57, 2971–2982. [Google Scholar] [CrossRef]
- Yamuna, R.; Ramakrishnan, S.; Dhara, K.; Devi, R.; Kothurkar, N.K.; Kirubha, E.; Palanisamy, P.K. Synthesis, characterization, and nonlinear optical properties of graphene oxide functionalized with tetra-amino porphyrin. J. Nanopart. Res. 2013, 15, 1399. [Google Scholar] [CrossRef]
- Yang, Y.E.; Yang, Y.R.; Yan, X.H. Universal optical properties of graphene nanoribbons: A first-principles study. Phys. E Low Dimens. Syst. Nano Struct. 2012, 44, 1406–1409. [Google Scholar] [CrossRef]
- Gao, Y.; Hao, P. Mechanical properties of monolayer graphene under tensile and compressive loading. Phys. E Low Dimens. Syst. Nanostruct. 2009, 41, 1561–1566. [Google Scholar] [CrossRef]
- Ferralis, N. Probing mechanical properties of graphene with Raman spectroscopy. J. Mater. Sci. 2010, 45, 5135–5149. [Google Scholar] [CrossRef]
- Xiao, J.R.; Staniszewski, J.; Gillespie, J.W., Jr. Tensile behaviors of graphene sheets and carbon nanotubes with multiple Stone–Wales defects. Mater. Sci. Eng. A 2010, 527, 715–723. [Google Scholar] [CrossRef]
- Park, H.J.; Meyer, J.; Roth, S.; Skákalová, V. Growth and properties of few-layer graphene prepared by chemical vapor deposition. Carbon 2010, 48, 1088–1094. [Google Scholar] [CrossRef]
- Georgantzinos, S.; Giannopoulos, G.; Anifantis, N.; Georgantzinos, S. Numerical investigation of elastic mechanical properties of graphene structures. Mater. Des. 2010, 31, 4646–4654. [Google Scholar] [CrossRef]
- Ni, Z.; Bu, H.; Zou, M.; Yi, H.; Bi, K.; Chen, Y. Anisotropic mechanical properties of graphene sheets from molecular dynamics. Phys. B Condens. Matter 2010, 405, 1301–1306. [Google Scholar] [CrossRef]
- Soldano, C.; Mahmood, A.; Dujardin, E. Production, properties and potential of graphene. Carbon 2010, 48, 2127–2150. [Google Scholar] [CrossRef]
- Kula, P.; Szymanski, W.; Kolodziejczyk, L.; Atraszkiewicz, R.; Grabarczyk, J.; Clapa, M.; Kaczmarek, L.; Jedrzejczak, A.; Niedzielski, P. High strength metallurgical graphene for hydrogen storage nanocomposites. Vacuum 2016, 129, 79–85. [Google Scholar] [CrossRef]
- Kula, P.; Kaczmarek, L.; Zawadzki, P.; Kołodziejczyk, L.; Szymanski, W.; Niedzielski, P.; Pietrasik, R.; Dybowski, K.; Kazimierski, D.; Nowak, D. Functionality of graphene as a result of its heterogenic growth on SiC nanoparticles on the basis of reversible hydrogen storage. Int. J. Hydrogen Energy 2014, 39, 19662–19671. [Google Scholar] [CrossRef]
- Tu, Z.C.; Ou-Yang, Z.C. Single-walled and multi-walled carbon nanotubes viewed as elastic tubes with the effective Young’s moduli dependent on layer number. Phys. Rev. B 2002, 65, 233407. [Google Scholar] [CrossRef]
- Meguid, S.; Wernik, J.; Cheng, Z. Atomistic-based continuum representation of the effective properties of nano-reinforced epoxies. Int. J. Solids Struct. 2010, 47, 1723–1736. [Google Scholar] [CrossRef]
- Zhao, P.; Shi, G. Study of poisson’s ratios of graphene and single-walled carbon nanotubes based on an improved molecular structural mechanics model. SL 2011, 5, 49–58. [Google Scholar]
- Zhao, H.; Min, K.; Aluru, N.R. Size and Chirality Dependent Elastic Properties of Graphene Nanoribbons under Uniaxial Tension. Nano Lett. 2009, 9, 3012–3015. [Google Scholar] [CrossRef]
- Baykasoglu, C.; Kirca, M.; Mugan, A. Nonlinear failure analysis of carbon nanotubes by using molecular-mechanics based models. Compos. Part B Eng. 2013, 50, 150–157. [Google Scholar] [CrossRef]
- Frank, I.W.; Tanenbaum, D.M.; Van Der Zande, A.M.; McEuen, P.L. Mechanical properties of suspended graphene sheets. J. Vac. Sci. Technol. B. 2007, 25, 2558–2561. [Google Scholar] [CrossRef]
- Cao, G. Atomistic Studies of Mechanical Properties of Graphene. Polymers 2014, 6, 2404–2432. [Google Scholar] [CrossRef]
- Akinwande, D.; Brennan, C.J.; Bunch, J.S.; Egberts, P.; Felts, J.R.; Gao, H.; Huang, R.; Kim, J.S.; Li, T.; Li, Y.; et al. A review on mechanics and mechanical properties of 2D materials—Graphene and beyond. Extrem. Mech. Lett. 2017, 13, 42–77. [Google Scholar] [CrossRef]
- Tian, W.; Li, W.; Yu, W.; Liu, X. A Review on Lattice Defects in Graphene: Types, Generation, Effects and Regulation. Micromachines 2017, 8, 163. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, Z.; De, S. A Density Functional Theory Study of the Mechanical Properties of Graphane with van der Waals Corrections. Mech. Adv. Mater. Struct. 2015, 22, 717–721. [Google Scholar] [CrossRef]
- Kvashnin, A.G.; Sorokin, P.B.D.; Kvashnin, G. The Theoretical Study of Mechanical Properties of Graphene Membranes. Fuller. Nanotub. Carbon Nanostruct. 2010, 18, 497–500. [Google Scholar] [CrossRef]
- Meo, M.; Rossi, M. A molecular-mechanics based finite element model for strength prediction of single wall carbon nanotubes. Mater. Sci. Eng. A 2007, 454, 170–177. [Google Scholar] [CrossRef]
- Liu, B.; Huang, Y.; Jiang, H.; Qu, S.; Hwang, K.C. The atomic-scale finite element method. Comput. Methods Appl. Mech. Eng. 2004, 193, 1849–1864. [Google Scholar] [CrossRef]
- Wernik, J.M.; Meguid, S.A. Recent Developments in Multifunctional Nanocomposites Using Carbon Nanotubes. Appl. Mech. Rev. 2010, 63, 050801. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, H.; Huang, Y.; Qu, S.; Yu, M.F.; Hwang, K.C. Atomic-scale finite element method in multiscale computation with applications to carbon nanotubes. Phys. Rev. B 2005, 72, 035435. [Google Scholar] [CrossRef]
- Song, Y.S.; Youn, J.R. Modeling of effective elastic properties for polymer based carbon nanotube composites. Polymer 2006, 47, 1741–1748. [Google Scholar] [CrossRef]
- Meo, M.; Rossi, M. Prediction of Young’s modulus of single wall carbon nanotubes by molecular-mechanics based finite element modelling. Compos. Sci. Technol. 2006, 66, 1597–1605. [Google Scholar] [CrossRef]
- Lei, X.; Natsuki, T.; Shi, J.; Ni, Q.Q. Analysis of Carbon Nanotubes on the Mechanical Properties at Atomic Scale. J. Nanomater. 2011, 2011, 805313. [Google Scholar] [CrossRef]
- Parvaneh, V.; Shariati, M.; Torabi, H. Bending buckling behavior of perfect and defective single-walled carbon nanotubes via a structural mechanics model. Acta Mech. 2012, 223, 2369–2378. [Google Scholar] [CrossRef]
- Tserpes, K.; Papanikos, P.; Labeas, G.; Pantelakis, S. Multi-scale modeling of tensile behavior of carbon nanotube-reinforced composites. Theor. Appl. Fract. Mech. 2008, 49, 51–60. [Google Scholar] [CrossRef]
- Tserpes, K.; Papanikos, P. The effect of Stone–Wales defect on the tensile behavior and fracture of single-walled carbon nanotubes. Compos. Struct. 2007, 79, 581–589. [Google Scholar] [CrossRef]
- Mohammadpour, E.; Awang, M. Predicting the nonlinear tensile behavior of carbon nanotubes using finite element simulation. Appl. Phys. A 2011, 104, 609–614. [Google Scholar] [CrossRef]
- Wernik, J.M.; Meguid, S.A. Atomistic-based continuum modeling of the nonlinear behaviour of carbon nanotubes. Acta Mech. 2010, 212, 167–179. [Google Scholar] [CrossRef]
- Xiao, J.R.; Staniszewski, J.; Gillespie, J.W. Fracture and progressive failure of defective graphene sheets and carbon nanotubes. Compos. Struct. 2009, 88, 602–609. [Google Scholar] [CrossRef]
- Rao, P.S.; Anandatheertha, S.; Naik, G.N.; Gopalakrishnan, S. Estimation of mechanical properties of single wall carbon nanotubes using molecular mechanics approach. Sadhana 2015, 40, 1301–1311. [Google Scholar] [CrossRef]
- Bernholc, J.; Brabec, C.J.; Yakobson, B.I. Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar]
- Chen, X.; Cao, G. A structural mechanics study of single-walled carbon nanotubes generalized from atomistic simulation. Nanotechnology 2006, 17, 1004–1015. [Google Scholar] [CrossRef] [PubMed]
- Tserpes, K.I.; Papanikos, P. Finite element modeling of single-walled carbon nanotubes. Compos. Part B 2005, 36, 468–477. [Google Scholar] [CrossRef]
- Nahas, M.N.; Abd-Rabou, M. Finite Element Modeling of Carbon Nanotubes. Int. J. Mech. Mechatron. Eng. 2010, 10, 19–24. [Google Scholar]
- Gupta, S.S.; Bosco, F.G.; Batra, R.C. Wall thickness and elastic moduli of single-walled carbon nanotubes from frequencies of axial, torsional and inextensional modes of vibration. Comput. Mater. Sci. 2010, 47, 1049–1059. [Google Scholar] [CrossRef]
- Belytschko, T.; Xiao, S.P.; Schatz, G.C.; Ruoff, R.S. Atomistic simulations of nanotube fracture. Phys. Rev. B 2002, 65, 235430. [Google Scholar] [CrossRef]
- Fan, N.; Ren, Z.; Jing, G.; Guo, J.; Peng, B.; Jiang, H. Numerical Investigation of the Fracture Mechanism of Defective Graphene Sheets. Materials 2017, 10, 164. [Google Scholar] [CrossRef]
- Tserpes, K.; Papanikos, P.; Tsirkas, S. A progressive fracture model for carbon nanotubes. Compos. Part B Eng. 2006, 37, 662–669. [Google Scholar] [CrossRef]
- Kim, J.; Lee, N.; Min, Y.H.; Noh, S.; Kim, N.K.; Jung, S.; Joo, M.; Yamada, Y. Distinguishing Zigzag and Armchair Edges on Graphene Nanoribbons by X-ray Photoelectron and Raman Spectroscopies. ACS Omega 2018, 3, 17789–17796. [Google Scholar] [CrossRef]
- Geim, A.; Novoselov, K. Graphene: Scientific Background on the Nobel Prize in Physics 2010; The Royal Swedish Academy of Sciences: Stockholm, Sweden, 2010. [Google Scholar]
- Timoshenko, S.; Gere, J.M. Theory of Elastic Stability, 2nd ed.; Dover Publications: Mineola, NY, USA, 2009. [Google Scholar]



| Number of Calculation Variant | Direction of Tension | l (Å) | a (Å) | h (Å) | d (Å) | Y (Tpa) | (-) | EGr (TPa) (Equation (10)) | (-) (Equation (12)) (Equation (17)) | (-) FEM |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | x | 1.42 | 2.46 | 0.44 | 0.44 | 1.15 | 0.3 | 40.95 | 0.800 | 0.812 |
| 2 | x | 1.42 | 2.46 | 0.75 | 0.75 | 1.15 | 0.3 | 13.09 | 0.663 | 0.666 |
| 3 | x | 1.42 | 2.46 | 0.89 | 0.89 | 1.15 | 0.3 | 9.630 | 0.580 | 0.620 |
| 4 | x | 1.42 | 2.46 | 1.00 | 1.00 | 1.15 | 0.3 | 7.932 | 0.546 | 0.59 |
| 5 | x | 1.42 | 2.46 | 1.42 | 1.42 | 1.15 | 0.3 | 4.727 | 0.463 | 0.515 |
| 6 | x | 1.42 | 2.46 | 2.00 | 2.00 | 1.15 | 0.3 | 3.058 | 0.411 | 0.471 |
| 7 | x | 1.42 | 2.46 | 2.42 | 2.42 | 1.15 | 0.3 | 2.448 | 0.392 | 0.453 |
| 8 | y | 1.42 | 2.46 | 0.44 | 0.44 | 1.15 | 0.3 | 40.94 | 0.800 | 0.791 |
| 9 | y | 1.42 | 2.46 | 0.75 | 0.75 | 1.15 | 0.3 | 13.08 | 0.633 | 0.618 |
| 10 | y | 1.42 | 2.46 | 0.89 | 0.89 | 1.15 | 0.3 | 9.620 | 0.580 | 0.564 |
| 11 | y | 1.42 | 2.46 | 1.00 | 1.00 | 1.15 | 0.3 | 7.930 | 0.546 | 0.527 |
| 12 | y | 1.42 | 2.46 | 1.42 | 1.42 | 1.15 | 0.3 | 4.726 | 0.463 | 0.445 |
| 13 | y | 1.42 | 2.46 | 2.00 | 2.00 | 1.15 | 0.3 | 3.057 | 0.411 | 0.394 |
| 14 | y | 1.42 | 2.46 | 2.42 | 2.42 | 1.15 | 0.3 | 2.448 | 0.392 | 0.373 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaroniek, M.; Czechowski, L.; Kaczmarek, Ł.; Warga, T.; Kubiak, T. A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites. Materials 2019, 12, 3918. https://doi.org/10.3390/ma12233918
Jaroniek M, Czechowski L, Kaczmarek Ł, Warga T, Kubiak T. A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites. Materials. 2019; 12(23):3918. https://doi.org/10.3390/ma12233918
Chicago/Turabian StyleJaroniek, Mieczysław, Leszek Czechowski, Łukasz Kaczmarek, Tomasz Warga, and Tomasz Kubiak. 2019. "A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites" Materials 12, no. 23: 3918. https://doi.org/10.3390/ma12233918
APA StyleJaroniek, M., Czechowski, L., Kaczmarek, Ł., Warga, T., & Kubiak, T. (2019). A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites. Materials, 12(23), 3918. https://doi.org/10.3390/ma12233918







