Material-Oriented Shape Functions for FGM Plate Finite Element Formulation
Abstract
1. Introduction
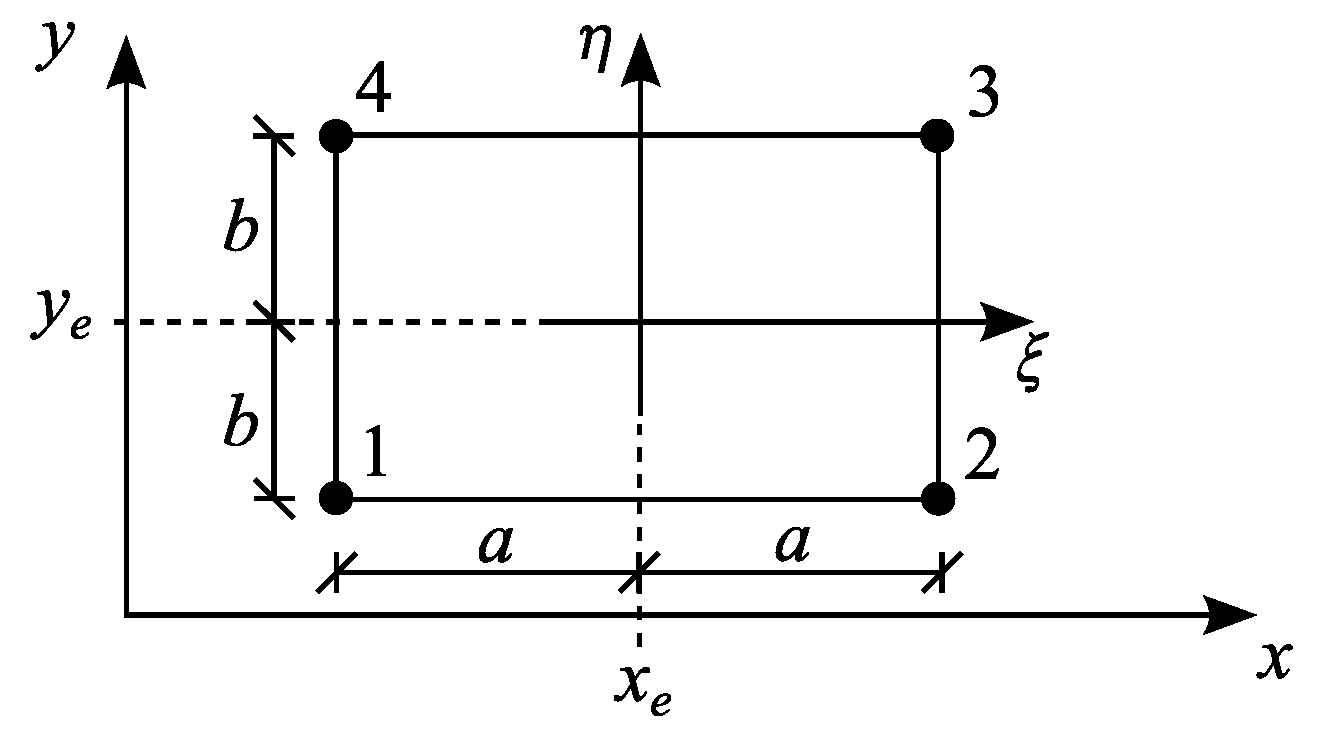
2. FGM plate Finite Elements
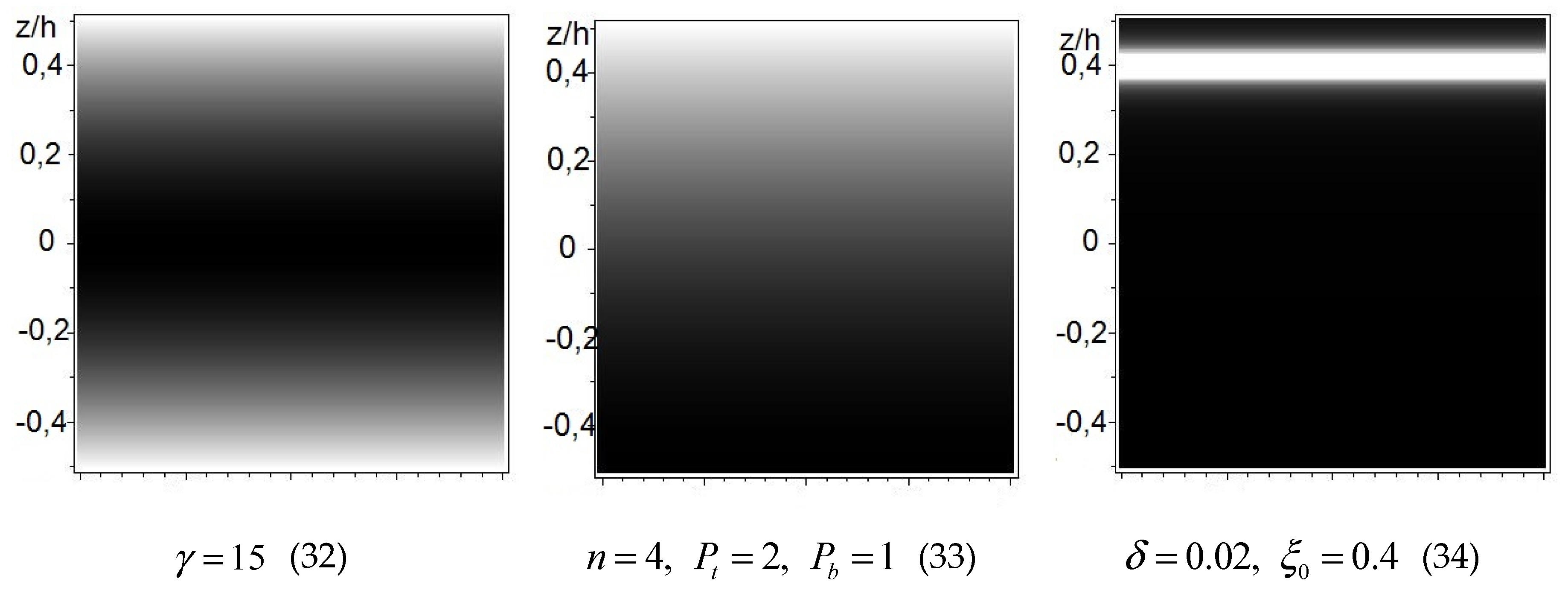
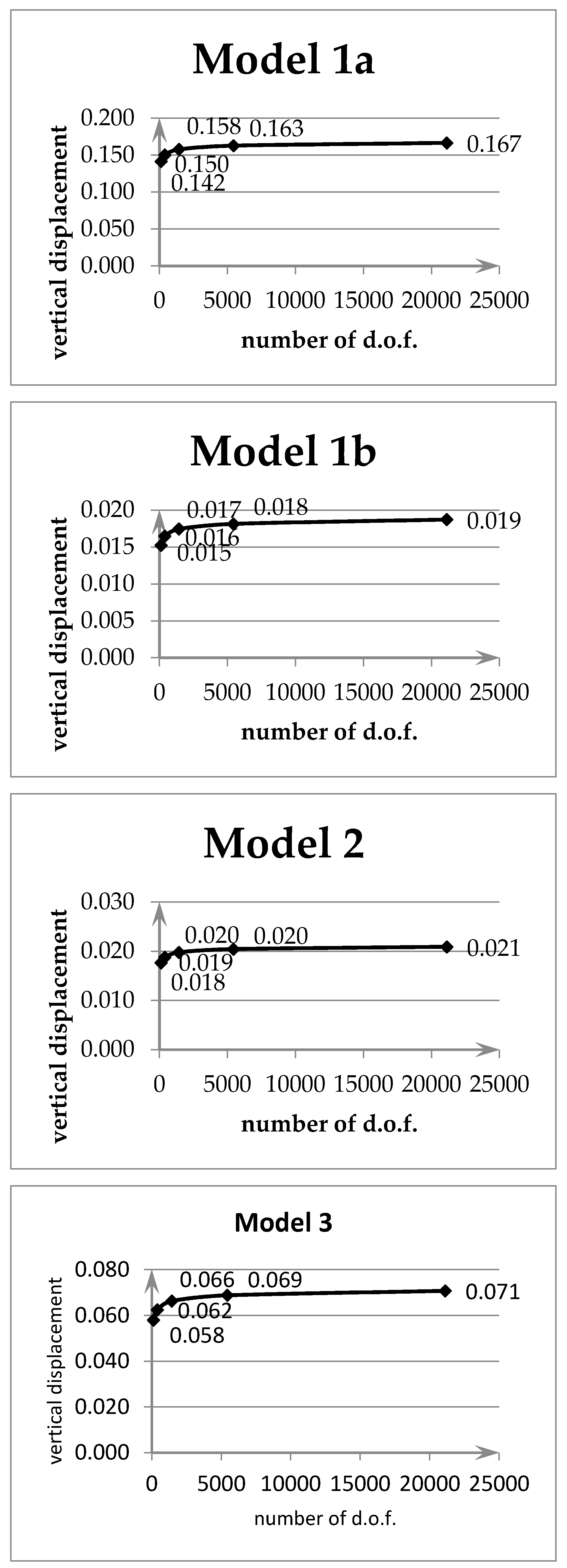
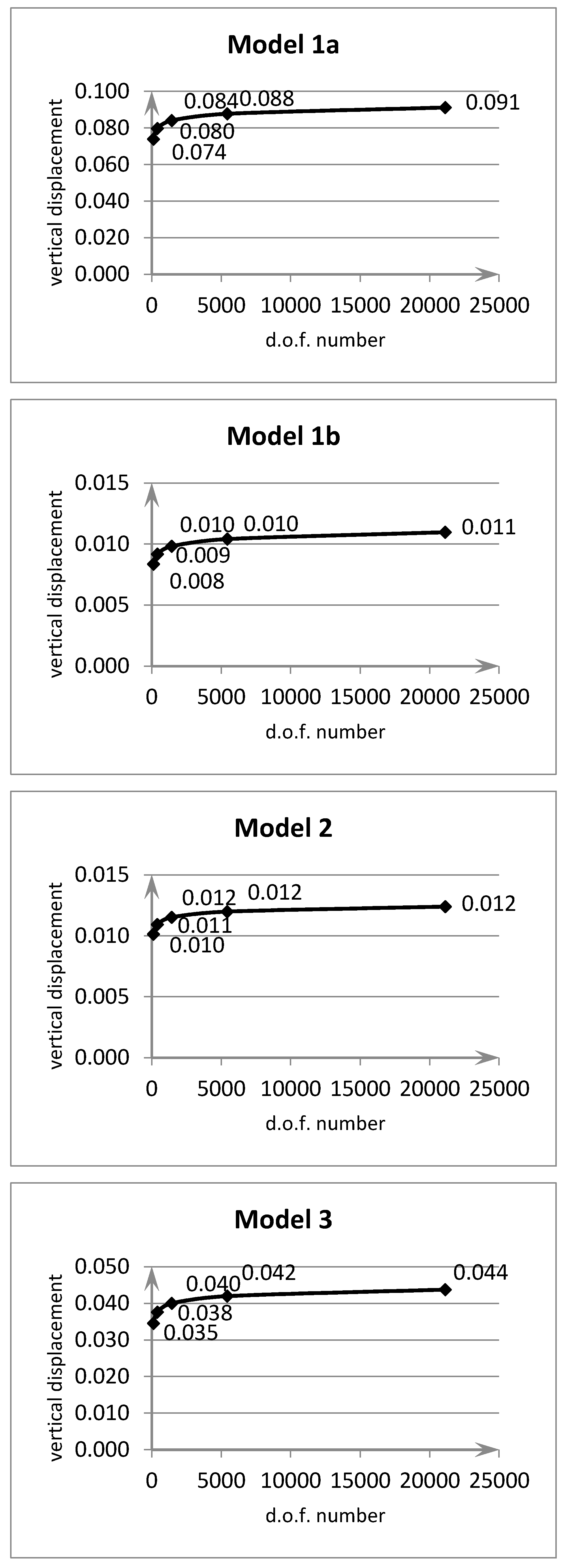
3. Numerical Examples
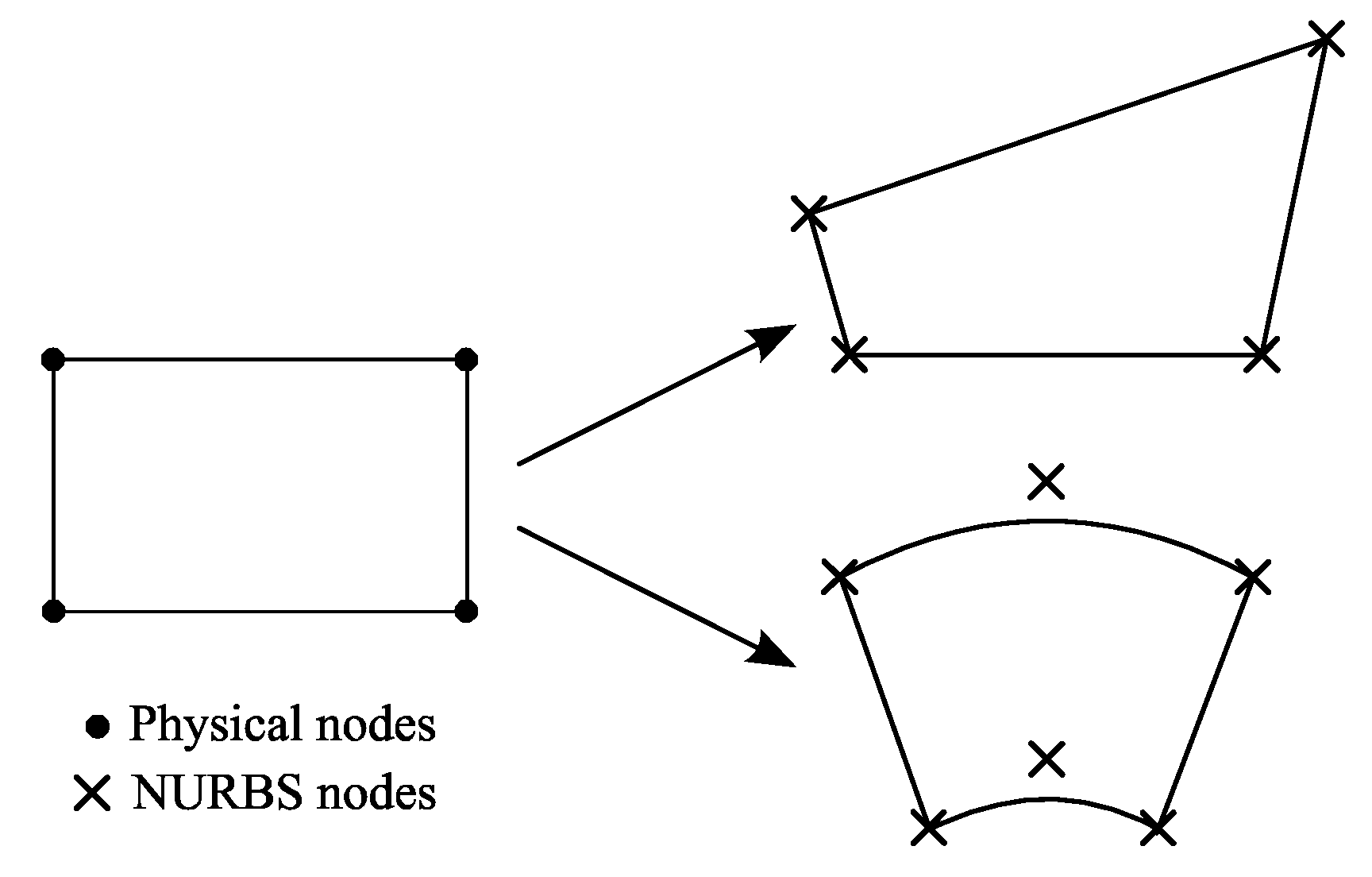
4. Free-Form Plate Finite Element—the Use of NURBS Functions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing and Applications; Kluwer Academy Publishers: Dordrecht/Boston/London, UK, 1999. [Google Scholar]
- Mahamood, R.M.; Akinalbi, E.T.; Shukla, M.; Pityana, S. Functionally graded material: An overview. In Proceedings of the World Congress on Engineering, London, UK, 4–6 July 2012. [Google Scholar]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Taylor, R.L.; Zienkiewicz, O.C. The Finite Element Method. Volume 2: Solid Mechanics; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Asemi, K.; Selehi, M.; Akhlaghi, M. Three dimensional static analysis of two dimensional functionally graded plates. Int. J. Recent Adv. Mech. Eng. 2013, 2, 21–32. [Google Scholar]
- Shariat, M.; Mohammadjani, R. Three-dimensional compatible finite element stress analysis of spinning two-directional FGM annular plates and disks with load and elastic foundation non-uniformities. Lat. Am. J. Solids Struct. 2013, 10, 859–890. [Google Scholar] [CrossRef][Green Version]
- Burlayenko, V.N.; Sadowski, T. Free vibrations and static analysis of functionally graded sandwich plates with three-dimensional finite elements. Meccanica 2019, 1–19. [Google Scholar] [CrossRef]
- Liew, K.M.; He, X.Q.; Ng, T.Y.; Sivashanker, S. Active control of FGM plates subjected to a temperature gradient: Modelling via finite element method based on FSDT. Int. J. Numer. Methods Eng. 2001, 52, 1253–1271. [Google Scholar] [CrossRef]
- He, X.Q.; Ng, T.Y.; Sivashanker, S.; Liew, K.M. Active control of FGM plates with integrated piezoelectric sensors and actuators. Int. J. Solids Struct. 2001, 38, 1641–1655. [Google Scholar] [CrossRef]
- Kurtaran, H. Shape effect on free vibration of functionally graded plates. Int. J. Eng. Appl. Sci. 2014, 6, 52–67. [Google Scholar] [CrossRef][Green Version]
- Sundararajan, N.; Prakash, T.; Ganapathi, M. Nonlinear free flexural vibrations of functionally graded rectangular and skew plates under thermal environments. Finite Elem. Anal. Des. 2005, 42, 152–168. [Google Scholar] [CrossRef]
- Ray, M.C.; Sachade, H.M. Finite element analysis of smart functionally graded plates. Int. J. Solids Struct. 2006, 43, 5468–5484. [Google Scholar] [CrossRef][Green Version]
- Park, W.T. Structural stability and dynamics of FGM plates using an improved 8-ANS finite element. Adv. Mater. Sci. Eng. 2016, 2016, 2821473. [Google Scholar] [CrossRef]
- Martinez-Paneda, E. On the finite element implementation of functionally graded materials. Materials 2019, 12, 287. [Google Scholar] [CrossRef] [PubMed]
- Nguyen-Xuan, H.; Tran, L.V.; Thai, C.H.; Nguyen-Thoi, T. Analysis of functionally graded plates by an efficient finite element method with node-based strain smoothing. Thin-Walled Struct. 2012, 54, 1–18. [Google Scholar] [CrossRef]
- Natarajan, S.; Ferreira, A.J.M.; Bordas, S.; Carrera, E.; Cinefra, M.; Zenkour, A.M. Analysis of functionally graded material plates using triangular elements with cell-based smooth discrete shear gap method. Math. Problems Eng. 2014, 2014, 247932. [Google Scholar] [CrossRef]
- Prakash, T.; Ganapathi, M. Asymmetric flexural vibration and thermoelastic stability of FGM circular plates using finite element method. Compos. Part B 2006, 37, 642–649. [Google Scholar] [CrossRef]
- Talha, M.; Singh, B.N. Static response and free vibration analysis of FGM plates using higher order shear deformation theory. Appl. Math. Model. 2010, 34, 3991–4011. [Google Scholar] [CrossRef]
- Talha, M.; Singh, B.N. Large amplitude free flexural vibration analysis of shear deformable FGM plates using nonlinear finite element method. Finite Elem. Anal. Des. 2011, 47, 394–401. [Google Scholar] [CrossRef]
- Kulkarni, S.D.; Trivedi, C.J.; Ishi, R.G. Static free vibration analysis of functionally graded skew plates using a four node quadrilateral element. In Advances in Structural Engineering; Matsagar, V., Ed.; Springer India: New Delhi, India, 2015; pp. 15–24. [Google Scholar]
- Ramu, I.; Mohanty, S.C. Modal analysis of functionally graded material plates using finite element method. Proced. Mater. Sci. 2014, 6, 460–467. [Google Scholar] [CrossRef]
- Valizadeh, N.; Natarajan, S.; Gonzalez-Estrada, O.A.; Rabczuk, T.; Bui, T.Q.; Bordas, S.P.A. NURBS-based finite element analysis of functionally graded plates: Static bending, vibrations, buckling and flutter. Compos. Struct. 2013, 99, 309–326. [Google Scholar] [CrossRef]
- Tran, L.V.; Thai, C.H.; Nguyen-Xuan, H. An isogeometric finite element formulation for thermal buckling analysis of functionally graded plates. Finite Elem. Anal. Des. 2013, 73, 65–76. [Google Scholar] [CrossRef]
- Koteswara Rao, D.; Blessington, P.J.; Tarapada, R. Finite element modeling and analysis of functionally graded (FG) composite shell structures. Proced. Eng. 2012, 38, 3192–3199. [Google Scholar]
- Daszkiewicz, K.; Chróścielewski, J.; Witkowski, W. Geometrically nonlinear analysis of functionally graded shells based on 2-D cosserat constitutive model. Eng. Trans. 2014, 62, 109–130. [Google Scholar]
- Chakraborty, A.; Gopalakrishnan, S.; Reddy, J.N. A new beam finite element for the analysis of functionally graded materials. Int. J. Mech. Sci. 2003, 45, 519–539. [Google Scholar] [CrossRef]
- Filippi, M.; Carrera, E.; Zenkour, A.M. Static analyses of FGM beams by various theories and finite elements. Compos. Part B 2015, 72, 1–9. [Google Scholar] [CrossRef]
- Kahya, V.; Turan, M. Finite element model for vibration and buckling of functionally graded beams based on the first-order shear deformation theory. Compos. Part B 2017, 109, 108–115. [Google Scholar] [CrossRef]
- Gilewski, W.; Gomuliński, A. Physical shape functions in finite element analysis of moderately thick plates. Int. J. Number. Methods Eng. 1991, 32, 1115–1135. [Google Scholar] [CrossRef]
- Kączkowski, Z. Plates—Static Calculations; Arkady: Warsaw, Poland, 1980. (In Polish) [Google Scholar]
- Gilewski, W. On the Criteria for Evaluation of Finite Elements—From Timoshenko Beam to Hencky-Bolle Plate; Warsaw University of Technology Publishing House: Warsaw, Poland, 2005. (In Polish) [Google Scholar]
- Gilewski, W. Physical Shape Functions in the Finite Element Method; Studies in Civil Engineering 81, Polish Academy of Sciences, Committee of Civil Engineering: Warsaw, Poland, 2013. (In Polish) [Google Scholar]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilievs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Compos. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Abaqus version 6.13. Simula, ABAQUS User Subroutine Reference Guide; Dassault Systemes Simula Corp.: Providence, RI, USA, 2013.
- Boulbes, R.J. Troubleshooting Finite-Element Modeling with Abaqus; With Applications in Structural Engineering Analysis; Springer Nature Switzerland AG: Basel, Switzerland, 2020. [Google Scholar]
- Maplesoft – Mathematics-Based Software and Services for Education, Engineering and Research. Available online: https://www.maplesoft.com/support/help (accessed on 1 February 2020).
- Daouadji, T.H.; Tounsi, A.; Adda Beida, E.A. Analytical solution for bensing analysis of functionally graded plates. Sci. Iran. Trans. B Mech. Eng. 2013, 20, 516–523. [Google Scholar]

| n | 0 | 1 | 2 | 3 | 5 | 10 | Infinity |
|---|---|---|---|---|---|---|---|
| Analytical solution [37] | 0.4665 | 0.9421 | 1.2228 | 1.3530 | 1.4647 | 1.6054 | 2.5328 |
| Present study | 0.4665 | 0.9280 | 1.1903 | 1.3124 | 1.4202 | 1.5692 | 2.5328 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilewski, W.; Pełczyński, J. Material-Oriented Shape Functions for FGM Plate Finite Element Formulation. Materials 2020, 13, 803. https://doi.org/10.3390/ma13030803
Gilewski W, Pełczyński J. Material-Oriented Shape Functions for FGM Plate Finite Element Formulation. Materials. 2020; 13(3):803. https://doi.org/10.3390/ma13030803
Chicago/Turabian StyleGilewski, Wojciech, and Jan Pełczyński. 2020. "Material-Oriented Shape Functions for FGM Plate Finite Element Formulation" Materials 13, no. 3: 803. https://doi.org/10.3390/ma13030803
APA StyleGilewski, W., & Pełczyński, J. (2020). Material-Oriented Shape Functions for FGM Plate Finite Element Formulation. Materials, 13(3), 803. https://doi.org/10.3390/ma13030803





