FE Analyses of Hyperelastic Solids under Large Bending: The Role of the Searle Parameter and Eulerian Slenderness
Abstract
1. Introduction
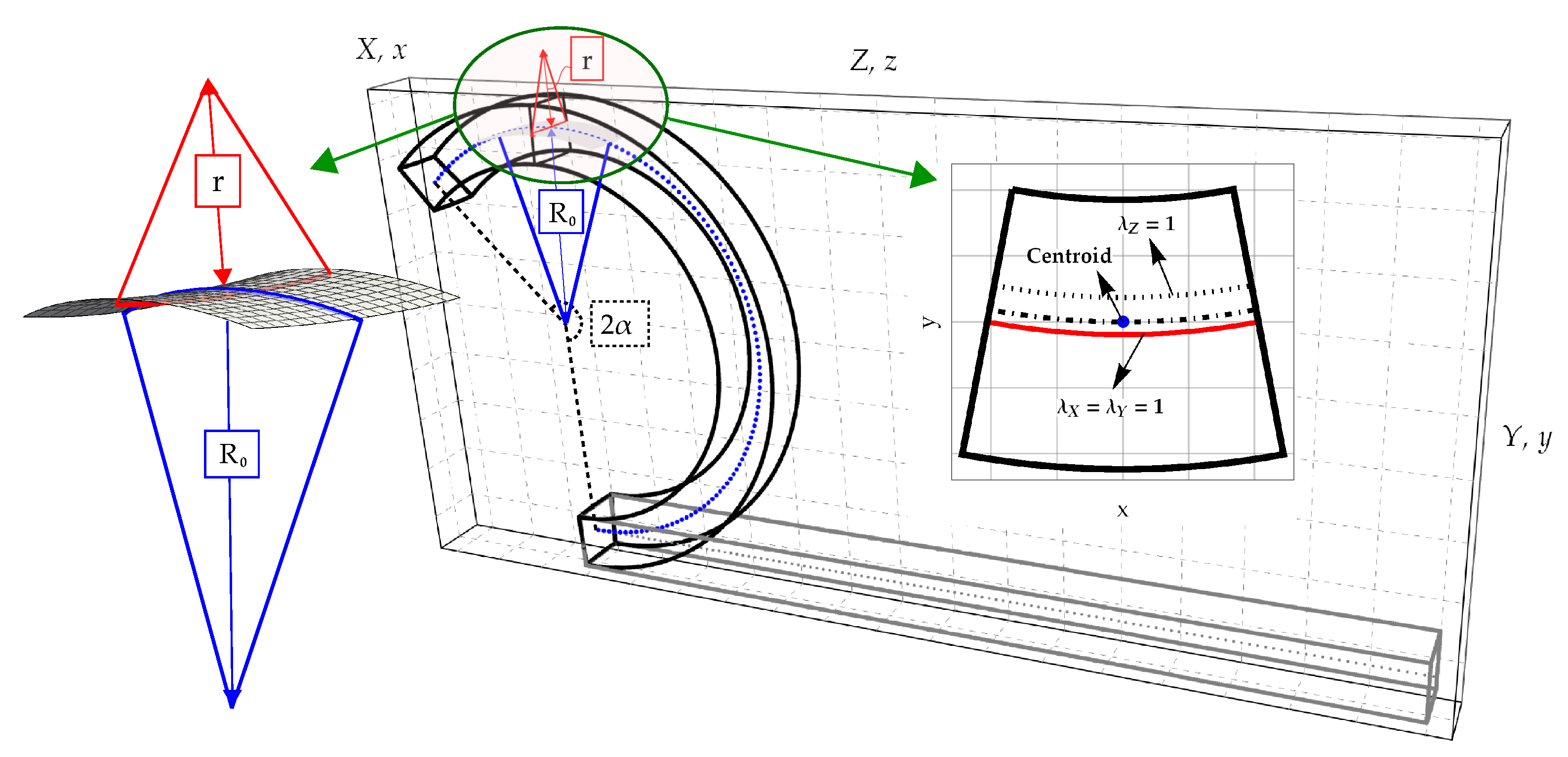
2. The Theoretical Model for the Finite Bending of Solids
2.1. Remarks on the Theoretical Model
- the longitudinal fibres, parallel to Z-axis, after bending are deformed into arcs of circumferences (blue curves in Figure 1). As reported above, the longitudinal radius of curvature of the deformed centroidal fibre is denoted as , whereas the longitudinal fibre with unitary transverse stretches () is characterized by the longitudinal radius of curvature R;
- during bending, transverse cross sections belonging to planes preserve their planarity and exhibit the same deformation;
- solid transverse fibres, parallel to X-axis, after bending are deformed into arcs of circumferences (red curves in Figure 1). The transversal fibre with unitary transverse stretches (), is characterized by the anticlastic (or transverse) radius if curvature r.
2.2. Generalization to Variable Bending Moment
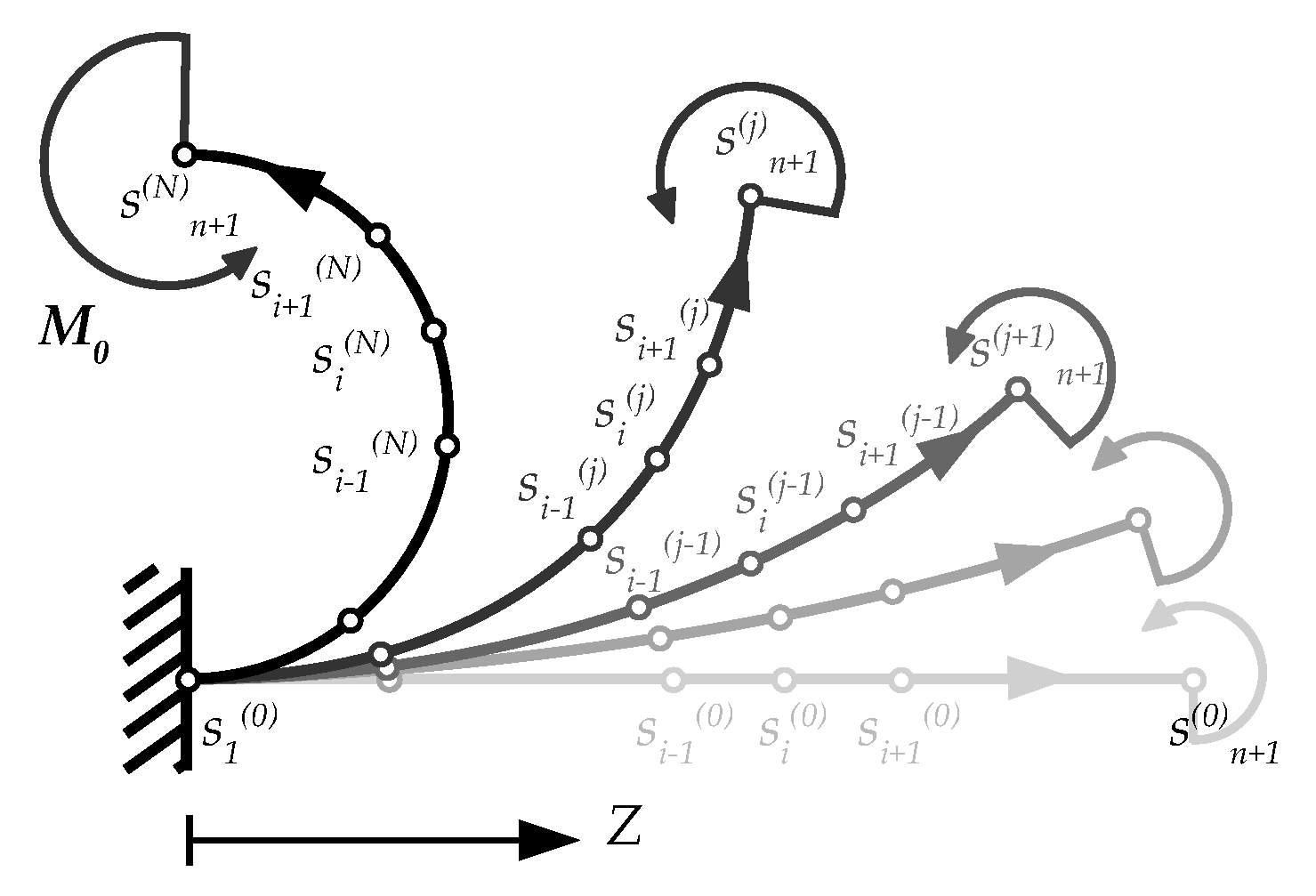
2.3. The Numerical Procedure
- starting from a trial solution corresponding to the linearized theory, the bending moment is obtained at the first iteration;
- for each node, Equation (6) is solved in the unknown radius of curvature ;
- then, the rotation and displacements fields are assessed from (9)–(11) for each node, providing the Eulerian coordinates of the beam axis, i.e., ;
- two convergence criteria have been adopted: The relative error between two subsequent iterations in terms of displacement norm and the potential energy;
- in case of not convergent results, the deformed configuration (not convergent) is used as guest solution for assessing a further bending moment distribution, . Therefore, the iterative procedure restarts from the second issue since both the convergence criteria are reached.
3. Study Cases
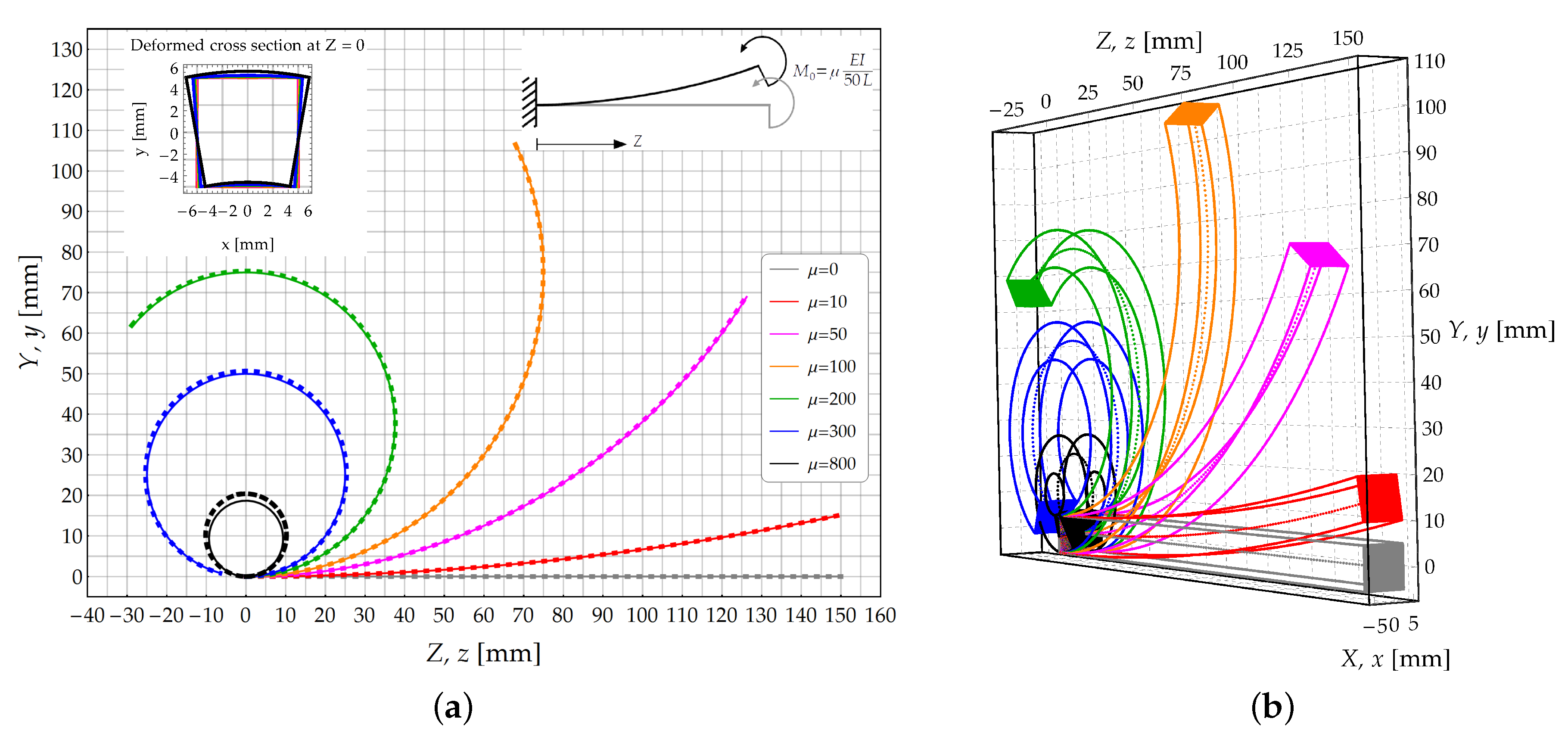
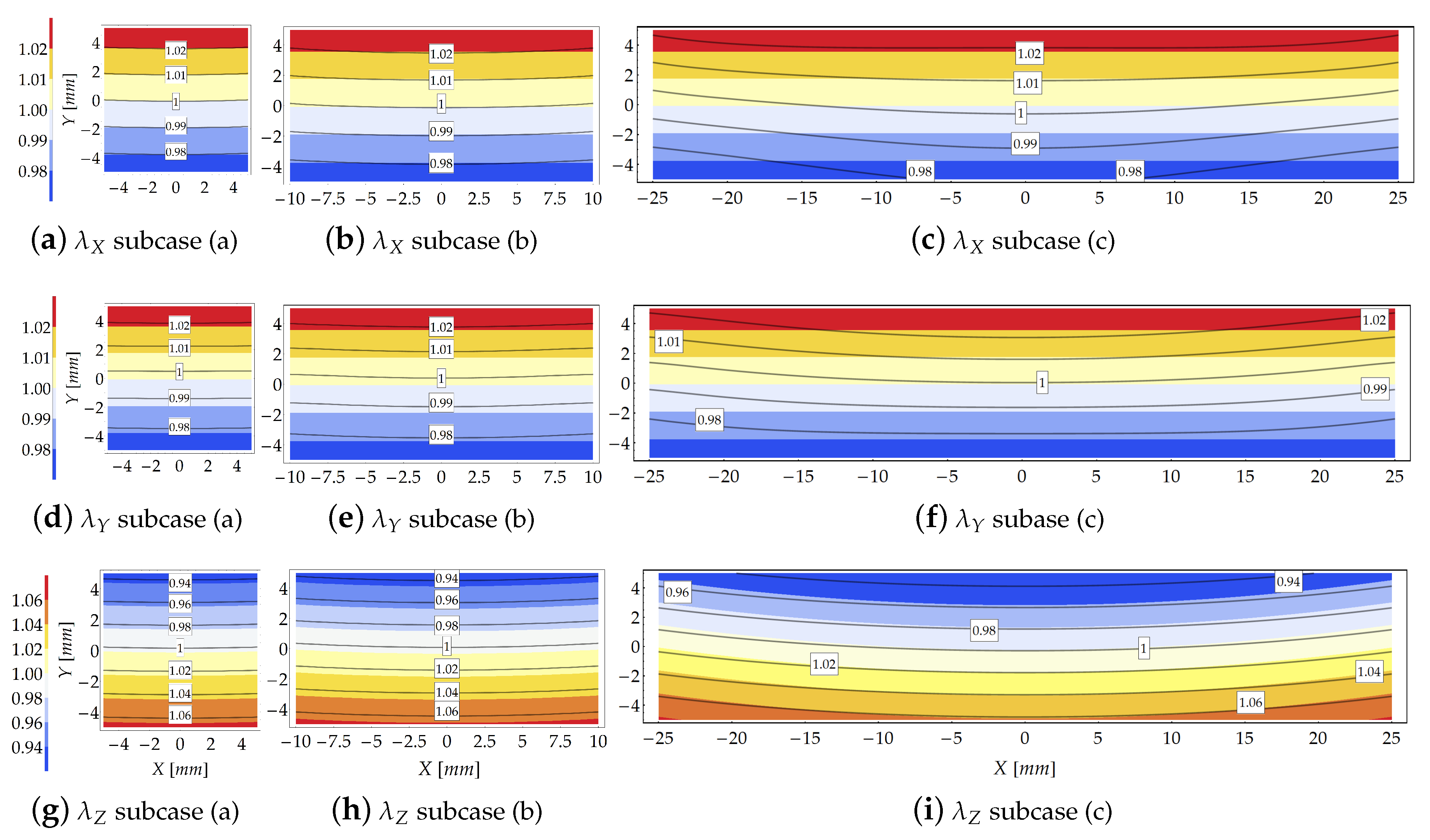
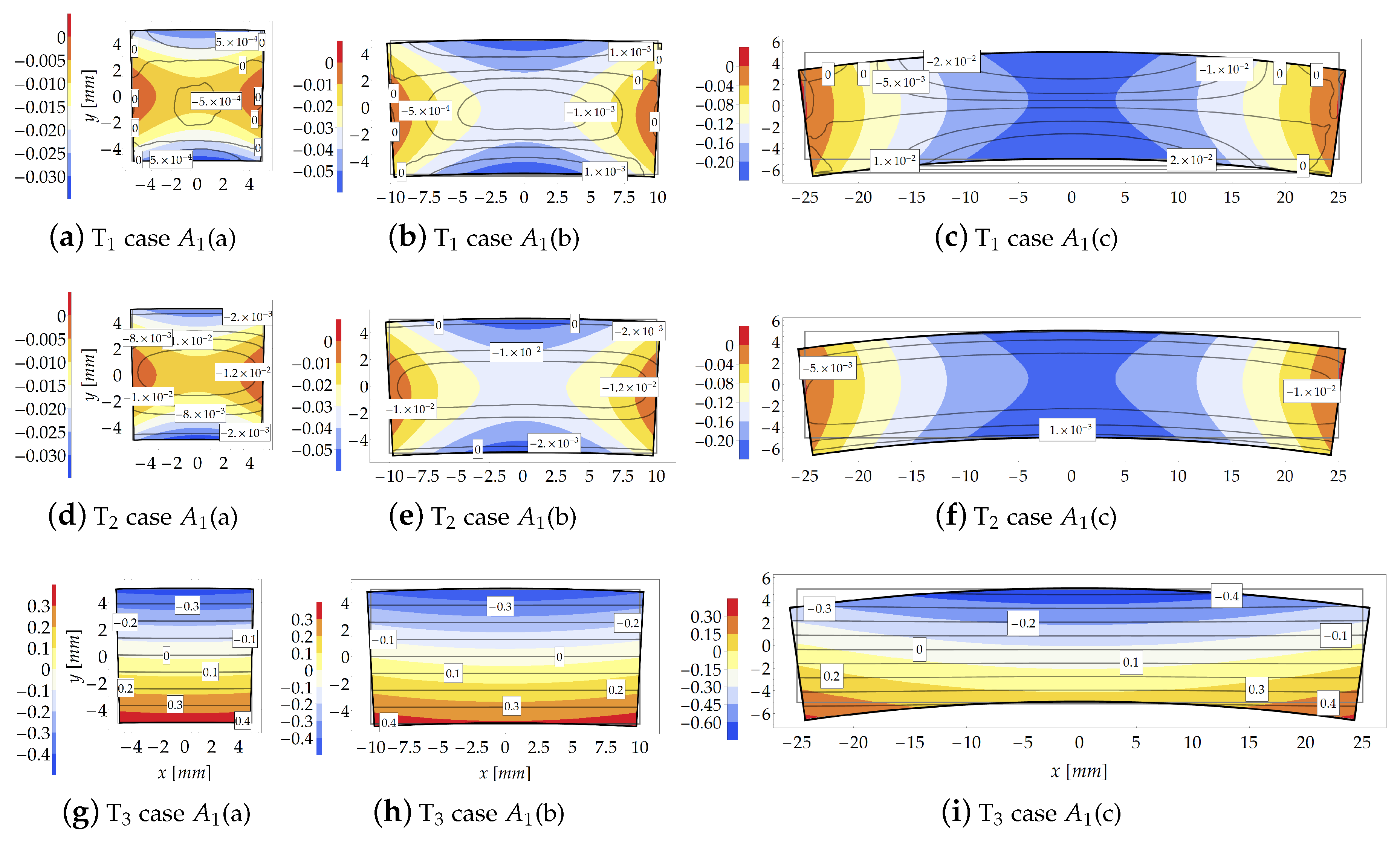
3.1. Cantilever Beam Subjected to a Couple at Its Free End (Case )
3.1.1. Theoretical Solution
3.1.2. The FE Model Solution
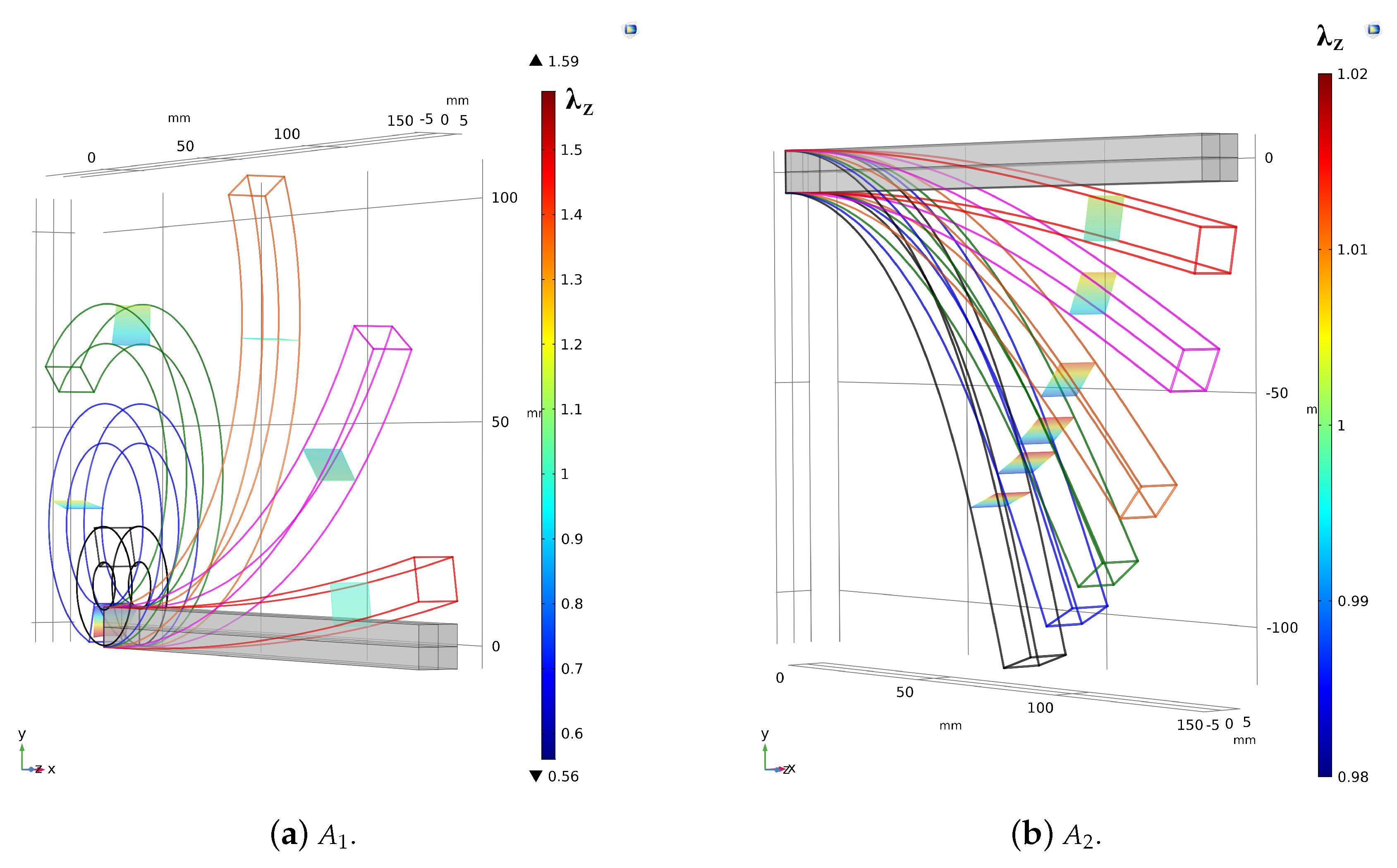
3.1.3. Results and Comparison
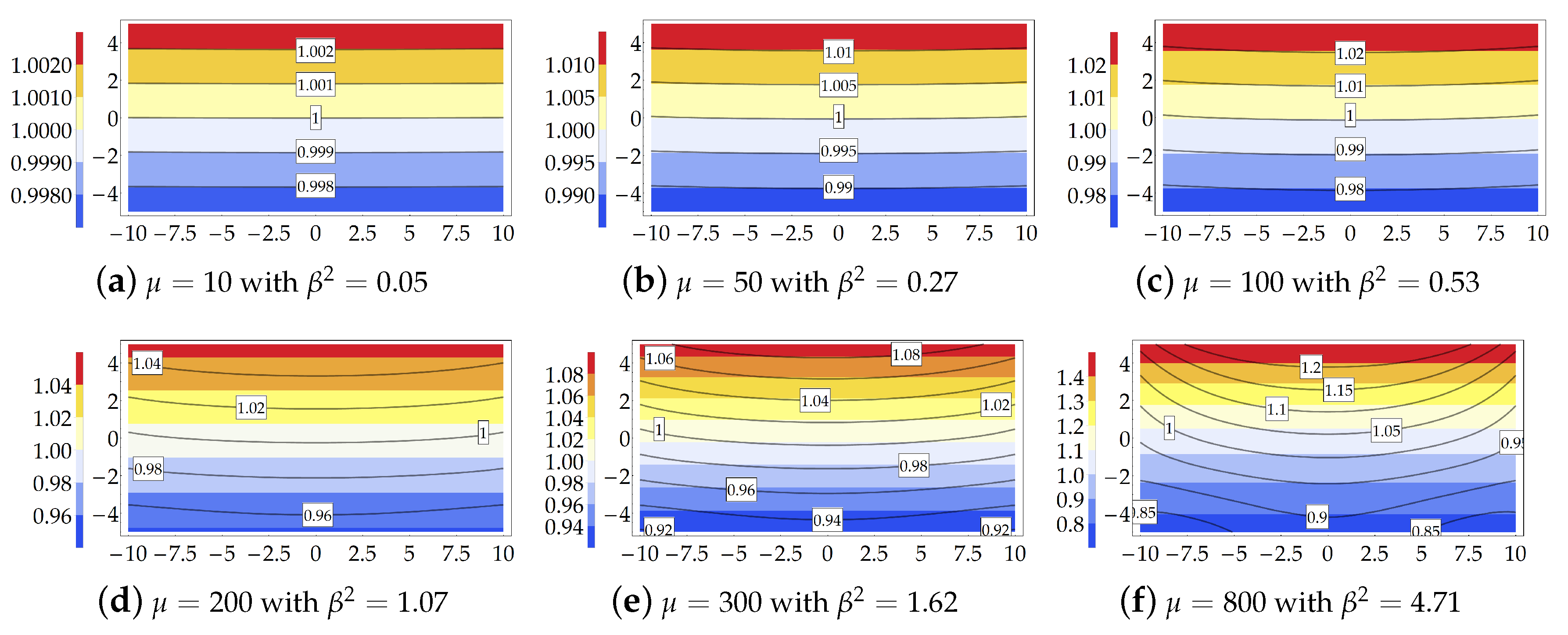
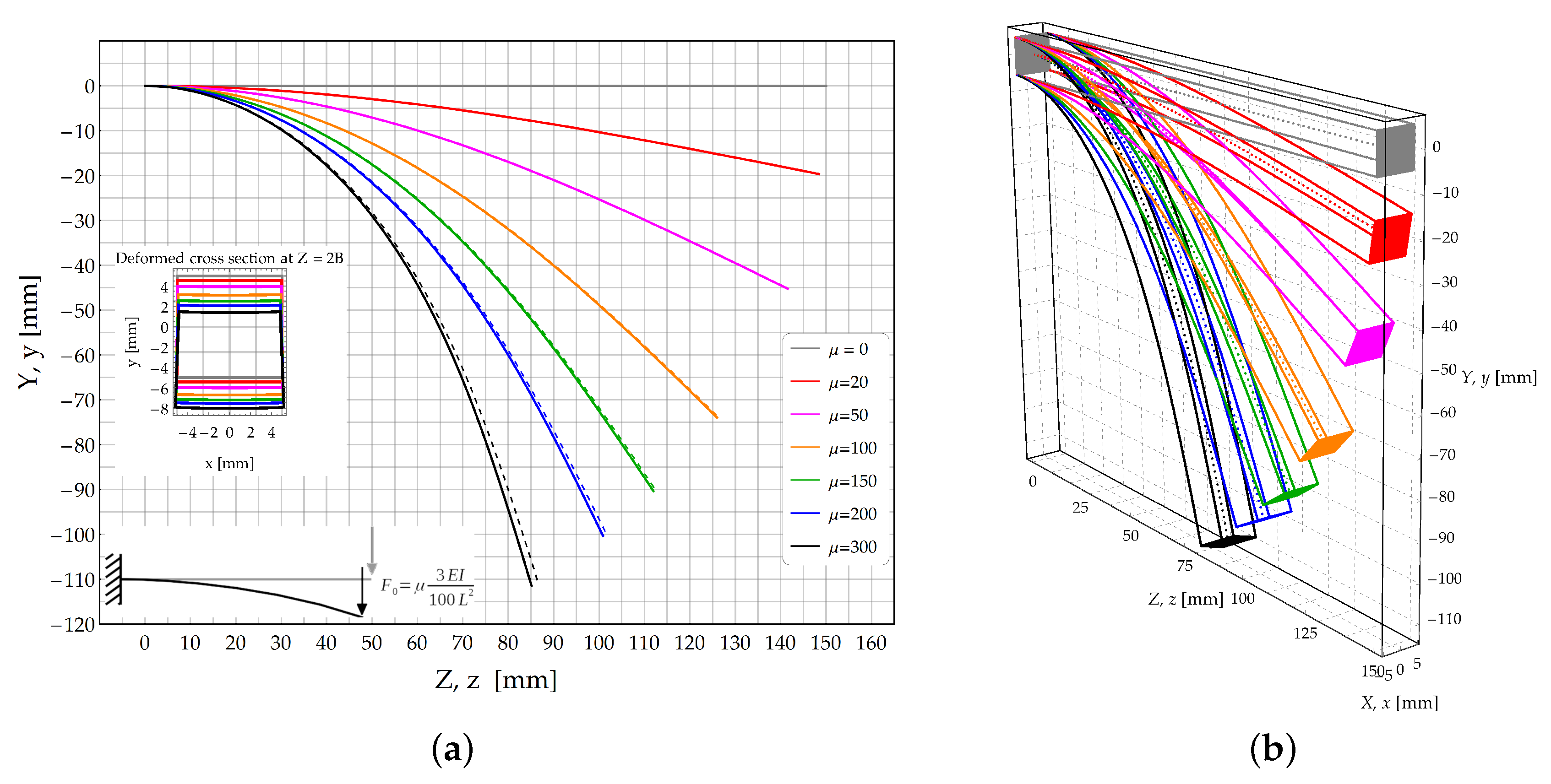
3.2. Cantilever Subjected to a Shear Force Acting at Its Free end (Case )
3.2.1. Theoretical Solution
3.2.2. The FE Solution
3.2.3. Results and Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| w.r.t. | with respect to |
| MR | Mooney–Rivlin |
References
- Schmitt, F.; Piccin, O.; Barbé, L.; Bayle, B. Soft robots manufacturing: A review. Front. Robot. AI 2018, 5, 84. [Google Scholar] [CrossRef]
- Martinez, R.V.; Branch, J.L.; Fish, C.R.; Jin, L.; Shepherd, R.F.; Nunes, R.M.; Suo, Z.; Whitesides, G.M. Robotic tentacles with three-dimensional mobility based on flexible elastomers. Adv. Mater. 2013, 25, 205–212. [Google Scholar] [CrossRef]
- Mac Murray, B.C.; An, X.; Robinson, S.S.; van Meerbeek, I.M.; O’Brien, K.W.; Zhao, H.; Shepherd, R.F. Poroelastic foams for simple fabrication of complex soft robots. Adv. Mater. 2015, 27, 6334–6340. [Google Scholar] [CrossRef]
- Wen, L.; Wang, T.; Wu, G.; Liang, J. Quantitative thrust efficiency of a self-propulsive robotic fish: Experimental method and hydrodynamic investigation. IEEE/ASME Trans. Mechatron. 2012, 18, 1027–1038. [Google Scholar] [CrossRef]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft robotics: Review of fluid-driven intrinsically soft devices; manufacturing, sensing, control, and applications in human-robot interaction. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Ilievski, F.; Mazzeo, A.D.; Shepherd, R.F.; Chen, X.; Whitesides, G.M. Soft robotics for chemists. Angew. Chem. Int. Ed. 2011, 50, 1890–1895. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ma, J.; Ren, Z.; Gong, Z.; Hao, Y.; Wang, T.; Wen, L. Fiber-reinforced soft robotic anthropomorphic finger. In Proceedings of the 2016 International Conference on Robotics and Automation Engineering (ICRAE), Jeju-Do, Korea, 24–29 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- De Haan, L.T.; Verjans, J.M.; Broer, D.J.; Bastiaansen, C.W.; Schenning, A.P. Humidity-responsive liquid crystalline polymer actuators with an asymmetry in the molecular trigger that bend, fold, and curl. J. Am. Chem. Soc. 2014, 136, 10585–10588. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Abbas, A. A low-cost soft coiled sensor for soft robots. In Proceedings of the ASME 2016 Dynamic Systems and Control Conference, Minneapolis, MN, USA, 12–14 October 2016. [Google Scholar]
- Timoshenko, S.; Timoshenko, S.; Goodier, J. Theory of Elasticity; McGraw-Hill Book Company Inc.: New York, NY, USA, 1951. [Google Scholar]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Lekhnitskii, S.G. Anisotropic Plates; Technical Report; Foreign Technology Div Wright-Patterson Afb Oh: Dayton, OH, USA, 1968. [Google Scholar]
- Lekhnitskii, S.; Fern, P.; Brandstatter, J.J.; Dill, E. Theory of elasticity of an anisotropic elastic body. Phys. Today 1964, 17, 84. [Google Scholar] [CrossRef]
- Barber, J.R. Elasticity; Springer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Tarantino, A.M. Homogeneous equilibrium configurations of a hyperelastic compressible cube under equitriaxial dead-load tractions. J. Elast. 2008, 92, 227. [Google Scholar] [CrossRef]
- Lanzoni, L.; Tarantino, A.M. Damaged hyperelastic membranes. Int. J. Non-Linear Mech. 2014, 60, 9–22. [Google Scholar] [CrossRef]
- Lanzoni, L.; Tarantino, A.M. Equilibrium configurations and stability of a damaged body under uniaxial tractions. Zeitschrift für angewandte Mathematik und Physik 2015, 66, 171–190. [Google Scholar] [CrossRef]
- Lanzoni, L.; Tarantino, A.M. A simple nonlinear model to simulate the localized necking and neck propagation. Int. J. Non-Linear Mech. 2016, 84, 94–104. [Google Scholar] [CrossRef]
- Rashid, B.; Destrade, M.; Gilchrist, M.D. Mechanical characterization of brain tissue in simple shear at dynamic strain rates. J. Mech. Behav. Biomed. Mater. 2013, 28, 71–85. [Google Scholar] [CrossRef] [PubMed]
- Rivlin, R. Large elastic deformations of isotropic materials. V. The problem of flexure. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1949, 195, 463–473. [Google Scholar]
- Ogden, R.W. Non-Linear Elastic Deformations; Courier Corporation: Chelmsford, MA, USA, 1997. [Google Scholar]
- Bruhns, O.T.; Xiao, H.; Meyers, A. Finite bending of a rectangular block of an elastic Hencky material. J. Elast. Phys. Sci. Solids 2002, 66, 237. [Google Scholar]
- Lanzoni, L.; Tarantino, A.M. Finite anticlastic bending of hyperelastic solids and beams. J. Elast. 2018, 131, 137–170. [Google Scholar] [CrossRef]
- Lanzoni, L.; Tarantino, A.M. The bending of beams in finite elasticity. J. Elast. 2020, 139, 91–121. [Google Scholar] [CrossRef]
- Lanzoni, L.; Tarantino, A. Mechanics of high-flexible beams under live loads. J. Elast. 2020, 1–26, IN PRESS. [Google Scholar] [CrossRef]
- Bigoni, D. Extremely Deformable Structures; Springer: Basel, Switzerland, 2015; Volume 562. [Google Scholar]
- Searle, G.F.C. Experimental Elasticity: A Manual for the Laboratory; Cambridge University Press: Cambridge, UK, 1908. [Google Scholar]
- Lamb, H. On the flexure of a flat elastic spring. Philos. Mag. J. Theor. Exp. Appl. Phys. 1891, 31, 182–188. [Google Scholar]
- Falope, F.; Lanzoni, L.; Tarantino, A. Bending device and anticlastic surface measurement of solids under large deformations and displacements. Mech. Res. Commun. 2019, 97, 52–56. [Google Scholar] [CrossRef]
- Falope, F.; Lanzoni, L.; Tarantino, A.M. The bending of fully nonlinear beams. Theoretical, numerical and experimental analyses. Int. J. Eng. Sci. 2019, 145, 103167. [Google Scholar] [CrossRef]
- Ciarlet, P.G.; Geymonat, G. Sur les lois de comportement en élasticité non linéaire compressible. CR Acad. Sci. Paris Sér. II 1982, 295, 423–426. [Google Scholar]
- Tarantino, A.M.; Lanzoni, L.; Falope, F.O. The Bending Theory of Fully Nonlinear Beams; Springer: Basel, Switzerland, 2019. [Google Scholar]
- Jourawski, D. Sur le Résistance d’un Corps Prismatique et d’une Pièce Composée en Bois ou on Tôle de Fer à une Force Perpendiculaire à leur Longeur. Annales des Ponts et Chaussées 1856, 12, 328–351. [Google Scholar]

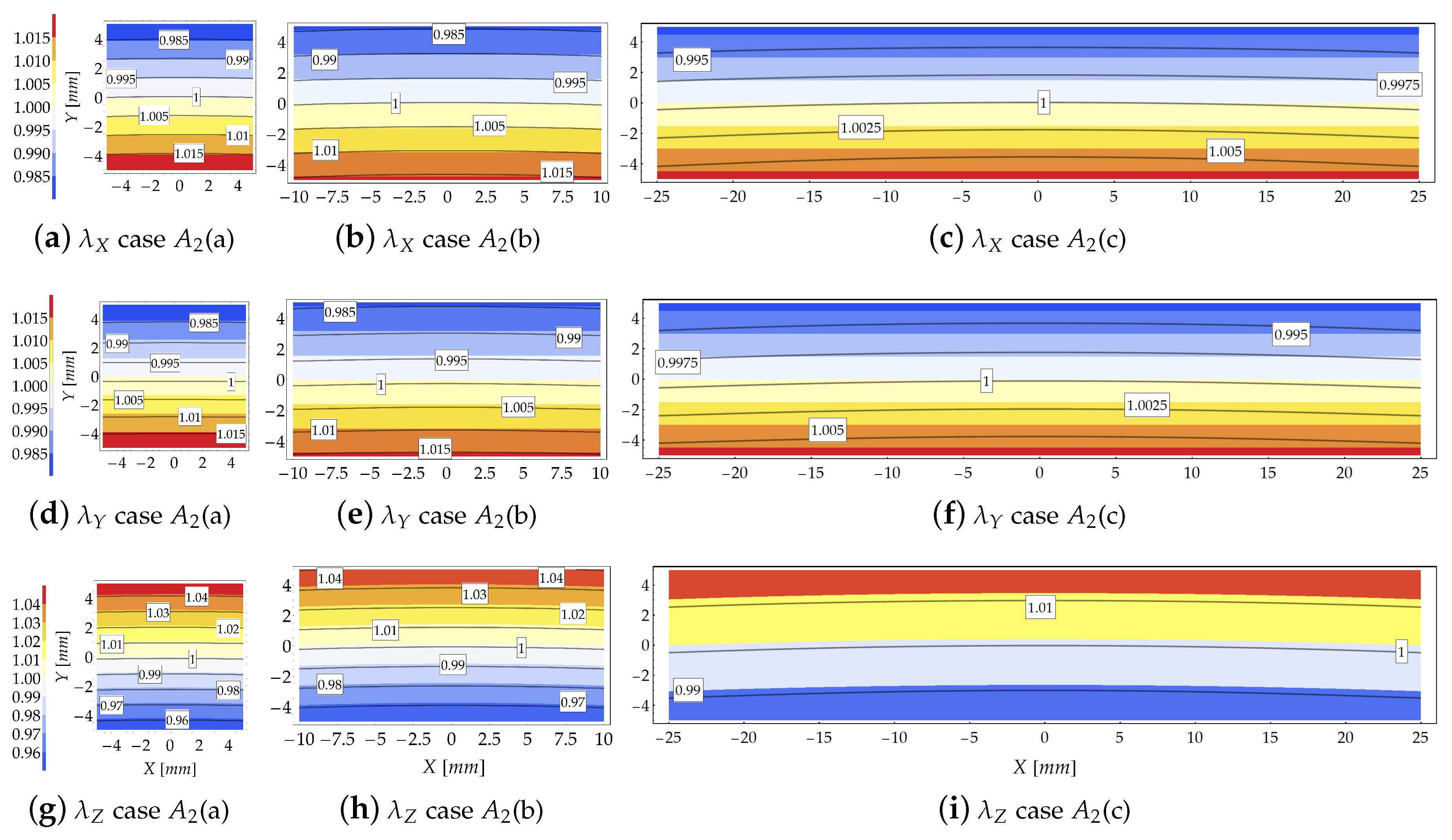
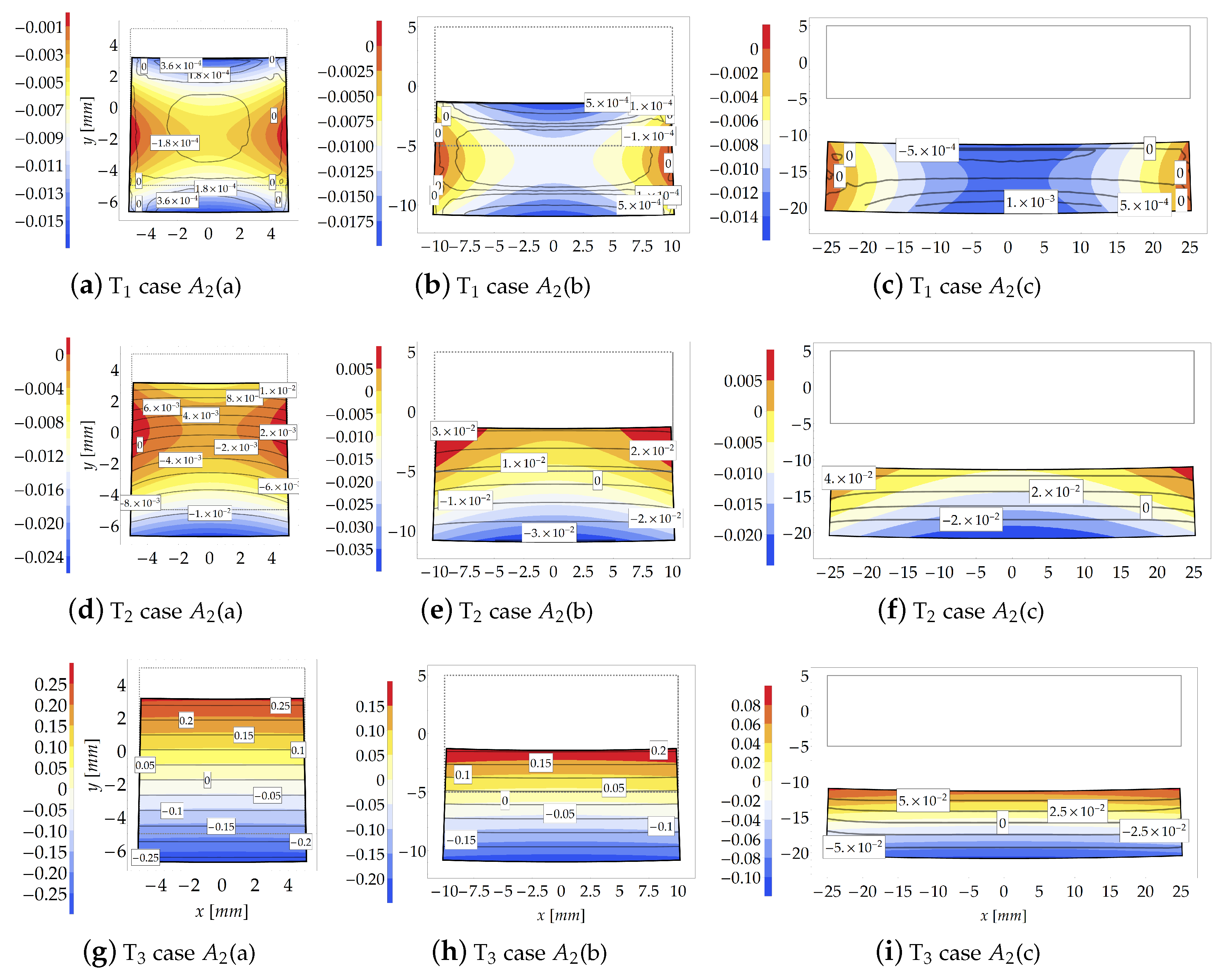
| Subcases | (a) | (b) | (c) |
|---|---|---|---|
| 1 | 2 | 5 | |
| 15 | 7.5 | 3 |
| Load | Subcases | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Mult. | (a) | (b) | (c) | ||||||
| 10 | |||||||||
| 50 | |||||||||
| 100 | |||||||||
| 200 | |||||||||
| 300 | |||||||||
| 800 | |||||||||
| Load Multiplier | 20 | 50 | 100 | 150 | 200 | 300 | |
|---|---|---|---|---|---|---|---|
| Subcases | (a) | 19.643 | 45.230 | 73.921 | 90.333 | 100.303 | 111.447 |
| (b) | 19.646 | 45.263 | 74.039 | 90.521 | 100.536 | 111.737 | |
| (c) | 19.666 | 45.494 | 74.917 | 91.970 | 102.423 | 115.291 | |
| Load | Subcases | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Mult. | (a) | (b) | (c) | ||||||
| 20 | |||||||||
| 50 | |||||||||
| 100 | |||||||||
| 150 | |||||||||
| 200 | |||||||||
| 300 | |||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oyedeji Falope, F.; Lanzoni, L.; Tarantino, A.M. FE Analyses of Hyperelastic Solids under Large Bending: The Role of the Searle Parameter and Eulerian Slenderness. Materials 2020, 13, 1597. https://doi.org/10.3390/ma13071597
Oyedeji Falope F, Lanzoni L, Tarantino AM. FE Analyses of Hyperelastic Solids under Large Bending: The Role of the Searle Parameter and Eulerian Slenderness. Materials. 2020; 13(7):1597. https://doi.org/10.3390/ma13071597
Chicago/Turabian StyleOyedeji Falope, Federico, Luca Lanzoni, and Angelo Marcello Tarantino. 2020. "FE Analyses of Hyperelastic Solids under Large Bending: The Role of the Searle Parameter and Eulerian Slenderness" Materials 13, no. 7: 1597. https://doi.org/10.3390/ma13071597
APA StyleOyedeji Falope, F., Lanzoni, L., & Tarantino, A. M. (2020). FE Analyses of Hyperelastic Solids under Large Bending: The Role of the Searle Parameter and Eulerian Slenderness. Materials, 13(7), 1597. https://doi.org/10.3390/ma13071597





