A Review on Cementitious Self-Healing and the Potential of Phase-Field Methods for Modeling Crack-Closing and Fracture Recovery
Abstract
1. Introduction
2. Self-Healing Mechanisms in Concrete
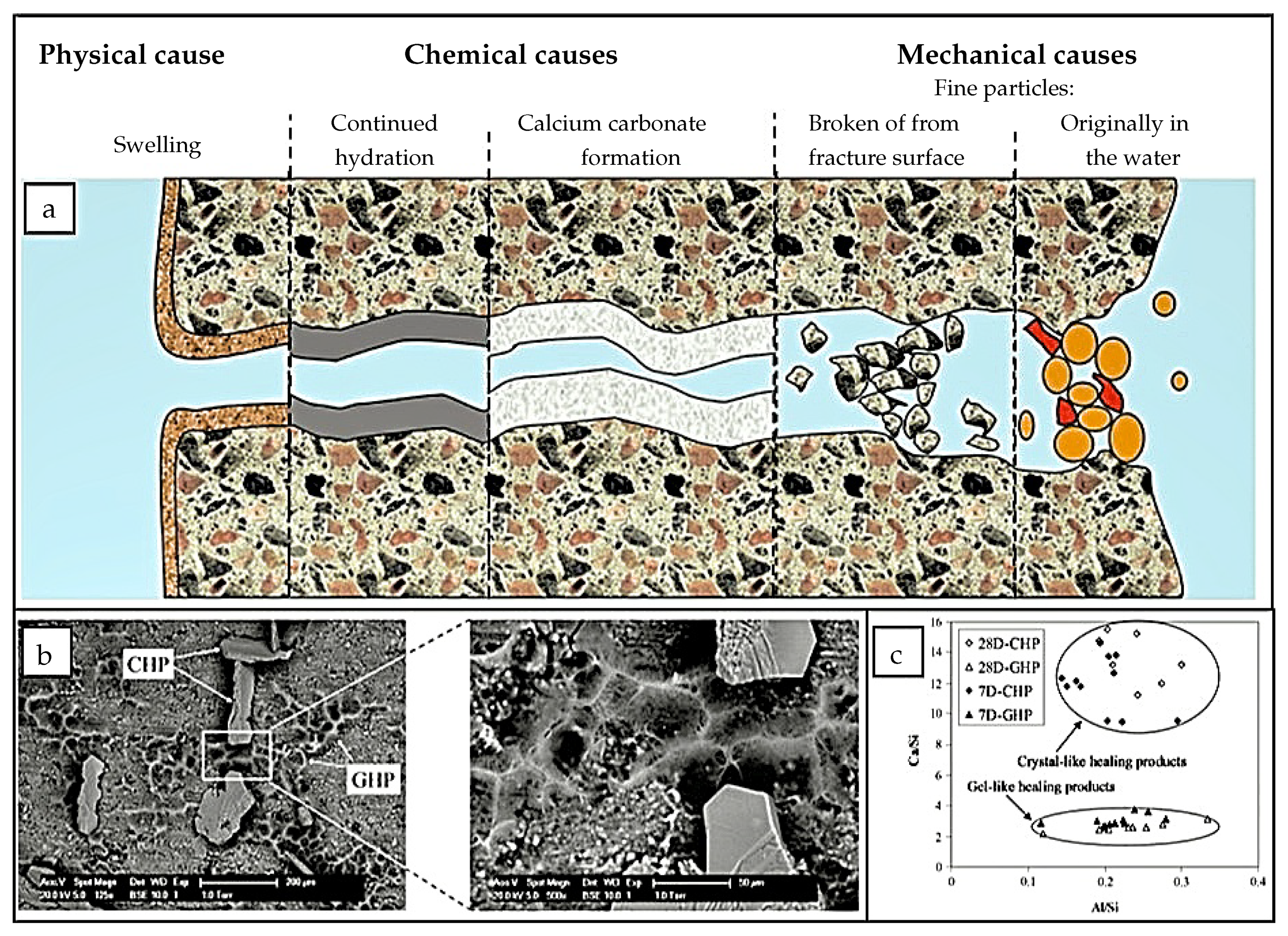
2.1. Autogenous Self-Healing
2.2. Autonomous Self-Healing
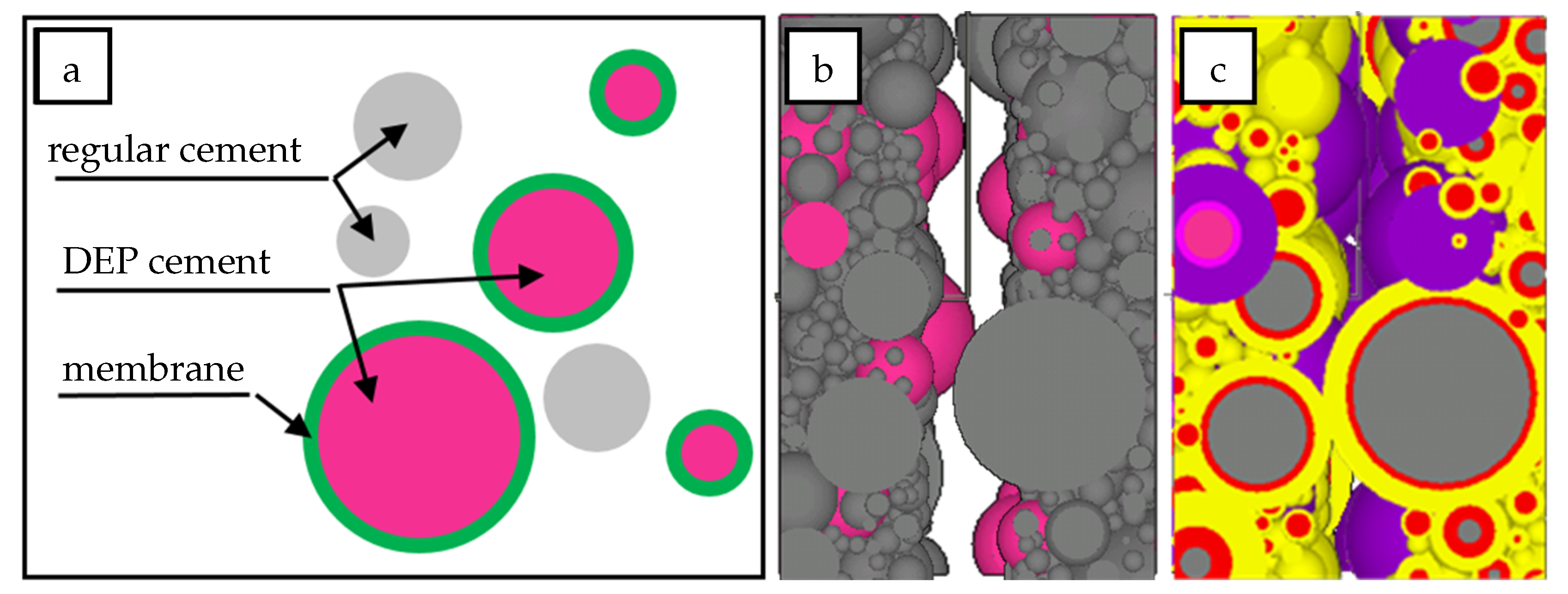
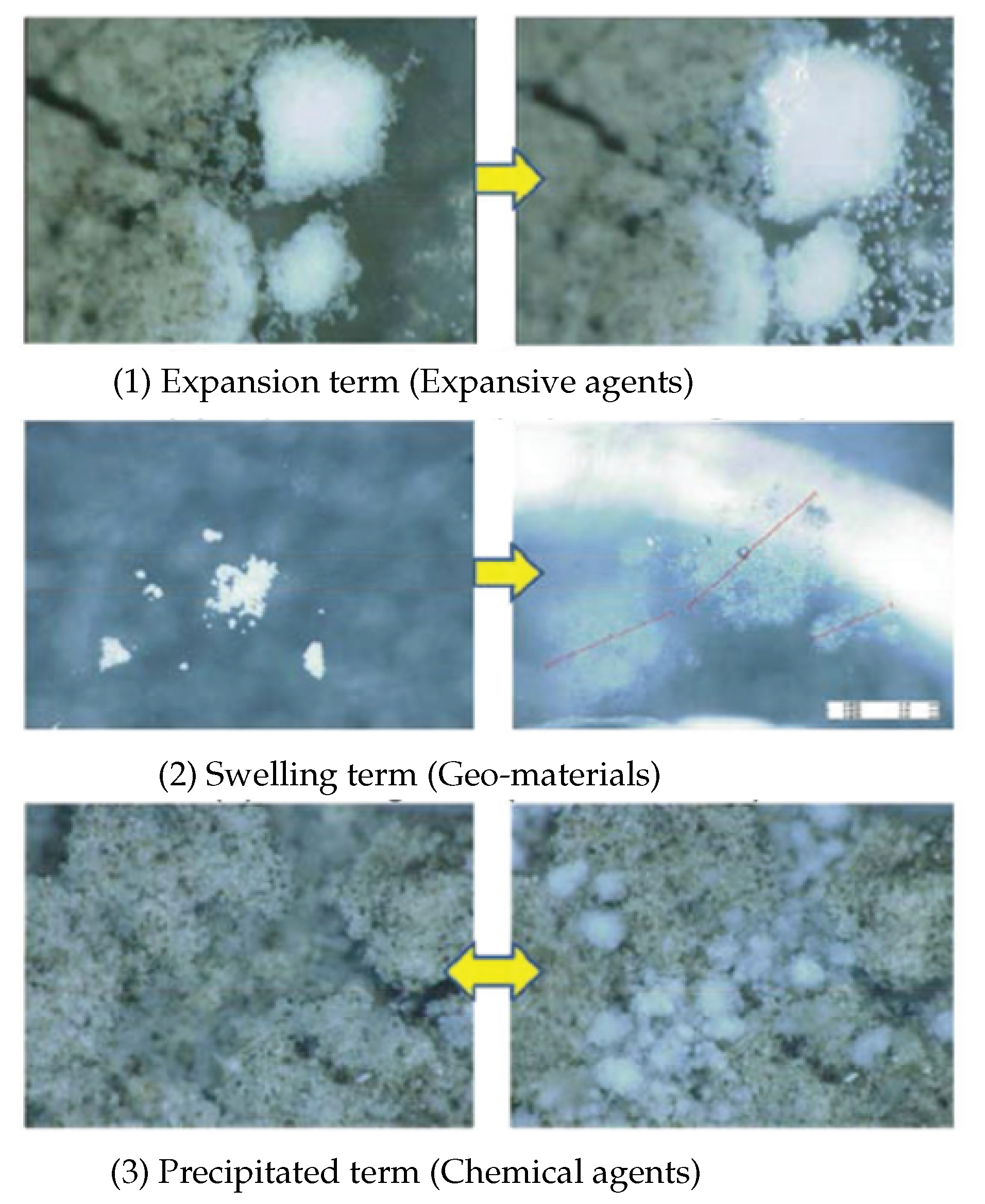
2.2.1. Self-Healing Based on Mineral Admixtures
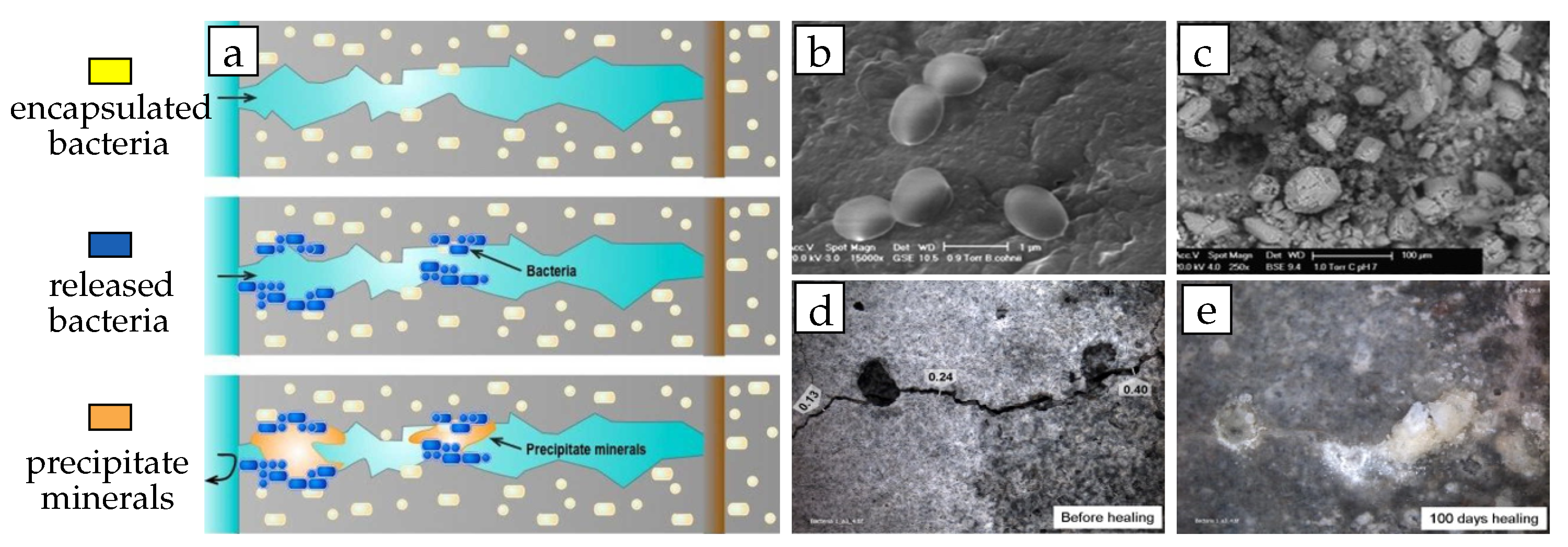
2.2.2. Self-Healing Based on Bacteria
2.2.3. Self-Healing Based on Adhesive Agents
3. Phase-Field Methods for Modeling Concrete Self-Healing
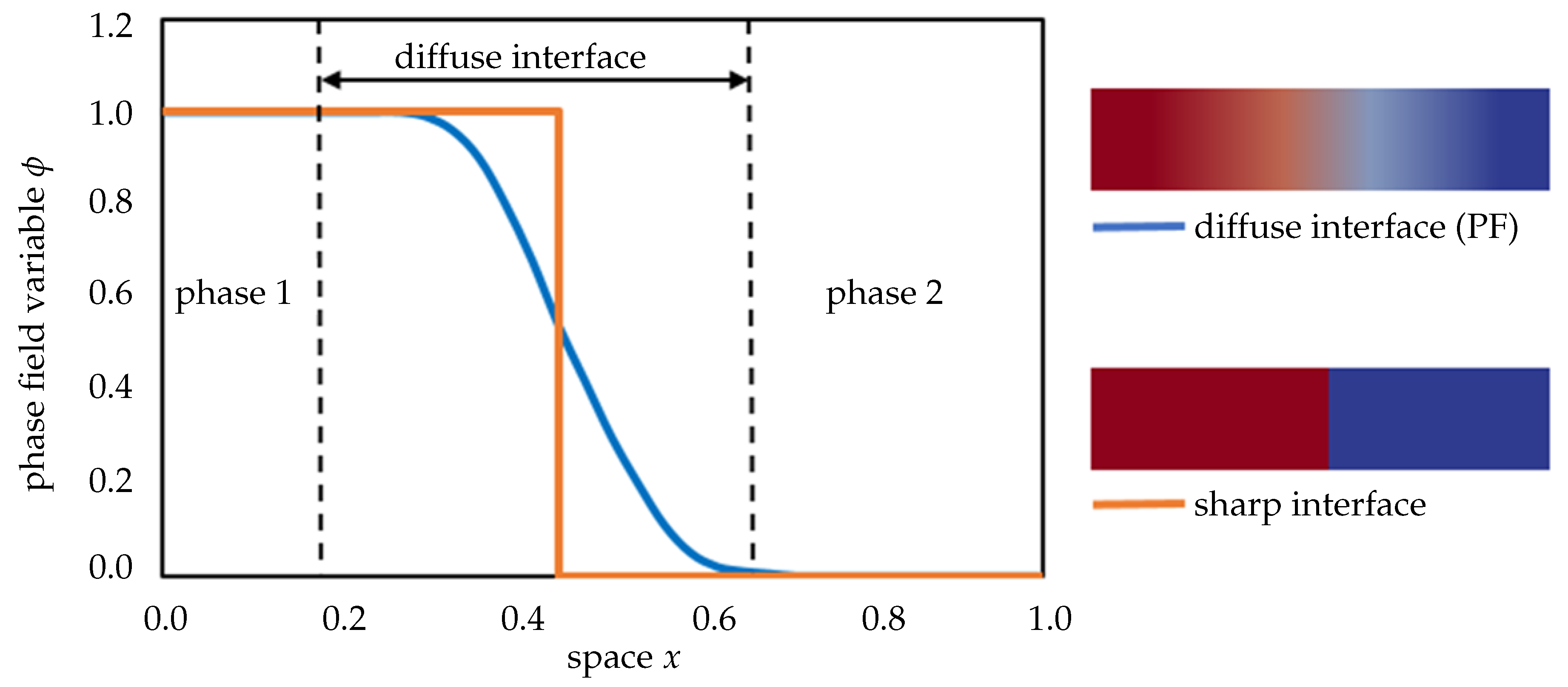
- PF is an extremely powerful mathematical modeling scheme for accurately describing physical movements of phase boundaries.
- PF was mainly employed for solving solidification dynamics, material phase changes/separations, growing phases driven by chemo-kinetics and transport phenomena, nucleation and coalescence processes between particles in micro-to-mesostructures.
- PF has been successfully employed in fracture mechanics to capture the cracking response of brittle/ductile materials without the need for employing Discrete Crack Approaches (DCAs) and/or Smeared Crack Approaches (SCA).
4. Main Equations of a Phase-Field Approach
4.1. Evolution Equation
4.2. Local Free Energy Function
5. Phase-Field Modeling of Precipitation Reaction Mechanisms
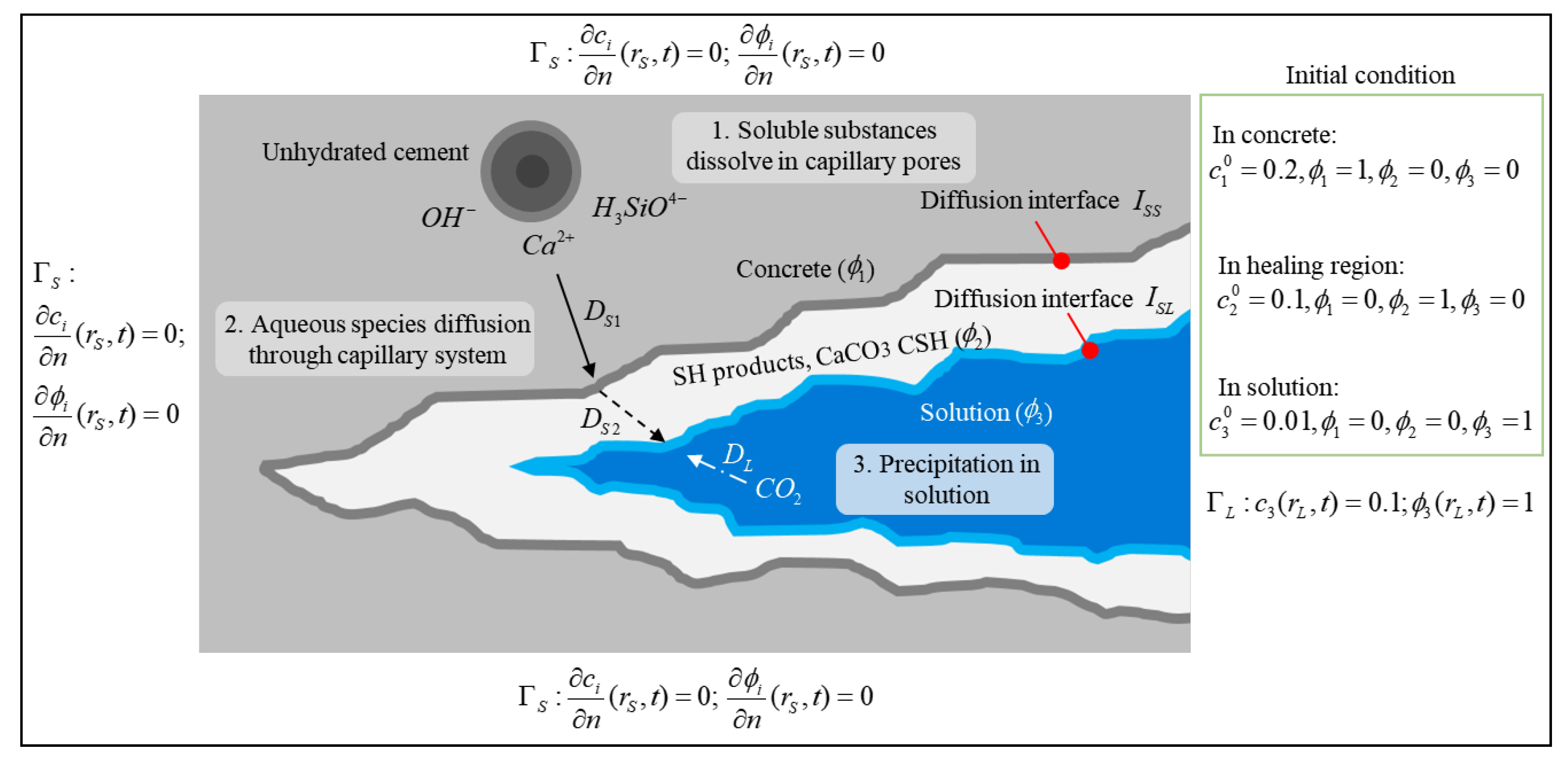
5.1. Solute Precipitation
5.1.1. Xu-Meakin Model, 2008
5.1.2. Noorden-Eck Model, 2011
5.2. Metal Precipitation
5.2.1. Wang–Chen Model, 1993
5.2.2. Rubin–Khachaturyan Model, 1999
5.2.3. Chen–Ma Model, 2004
6. Phase-Field Modeling for Fracture Mechanisms
6.1. Fundamental Variational Formulations
6.2. Regularized Variational Theory
7. Discussion and Conclusions
- Evolution of the pore structure at the crack surface:During the process of autonomous self-healing, soluble substances at the crack surface enter the solution and undergo various dissolution reactions, followed by hydration and carbonation crystallization reactions. Part of the solution will diffuse into the capillary pores of the concrete matrix, where crystallization and precipitation also occur. The growth of the cracked surface also forms a new pore structure, which further affects the diffusion and chemical reaction processes. Thus, the pore structure of the crack boundary is constantly changing with ongoing reaction. Its interaction with the crack morphology, reactant concentration, and mass transport needs to be investigated in the future.
- Influencing factors and simulations for mechanical repair of cracks:The fracture PF part is a combination of elastic and fracture energies. Elastic free energy will follow the classical assumptions while the fracture part will account for the fracture toughness, order formulation, evolution equations, and healing regain laws. Moreover, both are closely related to the packing density field. This is because the mechanical properties at fracture mainly depend on the solid-phase continuity. The mechanical properties are enhanced in a homogeneously dense position of the filler and, conversely, worse in the disconnected parts of the solid phase. The packing density field, in turn, is related to the mass transport. Therefore, a numerical transport–mechanical coupling strategy shall be developed to simulate the overall performance of the self-healing mechanism.
- Evolution of crack healing morphology:The morphology of the crack greatly influences its local healing effect. At the crack tip, healing products are produced faster and more frequently because of the higher concentration of reactants. The movement of the crack tip is faster than at other locations. Thus the crack morphology changes continuously with the healing process. As the PF model avoids tracking the boundary conditions at the interface and instead simulates the evolution of the auxiliary field. Therefore, the evolution of the interfacial morphology is easier to simulate. In addition, the simulation of interfacial morphology will take into account the distribution of bacteria, adhesive agents and mineral admixtures. Therefore, the macroscopic representation of a crack healing morphology shall be simulated from a micro-level point of view.
- Free energy to distinguish between various product phases:Self-healing products contain multiple substances (CSH, CH, or additional byproducts) that, although they have the same healing mechanism (aggregation, crystallization and precipitation), their chemical reaction kinetics are different. This affects the rate of healing of the cracks as a whole. Therefore, the free energies of the various product phases and the corresponding thermodynamic parameters will be distinguished in the future and reflected in specific simulations.
- Determination of PF parameters:A formulation for the determination of the PF parameters needs to be provided. Information on the PF parameters and their interrelationships will be obtained from thermodynamic and diffusion databases in combination with experimental data. Combined with the second law of thermodynamics and non-equilibrium thermodynamics, the self-diffusion, mutual diffusion, and chemical diffusion coefficients will be related to the diffusion mobility (M). The order parameter mobility (L) will be derived and their relationship to other phase-field parameters will be investigated.
- Development of a three-dimensional model:As a self-healing process includes complex physical-chemical-mechanical processes, these mechanisms can only be accurately simulated in a fully three-dimensional system. Therefore, a three-dimensional simulation of the self-healing process need to be performed with realistic boundary conditions. The simulation results need to be verified and compared with 3D computed tomography scan (CT scan) results of concrete specimens.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shetty, M. Concrete Technology, S; Chand and Company Ltd.: New Delhi, India, 2005. [Google Scholar]
- Perlovsky, L.I. Conundrum of combinatorial complexity. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 666–670. [Google Scholar] [CrossRef]
- Kaplan, M. Crack propagation and the fracture of concrete. J. Proc. 1961, 58, 591–610. [Google Scholar]
- Frosch, R.J. Another look at cracking and crack control in reinforced concrete. Struct. J. 1999, 96, 437–442. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Roumaldi, J.; Batson, G.B. Mechanics of Crack Arrest in Concrete. J. Eng. Mech. Div. ASCE Proc. 1963, 89, 147–168. [Google Scholar]
- Ferrara, L.; Asensio, E.C.; Monte, F.L.; Flores, M.R.; Moreno, M.S.; Snoeck, D.; Mullem, T.V.; Belie, N.D. Experimental characterization of the self-healing capacity of cement based materials: An overview. Proceedings 2018, 2, 454. [Google Scholar] [CrossRef]
- Ferrara, L.; Van Mullem, T.; Alonso, M.C.; Antonaci, P.; Borg, R.P.; Cuenca, E.; Jefferson, A.; Ng, P.L.; Peled, A.; Roig-Flores, M.; et al. Experimental characterization of the self-healing capacity of cement based materials and its effects on the material performance: A state of the art report by COST Action SARCOS WG2. Constr. Build. Mater. 2018, 167, 115–142. [Google Scholar] [CrossRef]
- Van Tittelboom, K.; De Belie, N. Self-healing in cementitious materials—A review. Materials 2013, 6, 2182–2217. [Google Scholar] [CrossRef]
- Hearn, N. Self-sealing, autogenous healing and continued hydration: What is the difference? Mater. Struct. 1998, 31, 563. [Google Scholar] [CrossRef]
- Koenders, E.; Ukrainczyk, N.; Caggiano, A. Modelling the Self-Healing Potential of Dissoluble Encapsulated Cement. In Proceedings of the 7th European Conference on Computational Fluid Dynamics (ECFD 7), Glasgow, UK, 11–15 June 2018. [Google Scholar]
- Yang, S.; Caggiano, A.; Yi, M.; Ukrainczyk, N.; Koenders, E. Modelling autogenous self-healing with dissoluble encapsulated particles using a phase field approach. In Conference: Mecánica Computacional, Santa Fe, Argentina, 5–7 Noviembre 2019; Asociación Argentina de Mecánica Computacional: Santa Fe, Argentina, 2019; Volume 37, pp. 1457–1467. [Google Scholar]
- Huang, H.; Ye, G.; Damidot, D. Effect of blast furnace slag on self-healing of microcracks in cementitious materials. Cem. Concr. Res. 2014, 60, 68–82. [Google Scholar] [CrossRef]
- Jonkers, H.M. Self healing concrete: A biological approach. In Self Healing Materials; Springer: Berlin/Heidelberg, Germany, 2007; pp. 195–204. [Google Scholar]
- Ghosh, S.K. Self-Healing Materials: Fundamentals, Design Strategies, and Applications; Wiley-vch: Weinheim, Germany, 2009. [Google Scholar]
- De Rooij, M.; Van Tittelboom, K.; De Belie, N.; Schlangen, E. Self-Healing Phenomena in Cement-Based Materials: State-of-the-Art Report of RILEM Technical Committee 221-SHC: Self-Healing Phenomena in Cement-Based Materials; Springer: Berlin/Heidelberg, Germany, 2013; Volume 11. [Google Scholar]
- Li, V.C.; Yang, E.H. Self healing in concrete materials. In Self Healing Materials; Springer: Berlin/Heidelberg, Germany, 2007; pp. 161–193. [Google Scholar]
- Van Tittelboom, K.; Gruyaert, E.; Rahier, H.; De Belie, N. Influence of mix composition on the extent of autogenous crack healing by continued hydration or calcium carbonate formation. Constr. Build. Mater. 2012, 37, 349–359. [Google Scholar] [CrossRef]
- Snoeck, D.; De Belie, N. Repeated autogenous healing in strain-hardening cementitious composites by using superabsorbent polymers. J. Mater. Civ. Eng. 2016, 28, 04015086. [Google Scholar] [CrossRef]
- Snoeck, D.; De Belie, N. From straw in bricks to modern use of microfibers in cementitious composites for improved autogenous healing—A review. Constr. Build. Mater. 2015, 95, 774–787. [Google Scholar] [CrossRef]
- Mihashi, H.; Nishiwaki, T. Development of engineered self-healing and self-repairing concrete-state-of-the-art report. J. Adv. Concr. Technol. 2012, 10, 170–184. [Google Scholar] [CrossRef]
- Rule, J.D.; Brown, E.N.; Sottos, N.R.; White, S.R.; Moore, J.S. Wax-protected catalyst microspheres for efficient self-healing materials. Adv. Mater. 2005, 17, 205–208. [Google Scholar] [CrossRef]
- Dong, B.; Ding, W.; Qin, S.; Han, N.; Fang, G.; Liu, Y.; Xing, F.; Hong, S. Chemical self-healing system with novel microcapsules for corrosion inhibition of rebar in concrete. Cem. Concr. Compos. 2018, 85, 83–91. [Google Scholar] [CrossRef]
- Snoeck, D.; Van Tittelboom, K.; Steuperaert, S.; Dubruel, P.; De Belie, N. Self-healing cementitious materials by the combination of microfibres and superabsorbent polymers. J. Intell. Mater. Syst. Struct. 2014, 25, 13–24. [Google Scholar] [CrossRef]
- Alghamri, R.; Kanellopoulos, A.; Litina, C.; Al-Tabbaa, A. Preparation and polymeric encapsulation of powder mineral pellets for self-healing cement based materials. Constr. Build. Mater. 2018, 186, 247–262. [Google Scholar] [CrossRef]
- Roig-Flores, M.; Moscato, S.; Serna, P.; Ferrara, L. Self-healing capability of concrete with crystalline admixtures in different environments. Constr. Build. Mater. 2015, 86, 1–11. [Google Scholar] [CrossRef]
- Roig-Flores, M.; Pirritano, F.; Serna, P.; Ferrara, L. Effect of crystalline admixtures on the self-healing capability of early-age concrete studied by means of permeability and crack closing tests. Constr. Build. Mater. 2016, 114, 447–457. [Google Scholar] [CrossRef]
- Van Tittelboom, K.; De Belie, N.; De Muynck, W.; Verstraete, W. Use of bacteria to repair cracks in concrete. Cem. Concr. Res. 2010, 40, 157–166. [Google Scholar] [CrossRef]
- Wang, J.; Soens, H.; Verstraete, W.; De Belie, N. Self-healing concrete by use of microencapsulated bacterial spores. Cem. Concr. Res. 2014, 56, 139–152. [Google Scholar] [CrossRef]
- Tan, N.P.B.; Keung, L.H.; Choi, W.H.; Lam, W.C.; Leung, H.N. Silica-based self-healing microcapsules for self-repair in concrete. J. Appl. Polym. Sci. 2016, 133. [Google Scholar] [CrossRef]
- Aliko-Benítez, A.; Doblaré, M.; Sanz-Herrera, J. Chemical-diffusive modeling of the self-healing behavior in concrete. Int. J. Solids Struct. 2015, 69, 392–402. [Google Scholar] [CrossRef]
- Huang, H.; Ye, G. Simulation of self-healing by further hydration in cementitious materials. Cem. Concr. Compos. 2012, 34, 460–467. [Google Scholar] [CrossRef]
- Ferrara, L.; Di Luzio, G.; Krelani, V. Experimental Assessment and Numerical Modeling of Self Healing Capacity of Cement Based Materials via Fracture Mechanics Concepts. In Proceedings of the 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures (FraMCoS-9), Berkeley, CA, USA, 29 May–1 June 2016; pp. 1–12. [Google Scholar]
- Di Luzio, G.; Ferrara, L.; Krelani, V. A numerical model for the self-healing capacity of cementitious composites. In Proceedings of the Computational Modelling of Concrete Structures, St. Anton am Arlberg, Austria, 24–27 March 2014. [Google Scholar]
- Zemskov, S.V.; Jonkers, H.M.; Vermolen, F.J. Mathematical models to predict the critical conditions for bacterial self-healing of concrete. In Proceedings of the International Conference on Mathematical Modeling and Computational Physics, Stará Lesná, Slovakia, 4–8 July 2011; pp. 108–121. [Google Scholar]
- Zemskov, S.V.; Jonkers, H.M.; Vermolen, F.J. A mathematical model for bacterial self-healing of cracks in concrete. J. Intell. Mater. Syst. Struct. 2014, 25, 4–12. [Google Scholar] [CrossRef]
- Hilloulin, B.; Grondin, F.; Matallah, M.; Loukili, A. Modelling of autogenous healing in ultra high performance concrete. Cem. Concr. Res. 2014, 61, 64–70. [Google Scholar] [CrossRef]
- Di Luzio, G.; Ferrara, L.; Krelani, V. Numerical modeling of mechanical regain due to self-healing in cement based composites. Cem. Concr. Compos. 2018, 86, 190–205. [Google Scholar] [CrossRef]
- Mergheim, J.; Steinmann, P. Phenomenological modelling of self-healing polymers based on integrated healing agents. Comput. Mech. 2013, 52, 681–692. [Google Scholar] [CrossRef]
- Darabi, M.K.; Al-Rub, R.K.A.; Little, D.N. A continuum damage mechanics framework for modeling micro-damage healing. Int. J. Solids Struct. 2012, 49, 492–513. [Google Scholar] [CrossRef]
- Hilloulin, B.; Hilloulin, D.; Grondin, F.; Loukili, A.; De Belie, N. Mechanical regains due to self-healing in cementitious materials: Experimental measurements and micro-mechanical model. Cem. Concr. Res. 2016, 80, 21–32. [Google Scholar] [CrossRef]
- Miao, S.; Wang, M.L.; Schreyer, H.L. Constitutive models for healing of materials with application to compaction of crushed rock salt. J. Eng. Mech. 1995, 121, 1122–1129. [Google Scholar] [CrossRef]
- Barbero, E.J.; Greco, F.; Lonetti, P. Continuum damage-healing mechanics with application to self-healing composites. Int. J. Damage Mech. 2005, 14, 51–81. [Google Scholar] [CrossRef]
- Barbero, E.J.; Ford, K.J. Characterization of self-healing fiber-reinforced polymer-matrix composite with distributed damage. J. Adv. Mater. Covina 2007, 39, 20–27. [Google Scholar]
- Hazelwood, T.; Jefferson, A.D.; Lark, R.J.; Gardner, D.R. Numerical simulation of the long-term behaviour of a self-healing concrete beam vs standard reinforced concrete. Eng. Struct. 2015, 102, 176–188. [Google Scholar] [CrossRef][Green Version]
- Davies, R.; Jefferson, A. Micromechanical modelling of self-healing cementitious materials. Int. J. Solids Struct. 2017, 113, 180–191. [Google Scholar] [CrossRef]
- Remmers, J.J.; de Borst, R. Numerical modelling of self healing mechanisms. In Self Healing Materials; Springer: Berlin/Heidelberg, Germany, 2007; pp. 365–380. [Google Scholar]
- Alsheghri, A.A.; Al-Rub, R.K.A. Thermodynamic-based cohesive zone healing model for self-healing materials. Mech. Res. Commun. 2015, 70, 102–113. [Google Scholar] [CrossRef]
- Alsheghri, A.A.; Al-Rub, R.K.A. Finite element implementation and application of a cohesive zone damage-healing model for self-healing materials. Eng. Fract. Mech. 2016, 163, 1–22. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, X. A softening-healing law for self-healing quasi-brittle materials: Analyzing with strong discontinuity embedded approach. Eng. Fract. Mech. 2018, 192, 290–306. [Google Scholar] [CrossRef]
- Gilabert, F.; Garoz, D.; Van Paepegem, W. Macro-and micro-modeling of crack propagation in encapsulation-based self-healing materials: Application of XFEM and cohesive surface techniques. Mater. Des. 2017, 130, 459–478. [Google Scholar] [CrossRef]
- Zhou, S.; Zhu, H.; Yan, Z.; Ju, J.W.; Zhang, L. A micromechanical study of the breakage mechanism of microcapsules in concrete using PFC2D. Constr. Build. Mater. 2016, 115, 452–463. [Google Scholar] [CrossRef]
- Caggiano, A.; Etse, G.; Ferrara, L.; Krelani, V. Zero-thickness interface constitutive theory for concrete self-healing effects. Comput. Struct. 2017, 186, 22–34. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-field models in materials science. Model. Simul. Mater. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Warren, J.A.; Beckermann, C.; Karma, A. Phase-field simulation of solidification. Annu. Rev. Mater. Res. 2002, 32, 163–194. [Google Scholar] [CrossRef]
- Chen, L.Q. Phase-field models for microstructure evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef]
- Pan, S.; Zhu, M. A three-dimensional sharp interface model for the quantitative simulation of solutal dendritic growth. Acta Mater. 2010, 58, 340–352. [Google Scholar] [CrossRef]
- Bangert, F.; Kuhl, D.; Meschke, G. Chemo-hygro-mechanical modelling and numerical simulation of concrete deterioration caused by alkali-silica reaction. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 689–714. [Google Scholar] [CrossRef]
- Wang, H.; Liu, F.; Zhai, H.; Wang, K. Application of the maximal entropy production principle to rapid solidification: A sharp interface model. Acta Mater. 2012, 60, 1444–1454. [Google Scholar] [CrossRef]
- Ma, L.; Chen, R.; Yang, X.; Zhang, H. Numerical approximations for Allen-Cahn type phase field model of two-phase incompressible fluids with moving contact lines. Commun. Comput. Phys. 2017, 21, 867–889. [Google Scholar] [CrossRef]
- Gómez, H.; Calo, V.M.; Bazilevs, Y.; Hughes, T.J. Isogeometric analysis of the Cahn–Hilliard phase-field model. Comput. Methods Appl. Mech. Eng. 2008, 197, 4333–4352. [Google Scholar] [CrossRef]
- Talaiekhozan, A.; Keyvanfar, A.; Shafaghat, A.; Andalib, R.; Majid, M.; Fulazzaky, M.A.; Zin, R.M.; Lee, C.T.; Hussin, M.W.; Hamzah, N.; et al. A review of self-healing concrete research development. J. Environ. Treat. Tech. 2014, 2, 1–11. [Google Scholar]
- Luhar, S.; Gourav, S. A review paper on self healing concrete. J. Civ. Eng. Res. 2015, 5, 53–58. [Google Scholar]
- Yang, Y.; Yang, E.H.; Li, V.C. Autogenous healing of engineered cementitious composites at early age. Cem. Concr. Res. 2011, 41, 176–183. [Google Scholar] [CrossRef]
- Edvardsen, C. Water permeability and autogenous healing of cracks in concrete. Mater. J. 1999, 96, 448–454. [Google Scholar]
- Van Tittelboom, K.; De Belie, N.; Lehmann, F.; Grosse, C.U. Acoustic emission analysis for the quantification of autonomous crack healing in concrete. Constr. Build. Mater. 2012, 28, 333–341. [Google Scholar] [CrossRef]
- De Belie, N.; Gruyaert, E.; Al-Tabbaa, A.; Antonaci, P.; Baera, C.; Bajare, D.; Darquennes, A.; Davies, R.; Ferrara, L.; Jefferson, T.; et al. A review of self-healing concrete for damage management of structures. Adv. Mater. Interfaces 2018, 5, 1800074. [Google Scholar] [CrossRef]
- Ferrara, L.; Krelani, V.; Carsana, M. A “fracture testing” based approach to assess crack healing of concrete with and without crystalline admixtures. Constr. Build. Mater. 2014, 68, 535–551. [Google Scholar] [CrossRef]
- Yang, Y.; Lepech, M.D.; Yang, E.H.; Li, V.C. Autogenous healing of engineered cementitious composites under wet–dry cycles. Cem. Concr. Res. 2009, 39, 382–390. [Google Scholar] [CrossRef]
- Reinhardt, H.; Jonkers, H.; Van Tittelboom, K.; Snoeck, D.; De Belie, N.; De Muynck, W.; Verstraete, W.; Wang, J.; Mechtcherine, V. Recovery against environmental action. In Self-Healing Phenomena in Cement-Based Materials; Springer: Berlin/Heidelberg, Germany, 2013; pp. 65–117. [Google Scholar]
- Qureshi, T.; Kanellopoulos, A.; Al-Tabbaa, A. Autogenous self-healing of cement with expansive minerals-I: Impact in early age crack healing. Constr. Build. Mater. 2018, 192, 768–784. [Google Scholar] [CrossRef]
- Clear, C. The Effects of Autogenous Healing upon the Leakage of Water through Cracks in Concrete; Tech Rpt. 559; Transport Research Laboratory: Crowthorne, UK, 1985. [Google Scholar]
- Meichsner, H. Über die Selbstdichtung von Trennrissen in Beton. Beton-Und Stahlbetonbau 1992, 87, 95–99. [Google Scholar] [CrossRef]
- Reinhardt, H.W.; Jooss, M. Permeability and self-healing of cracked concrete as a function of temperature and crack width. CEment Concr. Res. 2003, 33, 981–985. [Google Scholar] [CrossRef]
- Neville, A. Autogenous healing—A concrete miracle? Concr. Int. 2002, 24, 76–82. [Google Scholar]
- Huang, H.; Ye, G.; Damidot, D. Characterization and quantification of self-healing behaviors of microcracks due to further hydration in cement paste. Cem. Concr. Res. 2013, 52, 71–81. [Google Scholar] [CrossRef]
- Jefferson, T.; Javierre, E.; Freeman, B.; Zaoui, A.; Koenders, E.; Ferrara, L. Research progress on numerical models for self-healing cementitious materials. Adv. Mater. Interfaces 2018, 5, 1701378. [Google Scholar] [CrossRef]
- Lee, Y.S.; Ryou, J.S. Self healing behavior for crack closing of expansive agent via granulation/film coating method. Constr. Build. Mater. 2014, 71, 188–193. [Google Scholar] [CrossRef]
- Ahn, T.H.; Kishi, T. Crack self-healing behavior of cementitious composites incorporating various mineral admixtures. J. Adv. Concr. Technol. 2010, 8, 171–186. [Google Scholar] [CrossRef]
- Jonkers, H.M.; Thijssen, A.; Muyzer, G.; Copuroglu, O.; Schlangen, E. Application of bacteria as self-healing agent for the development of sustainable concrete. Ecol. Eng. 2010, 36, 230–235. [Google Scholar] [CrossRef]
- Wiktor, V.; Jonkers, H.M. Quantification of crack-healing in novel bacteria-based self-healing concrete. Cem. Concr. Compos. 2011, 33, 763–770. [Google Scholar] [CrossRef]
- Gupta, S.; Dai Pang, S.; Kua, H.W. Autonomous healing in concrete by bio-based healing agents—A review. Constr. Build. Mater. 2017, 146, 419–428. [Google Scholar] [CrossRef]
- Jonkers, H.M. Bacteria-based self-healing concrete. Heron 2011, 56. [Google Scholar]
- Wang, J.Y.; De Belie, N.; Verstraete, W. Diatomaceous earth as a protective vehicle for bacteria applied for self-healing concrete. J. Ind. Microbiol. Biotechnol. 2012, 39, 567–577. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Snoeck, D.; Van Vlierberghe, S.; Verstraete, W.; De Belie, N. Application of hydrogel encapsulated carbonate precipitating bacteria for approaching a realistic self-healing in concrete. Constr. Build. Mater. 2014, 68, 110–119. [Google Scholar] [CrossRef]
- Luo, M.; Qian, C.X.; Li, R.Y. Factors affecting crack repairing capacity of bacteria-based self-healing concrete. Constr. Build. Mater. 2015, 87, 1–7. [Google Scholar] [CrossRef]
- Wang, J.; Mignon, A.; Snoeck, D.; Wiktor, V.; Van Vliergerghe, S.; Boon, N.; De Belie, N. Application of modified-alginate encapsulated carbonate producing bacteria in concrete: A promising strategy for crack self-healing. Front. Microbiol. 2015, 6, 1088. [Google Scholar] [CrossRef]
- Khaliq, W.; Ehsan, M.B. Crack healing in concrete using various bio influenced self-healing techniques. Constr. Build. Mater. 2016, 102, 349–357. [Google Scholar] [CrossRef]
- Thao, T.D.P.; Johnson, T.J.S.; Tong, Q.S.; Dai, P.S. Implementation of self-healing in concrete–proof of concept. IES J. Part A Civ. Struct. Eng. 2009, 2, 116–125. [Google Scholar] [CrossRef]
- Van Belleghem, B.; Kessler, S.; Van den Heede, P.; Van Tittelboom, K.; De Belie, N. Chloride induced reinforcement corrosion behavior in self-healing concrete with encapsulated polyurethane. Cem. Concr. Res. 2018, 113, 130–139. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, W.; Yuan, Z. Influence of mineral additives and environmental conditions on the self-healing capabilities of cementitious materials. Cem. Concr. Compos. 2015, 57, 116–127. [Google Scholar] [CrossRef]
- Jaroenratanapirom, D.; Sahamitmongkol, R. Effects of different mineral additives and cracking ages on self-healing performance of mortar. In Proceedings of the 6th Annual Concrete Conference, Phetchaburi, Thailand, 20–23 October 2010; pp. 551–556. [Google Scholar]
- Jiang, Z.; Li, W.; Yuan, Z.; Yang, Z. Self-healing of cracks in concrete with various crystalline mineral additives in underground environment. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2014, 29, 938–944. [Google Scholar] [CrossRef]
- Kanellopoulos, A.; Qureshi, T.; Al-Tabbaa, A. Glass encapsulated minerals for self-healing in cement based composites. Constr. Build. Mater. 2015, 98, 780–791. [Google Scholar] [CrossRef]
- Qureshi, T.; Kanellopoulos, A.; Al-Tabbaa, A. Encapsulation of expansive powder minerals within a concentric glass capsule system for self-healing concrete. Constr. Build. Mater. 2016, 121, 629–643. [Google Scholar] [CrossRef]
- Sisomphon, K.; Copuroglu, O.; Koenders, E. Self-healing of surface cracks in mortars with expansive additive and crystalline additive. Cem. Concr. Compos. 2012, 34, 566–574. [Google Scholar] [CrossRef]
- Ahn, T.; Kishi, T. The effect of geo-materials on the autogenous healing behavior of cracked concrete. In Concrete Repair, Rehabilitation and Retrofitting II, Cape Town, South Africa; CRC Press: Boca Raton, FL, USA, 2008; pp. 125–126. [Google Scholar]
- Buller, A.S.; Lee, K.M.; Jang, S.Y. Mechanical recovery of cracked fiber-reinforced mortar incorporating crystalline admixture, expansive agent, and geomaterial. Adv. Mater. Sci. Eng. 2019, 2019, 3420349. [Google Scholar] [CrossRef]
- Lucas, S.S.; Moxham, C.; Tziviloglou, E.; Jonkers, H. Study of self-healing properties in concrete with bacteria encapsulated in expanded clay. Sci. Technol. Mater. 2018, 30, 93–98. [Google Scholar] [CrossRef]
- Jonkers, H.M.; Schlangen, E. A two component bacteria-based self-healing concrete. In Proceedings of the 2nd International Conference on Concrete Repair, Rehabilitation and Retrofitting, Cape Town, South Africa, 24–26 November 2008; pp. 119–120. [Google Scholar]
- Jonkers, H.M.; Schlangen, E. Crack repair by concrete-immobilized bacteria. In Proceedings of the First International Conference on Self Healing Materials, Noordwijk Aan Zee, The Netherlands, 18–20 April 2007; Volume 18, p. 20. [Google Scholar]
- Kua, H.W.; Gupta, S.; Aday, A.N.; Srubar III, W.V. Biochar-immobilized bacteria and superabsorbent polymers enable self-healing of fiber-reinforced concrete after multiple damage cycles. Cem. Concr. Compos. 2019, 100, 35–52. [Google Scholar] [CrossRef]
- Wu, M.; Hu, X.; Zhang, Q.; Xue, D.; Zhao, Y. Growth environment optimization for inducing bacterial mineralization and its application in concrete healing. Constr. Build. Mater. 2019, 209, 631–643. [Google Scholar] [CrossRef]
- Li, V.C.; Herbert, E. Robust self-healing concrete for sustainable infrastructure. J. Adv. Concr. Technol. 2012, 10, 207–218. [Google Scholar] [CrossRef]
- Lee, Y.S.; Park, W. Current challenges and future directions for bacterial self-healing concrete. Appl. Microbiol. Biotechnol. 2018, 102, 3059–3070. [Google Scholar] [CrossRef]
- Rao, M.; Reddy, V.S.; Hafsa, M.; Veena, P.; Anusha, P. Bioengineered concrete-a sustainable self-healing construction material. Res. J. Eng. Sci. ISSN 2013, 2278, 9472. [Google Scholar]
- Xu, J.; Yao, W. Multiscale mechanical quantification of self-healing concrete incorporating non-ureolytic bacteria-based healing agent. Cem. Concr. Res. 2014, 64, 1–10. [Google Scholar] [CrossRef]
- Alazhari, M.; Sharma, T.; Heath, A.; Cooper, R.; Paine, K. Application of expanded perlite encapsulated bacteria and growth media for self-healing concrete. Constr. Build. Mater. 2018, 160, 610–619. [Google Scholar] [CrossRef]
- Han, S.; Choi, E.K.; Park, W.; Yi, C.; Chung, N. Effectiveness of expanded clay as a bacteria carrier for self-healing concrete. Appl. Biol. Chem. 2019, 62, 19. [Google Scholar] [CrossRef]
- Alghamri, R.; Kanellopoulos, A.; Al-Tabbaa, A. Impregnation and encapsulation of lightweight aggregates for self-healing concrete. Constr. Build. Mater. 2016, 124, 910–921. [Google Scholar] [CrossRef]
- Seifan, M.; Samani, A.K.; Berenjian, A. Bioconcrete: Next generation of self-healing concrete. Appl. Microbiol. Biotechnol. 2016, 100, 2591–2602. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Hollar, J.; He, X.; Shi, X. A self-healing cementitious composite using oil core/silica gel shell microcapsules. Cem. Concr. Compos. 2011, 33, 506–512. [Google Scholar] [CrossRef]
- Dong, B.; Fang, G.; Ding, W.; Liu, Y.; Zhang, J.; Han, N.; Xing, F. Self-healing features in cementitious material with urea–formaldehyde/epoxy microcapsules. Constr. Build. Mater. 2016, 106, 608–617. [Google Scholar] [CrossRef]
- Muhammad, N.Z.; Shafaghat, A.; Keyvanfar, A.; Majid, M.Z.A.; Ghoshal, S.; Yasouj, S.E.M.; Ganiyu, A.A.; Kouchaksaraei, M.S.; Kamyab, H.; Taheri, M.M.; et al. Tests and methods of evaluating the self-healing efficiency of concrete: A review. Constr. Build. Mater. 2016, 112, 1123–1132. [Google Scholar] [CrossRef]
- Hu, Z.X.; Hu, X.M.; Cheng, W.M.; Zhao, Y.Y.; Wu, M.Y. Performance optimization of one-component polyurethane healing agent for self-healing concrete. Constr. Build. Mater. 2018, 179, 151–159. [Google Scholar] [CrossRef]
- Dry, C.M. Design of self-growing, self-sensing, and self-repairing materials for engineering applications. In Smart Materials and MEMS, Melbourne, Australia, 2000; International Society for Optics and Photonics: Bellingham, WA, USA, 2001; Volume 4234, pp. 23–29. [Google Scholar]
- Hilloulin, B.; Van Tittelboom, K.; Gruyaert, E.; De Belie, N.; Loukili, A. Design of polymeric capsules for self-healing concrete. Cem. Concr. Compos. 2015, 55, 298–307. [Google Scholar] [CrossRef]
- Van Tittelboom, K.; Tsangouri, E.; Van Hemelrijck, D.; De Belie, N. The efficiency of self-healing concrete using alternative manufacturing procedures and more realistic crack patterns. Cem. Concr. Compos. 2015, 57, 142–152. [Google Scholar] [CrossRef]
- Dry, C. Procedures developed for self-repair of polymer matrix composite materials. Compos. Struct. 1996, 35, 263–269. [Google Scholar] [CrossRef]
- Pang, J.W.; Bond, I.P. A hollow fibre reinforced polymer composite encompassing self-healing and enhanced damage visibility. Compos. Sci. Technol. 2005, 65, 1791–1799. [Google Scholar] [CrossRef]
- Zhu, Y.; Ye, X.J.; Rong, M.Z.; Zhang, M.Q. Self-healing glass fiber/epoxy composites with polypropylene tubes containing self-pressurized epoxy and mercaptan healing agents. Compos. Sci. Technol. 2016, 135, 146–152. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, H.; Yang, J. Synthesis of organic silane microcapsules for self-healing corrosion resistant polymer coatings. Corrosion Sci. 2012, 65, 561–566. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X.; Wang, Q. Mass and volume conservation in phase field models for binary fluids. Commun. Comput. Phys. 2013, 13, 1045–1065. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Phase-field method for computationally efficient modeling of solidification with arbitrary interface kinetics. Phys. Rev. E 1996, 53, R3017. [Google Scholar] [CrossRef]
- Flower, H.; Gregson, P. Solid state phase transformations in aluminium alloys containing lithium. Mater. Sci. Technol. 1987, 3, 81–90. [Google Scholar] [CrossRef]
- Steinbach, I.; Apel, M. Multi phase field model for solid state transformation with elastic strain. Phys. D Nonlinear Phenom. 2006, 217, 153–160. [Google Scholar] [CrossRef]
- Krill Iii, C.; Chen, L.Q. Computer simulation of 3-D grain growth using a phase-field model. Acta Mater. 2002, 50, 3059–3075. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. Quantitative analysis of grain boundary properties in a generalized phase field model for grain growth in anisotropic systems. Phys. Rev. B 2008, 78, 024113. [Google Scholar] [CrossRef]
- Kazaryan, A.; Wang, Y.; Dregia, S.; Patton, B.R. Generalized phase-field model for computer simulation of grain growth in anisotropic systems. Phys. Rev. B 2000, 61, 14275. [Google Scholar] [CrossRef]
- Zeng, Y.; Hunter, A.; Beyerlein, I.J.; Koslowski, M. A phase field dislocation dynamics model for a bicrystal interface system: An investigation into dislocation slip transmission across cube-on-cube interfaces. Int. J. Plast. 2016, 79, 293–313. [Google Scholar] [CrossRef]
- Levitas, V.I.; Roy, A.M. Multiphase phase field theory for temperature-induced phase transformations: Formulation and application to interfacial phases. Acta Mater. 2016, 105, 244–257. [Google Scholar] [CrossRef]
- Ravash, H.; Vanherpe, L.; Vleugels, J.; Moelans, N. Three-dimensional phase-field study of grain coarsening and grain shape accommodation in the final stage of liquid-phase sintering. J. Eur. Ceram. Soc. 2017, 37, 2265–2275. [Google Scholar] [CrossRef]
- Deckelnick, K.; Elliott, C.M.; Styles, V. Double obstacle phase field approach to an inverse problem for a discontinuous diffusion coefficient. Inverse Probl. 2016, 32, 045008. [Google Scholar] [CrossRef]
- Heinonen, V.; Achim, C.; Kosterlitz, J.; Ying, S.C.; Lowengrub, J.; Ala-Nissila, T. Consistent hydrodynamics for phase field crystals. Phys. Rev. Lett. 2016, 116, 024303. [Google Scholar] [CrossRef]
- Wang, N.; Bevan, K.H.; Provatas, N. Phase-field-crystal model for electromigration in metal interconnects. Phys. Rev. Lett. 2016, 117, 155901. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Spatschek, R.; Brener, E.; Karma, A. Phase field modeling of crack propagation. Philos. Mag. 2011, 91, 75–95. [Google Scholar] [CrossRef]
- Spatschek, R.; Hartmann, M.; Brener, E.; Müller-Krumbhaar, H.; Kassner, K. Phase field modeling of fast crack propagation. Phys. Rev. Lett. 2006, 96, 015502. [Google Scholar] [CrossRef]
- Karma, A.; Lobkovsky, A.E. Unsteady crack motion and branching in a phase-field model of brittle fracture. Phys. Rev. Lett. 2004, 92, 245510. [Google Scholar] [CrossRef] [PubMed]
- Henry, H.; Levine, H. Dynamic instabilities of fracture under biaxial strain using a phase field model. Phys. Rev. Lett. 2004, 93, 105504. [Google Scholar] [CrossRef] [PubMed]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Chen, L.Q. Phase-field method of phase transitions/domain structures in ferroelectric thin films: A review. J. Am. Ceram. Soc. 2008, 91, 1835–1844. [Google Scholar] [CrossRef]
- Gránásy, L.; Pusztai, T.; Börzsönyi, T.; Tóth, G.; Tegze, G.; Warren, J.; Douglas, J. Phase field theory of crystal nucleation and polycrystalline growth: A review. J. Mater. Res. 2006, 21, 309–319. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-field model for microstructure evolution at the mesoscopic scale. Annu. Rev. Mater. Res. 2013, 43, 89–107. [Google Scholar] [CrossRef]
- Greenwood, M.; Provatas, N.; Rottler, J. Free energy functionals for efficient phase field crystal modeling of structural phase transformations. Phys. Rev. Lett. 2010, 105, 045702. [Google Scholar] [CrossRef]
- Provatas, N.; Elder, K. Phase-Field Methods in Materials Science and Engineering; John Wiley & Sons: Weinheim, Germany, 2011. [Google Scholar]
- Caginalp, G.; Fife, P. Phase-field methods for interfacial boundaries. Phys. Rev. B 1986, 33, 7792. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. In On Superconductivity and Superfluidity; Springer: Berlin/Heidelberg, Germany, 2009; pp. 113–137. [Google Scholar]
- Aldakheel, F. Mechanics of Nonlocal Dissipative Solids: Gradient Plasticity and Phase Field Modeling of Ductile Fracture; Institut für Mechanik (Bauwesen), Lehrstuhl I, Universität Stuttgart: Stuttgart, Germany, 2016. [Google Scholar] [CrossRef]
- Aldakheel, F. A microscale model for concrete failure in poro-elasto-plastic media. Theor. Appl. Fract. Mech. 2020, 107, 102517. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Qin, R.; Bhadeshia, H. Phase field method. Mater. Sci. Technol. 2010, 26, 803–811. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Quantitative phase-field modeling of dendritic growth in two and three dimensions. Phys. Rev. E 1998, 57, 4323. [Google Scholar] [CrossRef]
- Steinbach, I.; Pezzolla, F.; Nestler, B.; Seeßelberg, M.; Prieler, R.; Schmitz, G.J.; Rezende, J.L. A phase field concept for multiphase systems. Phys. D Nonlinear Phenom. 1996, 94, 135–147. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Phase-field model of dendritic sidebranching with thermal noise. Phys. Rev. E 1999, 60, 3614. [Google Scholar] [CrossRef]
- Jafarzadeh, H.; Farrahi, G.H.; Javanbakht, M. Phase field modeling of crack growth with double-well potential including surface effects. Contin. Mech. Thermodyn. 2020, 32, 913–925. [Google Scholar] [CrossRef]
- Hu, S.; Li, Y.; Zheng, Y.; Chen, L. Effect of solutes on dislocation motion—A phase-field simulation. Int. J. Plast. 2004, 20, 403–425. [Google Scholar] [CrossRef]
- Koslowski, M.; Cuitino, A.M.; Ortiz, M. A phase-field theory of dislocation dynamics, strain hardening and hysteresis in ductile single crystals. J. Mech. Phys. Solids 2002, 50, 2597–2635. [Google Scholar] [CrossRef]
- Yu, Y.M.; Liu, B.G.; Voigt, A. Phase-field modeling of anomalous spiral step growth on Si (001) surface. Phys. Rev. B 2009, 79, 235317. [Google Scholar] [CrossRef]
- Caginalp, G.; Xie, W. Phase-field and sharp-interface alloy models. Phys. Rev. E 1993, 48, 1897. [Google Scholar] [CrossRef]
- Collins, J.B.; Levine, H. Diffuse interface model of diffusion-limited crystal growth. Phys. Rev. B 1985, 31, 6119. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, A.A.; Murray, B.T.; Schaefer, R.J. Computation of dendrites using a phase field model. Phys. D Nonlinear Phenom. 1993, 66, 243–262. [Google Scholar] [CrossRef]
- Wang, S.L.; Sekerka, R.F. Computation of the dendritic operating state at large supercoolings by the phase field model. Phys. Rev. E 1996, 53, 3760. [Google Scholar] [CrossRef] [PubMed]
- Beckermann, C.; Diepers, H.J.; Steinbach, I.; Karma, A.; Tong, X. Modeling melt convection in phase-field simulations of solidification. J. Comput. Phys. 1999, 154, 468–496. [Google Scholar] [CrossRef]
- Ma, X.; Shi, S.; Woo, C.; Chen, L. The phase field model for hydrogen diffusion and γ-hydride precipitation in zirconium under non-uniformly applied stress. Mech. Mater. 2006, 38, 3–10. [Google Scholar] [CrossRef]
- Lai, Z.W. Theory of ordering dynamics for Cu 3 Au. Phys. Rev. B 1990, 41, 9239. [Google Scholar] [CrossRef]
- Rubin, G.; Khachaturyan, A. Three-dimensional model of precipitation of ordered intermetallics. Acta Mater. 1999, 47, 1995–2002. [Google Scholar] [CrossRef]
- Pongsaksawad, W.; Powell, A.C.; Dussault, D. Phase-field modeling of transport-limited electrolysis in solid and liquid states. J. Electrochem. Soc. 2007, 154, F122–F133. [Google Scholar] [CrossRef]
- Takaki, T. A phase-field topology optimization model using a double-obstacle function. In ECCOMAS 2012-European Congress on Computational Methods in Applied Sciences and Engineering; e-Book Full Papers: Vienna, Austria, 2012; pp. 8761–8768. [Google Scholar]
- Leo, P.H.; Johnson, W. Spinodal decomposition and coarsening of stressed thin films on compliant substrates. Acta Mater. 2001, 49, 1771–1787. [Google Scholar] [CrossRef]
- Echebarria, B.; Folch, R.; Karma, A.; Plapp, M. Quantitative phase-field model of alloy solidification. Phys. Rev. E 2004, 70, 061604. [Google Scholar] [CrossRef]
- Karma, A.; Kessler, D.A.; Levine, H. Phase-field model of mode III dynamic fracture. Phys. Rev. Lett. 2001, 87, 045501. [Google Scholar] [CrossRef] [PubMed]
- Karma, A.; Rappel, W.J. Numerical simulation of three-dimensional dendritic growth. Phys. Rev. Lett. 1996, 77, 4050. [Google Scholar] [CrossRef] [PubMed]
- Warren, J.A.; Kobayashi, R.; Lobkovsky, A.E.; Carter, W.C. Extending phase field models of solidification to polycrystalline materials. Acta Mater. 2003, 51, 6035–6058. [Google Scholar] [CrossRef]
- Nestler, B.; Garcke, H.; Stinner, B. Multicomponent alloy solidification: Phase-field modeling and simulations. Phys. Rev. E 2005, 71, 041609. [Google Scholar] [CrossRef]
- Chen, Q.; Ma, N.; Wu, K.; Wang, Y. Quantitative phase field modeling of diffusion-controlled precipitate growth and dissolution in Ti–Al–V. Scr. Mater. 2004, 50, 471–476. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.Q.; Khachaturyan, A. Kinetics of strain-induced morphological transformation in cubic alloys with a miscibility gap. Acta Metall. Mater. 1993, 41, 279–296. [Google Scholar] [CrossRef]
- Van Noorden, T.; Eck, C. Phase field approximation of a kinetic moving-boundary problem modelling dissolution and precipitation. Interfaces Free. Boundaries 2011, 13, 29–55. [Google Scholar] [CrossRef]
- Xu, Z.; Meakin, P. Phase-field modeling of solute precipitation and dissolution. J. Chem. Phys. 2008, 129, 014705. [Google Scholar] [CrossRef]
- Chen, L.Q.; Yang, W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters: The grain-growth kinetics. Phys. Rev. B 1994, 50, 15752. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, T.; Ardell, A.; Zhou, S.; Liu, Z.; Chen, L. Three-dimensional phase-field simulations of coarsening kinetics of r particles in binary Ni–Al alloys. Acta Mater. 2004, 52, 2837–2845. [Google Scholar] [CrossRef]
- Lowengrub, J.S.; Rätz, A.; Voigt, A. Phase-field modeling of the dynamics of multicomponent vesicles: Spinodal decomposition, coarsening, budding, and fission. Phys. Rev. E 2009, 79, 031926. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Chen, L. Solute segregation and coherent nucleation and growth near a dislocation—A phase-field model integrating defect and phase microstructures. Acta Mater. 2001, 49, 463–472. [Google Scholar] [CrossRef]
- Rodney, D.; Le Bouar, Y.; Finel, A. Phase field methods and dislocations. Acta Mater. 2003, 51, 17–30. [Google Scholar] [CrossRef]
- Kassner, K.; Misbah, C.; Müller, J.; Kappey, J.; Kohlert, P. Phase-field modeling of stress-induced instabilities. Phys. Rev. E 2001, 63, 036117. [Google Scholar] [CrossRef] [PubMed]
- Kassner, K.; Misbah, C. A phase-field approach for stress-induced instabilities. EPL (Europhys. Lett.) 1999, 46, 217. [Google Scholar] [CrossRef]
- Du, Q.; Liu, C.; Wang, X. Simulating the deformation of vesicle membranes under elastic bending energy in three dimensions. J. Comput. Phys. 2006, 212, 757–777. [Google Scholar] [CrossRef]
- Biben, T.; Kassner, K.; Misbah, C. Phase-field approach to three-dimensional vesicle dynamics. Phys. Rev. E 2005, 72, 041921. [Google Scholar] [CrossRef]
- Léonard, F.; Desai, R.C. Alloy decomposition and surface instabilities in thin films. Phys. Rev. B 1998, 57, 4805. [Google Scholar] [CrossRef]
- Wen, Y.H.; Chen, L.Q.; Hawk, J.A. Phase-field modeling of corrosion kinetics under dual-oxidants. Model. Simul. Mater. Sci. Eng. 2012, 20, 035013. [Google Scholar] [CrossRef]
- Shibuta, Y.; Okajima, Y.; Suzuki, T. A phase-field simulation of bridge formation process in a nanometer-scale switch. Scr. Mater. 2006, 55, 1095–1098. [Google Scholar] [CrossRef]
- Shibuta, Y.; Okajima, Y.; Suzuki, T. Phase-field modeling for electrodeposition process. Sci. Technol. Adv. Mater. 2007, 8, 511. [Google Scholar] [CrossRef]
- Han, B.; Van der Ven, A.; Morgan, D.; Ceder, G. Electrochemical modeling of intercalation processes with phase field models. Electrochim. Acta 2004, 49, 4691–4699. [Google Scholar] [CrossRef]
- Guyer, J.E.; Boettinger, W.J.; Warren, J.A.; McFadden, G.B. Phase field modeling of electrochemistry. I. Equilibrium. Phys. Rev. E 2004, 69, 021603. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, A.; Nestler, B. Grand-potential formulation for multicomponent phase transformations combined with thin-interface asymptotics of the double-obstacle potential. Phys. Rev. E 2012, 85, 021602. [Google Scholar] [CrossRef]
- Böttger, B.; Eiken, J.; Steinbach, I. Phase field simulation of equiaxed solidification in technical alloys. Acta Mater. 2006, 54, 2697–2704. [Google Scholar] [CrossRef]
- Oono, Y.; Puri, S. Study of phase-separation dynamics by use of cell dynamical systems. I. Modeling. Phys. Rev. A 1988, 38, 434. [Google Scholar] [CrossRef]
- Blowey, J.; Elliott, C. A Phase-Field Model with Double Obstacle Potential; Citeseer: Princeton, NJ, USA, 1994. [Google Scholar]
- Bhate, D.N.; Kumar, A.; Bower, A.F. Diffuse interface model for electromigration and stress voiding. J. Appl. Phys. 2000, 87, 1712–1721. [Google Scholar] [CrossRef]
- Barrett, J.W.; Garcke, H.; Nürnberg, R. A phase field model for the electromigration of intergranular voids. Interfaces Free Boundaries 2007, 9, 171–210. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Y.; Cuitino, A.; Khachaturyan, A. Phase field microelasticity theory and modeling of multiple dislocation dynamics. Appl. Phys. Lett. 2001, 78, 2324–2326. [Google Scholar] [CrossRef]
- Wang, Y.U.; Jin, Y.; Cuitino, A.; Khachaturyan, A. Nanoscale phase field microelasticity theory of dislocations: Model and 3D simulations. Acta Mater. 2001, 49, 1847–1857. [Google Scholar] [CrossRef]
- Karma, A.; Plapp, M. Spiral surface growth without desorption. Phys. Rev. Lett. 1998, 81, 4444. [Google Scholar] [CrossRef]
- Braun, R.; Cahn, J.; McFadden, G.; Rushmeier, H.; Wheeler, A. Theory of anisotropic growth rates in the ordering of an fcc alloy. Acta Mater. 1998, 46, 1–12. [Google Scholar] [CrossRef]
- Wang, Y.; Banerjee, D.; Su, C.; Khachaturyan, A. Field kinetic model and computer simulation of precipitation of L12 ordered intermetallics from fcc solid solution. Acta Mater. 1998, 46, 2983–3001. [Google Scholar] [CrossRef]
- Kobayashi, R. Modeling and numerical simulations of dendritic crystal growth. Phys. D Nonlinear Phenom. 1993, 63, 410–423. [Google Scholar] [CrossRef]
- Wang, S.L.; Sekerka, R.; Wheeler, A.; Murray, B.; Coriell, S.; Braun, R.; McFadden, G. Thermodynamically-consistent phase-field models for solidification. Phys. D Nonlinear Phenom. 1993, 69, 189–200. [Google Scholar] [CrossRef]
- Wang, Y.U. Computer modeling and simulation of solid-state sintering: A phase field approach. Acta Mater. 2006, 54, 953–961. [Google Scholar] [CrossRef]
- Wang, Y.; Khachaturyan, A. Three-dimensional field model and computer modeling of martensitic transformations. Acta Mater. 1997, 45, 759–773. [Google Scholar] [CrossRef]
- Münch, I.; Krauß, M. An enhanced finite element technique for diffuse phase transition. Comput. Mech. 2015, 56, 691–708. [Google Scholar] [CrossRef]
- Assadi, H. Phase-field modelling of electro-deoxidation in molten salt. Model. Simul. Mater. Sci. Eng. 2006, 14, 963. [Google Scholar] [CrossRef]
- Li, Y.; Hu, S.; Liu, Z.; Chen, L. Effect of substrate constraint on the stability and evolution of ferroelectric domain structures in thin films. Acta Mater. 2002, 50, 395–411. [Google Scholar] [CrossRef]
- Li, Y.; Chen, L. Temperature-strain phase diagram for Ba TiO3 thin films. Appl. Phys. Lett. 2006, 88, 072905. [Google Scholar] [CrossRef]
- Xu, J.; Wang, X.; Wang, B. Biochemical process of ureolysis-based microbial CaCO3 precipitation and its application in self-healing concrete. Appl. Microbiol. Biotechnol. 2018, 102, 3121–3132. [Google Scholar] [CrossRef] [PubMed]
- Vijay, K.; Murmu, M.; Deo, S.V. Bacteria based self healing concrete—A review. Constr. Build. Mater. 2017, 152, 1008–1014. [Google Scholar] [CrossRef]
- Quayum, M.S.; Zhuang, X.; Rabczuk, T. Computational model generation and RVE design of self-healing concrete. Front. Struct. Civ. Eng. 2015, 9, 383–396. [Google Scholar] [CrossRef]
- Mersmann, A.; Angerhöfer, M.; Franke, J. Controlled precipitation. Chem. Eng. Technol. Ind. Chem.-Plant Equip.-Process Eng.-Biotechnol. 1994, 17, 1–9. [Google Scholar] [CrossRef]
- Mauludin, L.M.; Oucif, C. Modeling of self-healing concrete: A review. J. Appl. Comput. Mech. 2019, 5, 526–539. [Google Scholar]
- Xu, Z.; Huang, H.; Li, X.; Meakin, P. Phase field and level set methods for modeling solute precipitation and/or dissolution. Comput. Phys. Commun. 2012, 183, 15–19. [Google Scholar] [CrossRef]
- Redeker, M.; Rohde, C.; Sorin Pop, I. Upscaling of a tri-phase phase-field model for precipitation in porous media. IMA J. Appl. Math. 2016, 81, 898–939. [Google Scholar] [CrossRef]
- Rohde, C.; von Wolff, L. A Ternary Cahn-Hilliard Navier-Stokes Model for Two Phase Flow with Precipitation and Dissolution. arXiv 2019, arXiv:1912.09181. [Google Scholar]
- Xu, Z.; Meakin, P. A phase-field approach to no-slip boundary conditions in dissipative particle dynamics and other particle models for fluid flow in geometrically complex confined systems. J. Chem. Phys. 2009, 130, 234103. [Google Scholar] [CrossRef]
- Lin, G.; Bao, J.; Xu, Z. A three-dimensional phase field model coupled with a lattice kinetics solver for modeling crystal growth in furnaces with accelerated crucible rotation and traveling magnetic field. Comput. Fluids 2014, 103, 204–214. [Google Scholar] [CrossRef][Green Version]
- Xu, Z.; Meakin, P. Phase-field modeling of two-dimensional solute precipitation/dissolution: Solid fingers and diffusion-limited precipitation. J. Chem. Phys. 2011, 134, 044137. [Google Scholar] [CrossRef] [PubMed]
- Bringedal, C.; von Wolff, L.; Pop, I.S. Phase field modeling of precipitation and dissolution processes in porous media: Upscaling and numerical experiments. Multiscale Model. Simul. 2020, 18, 1076–1112. [Google Scholar] [CrossRef]
- Schwarze, C.; Gupta, A.; Hickel, T.; Kamachali, R.D. Phase-field study of ripening and rearrangement of precipitates under chemomechanical coupling. Phys. Rev. B 2017, 95, 174101. [Google Scholar] [CrossRef]
- Müller, S.; Wolverton, C.; Wang, L.W.; Zunger, A. Predicting the size-and temperature-dependent shapes of precipitates in Al–Zn alloys. Acta Mater. 2000, 48, 4007–4020. [Google Scholar] [CrossRef]
- Shi, R.; Wang, Y. Variant selection during α precipitation in Ti–6Al–4V under the influence of local stress—A simulation study. Acta Mater. 2013, 61, 6006–6024. [Google Scholar] [CrossRef]
- Silberberg, M. Principles of General Chemistry; McGraw-Hill Education: London, UK, 2012. [Google Scholar]
- Willard, H.H. Separation by precipitation from homogeneous solution. Anal. Chem. 1950, 22, 1372–1374. [Google Scholar] [CrossRef]
- Cartwright, P.; Newman, E.; Wilson, D. Precipitation from homogeneous solution: A review. Analyst 1967, 92, 663–679. [Google Scholar] [CrossRef]
- Collings, E. Physics of Solid Solution Strengthening; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Lifshitz, I.M.; Slyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Awan, I.Z.; Khan, A.Q. Precipitation from Solid Solutions. J. Chem. Soc. Pak. 2017, 39, 319–336. [Google Scholar]
- Callister, W.D. Fundamentals of Materials Science and Engineering; Wiley: London, UK, 2000; Volume 471660817. [Google Scholar]
- Hou, H.; Zhao, Y.; Zhao, Y. Simulation of the precipitation process of ordered intermetallic compounds in binary and ternary Ni–Al-based alloys by the phase-field model. Mater. Sci. Eng. A 2009, 499, 204–207. [Google Scholar] [CrossRef]
- Wen, Y.; Lill, J.; Chen, S.; Simmons, J. A ternary phase-field model incorporating commercial CALPHAD software and its application to precipitation in superalloys. Acta Mater. 2010, 58, 875–885. [Google Scholar] [CrossRef]
- Wittmann, F. Structure of concrete with respect to crack formation. Fract. Mech. Concr. 1983, 43, 6. [Google Scholar]
- Mazars, J.; Pijaudier-Cabot, G. Continuum damage theory—Application to concrete. J. Eng. Mech. 1989, 115, 345–365. [Google Scholar] [CrossRef]
- Schlangen, E.; Van Mier, J. Micromechanical analysis of fracture of concrete. Int. J. Damage Mech. 1992, 1, 435–454. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Meschke, G.; Lackner, R.; Mang, H.A. An anisotropic elastoplastic-damage model for plain concrete. Int. J. Numer. Methods Eng. 1998, 42, 703–727. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Kuna, M. Numerische Beanspruchungsanalyse von Rissen; Springer: Berlin, Germany, 2008; Volume 2. [Google Scholar]
- Sobolev, K.; Shah, S. Nanotechnology of Concrete: Recent Developments and Future Perspectives; ACI: Farmington Hills, MI, USA, 2008. [Google Scholar]
- Pedersen, R.; Simone, A.; Sluys, L. An analysis of dynamic fracture in concrete with a continuum visco-elastic visco-plastic damage model. Eng. Fract. Mech. 2008, 75, 3782–3805. [Google Scholar] [CrossRef]
- Hain, M.; Wriggers, P. Numerical homogenization of hardened cement paste. Comput. Mech. 2008, 42, 197–212. [Google Scholar] [CrossRef]
- Kim, S.M.; Al-Rub, R.K.A. Meso-scale computational modeling of the plastic-damage response of cementitious composites. Cem. Concr. Res. 2011, 41, 339–358. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardt, S.; Kooenke, C. A mesoscale model for concrete to simulate mechanical failure. Comput. Concr. 2011, 8, 401–423. [Google Scholar] [CrossRef]
- Lohaus, L.; Oneschkow, N.; Wefer, M. Design model for the fatigue behaviour of normal-strength, high-strength and ultra-high-strength concrete. Struct. Concr. 2012, 13, 182–192. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zreid, I.; Kaliske, M. A gradient enhanced plasticity–damage microplane model for concrete. Comput. Mech. 2018, 62, 1239–1257. [Google Scholar] [CrossRef]
- Schäfer, N.; Gudžulić, V.; Timothy, J.J.; Breitenbücher, R.; Meschke, G. Fatigue behavior of HPC and FRC under cyclic tensile loading: Experiments and modeling. Struct. Concr. 2019, 20, 1265–1278. [Google Scholar] [CrossRef]
- Gebuhr, G.; Pise, M.; Sarhil, M.; Anders, S.; Brands, D.; Schröder, J. Analysis and evaluation of the pull-out behavior of hooked steel fibers embedded in high and ultra-high performance concrete for calibration of numerical models. Struct. Concr. 2019, 20, 1254–1264. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef]
- Loehnert, S.; Mueller-Hoeppe, D.; Wriggers, P. 3D corrected XFEM approach and extension to finite deformation theory. Int. J. Numer. Methods Eng. 2011, 86, 431–452. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. The variational approach to fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Kuhn, C.; Müller, R. A continuum phase field model for fracture. Eng. Fract. Mech. 2010, 77, 3625–3634. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217, 77–95. [Google Scholar] [CrossRef]
- Hesch, C.; Weinberg, K. Thermodynamically consistent algorithms for a finite-deformation phase-field approach to fracture. Int. J. Numer. Methods Eng. 2014, 99, 906–924. [Google Scholar] [CrossRef]
- Miehe, C.; Schaenzel, L.M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Heister, T.; Wheeler, M.F.; Wick, T. A primal-dual active set method and predictor-corrector mesh adaptivity for computing fracture propagation using a phase-field approach. Comput. Methods Appl. Mech. Eng. 2015, 290, 466–495. [Google Scholar] [CrossRef]
- Heider, Y.; Markert, B. A phase-field modeling approach of hydraulic fracture in saturated porous media. Mech. Res. Commun. 2017, 80, 38–46. [Google Scholar] [CrossRef]
- Paggi, M.; Reinoso, J. Revisiting the problem of a crack impinging on an interface: A modeling framework for the interaction between the phase field approach for brittle fracture and the interface cohesive zone model. Comput. Methods Appl. Mech. Eng. 2017, 321, 145–172. [Google Scholar] [CrossRef]
- Pillai, U.; Heider, Y.; Markert, B. A diffusive dynamic brittle fracture model for heterogeneous solids and porous materials with implementation using a user-element subroutine. Comput. Mater. Sci. 2018, 153, 36–47. [Google Scholar] [CrossRef]
- Aldakheel, F.; Hudobivnik, B.; Hussein, A.; Wriggers, P. Phase-field modeling of brittle fracture using an efficient virtual element scheme. Comput. Methods Appl. Mech. Eng. 2018, 341, 443–466. [Google Scholar] [CrossRef]
- Seleš, K.; Jurčević, A.; Tonković, Z.; Sorić, J. Crack propagation prediction in heterogeneous microstructure using an efficient phase-field algorithm. Theor. Appl. Fract. Mech. 2019, 100, 289–297. [Google Scholar] [CrossRef]
- Noii, N.; Aldakheel, F.; Wick, T.; Wriggers, P. An adaptive global–local approach for phase-field modeling of anisotropic brittle fracture. Comput. Methods Appl. Mech. Eng. 2020, 361, 112744. [Google Scholar] [CrossRef]
- Heider, Y.; Sun, W. A phase field framework for capillary-induced fracture in unsaturated porous media: Drying-induced vs. hydraulic cracking. Comput. Methods Appl. Mech. Eng. 2020, 359, 112647. [Google Scholar] [CrossRef]
- Aldakheel, F.; Tomann, C.; Lohaus, L.; Wriggers, P. Water-induced failure mechanics for concrete. PAMM 2019, 19, e201900140. [Google Scholar] [CrossRef]
- Miehe, C.; Dal, H.; Schänzel, L.M.; Raina, A. A phase-field model for chemo-mechanical induced fracture in lithium-ion battery electrode particles. Int. J. Numer. Methods Eng. 2016, 106, 683–711. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Tomann, C.; Lohaus, L.; Aldakheel, F.; Wriggers, P. Influence of water-induced damage mechanisms on the fatigue deterioration of high-strength concrete. In Proceedings of the 6th International Fib Congress: Concrete–Innovations in Materials, Design and Structures, Kraków, Poland, 27–29 May 2019. [Google Scholar]
- Carollo, V.; Paggi, M.; Reinoso, J. The steady-state Archard adhesive wear problem revisited based on the phase field approach to fracture. Int. J. Fract. 2019, 215, 39–48. [Google Scholar] [CrossRef]
- Steinke, C.; Kaliske, M. A phase-field crack model based on directional stress decomposition. Comput. Mech. 2019, 63, 1019–1046. [Google Scholar] [CrossRef]
- Carrara, P.; Ambati, M.; Alessi, R.; De Lorenzis, L. A framework to model the fatigue behavior of brittle materials based on a variational phase-field approach. Comput. Methods Appl. Mech. Eng. 2020, 361, 112731. [Google Scholar] [CrossRef]
- Heider, Y.; Reiche, S.; Siebert, P.; Markert, B. Modeling of hydraulic fracturing using a porous-media phase-field approach with reference to experimental data. Eng. Fract. Mech. 2018, 202, 116–134. [Google Scholar] [CrossRef]
- Fantoni, F.; Bacigalupo, A.; Paggi, M.; Reinoso, J. A phase field approach for damage propagation in periodic microstructured materials. Int. J. Fract. 2019, 223, 53–76. [Google Scholar] [CrossRef]
- Aldakheel, F.; Noii, N.; Wick, T.; Wriggers, P. A global-local approach for hydraulic phase-field fracture in poroelastic media. Comput. Math. Appl. 2020. [Google Scholar] [CrossRef]
- Yin, B.; Kaliske, M. An anisotropic phase-field model based on the equivalent crack surface energy density at finite strain. Comput. Methods Appl. Mech. Eng. 2020, 369, 113202. [Google Scholar] [CrossRef]
- Khodadadian, A.; Noii, N.; Parvizi, M.; Abbaszadeh, M.; Wick, T.; Heitzinger, C. A Bayesian estimation method for variational phase-field fracture problems. Comput. Mech. 2020, 66, 827–849. [Google Scholar] [CrossRef] [PubMed]
- Teichtmeister, S.; Kienle, D.; Aldakheel, F.; Keip, M.A. Phase field modeling of fracture in anisotropic brittle solids. Int. J. Non-Linear Mech. 2017, 97, 1–21. [Google Scholar] [CrossRef]
- Bilgen, C.; Homberger, S.; Weinberg, K. Phase-field fracture simulations of the Brazilian splitting test. Int. J. Fract. 2019, 220, 85–98. [Google Scholar] [CrossRef]
- Makvandi, R.; Duczek, S.; Juhre, D. A phase-field fracture model based on strain gradient elasticity. Eng. Fract. Mech. 2019, 220, 106648. [Google Scholar] [CrossRef]
- Wriggers, P.; Aldakheel, F.; Lohaus, L.; Heist, M. Water-induced damage mechanisms of cyclically loaded High-performance concretes. Bauingenieur 2020, 95, 126–132. [Google Scholar]
- Denli, F.A.; Gültekin, O.; Holzapfel, G.A.; Dal, H. A phase-field model for fracture of unidirectional fiber-reinforced polymer matrix composites. Comput. Mech. 2020, 65, 1149–1166. [Google Scholar] [CrossRef]
- Schreiber, C.; Kuhn, C.; Müller, R.; Zohdi, T. A phase field modeling approach of cyclic fatigue crack growth. Int. J. Fract. 2020, 225, 89–100. [Google Scholar]
- Zhuang, X.; Zhou, S.; Sheng, M.; Li, G. On the hydraulic fracturing in naturally-layered porous media using the phase field method. Eng. Geol. 2020, 266, 105306. [Google Scholar] [CrossRef]
- Dittmann, M.; Krüger, M.; Schmidt, F.; Schuß, S.; Hesch, C. Variational modeling of thermomechanical fracture and anisotropic frictional mortar contact problems with adhesion. Comput. Mech. 2019, 63, 571–591. [Google Scholar] [CrossRef]
- Hussein, A.; Wriggers, P.; Hudobivnik, B.; Aldakheel, F.; Guidault, P.A.; Allix, O. Treatment of Brittle Fracture in Solids with the Virtual Element Method. In Virtual Design and Validation; Springer: Berlin/Heidelberg, Germany, 2020; pp. 201–228. [Google Scholar]
- Wick, T. Multiphysics Phase-Field Fracture: Modeling, Adaptive Discretizations, and Solvers; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2020; p. 28. [Google Scholar]
- Geelen, R.; Plews, J.; Tupek, M.; Dolbow, J. An extended/generalized phase-field finite element method for crack growth with global-local enrichment. Int. J. Numer. Methods Eng. 2020, 121, 2534–2557. [Google Scholar] [CrossRef]
- Ma, R.; Sun, W. FFT-based solver for higher-order and multi-phase-field fracture models applied to strongly anisotropic brittle materials. Comput. Methods Appl. Mech. Eng. 2020, 362, 112781. [Google Scholar] [CrossRef]
- Tarafder, P.; Dan, S.; Ghosh, S. Finite deformation cohesive zone phase field model for crack propagation in multi-phase microstructures. Comput. Mech. 2020, 66, 723–743. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Gerasimov, T. Numerical Implementation of Phase-Field Models of Brittle Fracture. In Modeling in Engineering Using Innovative Numerical Methods for Solids and Fluids; Springer: Berlin/Heidelberg, Germany, 2020; pp. 75–101. [Google Scholar]
- Miehe, C.; Hofacker, M.; Schänzel, L.M.; Aldakheel, F. Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic–plastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Li, P.; Yvonnet, J.; Combescure, C. An extension of the phase field method to model interactions between interfacial damage and brittle fracture in elastoplastic composites. Int. J. Mech. Sci. 2020, 179, 105633. [Google Scholar] [CrossRef]
- Ambati, M.; Kruse, R.; De Lorenzis, L. A phase-field model for ductile fracture at finite strains and its experimental verification. Comput. Mech. 2016, 57, 149–167. [Google Scholar] [CrossRef]
- Barfusz, O.; Brepols, T.; van der Velden, T.; Frischkorn, J.; Reese, S. A single Gauss point continuum finite element formulation for gradient-extended damage at large deformations. Comput. Methods Appl. Mech. Eng. 2021, 373, 113440. [Google Scholar] [CrossRef]
- Diehl, M.; Wicke, M.; Shanthraj, P.; Roters, F.; Brueckner-Foit, A.; Raabe, D. Coupled crystal plasticity–phase field fracture simulation study on damage evolution around a void: Pore shape versus crystallographic orientation. JOM 2017, 69, 872–878. [Google Scholar] [CrossRef]
- Miehe, C.; Aldakheel, F.; Teichtmeister, S. Phase-field modeling of ductile fracture at finite strains: A robust variational-based numerical implementation of a gradient-extended theory by micromorphic regularization. Int. J. Numer. Methods Eng. 2017, 111, 816–863. [Google Scholar] [CrossRef]
- Borden, M.J.; Hughes, T.J.; Landis, C.M.; Anvari, A.; Lee, I.J. A phase-field formulation for fracture in ductile materials: Finite deformation balance law derivation, plastic degradation, and stress triaxiality effects. Comput. Methods Appl. Mech. Eng. 2016, 312, 130–166. [Google Scholar] [CrossRef]
- Miehe, C.; Aldakheel, F.; Raina, A. Phase field modeling of ductile fracture at finite strains: A variational gradient-extended plasticity-damage theory. Int. J. Plast. 2016, 84, 1–32. [Google Scholar] [CrossRef]
- Alessi, R.; Marigo, J.J.; Maurini, C.; Vidoli, S. Coupling damage and plasticity for a phase-field regularisation of brittle, cohesive and ductile fracture: One-dimensional examples. Int. J. Mech. Sci. 2018, 149, 559–576. [Google Scholar] [CrossRef]
- Aldakheel, F.; Mauthe, S.; Miehe, C. Towards Phase Field Modeling of Ductile Fracture in Gradient-Extended Elastic-Plastic Solids. PAMM 2014, 14, 411–412. [Google Scholar] [CrossRef]
- Badnava, H.; Etemadi, E.; Msekh, M.A. A phase field model for rate-dependent ductile fracture. Metals 2017, 7, 180. [Google Scholar] [CrossRef]
- Dittmann, M.; Aldakheel, F.; Schulte, J.; Schmidt, F.; Krüger, M.; Wriggers, P.; Hesch, C. Phase-field modeling of porous-ductile fracture in non-linear thermo-elasto-plastic solids. Comput. Methods Appl. Mech. Eng. 2020, 361, 112730. [Google Scholar] [CrossRef]
- Choo, J.; Sun, W. Coupled phase-field and plasticity modeling of geological materials: From brittle fracture to ductile flow. Comput. Methods Appl. Mech. Eng. 2018, 330, 1–32. [Google Scholar] [CrossRef]
- Seiler, M.; Linse, T.; Hantschke, P.; Kästner, M. An efficient phase-field model for fatigue fracture in ductile materials. Eng. Fract. Mech. 2020, 224, 106807. [Google Scholar] [CrossRef]
- Dittmann, M.; Aldakheel, F.; Schulte, J.; Wriggers, P.; Hesch, C. Variational phase-field formulation of non-linear ductile fracture. Comput. Methods Appl. Mech. Eng. 2018, 342, 71–94. [Google Scholar] [CrossRef]
- Yin, B.; Kaliske, M. A ductile phase-field model based on degrading the fracture toughness: Theory and implementation at small strain. Comput. Methods Appl. Mech. Eng. 2020, 366, 113068. [Google Scholar] [CrossRef]
- Aldakheel, F.; Hudobivnik, B.; Wriggers, P. Virtual element formulation for phase-field modeling of ductile fracture. Int. J. Multiscale Comput. Eng. 2019, 17, 181–200. [Google Scholar] [CrossRef]
- Kuhn, C.; Noll, T.; Müller, R. On phase field modeling of ductile fracture. GAMM-Mitteilungen 2016, 39, 35–54. [Google Scholar] [CrossRef]
- Miehe, C.; Kienle, D.; Aldakheel, F.; Teichtmeister, S. Phase field modeling of fracture in porous plasticity: A variational gradient-extended Eulerian framework for the macroscopic analysis of ductile failure. Comput. Methods Appl. Mech. Eng. 2016, 312, 3–50. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Li, J.; Liu, Q.; Wu, C.; Sun, G.; Li, Q. Phase field fracture in elasto-plastic solids: Variational formulation for multi-surface plasticity and effects of plastic yield surfaces and hardening. Int. J. Mech. Sci. 2019, 156, 382–396. [Google Scholar] [CrossRef]
- Krüger, M.; Dittmann, M.; Aldakheel, F.; Härtel, A.; Wriggers, P.; Hesch, C. Porous-ductile fracture in thermo-elasto-plastic solids with contact applications. Comput. Mech. 2019, 1–26. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Schillinger, D. The multiscale finite element method for nonlinear continuum localization problems at full fine-scale fidelity, illustrated through phase-field fracture and plasticity. J. Comput. Phys. 2019, 396, 129–160. [Google Scholar] [CrossRef]
- Azinpour, E.; Sa, J.C.D.; Santos, A.D.D. Micromechanically-motivated phase field approach to ductile fracture. Int. J. Damage Mech. 2020. [Google Scholar] [CrossRef]
- Aldakheel, F.; Wriggers, P.; Miehe, C. A modified Gurson-type plasticity model at finite strains: Formulation, numerical analysis and phase-field coupling. Comput. Mech. 2018, 62, 815–833. [Google Scholar] [CrossRef]
- Brepols, T.; Wulfinghoff, S.; Reese, S. A gradient-extended two-surface damage-plasticity model for large deformations. Int. J. Plast. 2020, 129, 102635. [Google Scholar] [CrossRef]
- Dean, A.; Reinoso, J.; Jha, N.; Mahdi, E.; Rolfes, R. A phase field approach for ductile fracture of short fibre reinforced composites. Theor. Appl. Fract. Mech. 2020, 102495. [Google Scholar] [CrossRef]
- Kienle, D.; Aldakheel, F.; Keip, M.A. A finite-strain phase-field approach to ductile failure of frictional materials. Int. J. Solids Struct. 2019, 172, 147–162. [Google Scholar] [CrossRef]
- Amin, W.; Ali, M.A.; Vajragupta, N.; Hartmaier, A. Studying grain boundary strengthening by dislocation-based strain gradient crystal plasticity coupled with a multi-phase-field model. Materials 2019, 12, 2977. [Google Scholar] [CrossRef]
- Wolf, E. Fatigue crack closure under cyclic tension. Eng. Fract. Mech. 1970, 2, 37–45. [Google Scholar] [CrossRef]
- Elber, W. The significance of fatigue crack closure. In Damage Tolerance in Aircraft Structures; ASTM International: West Conshohocken, PA, USA, 1971. [Google Scholar]
- Vasudeven, A.; Sadananda, K.; Louat, N. A review of crack closure, fatigue crack threshold and related phenomena. Mater. Sci. Eng. A 1994, 188, 1–22. [Google Scholar] [CrossRef]
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Pippan, R.; Hohenwarter, A. Fatigue crack closure: A review of the physical phenomena. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 471–495. [Google Scholar] [CrossRef] [PubMed]
- Aldakheel, F.; Hudobivnik, B.; Artioli, E.; Beirao da Veiga, L.; Wriggers, P. Curvilinear Virtual Elements for Contact Mechanics. Comput. Methods Appl. Mech. Eng. 2020. accepted. [Google Scholar]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Mumford, D.B.; Shah, J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 1989, 42, 577–685. [Google Scholar] [CrossRef]

| Double-well | ||
where A is the height of the potential energy between the two states at the minimum free energy. | ||
| solidification | [54,55,147,154,156,172,173,174,175,176,177,178,179,180] |  |
| coarsening and grain growth | [127,128,181,182,183] | |
| dislocation dynamics | [184,185] | |
| crack propagation | [136,137,138,139,140] | |
| crystal growth under stress | [186,187] | |
| biological application | [188,189] | |
| phase transformations in thin films | [190] | |
| electrochemical process | [191,192,193,194,195] | |
| Double-obstacle | ||
where, when the phase transition only occurs in the narrow interface layer instead of in regions outside the interfacial layer. | ||
| solidification | [196,197] | 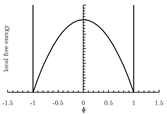 |
| cell dynamical system | [198,199] | |
| stiffness maximization | [170] | |
| electromigration | [200,201] | |
| Crystalline energy | ||
where A is the energy barrier between two neighboring minima. This function is formulated with an infinite number of degenerated minima. | ||
| dislocation system | [158,159,202,203] | 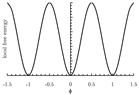 |
| spiral growth | [160,204] | |
| Potential with temperature field | ||
| , where is the difference between the current temperature and the melting temperature; is a positive constant. | ||
| solidification | [161,162,163,164,165] |  |
| Landau-polynomial | ||
| , where is the free energy of the disordered phase; are expansion coefficients related to temperature. | ||
| solidification | [168,205,206,207,208] | 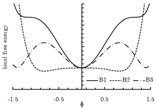 |
| solid-state phase transformations | [166,167,209,210,211] | |
| electrochemical process | [169,212] | |
| crystal growth under stress | [170] | |
| phase transformations in thin films | [171,213,214] | |
| MainApplication | PF Model | Reference | Feature |
| Solute precipitation | Xu-Meakin model | [180,220,223,224,225] | Discontinuity of the solute concentration gradient at the interface. |
| Noorden-Eck model | [179,221,222,226] | a Single-phase free boundary problem with dynamic conditions at the moving boundary. | |
| Metal precipitation | Wang-Chen model | [178,227] | Solid-state precipitation controlled by transformation-induced elastic strains. |
| Rubin-Khachaturyan model | [168,228] | 3D stochastic PF model. | |
| Chen-Ma model | [177,229] | Kinetic data of existing databases CALPHAD applied into the PF model. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Aldakheel, F.; Caggiano, A.; Wriggers, P.; Koenders, E. A Review on Cementitious Self-Healing and the Potential of Phase-Field Methods for Modeling Crack-Closing and Fracture Recovery. Materials 2020, 13, 5265. https://doi.org/10.3390/ma13225265
Yang S, Aldakheel F, Caggiano A, Wriggers P, Koenders E. A Review on Cementitious Self-Healing and the Potential of Phase-Field Methods for Modeling Crack-Closing and Fracture Recovery. Materials. 2020; 13(22):5265. https://doi.org/10.3390/ma13225265
Chicago/Turabian StyleYang, Sha, Fadi Aldakheel, Antonio Caggiano, Peter Wriggers, and Eddie Koenders. 2020. "A Review on Cementitious Self-Healing and the Potential of Phase-Field Methods for Modeling Crack-Closing and Fracture Recovery" Materials 13, no. 22: 5265. https://doi.org/10.3390/ma13225265
APA StyleYang, S., Aldakheel, F., Caggiano, A., Wriggers, P., & Koenders, E. (2020). A Review on Cementitious Self-Healing and the Potential of Phase-Field Methods for Modeling Crack-Closing and Fracture Recovery. Materials, 13(22), 5265. https://doi.org/10.3390/ma13225265








