The numerical modeling of various types of structures has become an indispensable part of engineering design work. The problems that are related to the analysis of structures made of metal, timber, or composite materials are often addressed through numerical analyses. Such analyses are particularly useful when a structure becomes increasingly anisotropic, which is often the case with composite structures. There is a large variability of types of composite structures. Consequently, numerical tools for analyzing composite structures’ behavior are constantly being developed and improved upon. One type of these structures is a sandwich composite with a pyramidal truss core. This particular type of composite has recently gained the attention of the scientific community due to its engineering advantages [
1,
2,
3,
4,
5]. Among these advantags, they possess high specific bending stiffness, weight efficiency, and good thermal and acoustical insulation [
6]. The static and dynamic behavior of sandwich structures is governed by the configurations of the parent components (face sheets and core), as well as their constituent materials’ properties. The face sheets of these structures mainly contribute to the bending stiffness, whereas the core mainly contributes to the shear stiffness. The manufacturing of such composites is realized while using adhesive joints between the core and the face sheets [
7]. If the parent materials are made of metal, the joints are mostly manufactured by brazing or laser welding [
8]. However, if the parent components are made of different materials, e.g., fiber-reinforced laminated face sheets and aluminum core, then the joints must be manufactured by the application of an adhesive material such as epoxy resin. For the first case, it is customary to assume that the brazed or welded joints possess similar material properties to those of the parent material and, therefore, there is no need for special modeling of the joints. For the latter case, the adhesive material’s properties differ from those of the parent components. This may result in a significant mutual displacements between them. For such a case, it is important to properly model the adhesive joint in order to capture additional effects that are associated with the mutual movements of the parent components. The current state-of-the-art regarding the modeling of sandwich beams with a pyramidal truss core is mostly governed by two approaches, namely equivalent modeling [
9,
10] or the finite element method (FEM) [
11,
12]. The first approach has usually been used for static analyses including linear and non-linear responses as well as fracture analysis. The equivalent model of the sandwich beam is mostly derived from the geometrical characteristics of the core and the stiffness parameters of parent components. Such models are suitable for analyzing full metal sandwich beams as well as different combinations of parent components, such as metal face sheets with a laminated carbon fiber composites (CFRP) truss core or CFRP face sheets with a metal truss core. However, for this kind of model, the adhesive joints’ compliance is not accounted for. For this reason, this type of structural modeling does not provide any information on the local behavior of the sandwich beams. The FEM approach has been used for either static or dynamic (vibration and crashworthiness) analyses. It allows for the detailed modeling of structures. However, this approach requires careful planning of the model development. It must start with proper assumptions made regarding the geometry, element type, material models, interactions between parts that are in contact (for the current case parent components), number of elements, type of solution, etc. The most attention is commonly given to the exact representation of the geometry of the beams, as seen in the up-to-date literature. The mutual contact between parent components is mostly defined as a tied contact (no mutual displacements between parent materials are allowed) [
13] or by the introduction of a mathematical model for adhesive joints (small displacements between parent materials are allowed) [
14]. However, the motivation for such approaches has been not justified, unless the parent components are made of the same material [
15]. There is also a number of research studies devoted to the sandwich beams with an adhesive layer made of viscoelastic layer [
16,
17,
18]. However, for the above cases, the viscoelastic layer was designed in order to enhance damping behaviour only, rather than the bound between the face sheets.
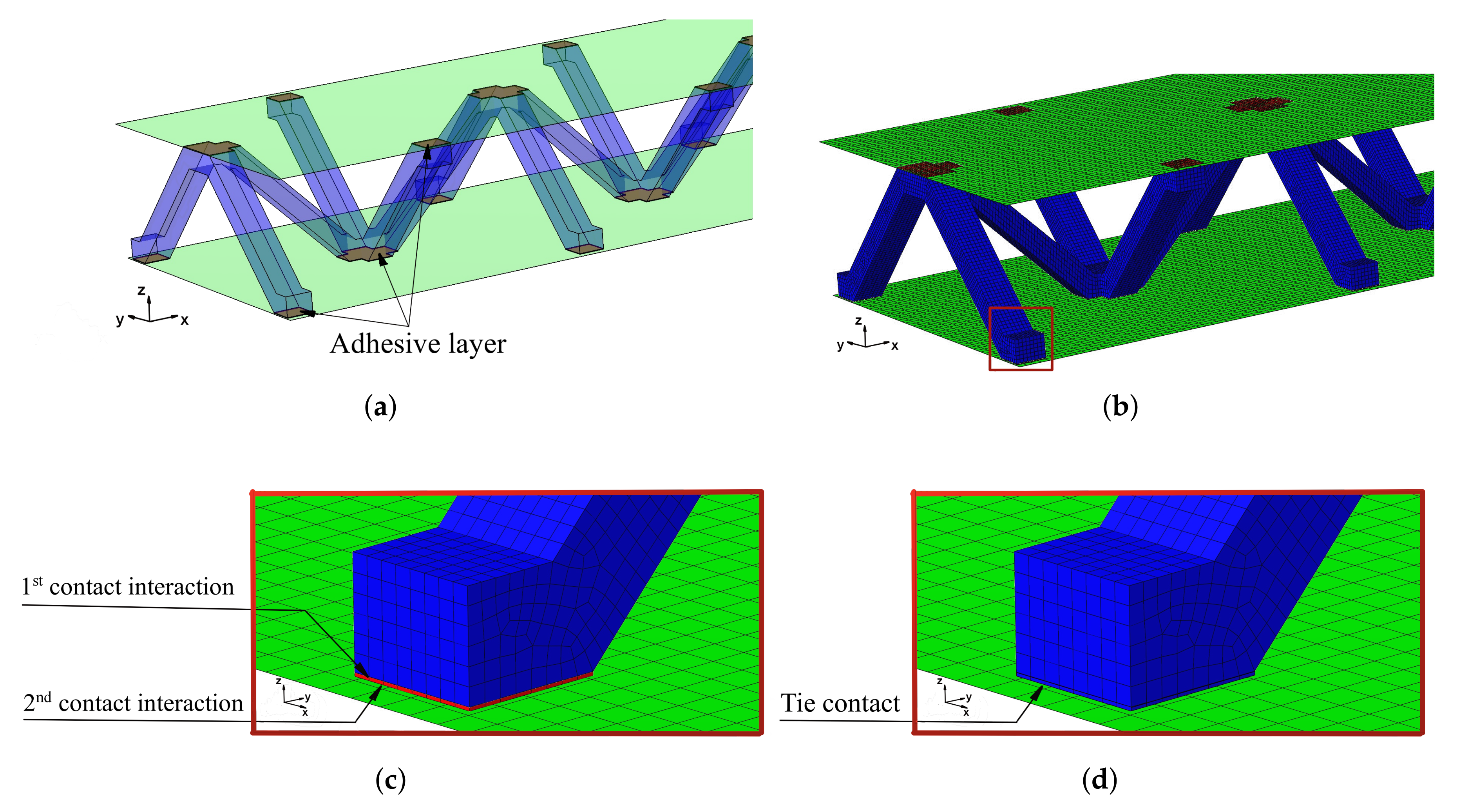
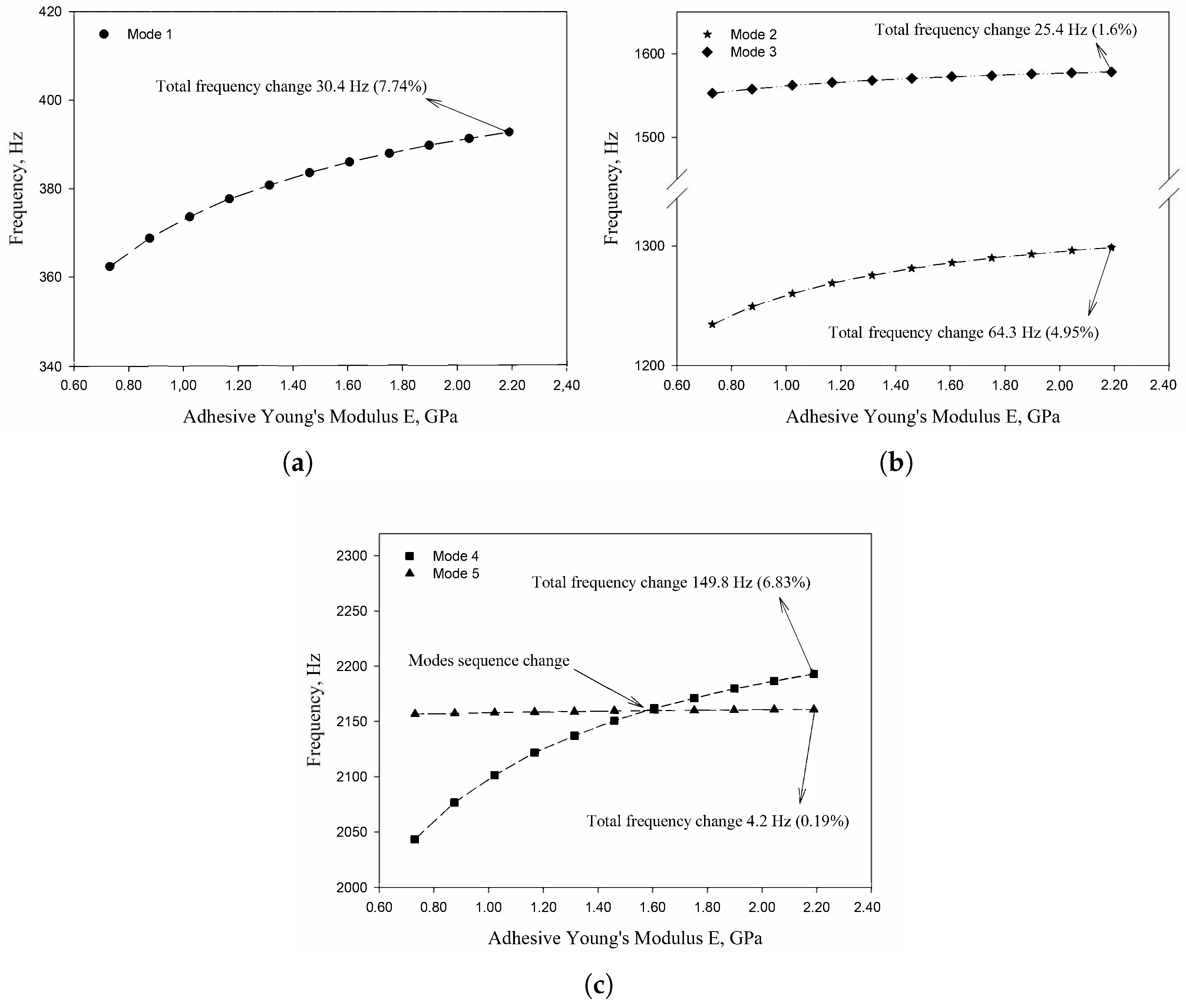
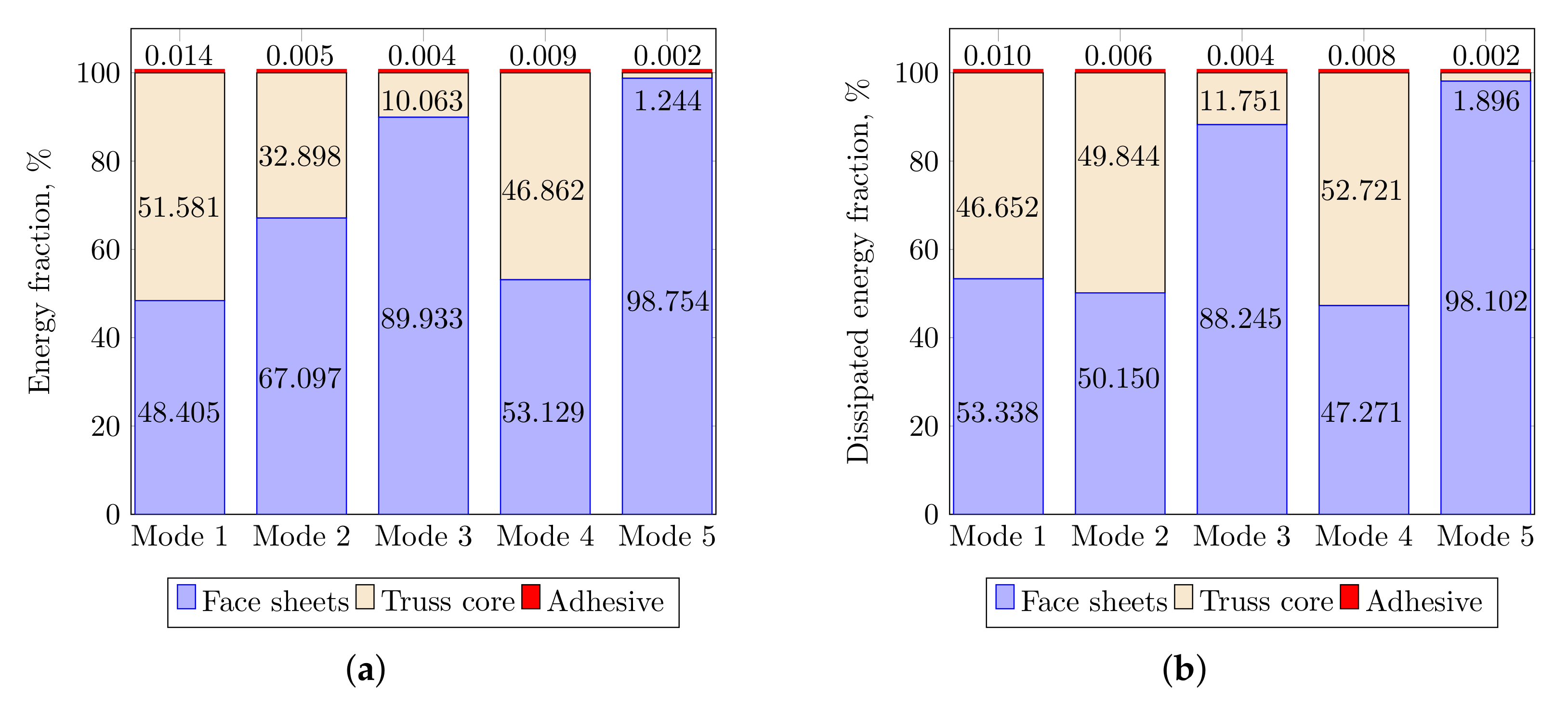
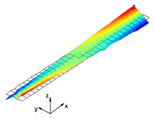
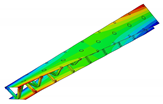
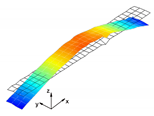
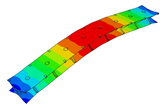
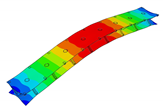
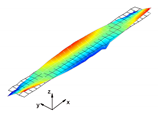
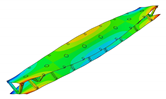
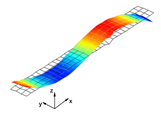
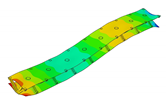
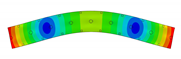
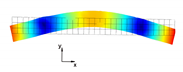
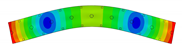
In the present paper, the authors aim to establish the role of the locally applied adhesive joints in the dynamic response of the sandwich beam. For this purpose a detailed three dimensional finite element model of the beam is developed. The beam is composed of laminated face sheets and the pyramidal aluminum truss core. The model accounts for a layer of the adhesive material that is placed between the parent components. The authors assume that the adhesive material behaves as an elastic solid but possess the both stiffness and dynamic properties. As a consequence, the overall beam’s compliance changes and affects the dynamic parameters of the beam. In order to model the adhesive layer a continuum hybrid solid-shell element is used which allows considerably reducing the total number of finite elements. The dynamic parameters of interest are eigenfrequencies, mode shapes, and modal loss factors. The significance of the adhesive joint modeling is verified by developing two numerical models of the sandwich beam with a different approach for the joint definition. The first approach accounts for additional layers of material that are placed between parent components. In the second approach, the joint is defined as a tided contact with no mutual displacement between parent components allowed. In addition, the sensitivity of the beam’s eigenfrequencies to the stiffness variation of the adhesive material is presented. The most appropriate model will be used for the modal parameters prediction. The modal loss factors are predicted based on the strain energy method, for which a theoretical background is presented. The scope of the present investigation is then expanded to a series of experimental vibration tests on a real sandwich beam samples. The vibration tests are meant to validate the correctness of the developed numerical models. For the vibration tests, a system of three laser vibrometers is used, which are capable of sensing vibrations in three mutually perpendicular directions. The in-plane and out-of-plane vibration modes of the sandwich beam can be therefore investigated, which is seldom reported in the up to date literature. The results presented in the current paper will contribute to field of sandwich structures dynamics by defining the extent and circumstances for the possible model simplifications in terms of adhesive layer modeling. The above will be achieved by comparing the numerical and experimental analyses.