Experimental Investigation of Delamination in Composite Continuous Fiber-Reinforced Plastic Laminates with Elastic Couplings
Abstract
1. Introduction
2. Elastic Coupling Phenomenon in Composites
3. Experimental Procedures
3.1. DCB Specimens
3.2. Test Procedure
3.3. Data Reduction Schemes
3.3.1. Classical Methods
3.3.2. Compliance-Based Beam Method (CBBM)
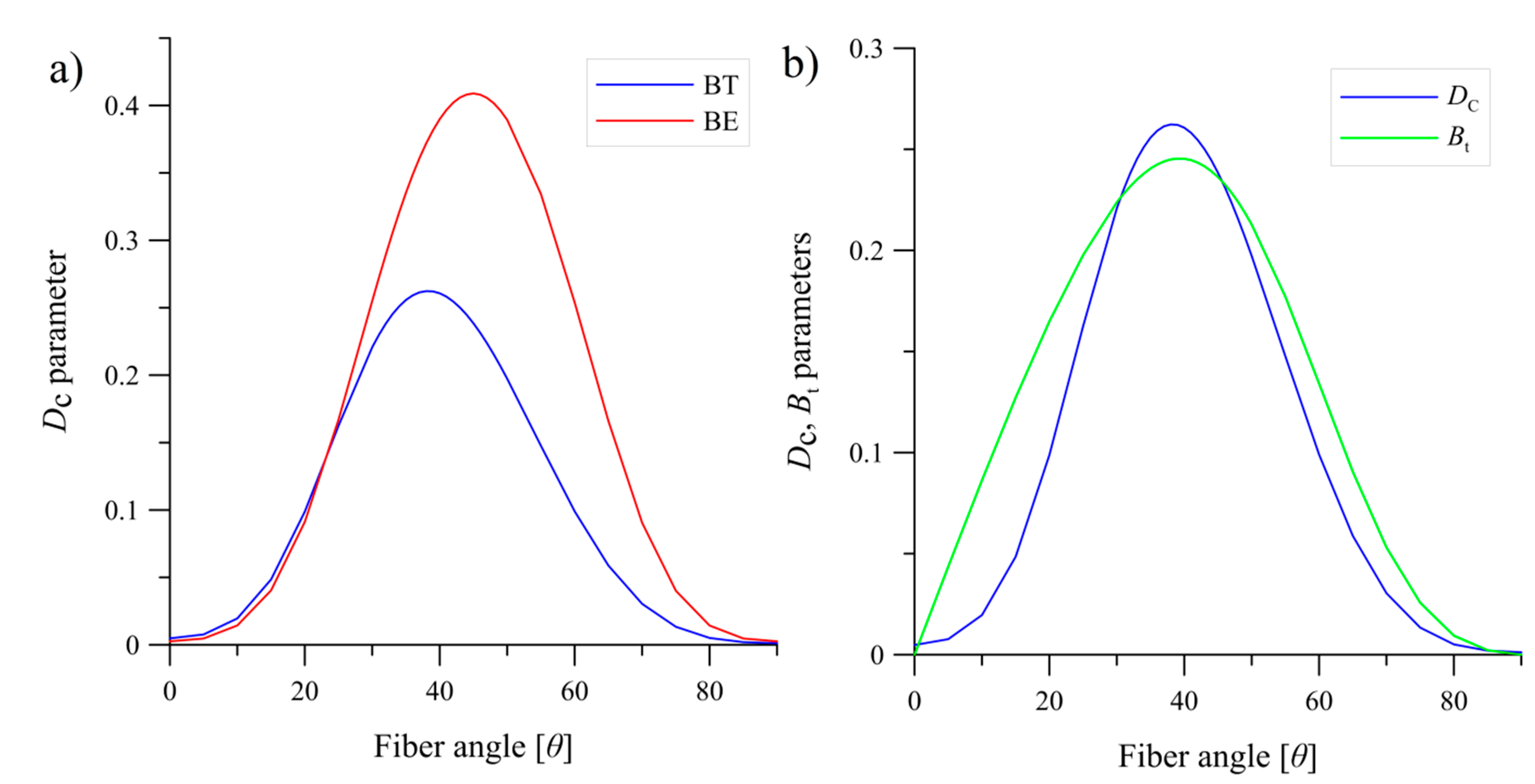
4. Effect of Elastic Couplings on Composite Laminates
5. Experimental Results
5.1. Critical Strain Energy Release Rate (c-SERR)
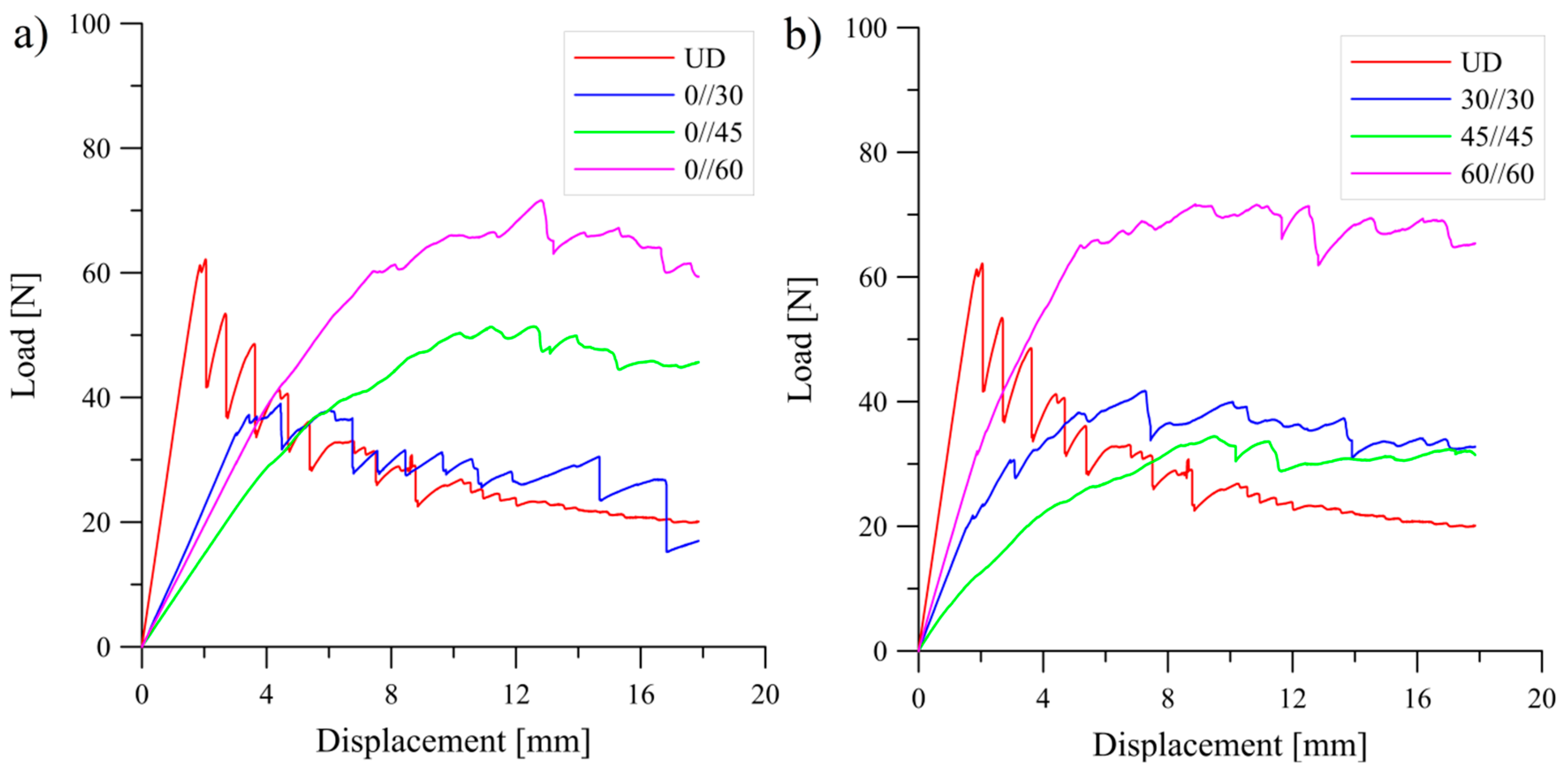
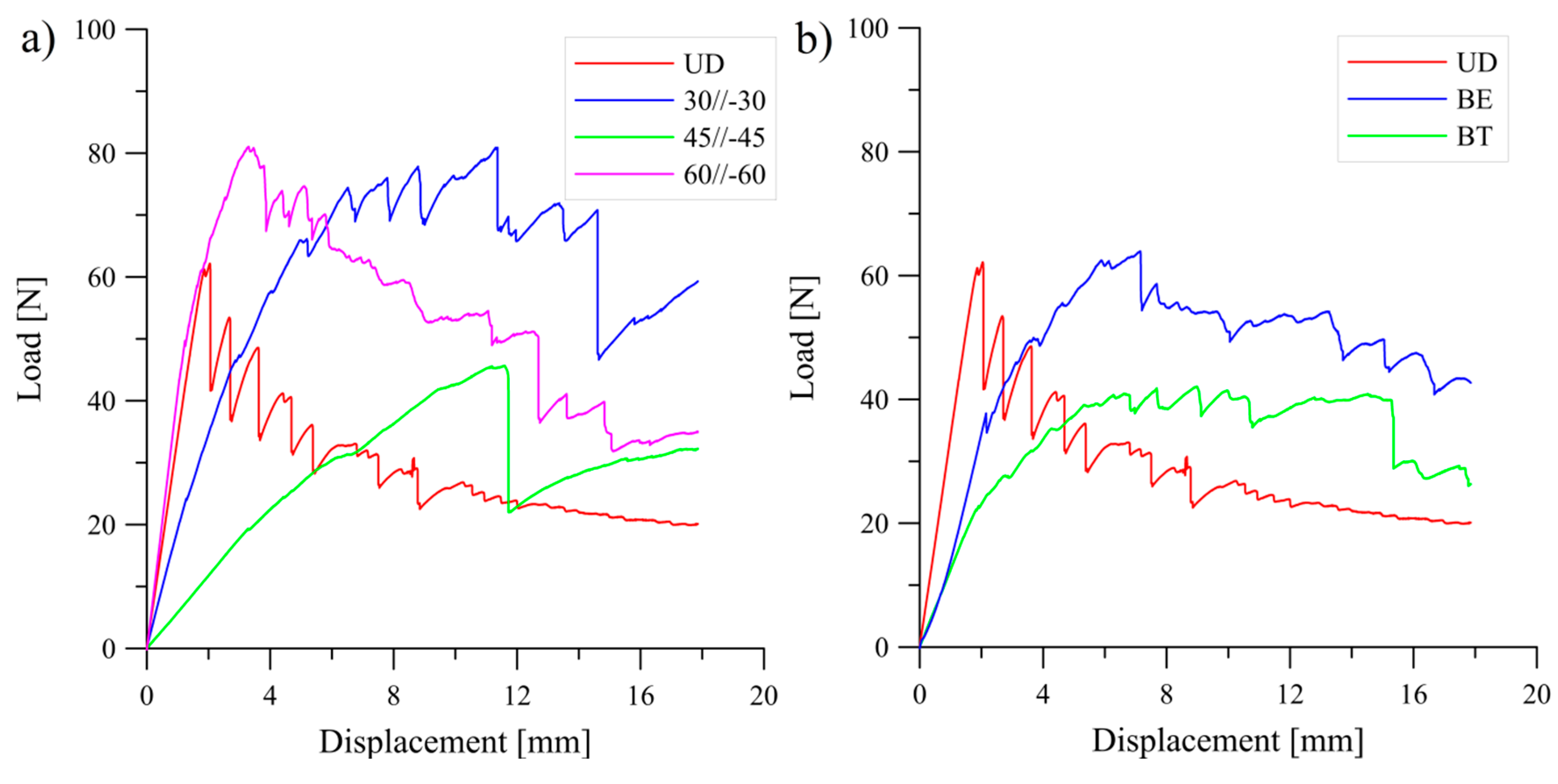
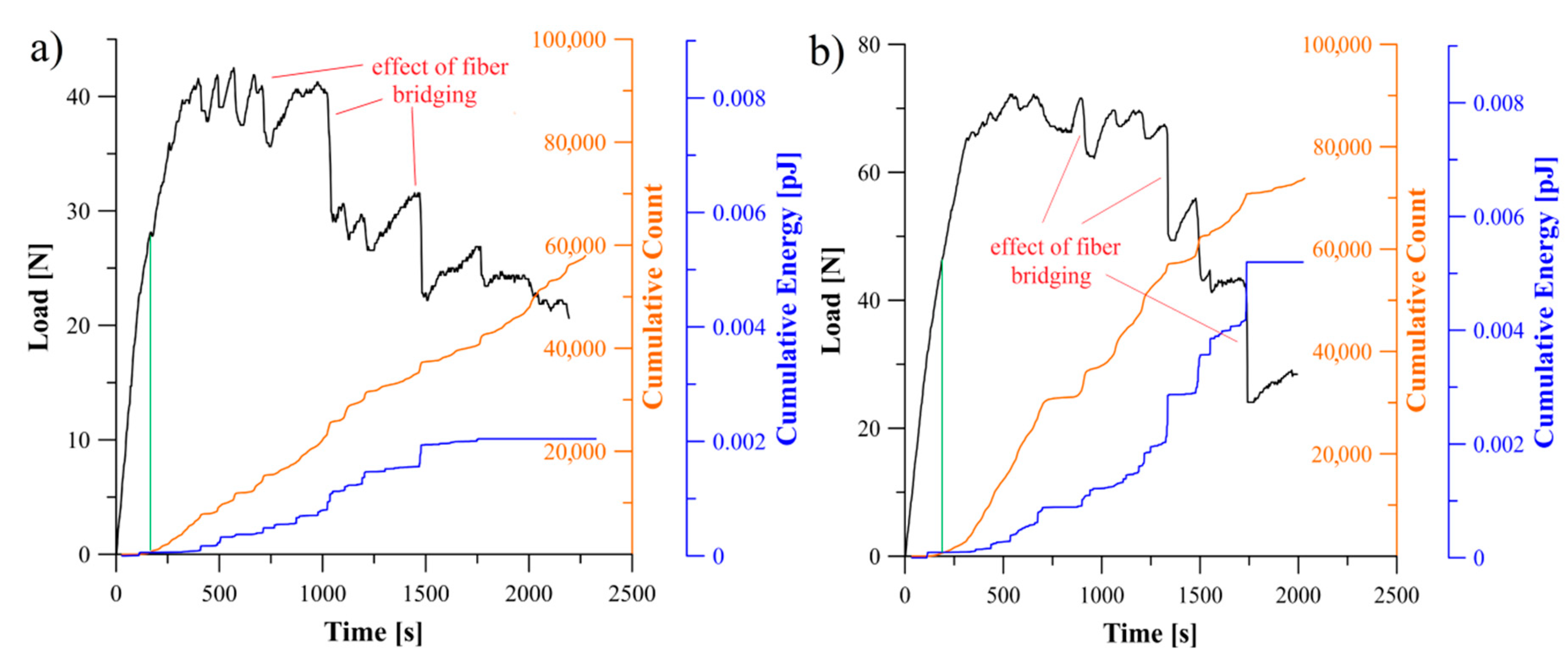
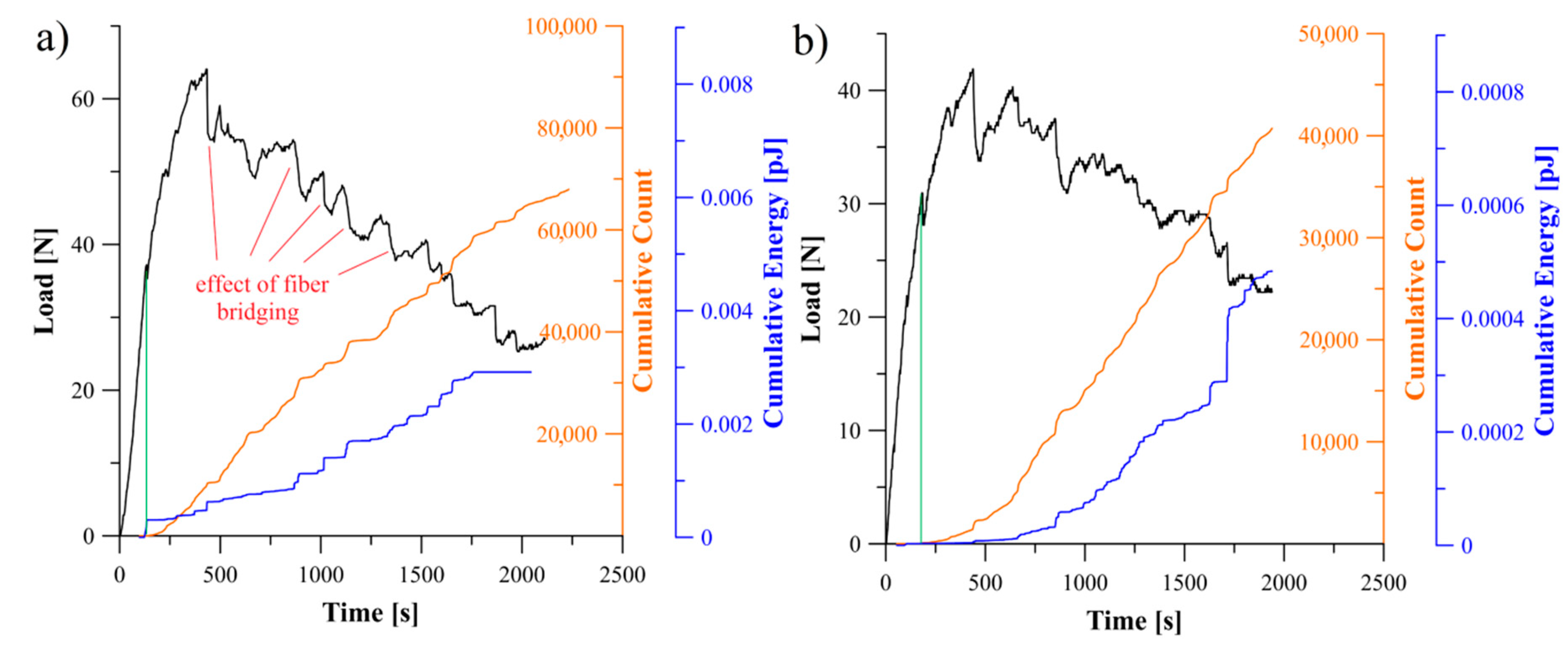
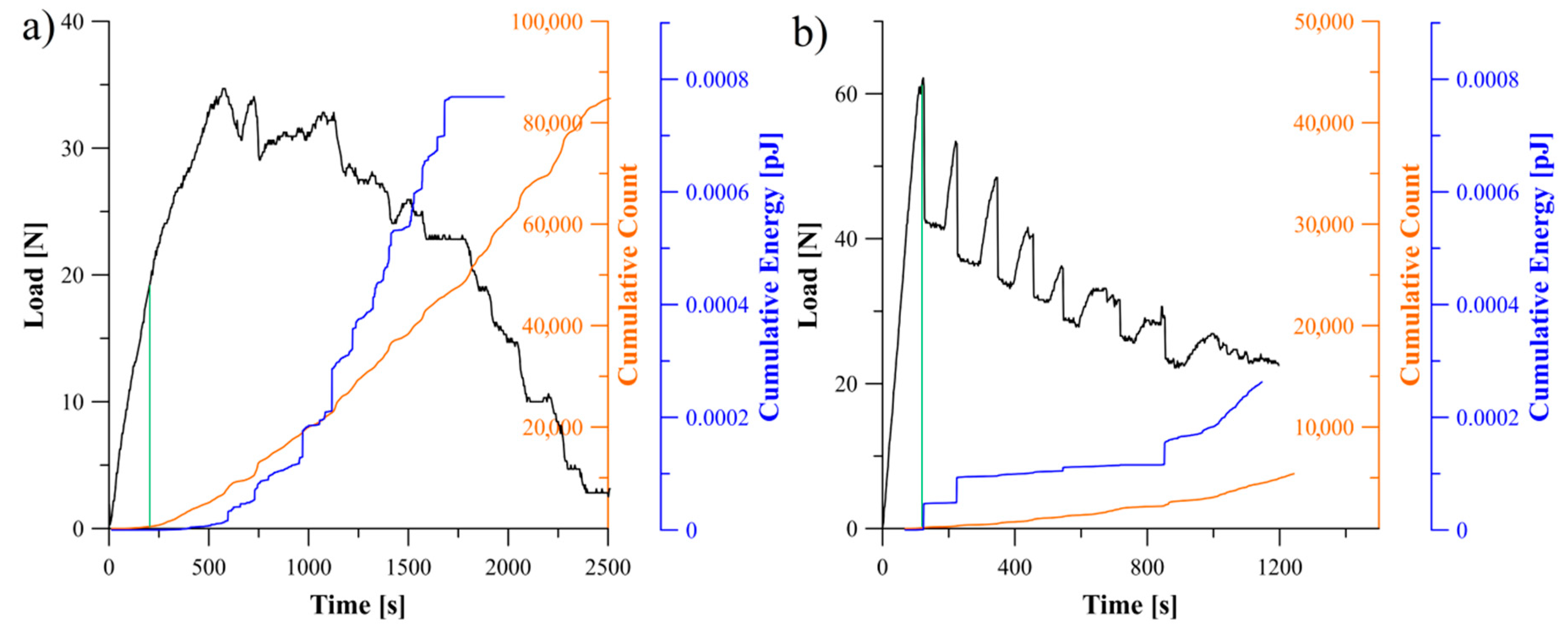
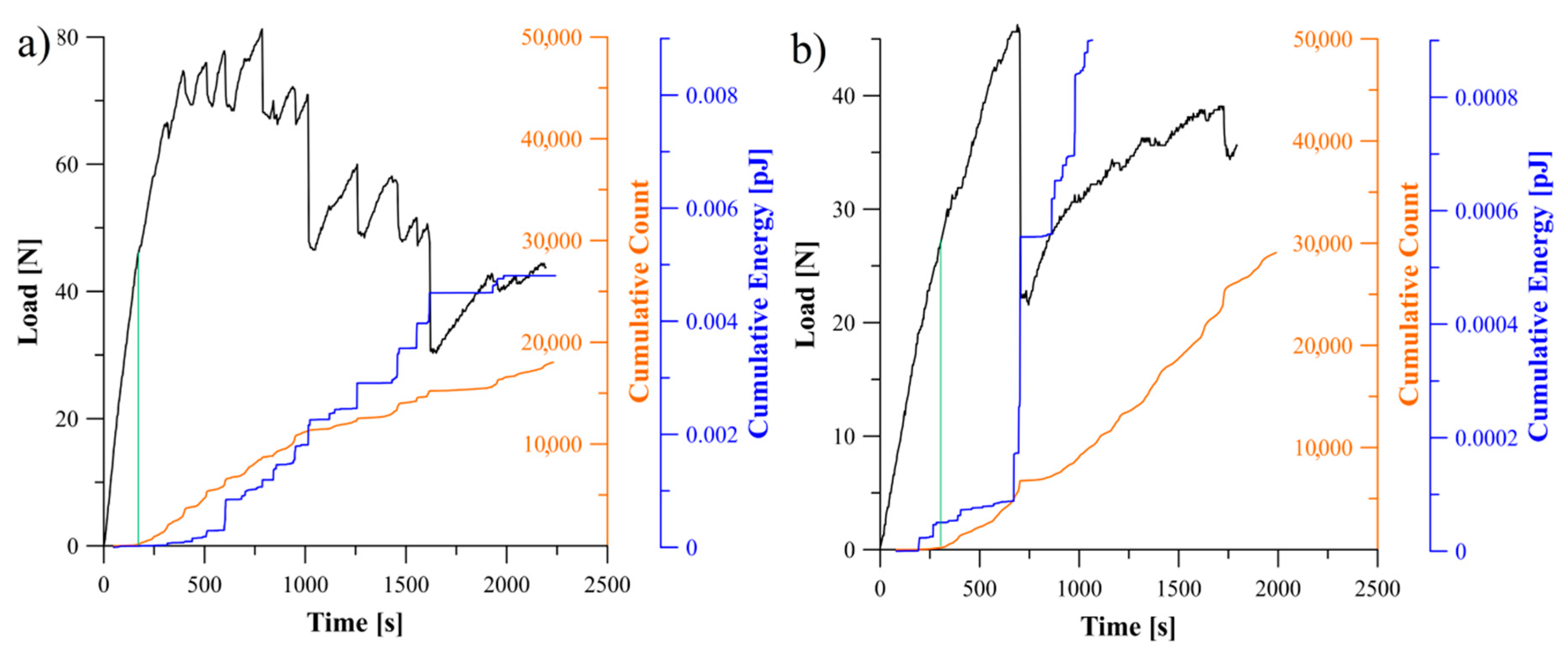
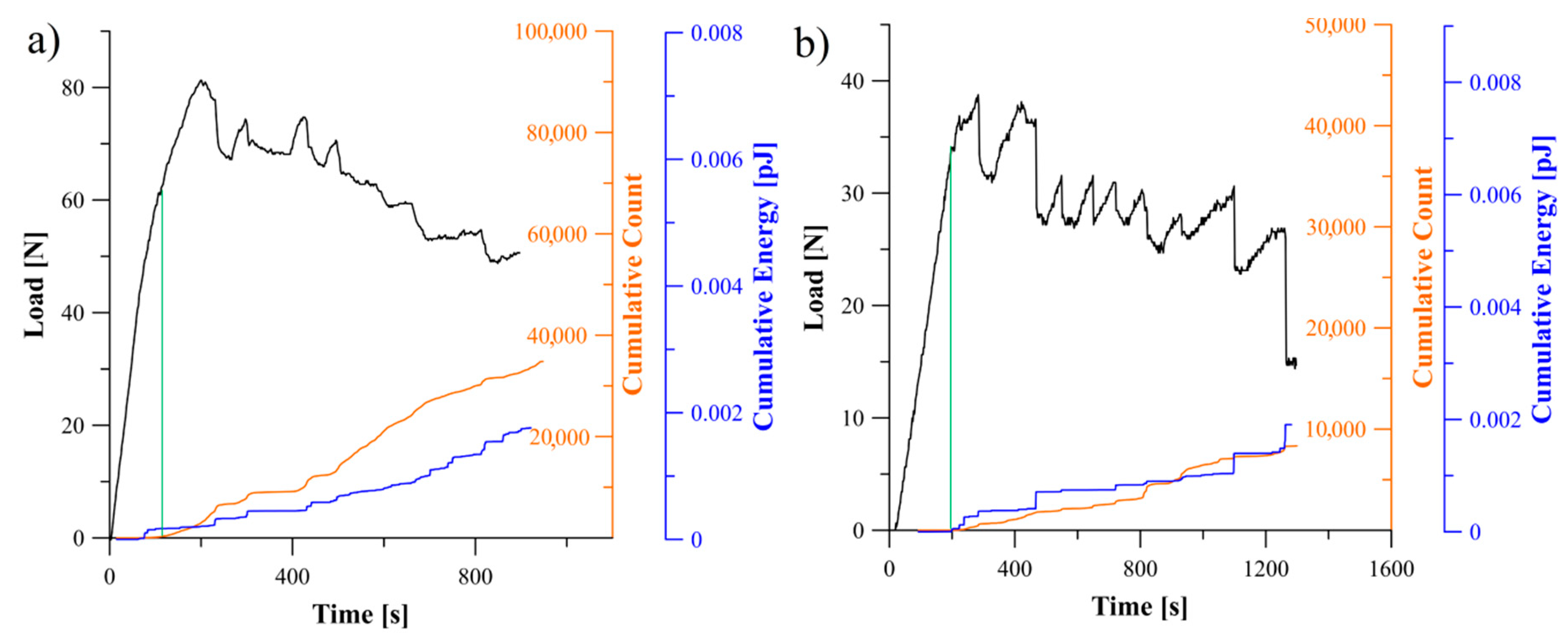
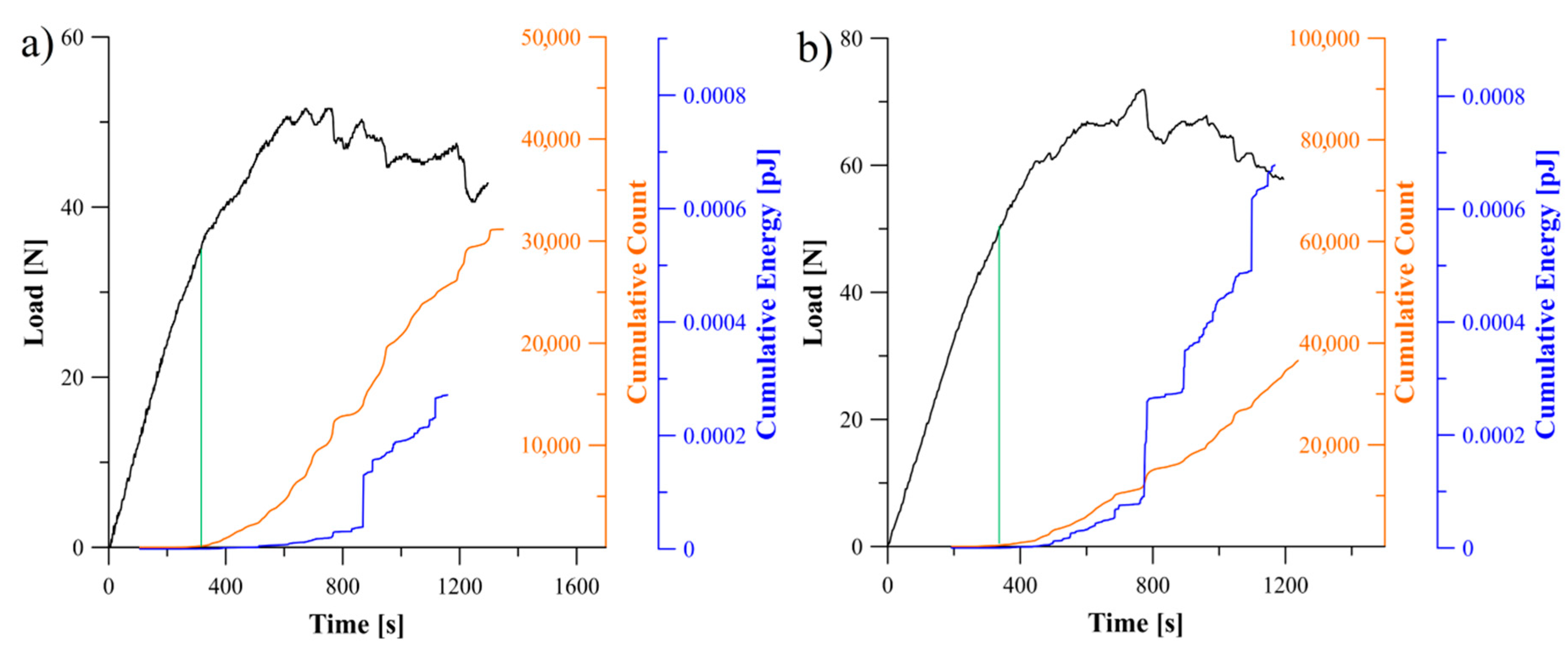
5.2. Analysis of Delamination Initiation and Propagation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | crack length |
| aeq | equivalent crack length |
| a0 | initial crack length |
| h | half thickness of specimen |
| n | correction parameter |
| A | extensional stiffness matrix |
| Aij | component of the extensional stiffness matrix |
| A1 | correction parameter |
| B | coupling stiffness matrix |
| B | specimen width |
| Bij | component of the coupling stiffness matrix |
| Bt | non-dimensional parameter |
| C | compliance |
| C0 | initial compliance |
| D | bending stiffness matrix |
| Dij | component of the bending stiffness matrix |
| Dc | non-dimensional parameter |
| E1 | longitudinal Young’s modulus |
| E2 | transversal Young’s modulus |
| Ef | flexural modulus |
| G12 | shear modulus |
| GIC | critical strain energy release rate |
| L | specimen length |
| M | moment vector |
| N | force vector |
| P | applied load |
| ν12 | Poisson’s ratio |
| δ | displacement |
| Δ | correction parameter |
| Γ | correction parameter |
| List of acronyms | |
| AE | acoustic emission |
| BE | bending-extension coupled specimen |
| BT | bending-twisting coupled specimen |
| CBBM | Compliance-Based Beam Method |
| DCB | Double Cantilever Beam |
| MCC | Modified Compliance Calibration |
| CCM | Compliance Calibration Method |
| MBT | Modified Beam Theory |
| SEM | scanning electron microscope |
References
- D5528 Standard Test. Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2013.
- D7905 Standard Test. Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2018.
- De Gracia, J.; Boyano, A.; Arrese, A.; Mujika, F. Analysis of the DCB test of angle-ply laminates including residual stresses. Theor. Appl. Fract. Mech. 2018, 94, 197–204. [Google Scholar] [CrossRef]
- Pereira, A.B.; de Morais, A.B. Mode II interlaminar fracture of glass/epoxy multidirectional laminates. Compos. Part A 2004, 35, 265–272. [Google Scholar] [CrossRef]
- Alfano, G.; Crisfield, M.A. Finite element interface models for the delamination analysis of laminated composites: Mechanical and computational issues. Int. J. Numer. Meth. Eng. 2001, 50, 1701–1736. [Google Scholar] [CrossRef]
- de Borst, R. Numerical aspects of cohesive-zone models. Eng. Fract. Mech. 2003, 70, 1743–1757. [Google Scholar] [CrossRef]
- Gliszczynski, A.; Samborski, S.; Wiacek, N.; Rzeczkowski, J. Mode I Interlaminar Fracture of Glass/Epoxy Unidirectional Laminates. Part II: Numerical Analysis. Materials (Basel) 2019, 12, 1607. [Google Scholar] [CrossRef]
- Herráez, M.; González, C.; Lopes, C.S. A numerical framework to analyze fracture in composite materials: From R-curves to homogenized softening laws. Int. J. Solids Struct. 2018, 134, 216–228. [Google Scholar] [CrossRef]
- Orifici, A.C.; Krueger, R. Benchmark assessment of automated delamination propagation capabilities in finite element codes for static loading. Finite Elem. Anal. Des. 2012, 54, 28–36. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Kanninen, M.F. A finite element calculation of stress intensity factors by a modified crack closure integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, B.; Zhao, L.; Zhang, J.; Hu, N.; Zhang, C. R-curve behaviour of the mixed-mode I/II delamination in carbon/epoxy laminates with unidirectional and multidirectional interfaces. Compos. Struct. 2019, 223, 110949. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, B.; Mukhopadhyay, S.; Hallett, S.R. Experimental study on delamination migration in multidirectional laminates under mode II static and fatigue loading, with comparison to mode I. Compos. Struct. 2018, 261, 683–698. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Heidari-Rarani, M. Effect of stacking sequence on R-curve behavior of glass/epoxy DCB laminates with 0°//0° crack interface. Mater. Sci. Eng. A 2011, 529, 265–269. [Google Scholar] [CrossRef]
- Schön, J.; Nyman, T.; Blom, A.; Ansell, H. A numerical and experimental investigation of delamination behaviour in the DCB specimen. Compos. Sci. Technol. 2000, 60, 173–184. [Google Scholar] [CrossRef]
- Davidson, B.D. Three Dimensional Analysis and Resulting Design Recommendations for Unidirectional and Multidirectional End-Notched Flexure Tests. J. Compos. Mater. 1995, 29, 2018–2033. [Google Scholar] [CrossRef]
- Olsson, R.A. Simplified improved beam analysis of the DCB specimen. Compos. Sci. Technol. 1992, 43, 329–338. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Heidari-Rarani, M.; Rahimi, S. Influence of curved delamination front on toughness of multidirectional DCB specimens. Compos. Struct. 2012, 94, 1359–1365. [Google Scholar] [CrossRef]
- York, C.B.; de Almeida, S.F.M. On Extension-Shearing Bending-Twisting coupled laminates. Compos. Struct. 2017, 164, 10–22. [Google Scholar] [CrossRef]
- Rzeczkowski, J.; Samborski, S.; Valvo, P.S. Effect of stiffness matrices terms on delamination front shape in laminates with elastic couplings. Compos. Struct. 2020, 23, 111547. [Google Scholar] [CrossRef]
- Jiang, Z.; Wan, S.; Keller, T.; Fang, Z.; Vassilopoulos, A.P. Vassilopoulos. Influence of curved delamination front on R-curve of DCB specimen. Compos. Struct. 2019, 223, 111311. [Google Scholar] [CrossRef]
- Jiang, Z.; Wan, S.; Zhong, Z.; Li, S.; Shen, K. Effect of curved delamination front on mode-I fracture toughness of adhesively bonded joints. Eng. Fract. Mech. 2015, 138, 73–91. [Google Scholar] [CrossRef]
- Amrutharaj, G.S.; Lam, K.Y.; Cotterell, B. Fracture process zone concept and delamination of composite laminates. Theor. Appl. Fract. Mech. 1995, 24, 57–64. [Google Scholar] [CrossRef]
- de Moura, M.F.S.F.; de Morais, A.B. Equivalent crack based analyses of ENF and ELS tests. Eng. Fract. Mech. 2008, 75, 2584–2596. [Google Scholar] [CrossRef]
- Rzeczkowski, J. An experimental analysis of the end-notched flexure composite laminates beams with elastic couplings. Contin. Mech. 2020, 98, 210. [Google Scholar]
- Rzeczkowski, J.; Samborski, S.; Paśnik, J. Experimental Verification of the DCB Test Configuration Applicability to Mechanically Coupled Composite Laminates. IOP Conf. Ser. Mater. Sci. Eng. 2018, 416, 12055. [Google Scholar] [CrossRef]
- De Moura, M.F.S.F.; Campilho, R.D.S.G.; Gonçalves, J.P.M. Crack equivalent concept applied to the fracture characterization of bonded joints under pure mode I loading. Compos. Sci. Technol. 2008, 68, 2224–2230. [Google Scholar] [CrossRef]
- Lissek, F.; Haeger, A.; Knoblauch, V.; Hloch, S.; Pude, F.; Kaufeld, M. Acoustic emission for interlaminar toughness testing of CFRP: Evaluation of the crack growth due to burst analysis. Compos. Part B Eng. 2018, 136, 55–62. [Google Scholar] [CrossRef]
- Nikbakht, M.; Yousefi, J.; Hosseini-Toudeshky, H.; Minak, G. Delamination evaluation of composite laminates with different interface fiber orientations using acoustic emission features and micro visualization. Compos. Part. B Eng. 2017, 113, 185–196. [Google Scholar] [CrossRef]
- Saeedifar, M.; Fotouhi, M.; Najafabadi, M.A.; Toudeshky, H.H.; Minak, G. Prediction of quasi-static delamination onset and growth in laminated composites by acoustic emission. Compos. Part. B Eng. 2016, 85, 113–122. [Google Scholar] [CrossRef]
- Kaw, A.K. Mechanics of Composite Materials, 2nd ed.; CRC, Taylor & Francis: Boca Raton, FL, USA, 2006; ISBN 9780849313431. [Google Scholar]
- Hashemi, S.; Kinloch, A.J.; Williams, J.G. The analysis of interlaminar fracture in uniaxial fibre-polymer composites. Proc. R. Soc. A 1990, 427, 173–199. [Google Scholar]
- Samborski, S. Analysis of the end-notched flexure test configuration applicability for mechanically coupled fiber reinforced composite laminates. Compos. Struct. 2017, 163, 342–349. [Google Scholar] [CrossRef]
- Samborski, S. Numerical analysis of the DCB test configuration applicability to mechanically coupled Fiber Reinforced Laminated Composite beams. Compos. Struct. 2016, 152, 477–487. [Google Scholar] [CrossRef]
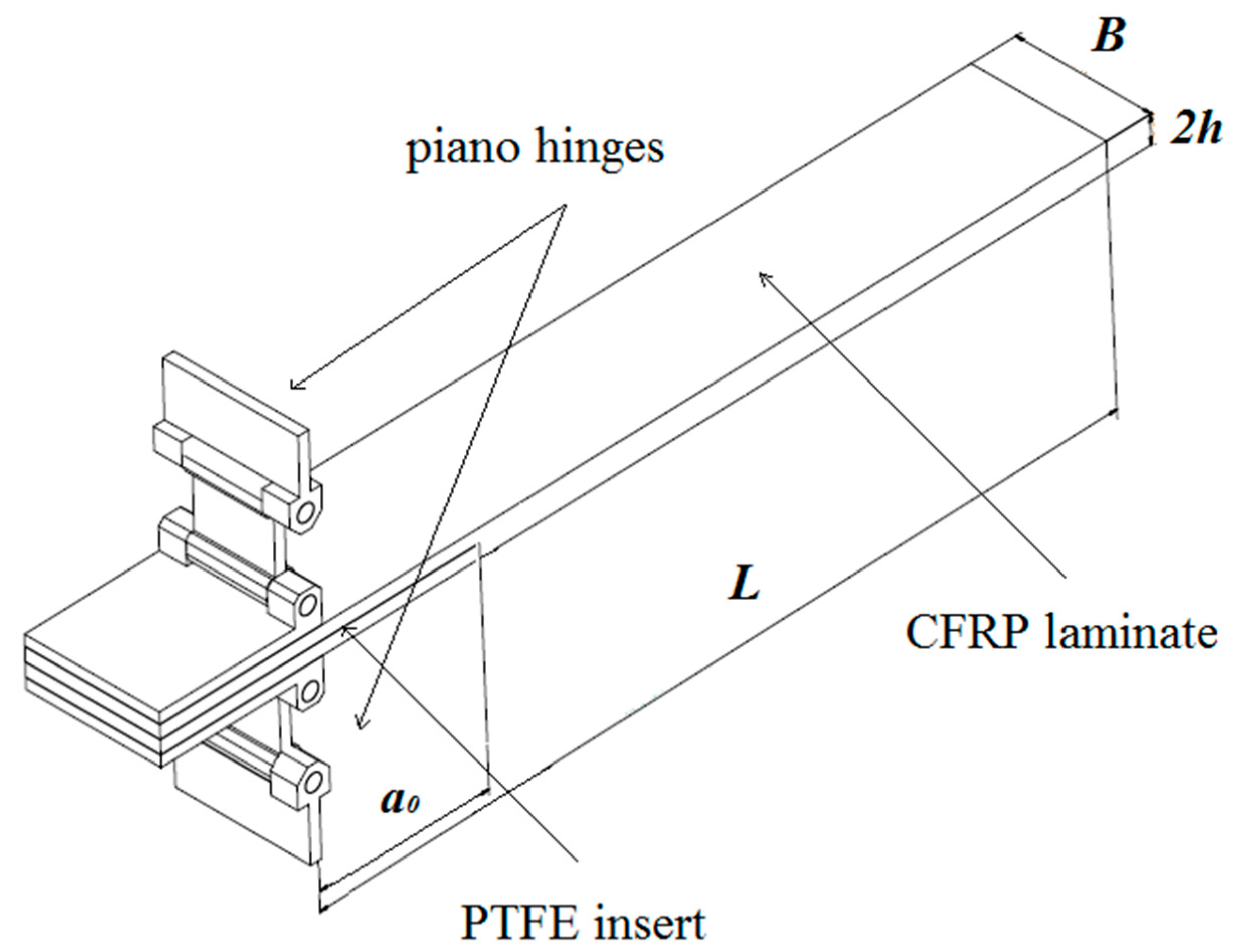


| Laminate | Stacking Sequence (for One Sub-laminate) |
|---|---|
| BT | (45°/0°/45°/45°/0°/−45°/0°/−45°/−45°/−45°/−45°/0°/−45°/45°/0°/0°/45°/45°) |
| BE | (45°/−45°/0°/−45°/0°/45°/90°/45°/−45°) |
| E1 (GPa) | E2 (GPa) | ν12 (-) | G12 (GPa) |
|---|---|---|---|
| 112.105 | 7.421 | 0.270 | 3.338 |
| Interface | A (MPa × mm) × 105 | B (MPa × mm2) × 10−10 | D (MPa × mm3) × 105 | Dc | Bt | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0°//0° | 5.0174 | 0.0897 | 0 | −0.2910 | 0.0034 | 0 | 8.2946 | 0.1483 | 0 | 0.0048 | 0 |
| 0.0897 | 0.3321 | 0 | 0.0034 | 0.0045 | 0 | 0.1483 | 0.5491 | 0 | |||
| 0 | 0 | 0.1487 | 0 | 0 | −0.0011 | 0 | 0 | 0.2458 | |||
| 30°//30° | 4.8980 | 0.1401 | 0.0888 | −0.2910 | 0.0034 | 0 | 8.2939 | 0.1485 | 0.0005 | 0.0048 | 0 |
| 0.1401 | 0.3506 | 0.0305 | 0.0034 | 0.0045 | 0 | 0.1485 | 0.5492 | 0.0002 | |||
| 0.0888 | 0.0305 | 0.1991 | 0 | 0 | −0.0011 | 0.0005 | 0.0002 | 0.2461 | |||
| 45°//45° | 4.8123 | 0.1570 | 0.0689 | −0.2910 | 0.0034 | 0 | 8.2934 | 0.1486 | 0.0004 | 0.0048 | 0 |
| 0.1570 | 0.4026 | 0.0689 | 0.0034 | 0.0045 | 0 | 0.1486 | 0.5495 | 0.0004 | |||
| 0.0689 | 0.0689 | 0.2160 | 0 | 0 | 0.0011 | 0.0004 | 0.0004 | 0.2462 | |||
| 60°//60° | 4.7602 | 0.1401 | 0.0305 | −0.2910 | 0.0034 | 0 | 8.2931 | 0.1485 | 0.0002 | 0.0048 | 0 |
| 0.1401 | 0.4884 | 0.0888 | 0.0034 | 0.0045 | 0 | 0.1485 | 0.5500 | 0.0005 | |||
| 0.0305 | 0.0888 | 0.1991 | 0 | 0 | −0.0011 | 0.0002 | 0.0005 | 0.2461 | |||
| Laminate | A (MPa × mm) × 105 | B (MPa × mm2) × 10−11 | D (MPa × mm3) × 104 | Dc | Bt | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BT | 1.4257 | 0.4512 | 0 | 0.0909 | 0 | 0.0909 | 6.6061 | 2.0906 | 1.5608 | 0.2384 | 0.2363 |
| 0.4512 | 0.5989 | 0 | 0 | −0.0909 | 0 | 2.0906 | 2.7751 | 1.5608 | |||
| 0 | 0 | 0.4824 | 0.0909 | 0 | 0.1819 | 1.5608 | 1.5608 | 2.2353 | |||
| Laminate | A (MPa × mm) × 104 | B (MPa × mm2) × 103 | D (MPa × mm3) × 103 | Dc | Bt | ||||||
| BE | 5.7506 | 2.2560 | 0 | −3.6104 | 0 | 0 | 5.1803 | 3.3060 | 0 | 0.4089 | 0 |
| 2.2560 | 4.3726 | 0 | 0 | 3.6104 | 0 | 3.3060 | 5.1606 | 0 | |||
| 0 | 0 | 2.4121 | 0 | 0 | 0 | 0 | 0 | 3.4870 | |||
| Interface | CCM | MBT | MCC | CBBM | ||||
|---|---|---|---|---|---|---|---|---|
| GIC (N/mm) | Error (%) | GIC (N/mm) | Error (%) | GIC (N/mm) | Error (%) | GIC (N/mm) | Error (%) | |
| 0°//0° | 0.14 | 0.08 | 0.14 | 0.17 | 0.14 | 2.08 | 0.15 | 0.26 |
| 0°//30° | 0.18 | 2.50 | 0.19 | 2.61 | 0.19 | 1.95 | 0.21 | 6.28 |
| 0°//45° | 0.39 | 3.49 | 0.38 | 4.07 | 0.38 | 4.68 | 0.39 | 2.21 |
| 0°//60° | 0.53 | 4.33 | 0.51 | 1.16 | 0.50 | 1.93 | 0.74 | 10.08 |
| 0°//90° | 0.40 | 10.28 | 0.42 | 13.40 | 0.40 | 10.55 | 0.45 | 12.29 |
| 30°//30° | 0.16 | 1.68 | 0.17 | 2.25 | 0.17 | 2.11 | 0.17 | 2.37 |
| 30°//−30° | 0.49 | 11.54 | 0.5 | 11.92 | 0.51 | 11.04 | 0.56 | 16.66 |
| 45°//45° | 0.16 | 1.59 | 0.16 | 1.44 | 0.16 | 1.36 | 0.18 | 0.76 |
| 45°//−45° | 0.22 | 7.32 | 0.22 | 8.64 | 0.23 | 8.76 | 0.24 | 8.94 |
| 60°//60° | 0.67 | 3.10 | 0.66 | 4.11 | 0.63 | 5.26 | 0.79 | 4.64 |
| 60°//−60° | 0.46 | 4.21 | 0.46 | 4.87 | 0.42 | 3.59 | 0.45 | 3.75 |
| 90°//90° | 0.54 | 2.20 | 0.54 | 3.60 | 0.54 | 6.83 | 0.61 | 9.33 |
| BE | 0.51 | 3.56 | 0.50 | 2.32 | 0.49 | 5.38 | 0.65 | 9.06 |
| BT | 0.36 | 3.06 | 0.36 | 2.59 | 0.34 | 2.11 | 0.38 | 1.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rzeczkowski, J.; Samborski, S.; de Moura, M. Experimental Investigation of Delamination in Composite Continuous Fiber-Reinforced Plastic Laminates with Elastic Couplings. Materials 2020, 13, 5146. https://doi.org/10.3390/ma13225146
Rzeczkowski J, Samborski S, de Moura M. Experimental Investigation of Delamination in Composite Continuous Fiber-Reinforced Plastic Laminates with Elastic Couplings. Materials. 2020; 13(22):5146. https://doi.org/10.3390/ma13225146
Chicago/Turabian StyleRzeczkowski, Jakub, Sylwester Samborski, and Marcelo de Moura. 2020. "Experimental Investigation of Delamination in Composite Continuous Fiber-Reinforced Plastic Laminates with Elastic Couplings" Materials 13, no. 22: 5146. https://doi.org/10.3390/ma13225146
APA StyleRzeczkowski, J., Samborski, S., & de Moura, M. (2020). Experimental Investigation of Delamination in Composite Continuous Fiber-Reinforced Plastic Laminates with Elastic Couplings. Materials, 13(22), 5146. https://doi.org/10.3390/ma13225146






