1. Introduction
Ease of fabrication, transparency in the UV visible range, chemical inertness, low electrical conductivity, and their elasticity are some of the useful characteristics of Polydimethylsiloxane (PDMS) [
1]. Therefore, PDMS, a silicon elastomer, is widely found in applications of fluidics, optical systems and sensors [
2]. In addition, there is a growing interest in using PDMS in the field of robotics, as stretchable electronic skins [
3], among many other applications. Martensitic phase transforming metals such as shape memory alloys (SMA) are, contrarily, hard inorganic materials (e.g., NiTi-alloys). Both materials have in common that they exhibit a nonlinear mechanical behavior. SMA’s behavior is also temperature, mechanical loading and in special cases magnetic field dependent [
4]. These physical quantities induce a spontaneous change of the crystallographic lattice and lead to a change of the mechanical properties [
4]. Due to their viscoelastic nature, PDMS’s mechanical behavior is time and temperature dependent. Both materials would exhibit a hysteretic behavior during mechanical cyclic excitation and, therefore, they are suitable for vibration damping [
5,
6].
In the literature various SMA hybrid composites were reported to achieve (large displacement) actuators [
7,
8,
9], enhanced damping capacity as well as toughness within a thermoset polymer matrix [
6,
10], improved performance of self-healing polymers by embedding SMA wires [
11,
12], surface topography modulation [
13], among others. Elastomer-SMA composites were of particular interest due to the combination of flexibility and shape memory effect initiated by the embedded shape memory alloy (long, short wires, plates, shells etc.). Applications were related to robotics and smart structures, as robot hands made of polyurethane-SMA composite [
14] or dynamically programmable micro-wrinkles made of PDMS-SMA [
13]. Moreover, in earlier investigations special emphases were given to actuator of any regard [
15,
16] and Huang (2002) [
17] studied different SMAs for actuators and concluded that NiTi alloys revealed the best performance in terms of thermomechanical behavior.
Motivated by the idea of merging the shape memory characteristic of NiTi and the soft flexible viscoelastic behavior of PDMS, we present a composite for enhanced damping capacity. Basically, PDMS is the matrix material and shape memory NiTi alloy is incorporated as wires.
Figure 1 shows the barbell-shaped specimen made of PDMS with 4.4 vol% NiTi wires. Additionally, it illustrates the actuation capability of the composite. A mechanical deformation is temporarily preserved due to the metal wires and the flexible elastomer. When the temperature is elevated to the transition temperature, the SMA will regain the permanent shape resulting in the original straight shape of the sample. The temperature increase could be achieved by an external heating source or easily by electric heating through the SMA wires. Unlike shape memory NiTi wires, the temporary shape would never be preserved by the neat silicon elastomer without any external loading at ambient temperatures.
Besides the actuation capability, also the damping performance of a PDMS can be enhanced by introducing SMA wires [
5,
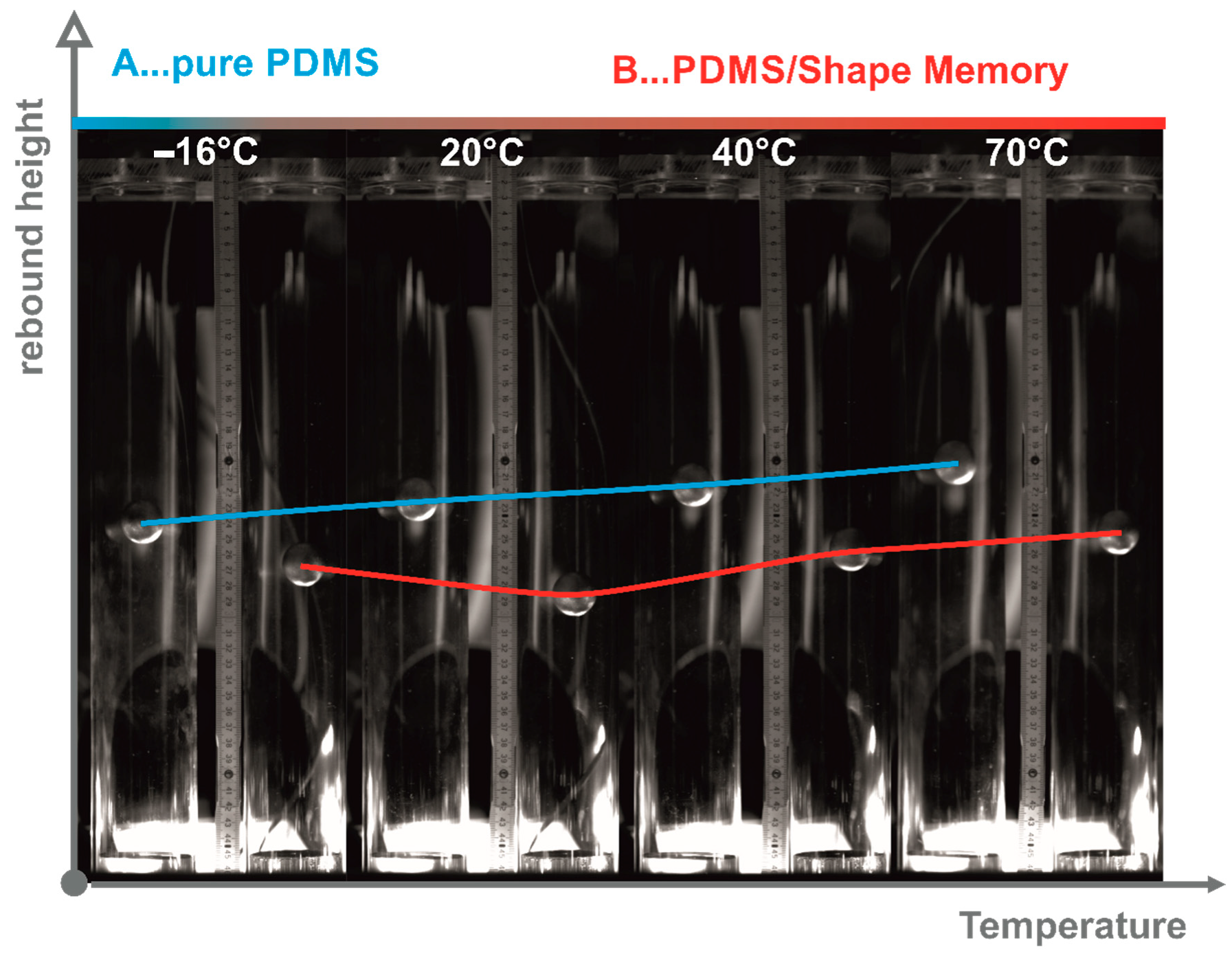
6], however, it is less investigated compared to actuator designs. To demonstrate the damping capacity, a ball drop test is realized and shown in
Figure 2. Two acrylic glass tubes were placed in a temperature chamber, where at the bottom of one tube the PDMS-SMA composite was fixed and the neat PDMS in the other tube for comparison purposes. The balls were held by electromagnets at the top of the tubes and by a trigger the balls could be released simultaneously. In
Figure 2 the right tube belongs to the neat PDMS and the left one to the PDMS-SMA. A high-speed camera was utilized to record the ball drop. Sequences at four different temperatures of the first maximum rebound height are presented in
Figure 2. Essential is the rebound height difference between the neat PDMS and the composite. From these observations it can be concluded that PDMS-SMA dissipates the energy more and faster; thereby it should be noted that the damping element made of PDMS-SMA is stiffer than that of neat PDMS of same volume, simply a result of the higher stiffness of the SMA.
To gain more insight into the interplay between PDMS and SMA, on the one hand, and the dynamic thermomechanical behavior, on the other hand, a comprehensive characterization methodology including an attempt to model the investigated mechanical properties and their temperature as well as loading rate dependency will be presented in the following. In this paper, we report the first study of combining NiTi wires with PDMS matrix, and investigate their stiffness as well as damping behaviors under dynamic thermomechanical loadings.
3. Results and Discussion
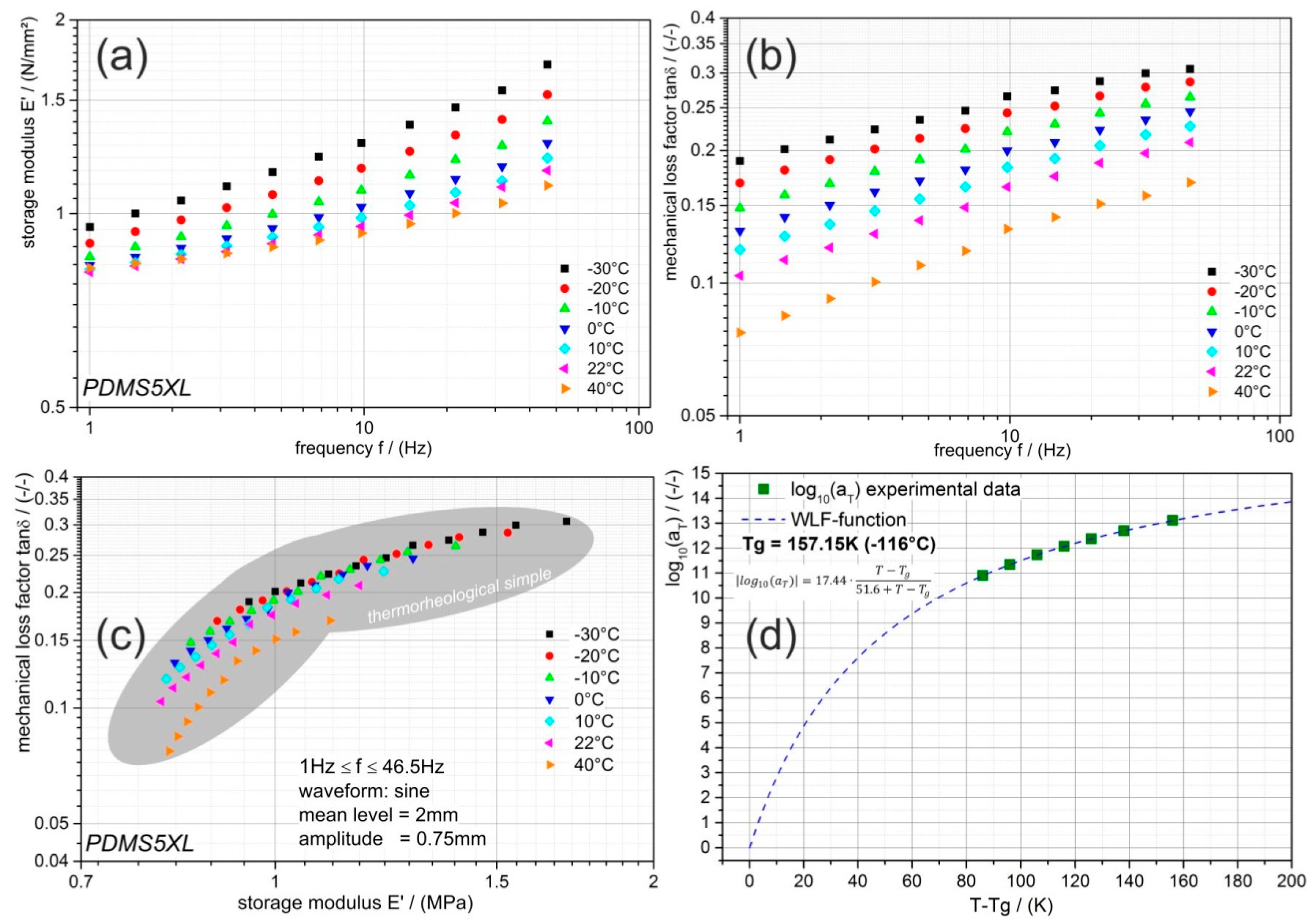
The fundamental characterization of the neat PDMS in terms of its viscoelastic behavior is presented in
Figure 4. In the diagrams of
Figure 4a–c, each color represents an isothermal measurement. The storage modulus E′ and the mechanical loss factor tanδ exhibit with increasing temperature a decline (cf.
Figure 4a,b). Interestingly, the modulus measurements reveal that the temperature-dependency at higher frequencies is more pronounced while at 1 Hz it is almost not evident (see
Figure 4a); the opposite is observable for the mechanical loss factor in
Figure 4b. To determine the thermorheological behavior of the investigated PDMS, we have considered the wicket-plot in
Figure 4c. This diagram is very convenient for analyzing the trend of the inherent respond timE′s temperature dependency as a result of the external mechanical loading. If all examined data reveal that tanδ is a unique function of E′, then the respond times (here the relaxation times) are equally temperature dependent and time–temperature superposition (TTSP) is applicable [
19,
23]. Here, we concluded that the measured data are with good approximation thermorheologically simple and TTSP can be applied. Moreover, from a generated master curve, shift factors can be determined and WLF-function (Equation (3)) could be applicable to model these factors. We constructed the master curve at the glass transition temperature Tg of the neat PDMS (157.15 K) and the determined shift factors revealed a temperature dependency, which is perfectly expressed by the WLF-function (see
Figure 4d).
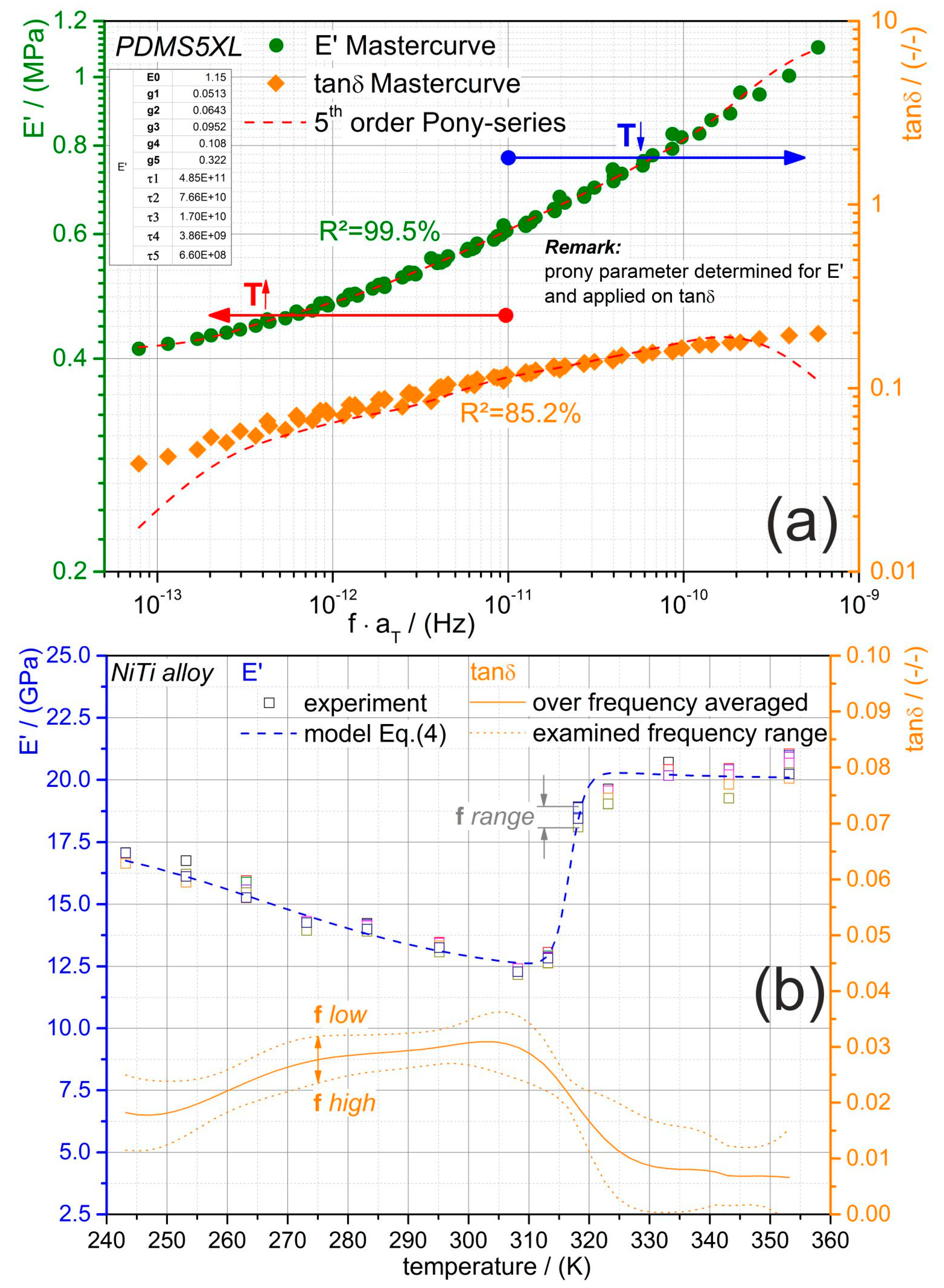
It is very convenient that the neat PDMS’s thermorheological behavior is simple, as the temperature- and rate-dependent mechanical behavior can be easily modeled. Moreover, its influence may be ascribable when the PDMS-SMA composite is characterized and in return we may get more insight into the effects of NiTi within the composite. The master curves of the neat PDMS’s storage modulus E′ and mechanical loss factor tanδ are illustrated in
Figure 5a. Reference temperature therefor was the glass transition temperature of 157.15 K and it perfectly fitted the experimental data. The parameters of a 5th order Prony series were identified (see
Table 2) for the modulus master curve and applied to tanδ according to Equation (2). In
Figure 5a the predicted curves are illustrated with the respective correlation coefficients (R
2) to the experimental data. At low and high frequencies the fit of the Prony series to the tanδ master curve is not as good as in the other frequency range. As the Prony series was optimized to the storage modulus, this misfit could be related to the earlier mentioned opposite temperature dependency of tanδ and E′ at low and high frequencies (cf.
Figure 4a vs.
Figure 4b). The macroscopic storage modulus and the tanδ of the NiTi alloy are shown in
Figure 5b. In contrast to the earlier discussed neat PDMS, the time–temperature superposition principle is not applicable to the NiTi alloy. However, a pronounced temperature dependency can be observed for both dynamic mechanical properties. In addition, the mechanical loss factor seems to be loading frequency-dependent, while the storage modulus is almost independent. The varying mechanical properties are mainly caused by the diffusionless phase transformation of the microstructure from austenite to martensite passing through an intermediate phase (rhombohedral-phase). From low to high temperature, the storage modulus declines until a minimum of 12.5 GPa, followed by a steep increase to a rather plateau with small variations around 20 GPa. The tanδ behavior is opposite within the investigated temperatures, showing an increase until the peak is reached and declines subsequently. The peak of the martensitic phase transformation is measured at around the same temperature of 310 K as the minimum of the storage modulus. This seems to be reliable, as the damping is higher the lower the storage modulus is. From modeling point of view, we have not found any constitutive law to describe (predict) the macroscopic behavior of NiTi alloys in the literature. Therefore, some of the authors conducted an investigation focusing on the dynamic thermomechanical behavior of NiTi alloys [
22]. The frequency discrepancy was highlighted and reported there, including an empirical model for the temperature-dependent modulus of NiTi alloys. It was found that the biphasic function according to Equation (4) is capable of predicting the storage modulus characteristic. The fit is demonstrated in
Figure 5b as a dashed line and the determined model parameters are listed in
Table 3.
The diagrams of
Figure 4 and
Figure 5 showed that the inherent viscoelastic characteristics of the silicon elastomer can be described by the well-known models for thermorheological simple behavior and the NiTi alloy’s temperature-dependent modulus can be modeled by an empirical proposed biphasic function. Now, the dynamic thermomechanical behavior of the PDMS-SMA composite will be discussed based on the evaluations summarized in the diagrams of
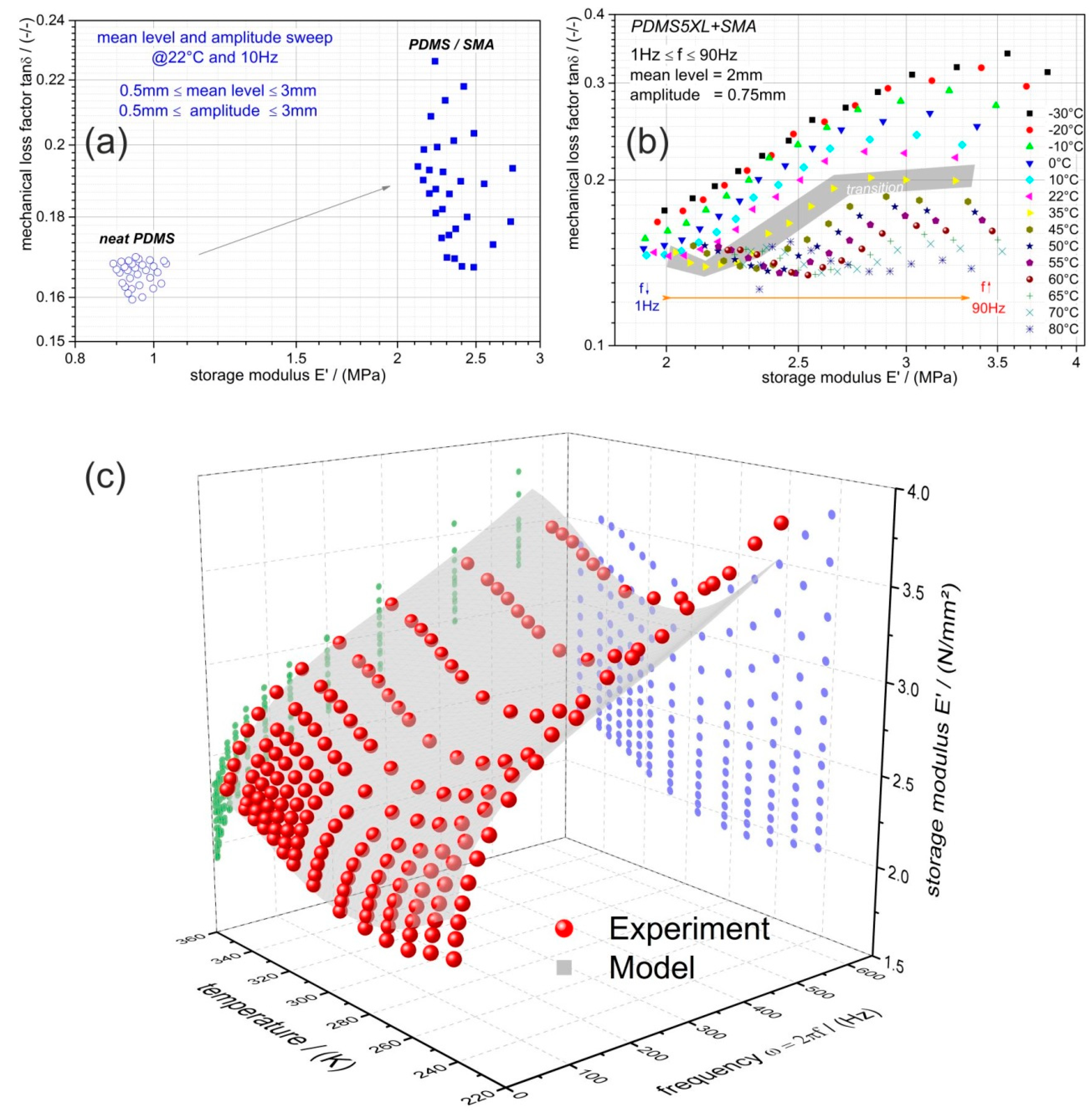
Figure 6. The composite was evaluated and analyzed with a similar methodology as previously discussed. Wicket-plots (dissipative vs. storage properties) were considered to illustrate the loading-rate and temperature dependency of the PDMS-SMA. First of all,
Figure 6a compares the neat PDMS performance with PDMS-SMA obtained by the amplitude and mean level sweep procedure at 10 Hz and room temperature. As expected the stiffness of the PDMS-SMA is higher, caused by the much higher modulus of the introduced NiTi wires into the PDMS matrix, while the volume of the investigated barbell-specimen is unchanged. However, it is interesting to note that tanδ is increased as well, meaning that the damping capability is also enhanced. Recalling the drop-ball test illustrated in
Figure 2, we can conclude that the higher and faster dissipation of the PDMS-SMA damping element is a consequence of the increased stiffness as well as mechanical loss factor. The thermomechanical behavior of the composite measured at various frequencies is shown in
Figure 6b. Each color represents an isothermal measurement. The frequency range is indicated by an arrow within the diagram. Generally, the higher the frequency, the higher is the modulus of the PDMS-SMA composite. To some extent this trend can also be observed for tanδ; although at low frequencies the mechanical loss factor is rather constant. An opposite observation is made for the temperature dependency of tanδ; the lower the temperature, the higher the value, however, at high temperatures and low frequencies the tanδ is approximately 0.15 and almost unaffected. While the tanδ is constantly increasing with decreasing temperature, the storage modulus reveals a decrease up to 35 °C (308.15 K) followed by an increase. Comparing this temperature with the transition temperature obtained from the diagram in
Figure 5b, where the modulus of the NiTi alloy exhibits a minimum and tanδ a maximum, it follows that the PDMS-SMA’s modulus characteristic is dominated by the NiTi wires and shows also the same transition at around 310 K. On the other hand, the tanδ characteristic reveals no maximum at this temperature and, consequently, it must be dominated by the matrix material (PDMS). From this point of view, the observed frequency dependency is related to the PDMS matrix behavior, as the trend is similar to the earlier discussed and shown
Figure 4a,b.
Moreover, at the boundary of the NiTi wires and the PDMS matrix is no perfectly bonding and so small relative movements between them cannot be prevented, leading to frictional dissipation of the external mechanical loading. A dissipative process is introduced by the non-perfectly bonded boundaries additionally to the bulk dissipation due to the viscoelastic behavior of the elastomer.
Focusing on the storage modulus, a 3D plot is presented in
Figure 6c for the sake of better illustration of the compositE′s loading rate (frequency) and temperature dependencies (red data points). The 2D projected data for each parameter (blue and green) are also shown. Here, again the transition region of the modulus is visible and its frequency dependency.
In addition, a coupled model is utilized according to Equation (5) to predict the frequency- and temperature-dependent storage modulus characteristics. A 3rd order Prony series was combined with the proposed biphasic function. Thereby, the biphasic function was used to compute the instantaneous temperature-dependent modulus of the composite; the frequency dependency was covered by the Prony series. This approach is justified by the earlier argumentation, that the modulus and its temperature dependency are determined by the NiTi phase of the composite and the frequency dependency by the PDMS matrix. A correlation coefficient (R
2) of 97.75% is achieved by this approach and the corresponding model parameters are summarized in
Table 4. For the model parameter determination, the relaxation times were predefined in order to reduce the number of dependent variables and the well-known Levenberg-Marquardt algorithm was utilized. The evaluated standard errors for the derived parameters are presented in
Table 4.