Determination of the Bending Properties of Wire Rope Used in Cable Barrier Systems
Abstract
1. Introduction
2. The 3 × 7 19-mm Wire Rope
2.1. Characteristics of the Wire Rope
2.2. Geometry of the Wire Rope
3. Moment–Curvature Relationship
4. Experimental Bending Testing
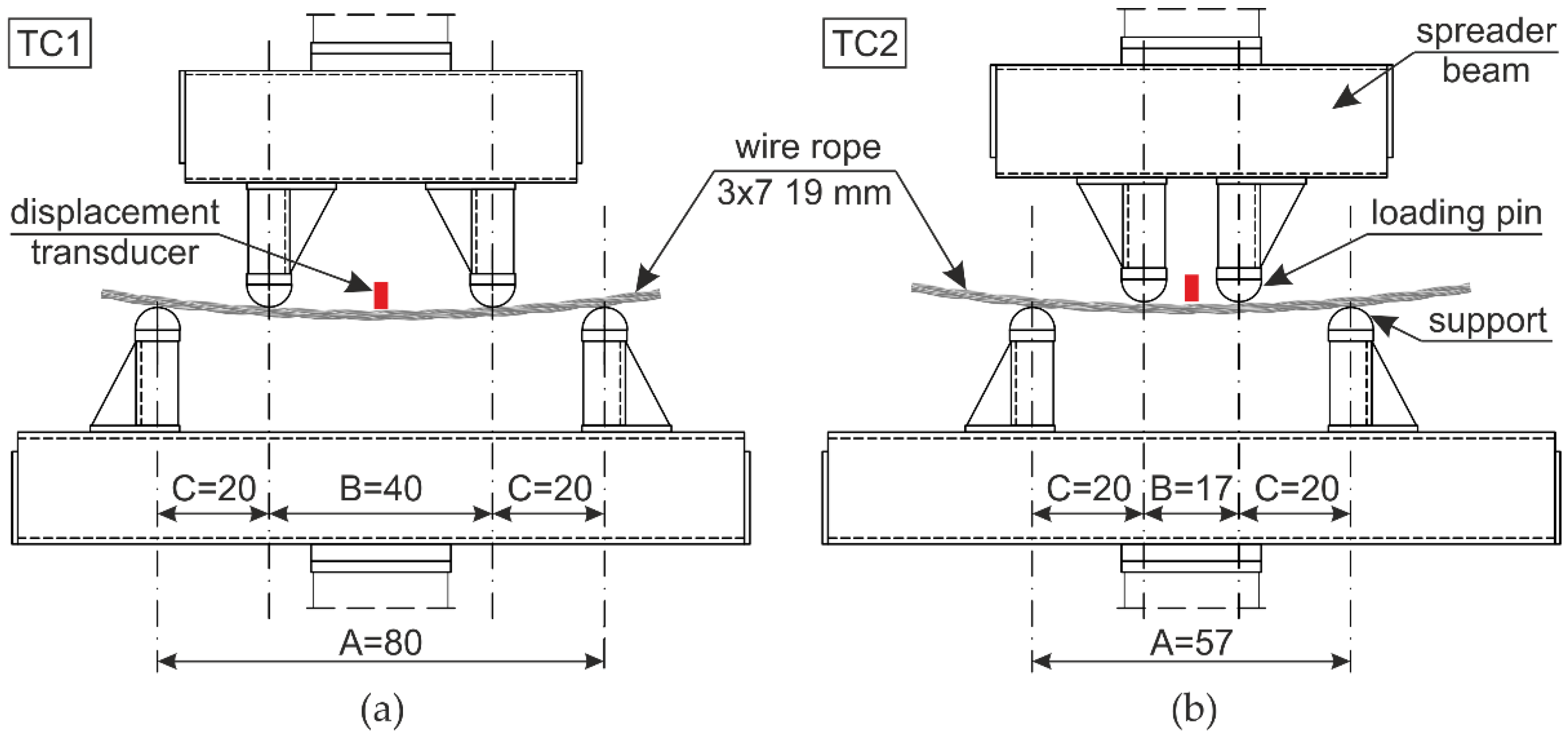
4.1. Test Specimens
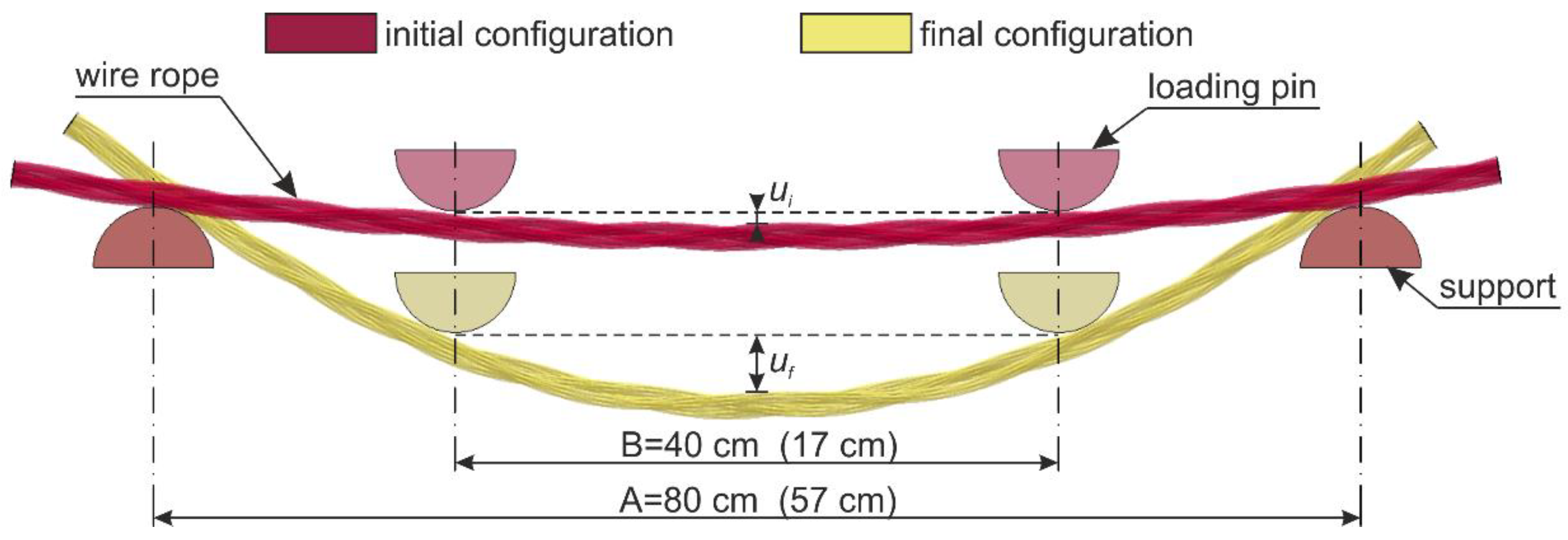
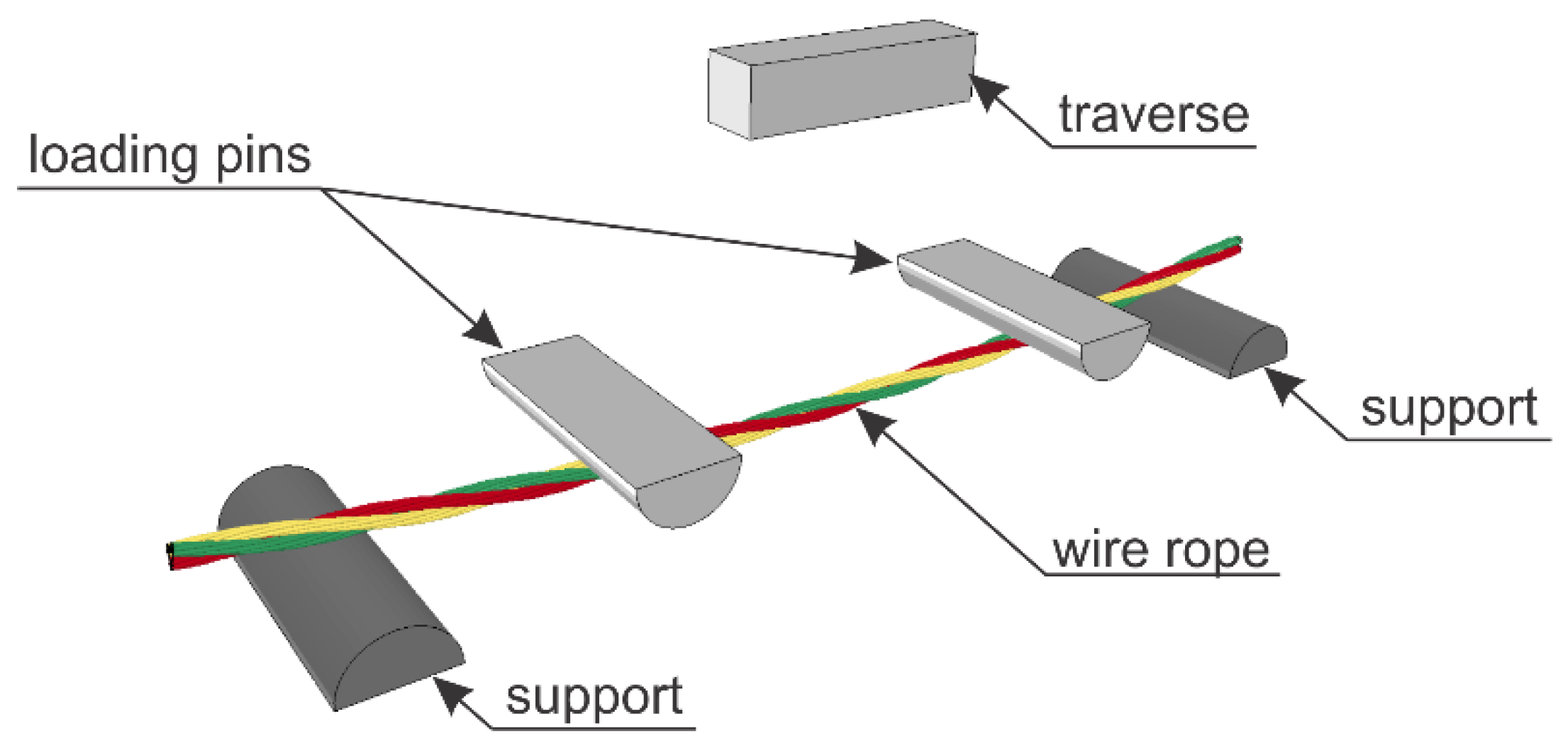
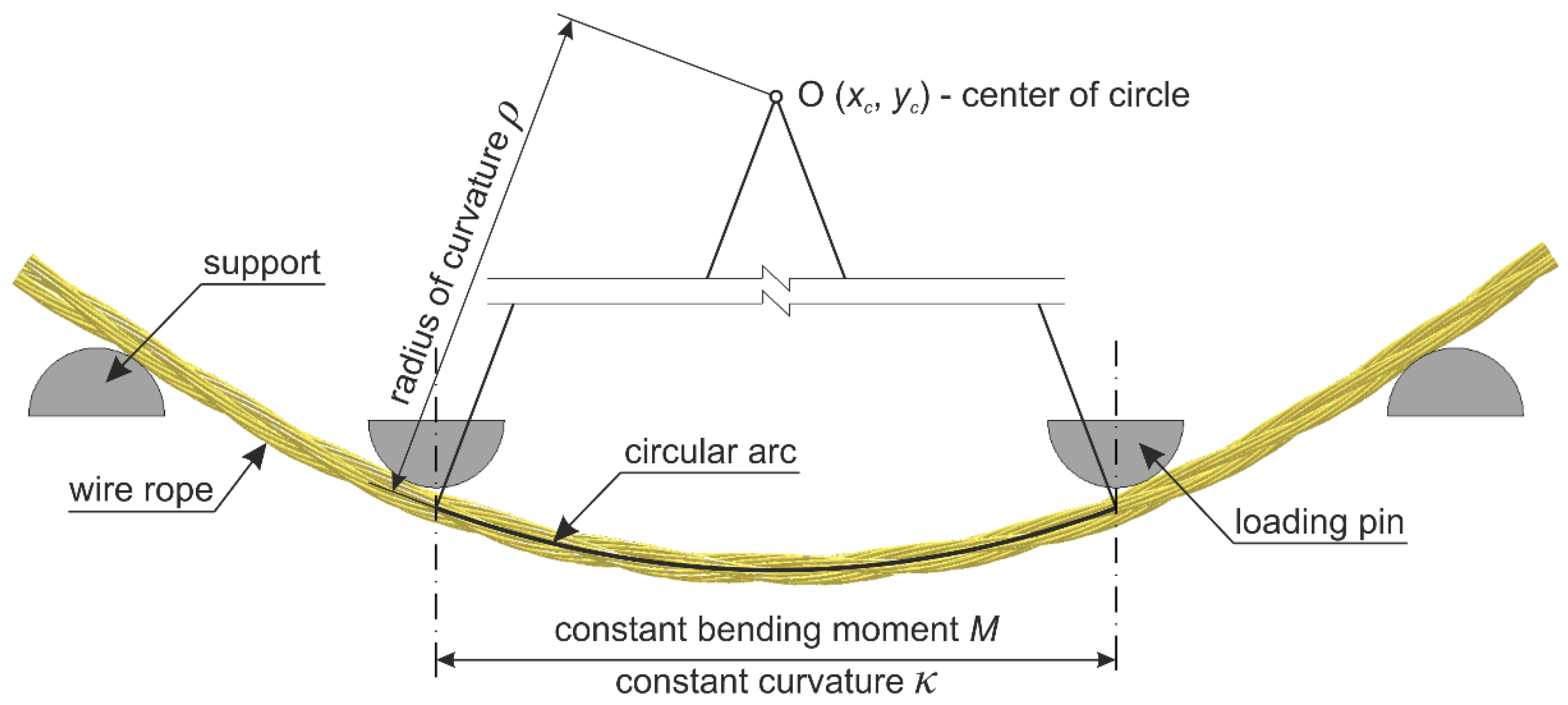
4.2. Test Stand
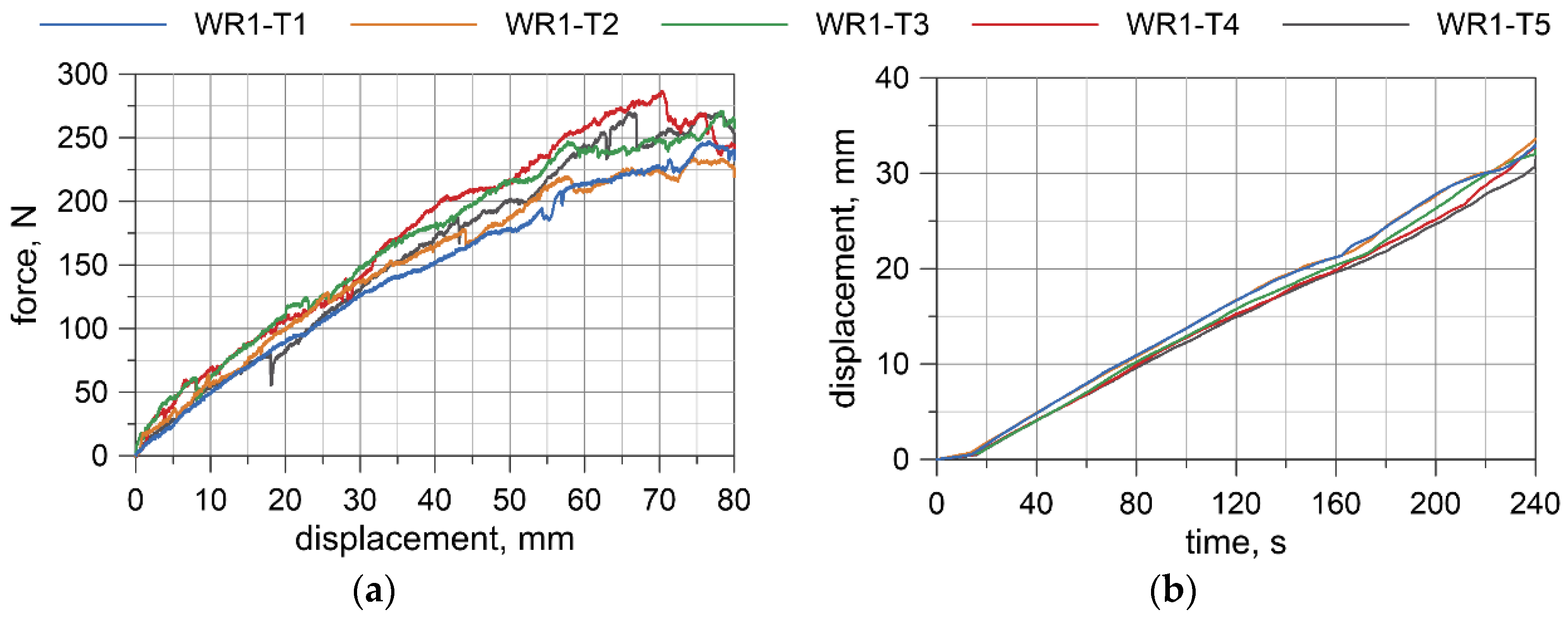
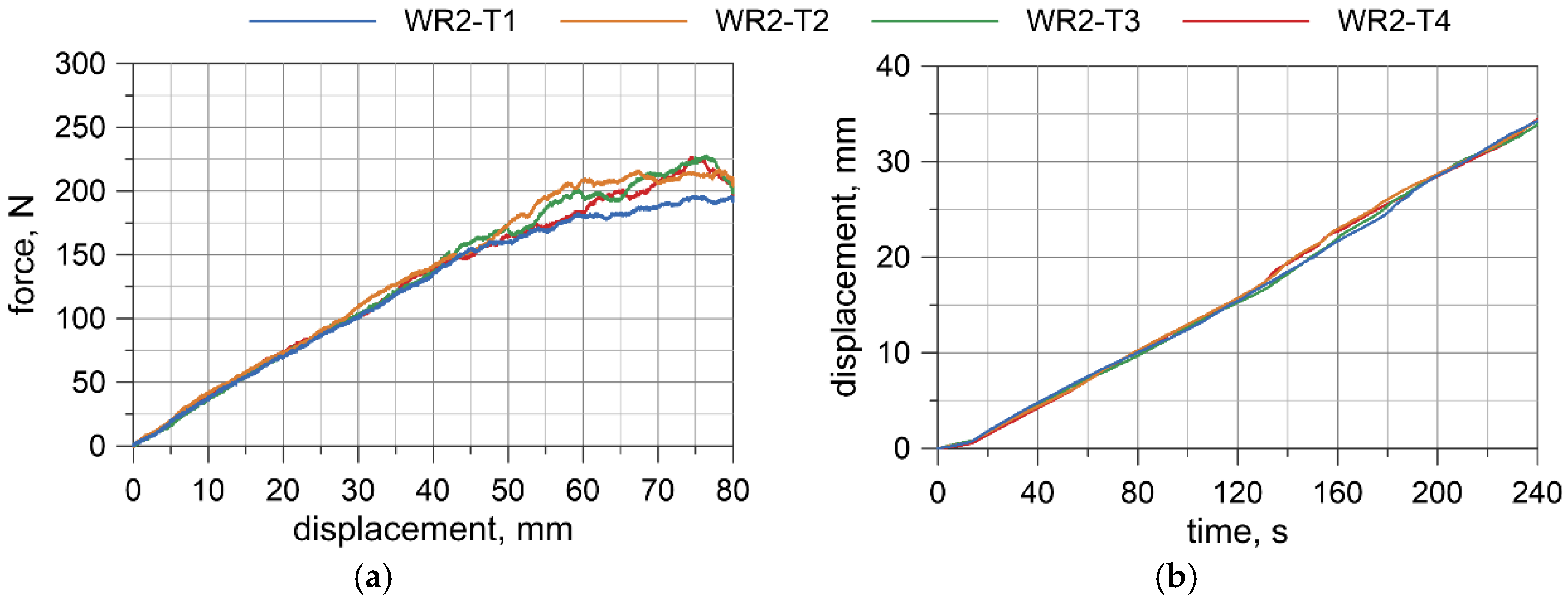
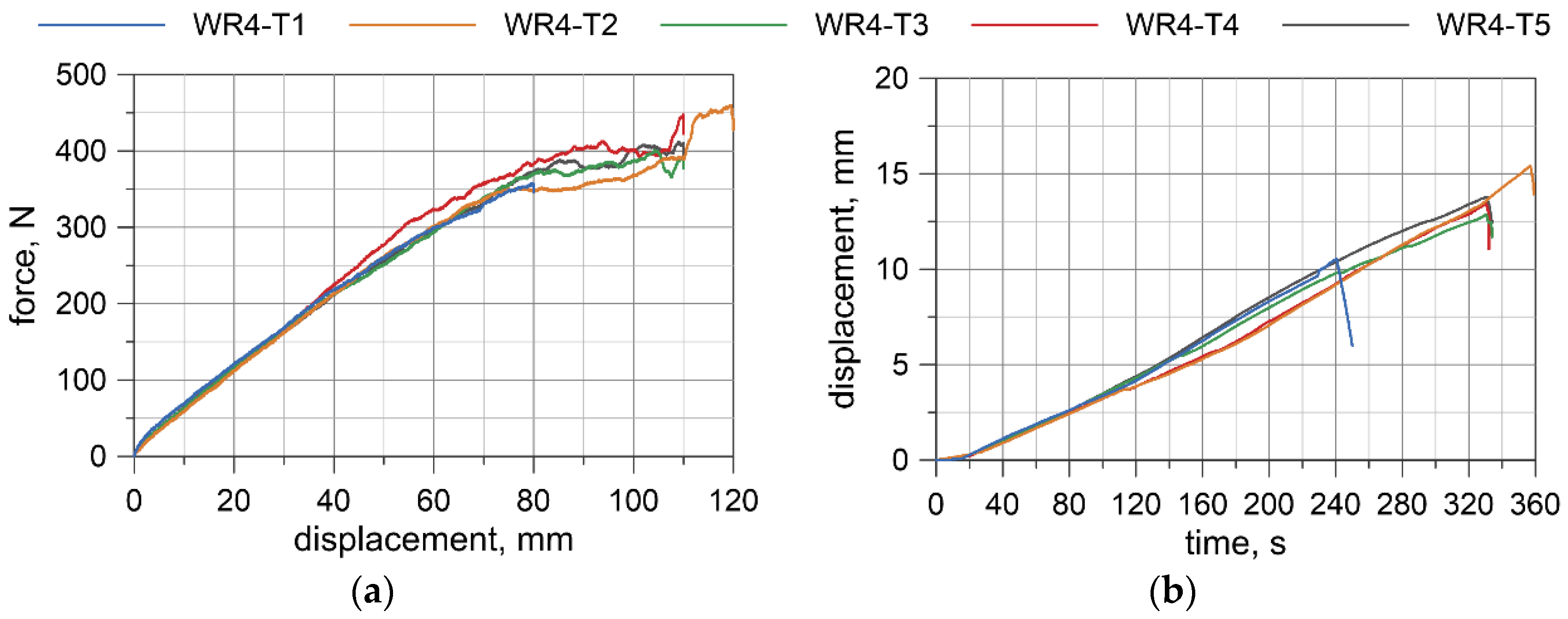
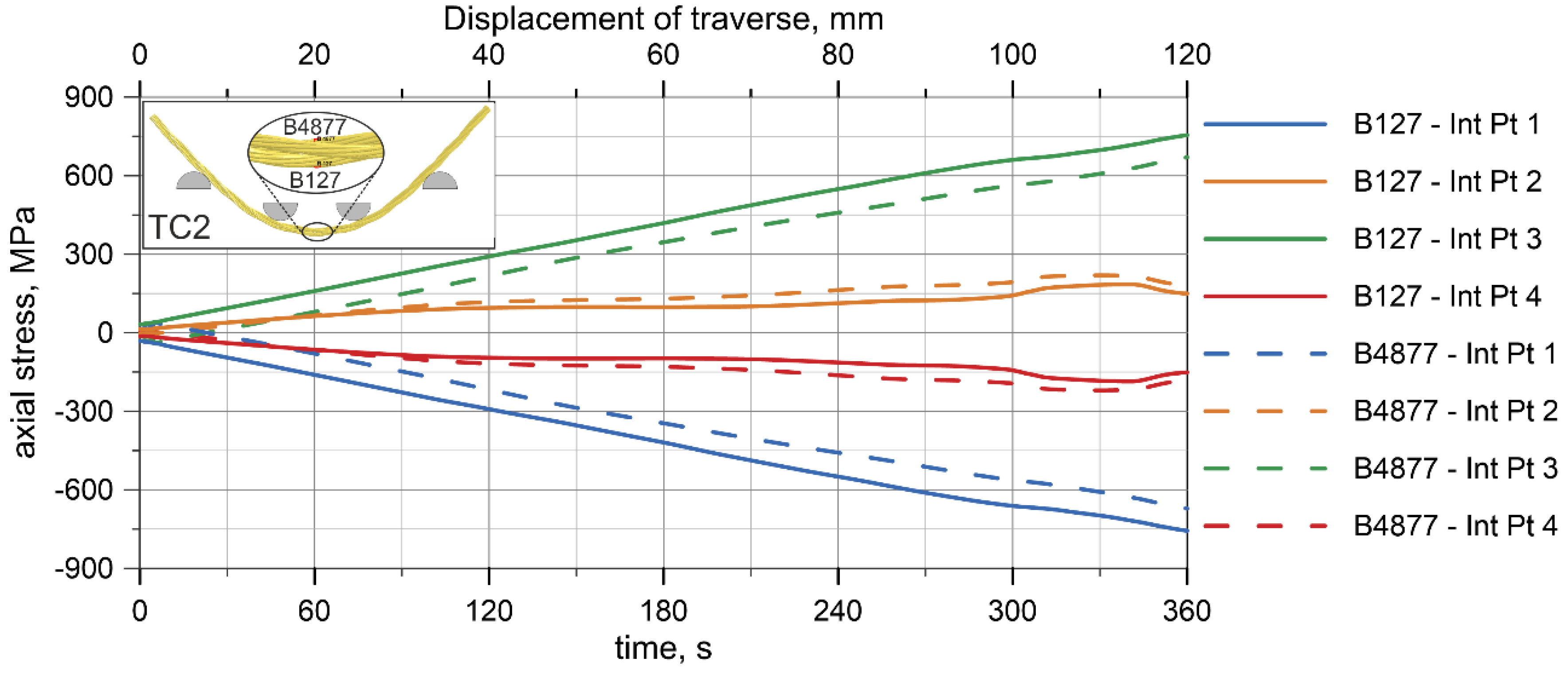
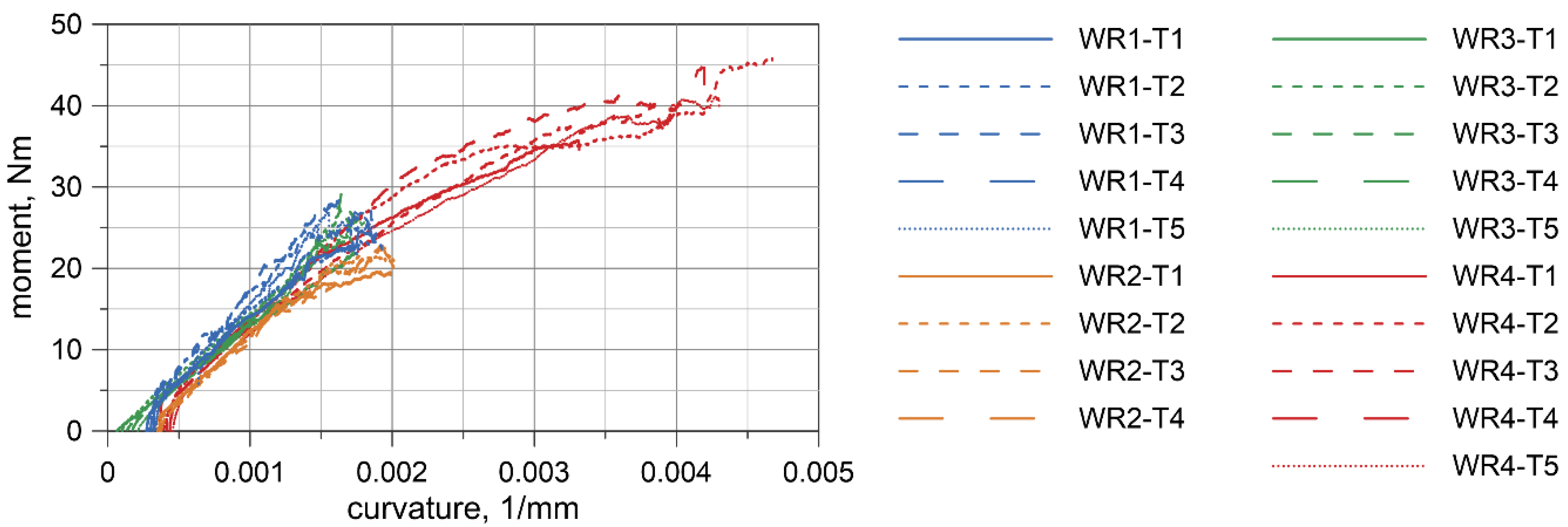
4.3. Test Results
5. Numerical Bending Testing
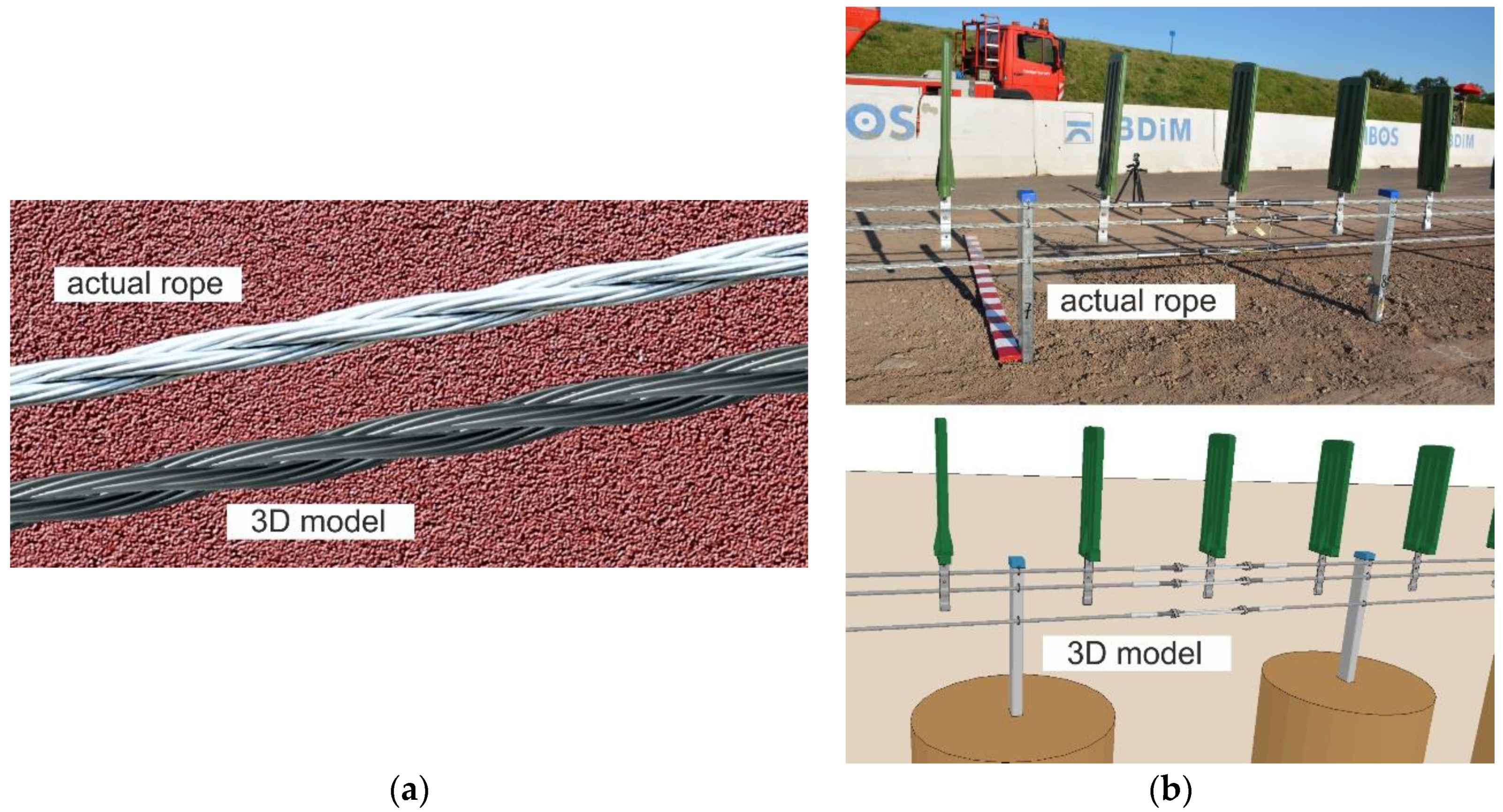
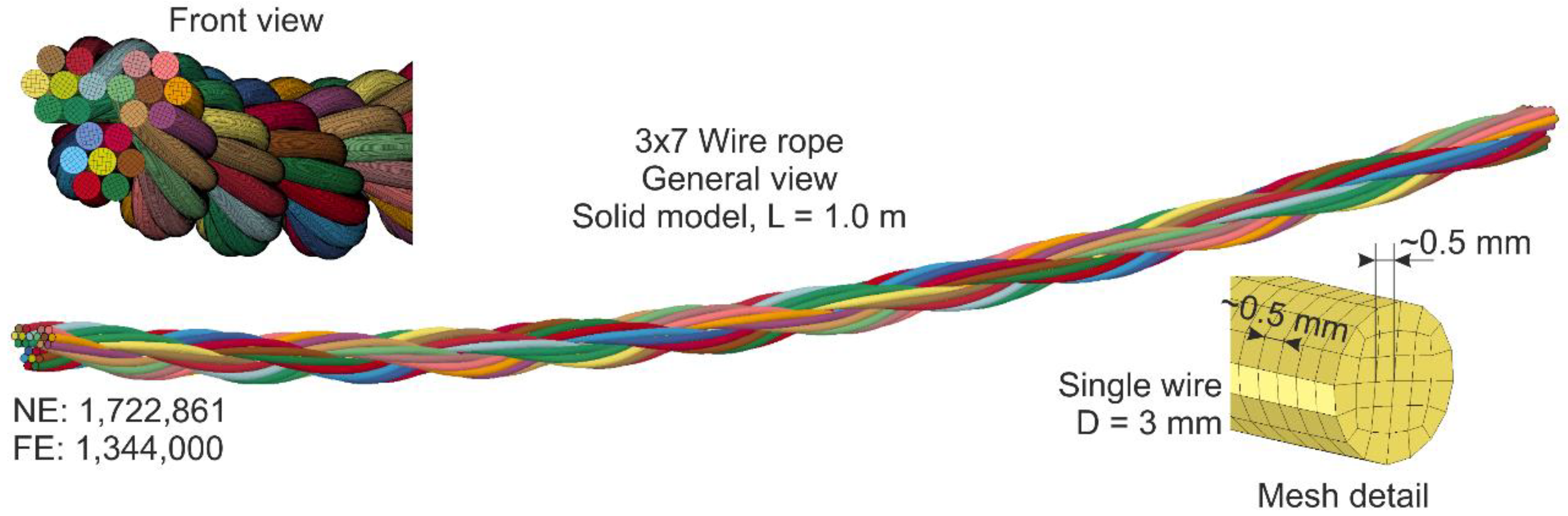
5.1. Numerical Model
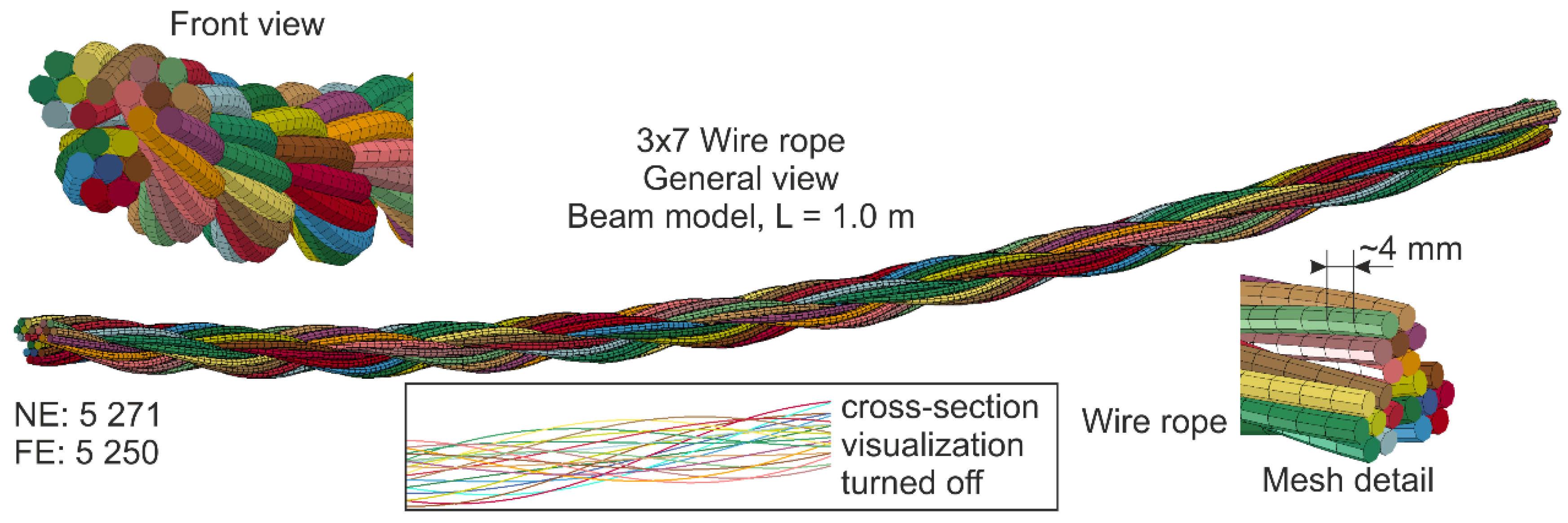
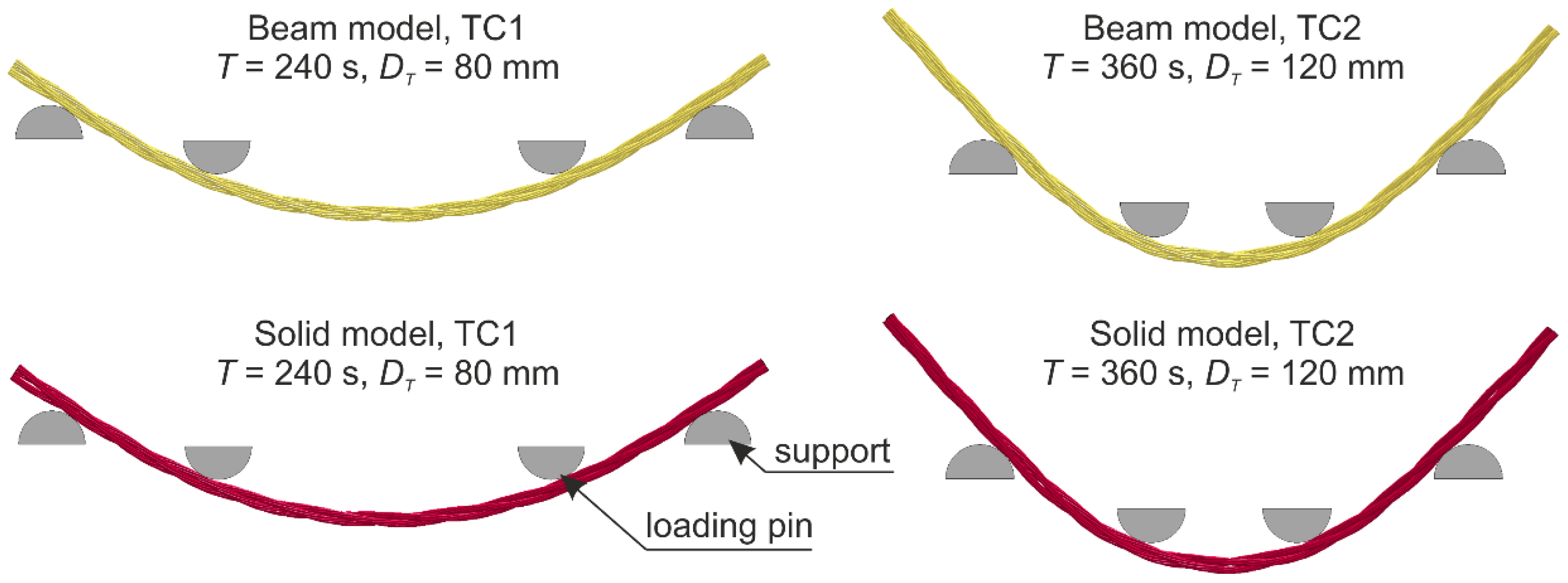
5.1.1. Beam Model
5.1.2. Solid Model
5.1.3. Parts of the Universal Testing Machine
5.2. Numerical Test Results
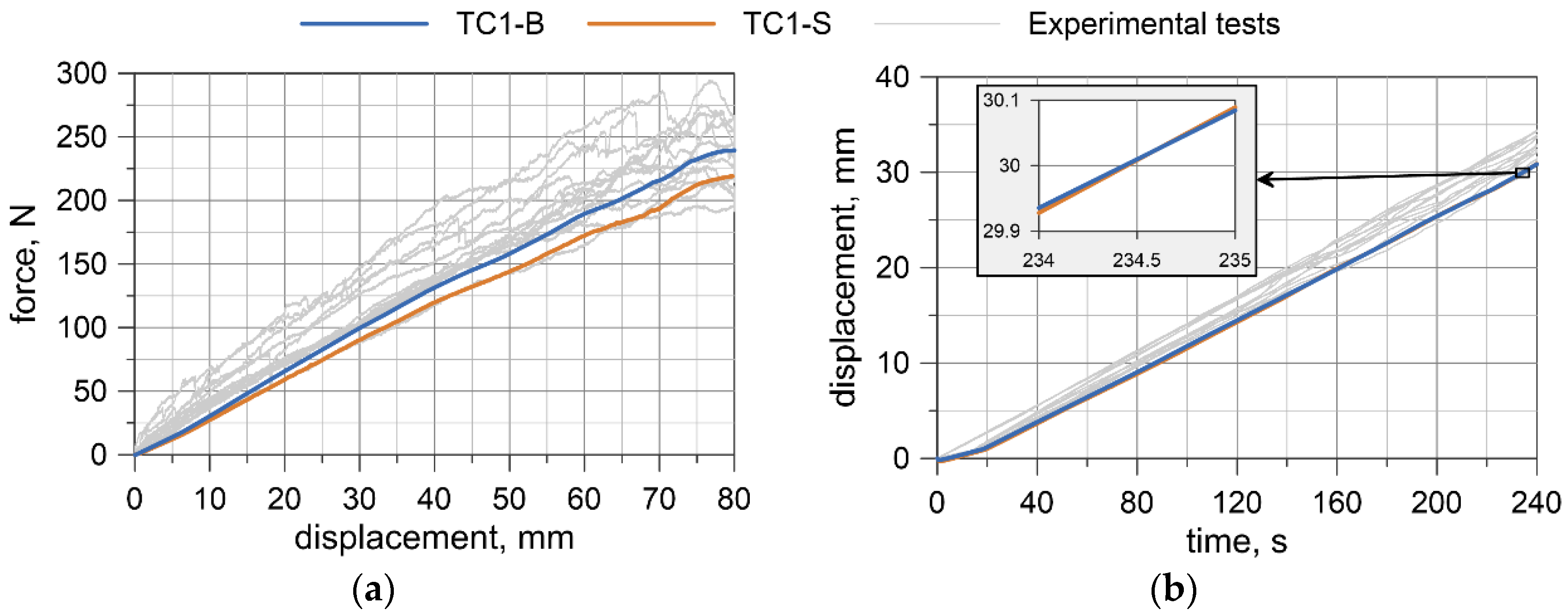
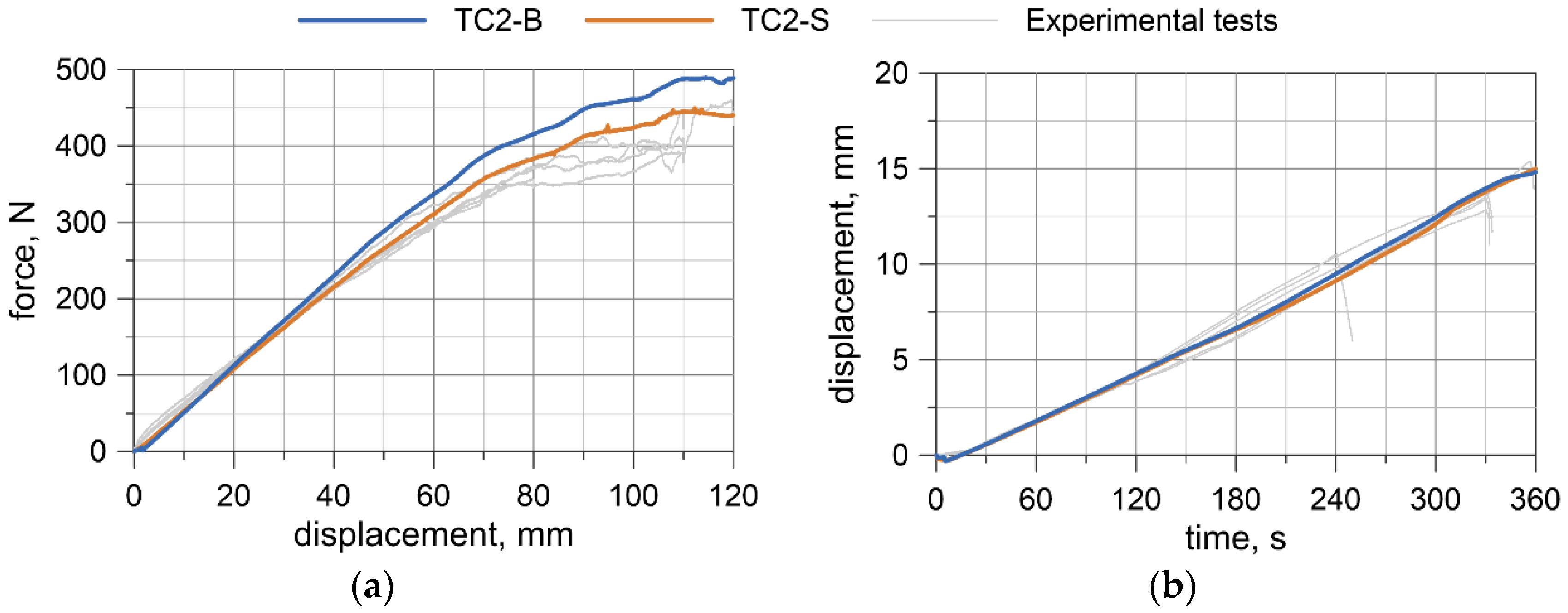
5.2.1. Comparison with Experimental Results
5.2.2. Analysis of Numerical Results
6. Results and Discussion
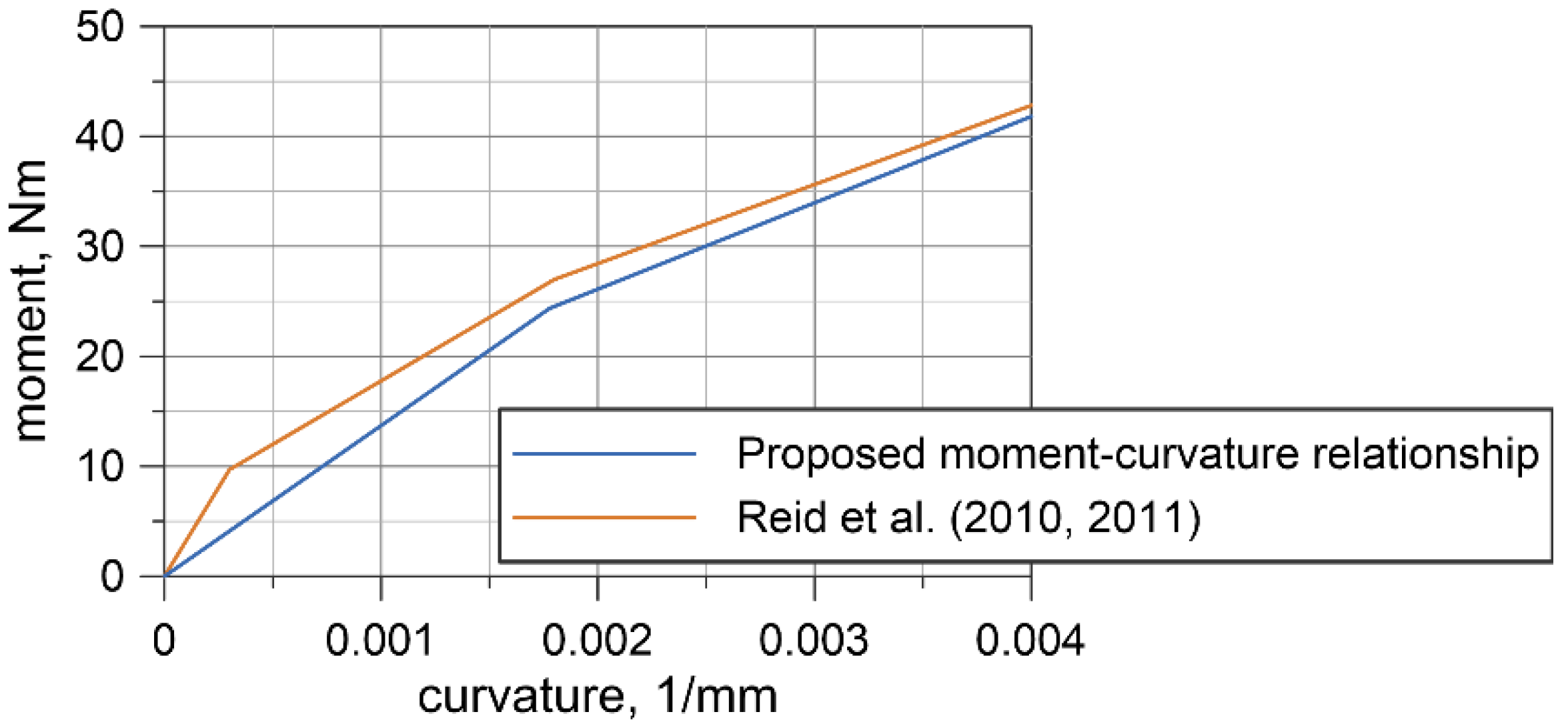
6.1. Moment–Curvature Relationship for the Wire Rope
6.2. Discussion
7. Conclusions
- Developing equations for a wire rope geometry;
- Developing two advanced nonlinear FE models of wire rope utilizing beam and solid finite elements;
- Conducting an analysis of 19 experimental tests and four numerical simulations of four-point bending. The simulations were validated against the experimental results;
- Detailed analysis of numerical results including both cross-sectional and contact stress analyses;
- Determination of the nonlinear elastic moment–curvature relation for the wire rope.
- The responses of non-prestretched and prestretched wire rope in the range of curvatures up to 0.004 mm−1 (i.e., the radius of curvature equals 25 cm) are similar and one moment–curvature relation is assumed for both prestretched and non-prestretched ropes;
- In the analyzed range of curvatures, the wire rope worked in the elastic range. Plastic strains in wires appeared solely locally under the loading pins. This suggests that in real-life accidents, the wire rope may work in the elastic range as well; however locally, in the vicinity of a point where a vehicle impacts the barrier, plastic strain may emerge;
- The considered wire rope works more as a set of 21 separated wires than as one single solid section;
- The interwire friction coefficient does not substantially affect the results. This is due to the wire rope geometry as most of the wire surfaces are not in contact with other wires.
Funding
Acknowledgments
Conflicts of Interest
References
- Mouhib, N.; Ouaomar, H.; Lahlou, M.; Ennaji, A.; El Ghorba, M. Tensile test of a strand with 2 broken wires artificially damaged and life prediction. Int. J. Eng. Sci. 2015, 4, 11–16. [Google Scholar]
- Karathanasopoulos, N.; Reda, H.; Ganghoffer, J. Francois finite element modeling of the elastoplastic axial-torsional response of helical constructions to traction loads. Int. J. Mech. Sci. 2017, 133, 368–375. [Google Scholar] [CrossRef]
- Argatov, I. Response of a wire rope strand to axial and torsional loads: Asymptotic modeling of the effect of interwire contact deformations. Int. J. Solids Struct. 2011, 48, 1413–1423. [Google Scholar] [CrossRef]
- Argatov, I.I.; Gómez, X.; Tato, W.; Urchegui, M.A. Wear evolution in a stranded rope under cyclic bending: Implications to fatigue life estimation. Wear 2011, 271, 2857–2867. [Google Scholar] [CrossRef]
- Meknassi, M.; Barakat, M.; Tijani, A.; El Ghorba, M. Characterization of Residual Energy Loss and Damage Prediction of wire Rope wires Exposed to Sulfuric Acid. Int. J. Eng. Res. Dev. 2017, 13, 94–99. [Google Scholar]
- Zhou, H.; Kodur, V.K.R.; Nie, H.; Wang, Y.; Naser, M.Z. Behavior of prestressed stayed steel columns under fire conditions. Int. J. Steel Struct. 2017, 17, 195–204. [Google Scholar] [CrossRef]
- Li, D.; Ou, J.; Lan, C.; Li, H. Monitoring and failure analysis of corroded bridge cables under fatigue loading using acoustic emission sensors. Sensors 2012, 12, 3901–3915. [Google Scholar] [CrossRef]
- Utting, W.S.; Jones, N. The response of wire rope strands to axial tensile loads-Part I. Experimental results and theoretical predictions. Int. J. Mech. Sci. 1987, 29, 605–619. [Google Scholar] [CrossRef]
- Nawrocki, A.; Labrosse, M. Finite element model for simple straight wire rope strands. Comput. Struct. 2000, 77, 345–359. [Google Scholar] [CrossRef]
- Wu, J. The finite element modeling of spiral ropes. Int. J. Coal Sci. Technol. 2014, 1, 346–355. [Google Scholar] [CrossRef]
- Smyth, A. Simulation of Overhead Crane Wire Ropes Utilizing LS-DYNA. In Proceedings of the 15th International LS-DYNA Users Conference, Detroit, MI, USA, 10–14 June 2018; pp. 1–12. [Google Scholar]
- Vukelic, G.; Vizentin, G. Damage-induced stresses and remaining service life predictions of wire ropes. Appl. Sci. 2017, 7, 107. [Google Scholar] [CrossRef]
- Costello, G.A. Theory of Wire Ropes; Springer: New York, NY, USA, 1997. [Google Scholar]
- Papailiou, K.O. On the bending stiffness of transmission line conductors. IEEE Power Eng. Rev. 1997, 17, 46. [Google Scholar] [CrossRef]
- Elata, D.; Eshkenazy, R.; Weiss, M.P. The mechanical behavior of a wire rope with an independent wire rope core. Int. J. Solids Struct. 2004, 41, 1157–1172. [Google Scholar] [CrossRef]
- Jiang, W.G.; Henshall, J.L.; Walton, J.M. Concise finite element model for three-layered straight wire rope strand. Int. J. Mech. Sci. 2000, 42, 63–86. [Google Scholar] [CrossRef]
- Wang, H.; Fu, C.; Cui, W.; Zhao, X.; Qie, S. Numerical simulation and experimental study on stress deformation of braided wire rope. J. Strain Anal. Eng. Des. 2017, 52, 69–76. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, X.; Chen, Z. A simplified finite element model for structural cable bending mechanism. Int. J. Mech. Sci. 2016, 113, 196–210. [Google Scholar] [CrossRef]
- Kim, S.Y.; Lee, P.S. Modeling of helically stranded cables using multiple beam finite elements and its application to torque balance design. Constr. Build. Mater. 2017, 151, 591–606. [Google Scholar] [CrossRef]
- Reid, J.D.; Lechtenberg, K.; Stolle, C.S. Development of Advanced Finite Element Material Models for Cable Barrier Wire Rope; MwRSF Research Report No. TRP-03-233-10; Mid-America Transportation Center: Lincoln, NE, USA, 2010.
- Erdönmez, C.; Imrak, C.E. Modeling and numerical analysis of the wire strand. J. Nav. Sci. Eng. 2009, 6, 30–38. [Google Scholar]
- Judge, R.; Yang, Z. Numerical Simulation of Spiral-Strand Cables Subjected To High Velocity Fragment Impact. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Boroška, J.; Pauliková, A.; Ivančo, V. Determination of elastic modulus of steel wire ropes for computer simulation. Appl. Mech. Mater. 2014, 683, 22–27. [Google Scholar] [CrossRef]
- Foti, F.; de Luca di Roseto, A. Analytical and finite element modelling of the elastic–plastic behaviour of metallic strands under axial–torsional loads. Int. J. Mech. Sci. 2016, 115–116, 202–214. [Google Scholar] [CrossRef]
- Ray, M.H.; Silvestri, C.; Conron, C.E.; Mongiardini, M. Experience with cable median barriers in the United States: Design standards, policies, and performance. J. Transp. Eng. 2009, 711–720. [Google Scholar] [CrossRef]
- Fang, H.; Wang, Q.; Weggel, D.C. Crash analysis and evaluation of cable median barriers on sloped medians using an efficient finite element model. Adv. Eng. Softw. 2015, 82, 1–13. [Google Scholar] [CrossRef]
- Budzyński, M.; Gobis, A.; Jamroz, K.; Jeliński, Ł.; Ostrowski, K. Road Restraint Systems as a Basis for Roadside Safety Improvement. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 1–10. [Google Scholar] [CrossRef]
- Alberson, D.C.; Bligh, R.P.; Buth, C.E.; Bullard, D.L. A Review Of Cable/Wire Rope Barrier Design Considerations. Transp. Res. Rec. 2003, 1851, 95–104. [Google Scholar] [CrossRef]
- Cooner, S.A.; Rathod, Y.K.; Alberson, D.C.; Bligh, R.P.; Ranft, S.E.; Sun, D. Development of Guidelines for Cable Median Barrier Systems in Texas; Texas Department of Transportation: Austin, TX, USA, 2009.
- Kampschneider, L.; Homan, D.M.; Lechtenberg, K.A.; Faller, R.K.; Bielenberg, R.W.; Sicking, D.L.; Reid, J.D.; Rosenbaugh, S.K. Evaluation Of A Non-Proprietary, High- Tension, Four-Cable Median Barrier On Level; MwRSF Research Report No. TRP-03-258-12; Midwest States Regional Pooled Fund Program: Lincoln, NE, USA, 2012. [Google Scholar]
- Savolainen, B.P.T.; Gates, T.J.; Russo, B.J.; Kay, J.J. Study of High-Tension Cable Barriers on Michigan Roadways; MDOT ORBP Project Number: OR10-036, FINAL REPORT RC-1612; Michigan Department of Transportation: Lansing, MI, USA, 2014.
- Stolle, C.S.; Reid, J.D.; Lechtenberg, K.A. Update To Cable Barrier Literature Review; MwRSF Research Report No. TRP-03-227-10; Midwest States Regional Pooled Fund Program: Lincoln, NE, USA, 2010. [Google Scholar]
- Bruski, D.; Burzyński, S.; Chróścielewski, J.; Jamroz, K.; Pachocki, Ł.; Witkowski, W.; Wilde, K. Experimental and numerical analysis of the modified TB32 crash tests of the cable barrier system. Eng. Fail. Anal. 2019, 104, 227–246. [Google Scholar] [CrossRef]
- Bruski, D.; Witkowski, W. Numerical studies on the influence of selected construction features and road conditions on the performance of road cable barriers. MATEC Web Conf. 2018, 1003, 1–8. [Google Scholar] [CrossRef]
- Stolle, C.S.; Reid, J.D. Development of a wire rope model for cable guardrail simulation. Int. J. Crashworth. 2011, 16, 331–341. [Google Scholar] [CrossRef]
- Stolle, C.S.; Reid, J.D. Modeling Wire Rope Used in Cable Barrier Systems. In Proceedings of the 11th International LS-DYNA Users Conference, Detroit, MI, USA, 6–8 June 2010; pp. 1–10. [Google Scholar]
- Report: Tensile Strength Test. 2016, pp. 1–3. Available online: http://www.swedwire.se/uploads/file/14f878ba876f48f8864c29d45a34c9b1/Tensile_strength_test_on_ropes_2016_SP.pdf (accessed on 15 April 2020).
- Wilde, K.; Bruski, D.; Budzyński, M.; Burzyński, S.; Chróścielewski, J.; Jamroz, K.; Pachocki, Ł.; Witkowski, W. Numerical analysis of TB32 crash tests for 4-cable guardrail barrier system installed on the horizontal convex curves of road. Int. J. Nonlinear Sci. Numer. Simul. 2019, 21, 65–81. [Google Scholar] [CrossRef]
- Wilde, K.; Bruski, D.; Burzyński, S.; Chróścielewski, J.; Pachocki, Ł.; Witkowski, W. LS-DYNA simulations of the impacts of a 38-ton Heavy Goods Vehicle into a road cable barrier. In Proceedings of the 12th European LS-DYNA Conference, Koblenz, Germany, 14–16 May 2019; pp. 1–12. [Google Scholar]
- Hibbeler, R.C. Mechanics of Materials; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Gere, J.M.; Goodno, B.J. Mechanics of Materials; Cengage Learning: Stamford, CT, USA, 2009. [Google Scholar]
- LS-DYNA, Keyword User’s Manual. Volume I.; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2015.
- LS-DYNA, Keyword User’s Manual. Volume II. Material Models; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2015.
- Hallquist, J. LS-DYNA, Theory Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2006. [Google Scholar]
- Borrvall, T. Mortar Contact Algorithm for Implicit Stamping Analyses in LS-DYNA®. In Proceedings of the 10th International LS-DYNA Users Conference, Detroit, MI, USA, 8–10 June 2008; pp. 1–10. [Google Scholar]
- Pathy, S.; Borrvall, T. Quasi-Static Simulations using Implicit LS-DYNA. In Proceedings of the 14th International LS-DYNA Users Conference, Detroit, MI, USA, 12–14 June 2016; pp. 1–8. [Google Scholar]






© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruski, D. Determination of the Bending Properties of Wire Rope Used in Cable Barrier Systems. Materials 2020, 13, 3842. https://doi.org/10.3390/ma13173842
Bruski D. Determination of the Bending Properties of Wire Rope Used in Cable Barrier Systems. Materials. 2020; 13(17):3842. https://doi.org/10.3390/ma13173842
Chicago/Turabian StyleBruski, Dawid. 2020. "Determination of the Bending Properties of Wire Rope Used in Cable Barrier Systems" Materials 13, no. 17: 3842. https://doi.org/10.3390/ma13173842
APA StyleBruski, D. (2020). Determination of the Bending Properties of Wire Rope Used in Cable Barrier Systems. Materials, 13(17), 3842. https://doi.org/10.3390/ma13173842




