Comparative Study of Phenomenological Residual Strength Models for Composite Materials Subjected to Fatigue: Predictions at Constant Amplitude (CA) Loading
Abstract
:1. Introduction
2. Residual Strength Models
2.1. Sendeckyj’s Model
2.2. Kassapogoulos’ Model
2.3. Caprino’s Model
2.4. D’Amore’s Model
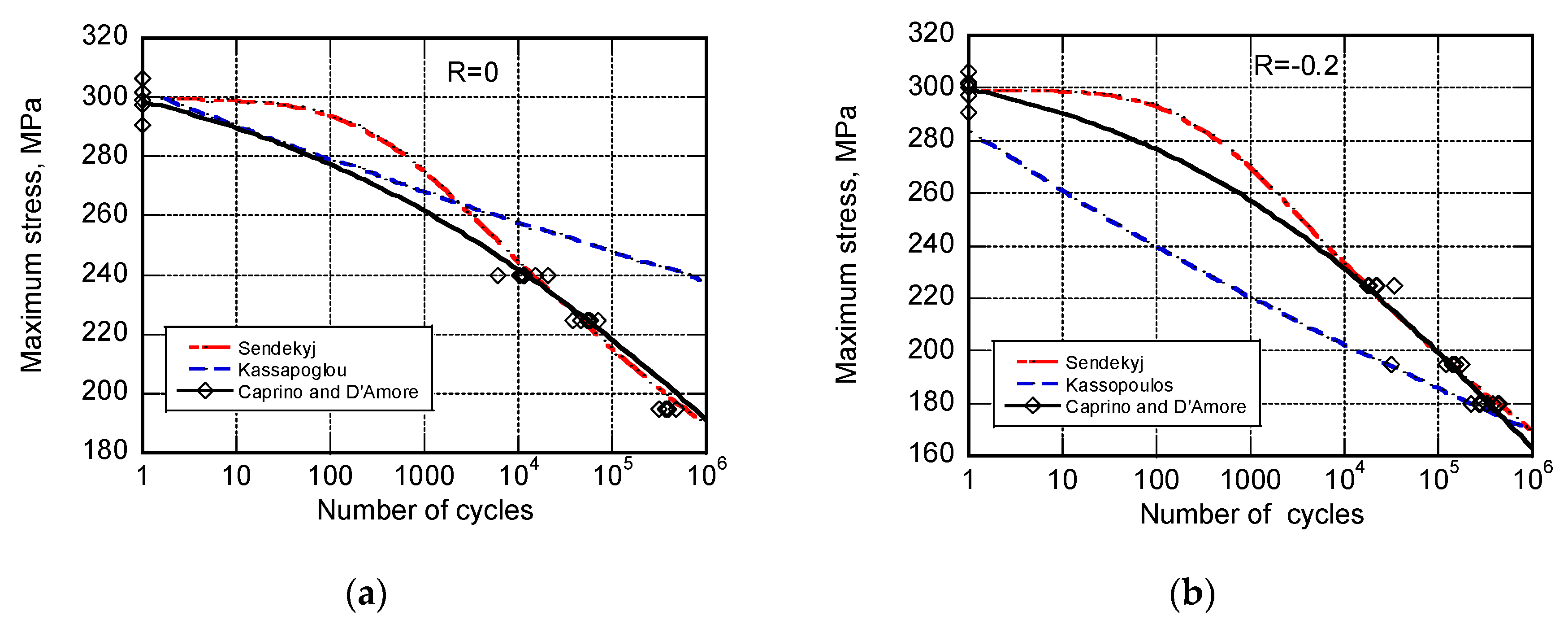
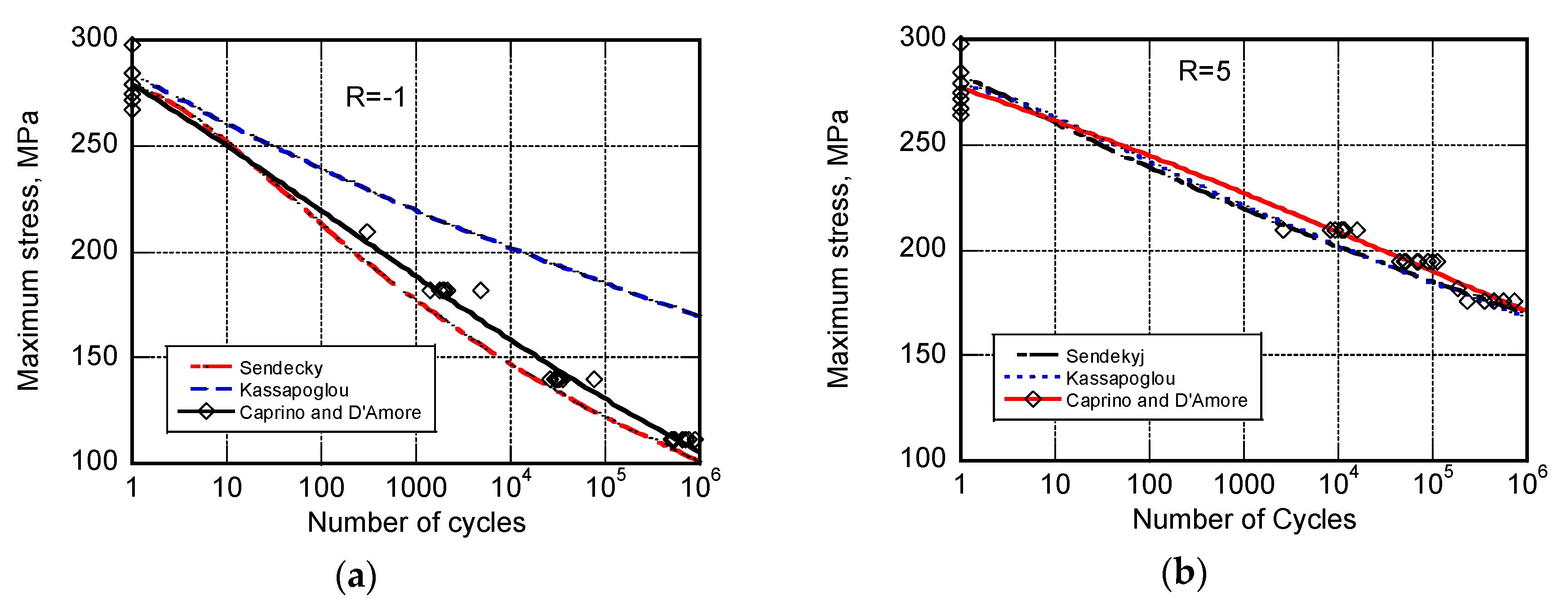
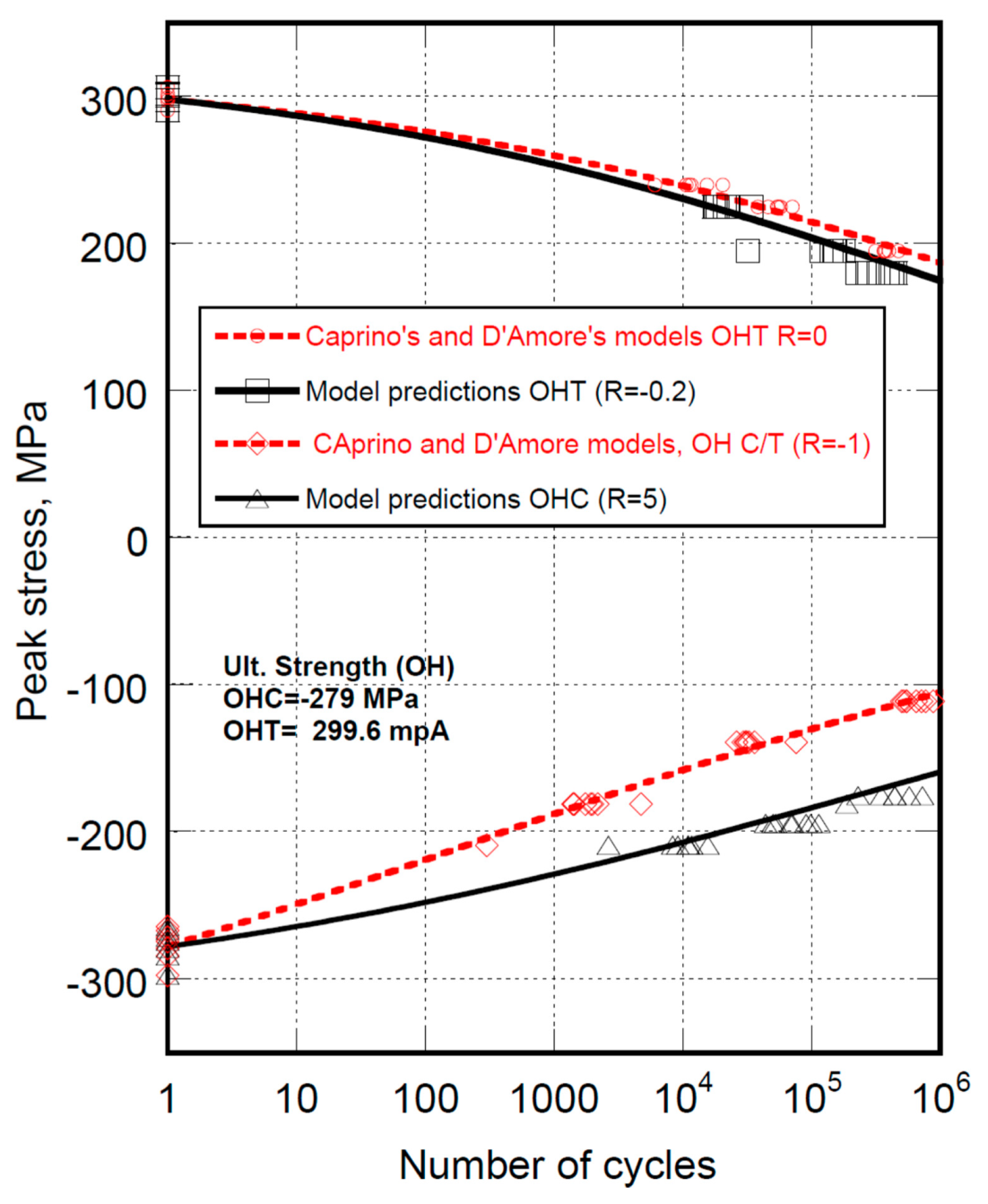
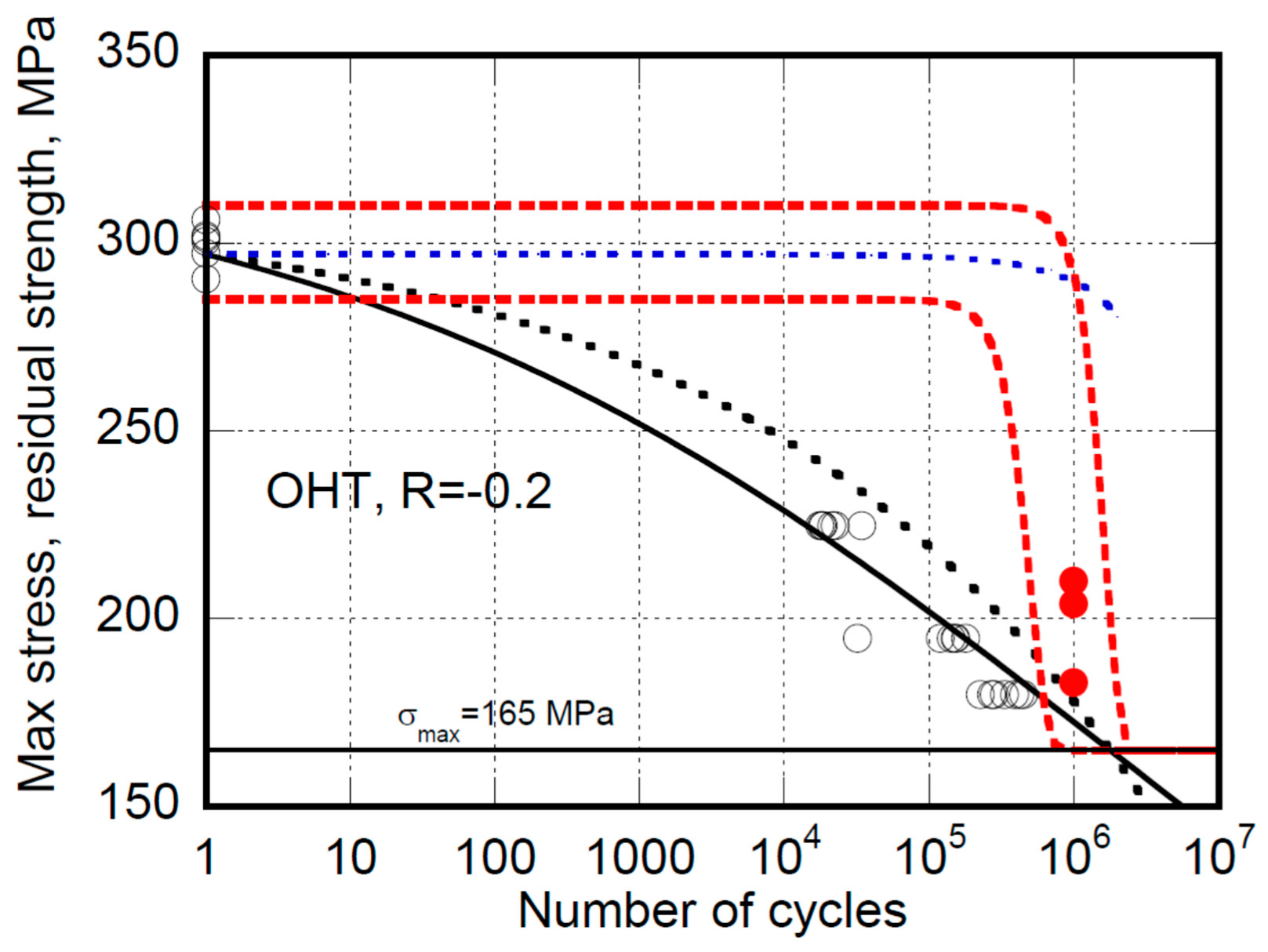
3. Experimental Data
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reifsneider, K.L. Fatigue of Composite Materials; Elsevier: New York, NY, USA, 1990. [Google Scholar]
- Vassilopoulos, A.P.; Keller, T. Fatigue of Fiber-Reinforced Composites; Springer: London, UK, 2013. [Google Scholar]
- Sevenois, R.D.B.; Van Paepegem, W. Fatigue damage modeling techniques for textile composites: Review and comparison with unidirectional composites modeling techniques. ASME Appl. Mech. Rev 2015, 67, 1–12. [Google Scholar] [CrossRef]
- Degrieck, J.; Paepegem, W.V. Fatigue damage modelling of fibre-reinforced composite materials. Rev. Appl. Mech. Rev. 2004, 54, 279–300. [Google Scholar] [CrossRef]
- Halpin, J.C.; Jerina, K.L.; Johnson, T.A. Characterization of composites for the purpose of reliability evaluation. In Analysis of Test Methods for High Modulus Fibers and Composites; ASTM STP: West Conshohocken, PA, USA, 1973; pp. 5–64. [Google Scholar]
- Halpin, J.C.; Johnson, T.A.; Waddoups, M.E. Kinetics fracture models and structural reliability. Int. J. Fract. Mech. 1972, 8, 465–468. [Google Scholar] [CrossRef]
- Wolff, R.V.; Lemon, G.H. Reliability Predictions for Adhesive Bonds; Air Force Materials Laboratory: Dayton, OH, USA, 1972. [Google Scholar]
- Passipoularidis, V.A.; Philippidis, T.P. Strength degradation due to fatigue in fiber dominated glass/epoxy composites: A statistical approach. J. Compos. Mater. 2009, 43, 997–1013. [Google Scholar] [CrossRef]
- Philippidis, T.P.; Passipoularidis, V.A. Residual strength after fatigue in composites: Theory vs. experiment. Int. J. Fatigue 2007, 29, 2104–2116. [Google Scholar] [CrossRef]
- Yang, J.N. Fatigue and residual strength degradation for graphite/epoxy composites under tension-compression cyclic loading. J. Compos. Mater. 1978, 12, 19–39. [Google Scholar] [CrossRef]
- Sendeckyj, G.P. Fitting Models to Composite Materials Fatigue Data. In Test Methods and Design Allowables for Fibrous Composites; ASTM STP 734; Chamis, C.C., Ed.; ASTM: Philadelphia, PA, USA, 1981; pp. 245–260. [Google Scholar]
- Yang, J.N.; Jones, D.L. Load Sequence Effects on Graphite/Epoxy [±35]2S Laminate; ASTM STP: West Conshohocken, PA, USA, 1983; Volume 813, pp. 246–262. [Google Scholar]
- Andersons, J.; Korsgaard, J. Residual strength of GRP at high cycle fatigue. ICCM 1997, II, 135–144. [Google Scholar]
- D’Amore, A.; Caprino, G.; Stupak, P.; Zhou, J.; Nicolais, L. Effect of stress ratio on the flexural fatigue behaviour of continuous strand mat reinforced plastics. Sci. Eng. Compos. Mater. 1996, 5, 1–8. [Google Scholar] [CrossRef]
- D’Amore, A.; Giorgio, M.; Grassia, L. Modeling the residual strength of carbon fiber reinforced composites subjected to cyclic loading. Int. J. Fatigue 2015, 78, 31–37. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L. Constitutive law describing the strength degradation kinetics of fibre-reinforced composites subjected to constant amplitude cyclic loading. Mech. Time-Depend. Mater. 2016, 20, 1–12. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L. Phenomenological approach to the study of Hierarchical damage mechanisms in composite materials subjected to fatigue loadings. Compos. Struct. 2017, 175, 1–6. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L. Calculation of the shrinkage-induced residual stress in a viscoelastic dental restorative material. Mech. Time-Depend. Mater. 2013, 17, 1–13. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L. A method to predict the fatigue life and the residual strength of composite materials subjected to variable (VA) amplitude loadings. Compos. Struct. 2019, 228, 111338. [Google Scholar] [CrossRef]
- Hahn, H.T.; Kim, R.Y. Proof Testing of Composite Materials. J. Compos. Mater. 1975, 9, 297–311. [Google Scholar] [CrossRef]
- Chou, P.C.; Croman, R. Residual strength in fatigue based on strength-life equal rank assumption. J. Compos. Mater. 1978, 12, 177–194. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L. Principal features of fatigue and residual strength of composite materials subjected to Constant Amplitude (CA) loading. Materials 2019, 12, 2586. [Google Scholar] [CrossRef]
- Kassapoglou, C. Fatigue Life Prediction of Composite Structures Under Constant Amplitude Loading. J. Compos. Mater. 2007, 41, 2737–2754. [Google Scholar] [CrossRef]
- Zhou, J.; D’Amore, A.; Zhuang, G.; He, T.; Li, B.; Nicolais, L. Tension-tension fatigue failure behaviour of poly(phenylene ether ketone) (PEK-C). Polymer 1996, 37, 2103–2111. [Google Scholar] [CrossRef]
- Zhou, J.; D’Amore, A.; Nicolais, L. The effect of loading parameters parameters on fatigue behaviour of injection moulded composite. Sci. Eng. Compos. Mater. 1995, 4, 17–26. [Google Scholar] [CrossRef]
- Stupak, P.R.; D’Amore, A.; Rigale, F.; Nicolais, L. Uniaxial and biaxial flexural fatigue of glass reinforced inter-penetrated network polymer composites. Appl. Compos. Mater. 1994, 1, 19–33. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L.; Verde, P. Modeling the flexural fatigue behavior of glass-fiber-reinforced thermoplastic matrices. Mech. Time-Depend. Mater. 2013, 17, 15–23. [Google Scholar] [CrossRef]
- Caprino, G.; D’Amore, A.; Facciolo, F. Fatigue sensitivity of random glass fibre reinforced plastics. J. Compos. Mater. 1998, 32, 1203–1220. [Google Scholar] [CrossRef]
- Caprino, G.; D’Amore, A. Flexural fatigue behaviour of random continous-fibre-reinforced thermoplastic composites. Compos. Sci. Technol. 1998, 58, 957–965. [Google Scholar] [CrossRef]
- Caprino, G.; D’Amore, A. Fatigue life of graphite/epoxy laminates subjected to tension-compression loadings. Mech. Time-Depend. 2000, 4, 139–154. [Google Scholar] [CrossRef]
- DOT/FAA/AR-10/6. Determining the Fatigue Life of Composites Aircraft Structures Using Life and Load-Enhancement Factors. 2011. Available online: http://www.tc.faa.gov/its/worldpac/techrpt/ar10-6.pdf (accessed on 1 February 2015).

| Parameters | ||
|---|---|---|
| - | s | f |
| W1 | S0 | 1 |
| W2 | S0 | C |
| W3 | S0 | C(1 − R)G |
| W3A | S0(1 − R)G | C(1 − R)G |
| W4 | S0 + D(1 − R)G | C(1 − R)G |
| W4A | S0(1 − R)G | C(1 − R)G |
| - | Number of Parameters | Recovery of The Static Strength Distribution from Fatigue Data (The Concept of Equivalent Static Strength) | Predictions of Fatigue Life under Different Loading Conditions | Prediction of “Sudden Drop” of Strength with Fixed Parameters Optimized on The Basis of Fatigue Life and Static Strength Data | Easy Use for Reliability Analysis (Based on Few, Fixed Parameters) | Easy Use for The Optimization Of Test Campaign. The Development of Generalized Softwares and Predictions under Variable Amplitude Loadings |
|---|---|---|---|---|---|---|
| D’Amore (2015) | 2 | Excellent | Excellent | Excellent (no adjustments allowed). The parameters are fixed once and for all. | Excellent | Excellent |
| Caprino (1996) | 2 | Excellent | Excellent | poor | poor | poor |
| Sendekyj (1980) | >2 each loading condition | Excellent | Poor: Only fit to the data (no predictions). Different set of parameters each loading condition | poor | poor | poor |
| Kassapouglos (2011) | No parameters needed. Only the two parameters of the Weibull distribution function are claimed to be sufficient to predict the fatigue life (No fatigue life data are required) | Not shown | Prediction are un-conservative. Fatigue curves are shifted some 2 or more decades of cycles in respect to the experimental data | Not shown | Not shown | Not shown |
| - | Equation for The Rate of Strength Degradation | Residual Strength Evolution Equation | Fatigue Life Equation |
|---|---|---|---|
| D’Amore (2015) | |||
| Caprino (1996) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Amore, A.; Grassia, L. Comparative Study of Phenomenological Residual Strength Models for Composite Materials Subjected to Fatigue: Predictions at Constant Amplitude (CA) Loading. Materials 2019, 12, 3398. https://doi.org/10.3390/ma12203398
D’Amore A, Grassia L. Comparative Study of Phenomenological Residual Strength Models for Composite Materials Subjected to Fatigue: Predictions at Constant Amplitude (CA) Loading. Materials. 2019; 12(20):3398. https://doi.org/10.3390/ma12203398
Chicago/Turabian StyleD’Amore, Alberto, and Luigi Grassia. 2019. "Comparative Study of Phenomenological Residual Strength Models for Composite Materials Subjected to Fatigue: Predictions at Constant Amplitude (CA) Loading" Materials 12, no. 20: 3398. https://doi.org/10.3390/ma12203398
APA StyleD’Amore, A., & Grassia, L. (2019). Comparative Study of Phenomenological Residual Strength Models for Composite Materials Subjected to Fatigue: Predictions at Constant Amplitude (CA) Loading. Materials, 12(20), 3398. https://doi.org/10.3390/ma12203398




