Principal Features of Fatigue and Residual Strength of Composite Materials Subjected to Constant Amplitude (CA) Loading
Abstract
:1. Introduction
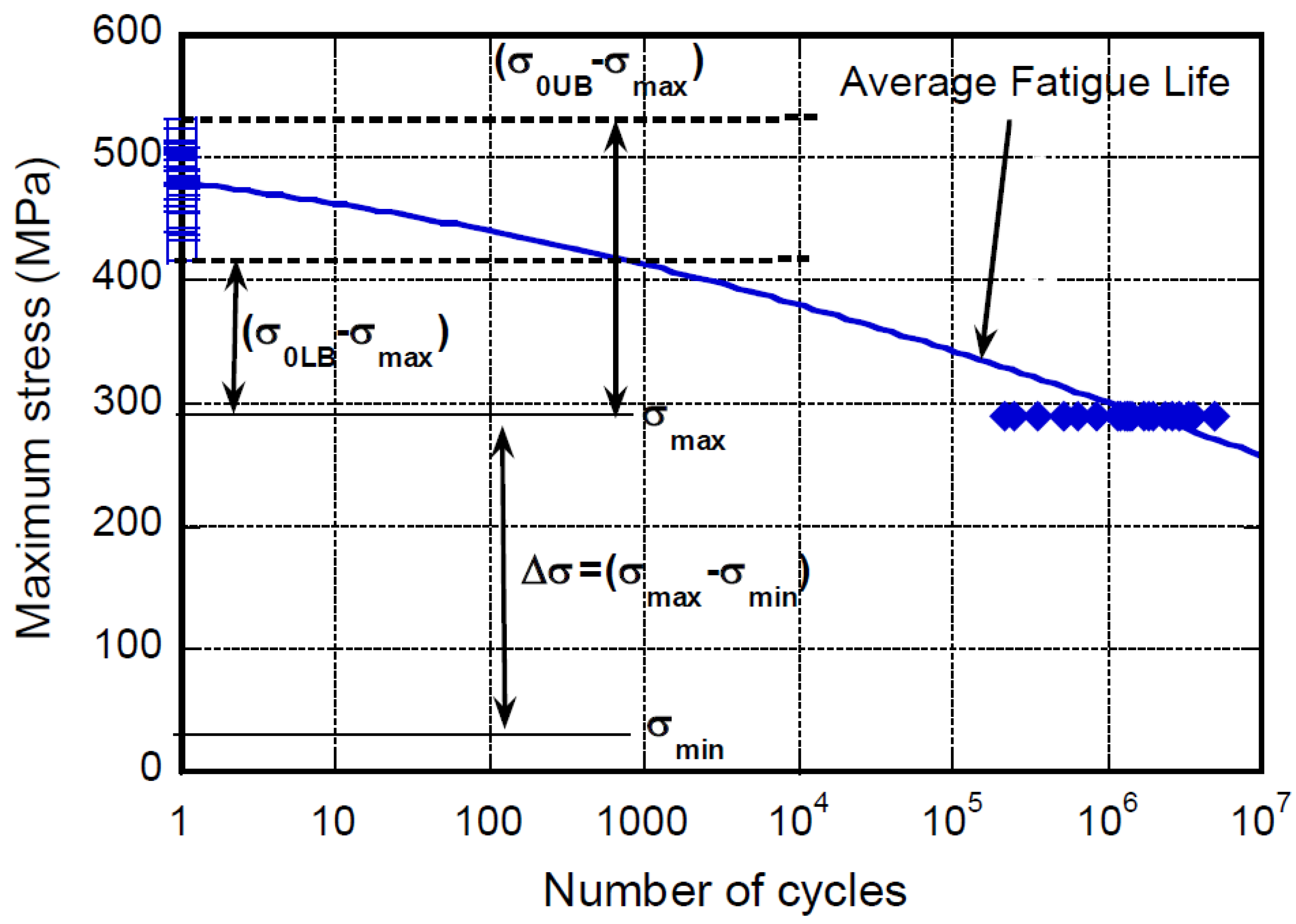
2. Phenomenology of Fatigue
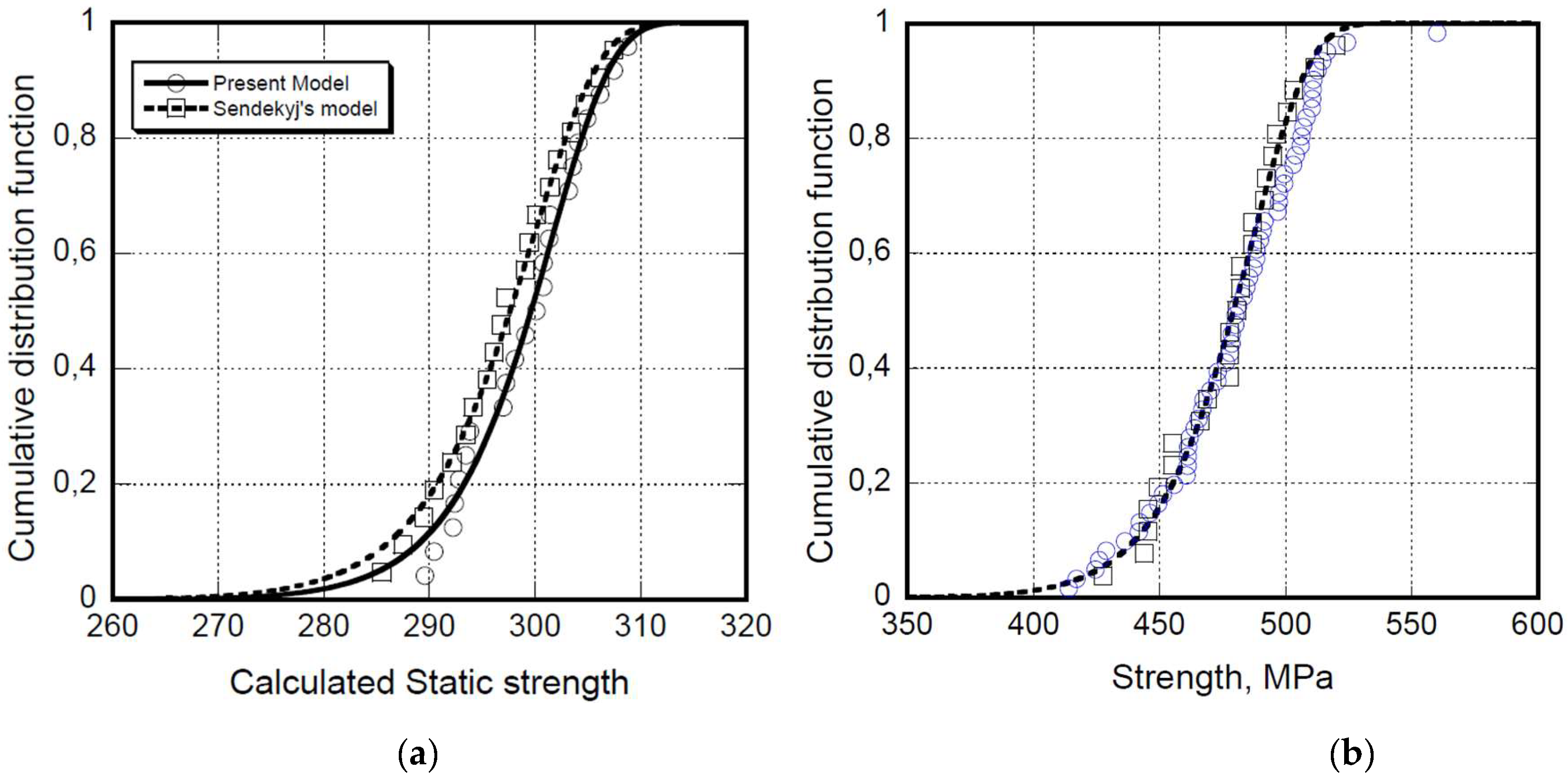
2.1. Static Strength
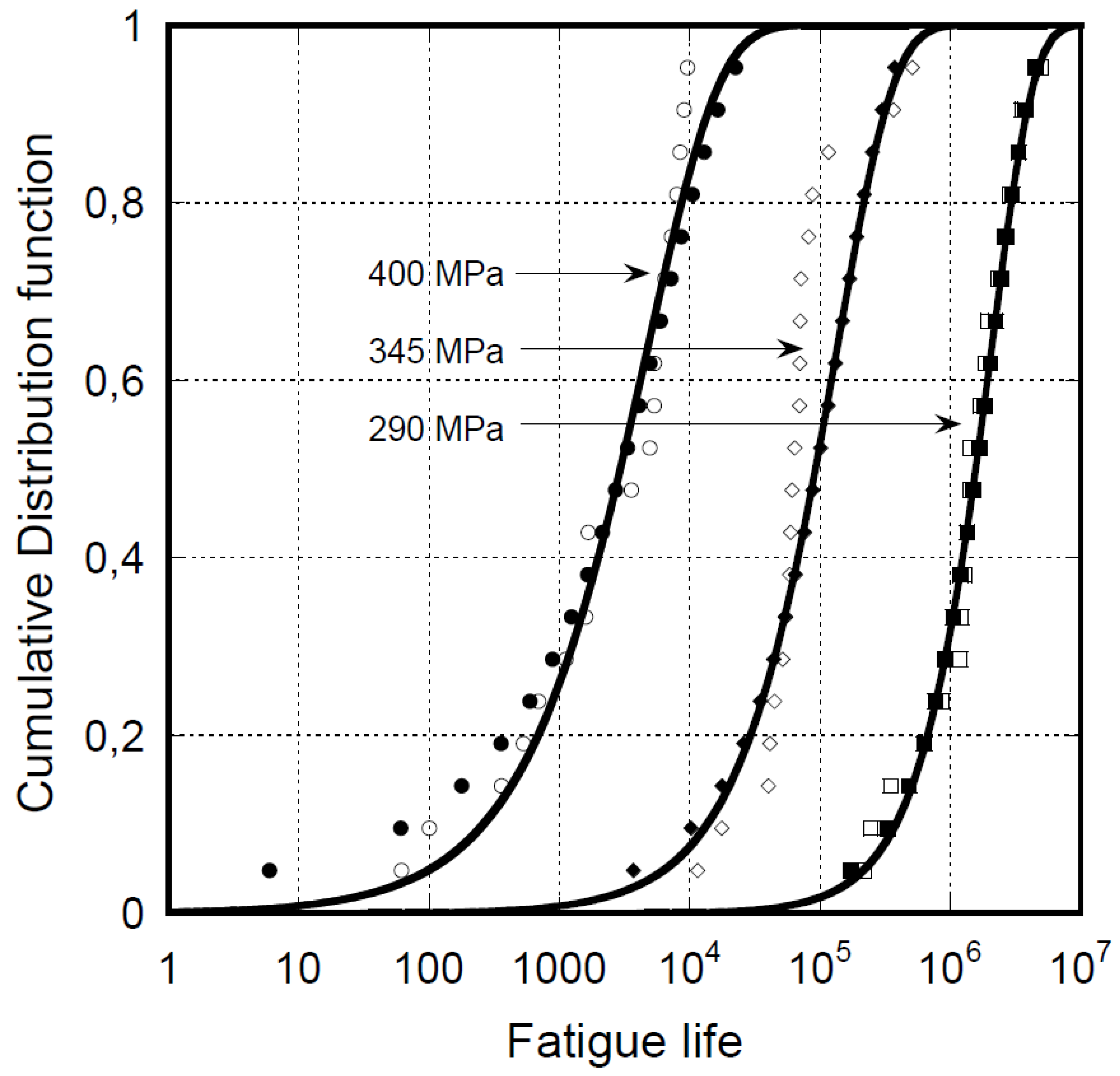
2.2. The Strength-Life Equal Rank Assumption (SLERA)
2.3. Fatigue Limit
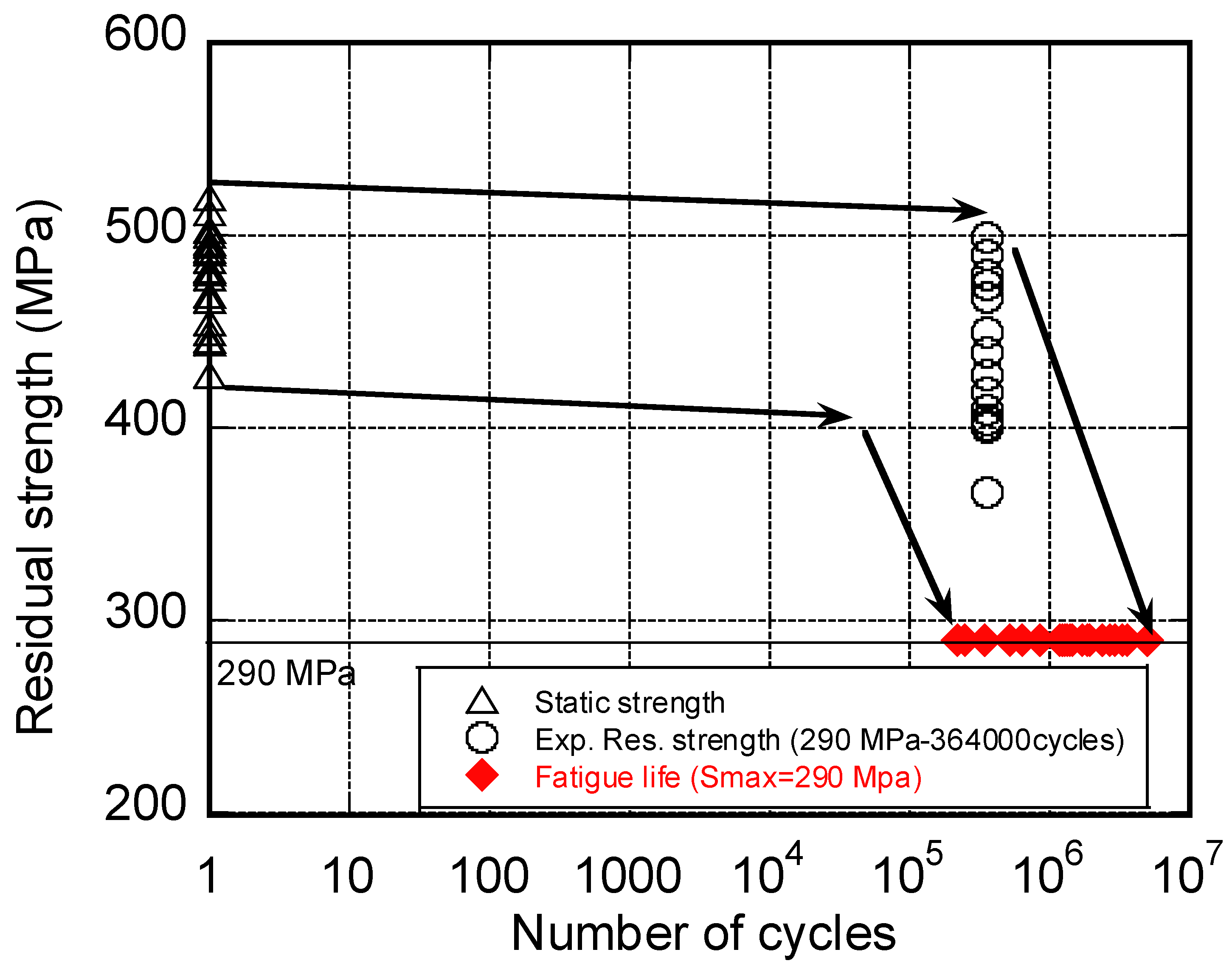
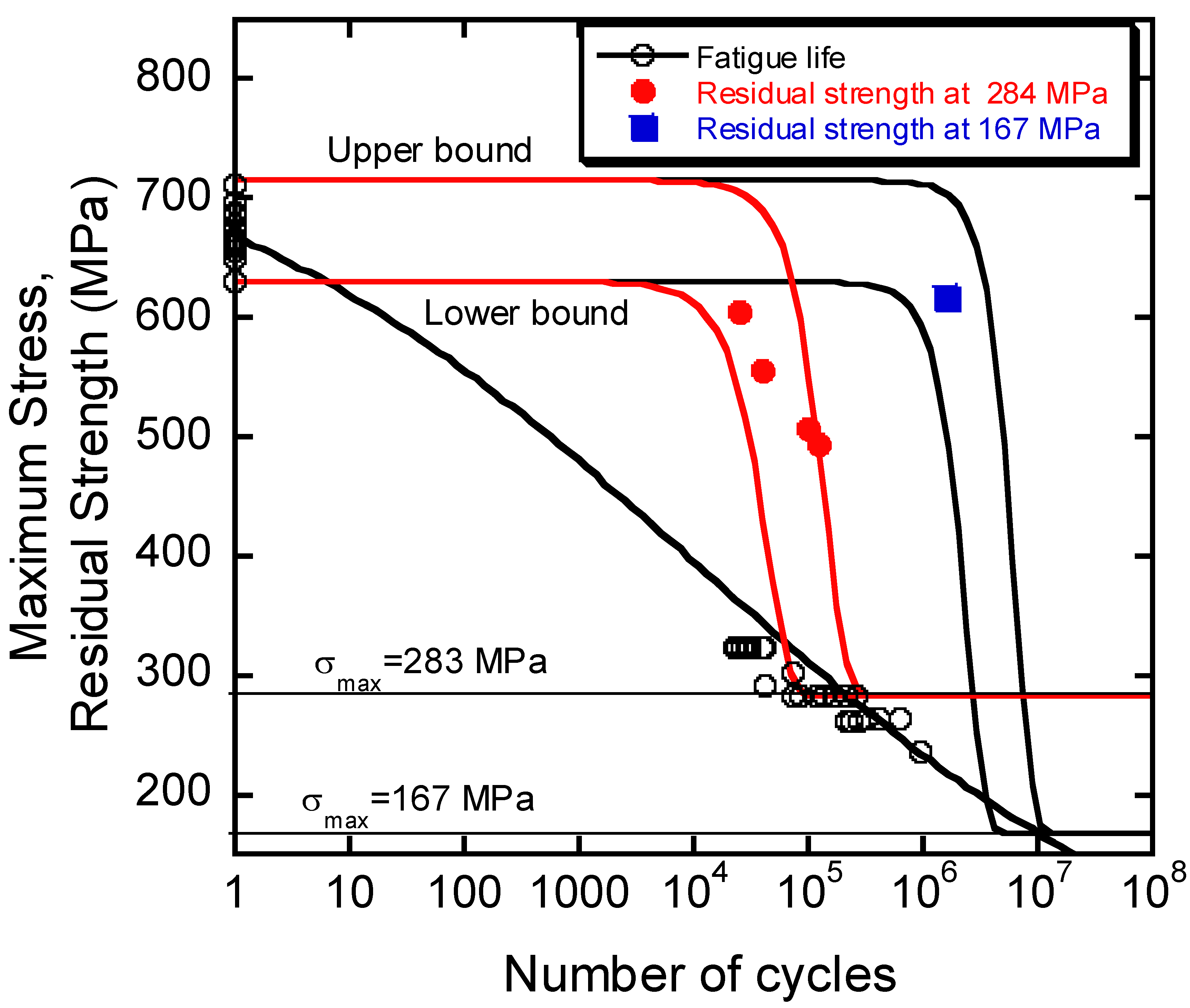
2.4. Residual Strength
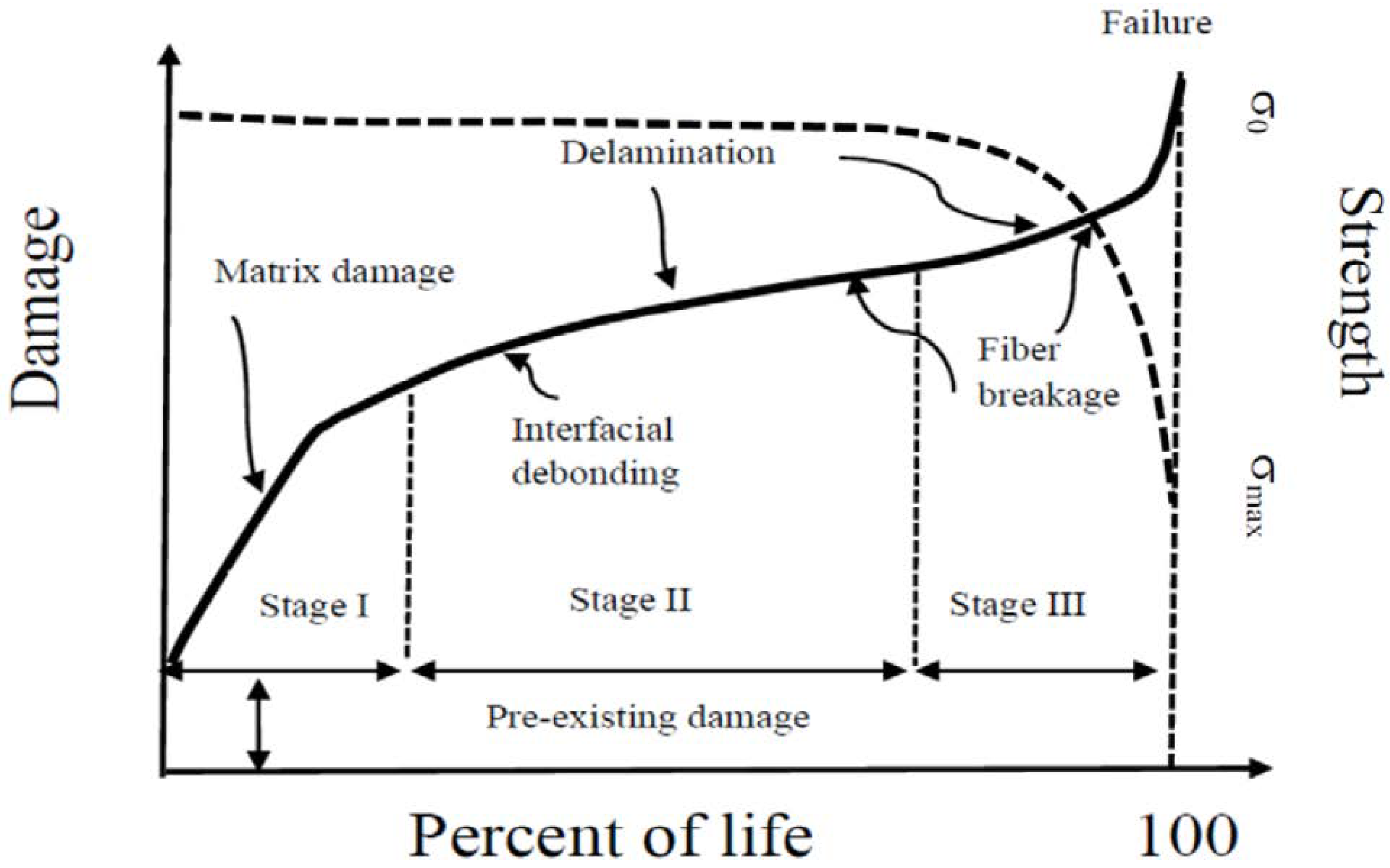
2.5. The Hierarchy of Damage
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reifsneider, K.L. Fatigue of Composite Materials; Elsevier: New York, NY, USA, 1990. [Google Scholar]
- Vassilopoulos, A.P.; Keller, T. Fatigue of Fiber-reinforced Composites; Springer-Verlag: London, UK, 2013. [Google Scholar]
- Halpin, J.C.; Jerina, K.L.; Johnson, T.A. Characterization of composites for the purpose of reliability evaluation. In Analysis of Test Methods for High Modulus Fibers and Composites; ASTM STP: West Conshohocken, PA, USA, 1973; pp. 5–64. [Google Scholar]
- Halpin, J.C.; Johnson, T.A.; Waddoups, M.E. Kinetics fracture models and structural reliability. Int. J. Fracture Mech. 1972, 8, 465–468. [Google Scholar] [CrossRef]
- Wolff, R.V.; Lemon, G.H. Reliability Predictions for Adhesive Bonds; Air Force Materials Laboratory: Dayton, OH, USA, 1972. [Google Scholar]
- Yang, J.N.; Sun, C.T. Proof test and fatigue of unnotched composite laminates. J. Compos. Mater. 1980, 14, 168–176. [Google Scholar] [CrossRef]
- Yang, J.N.; Jones, D.L. Load sequence effects on the fatigue of unnotched composite materials. In Fatigue of Fibrous Composite Materials; ASTM STP: West Conshohocken, PA, USA, 1981; pp. 213–232. [Google Scholar]
- Reifsneider, K.L.; Stinchcomb, W.W. A critical element model of the residual strength and life of fatigue-loaded composite coupons. In Composite Materials: Fatigue and Fracture; STP 907; ASTM STP: West Conshohocken, PA, USA, 1986; pp. 298–313. [Google Scholar]
- Sendeckyj, G.P. Life prediction for resin-matrix composite materials. In Fatigue of Composite Materials; Elsevier Science Publishers: Amsterdam, The Netherlands, 1990; pp. 431–483. [Google Scholar]
- Passipoularidis, V.A.; Philippidis, T.P. A study of factors affecting life prediction of composites under spectrum loading. Int. J. Fatigue 2009, 31, 408–417. [Google Scholar] [CrossRef]
- Passipoularidis, V.A.; Philippidis, T.P. Strength degradation due to fatigue in fiber dominated glass/epoxy composites: A statistical approach. J. Compos. Mater. 2009, 43, 997–1013. [Google Scholar] [CrossRef]
- Degrieck, J.; Paepegem, W.V. Fatigue damage modelling of fibre-reinforced composite materials: Review. Appl. Mech. Rev. 2004, 54. [Google Scholar] [CrossRef]
- Quaresimin, M.; Carraro, P.A.; Pilgaard, M.L.; Lucato, N.; Vivian, L.; Brøndsted, P.; Sørensen, B.F.; Varna, J.; Talreja, R. Damage evolution under internal and external multiaxial cyclic stress state: A comparative analysis. Compos. Part B 2014, 61, 282–290. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Papanikos, P.; Labeas, G.; Pantelakis, S. Fatigue damage accumulation and residual strength assessment of CFRP laminates. Compos. Struct. 2004, 63, 219–230. [Google Scholar] [CrossRef]
- Sevenois, R.D.B.; Van-Paepegem, W. Fatigue damage modeling techniques for textile composites: review and comparison with unidirectional composites modeling techniques. ASME Appl. Mech. Rev 2015, 67, 1–12. [Google Scholar] [CrossRef]
- Chou, P.C.; Croman, R. Residual strength in fatigue based on strength-life equal rank assumption. J. Compos. Mater. 1978, 12, 177–194. [Google Scholar] [CrossRef]
- D’Amore, A.; Giorgio, M.; Grassia, L. Modeling the residual strength of carbon fiber reinforced composites subjected to cyclic loading. Int. J. Fatigue 2015, 78, 31–37. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L. Constitutive law describing the strength degradation kinetics of fibre-reinforced composites subjected to constant amplitude cyclic loading. Mech. Time-Depend. Mater. 2016, 20, 1–12. [Google Scholar] [CrossRef]
- Yang, J.N.; Liu, M.D. Residual strength degradation model and theory of periodic proof tests for graphite/epoxy laminates. J. Compos. Mater. 1977, 11, 176–203. [Google Scholar] [CrossRef]
- Wang, H.H.; Han, K.S. Statistical study of strength and fatigue life of composite materials. Composites 1987, 18, 47–53. [Google Scholar] [CrossRef]
- Determining the Fatigue Life of Composites Aircraft Structures Using Life and Load-Enhancement Factors. Available online: http://www.tc.faa.gov/its/worldpac/techrpt/ar10-6.pdf (accessed on 14 August 2011).
- Yang, J.N.; Jones, D.L. Load Sequence Effects on Graphite/Epoxy [±35]2S Laminate; ASTM STP: West Conshohocken, PA, USA, 1983; pp. 246–262. [Google Scholar]
- D’Amore, A.; Caprino, G.; Stupak, P.; Zhou, J.; Nicolais, L. Effect of stress ratio on the flexural fatigue behaviour of continuous strand mat reinforced plastics. Sci. Eng. Compos. Mater. 1996, 5, 1–8. [Google Scholar] [CrossRef]
- Dick, T.M.; Jar, P.Y.B.; Cheng, J.J.R. Prediction of fatigue resistance of short-fiber-reinforced polymers. Int. J. Fatigue 2009, 31, 284–291. [Google Scholar] [CrossRef]
- Sendeckyj, G.P. Fitting models to composite materials fatigue data. In Test Methods and Design Allowables for Fibrous Composites; STP 734; Chamis, C.C., Ed.; ASTM STP: West Conshohocken, PA, USA, 1981; pp. 245–260. [Google Scholar]
- D’Amore, A.; Caprino, G.; Nicolais, L.; Marino, G. Long-term behaviour of PEI and PEI-based composites subjected to physical aging. Compos. Sci. Technol. 1999, 59, 1993–2003. [Google Scholar] [CrossRef]
- Caprino, G.; D’Amore, A.; Facciolo, F. Fatigue sensitivity of random glass fibre reinforced plastic. J. Compos. Mater. 1998, 32, 1203–1220. [Google Scholar] [CrossRef]
- Caprino, G.; D’Amore, A. Flexural fatigue behaviour of random continuous-fibre-reinforced thermoplastic composites. Compos. Sci. Technol. 1998, 58, 957–965. [Google Scholar] [CrossRef]
- Caprino, G.; D’Amore, A. Fatigue life of graphite/epoxy laminates subjected to tension-compression loadings. Mech. Time-Depend. Mater. 2000, 4, 139–154. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L. Phenomenological approach to the study of hierarchical damage mechanisms in composite materials subjected to fatigue loadings. Compos. Struct. 2017, 175, 1–6. [Google Scholar] [CrossRef]
- Hahn, H.T.; Kim, R.Y. Proof Testing of Composite Materials. J. Compos. Mater. 1975, 9, 297–311. [Google Scholar] [CrossRef]
- Barnard, P.M.; Butler, R.J.; Curtis, P.T. The strength-life equal rank assumption and its application to the fatigue life prediction of composite materials. Int. J. Fatigue 1988, 10, 171–177. [Google Scholar] [CrossRef]
- Hao, J.S.; Wei, Y.X.; Yi, W.T. Synergistic damage mechanic model for stiffness properties of early fatigue damage in composite laminates. Proc. Eng. 2014, 74, 199–209. [Google Scholar]

| Max. Stress MPa | Shape Factor | Scale Factor |
|---|---|---|
| 290 | 1.337 | 2.06 × 106 |
| 345 | 0.987 | 1.33 × 105 |
| 400 | 0.78 | 4.68 × 103 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Amore, A.; Grassia, L. Principal Features of Fatigue and Residual Strength of Composite Materials Subjected to Constant Amplitude (CA) Loading. Materials 2019, 12, 2586. https://doi.org/10.3390/ma12162586
D’Amore A, Grassia L. Principal Features of Fatigue and Residual Strength of Composite Materials Subjected to Constant Amplitude (CA) Loading. Materials. 2019; 12(16):2586. https://doi.org/10.3390/ma12162586
Chicago/Turabian StyleD’Amore, Alberto, and Luigi Grassia. 2019. "Principal Features of Fatigue and Residual Strength of Composite Materials Subjected to Constant Amplitude (CA) Loading" Materials 12, no. 16: 2586. https://doi.org/10.3390/ma12162586
APA StyleD’Amore, A., & Grassia, L. (2019). Principal Features of Fatigue and Residual Strength of Composite Materials Subjected to Constant Amplitude (CA) Loading. Materials, 12(16), 2586. https://doi.org/10.3390/ma12162586




