The Effect of Internal Pressure on Radial Strain of Steel Pipe Subjected to Monotonic and Cyclic Loading
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Descriptions
2.2. Experimental Setup
2.2.1. Static Loading
2.2.2. Cyclic Loading
3. Results and Discussion
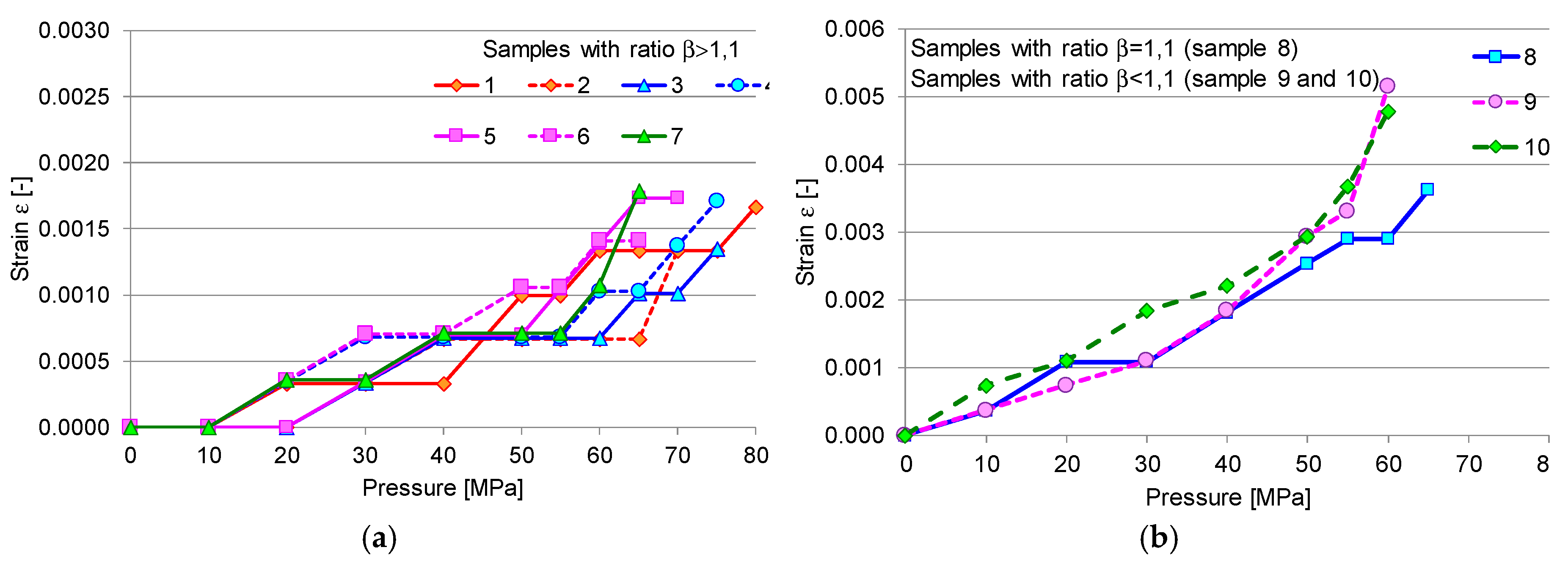
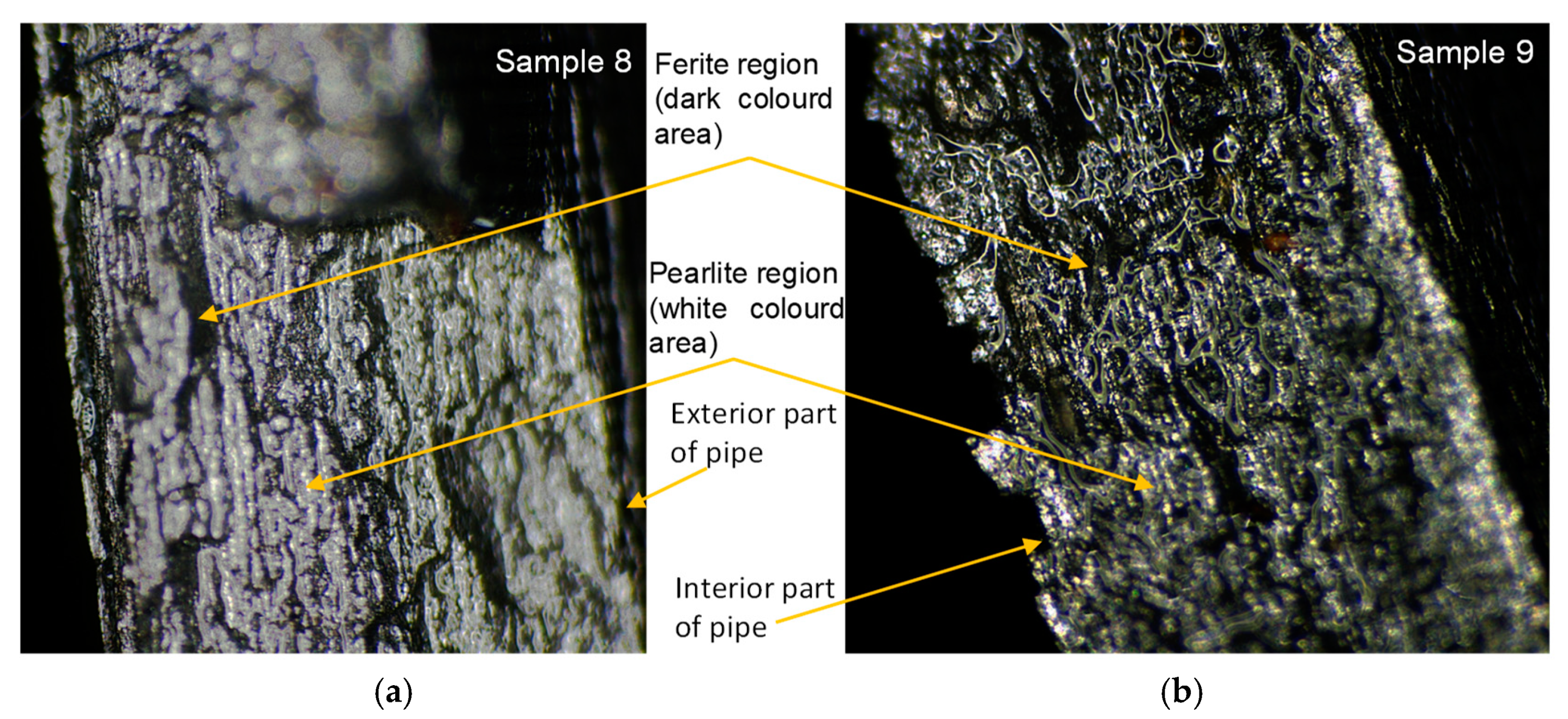
3.1. Monotonic Load
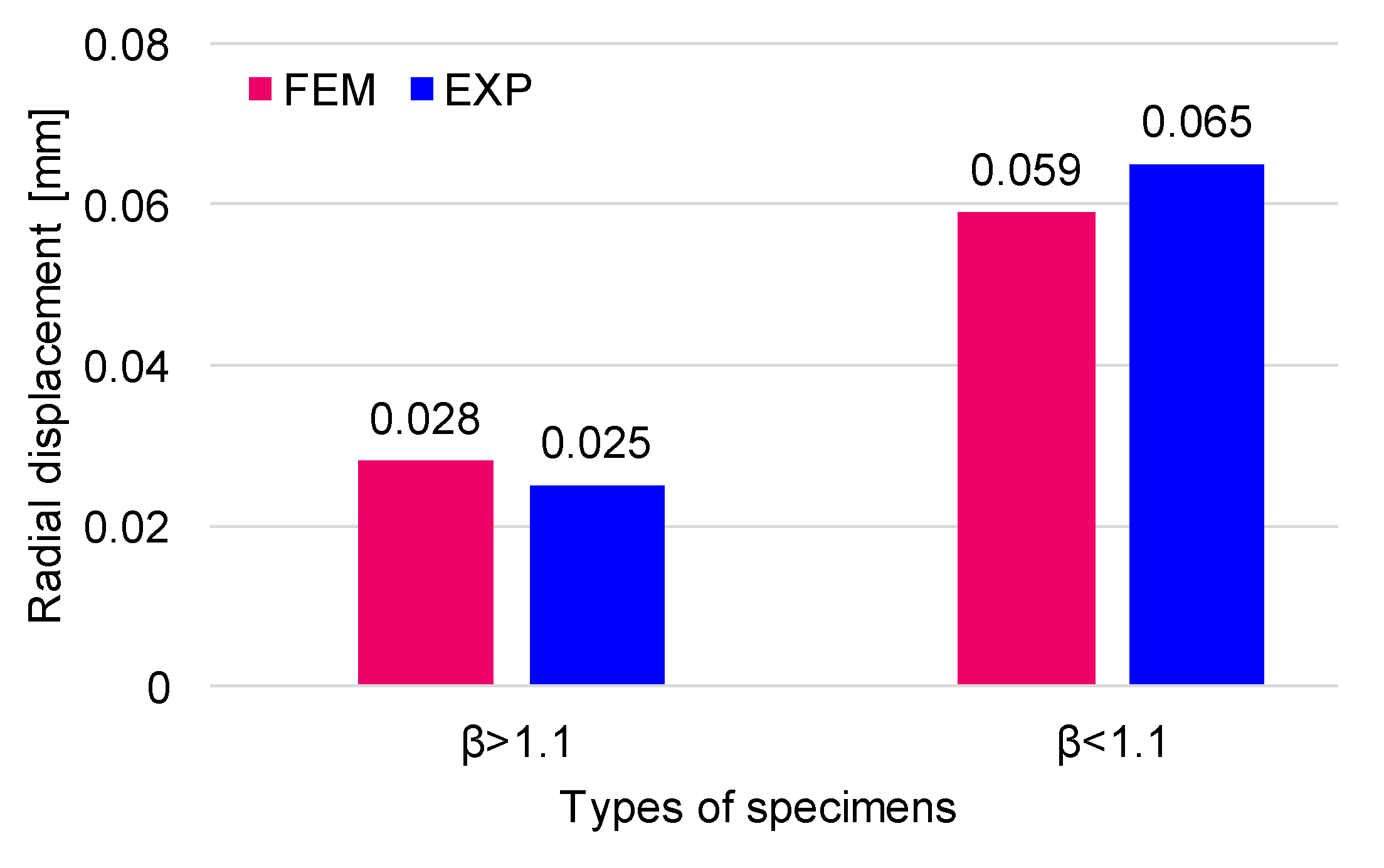
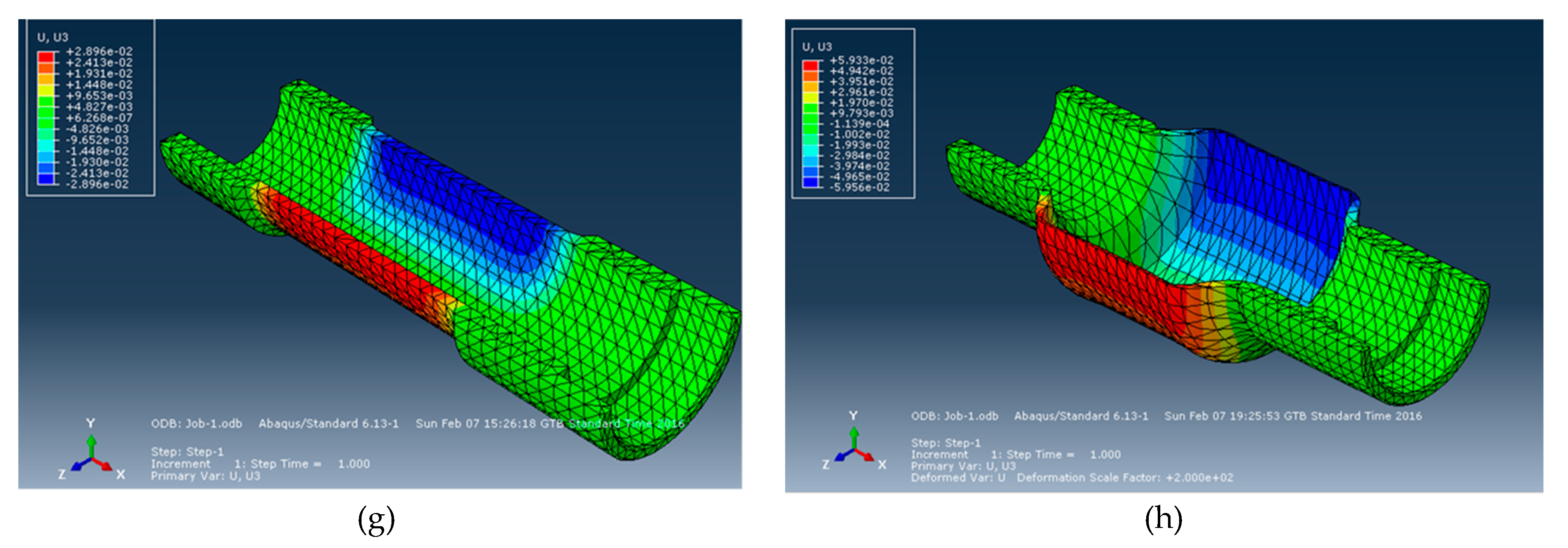
3.2. Finite Element Analysis (FEA) of Strain and Stress States of Small Pipes
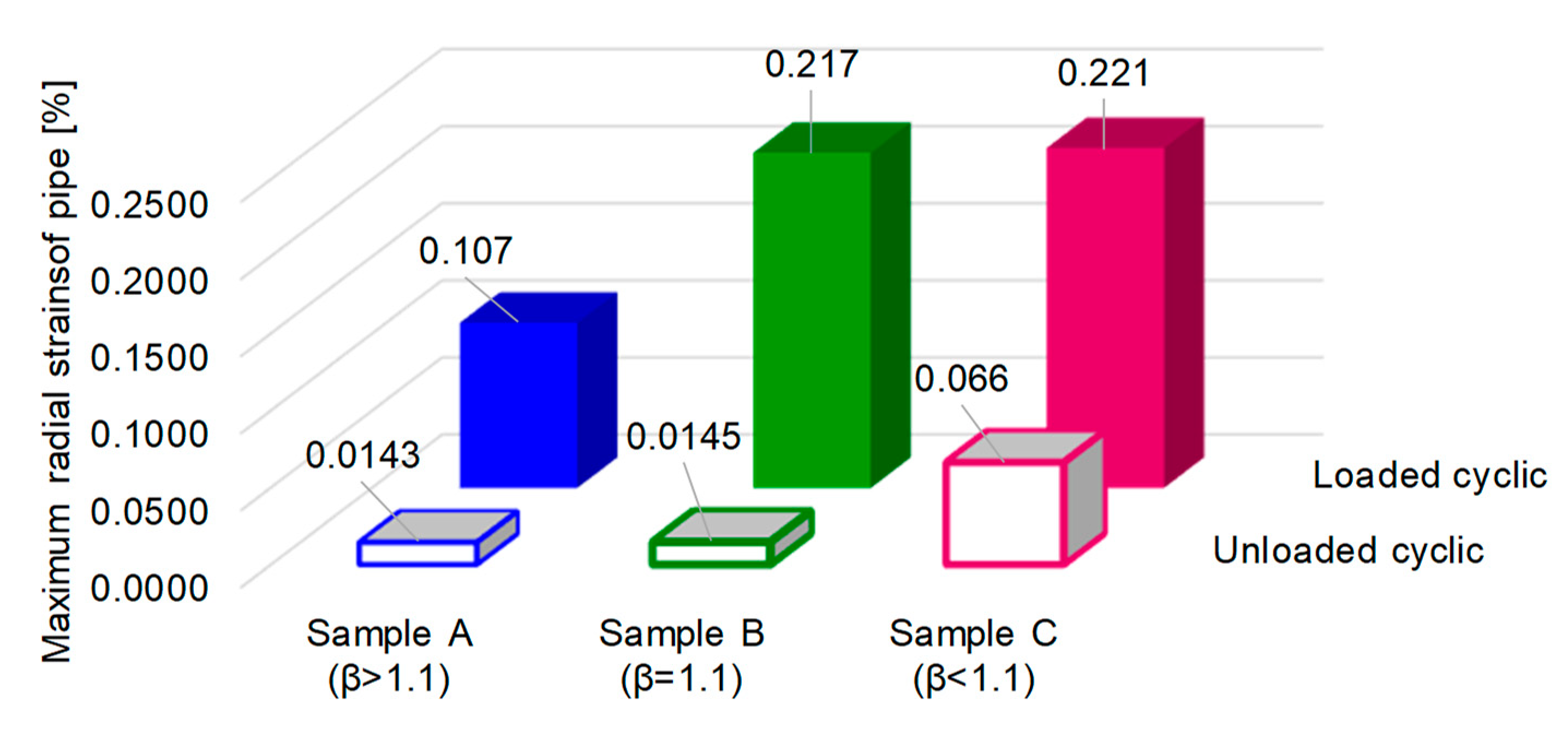
3.3. Cyclic Loading
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Elliotis, M.C. A Finite Element Approach for the Elastic Plastic Behavior of a Steel Pipe Used to Transport Natural Gas. In Proceedings of the Conference Papers in Energy, Limassol, Cyprus, 19–21 November 2013; Hindawi Publishing Corporation: London, UK, 2013; Volume 2013, p. 267095. [Google Scholar] [CrossRef]
- Robertson, A.; Li, H.; Mackenzie, D. Plastic collapse of pipe bends under combined internal pressure and in-plane bending. Int. J. Press. Vessel. Pip. 2005, 82, 407–416. [Google Scholar] [CrossRef]
- Zhu, X.K.; Leis, B.N. Theoretical and numerical predictions of burst pressure of pipelines. J. Press. Vessel. Technol. 2007, 129, 644–652. [Google Scholar] [CrossRef]
- Zhu, X.K.; Leis, B.N. Evaluation of burst pressure prediction models for line pipes. Int. J. Press. Vessel. Pip. 2012, 89, 85–97. [Google Scholar] [CrossRef]
- Gajdos, L.; Sperl, M. Evaluating the integrity of pressure pipelines by fracture mechanics. INTECH Appl. Fract. Mech. 2012, 10, 283–310. [Google Scholar]
- Law, M.; Bowie, G. Failure strain in high yield-to-tensile ratio line pipes. J. Pipeline Integr. 2006, 5, 25–36. [Google Scholar]
- El-Sayed, M.; El-Domiaty, A.; Mourad, A.I. Fracture Assessment of Axial Crack in Steel Pipe under Internal Pressure. Procedia Eng. 2015, 130, 1273–1287. [Google Scholar] [CrossRef]
- Tomita, Y.; Shindo, A.; Nagai, M. Axisymmetric deformation of circular elastic-plastic tubes under axial tension and internal pressure. Int. J. Mech. Sci. 1984, 26, 437–444. [Google Scholar] [CrossRef]
- Majid, Z.A.; Mohsin, R.; Yusof, M.Z. Experimental and computational failure analysis of natural gas pipe. Eng. Fail. Anal. 2012, 19, 32–42. [Google Scholar] [CrossRef]
- Qiao, Q.; Cheng, G.; Wu, W.; Li, Y.; Huang, H.; Wei, Z. Failure analysis of corrosion at an inhomogeneous welded joint in a natural gas gathering pipeline considering the combined action of multiple factors. Eng. Fail. Anal. 2016, 64, 126–143. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, T.; Wang, Y.; Qiao, J.; Wang, Z. Corrosion failure mechanism of associated gas transmission pipeline. Materials 2018, 11, 1935. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Liu, X.L.; Xiong, Z.X.; Cheng, J.C.; Yang, B.; Yu, C. Corrosion reasons and control measures of a natural gas pipeline. Surf. Technol. 2018, 47, 89–94. [Google Scholar] [CrossRef]
- Steigmann, R.; Stanciu, M.D.; Szasz, M.; Curtu, I.; Sturzu, T.; Savin, A. The evaluation of the elasto-plastic behavior in case of the honed steel pipes subjected to variable internal pressure. In Proceedings of the ModTech International Conference—Modern Technologies in Industrial Engineering IV Iasi, IOP Science Materials Science and Engineering, Iasi, Romania, 15–18 June 2016; Volume 145, p. 022036. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Curtu, I.; Szasz, M. The assessment of the probabilistic burst of honed steel pipes based on elastic plastic behavior. Procedia Eng. 2017, 181, 28–35. [Google Scholar]
- Lasebikan, B.A.; Akisanya, A.R. Burst pressure of super duplex stainless steel pipes subject to combined axial tension, internal pressure and elevated temperature. Int. J. Press. Vessel. Pip. 2014, 119, 62–68. [Google Scholar] [CrossRef]
- Rahman, S. Probabilistic elastic-plastic fracture analysis of circumferentially cracked pipes with finite length surface flaws. Nucl. Eng. Des. 2000, 195, 239–260. [Google Scholar] [CrossRef]
- Mushiri, T.; Mbohva, C. Elasto-plastic collapse analysis of pipe bends using finite elements analysis. In Proceedings of the 6th International Conference in Mechanical, Production & Automobile Engineering, Cape Town, South Africa, 24–25 September 2014; pp. 26–29. [Google Scholar]
- Vaičiulis, D.; Bražėnas, A. Determination of stress strain state in pipe subjected to internal pressure at plane strain condition under elasto plastic loading. Mechanika 2011, 17, 346–351. [Google Scholar] [CrossRef]
- Lin, Y.; Deng, K.; Sun, Y.; Zeng, D.; Liu, W.; Kong, X.; Singh, A. Burst strength of tubing and casing based on twin shear unified strength theory. PLoS ONE 2014, 9, e111426. [Google Scholar] [CrossRef] [PubMed]
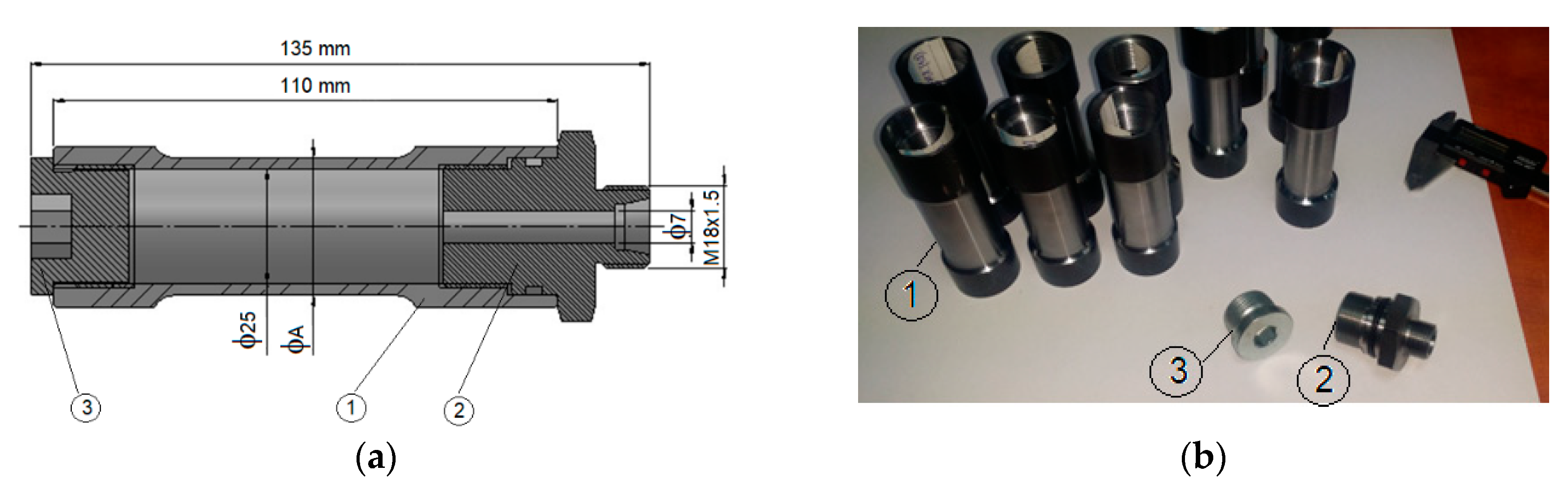
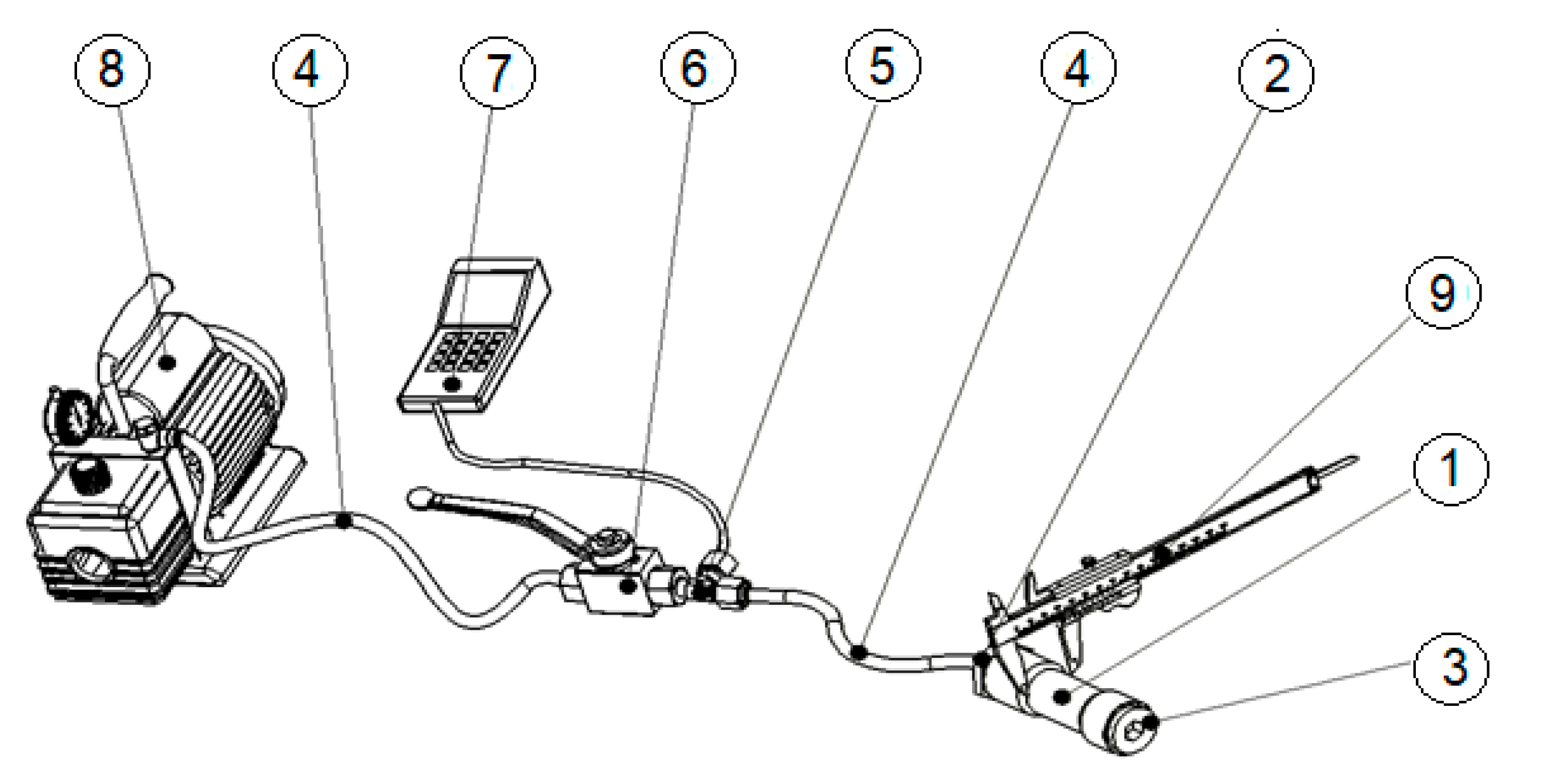
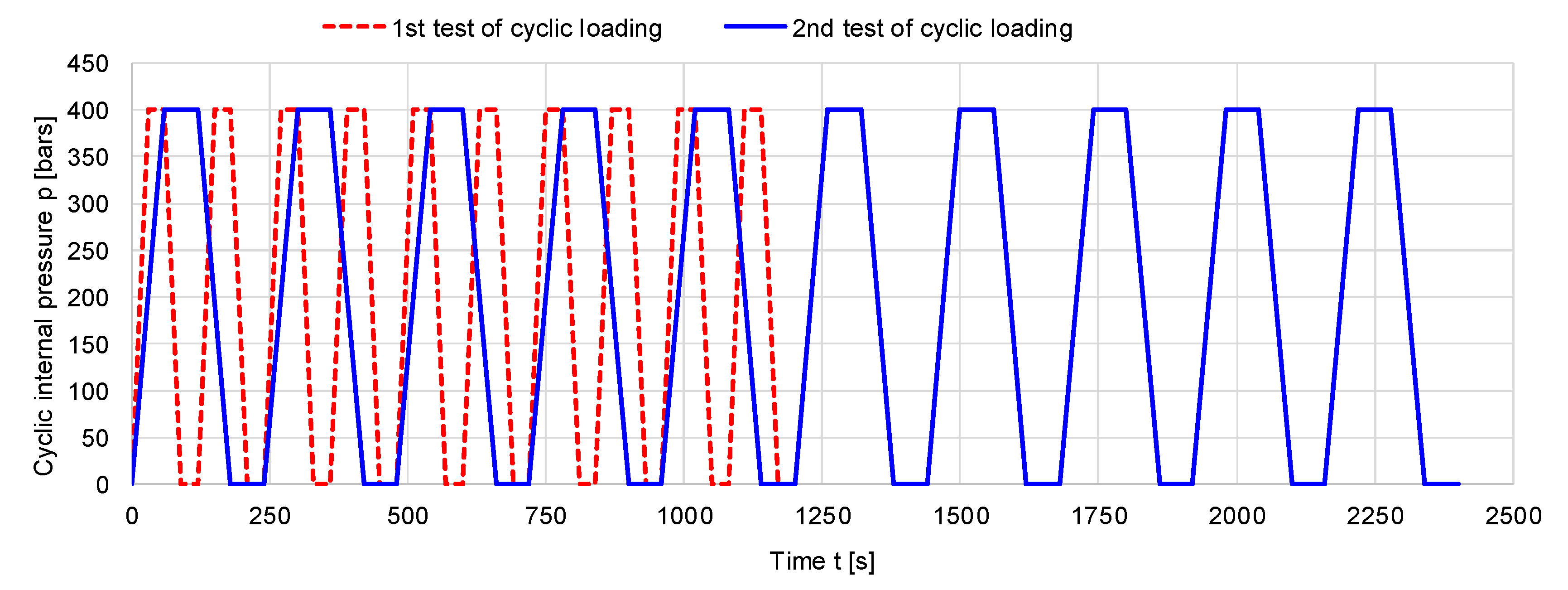

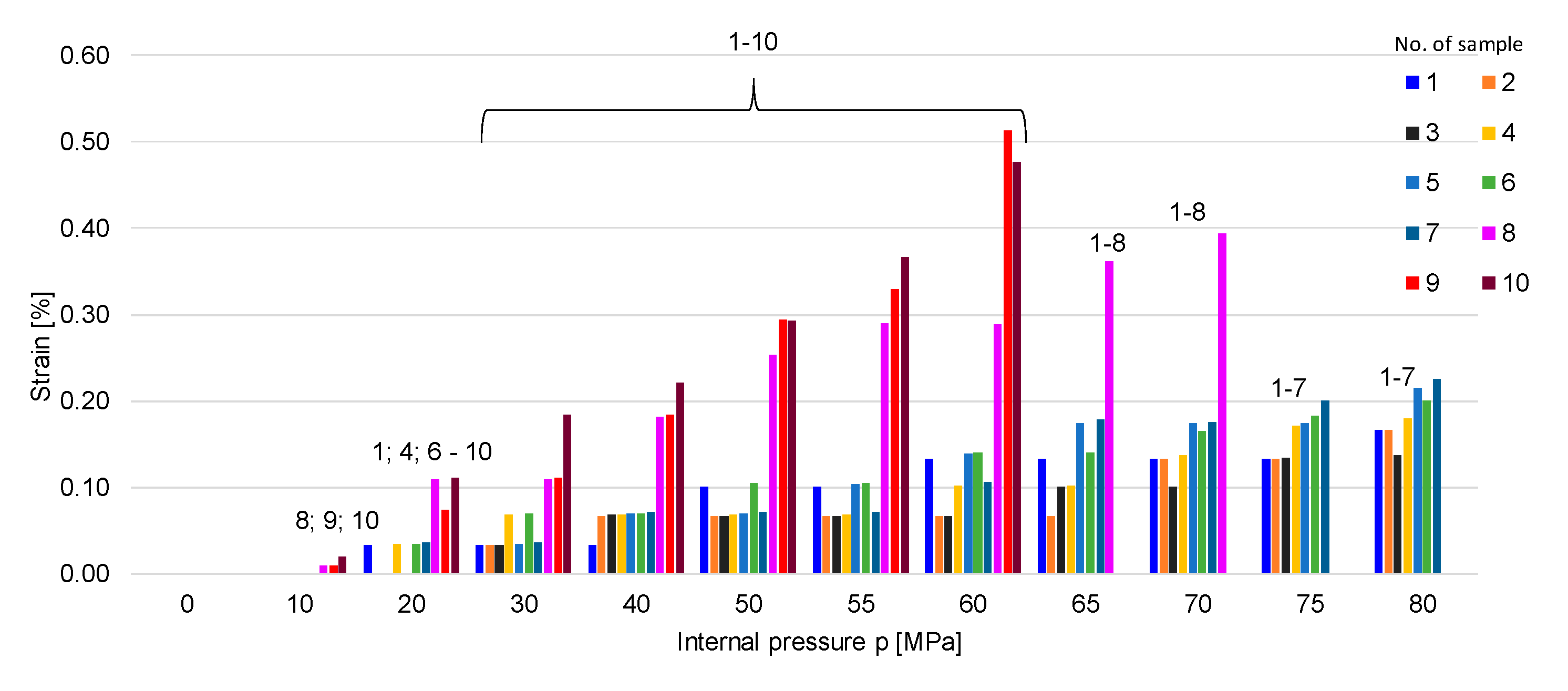




| Sample Code | Interior Diameter Φ25 (mm) | Outside Diameter ΦA (mm) | Wall Thickness s1 = (ΦA − Φ25)/2 (mm) | Ratio B = ΦA/Φ25 |
|---|---|---|---|---|
| 1 | 25 | 30.01 | 2.505 | 1.20 |
| 2 | 25 | 29.99 | 2.495 | 1.19 |
| 3 | 25 | 29.60 | 2.300 | 1.18 |
| 4 | 25 | 29.20 | 2.100 | 1.16 |
| 5 | 25 | 28.80 | 1.900 | 1.15 |
| 6 | 25 | 28.40 | 1.700 | 1.13 |
| 7 | 25 | 28.00 | 1.500 | 1.12 |
| 8 | 25 | 27.60 | 1.300 | 1.10 |
| 9 | 25 | 27.22 | 1.110 | 1.08 |
| 10 | 25 | 27.21 | 1.105 | 1.08 |
| Sample Code | Interior Diameter Φ25 (mm) | Outside Diameter ΦA (mm) | Wall Thickness s1 = (ΦA − Φ25)/2 (mm) | Ratio β = ΦA/Φ25 |
|---|---|---|---|---|
| A | 25 | 28.010 | 1.505 | 1.12 |
| B | 25 | 27.600 | 1.300 | 1.10 |
| C | 25 | 27.210 | 1.105 | 1.08 |
| Samples | Pressure (MPa) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | |
| 1 | 30.01 | 30.01 | 30.02 | 30.02 | 30.02 | 30.04 | 30.04 | 30.05 | 30.05 | 30.05 | 30.05 | 30.06 |
| 2 | 29.99 | 29.99 | 29.99 | 30.00 | 30.01 | 30.01 | 30.01 | 30.01 | 30.01 | 30.03 | 30.03 | 30.04 |
| 3 | 29.60 | 29.60 | 29.60 | 29.61 | 29.62 | 29.62 | 29.62 | 29.62 | 29.63 | 29.63 | 29.64 | 29.64 |
| 4 | 29.20 | 29.20 | 29.21 | 29.22 | 29.22 | 29.22 | 29.22 | 29.23 | 29.23 | 29.24 | 29.25 | 29.25 |
| 5 | 28.80 | 28.80 | 28.80 | 28.81 | 28.82 | 28.82 | 28.83 | 28.84 | 28.85 | 28.85 | 28.85 | 28.86 |
| 6 | 28.40 | 28.40 | 28.41 | 28.42 | 28.42 | 28.43 | 28.43 | 28.44 | 28.44 | 28.45 | 28.45 | 28.46 |
| 7 | 28.00 | 28.00 | 28.01 | 28.01 | 28.02 | 28.02 | 28.02 | 28.03 | 28.05 | 28.05 | 28.06 | 28.06 |
| 8 | 27.60 | 27.61 | 27.63 | 27.63 | 27.65 | 27.67 | 27.68 | 27.68 | 27.70 | 27.71 | burst | burst |
| 9 | 27.22 | 27.23 | 27.24 | 27.25 | 27.27 | 27.30 | 27.31 | 27.36 | burst | burst | burst | burst |
| 10 | 27.21 | 27.23 | 27.24 | 27.26 | 27.27 | 27.29 | 27.31 | 27.34 | burst | burst | burst | burst |
| Type of Pipe | Ratio β | Pressure P (N/mm2) | Maximum Stress: Von Mises σmax (MPa) | Displacement Utot (mm) | Displacement | ||
|---|---|---|---|---|---|---|---|
| Ux (mm) | Uy (mm) | Uz (mm) | |||||
| Thick wall | β > 1.1 | 80 | 485 | 0.0292 | 0.009 | 0.028 | 0.028 |
| Thin wall | β < 1.1 | 65 | 491 | 0.0601 | 0.015 | 0.059 | 0.059 |
| t1 = 30 s | Diameter Measured after Each Cycle ΦA (mm) Sample A (β > 1.1) | |||||||||
| d1 | d2 | d3 | d4 | d5 | d6 | d7 | d8 | d9 | d10 | |
| pactive * | 28.033 | 28.033 | 28.034 | 28.034 | 28.034 | 28.034 | 28.035 | 28.035 | 28.035 | 28.035 |
| pinactive * | 28.010 | 28.010 | 28.010 | 28.011 | 28.011 | 28.011 | 28.012 | 28.012 | 28.012 | 28.012 |
| t2 = 60 s | d11 | d12 | d13 | d14 | d15 | d16 | d17 | d18 | d19 | d20 |
| pactive * | 28.040 | 28.040 | 28.040 | 28.040 | 28.040 | 28.040 | 28.040 | 28.040 | 28.040 | 28.040 |
| pinactive * | 28.012 | 28.013 | 28.013 | 28.013 | 28.013 | 28.013 | 28.013 | 28.013 | 28.014 | 28.014 |
| t1 = 30 s | Sample B (β = 1.1) | |||||||||
| pactive * | 27.620 | 27.630 | 27.630 | 27.630 | 27.630 | 27.630 | 27.630 | 27.630 | 27.640 | 27.640 |
| pinactive * | 27.600 | 27.600 | 27.600 | 27.600 | 27.600 | 27.600 | 27.600 | 27.600 | 27.600 | 27.600 |
| t2 = 60 s | d11 | d12 | d13 | d14 | d15 | d16 | d17 | d18 | d19 | d20 |
| pactive * | 27.640 | 27.640 | 27.640 | 27.650 | 27.650 | 27.650 | 27.650 | 27.650 | 27.660 | 27.660 |
| pinactive * | 27.603 | 27.604 | 27.603 | 27.603 | 27.603 | 27.603 | 27.603 | 27.604 | 27.604 | 27.604 |
| t1 = 30 s | Sample C (β < 1.1) | |||||||||
| pactive * | 27.240 | 27.240 | 27.242 | 27.243 | 27.250 | 27.250 | 27.250 | 27.250 | 27.260 | 27.260 |
| pinactive * | 27.21 | 27.212 | 27.213 | 27.214 | 27.214 | 27.215 | 27.216 | 27.216 | 27.217 | 27.218 |
| t2 = 60 s | d11 | d12 | d13 | d14 | d15 | d16 | d17 | d18 | d19 | d20 |
| pactive * | 27.260 | 27.260 | 27.266 | 27.266 | 27.266 | 27.270 | 27.270 | 27.270 | 27.270 | 27.270 |
| 27.220 | 27.220 | 27.220 | 27.220 | 27.224 | 27.224 | 27.225 | 27.226 | 27.227 | 27.228 | 27.220 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pleșcan, C.; Stanciu, M.D.; Szasz, M. The Effect of Internal Pressure on Radial Strain of Steel Pipe Subjected to Monotonic and Cyclic Loading. Materials 2019, 12, 2849. https://doi.org/10.3390/ma12182849
Pleșcan C, Stanciu MD, Szasz M. The Effect of Internal Pressure on Radial Strain of Steel Pipe Subjected to Monotonic and Cyclic Loading. Materials. 2019; 12(18):2849. https://doi.org/10.3390/ma12182849
Chicago/Turabian StylePleșcan, Costel, Mariana D. Stanciu, and Matyas Szasz. 2019. "The Effect of Internal Pressure on Radial Strain of Steel Pipe Subjected to Monotonic and Cyclic Loading" Materials 12, no. 18: 2849. https://doi.org/10.3390/ma12182849
APA StylePleșcan, C., Stanciu, M. D., & Szasz, M. (2019). The Effect of Internal Pressure on Radial Strain of Steel Pipe Subjected to Monotonic and Cyclic Loading. Materials, 12(18), 2849. https://doi.org/10.3390/ma12182849







