On the Application of a Diffusive Memristor Compact Model to Neuromorphic Circuits
Abstract
1. Introduction
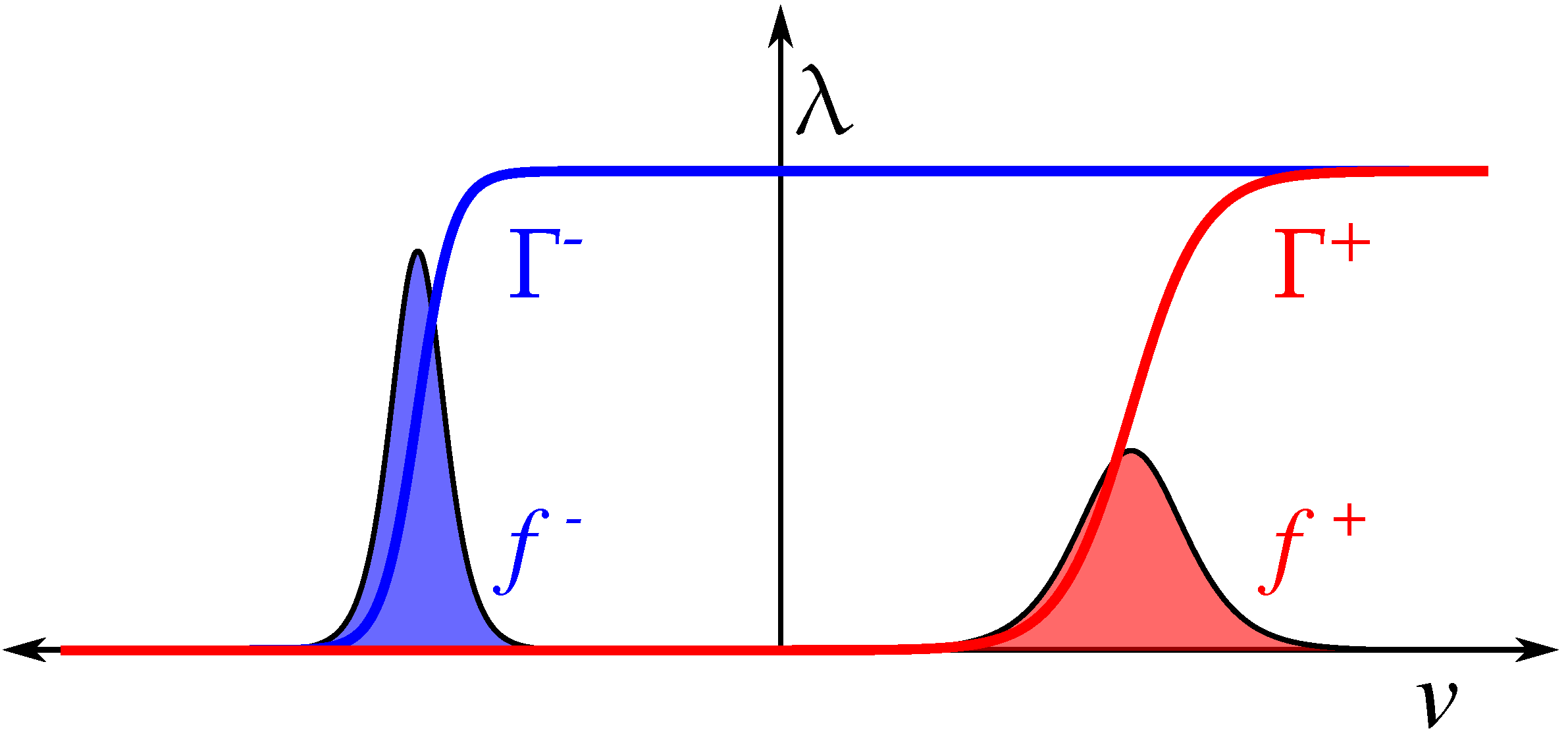
1.1. Compact Model of Memristive Behavior
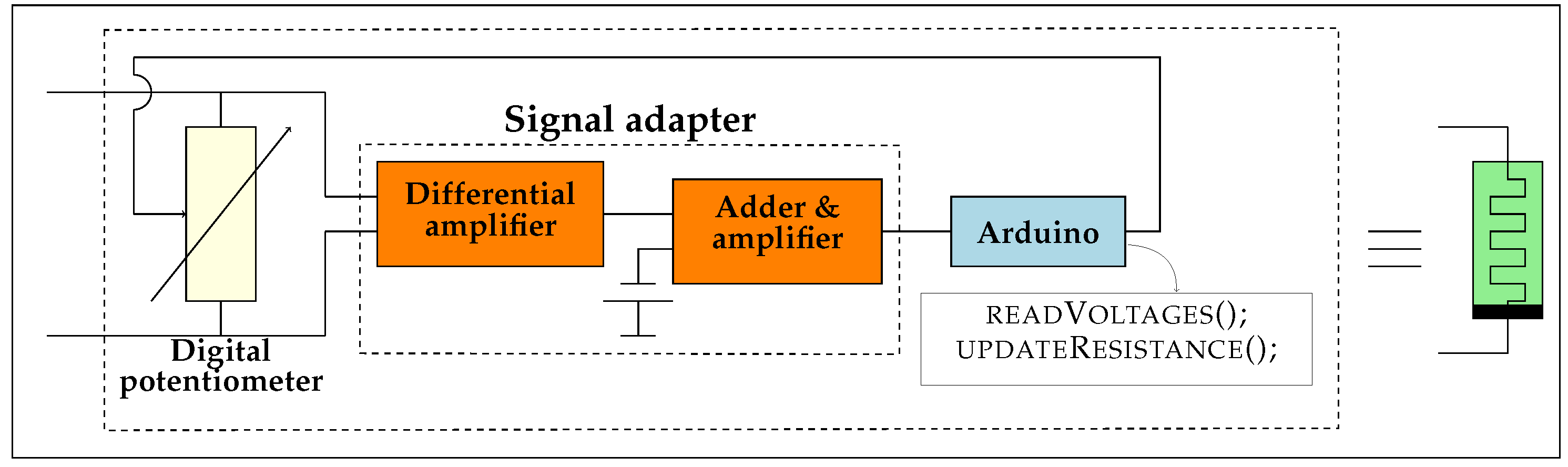
1.2. Emulation Architecture
1.3. Memristors for Neuromorphic Applications
2. Results and Discussion
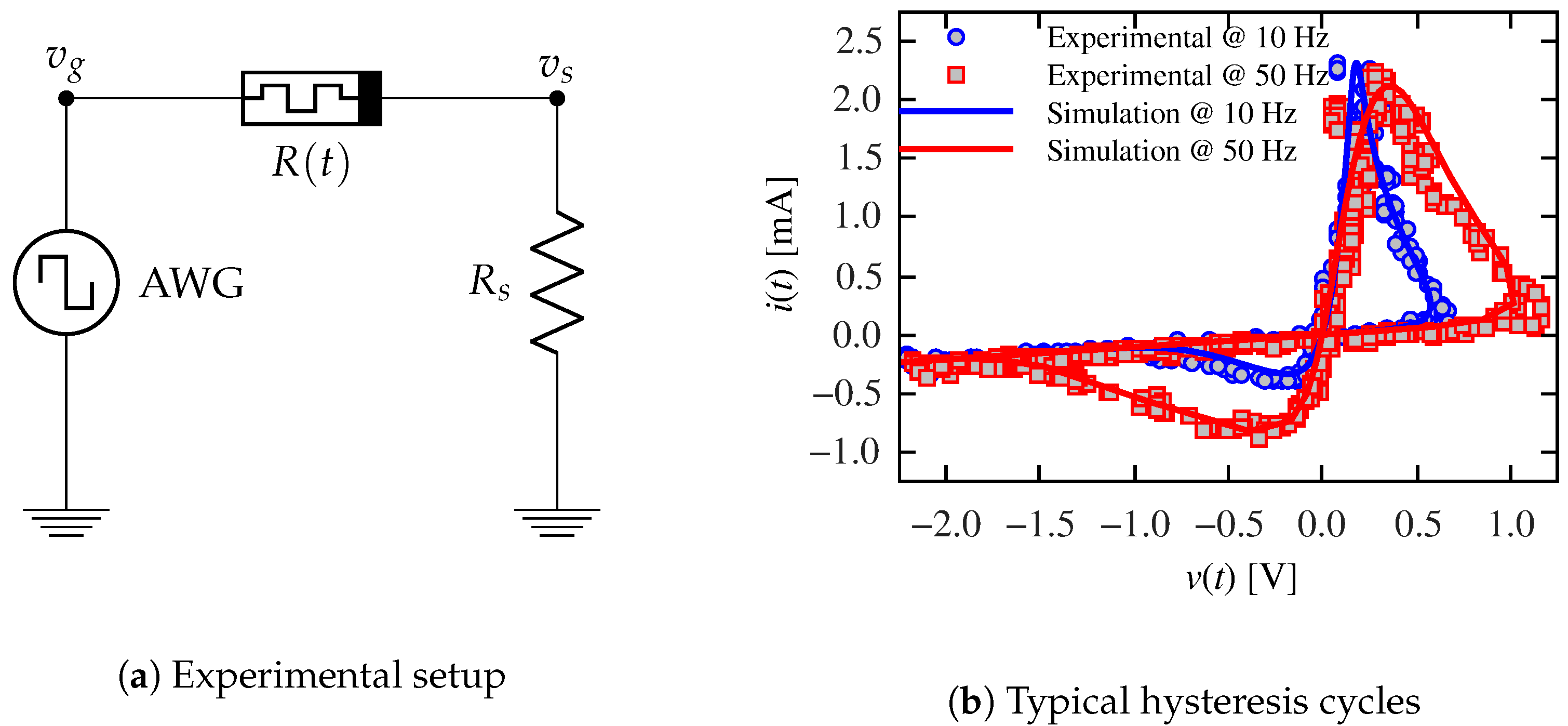
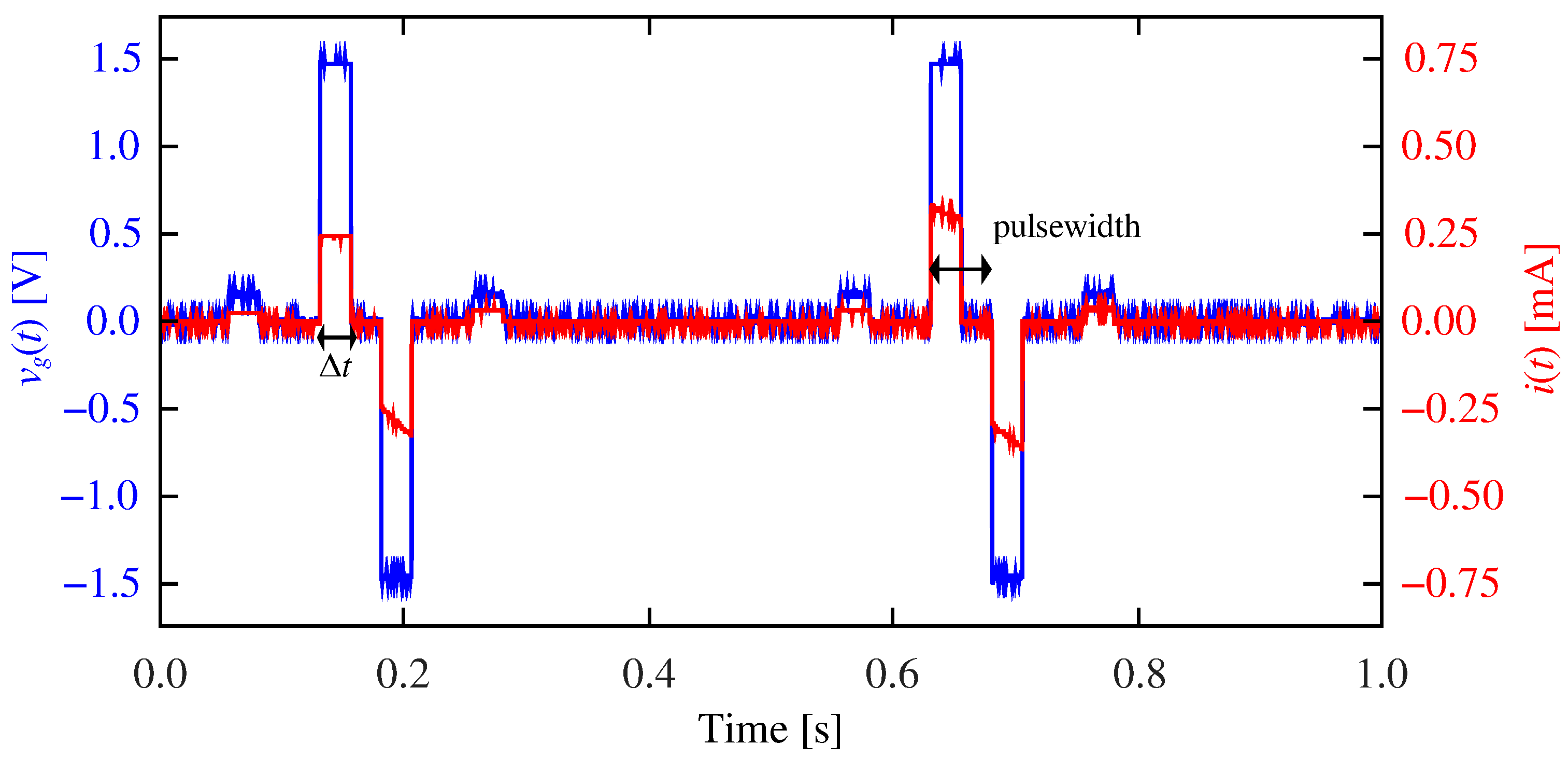
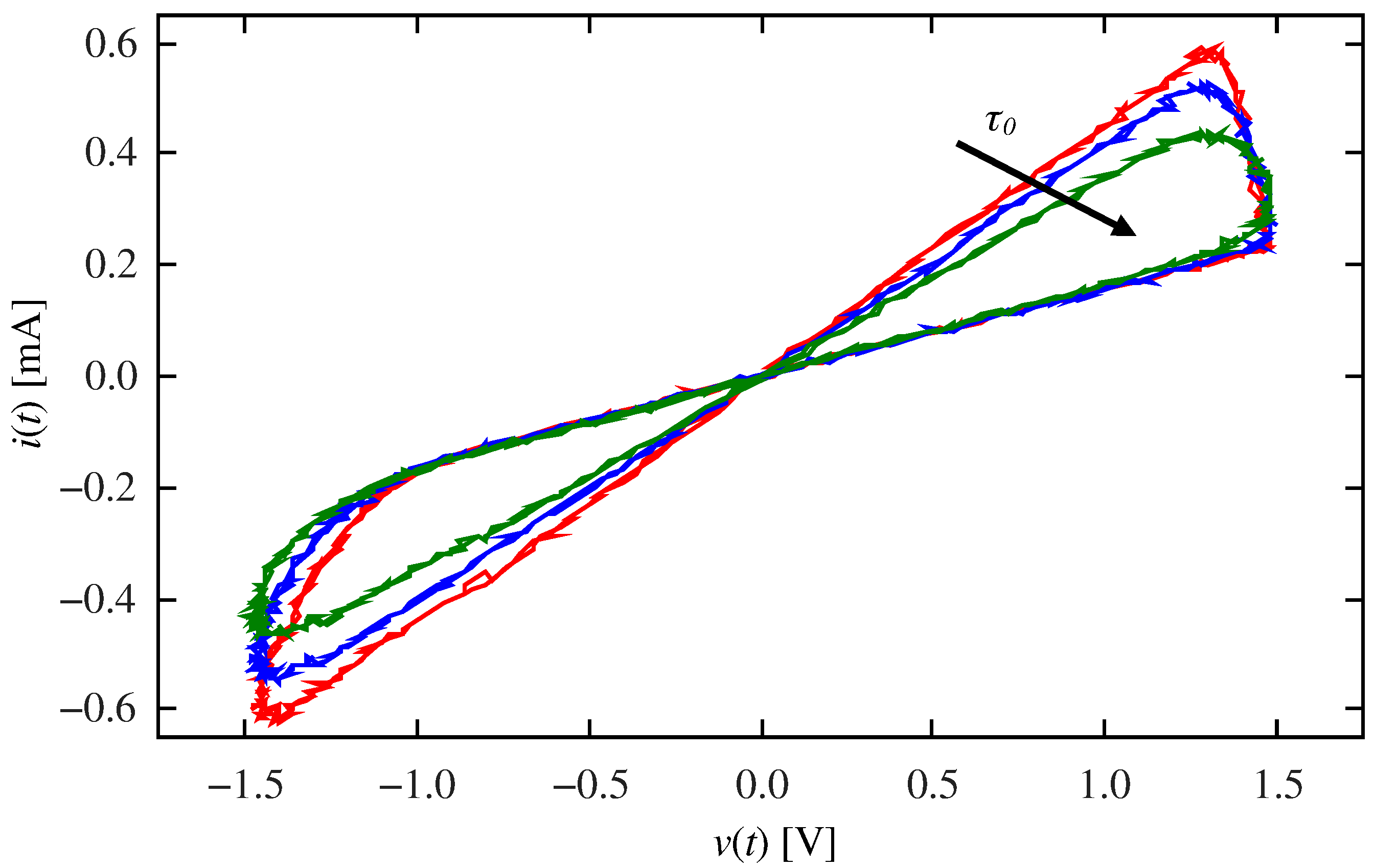
2.1. Validation of the Emulation Architecture
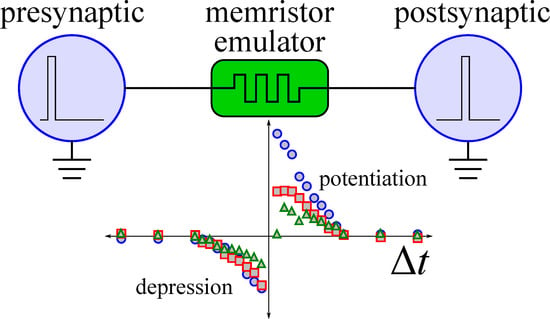
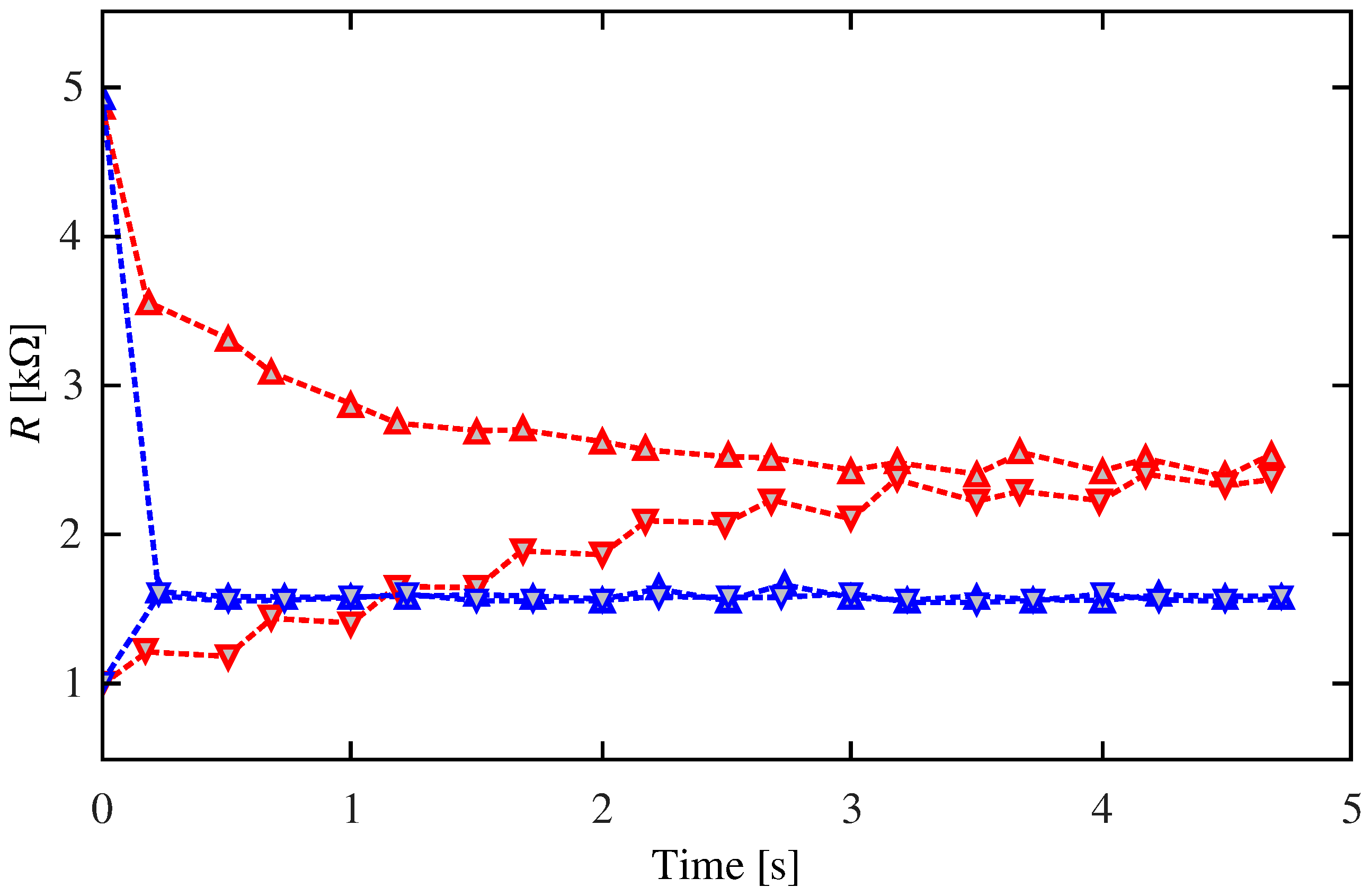
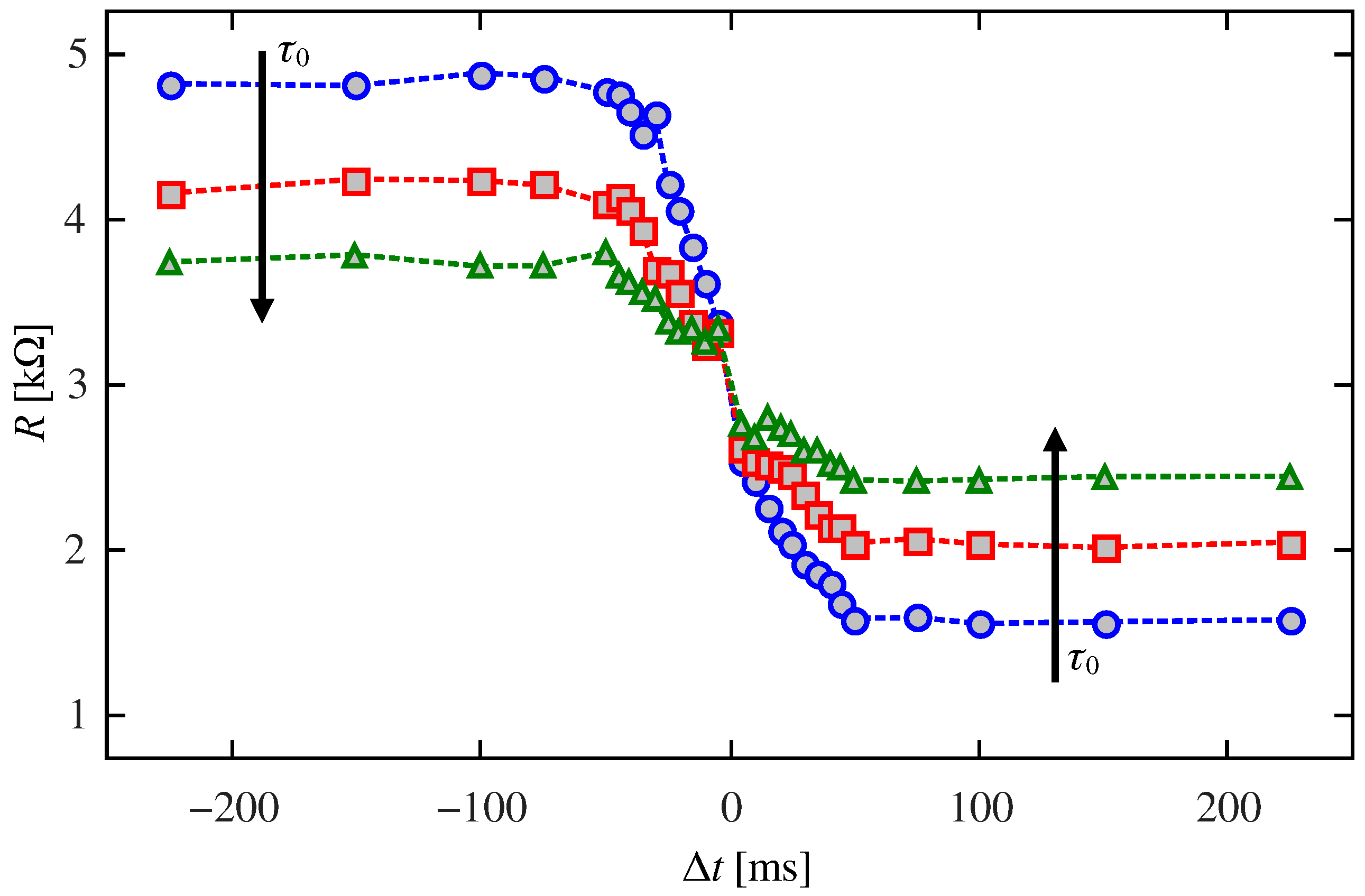
2.2. Synapse Mimicking
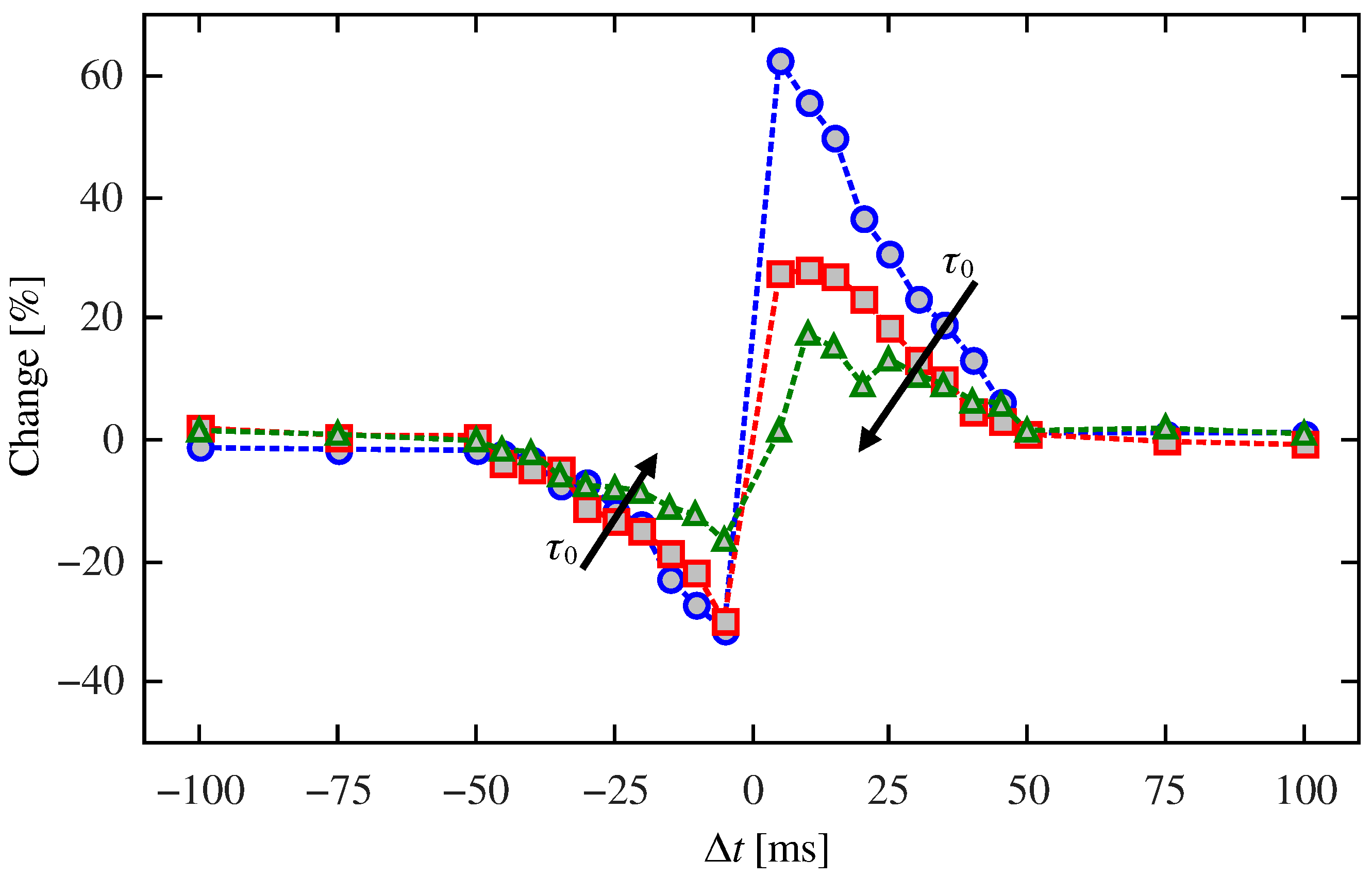
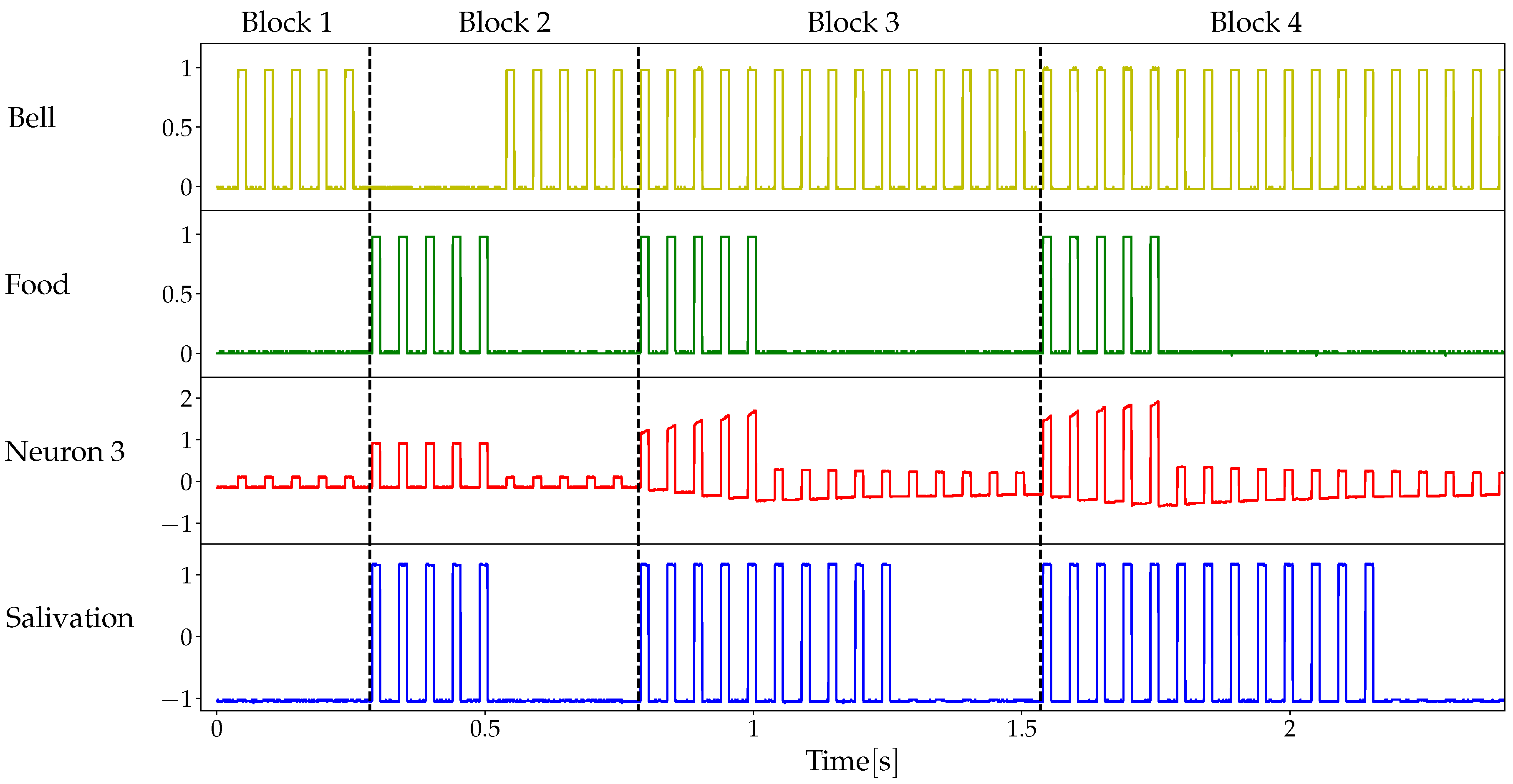
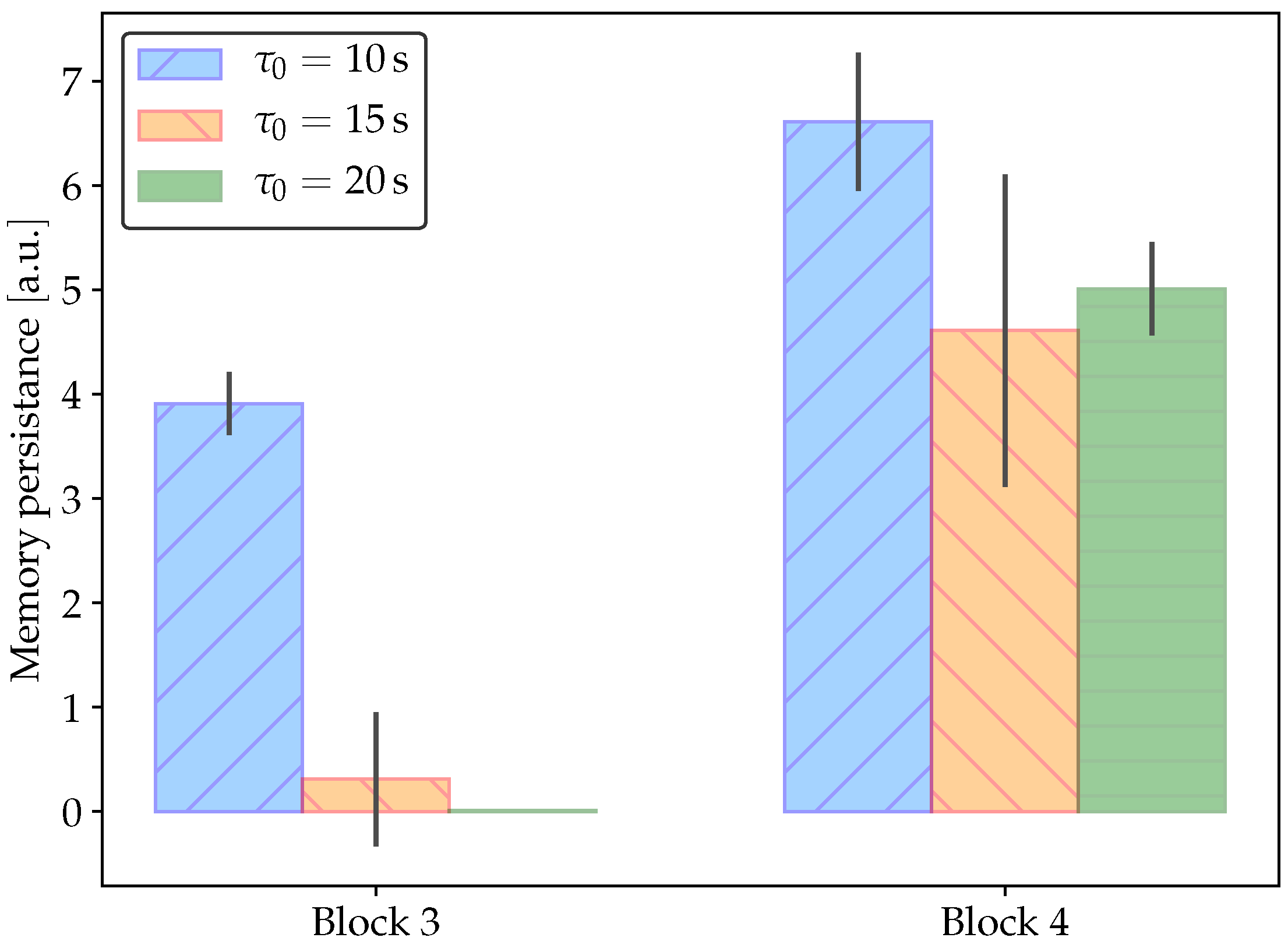
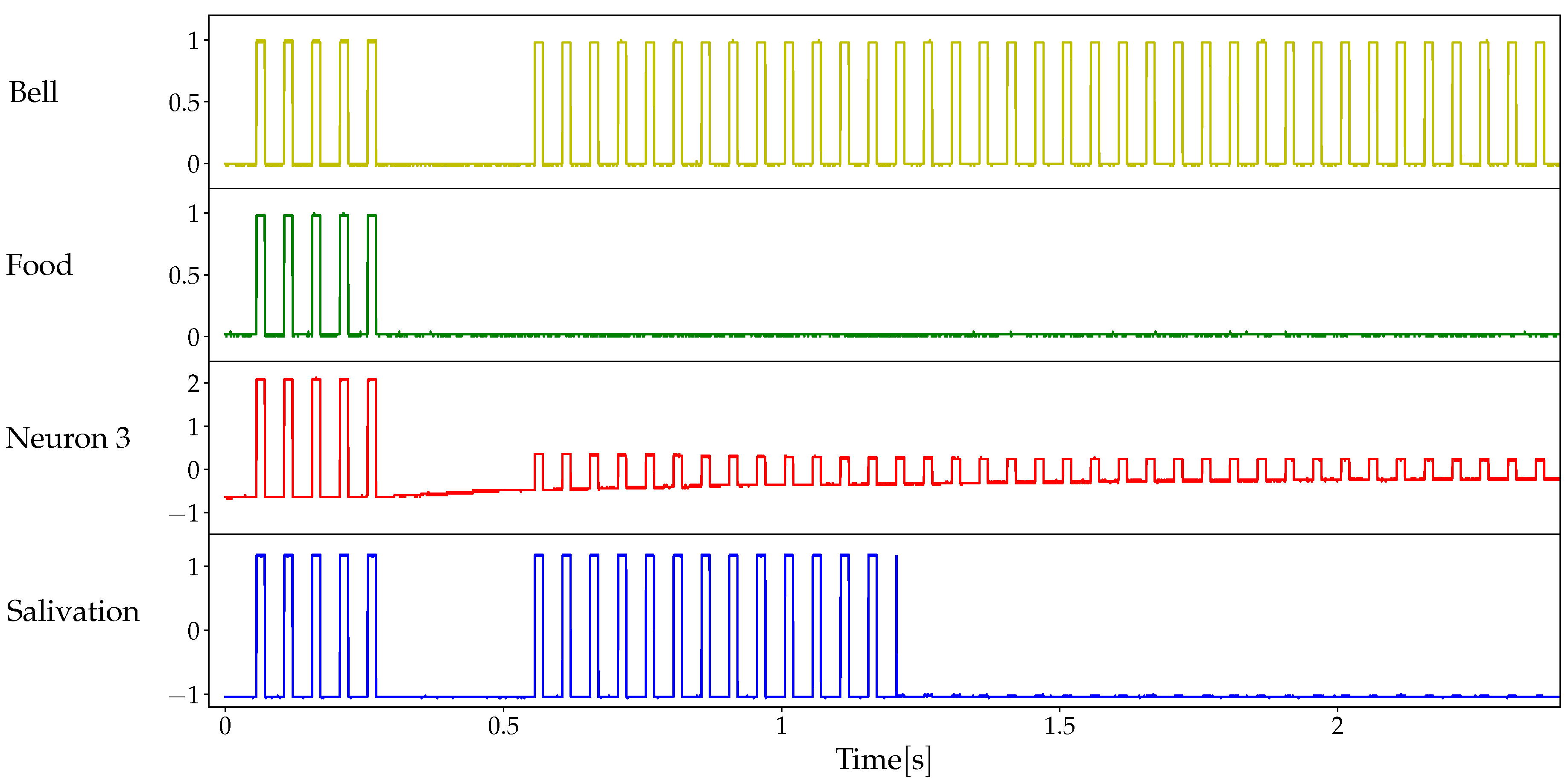
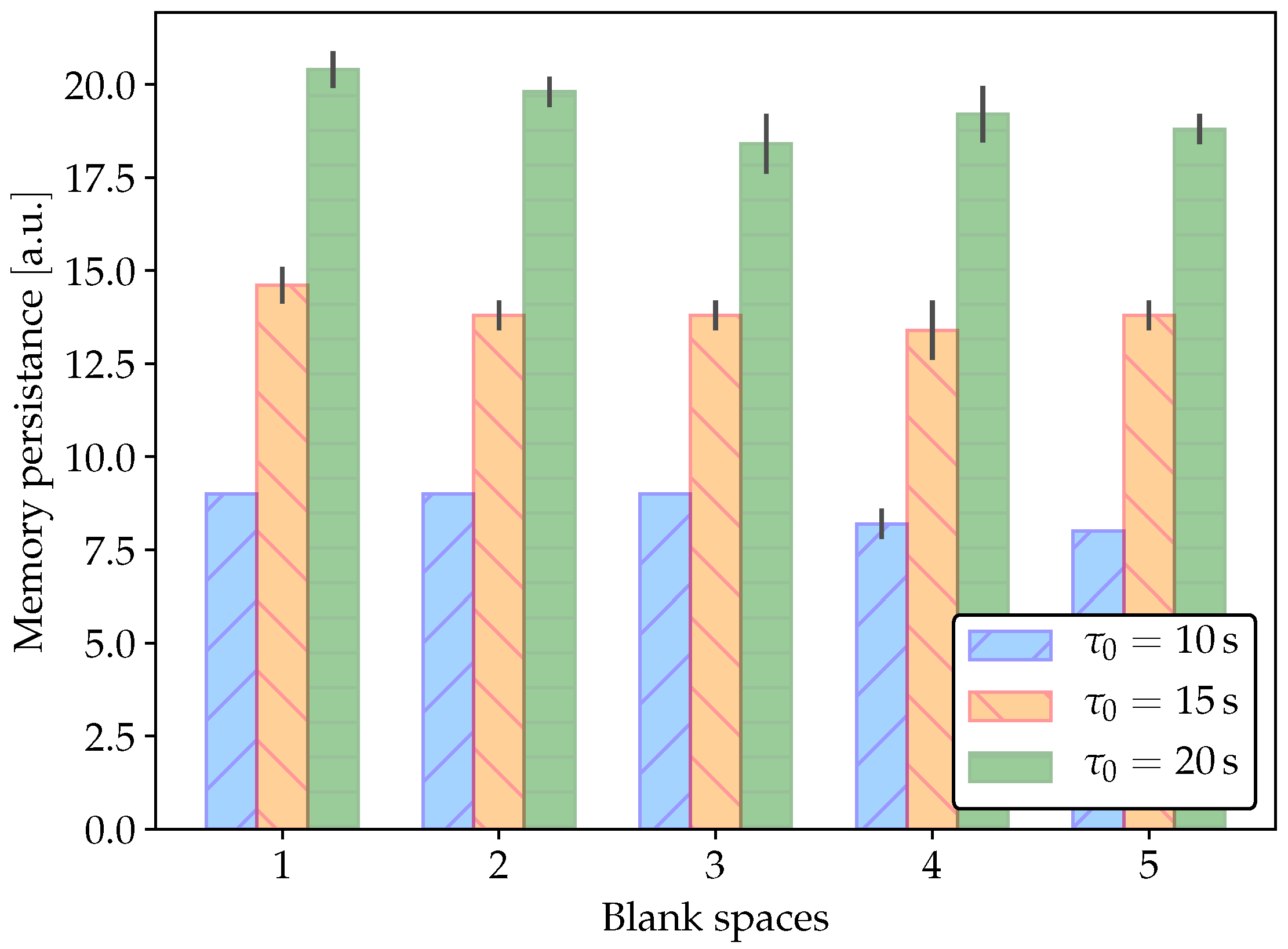
2.3. Classical Conditioning
3. Materials and Methods
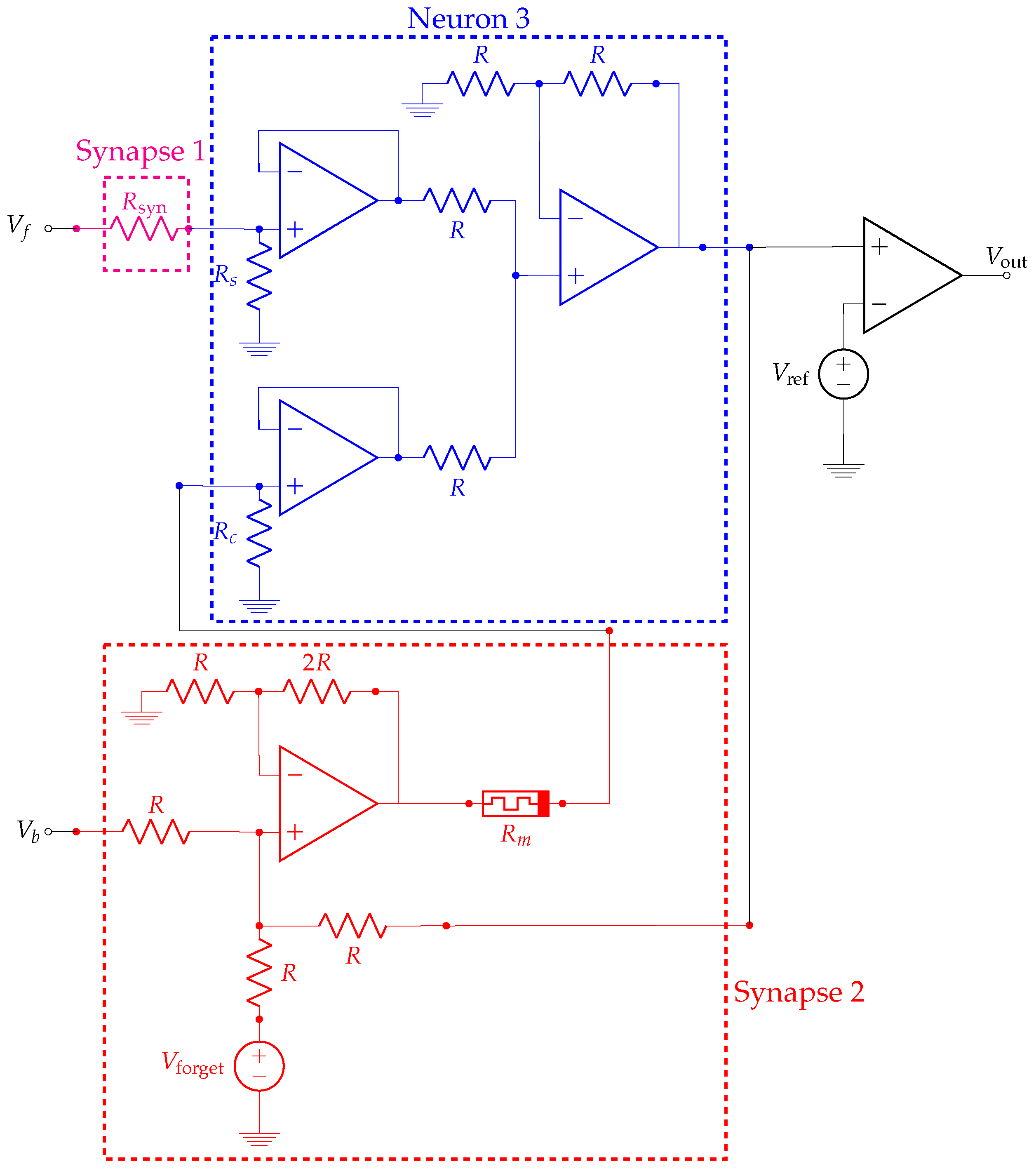
3.1. Details of the Emulator Architecture
| Algorithm 1 Model implementation in Arduino Due: Main loop |
|
| Algorithm 2 Model implementation in Arduino Due: Integration time step |
|
| Algorithm 3 Model implementation in Arduino Due: Numerical Integration |
|
3.2. Details of the Conditioned Learning Experiment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Chua, L.O. The fourth element. Proc. IEEE 2012, 100, 1920–1927. [Google Scholar] [CrossRef]
- Jo, S.H.; Chang, T.; Ebong, I.; Bhadviya, B.B.; Mazumder, P.; Lu, W. Nanoscale Memristor Device as Synapse in Neuromorphic Systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef] [PubMed]
- Querlioz, D.; Bichler, O.; Gamrat, C. Simulation of a memristor-based spiking neural network immune to device variations. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 1775–1781. [Google Scholar] [CrossRef]
- Linares-Barranco, B.; Serrano-Gotarredona, T.; Camuñas-Mesa, L.; Perez-Carrasco, J.; Zamarreño-Ramos, C.; Masquelier, T. On Spike-Timing-Dependent-Plasticity, Memristive Devices, and Building a Self-Learning Visual Cortex. Front. Neurosci. 2011, 5, 26. [Google Scholar] [CrossRef]
- Hu, S.G.; Wu, H.T.; Liu, Y.; Chen, T.P.; Liu, Z.; Yu, Q.; Yin, Y.; Hosaka, S. Design of an electronic synapse with spike time dependent plasticity based on resistive memory device. J. Appl. Phys. 2013, 113, 114502. [Google Scholar] [CrossRef]
- Serrano-Gotarredona, T.; Masquelier, T.; Prodromakis, T.; Indiveri, G.; Linares-Barranco, B. STDP and STDP variations with memristors for spiking neuromorphic learning systems. Front. Neurosci. 2013, 7, 2. [Google Scholar] [CrossRef] [PubMed]
- Bill, J.; Legenstein, R. A compound memristive synapse model for statistical learning through STDP in spiking neural networks. Front. Neurosci. 2014, 8, 412. [Google Scholar] [CrossRef] [PubMed]
- Prezioso, M.; Merrikh-Bayat, F.; Hoskins, B.; Adam, G.C.; Likharev, K.K.; Strukov, D.B. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 2015, 521, 61. [Google Scholar] [CrossRef]
- Saïghi, S.; Mayr, C.G.; Serrano-Gotarredona, T.; Schmidt, H.; Lecerf, G.; Tomas, J.; Grollier, J.; Boyn, S.; Vincent, A.F.; Querlioz, D.; et al. Plasticity in memristive devices for spiking neural networks. Front. Neurosci. 2015, 9, 51. [Google Scholar] [CrossRef]
- Covi, E.; Brivio, S.; Serb, A.; Prodromakis, T.; Fanciulli, M.; Spiga, S. Analog Memristive Synapse in Spiking Networks Implementing Unsupervised Learning. Front. Neurosci. 2016, 10, 482. [Google Scholar] [CrossRef]
- Shen, J.X.; Shang, D.S.; Chai, Y.S.; Wang, S.G.; Shen, B.G.; Sun, Y. Mimicking Synaptic Plasticity and Neural Network Using Memtranstors. Adv. Mater. 2018, 30, 1706717. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kwon, Y.J.; Kwon, D.E.; Yoon, K.J.; Yoon, J.H.; Yoo, S.; Kim, H.J.; Park, T.H.; Han, J.W.; Kim, K.M.; et al. Nociceptive Memristor. Adv. Mater. 2018, 30, 1704320. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.H.; Wang, Z.; Kim, K.M.; Wu, H.; Ravichandran, V.; Xia, Q.; Hwang, C.S.; Yang, J.J. An artificial nociceptor based on a diffusive memristor. Nat. Commun. 2018, 9, 417. [Google Scholar] [CrossRef] [PubMed]
- Borghetti, J.; Li, Z.; Straznicky, J.; Li, X.; Ohlberg, D.A.; Wu, W.; Stewart, D.R.; Williams, R.S. A hybrid nanomemristor/transistor logic circuit capable of self-programming. Proc. Natl. Acad. Sci. USA 2009, 106, 1699–1703. [Google Scholar] [CrossRef] [PubMed]
- Xia, Q.; Robinett, W.; Cumbie, M.W.; Banerjee, N.; Cardinali, T.J.; Yang, J.J.; Wu, W.; Li, X.; Tong, W.M.; Strukov, D.B.; et al. Memristor-CMOS hybrid integrated circuits for reconfigurable logic. Nano Lett. 2009, 9, 3640–3645. [Google Scholar] [CrossRef]
- Gao, L.; Alibart, F.; Strukov, D.B. Programmable CMOS/memristor threshold logic. IEEE Trans. Nanotechnol. 2013, 12, 115–119. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Memristor oscillators. Int. J. Bifurc. Chaos 2008, 18, 3183–3206. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Chua, L.O. Simplest chaotic circuit. Int. J. Bifurc. Chaos 2010, 20, 1567–1580. [Google Scholar] [CrossRef]
- Muthuswamy, B. Implementing memristor based chaotic circuits. Int. J. Bifurc. Chaos 2010, 20, 1335–1350. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-based resistive switching memories–nanoionic mechanisms, prospects, and challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef]
- Waser, R.; Aono, M. Nanoionics-based resistive switching memories. In Nanoscience in Addition, Technology: A Collection of Reviews from Nature Journals; World Scientific: Singapore, 2010; pp. 158–165. [Google Scholar]
- Gale, E. TiO2-based memristors and ReRAM: Materials, mechanisms and models (a review). Semicond. Sci. Technol. 2014, 29, 104004. [Google Scholar] [CrossRef]
- Lastras-Montaño, M.A.; Cheng, K.T. Resistive random-access memory based on ratioed memristors. Nat. Electron. 2018, 1, 466. [Google Scholar] [CrossRef]
- Abdalla, H.; Pickett, M.D. SPICE modeling of memristors. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 1832–1835. [Google Scholar]
- Kvatinsky, S.; Friedman, E.G.; Kolodny, A.; Weiser, U.C. TEAM: Threshold adaptive memristor model. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 211–221. [Google Scholar] [CrossRef]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N.; Tlelo-Cuautle, E.; Vaidyanathan, S. Memristor: A New Concept in Synchronization of Coupled Neuromorphic Circuits. J. Eng. Sci. Technol. Rev. 2014, 8, 157–173. [Google Scholar] [CrossRef]
- Wang, Z.; Joshi, S.; Savel’ev, S.E.; Jiang, H.; Midya, R.; Lin, P.; Hu, M.; Ge, N.; Strachan, J.P.; Li, Z.; et al. Memristors with diffusive dynamics as synaptic emulators for neuromorphic computing. Nat. Mater. 2017, 16, 101. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.; Li, B.; Tang, T.; Gu, P.; Chen, P.; Yu, S.; Cao, Y.; Wang, Y.; Xie, Y.; Yang, H. MNSIM: Simulation Platform for Memristor-Based Neuromorphic Computing System. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 1009–1022. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Ventra, M.D. Experimental demonstration of associative memory with memristive neural networks. Neural Netw. 2010, 23, 881–886. [Google Scholar] [CrossRef]
- Kim, H.; Sah, M.P.; Yang, C.; Cho, S.; Chua, L.O. Memristor Emulator for Memristor Circuit Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2422–2431. [Google Scholar] [CrossRef]
- Ascoli, A.; Corinto, F.; Tetzlaff, R. A class of versatile circuits, made up of standard electrical components, are memristors. Int. J. Circuit Theory Appl. 2016, 44, 127–146. [Google Scholar] [CrossRef]
- Yesil, A. A new grounded memristor emulator based on MOSFET-C. AEU-Int. J. Electron. Commun. 2018, 91, 143–149. [Google Scholar] [CrossRef]
- Yu, D.S.; Sun, T.T.; Zheng, C.Y.; Iu, H.H.C.; Fernando, T. A Simpler Memristor Emulator Based on Varactor Diode. Chin. Phys. Lett. 2018, 35, 058401. [Google Scholar] [CrossRef]
- Olumodeji, O.A.; Gottardi, M. Arduino-controlled HP memristor emulator for memristor circuit applications. Integration 2017, 58, 438–445. [Google Scholar] [CrossRef]
- Ermini, M.A.; Dhanasekar, J.; Sudha, V. Memristor emulator using MCP3208 and digital potentiometer. ICTACT J. Microelectron. 2018, 3. [Google Scholar] [CrossRef]
- Sánchez-López, C.; Mendoza-Lopez, J.; Carrasco-Aguilar, M.; Muñiz-Montero, C. A floating analog memristor emulator circuit. IEEE Trans. Circuits Syst. II Express Br. 2014, 61, 309–313. [Google Scholar]
- Bi, G.q.; Poo, M.m. Synaptic Modifications in Cultured Hippocampal Neurons: Dependence on Spike Timing, Synaptic Strength, and Postsynaptic Cell Type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar] [CrossRef]
- Bi, G.q.; Poo, M.m. Synaptic Modification by Correlated Activity: Hebb’s Postulate Revisited. Annu. Rev. Neurosci. 2001, 24, 139–166. [Google Scholar] [CrossRef]
- Dan, Y.; Poo, M.M. Spike Timing-Dependent Plasticity of Neural Circuits. Neuron 2004, 44, 23–30. [Google Scholar] [CrossRef]
- Najem, J.S.; Taylor, G.J.; Weiss, R.J.; Hasan, M.S.; Rose, G.; Schuman, C.D.; Belianinov, A.; Collier, C.P.; Sarles, S.A. Memristive Ion Channel-Doped Biomembranes as Synaptic Mimics. ACS Nano 2018, 12, 4702–4711. [Google Scholar] [CrossRef]
- Hu, S.G.; Liu, Y.; Liu, Z.; Chen, T.P.; Yu, Q.; Deng, L.J.; Yin, Y.; Hosaka, S. Synaptic long-term potentiation realized in Pavlov’s dog model based on a NiOx-based memristor. J. Appl. Phys. 2014, 116, 214502. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Duan, S.; Huang, T.; Wang, H. Pavlov associative memory in a memristive neural network and its circuit implementation. Neurocomputing 2016, 171, 23–29. [Google Scholar] [CrossRef]
- Tan, Z.H.; Yin, X.B.; Yang, R.; Mi, S.B.; Jia, C.L.; Guo, X. Pavlovian conditioning demonstrated with neuromorphic memristive devices. Sci. Rep. 2017, 7, 713. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, P.I. Conditioned reflexes: An investigation of the physiological activity of the cerebral cortex. Ann. Neurosci. 2010, 17, 136. [Google Scholar] [CrossRef] [PubMed]
- Lorenzi, P.; Rao, R.; Irrera, F.; Suñé, J.; Miranda, E. A thorough investigation of the progressive reset dynamics in HfO2-based resistive switching structures. Appl. Phys. Lett. 2015, 107, 113507. [Google Scholar] [CrossRef]
- Miranda, E.; Hudec, B.; Suñé, J.; Fröhlich, K. Model for the Current–Voltage Characteristic of Resistive Switches Based on Recursive Hysteretic Operators. IEEE Electron Device Lett. 2015, 36, 944–946. [Google Scholar] [CrossRef]
- Patterson, G.A.; Suñé, J.; Miranda, E. Voltage-Driven Hysteresis Model for Resistive Switching: SPICE Modeling and Circuit Applications. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2017, 36, 2044–2051. [Google Scholar] [CrossRef]
- Cisternas Ferri, A.; Rapoport, A.; Fierens, P.I.; Patterson, G.A. Mimicking Spike-Timing-Dependent Plasticity with Emulated Memristors. In Proceedings of the 2019 Argentine Conference on Electronics (CAE), Mar del Plata, Argentina, 14–15 March 2019; pp. 58–64. [Google Scholar] [CrossRef]
- Patterson, G.A.; Suñé, J.; Miranda, E. SPICE simulation of memristive circuits based on memdiodes with sigmoidal threshold functions. Int. J. Circuit Theory Appl. 2018, 46, 39–49. [Google Scholar] [CrossRef]
- Miranda, E. Compact Model for the Major and Minor Hysteretic I–V Loops in Nonlinear Memristive Devices. IEEE Trans. Nanotechnol. 2015, 14, 787–789. [Google Scholar] [CrossRef]
- Patterson, G.A.; Rodriguez-Fernandez, A.; Suñé, J.; Miranda, E.; Cagli, C.; Perniola, L. SPICE simulation of 1T1R structures based on a logistic hysteresis operator. In Proceedings of the 2017 Spanish Conference on Electron Devices (CDE), Barcelona, Spain, 8–10 Feburary 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Pershin, Y.V.; La Fontaine, S.; Di Ventra, M. Memristive model of amoeba learning. Phys. Rev. E 2009, 80, 021926. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Di Ventra, M. Memcomputing: A computing paradigm to store and process information on the same physical platform. In Proceedings of the 2014 International Workshop on Computational Electronics (IWCE), Paris, France, 3–6 June 2014; pp. 1–2. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Castelano, L.K.; Hartmann, F.; Lopez-Richard, V.; Di Ventra, M. A Memristive Pascaline. IEEE Trans. Circuits Syst. II Express Br. 2016, 63, 558–562. [Google Scholar] [CrossRef]
- Jeong, D.S.; Kim, K.M.; Kim, S.; Choi, B.J.; Hwang, C.S. Memristors for Energy-Efficient New Computing Paradigms. Adv. Electron. Mater. 2016, 2, 1600090. [Google Scholar] [CrossRef]
- Schuman, C.D.; Potok, T.E.; Patton, R.M.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A Survey of Neuromorphic Computing and Neural Networks in Hardware. arXiv 2017, arXiv:1705.06963. [Google Scholar]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; John Wiley & Sons Inc.: New York, NY, USA, 1949. [Google Scholar]
- Kulkarni, M.S.; Teuscher, C. Memristor-based reservoir computing. In Proceedings of the 2012 IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), Amsterdam, The Netherlands, 4–6 July 2012; pp. 226–232. [Google Scholar] [CrossRef]
- Ziegler, M.; Soni, R.; Patelczyk, T.; Ignatov, M.; Bartsch, T.; Meuffels, P.; Kohlstedt, H. An Electronic Version of Pavlov’s Dog. Adv. Funct. Mater. 2012, 22, 2744–2749. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, A.; Cagli, C.; Perniola, L.; Suñé, J.; Miranda, E. Effect of the voltage ramp rate on the set and reset voltages of ReRAM devices. Microelectron. Eng. 2017, 178, 61–65. [Google Scholar] [CrossRef]
- Jo, S.H.; Kim, K.H.; Lu, W. Programmable Resistance Switching in Nanoscale Two-Terminal Devices. Nano Lett. 2009, 9, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Gaba, S.; Sheridan, P.; Zhou, J.; Choi, S.; Lu, W. Stochastic memristive devices for computing and neuromorphic applications. Nanoscale 2013, 5, 5872–5878. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Wu, Y.; Wong, H.S.P. Investigating the switching dynamics and multilevel capability of bipolar metal oxide resistive switching memory. Appl. Phys. Lett. 2011, 98, 103514. [Google Scholar] [CrossRef]
- Cao, M.G.; Chen, Y.S.; Sun, J.R.; Shang, D.S.; Liu, L.F.; Kang, J.F.; Shen, B.G. Nonlinear dependence of set time on pulse voltage caused by thermal accelerated breakdown in the Ti/HfO2/Pt resistive switching devices. Appl. Phys. Lett. 2012, 101, 203502. [Google Scholar] [CrossRef]
- Strachan, J.P.; Torrezan, A.C.; Miao, F.; Pickett, M.D.; Yang, J.J.; Yi, W.; Medeiros-Ribeiro, G.; Williams, R.S. State Dynamics and Modeling of Tantalum Oxide Memristors. IEEE Trans. Electron Devices 2013, 60, 2194–2202. [Google Scholar] [CrossRef]
- Atmel. SMART ARM-Based MCU SAM3X/SAM3A Series; Atmel: San Jose, CA, USA, 2015. [Google Scholar]
- Renesas. X9C102, X9C103, X9C104, X9C503. Digitally Controlled Potentiometer (XDCP); Renesas: Tokyo, Japan, 2009. [Google Scholar]
- Fager, T. Arduino Library for Managing Digital Potentiometers X9Cxxx. Available online: https://sites.google.com/site/tfagerscode/home/digipotx9cxxx (accessed on 30 May 2019).

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cisternas Ferri, A.; Rapoport, A.; Fierens, P.I.; Patterson, G.A.; Miranda, E.; Suñé, J. On the Application of a Diffusive Memristor Compact Model to Neuromorphic Circuits. Materials 2019, 12, 2260. https://doi.org/10.3390/ma12142260
Cisternas Ferri A, Rapoport A, Fierens PI, Patterson GA, Miranda E, Suñé J. On the Application of a Diffusive Memristor Compact Model to Neuromorphic Circuits. Materials. 2019; 12(14):2260. https://doi.org/10.3390/ma12142260
Chicago/Turabian StyleCisternas Ferri, Agustín, Alan Rapoport, Pablo I. Fierens, German A. Patterson, Enrique Miranda, and Jordi Suñé. 2019. "On the Application of a Diffusive Memristor Compact Model to Neuromorphic Circuits" Materials 12, no. 14: 2260. https://doi.org/10.3390/ma12142260
APA StyleCisternas Ferri, A., Rapoport, A., Fierens, P. I., Patterson, G. A., Miranda, E., & Suñé, J. (2019). On the Application of a Diffusive Memristor Compact Model to Neuromorphic Circuits. Materials, 12(14), 2260. https://doi.org/10.3390/ma12142260