Thermal and Electronic Transport Properties of the Half-Heusler Phase ScNiSb
Abstract
1. Introduction
2. Materials and Methods
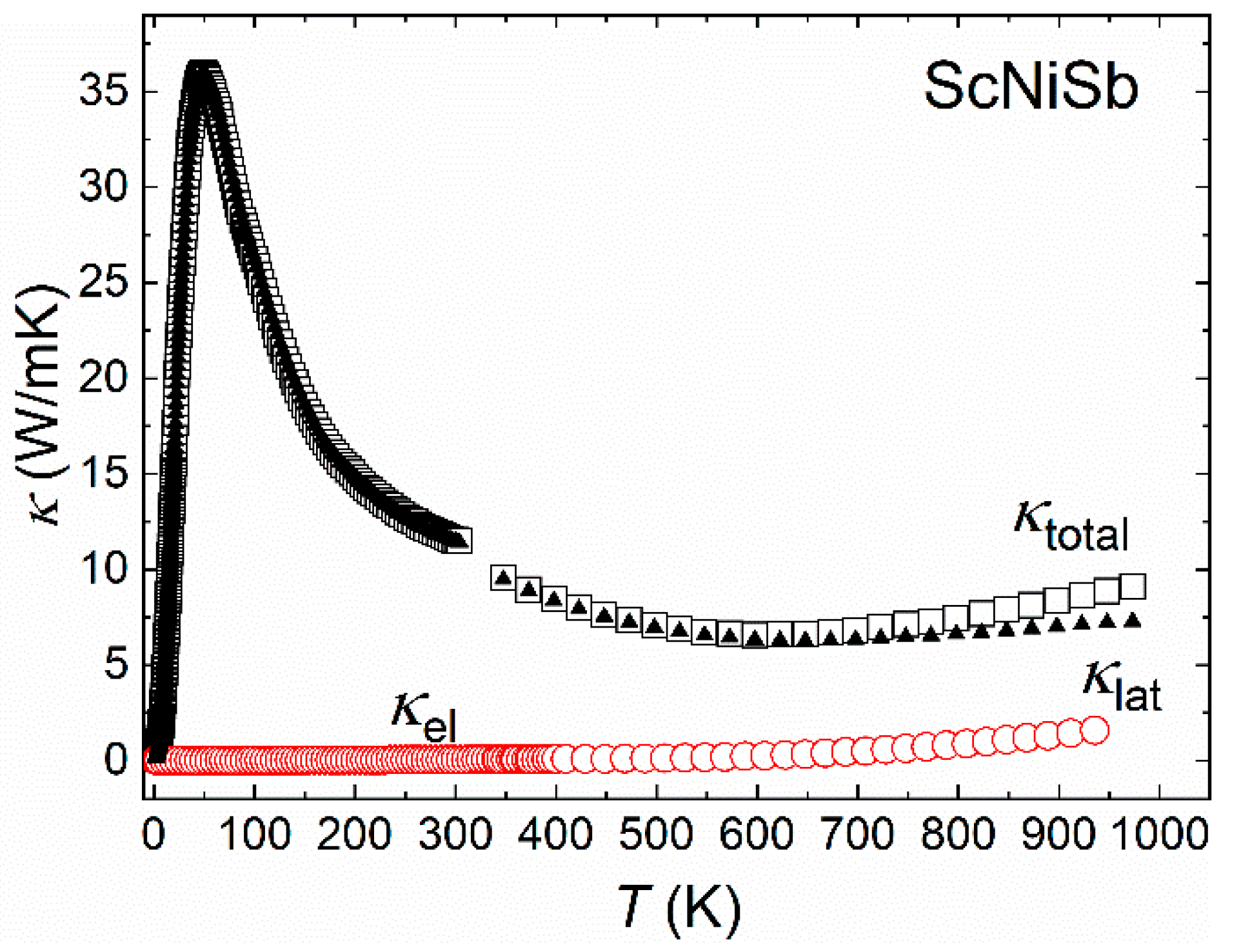
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mastronardi, K.; Young, D.; Wang, C.-C.; Khalifah, P.; Cava, R.J.; Ramirez, A.P. Antimonides with the half-Heusler structure: New thermoelectric materials. Appl. Phys. Lett. 1999, 74, 1415. [Google Scholar] [CrossRef]
- Sportouch, S.; Rocci-Lane, M.A.; Ireland, J.; Brazis, P.; Kannewurf, C.R.; Kanatzidis, M.G. Thermoelectric properties of half-Heusler phases: ErNi1-xCu xSb, YNi 1-xCuxSb and ZrxHfyTizNiSn. In Proceedings of the 18th International Conference on Thermoelectrics (IEEE), Baltimore, MD, USA, 29 August–2 September 1999; pp. 344–347. [Google Scholar]
- Sekimoto, T.; Kurosaki, K.; Muta, H.; Yamanaka, S. Thermoelectric and thermophysical properties of ErPdX (X=Sb and Bi) half-Heusler compounds. J. Appl. Phys. 2006, 99, 103701. [Google Scholar] [CrossRef]
- Gofryk, K.; Kaczorowski, D.; Plackowski, T.; Mucha, J.; Leithe-Jasper, A.; Schnelle, W.; Grin, Y. Magnetic, transport, and thermal properties of the half-Heusler compounds ErPdSb and YPdSb. Phys. Rev. B 2007, 75, 224426. [Google Scholar] [CrossRef]
- Kawano, K.; Kurosaki, K.; Muta, H.; Yamanaka, S. Substitution effect on the thermoelectric properties of p-type half-Heusler compounds: ErNi1−xPdxSb. J. Appl. Phys. 2008, 104, 013714. [Google Scholar] [CrossRef]
- Shutoh, N.; Sakurada, S.; Kondo, N.; Takezawa, N. Thermoelectric material and thermoelectric element. U.S. Patent 8,067,686, 19 November 2011. [Google Scholar]
- Ouardi, S.; Fecher, G.H.; Felser, C.; Hamrle, J.; Postava, K.; Pištora, J. Transport and optical properties of the gapless Heusler compound PtYSb. Appl. Phys. Lett. 2011, 99, 211904. [Google Scholar] [CrossRef]
- Li, G.; Kurosaki, K.; Ohishi, Y.; Muta, H.; Yamanaka, S. High Temperature Thermoelectric Properties of Half-Heusler Compound PtYSb. Jap. J. Appl. Phys. 2013, 52, 041804. [Google Scholar] [CrossRef]
- Ding, G.; Gao, G.Y.; Yao, K.L. Thermoelectric performance of half-Heusler compounds MYSb (M = Ni, Pd, Pt). J. Phys. D Appl. Phys. 2014, 47, 385305. [Google Scholar] [CrossRef]
- Li, S.; Zhao, H.; Li, D.; Jin, S.; Gu, L. Synthesis and thermoelectric properties of half-Heusler alloy YNiBi. J. Appl. Phys. 2015, 117, 205101. [Google Scholar] [CrossRef]
- Xue, Q.Y.; Liu, H.J.; Fan, D.D.; Cheng, L.; Zhao, B.Y.; Shi, J. LaPtSb: a half-Heusler compound with high thermoelectric performance. Phys. Chem. Chem. Phys. 2016, 18, 17912–17916. [Google Scholar] [CrossRef]
- Huang, S.; Liu, X.; Zheng, W.; Guo, J.; Xiong, R.; Wang, Z.; Shi, J. Dramatically improving thermoelectric performance of topological half-Heusler compound LuPtSb via hydrostatic pressure. J. Mater. Chem. A 2018, 6, 20069–20075. [Google Scholar] [CrossRef]
- Xie, W.; Weidenkaff, A.; Tang, X.; Zhang, Q.; Poon, J.; Tritt, T. Recent Advances in Nanostructured Thermoelectric Half-Heusler Compounds. Nanomaterials 2012, 2, 379–412. [Google Scholar] [CrossRef]
- Bos, J.-W.G.; Downie, R.A. Half-Heusler thermoelectrics: a complex class of materials. J. Phys. Condens. Matter 2014, 26, 433201. [Google Scholar] [CrossRef]
- Zhu, T.; Fu, C.; Xie, H.; Liu, Y.; Zhao, X. High Efficiency Half-Heusler Thermoelectric Materials for Energy Harvesting. Adv. Energy Mater. 2015, 5, 1500588. [Google Scholar] [CrossRef]
- Yu, J.; Xia, K.; Zhao, X.; Zhu, T. High performance p-type half-Heusler thermoelectric materials. J. Phys. D Appl. Phys. 2018, 51, 113001. [Google Scholar] [CrossRef]
- Poon, S. Recent Advances in Thermoelectric Performance of Half-Heusler Compounds. Metals 2018, 8, 989. [Google Scholar] [CrossRef]
- Fang, T.; Zhao, X.; Zhu, T. Band Structures and Transport Properties of High-Performance Half-Heusler Thermoelectric Materials by First Principles. Materials 2018, 11, 847. [Google Scholar] [CrossRef]
- Nowak, B.; Pavlosiuk, O.; Kaczorowski, D. Band Inversion in Topologically Nontrivial Half-Heusler Bismuthides: 209 Bi NMR Study. J. Phys. Chem. C 2015, 2770–2774. [Google Scholar] [CrossRef]
- Pavlosiuk, O.; Filar, K.; Wiśniewski, P.; Kaczorowski, D. Magnetic Order and SdH Effect in Half-Heusler Phase ErPdBi. Acta Phys. Pol. A 2015, 127, 656–658. [Google Scholar] [CrossRef]
- Nikitin, A.M.; Pan, Y.; Mao, X.; Jehee, R.; Araizi, G.K.; Huang, Y.K.; Paulsen, C.; Wu, S.C.; Yan, B.H.; de Visser, A. Magnetic and superconducting phase diagram of the half-Heusler topological semimetal HoPdBi. J. Phy. Condens. Matter 2015, 27, 275701. [Google Scholar] [CrossRef]
- Heusler Alloys; Felser, C., Hirohata, A., Eds.; Springer Series in Materials Science; Springer International Publishing: New York, NY, USA, 2016. [Google Scholar]
- Pavlosiuk, O.; Kaczorowski, D.; Wiśniewski, P. Superconductivity and Shubnikov–de Haas oscillations in the noncentrosymmetric half-Heusler compound YPtBi. Phys. Rev. B 2016, 94, 035130. [Google Scholar] [CrossRef]
- Pavlosiuk, O.; Fabreges, X.; Gukasov, A.; Meven, M.; Kaczorowski, D.; Wiśniewski, P. Magnetic structures of RE PdBi half-Heusler bismuthides (RE =Gd, Tb, Dy, Ho, Er). Phys. B Condens. Matter 2017, 536, 56–59. [Google Scholar] [CrossRef]
- Synoradzki, K.; Ciesielski, K.; Kaczorowski, D. Magnetocaloric Effect in Antiferromagnetic Half-Heusler Alloy DyNiSb. Acta Phys. Pol. A 2018, 133, 691–693. [Google Scholar] [CrossRef]
- Pavlosiuk, O.; Kleinert, M.; Wiśniewski, P.; Kaczorowski, D. Antiferromagnetic Order in the Half-Heusler Phase TbPdBi. Acta Phys. Pol. A 2018, 133, 498–500. [Google Scholar] [CrossRef]
- Dwight, A.E. The crystal structure of DyNiSb, DyPtSb and related compounds. In Proceedings of the 11th Rare Earth Research Conference, Traverse City, MI, USA, 7–10 October 1974. [Google Scholar]
- Pecharsky, V.K.; Pankevich, J.V.; Bodak, O.I. Crystal structures of the compounds RNiSb with various rare earth elements. Sov. Phys. Crystallogr. 1983, 28, 97–98. [Google Scholar]
- Harmening, T.; Eckert, H.; Pöttgen, R. Defects in half-Heusler type antimonides ScTSb (T=Ni, Pd, Pt). Solid State Sci. 2009, 11, 900–906. [Google Scholar] [CrossRef]
- Oestreich, J.; Probst, U. Thermoelectric properties of the compounds YMSb and ScMSb (M = Ni, Pd, Pt). In Proceedings of the 21th International Conference on Thermoelectrics (IEEE), Long Beach, CA, USA, 25–29 August 2002; pp. 135–137. [Google Scholar]
- Oestreich, J.; Probst, U.; Richardt, F.; Bucher, E. Thermoelectrical properties of the compounds ScMVIIISb and YMVIIISb (M VIII = Ni, Pd, Pt). J. Phys. Condens. Matter 2003, 15, 635–640. [Google Scholar] [CrossRef]
- Ishida, S.; Masaki, T.; Fujii, S.; Asano, S. Effects on electronic structures of atomic configurations in ternary compounds Ni-M-Z (M = Sc, Ti, Zr, Hf; Z = Sn, Sb). Phys. B Condens. Matter 1997, 237–238, 363–364. [Google Scholar] [CrossRef]
- Bende, D.; Grin, Y.; Wagner, F.R. Covalence and Ionicity in MgAgAs-Type Compounds. Chem. A Eur. J. 2014, 20, 9702–9708. [Google Scholar] [CrossRef] [PubMed]
- Kocak, B.; Ciftci, Y.O. The effect of pressure on structural, electronic, elastic, vibration and optical properties of ScXSb (X=Ni, Pd, Pt) compounds. Comp. Condens. Matter 2018, 14, 176–185. [Google Scholar] [CrossRef]
- Winiarski, M.J.; Bilińska, K.; Ciesielski, K.; Kaczorowski, D. Thermoelectric performance of p -type half-Heusler alloys ScMSb (M = Ni, Pd, Pt) by ab initio calculations. J. Alloys Comp. 2018, 762, 901–905. [Google Scholar] [CrossRef]
- Attema, J.J.; Fang, C.M.; Chioncel, L.; de Wijs, G.A.; Lichtenstein, A.I.; Groot, R.A. de Defects in half-metals and finite temperature. J. Phys. Condens. Matter 2004, 16, S5517–S5524. [Google Scholar] [CrossRef]
- Attema, J.J.; de Wijs, G.A.; de Groot, R.A. Optimizing performance of half-metals at finite temperature. J. Phys. Condens. Matter 2007, 19, 315212. [Google Scholar] [CrossRef][Green Version]
- Synoradzki, K.; Ciesielski, K.; Kępiński, L.; Kaczorowski, D. Thermoelectric properties of (DyNiSn)1−x(DyNiSb)x composite. Phys. B Condens. Matter 2018, 536, 659–663. [Google Scholar] [CrossRef]
- Synoradzki, K.; Ciesielski, K.; Kępiński, L.; Kaczorowski, D. Power factor enhancement in a composite based on the half-Heusler antimonide TmNiSb. J. Appl. Phys. 2018, 123, 235101. [Google Scholar] [CrossRef]
- Synoradzki, K.; Ciesielski, K.; Kępiński, L.; Kaczorowski, D. Effect of secondary LuNiSn phase on thermoelectric properties of half-Heusler alloy LuNiSb. Mater. Today: Proc. 2019, 8, 567–572. [Google Scholar] [CrossRef][Green Version]
- Ciesielski, K.; Synoradzki, K.; Wolańska, I.; Stuglik, P.; Kaczorowski, D. High-temperature thermoelectric properties of half-Heusler phases Er1-xHoxNiSb. Mater. Today: Proc. 2019, 8, 562–566. [Google Scholar] [CrossRef][Green Version]
- Wolańska, I.; Synoradzki, K.; Ciesielski, K.; Załęski, K.; Skokowski, P.; Kaczorowski, D. Enhanced thermoelectric power factor of half-Heusler solid solution Sc1-xTmxNiSb prepared by high-pressure high-temperature sintering method. Mater. Chem. Phys. 2019, 227, 29–35. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Akselrud, L.; Grin, Y. WinCSD : software package for crystallographic calculations (Version 4). J. Appl. Crystallogr. 2014, 47, 803–805. [Google Scholar] [CrossRef]
- Lory, P.-F.; Pailhès, S.; Giordano, V.M.; Euchner, H.; Nguyen, H.D.; Ramlau, R.; Borrmann, H.; Schmidt, M.; Baitinger, M.; Ikeda, M.; et al. Direct measurement of individual phonon lifetimes in the clathrate compound Ba7.81Ge40.67Au5.33. Nature Commun. 2017, 8, 491. [Google Scholar] [CrossRef]
- Yang, J.; Li, H.; Wu, T.; Zhang, W.; Chen, L.; Yang, J. Evaluation of Half-Heusler Compounds as Thermoelectric Materials Based on the Calculated Electrical Transport Properties. Adv. Funct. Mater. 2008, 18, 2880–2888. [Google Scholar] [CrossRef]
- Goldsmid, H.J.; Sharp, J.W. Estimation of the thermal band gap of a semiconductor from seebeck measurements. J. Electron. Mater. 1999, 28, 869–872. [Google Scholar] [CrossRef]
- Gibbs, Z.M.; Kim, H.-S.; Wang, H.; Snyder, G.J. Band gap estimation from temperature dependent Seebeck measurement—Deviations from the 2e|S|maxTmax relation. Appl. Phys. Lett. 2015, 106, 022112. [Google Scholar] [CrossRef]
- Mehdizadeh Dehkordi, A.; Zebarjadi, M.; He, J.; Tritt, T.M. Thermoelectric power factor: Enhancement mechanisms and strategies for higher performance thermoelectric materials. Mater. Sci. Eng. R Rep. 2015, 97, 1–22. [Google Scholar] [CrossRef]
- Jonker, G.H. The Application of Combined Conductivity and Seebeck-Effect Plots for the Analysis of Semiconductor Properties. Philips Res. Rep. 1968, 23, 131–138. [Google Scholar]
- Sekimoto, T.; Kurosaki, K.; Muta, H.; Yamanaka, S. High-temperature Hall measurements of lanthanide based ternary intermetallics. J. Appl. Phys. 2007, 102, 023705. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Kim, H.-S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef]
- Cahill, D.G.; Watson, S.K.; Pohl, R.O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 1992, 46, 6131–6140. [Google Scholar] [CrossRef]
- Hohl, H.; Ramirez, A.P.; Kaefer, W.; Fess, K.; Thurner, C.; Kloc, C.; Bucher, E. A New Class of Materials with Promising Thermoelectric Properties: MNiSn (M = Ti, Zr, Hf). MRS Online Proc. Libr. Arch. 1997, 478, 109. [Google Scholar] [CrossRef]
- Culp, S.R.; Poon, S.J.; Hickman, N.; Tritt, T.M.; Blumm, J. Effect of substitutions on the thermoelectric figure of merit of half-Heusler phases at 800 °C. Appl. Phys. Lett. 2006, 88, 042106. [Google Scholar] [CrossRef]
- Ackerbauer, S.-V.; Senyshyn, A.; Borrmann, H.; Burkhardt, U.; Ormeci, A.; Rosner, H.; Schnelle, W.; Gamża, M.; Gumeniuk, R.; Ramlau, R.; et al. Structural Transformation with “Negative Volume Expansion”: Chemical Bonding and Physical Behavior of TiGePt. Chem. A Eur. J. 2012, 18, 6272–6283. [Google Scholar] [CrossRef] [PubMed]
- Ackerbauer, S.-V.; Borrmann, H.; Bürgi, H.-B.; Flack, H.D.; Grin, Y.; Linden, A.; Palatinus, L.; Schweizer, W.B.; Warshamanage, R.; Wörle, M. TiGePt – a study of Friedel differences. Acta Crystallogr. B 2013, 69, 457–464. [Google Scholar] [CrossRef]
- Grin, Y. Inhomogeneity and anisotropy of chemical bonding and thermoelectric properties of materials. J. Solid State Chem. 2019, 274, 329–336. [Google Scholar] [CrossRef]
- Schierning, G.; Chavez, R.; Schmechel, R.; Balke, B.; Rogl, G.; Rogl, P. Concepts for medium-high to high temperature thermoelectric heat-to-electricity conversion: a review of selected materials and basic considerations of module design. Transl. Mater. Res. 2015, 2, 025001. [Google Scholar] [CrossRef]
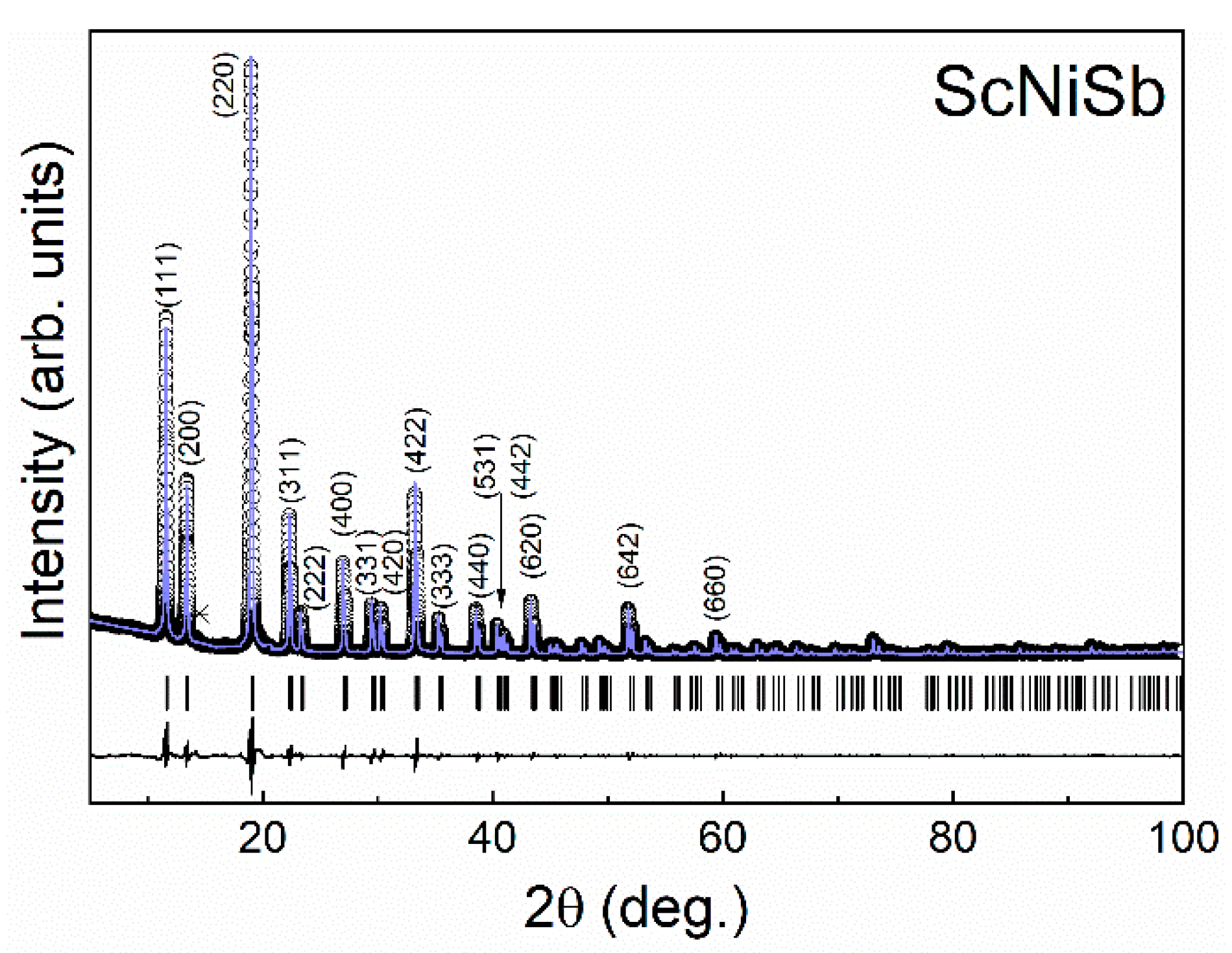

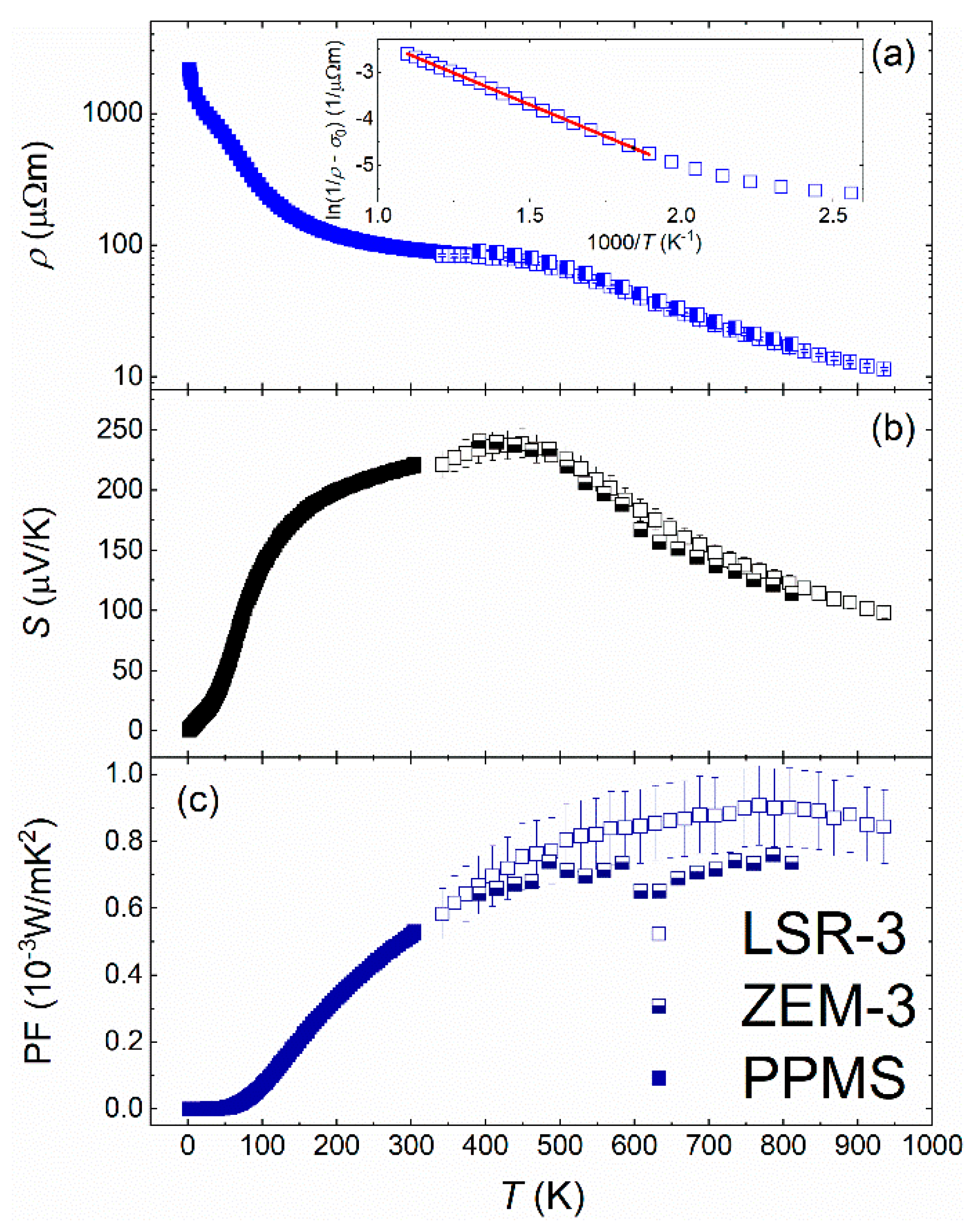
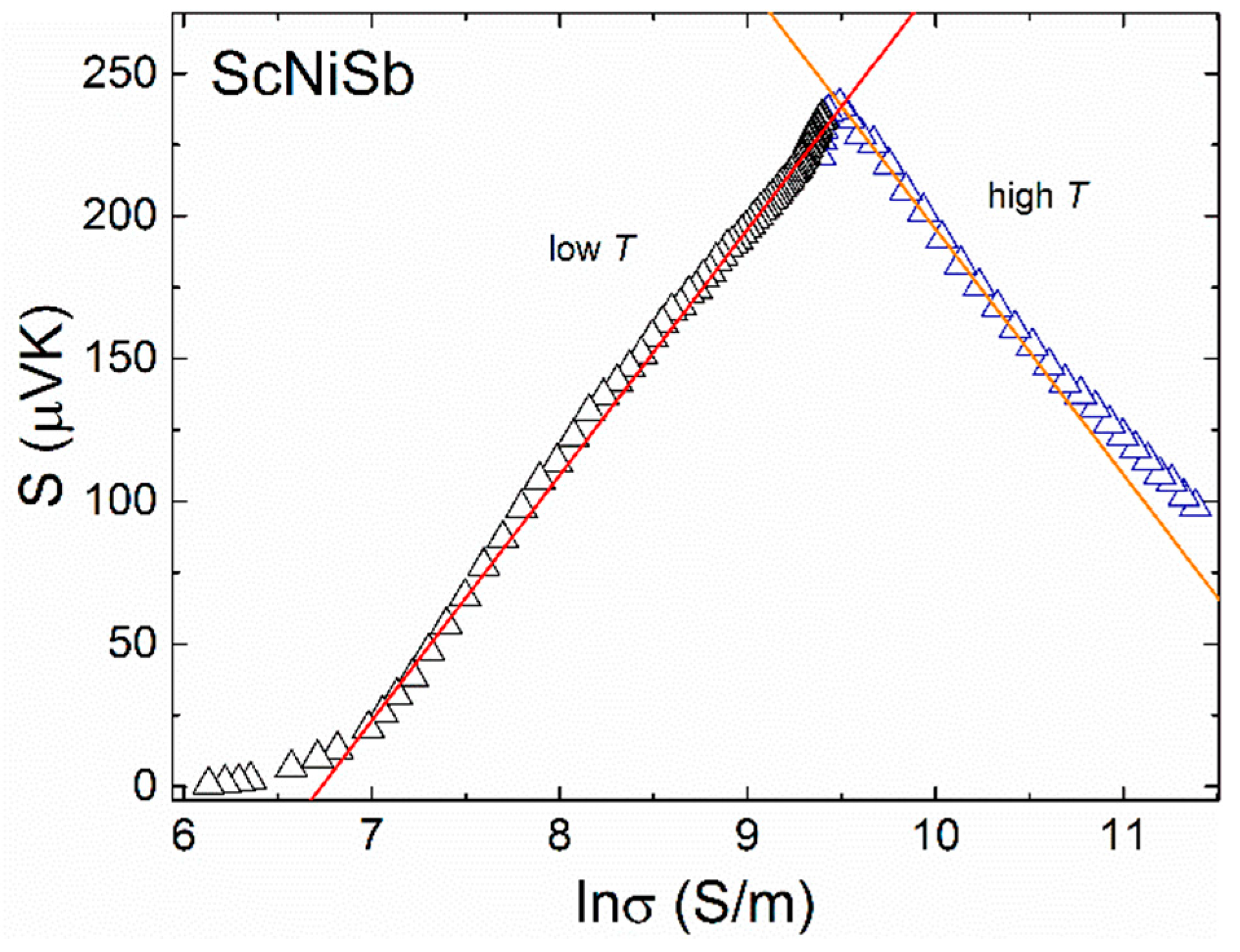
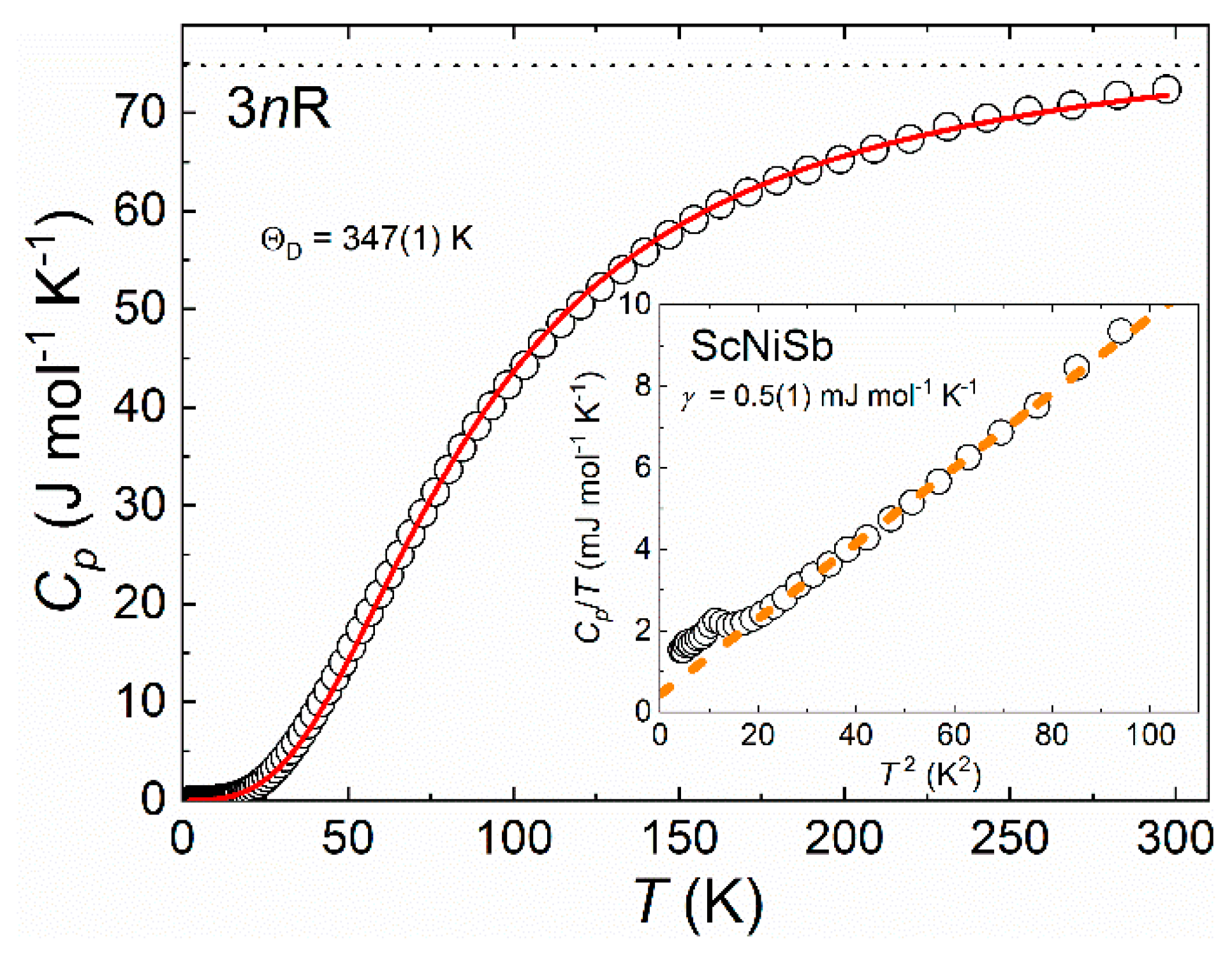

| Nominal Composition | Estimated Composition | a (Å) | V (Å3) | Theoretical Density (g/cm3) | Measured Density (g/cm3) |
|---|---|---|---|---|---|
| 33.3:33.3:33.3 | 33.7(4):32.9(2):33.4(2) | 6.0761(4) | 224.32(5) | 6.674(2) | 6.58(1) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Synoradzki, K.; Ciesielski, K.; Veremchuk, I.; Borrmann, H.; Skokowski, P.; Szymański, D.; Grin, Y.; Kaczorowski, D. Thermal and Electronic Transport Properties of the Half-Heusler Phase ScNiSb. Materials 2019, 12, 1723. https://doi.org/10.3390/ma12101723
Synoradzki K, Ciesielski K, Veremchuk I, Borrmann H, Skokowski P, Szymański D, Grin Y, Kaczorowski D. Thermal and Electronic Transport Properties of the Half-Heusler Phase ScNiSb. Materials. 2019; 12(10):1723. https://doi.org/10.3390/ma12101723
Chicago/Turabian StyleSynoradzki, Karol, Kamil Ciesielski, Igor Veremchuk, Horst Borrmann, Przemysław Skokowski, Damian Szymański, Yuri Grin, and Dariusz Kaczorowski. 2019. "Thermal and Electronic Transport Properties of the Half-Heusler Phase ScNiSb" Materials 12, no. 10: 1723. https://doi.org/10.3390/ma12101723
APA StyleSynoradzki, K., Ciesielski, K., Veremchuk, I., Borrmann, H., Skokowski, P., Szymański, D., Grin, Y., & Kaczorowski, D. (2019). Thermal and Electronic Transport Properties of the Half-Heusler Phase ScNiSb. Materials, 12(10), 1723. https://doi.org/10.3390/ma12101723





