A Novel Multiscale Mathematical Model for Building Bone Substitute Materials for Children
Abstract
1. Introduction
2. Model and Results
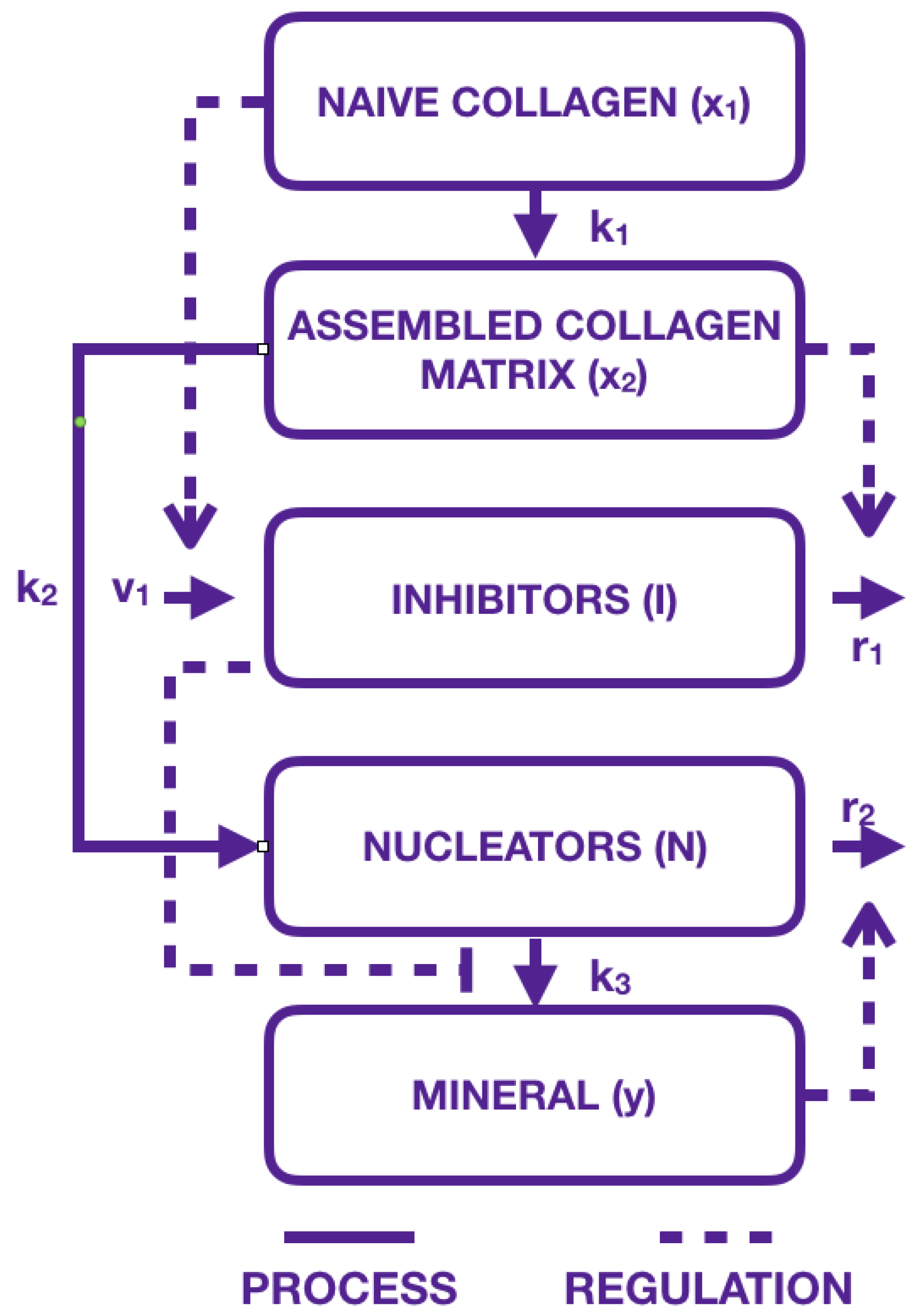
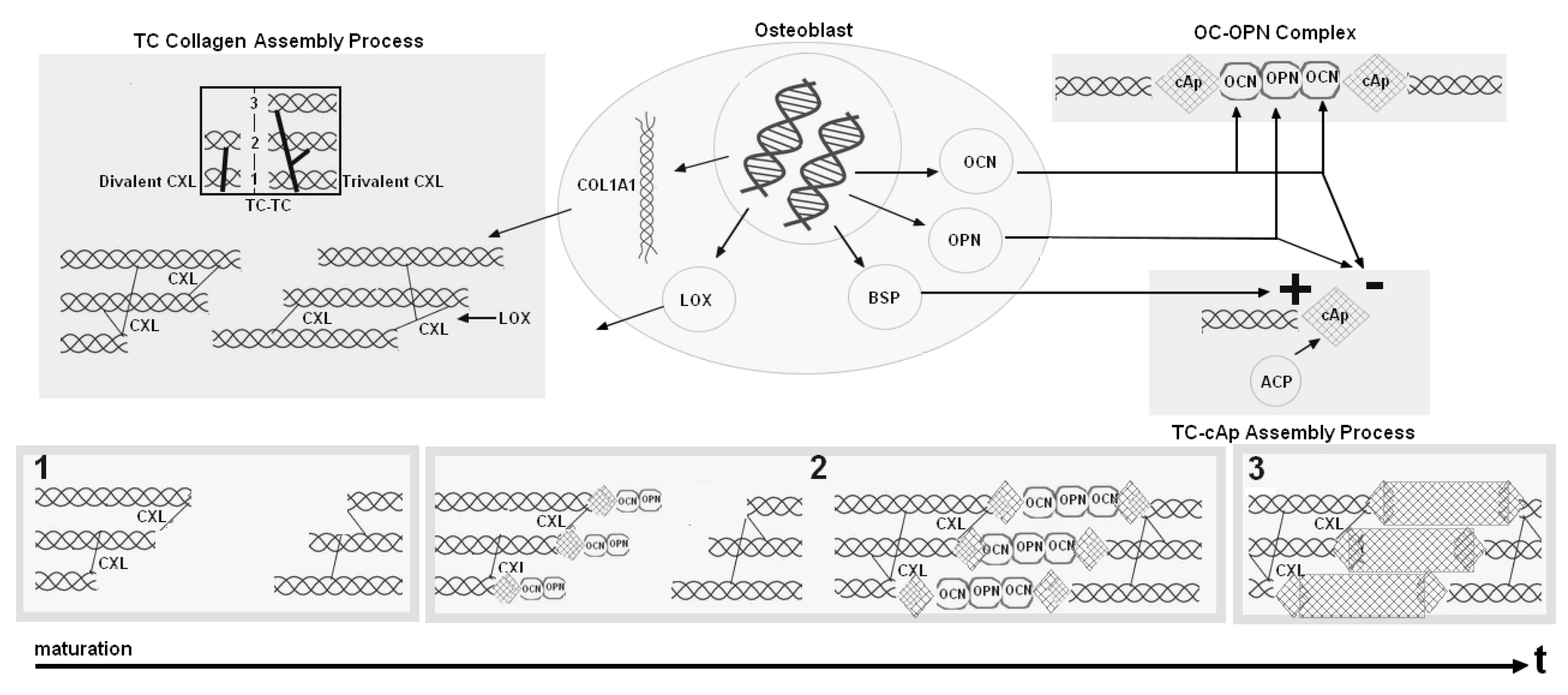
2.1. Modeling the Biological Components: An Inspirational Model
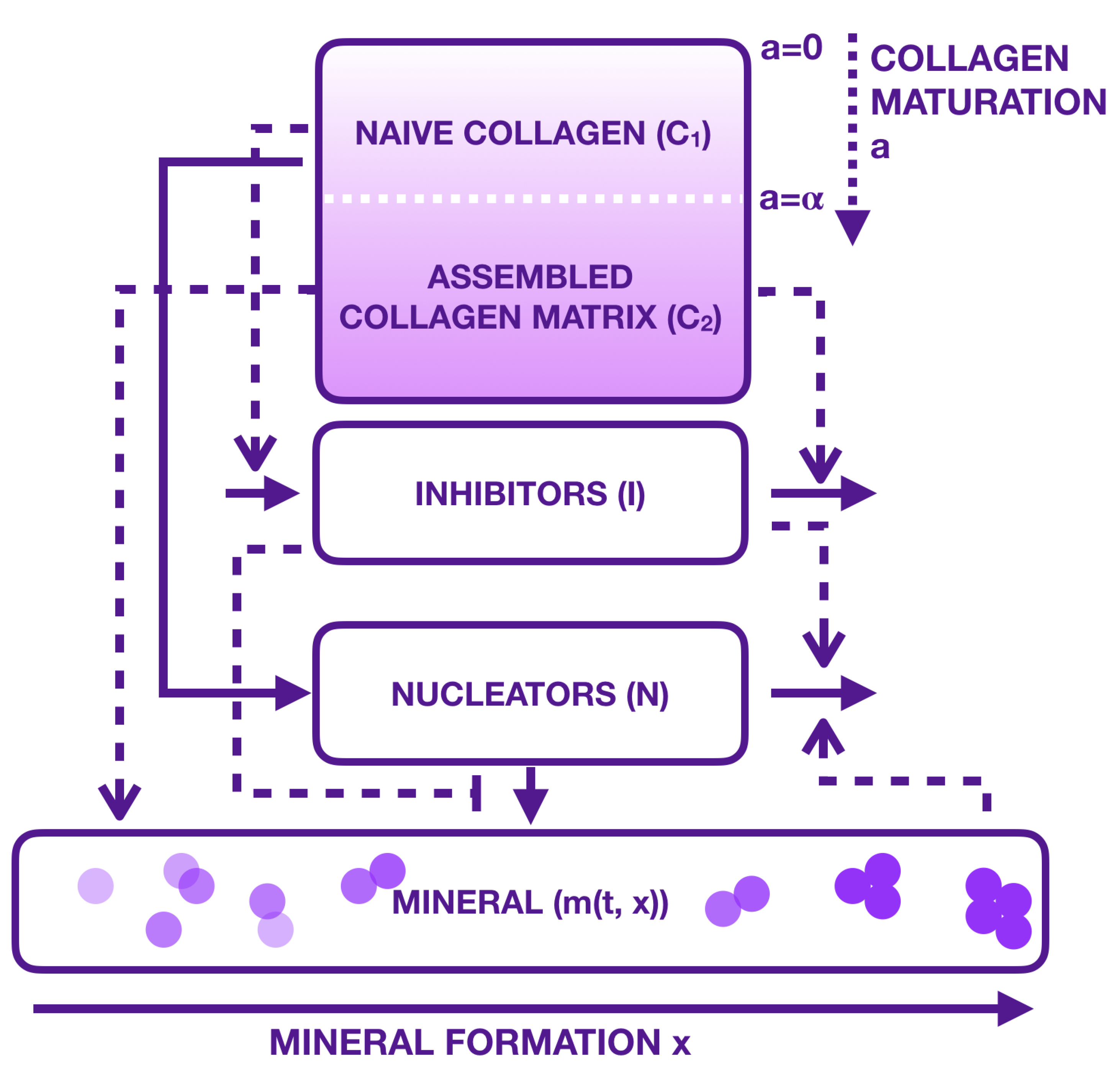
2.2. Our Mathematical Model
- -
- collagen compartments and have been replaced by a single compartment where immature collagen crosslinks progressively moves toward the assembled collagen matrix;
- -
- mineral formation is created from precipitated crystal growing in function of collagen and aggregating in function of inhibitors and nucleators.
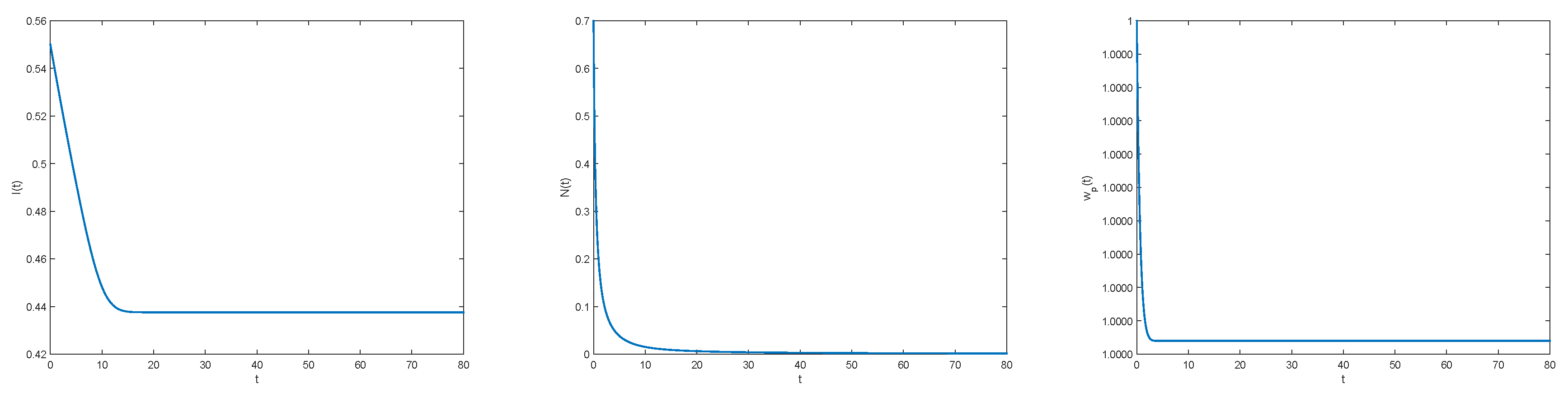
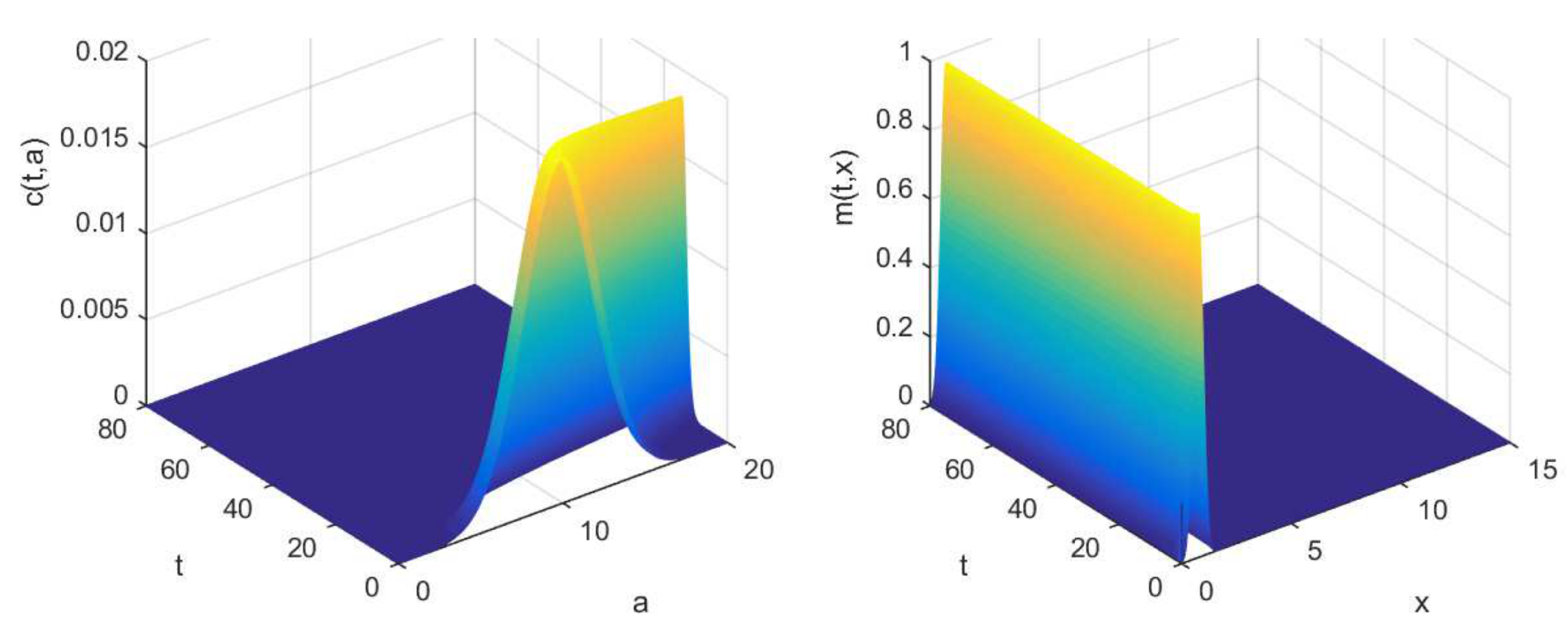
2.3. Results
2.4. Multiscale Modelling
3. Materials and Methods
3.1. An Associated System of Ordinary Differential Equation
3.2. Numerical Illustrations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, Z.; Najeeb, S.; Khurshid, Z.; Verma, V.; Rashid, H.; Glogauer, M. Biodegradable Materials for Bone Repair and Tissue Engineering Applications. Materials 2015, 8, 5744–5794. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.R.; Passi, D.; Singh, P.; Bhuibhar, A. Ceramic and non-ceramic hydroxyapatite as a bone graft material: A brief review. Ir. J. Med. Sci. 2015, 184, 101–106. [Google Scholar] [CrossRef] [PubMed]
- Fitoussi, F.; Ilharreborde, B. Is the induced-membrane technique successful for limb reconstruction after resecting large bone tumors in children? Clin. Orthop. Relat. Res. 2015, 473, 2067–2075. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Pan, Z.; Yan, S.; Zhao, X. Single-cortex is better than double-cortex in fibula grafts for large tibia bone defect in a 2-year-old child: A case report of a successful surgery and discussion of bone graft choices. Medicine 2017, 96, e5965. [Google Scholar] [CrossRef] [PubMed]
- Leet, A.I.; Boyce, A.M.; Ibrahim, K.A.; Wientroub, S.; Kushner, H.; Collins, M.T. Bone-Grafting in Polyostotic Fibrous Dysplasia. J. Bone Joint Surg. Am. Vol. 2016, 98, 211–219. [Google Scholar] [CrossRef] [PubMed]
- Zioupos, P.; Currey, J. Changes in the Stiffness, Strength, and Toughness of Human Cortical Bone With Age. Bone 1998, 22, 57–66. [Google Scholar] [CrossRef]
- Zimmermann, E.A.; Ritchie, R.O. Bone as a Structural Material. Adv. Healthc. Mater. 2015, 4, 1287–1304. [Google Scholar] [CrossRef] [PubMed]
- Boskey, A.L.; Imbert, L. Bone quality changes associated with aging and disease: A review. Ann. N. Y. Acad. Sci. 2017, 1410, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Garnero, P. The Role of Collagen Organization on the Properties of Bone. Calcif. Tissue Int. 2015, 97, 241. [Google Scholar] [CrossRef] [PubMed]
- Fyhrie, D.P.; Christiansen, B.A. Bone Material Properties and Skeletal Fragility. Calcif. Tissue Int. 2015, 97, 213–228. [Google Scholar] [CrossRef] [PubMed]
- Burr, D. The contribution of the organic matrix to bone’s material properties. Bone 2002, 31, 8–11. [Google Scholar] [CrossRef]
- Unal, M.; Creecy, A.; Nyman, J.S. The Role of Matrix Composition in the Mechanical Behavior of Bone. Curr. Osteoporos. Rep. 2018, 16, 205–215. [Google Scholar] [CrossRef] [PubMed]
- Saito, M.; Marumo, K. Effects of Collagen Crosslinking on Bone Material Properties in Health and Disease. Calcif. Tissue Int. 2015, 97, 242–261. [Google Scholar] [CrossRef] [PubMed]
- Eyre, D.R.; Koob, T.J.; Ness, K.P.V. Quantitation of hydroxypyridinium crosslinks in collagen by high-performance liquid chromatography. Anal. Biochem. 1984, 137, 380–388. [Google Scholar] [CrossRef]
- Gineyts, E.; Borel, O.; Chapurlat, R.; Garnero, P. Quantification of immature and mature collagen crosslinks by liquid chromatography-electrospray ionization mass spectrometry in connective tissues. J. Chromatogr. B 2010, 878, 1449–1454. [Google Scholar] [CrossRef] [PubMed]
- Berteau, J.; Gineyts, E.; Pithioux, M.; Baron, C.; Boivin, G.; Lasaygues, P.; Chabrand, P.; Follet, H. Ratio between mature and immature enzymatic cross-links correlates with post-yield cortical bone behavior: An insight into greenstick fractures of the child fibula. Bone 2015, 79, 190–195. [Google Scholar] [CrossRef] [PubMed]
- Roach, H. Why does bone matrix contain non-collagenous proteins? The possible roles of osteocalcin, osteonectin, osteopontin and bone sialoprotein in bone mineralisation and resorption. Cell Biol. Int. 1994, 18, 617–628. [Google Scholar] [CrossRef] [PubMed]
- Gamsjaeger, S.; Hofstetter, B.; Fratzl-Zelman, N.; Roschger, P.; Roschger, A.; Fratzl, P.; Brozek, W.; Masic, A.; Misof, B.; Glorieux, F.; et al. Pediatric reference Raman data for material characteristics of iliac trabecular bone. Bone 2014, 69, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Lefèvre, E.; Lasaygues, P.; Baron, C.; Payan, C.; Launay, F.; Follet, H.; Pithioux, M. Analyzing the anisotropic Hookeś law for childrenś cortical bone. J. Mech. Behav. Biomed. Mater. 2015, 49, 370–377. [Google Scholar] [CrossRef] [PubMed]
- Berteau, J.P.; Baron, C.; Pithioux, M.; Launay, F.; Chabrand, P.; Lasaygues, P. In vitro ultrasonic and mechanic characterization of the modulus of elasticity of children cortical bone. Ultrasonics 2014, 54, 1270–1276. [Google Scholar] [CrossRef] [PubMed]
- Irwin, A.; Mertz, H. Biomechanical Bases for the CRABI and Hybrid III Child Dummies. Proc. Stapp Car Crash Conf. 1997, 41, 1–12. [Google Scholar]
- Roth, S.; Raul, J.; Willinger, R. Limitation of scaling methods in child head finite elements modelling. Int. J. Veh. Saf. 2007, 2, 404–421. [Google Scholar] [CrossRef]
- Bala, Y.; Depalle, B.; Douillard, T.; Meille, S.; Clément, P.; Follet, H.; Chevalier, J.; Boivin, G. Respective roles of organic and mineral components of human cortical bone matrix in micromechanical behavior: An instrumented indentation study. J. Mech. Behav. Biomed. Mater. 2011, 4, 1473–1482. [Google Scholar] [CrossRef] [PubMed]
- Komarova, S.; Safranek, L.; Gopalakrishnan, J.; Ou, M.Y.; McKee, M.; Murshed, M.; Rauch, F.; Zuhr, E. Mathematical model for bone mineralization. Front. Cell Devel. Biol. 2015, 3, 51. [Google Scholar] [CrossRef] [PubMed]
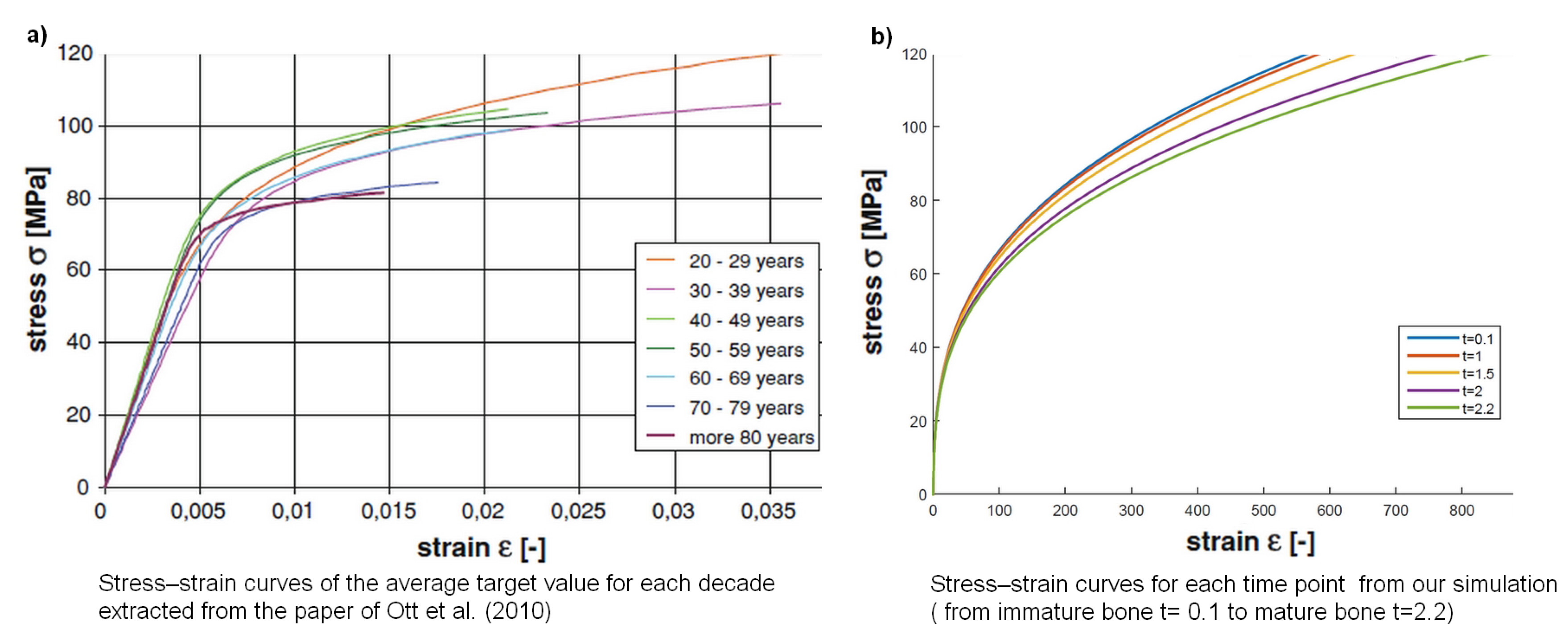
- Ott, I.; Kienzler, R.; Schröder, R. Aging in the cortical bone: A constitutive law and its application. Arch. Appl. Mech. 2010, 80, 527–541. [Google Scholar] [CrossRef]
- Depalle, B.; Duarte, A.G.; Fiedler, I.A.; Pujo-Menjouet, L.; Buehler, M.J.; Berteau, J.P. The different distribution of enzymatic collagen cross-links found in adult and children bone result in different mechanical behavior of collagen. Bone 2018, 110, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Uzel, S.G.; Buehler, M.J. Molecular structure, mechanical behavior and failure mechanism of the C-terminal cross-link domain in type I collagen. J. Mech. Behav. Biomed. Mater. 2011, 4, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Demers, J.-L.H.; Esmonde-White, F.W.; Esmonde-White, K.A.; Morris, M.D.; Pogue, B.W. ext-generation Raman tomography instrument for non-invasive in vivobone imaging. Biomed. Opt. Express. 2015, 6, 793–806. [Google Scholar] [CrossRef] [PubMed]
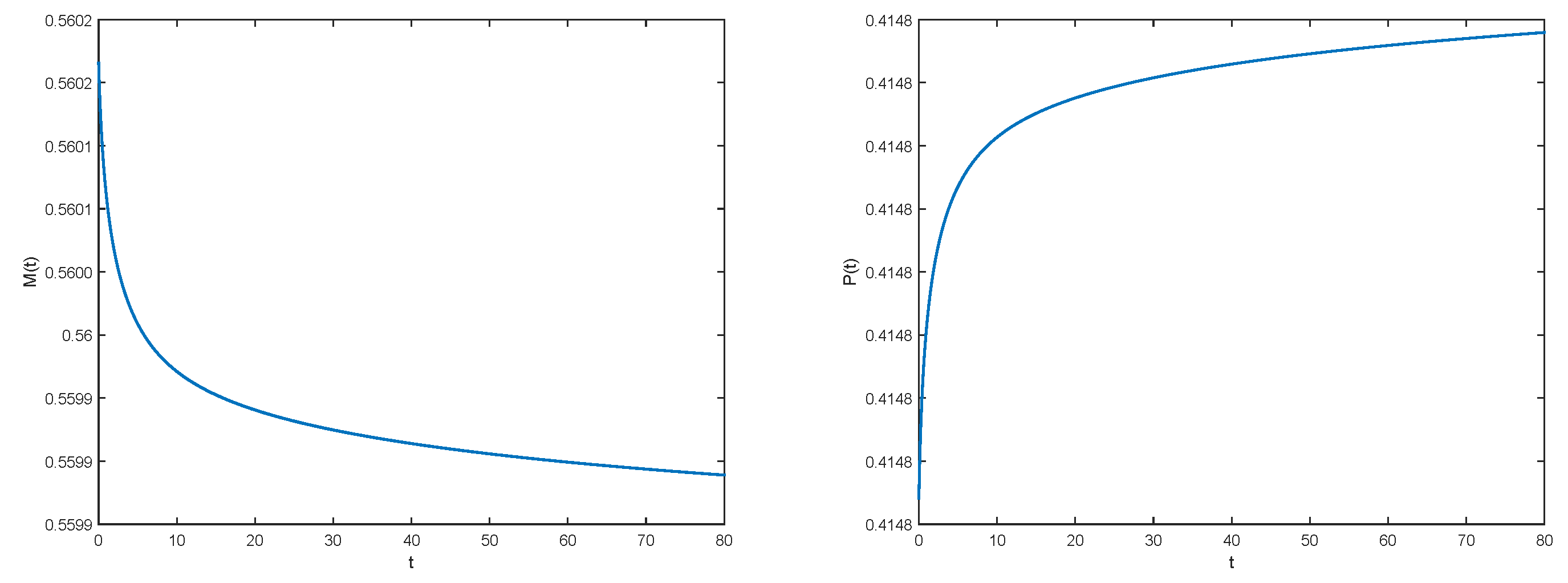
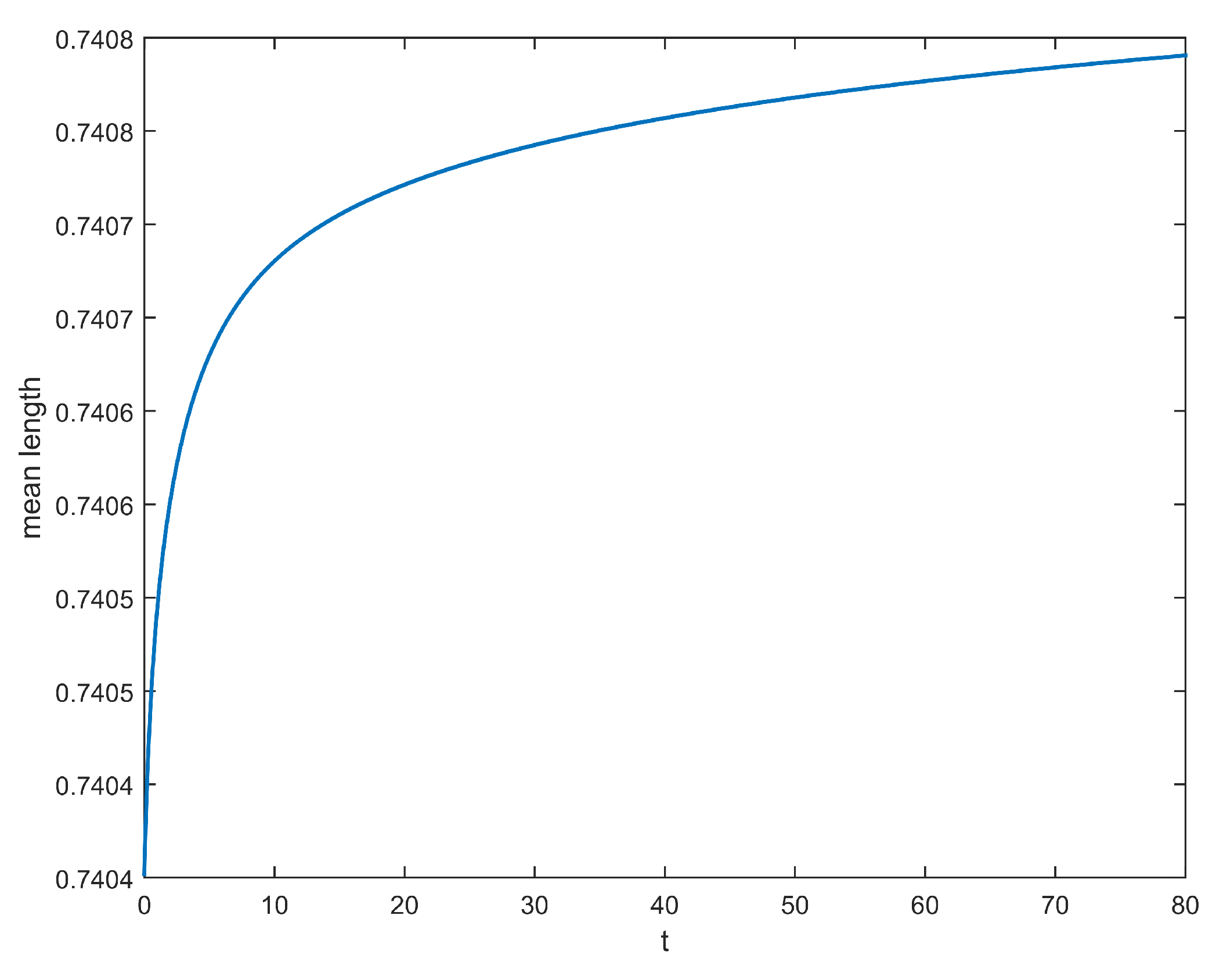
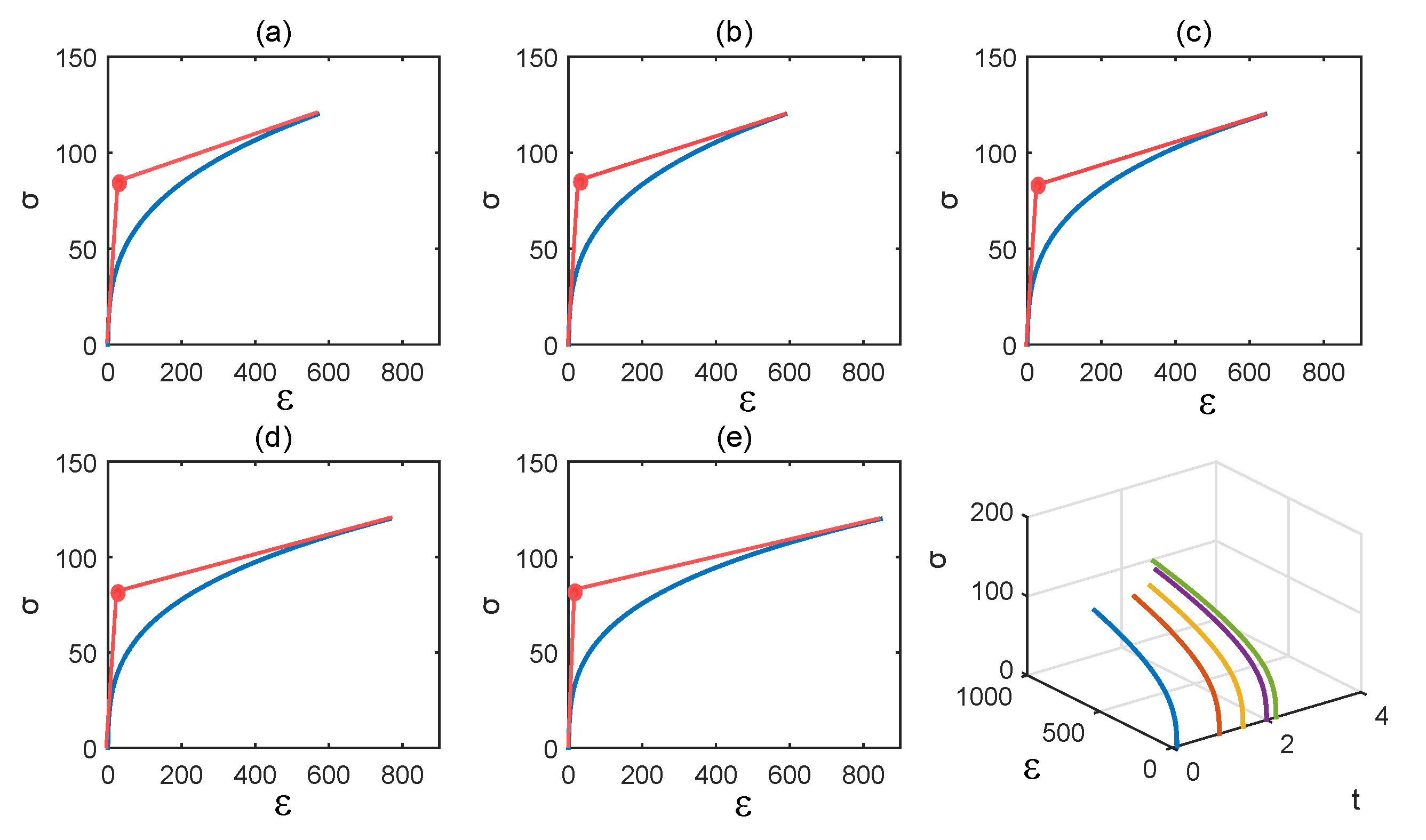
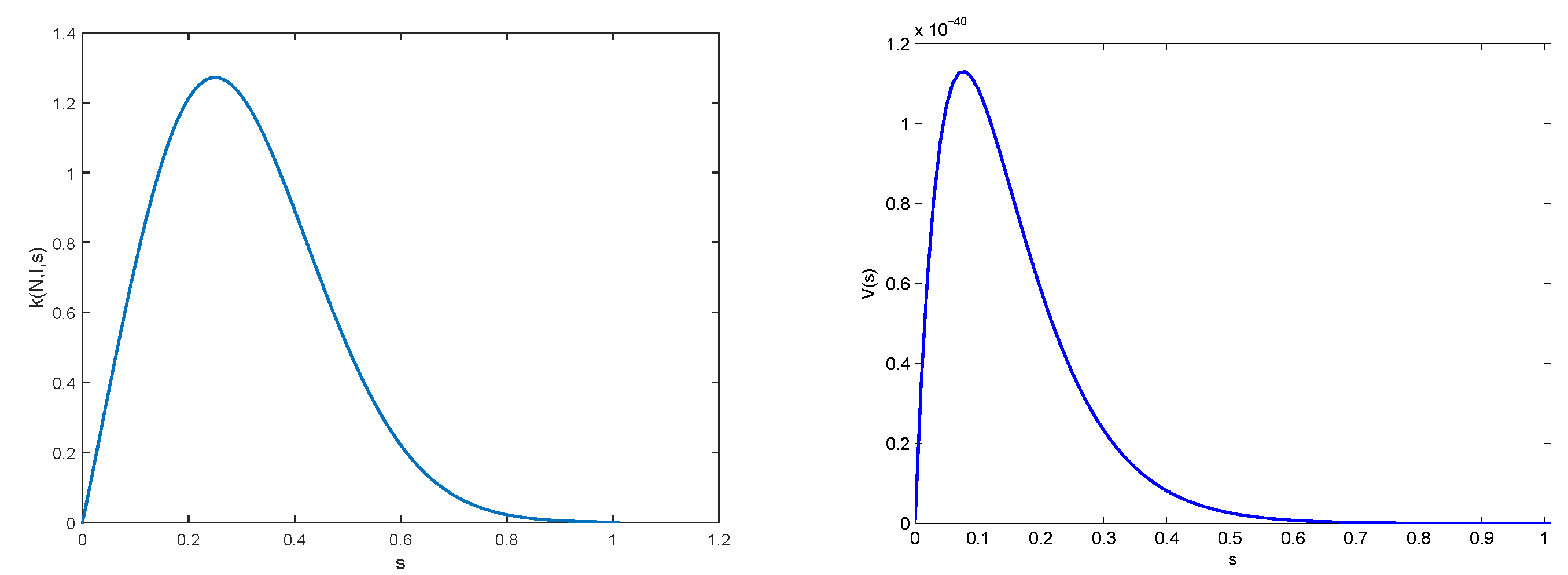
| t | Elastic Energy + Plastic Energy | ||||
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chekroun, A.; Pujo-Menjouet, L.; Berteau, J.-P. A Novel Multiscale Mathematical Model for Building Bone Substitute Materials for Children. Materials 2018, 11, 1045. https://doi.org/10.3390/ma11061045
Chekroun A, Pujo-Menjouet L, Berteau J-P. A Novel Multiscale Mathematical Model for Building Bone Substitute Materials for Children. Materials. 2018; 11(6):1045. https://doi.org/10.3390/ma11061045
Chicago/Turabian StyleChekroun, Abdennasser, Laurent Pujo-Menjouet, and Jean-Philippe Berteau. 2018. "A Novel Multiscale Mathematical Model for Building Bone Substitute Materials for Children" Materials 11, no. 6: 1045. https://doi.org/10.3390/ma11061045
APA StyleChekroun, A., Pujo-Menjouet, L., & Berteau, J.-P. (2018). A Novel Multiscale Mathematical Model for Building Bone Substitute Materials for Children. Materials, 11(6), 1045. https://doi.org/10.3390/ma11061045







