Quadratic Solid–Shell Finite Elements for Geometrically Nonlinear Analysis of Functionally Graded Material Plates
Abstract
1. Introduction
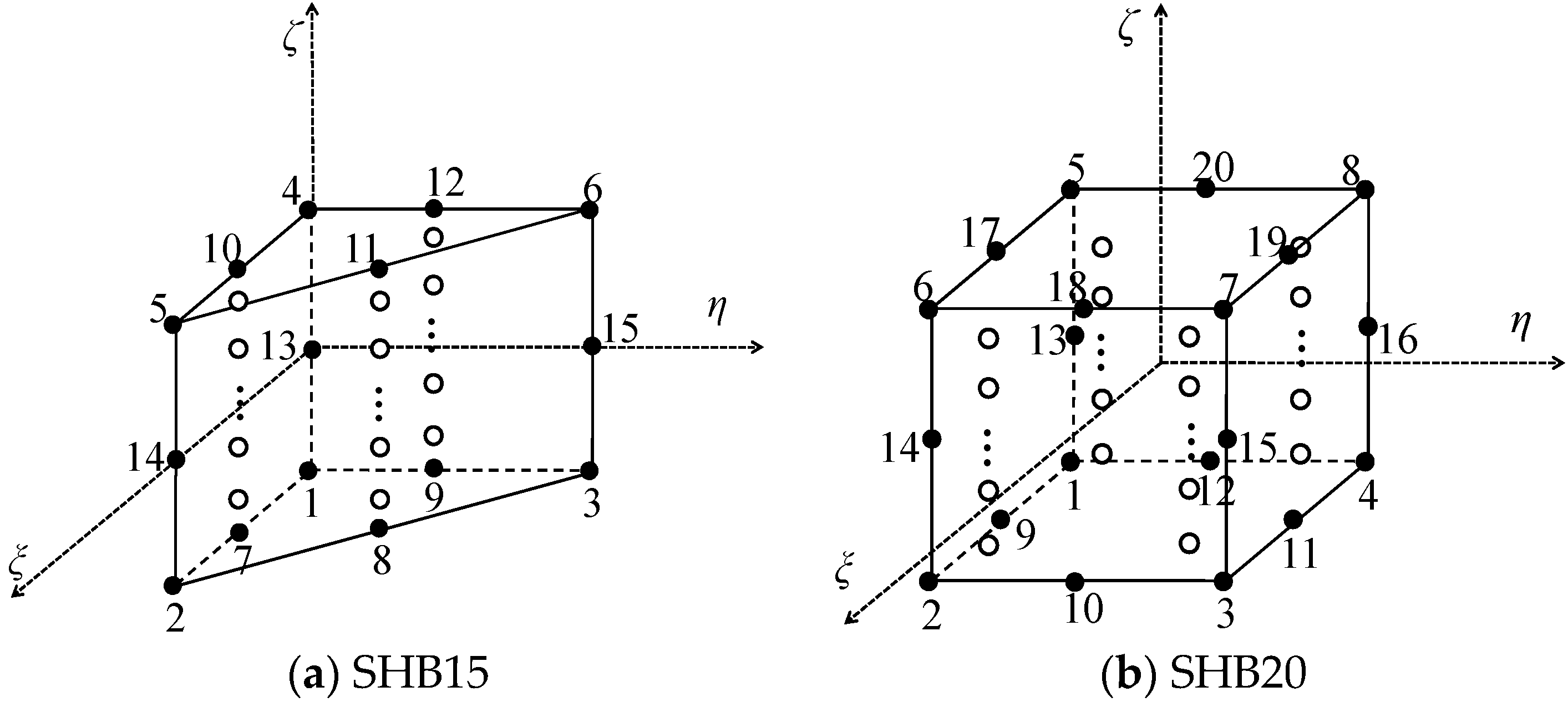
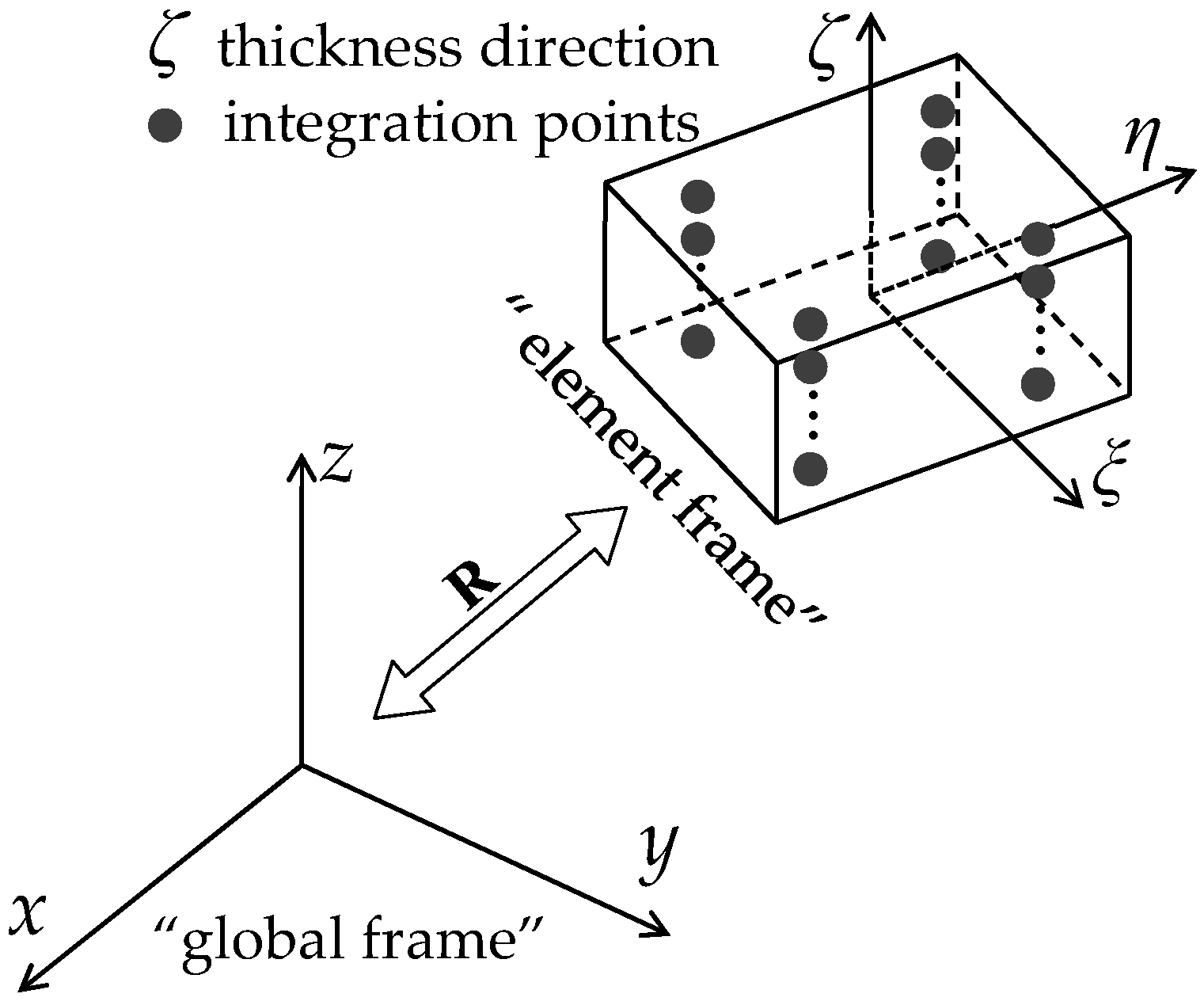
2. SHB15 and SHB20 Solid‒Shell Elements
2.1. Element Reference Geometries
2.2. Quadratic Approximation for the SHB Elements
2.3. Strain Field and Gradient Operator
2.4. Hu–Washizu Variational Principle
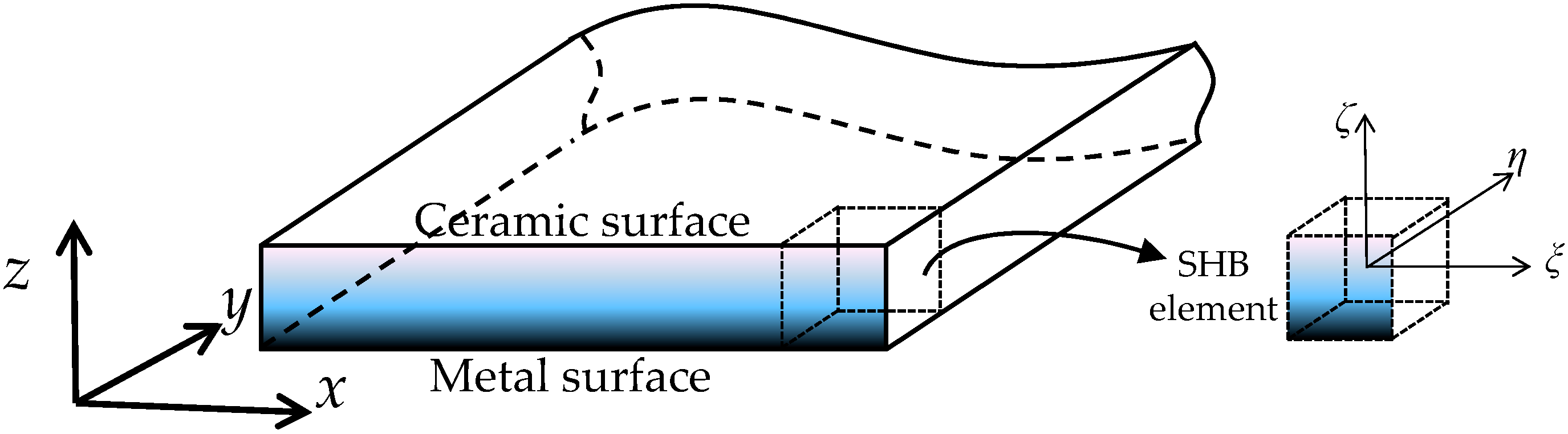
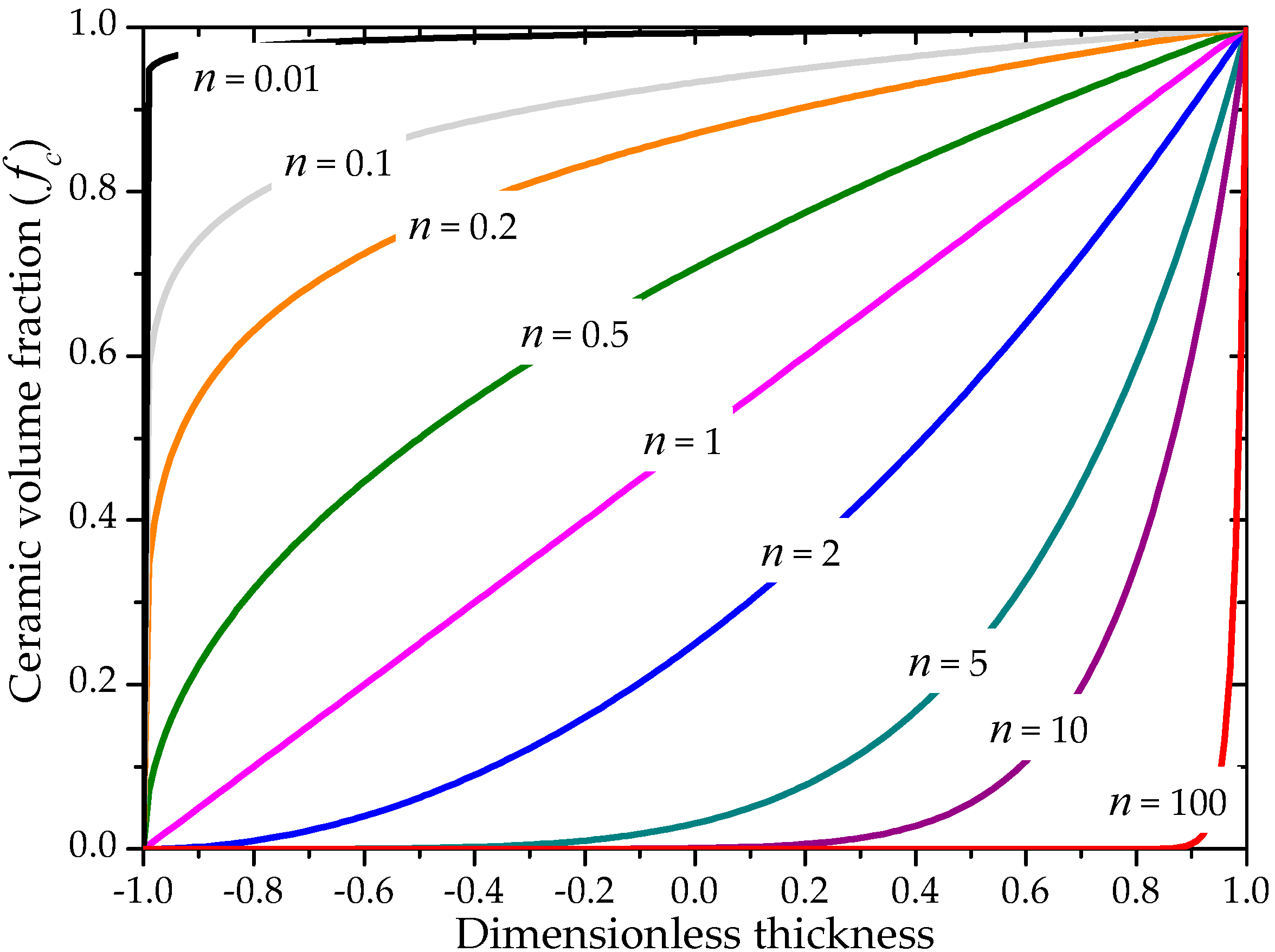
2.5. Description of Functionally Graded Elastic Behavior
3. Nonlinear Benchmark Problems
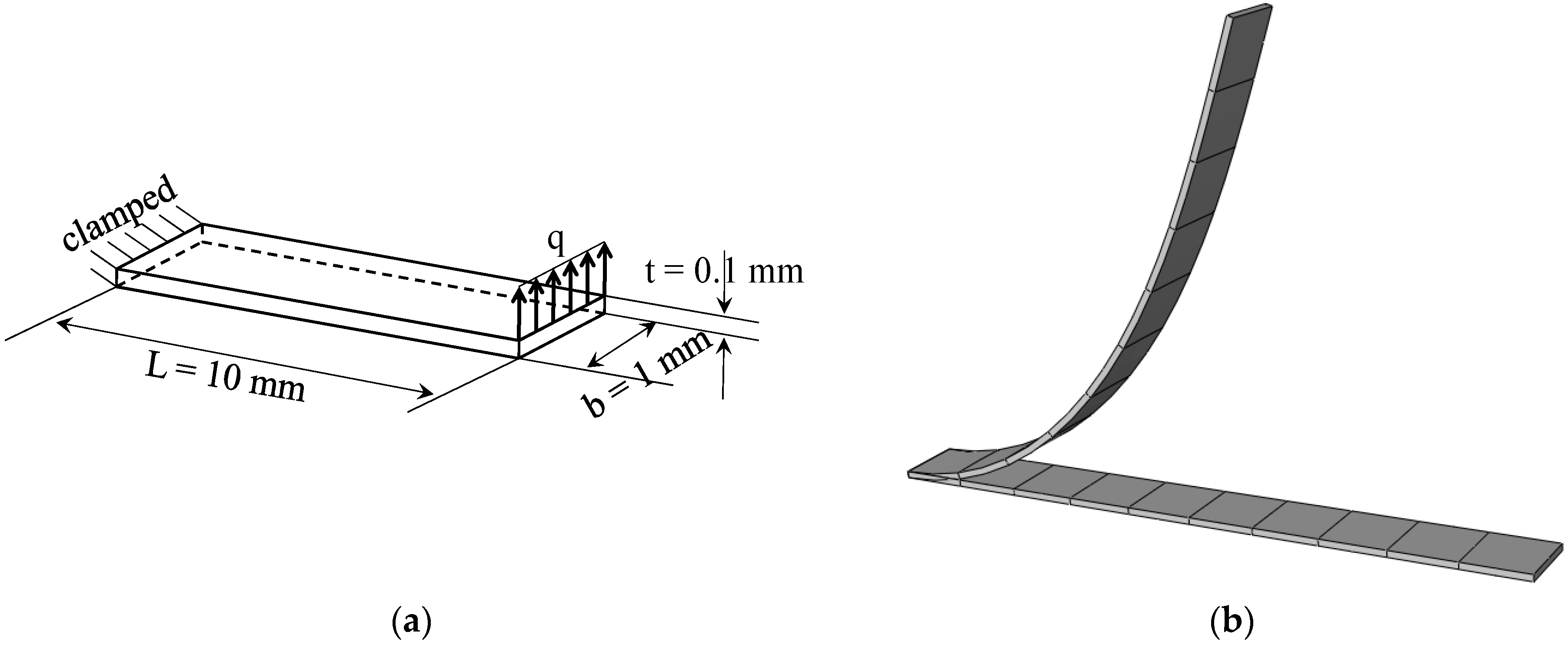
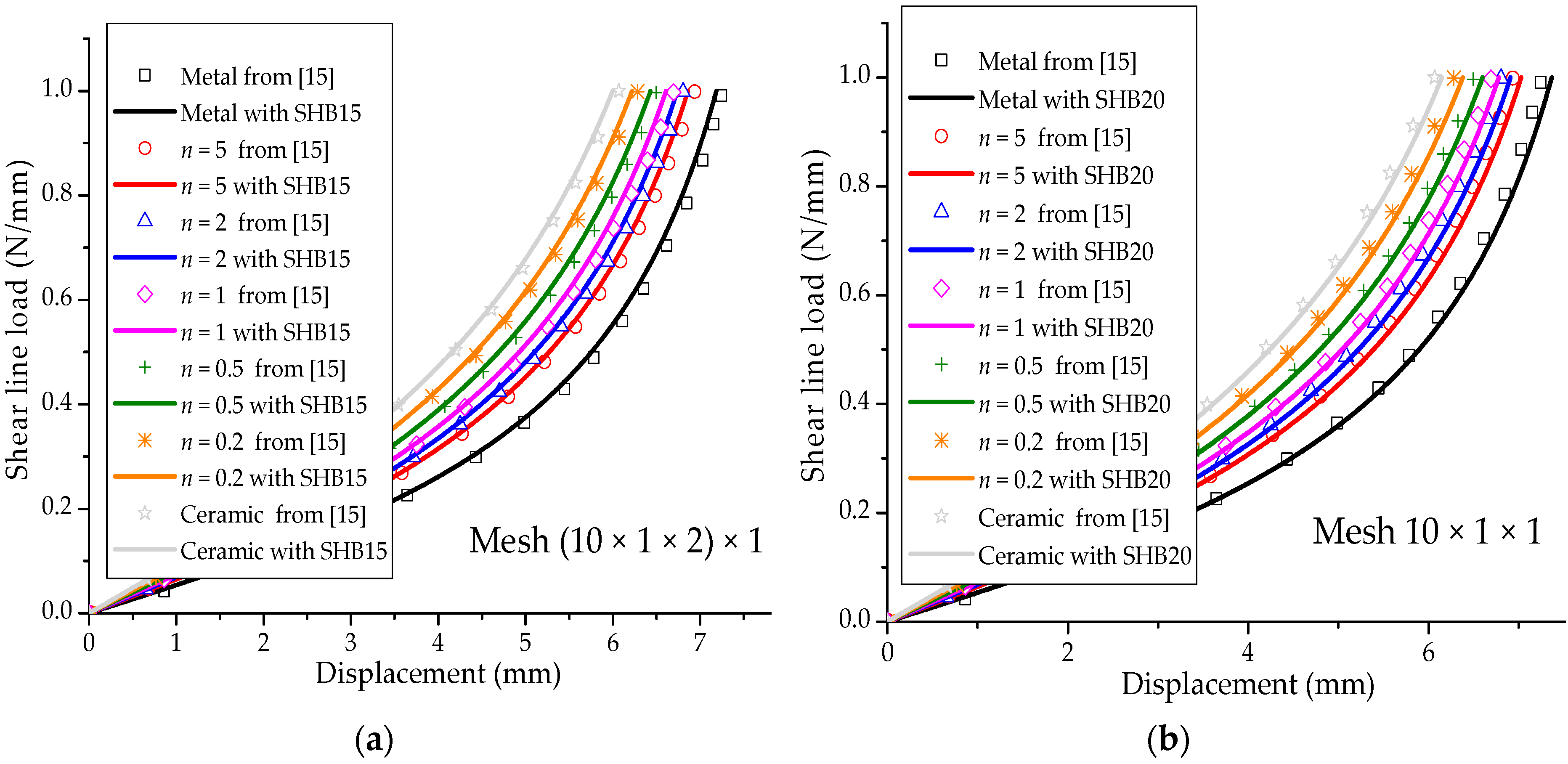
3.1. Cantilever Beam Sujected to End Shear Force
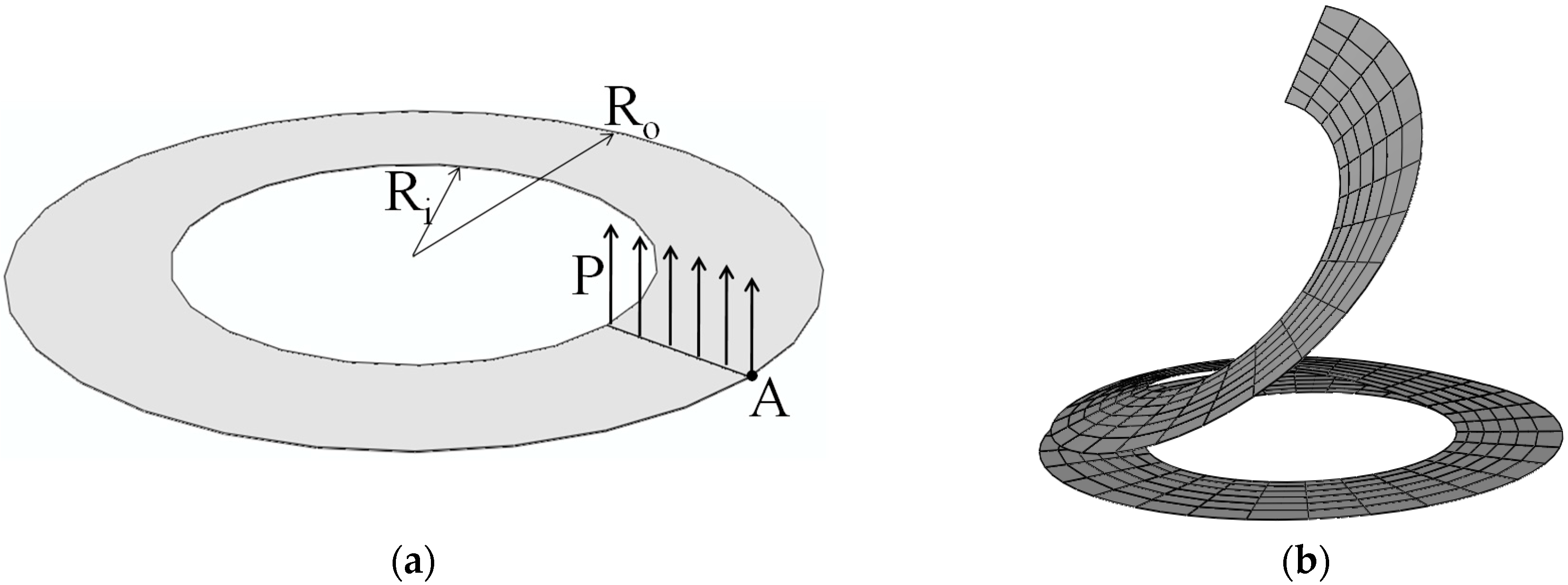
3.2. Slit Annular Plate
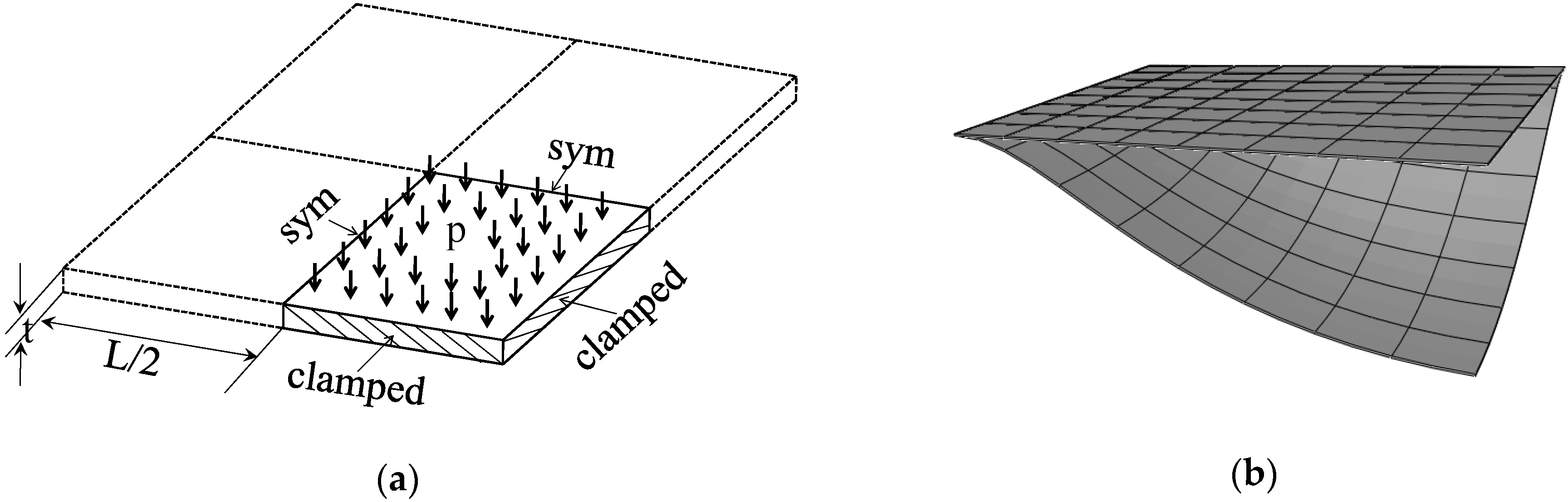
3.3. Clamped Square Plate under Pressure
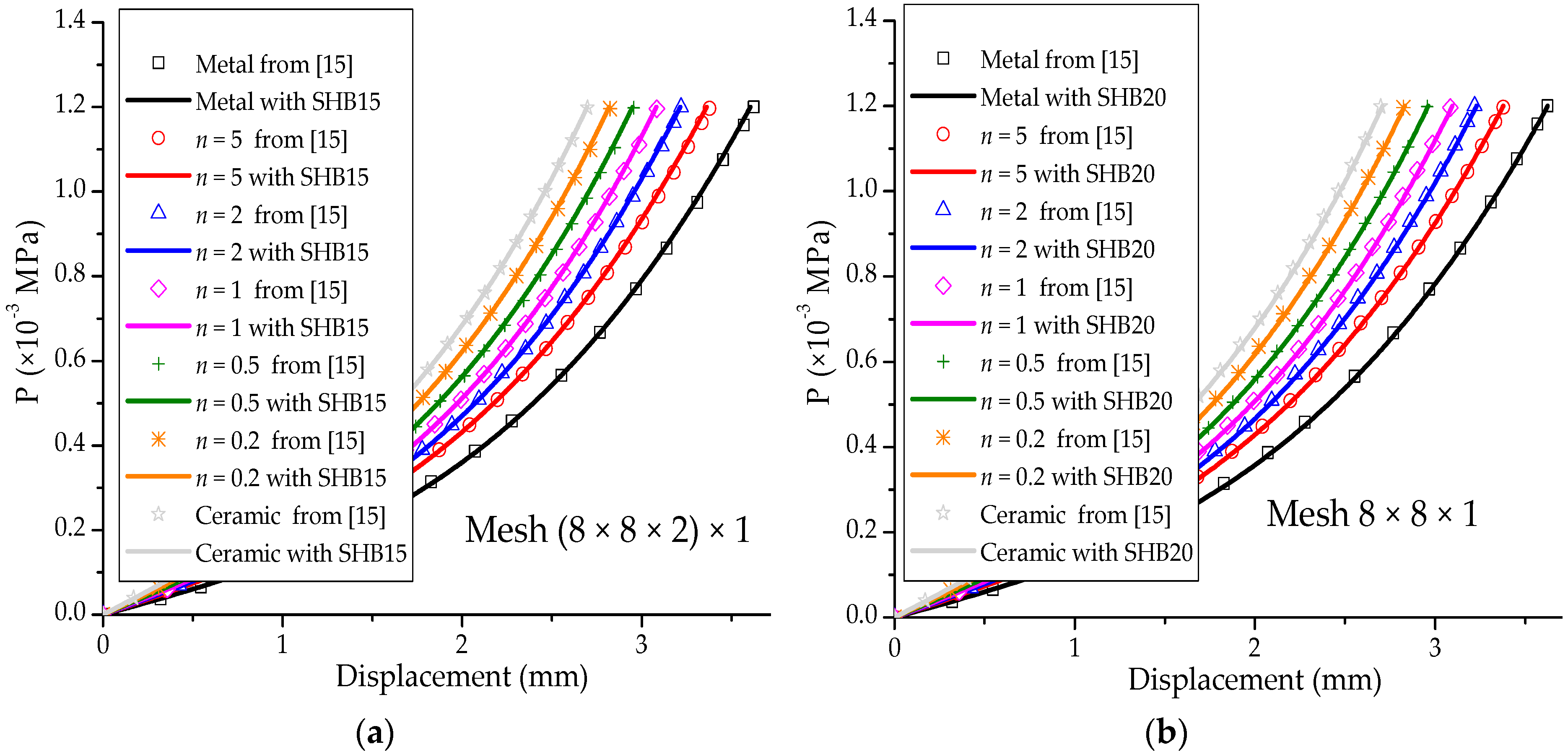
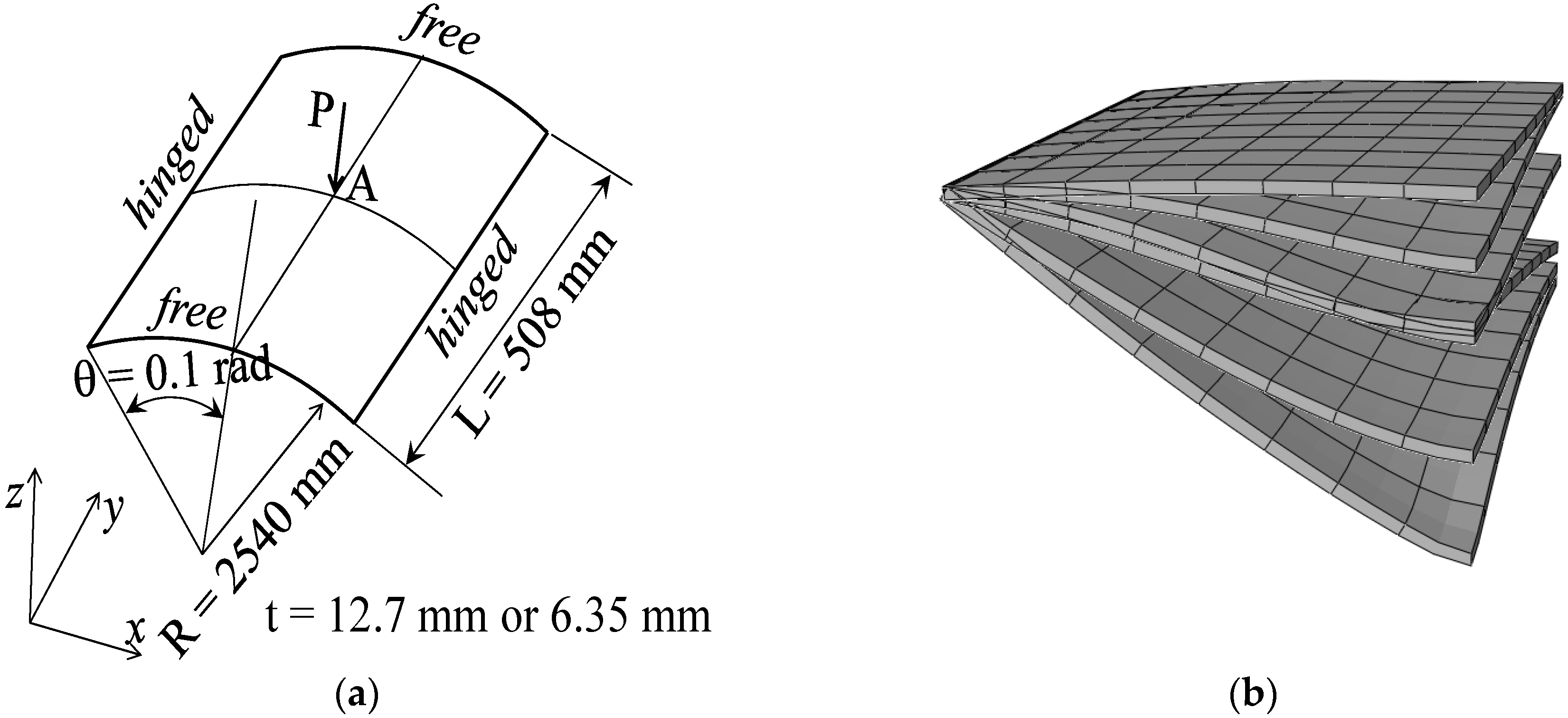
3.4. Hinged Cylindrical Roof
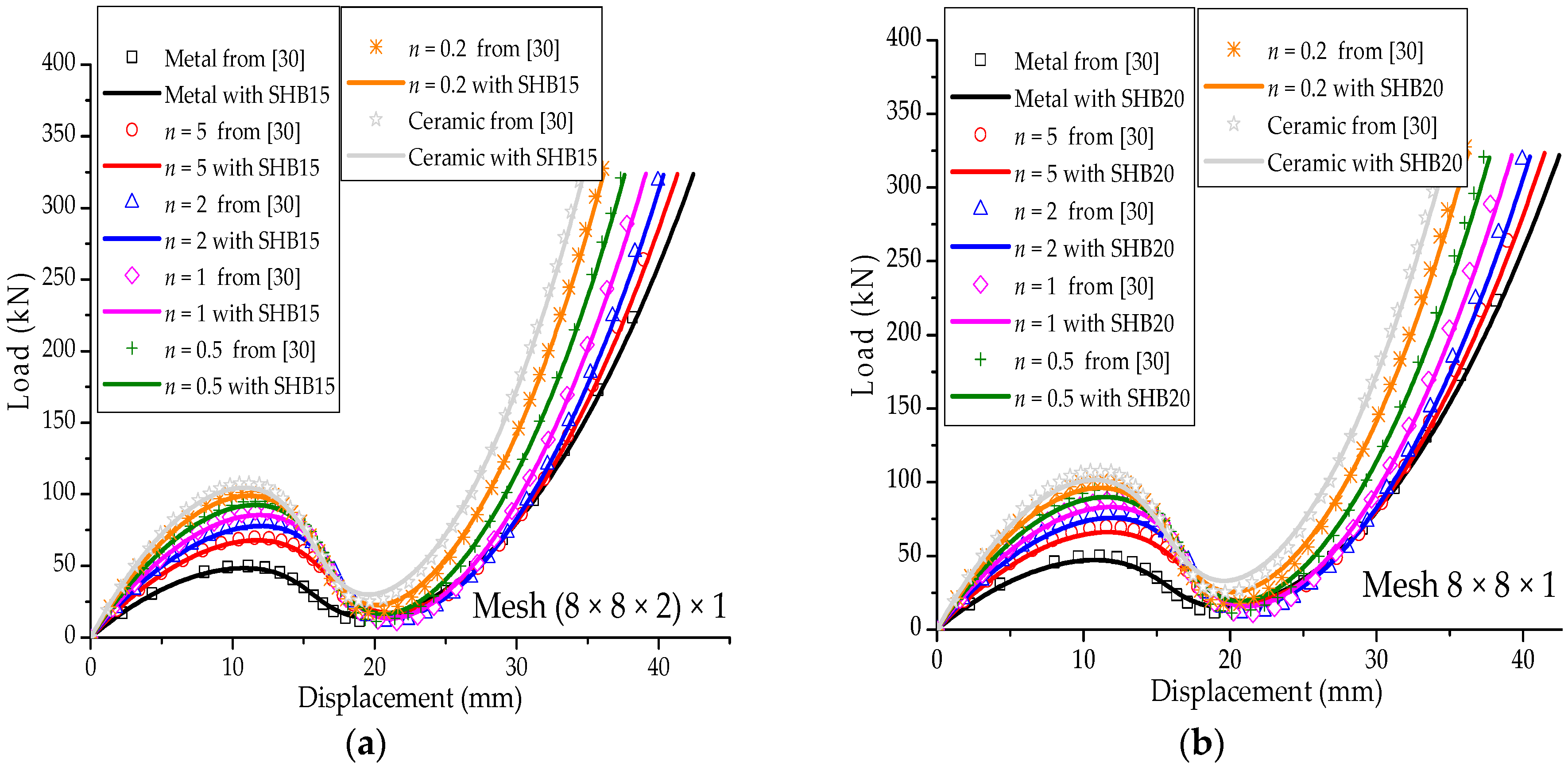
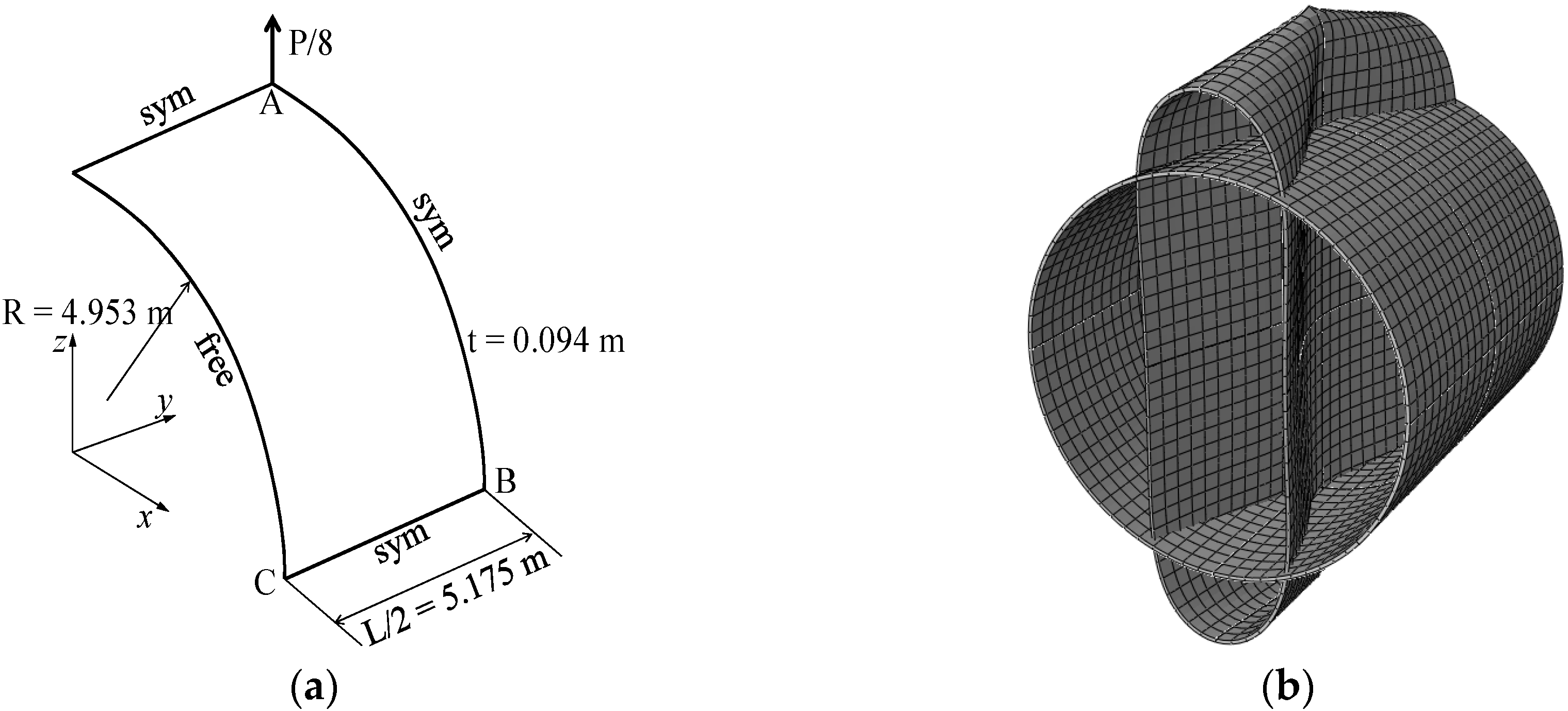
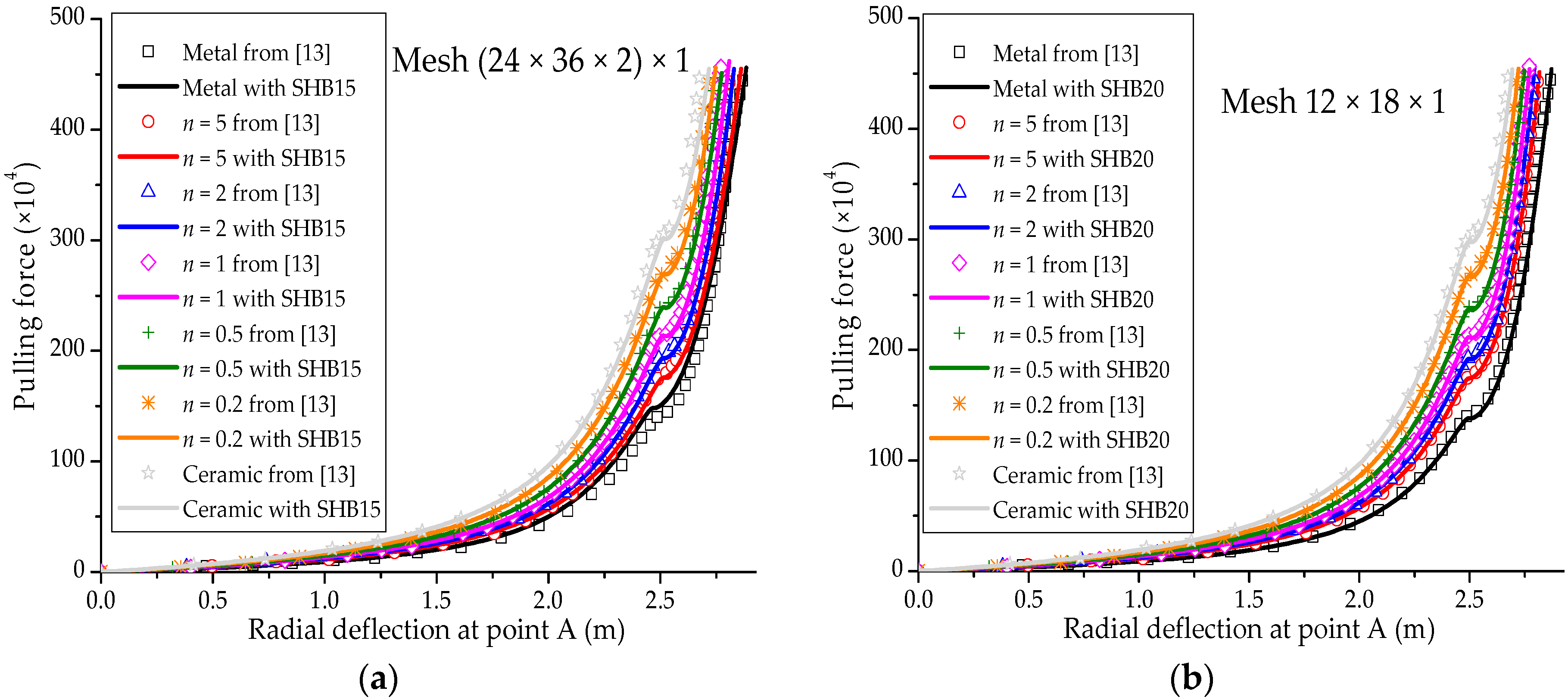
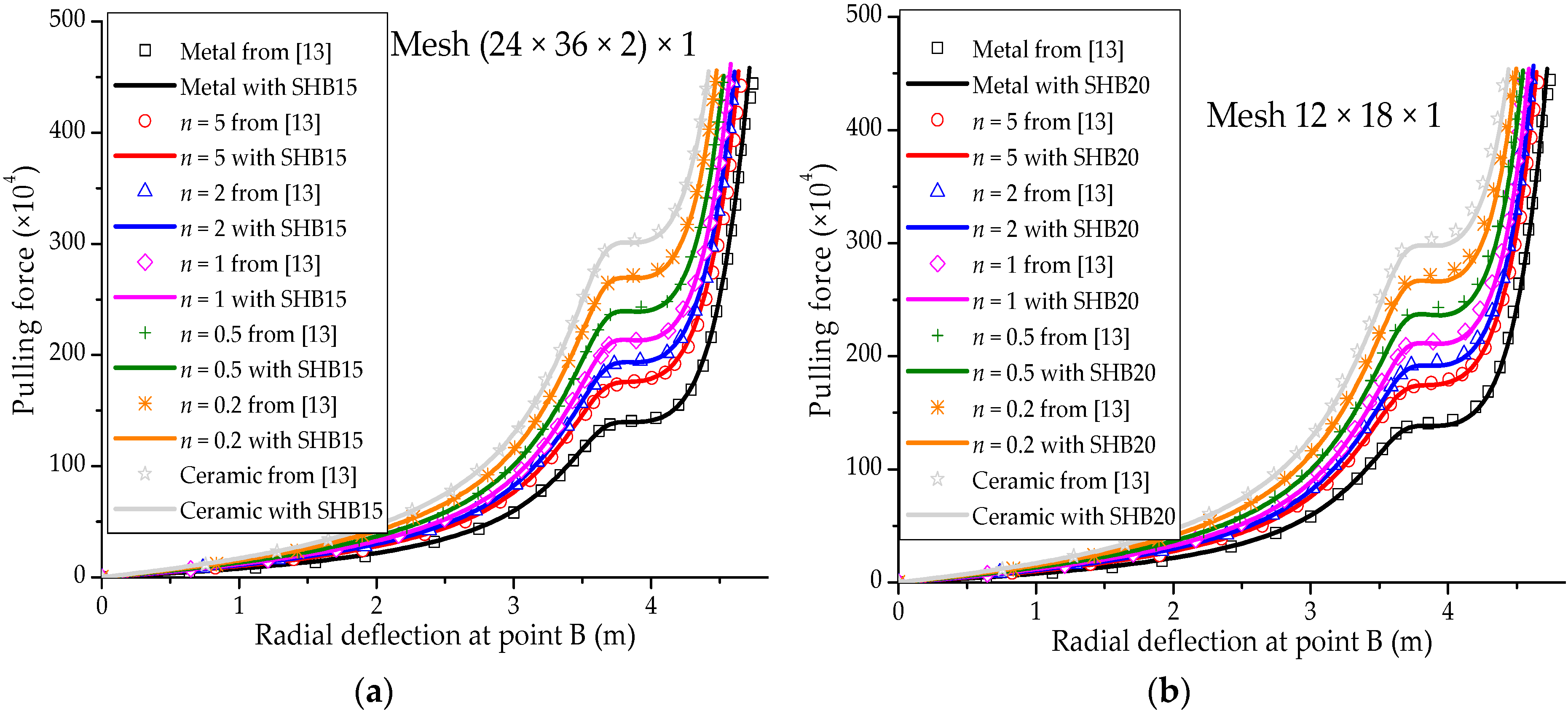
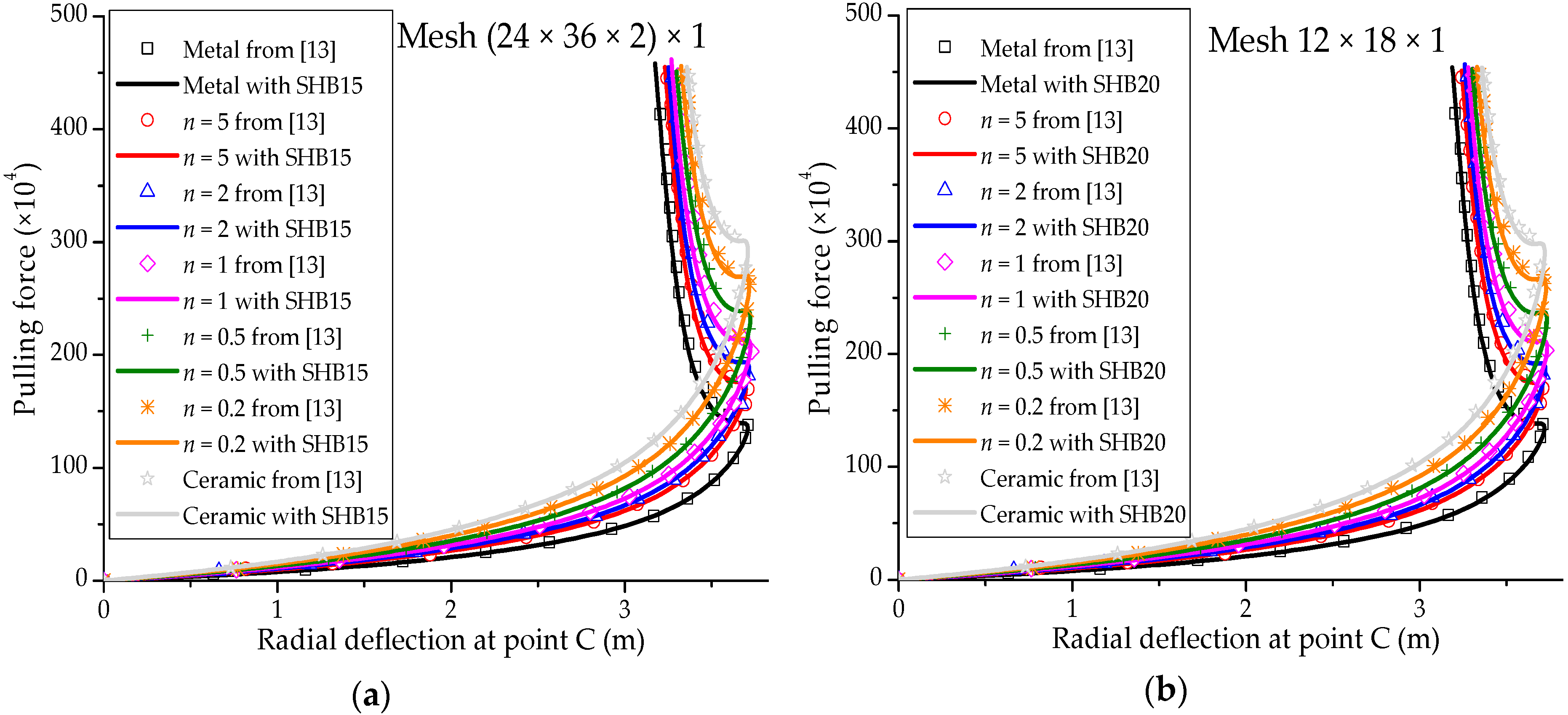
3.5. Pull-Out of an Open-Ended Cylinder
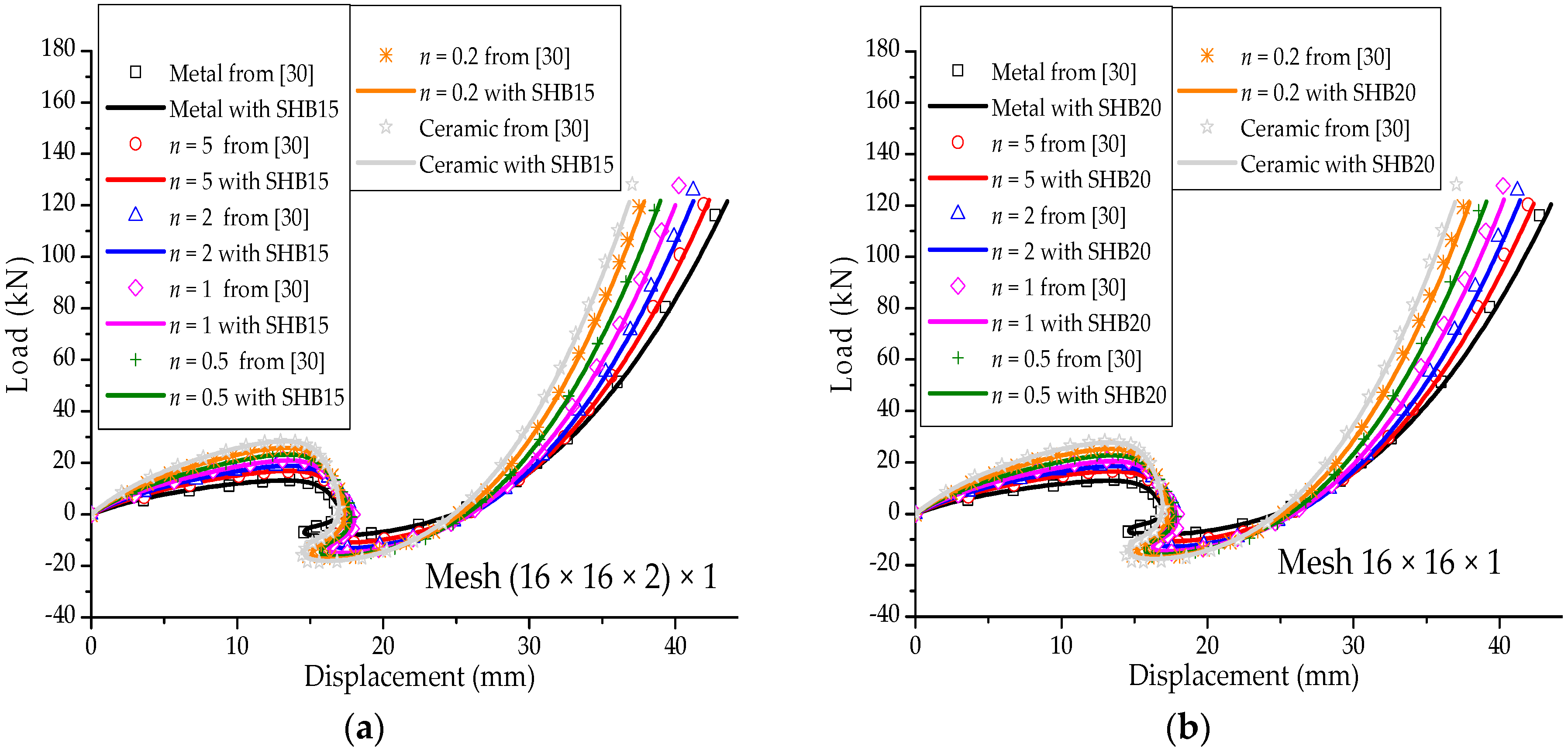
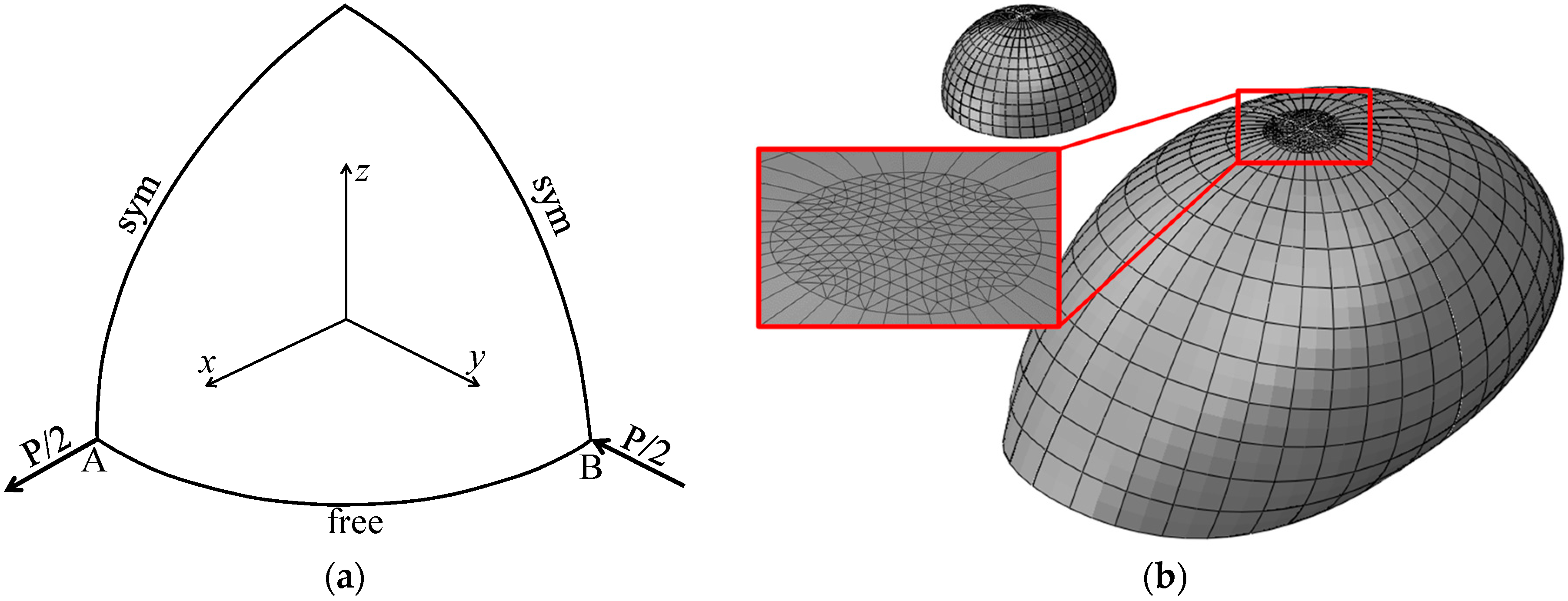
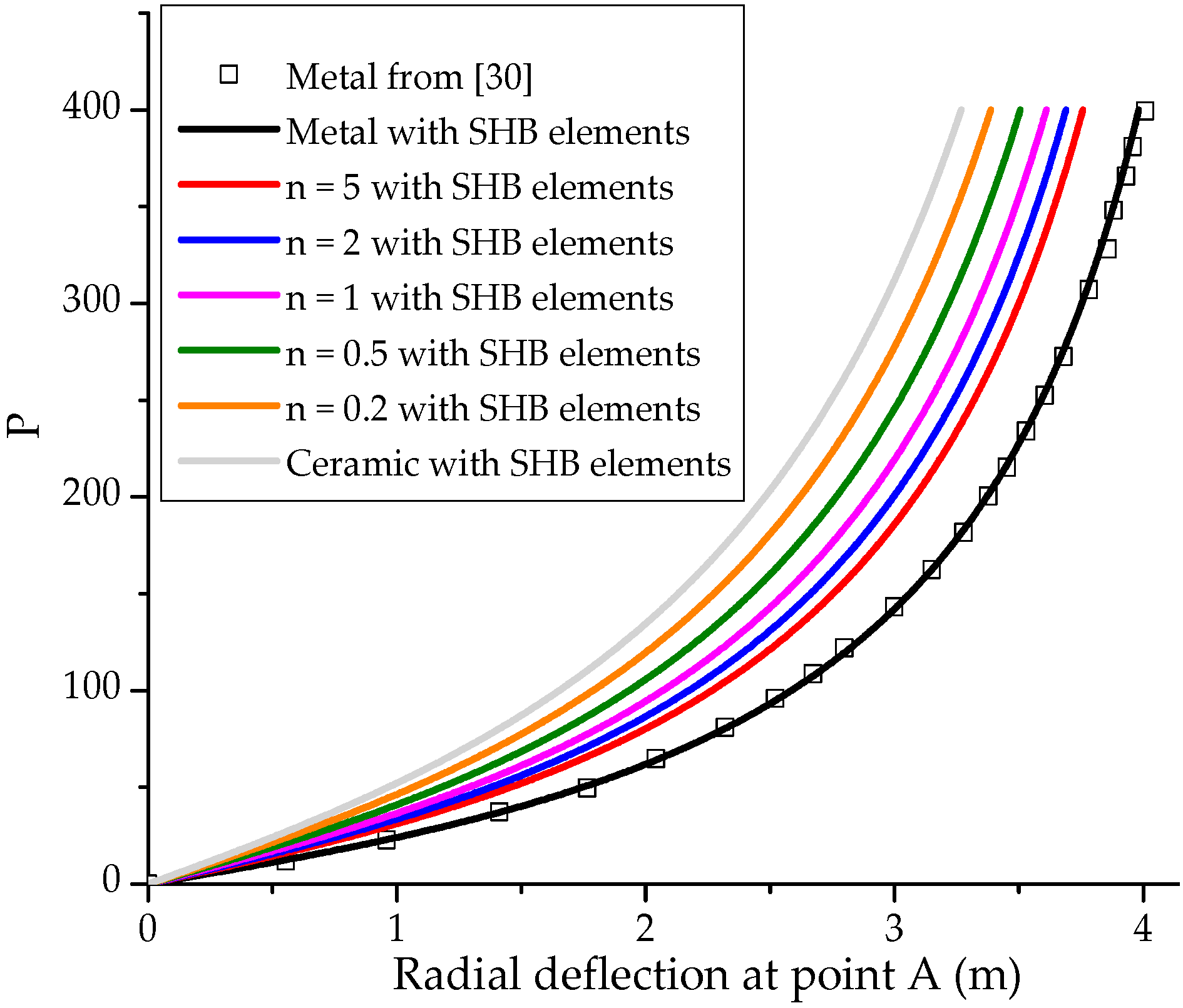
3.6. Pinched Hemispherical Shell
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yamanoushi, M.; Koizumi, M.; Hiraii, T.; Shiota, I. FGM-90. In Proceedings of the First International Symposium on Functionally Gradient Materials, Sendai, Japan, 8–9 October 1990. [Google Scholar]
- Koizumi, M. The concept of FGM. Ceram. Trans. Funct. Gradient Mater. 1993, 34, 3–10. [Google Scholar]
- Hauptmann, R.; Schweizerhof, K. A systematic development of solid–shell element formulations for linear and nonlinear analyses employing only displacement degrees of freedom. Int. J. Numer. Methods Eng. 1998, 42, 49–70. [Google Scholar] [CrossRef]
- Abed-Meraim, F.; Combescure, A. SHB8PS—A new adaptive, assumed-strain continuum mechanics shell element for impact analysis. Comput. Struct. 2002, 80, 791–803. [Google Scholar] [CrossRef]
- Reese, S. A large deformation solid-shell concept based on reduced integration with hourglass stabilization. Int. J. Numer. Methods Eng. 2007, 69, 1671–1716. [Google Scholar] [CrossRef]
- Abed-Meraim, F.; Combescure, A. An improved assumed strain solid–shell element formulation with physical stabilization for geometric non-linear applications and elastic–plastic stability analysis. Int. J. Numer. Methods Eng. 2009, 80, 1640–1686. [Google Scholar] [CrossRef]
- Salahouelhadj, A.; Abed-Meraim, F.; Chalal, H.; Balan, T. Application of the continuum shell finite element SHB8PS to sheet forming simulation using an extended large strain anisotropic elastic-plastic formulation. Arch. Appl. Mech. 2012, 82, 1269–1290. [Google Scholar] [CrossRef]
- Pagani, M.; Reese, S.; Perego, U. Computationally efficient explicit nonlinear analyses using reduced integration-based solid–shell finite elements. Comput. Methods Appl. Mech. Eng. 2014, 268, 141–159. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Too, J.M. Reduced integration technique in general analysis of plates and shells. Int. J. Numer. Methods Eng. 1971, 3, 275–290. [Google Scholar] [CrossRef]
- Alves de Sousa, R.J.; Cardoso, R.P.R.; Fontes Valente, R.A.; Yoon, J.W.; Grácio, J.J.; Natal Jorge, R.M. A new one-point quadrature enhanced assumed strain (EAS) solid-shell element with multiple integration points along thickness: Part I—Geometrically linear applications. Int. J. Numer. Methods Eng. 2005, 62, 952–977. [Google Scholar] [CrossRef]
- Edem, I.B.; Gosling, P.D. Physically stabilised displacement-based ANS solid–shell element. Finite Elem. Anal. Des. 2013, 74, 30–40. [Google Scholar] [CrossRef]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Arciniega, R.A.; Reddy, J.N. Large deformation analysis of functionally graded shells. Int. J. Solids Struct. 2007, 44, 2036–2052. [Google Scholar] [CrossRef]
- Cao, Z.-Y.; Wang, H.-N. Free vibration of FGM cylindrical shells with holes under various boundary conditions. J. Sound Vib. 2007, 306, 227–237. [Google Scholar] [CrossRef]
- Beheshti, A.; Ramezani, S. Nonlinear finite element analysis of functionally graded structures by enhanced assumed strain shell elements. Appl. Math. Model. 2015, 39, 3690–3703. [Google Scholar] [CrossRef]
- Asemi, K.; Salami, S.J.; Salehi, M.; Sadighi, M. Dynamic and Static analysis of FGM Skew plates with 3D Elasticity based Graded Finite element Modeling. Lat. Am. J. Solids Struct. 2014, 11, 504–533. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Nguyen-Xuan, H. An isogeometric finite element approach for three-dimensional static and dynamic analysis of functionally graded material plate structures. Compos. Struct. 2015, 132, 423–439. [Google Scholar] [CrossRef]
- Vel, S.S.; Batra, R.C. Three dimensional exact solution for the vibration of FGM rectangular plates. J. Sound Vib. 2004, 272, 703–730. [Google Scholar] [CrossRef]
- Zheng, S.J.; Dai, F.; Song, Z. Active control of piezothermoelastic FGM shells using integrated piezoelectric sensor/actuator layers. Int. J. Appl. Electromagn. 2009, 30, 107–124. [Google Scholar] [CrossRef]
- Hajlaoui, A.; Jarraya, A.; El Bikri, K.; Dammak, F. Buckling analysis of functionally graded materials structures with enhanced solid-shell elements and transverse shear correction. Compos. Struct. 2015, 132, 87–97. [Google Scholar] [CrossRef]
- Hajlaoui, A.; Triki, E.; Frikha, A.; Wali, M.; Dammak, F. Nonlinear dynamics analysis of FGM shell structures with a higher order shear strain enhanced solid-shell element. Lat. Am. J. Solids Struct. 2017, 14, 72–91. [Google Scholar] [CrossRef]
- Abed-Meraim, F.; Trinh, V.D.; Combescure, A. New quadratic solid–shell elements and their evaluation on linear benchmark problems. Computing 2013, 95, 373–394. [Google Scholar] [CrossRef]
- Wang, P.; Chalal, H.; Abed-Meraim, F. Quadratic solid-shell elements for nonlinear structural analysis and sheet metal forming simulation. Comput. Mech. 2017, 59, 161–186. [Google Scholar] [CrossRef]
- Hallquist, J.O. Theoretical Manual for DYNA3D; Report UC1D-19041; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1983. [Google Scholar]
- Simo, J.C.; Hughes, T.J.R. On the variational foundations of assumed strain methods. J. Appl. Mech. 1986, 53, 51–54. [Google Scholar] [CrossRef]
- Chi, S.H.; Chung, Y.L. Mechanical behavior of functionally graded material plates under transverse load—Part I: Analysis. Int. J. Solids Struct. 2006, 43, 3657–3674. [Google Scholar] [CrossRef]
- Chi, S.H.; Chung, Y.L. Mechanical behavior of functionally graded material plates under transverse load—Part II: Numerical results. Int. J. Solids Struct. 2006, 43, 3675–3691. [Google Scholar] [CrossRef]
- Betsch, P.; Gruttmann, F.; Stein, E. A 4-node finite shell element for the implementation of general hyperelastic 3D-elasticity at finite strains. Comput. Methods Appl. Mech. Eng. 1996, 130, 57–79. [Google Scholar] [CrossRef]
- Sze, K.Y.; Liu, X.H.; Lo, S.H. Popular benchmark problems for geometric nonlinear analysis of shells. Finite Elem. Anal. Des. 2004, 40, 1551–1569. [Google Scholar] [CrossRef]
- Arciniega, R.A.; Reddy, J.N. Tensor-based finite element formulation for geometrically nonlinear analysis of shell structures. Comput. Methods Appl. Mech. Eng. 2007, 196, 1048–1073. [Google Scholar] [CrossRef]
- Andrade, L.G.; Awruch, A.M.; Morsch, I.B. Geometrically nonlinear analysis of laminate composite plates and shells using the eight-node hexahedral element with one-point integration. Compos. Struct. 2007, 79, 571–580. [Google Scholar] [CrossRef]
- Sansour, C.; Kollmann, F.G. Families of 4-node and 9-node finite elements for a finite deformation shell theory. An assessment of hybrid stress, hybrid strain and enhanced strain elements. Comput. Mech. 2000, 24, 435–447. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalal, H.; Abed-Meraim, F. Quadratic Solid–Shell Finite Elements for Geometrically Nonlinear Analysis of Functionally Graded Material Plates. Materials 2018, 11, 1046. https://doi.org/10.3390/ma11061046
Chalal H, Abed-Meraim F. Quadratic Solid–Shell Finite Elements for Geometrically Nonlinear Analysis of Functionally Graded Material Plates. Materials. 2018; 11(6):1046. https://doi.org/10.3390/ma11061046
Chicago/Turabian StyleChalal, Hocine, and Farid Abed-Meraim. 2018. "Quadratic Solid–Shell Finite Elements for Geometrically Nonlinear Analysis of Functionally Graded Material Plates" Materials 11, no. 6: 1046. https://doi.org/10.3390/ma11061046
APA StyleChalal, H., & Abed-Meraim, F. (2018). Quadratic Solid–Shell Finite Elements for Geometrically Nonlinear Analysis of Functionally Graded Material Plates. Materials, 11(6), 1046. https://doi.org/10.3390/ma11061046





