1. Introduction
In comparison with other methods for the joint of materials, welding is one of the most used ones. However, it holds diverse flaws related to the manufacturing process. The most common imperfections are discontinuities, porosities, undercuts, cracks, inclusions, and lack of fusion, among others. These flaws are produced by the increase of speed, change in polarity of the current, and the extension and diameter of the electrode. Additionally, these variables modify the grain size and the areas surrounding the weld bead, such as: the fusion zone (FZ), the heat affected zone (HAZ), and the base metal (BM) [
1].
An evaluation of fatigue strength for welded joints consist of the study of crack initiation and propagation phenomena. Due to this, it is necessary to know the mechanisms to determine the various typical factors of fracture mechanics, with the aim to explain the behavior of cracked material when subjected to stresses and the mechanisms that lead to premature failure in load conditions below the yield and breakage limits [
2]. The fracture mechanics shows that the parameters tenacity, crack size, and level of strength can be related to predict the possibility of a fracture, such as stress intensity factors (SIF) in butt welds [
3,
4,
5]. This parameter depends on the geometry and the load and it is a measure of the degree to which a load is amplified at the tip of a crack. Additionally, the fracture mechanics raises other expressions for the evaluation of the crack propagation rate (da/dN), as function of the SIF range (∆K), where C and m are material constant values. This relationship is known as the Paris law [
6].
Several researches have been developed aimed at determining the areas that make up the welded joint [
7,
8,
9]. They have generally identified the fusion zone (FZ), which presents a grain growth from the fusion line into the interior of the fusion zone, the heat affected zone (HAZ) characterized by the hardening during the heating. In the cooling, the microstructure can present evidences of liquefaction in edges of grain and the base metal (BM), corresponding to the formation limit of the hardener precipitate. In the research of [
10], there are observed microstructural variations in a series of low-alloy steel weld which deposit different carbon concentrations (product from experimental electrodes), getting allotriomorphic ferrite growth is assumed to occur by an equilibrium transformation mechanism; its formation is found to determine the development of both Widmanstätten and acicular ferrite.
The observation of the fault surfaces in welding are useful to estimate the mechanisms of crack propagation, using the mark counting. In the research of [
11], it has been observed that the marks are normally formed when the load is intermittent during the service and the marks in a much finer scale. They can show the tip position on the crack after each cycle. The observation of the marks always suggests a fatigue failure, but the absence of this pattern does not rule it out. The crack origin and, in some cases, the marks can be observed through a scanning electron microscope (SEM). In the work of [
12], the modeling and implementation of criteria for multiple crack propagation, including interaction and coalescence was made. In this research, the correlation between the number of initiation sites and the applied stress level, showing that crack propagation is related with fatigue strength of weld.
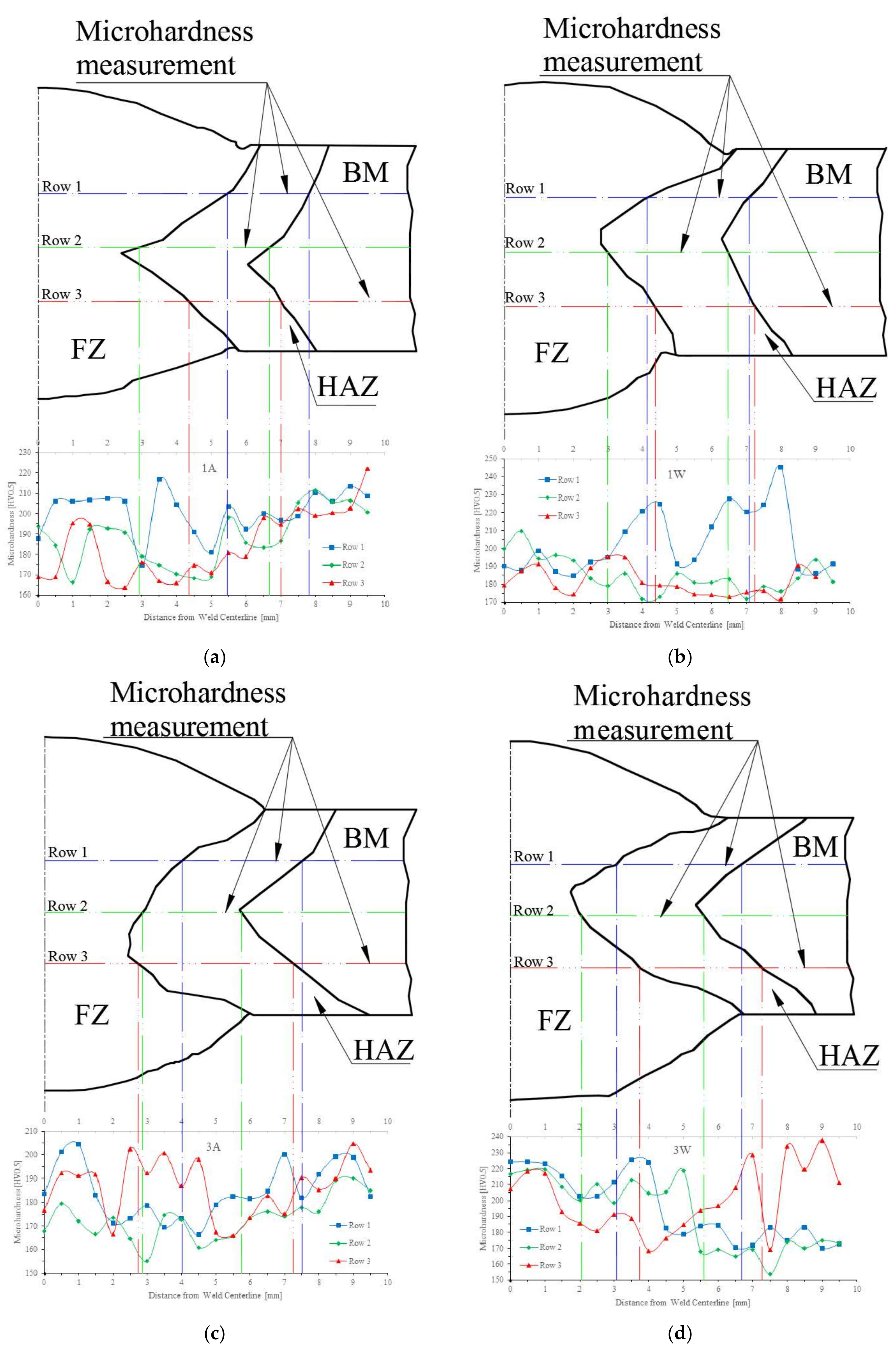
The determination of the mechanical properties of the weld joints such as hardness, fracture toughness, yield strength, and tensile strength are not constant, Bullón et al. [
13] indicates that they are affected by the thermodynamics or thermal field (temperature field) due to the high gradient temperature changes that are generated causing microstructural transformations, which affect the mechanical field (field of stresses and strain) and metallographic field (field of microstructural state) causing morphological changes. In addition, there is a mutual influence between this fields represented by the continuous and discontinuous lines.
Other researchers have studied the effect of microstructural changes and mechanical properties on the welded joint. Various researchers [
14,
15] show that geometric discontinuities affect the fatigue strength of welded joints. It is in the HAZ where the discontinuities can nucleate, which in general are the initiators of fatigue cracks in the welded joints. The fatigue fissure begins in a local flaw of the structure, either internal or external. In fact, the bead geometry already constitutes a geometric discontinuity, which turns out to be a stress concentrator.
In regards to the analysis by fracture mechanics on welded joints, several authors have researched the topic over the years through the selection of a combination of factors, such as material, the model geometry, and load conditions. However, most researchers have opted for the use of computational tools and the finite element method (FEM). A study using this technique by the Berrios’ researcher [
16], found a remarkable correspondence between the experimental trajectories of crack propagation on high resistance-steel and the propagation trajectories obtained using the software ANSYS APDL. The research carried out by Araque and Arzola [
17], developed an experimental-theoretical analysis about the influence of the cooling medium and the geometry of the welding bead profile in fatigue life and the associated parameters with structural integrity of welded joints. The results were a set of analytical expressions for the weld magnification factor Mk, the obtained models of behavior of the weld magnification factor are compared with the results from other researchers with some small differences.
On the other hand, Toribio [
18] has identified life fatigue for a pressure vessel under cyclic loads of thermal origin, as well as proposal on a general procedure to calculate the life fatigue on any structure subjected to cyclic load. He has been determined that shorter fracture trajectories during the life service generate leaks prior to break.
On the same field of research, Lewandowski [
19] has analyzed the behavior of crack growth in ferritic-perlitic structures subjected to cyclic flexion and has determined that, in all cases, life fatigue on welded specimens is less than on completely solid specimens, due to different mechanical properties to the characteristics of the welded joints (base material, weld bead, HAZ thermal affectated area).
About the use of software to analyze fractures, Franc3D has gained popularity among researchers in the last decade. Yang [
20], has proposed an algorithm based on the linear elastic fracture mechanics for the simulation of fatigue crack growth under non-proportional loads. He has found that cycles of growth calculated on the basis of stress intensity factors (SIF) correspond to the experimental data for specimens subjected to slightly lower loads. Similarly, Xiao [
21] has made a numerical analysis for surface cracks in on a hemispherical hole and has concluded that the geometry of the whole surface is a determining factor in the SIF. By using this software, researcher Chin [
22] has estimated how a crack spreads on a support made from an alloy of titanium and aluminum (very common in the aerospace industry) and has found that the Type I (SIF’s) is below the fracture toughness to the fracture material. Then, he has concluded this support could tolerate a certain type of cracks.
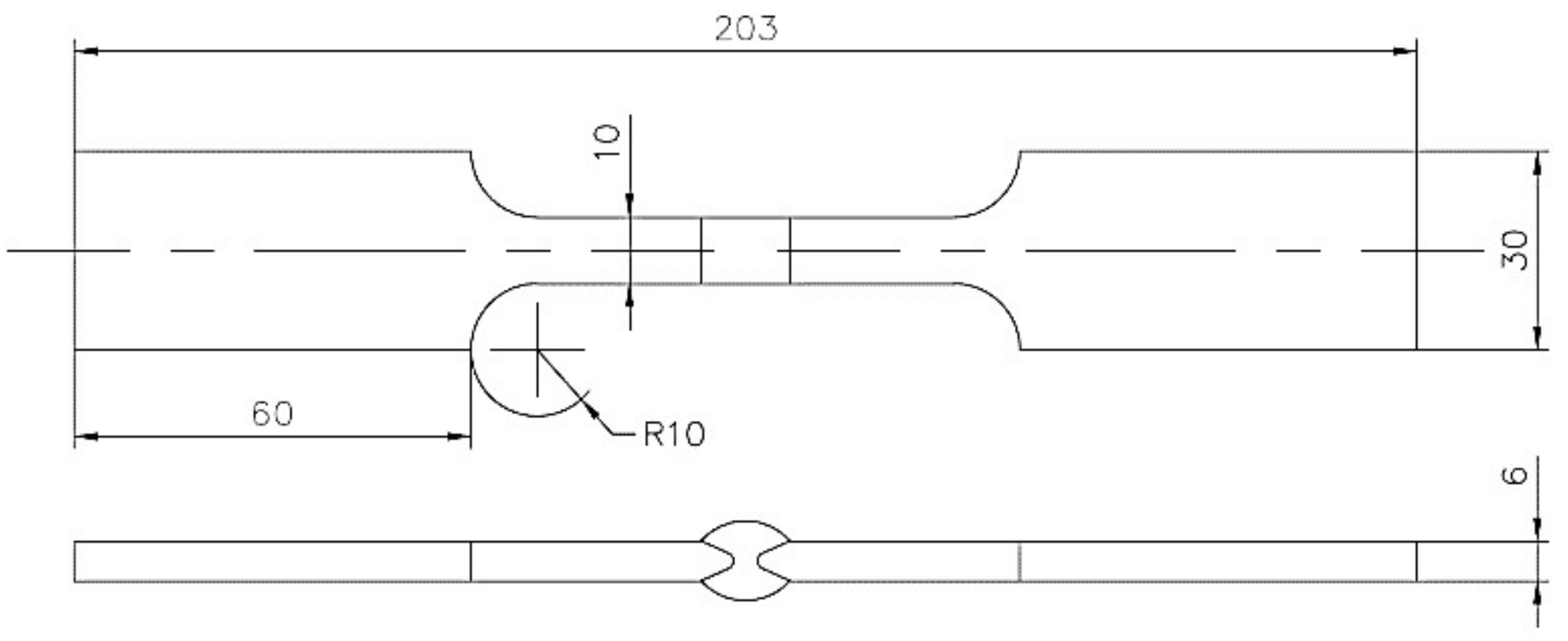
This article shows an experimental and theoretical study of the fatigue failures on butt welded joints for structural carbon steel ASTM A36 HR that used shielded metal arc welding (SMAW) with electrode E6013. The influence of the weld reinforcement was evaluated, as well as the post weld cooling environment by the uniaxial fatigue tests and the failure mechanism analysis present in the fracture surface. In other tests, the mechanical and fractomechanical properties from the welded joints were analyzed in relation with the crack origin and propagation caused by fatigue.
4. Conclusions
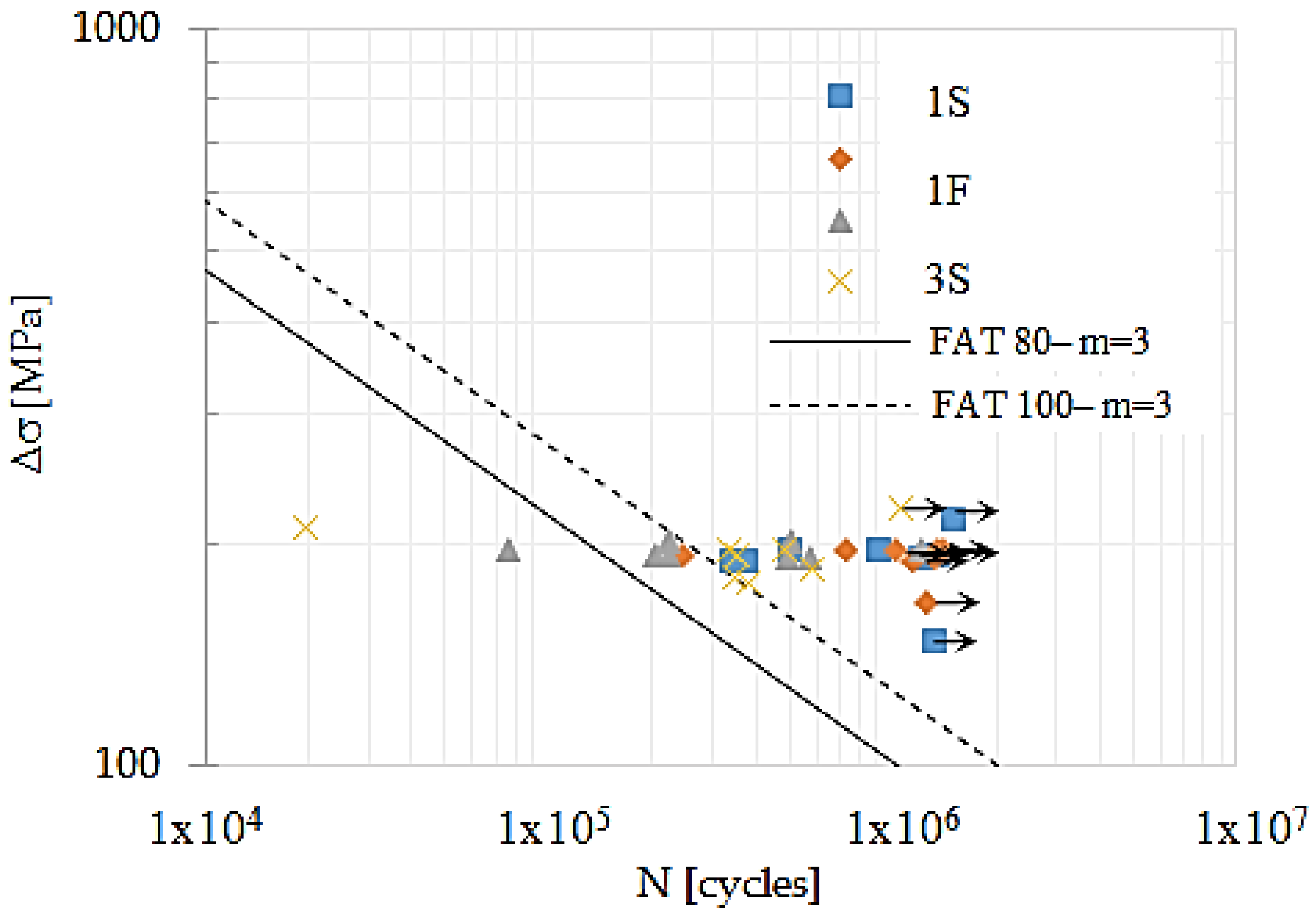
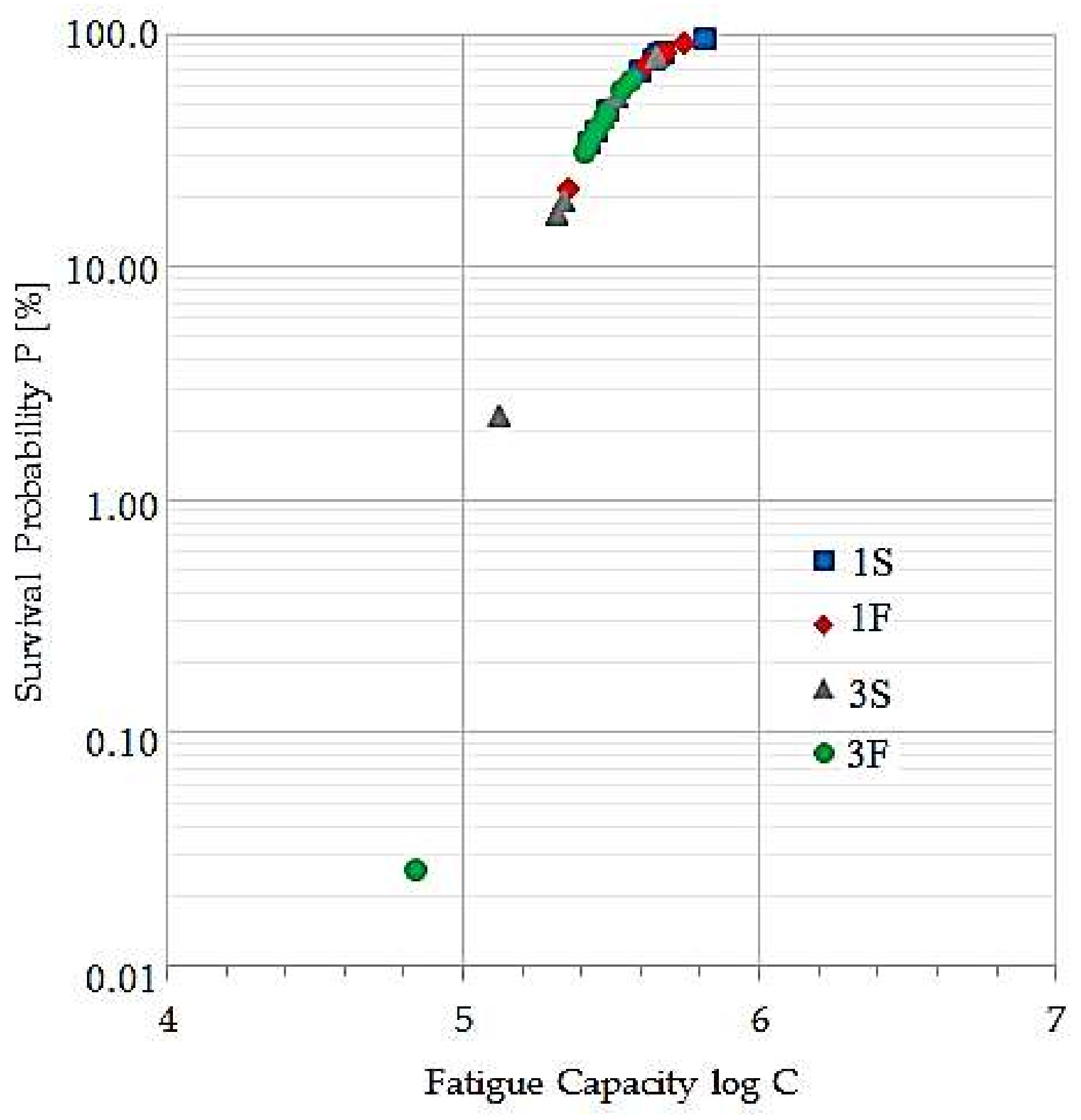
According with the results experimentally obtained in this research, welded joints with a welding reinforcement of 1 mm and cooled in water reached the highest probability of survival to fatigue. While the welded joints with a welding reinforcement of 3 mm and cooled in calm air, reached the worst probability of survival to fatigue. In general, fatigue strength in butt welded joints is strongly influenced by the welding reinforcement. In this research, 93.8% of the specimens presented a fatigue strength superior to the one of class FAT 90, while about 78.1% of the specimens reached a fatigue strength higher than the recommended one by class FAT 100.
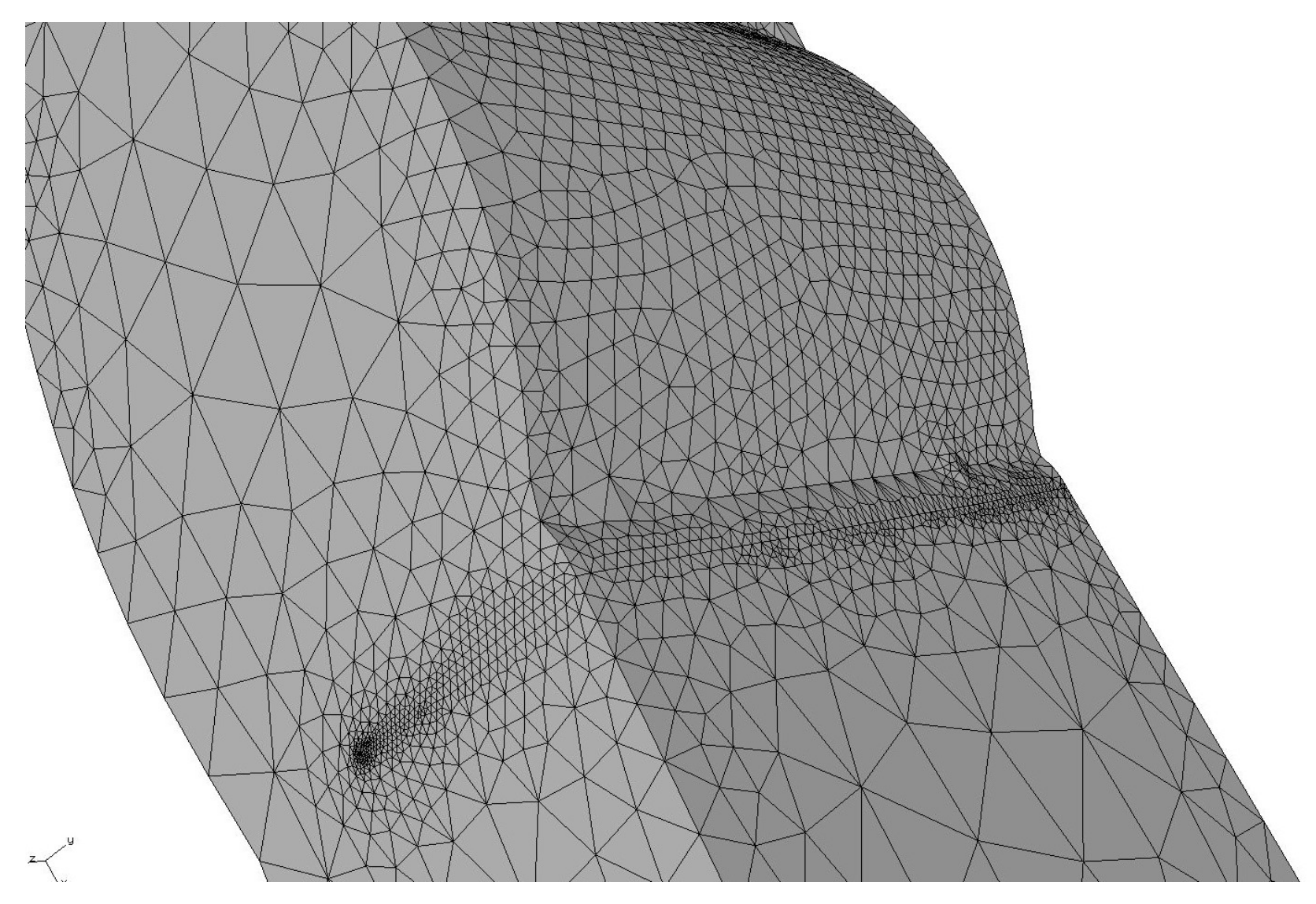
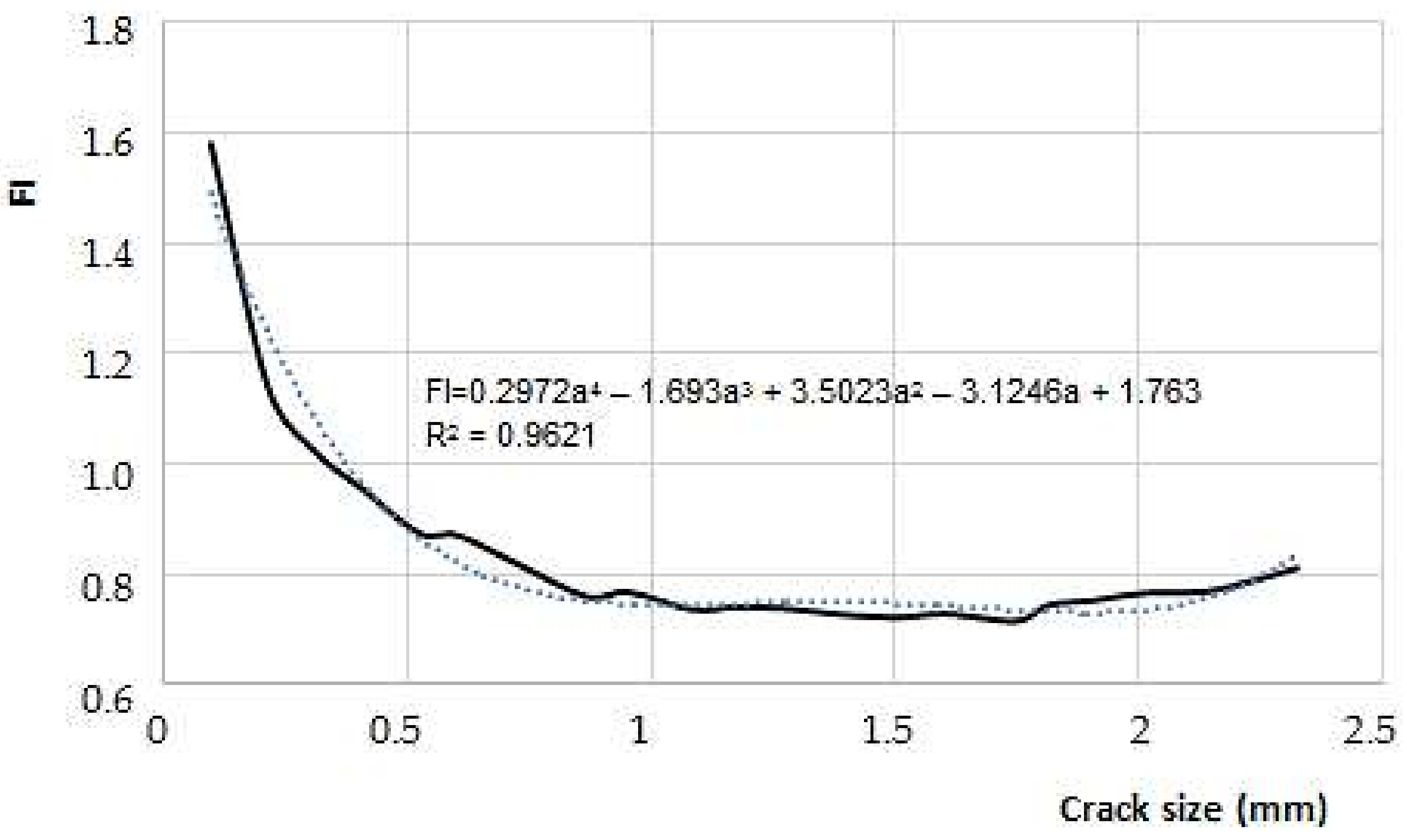
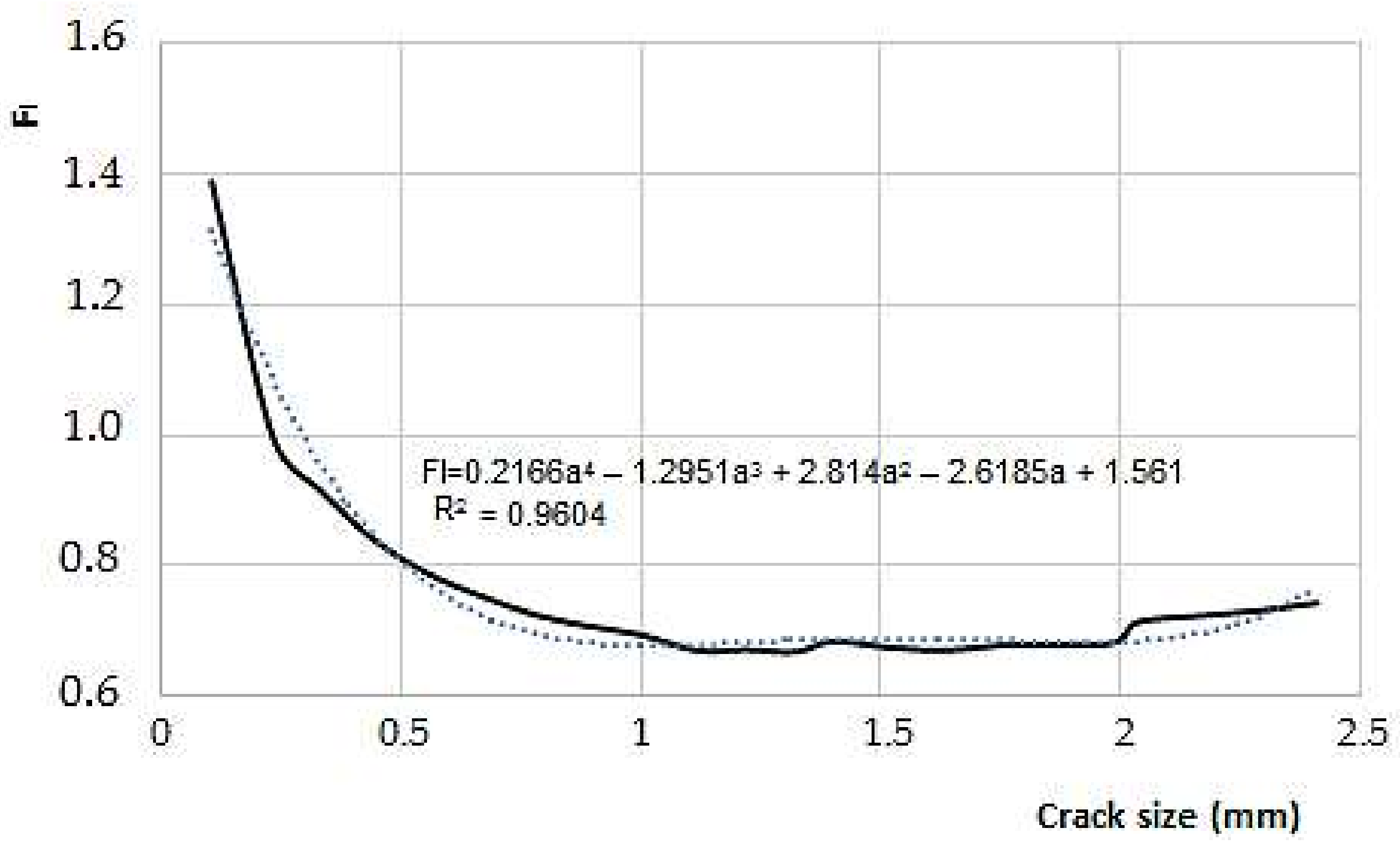
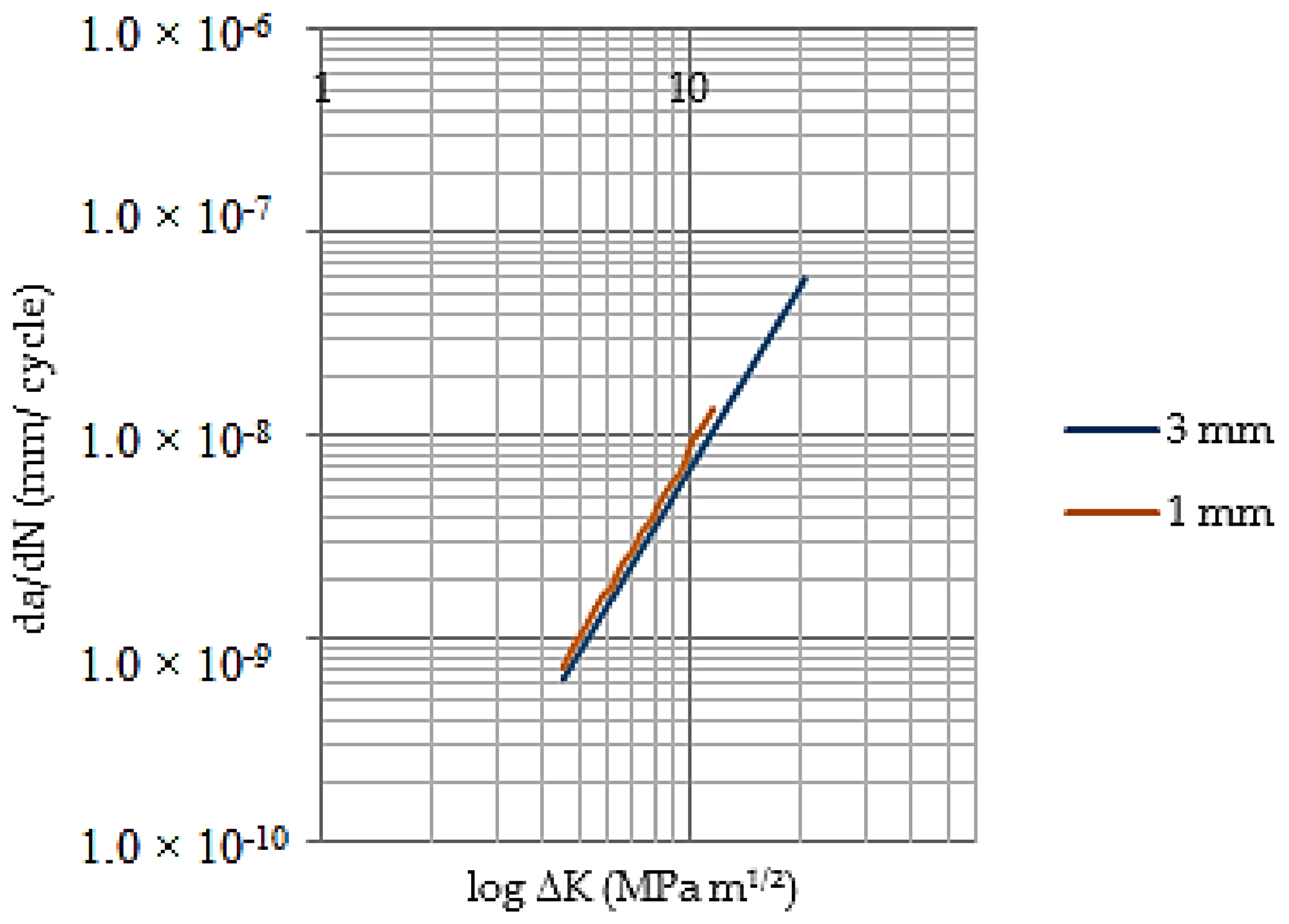
The use of the finite element method, along with the fracture mechanics, allowed one to have an adequate simulation of the stable propagation of cracks. The integration of the results obtained for the variation range for stress intensity factor and the separation between striations, obtained through SEM observation, allowed the estimation of the parameters C and m from Paris’ expression. For some measurements, C values and m atypical were obtained. The latter could be due to the high gradient change for the local mechanical properties next to the welding bead and the inherent distance difficulties of the measuring method between striations. However, the numerical propagation rates in the order of those found through experimental measurements were obtained.
The crack front on the failure surface presented an approximated semielliptical shape. This allows one to establish the finite element modelling for butt welded joints to establish correlations between experimental results and theoretical calculations. On the other hand, the importance of performing additional studies where the crack nucleation stage is included is highlighted. Where a fatigue model for this first stage should cover the influence of the microstructural phases and the grains shape and size. Moreover, further improvement of this assessment is expected by implementing other specific models for predicting changes in the microstructure and mechanical properties during the thermal cycle of the welding process.
In consistency with welding and post-welding processes applied to butt welded joints, it was observed that the post welding cooling cycle and the quantity of weld passes influence the material ductility and, thus the fracture toughness of the material, as well. In general, higher post-welding cooling speed caused significant lower measured values for the Charpy impact energy. Lower values of the Charpy impact energy are reported for the FZ and the HAZ compared to the base metal. On the other hand, no significant differences were found between experimental treatments for the mechanical properties obtained by the tension tests.