Linear Versus Nonlinear Acoustic Probing of Plasticity in Metals: A Quantitative Assessment
Abstract
1. Introduction
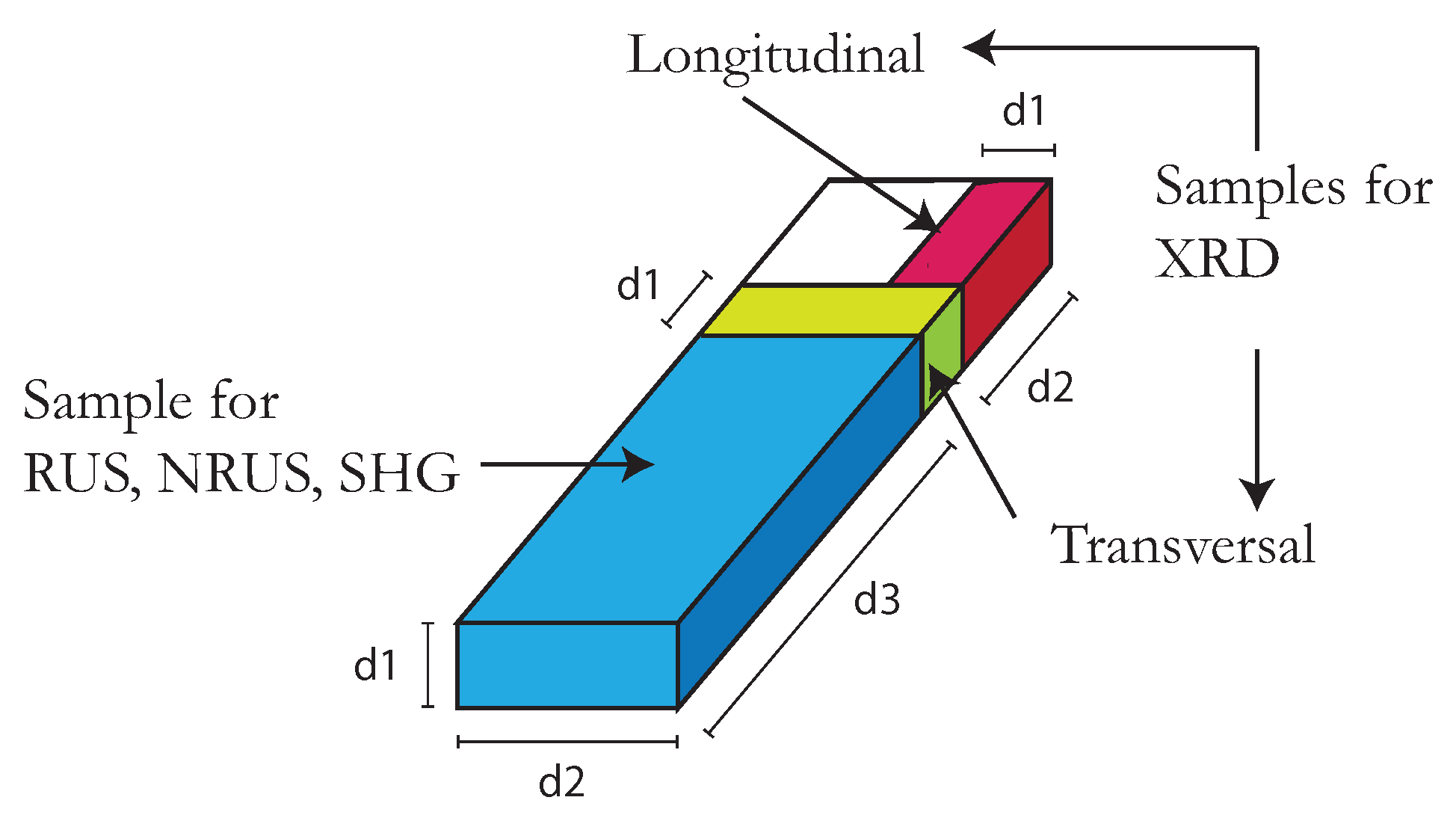
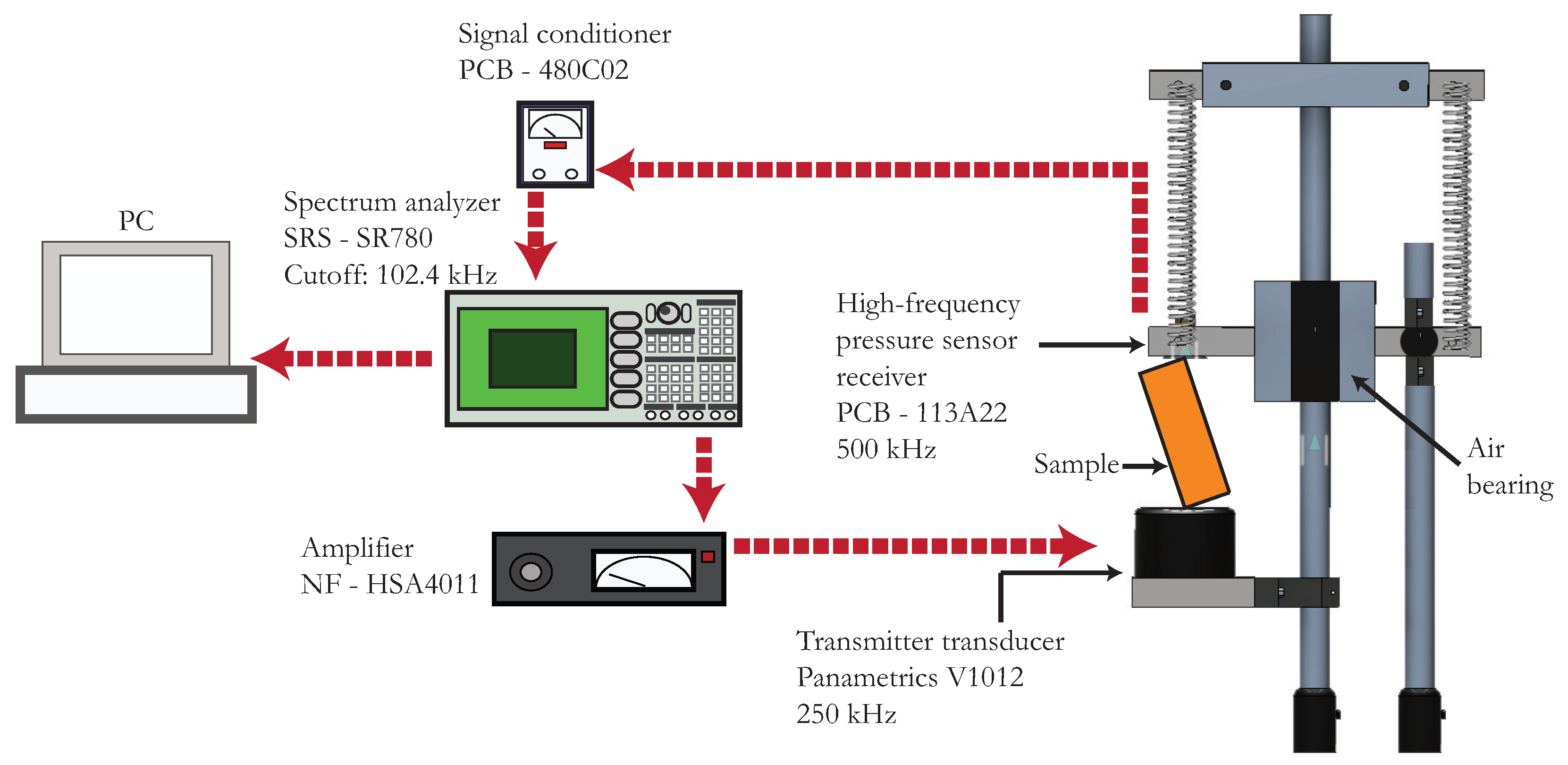
2. Materials and Methods
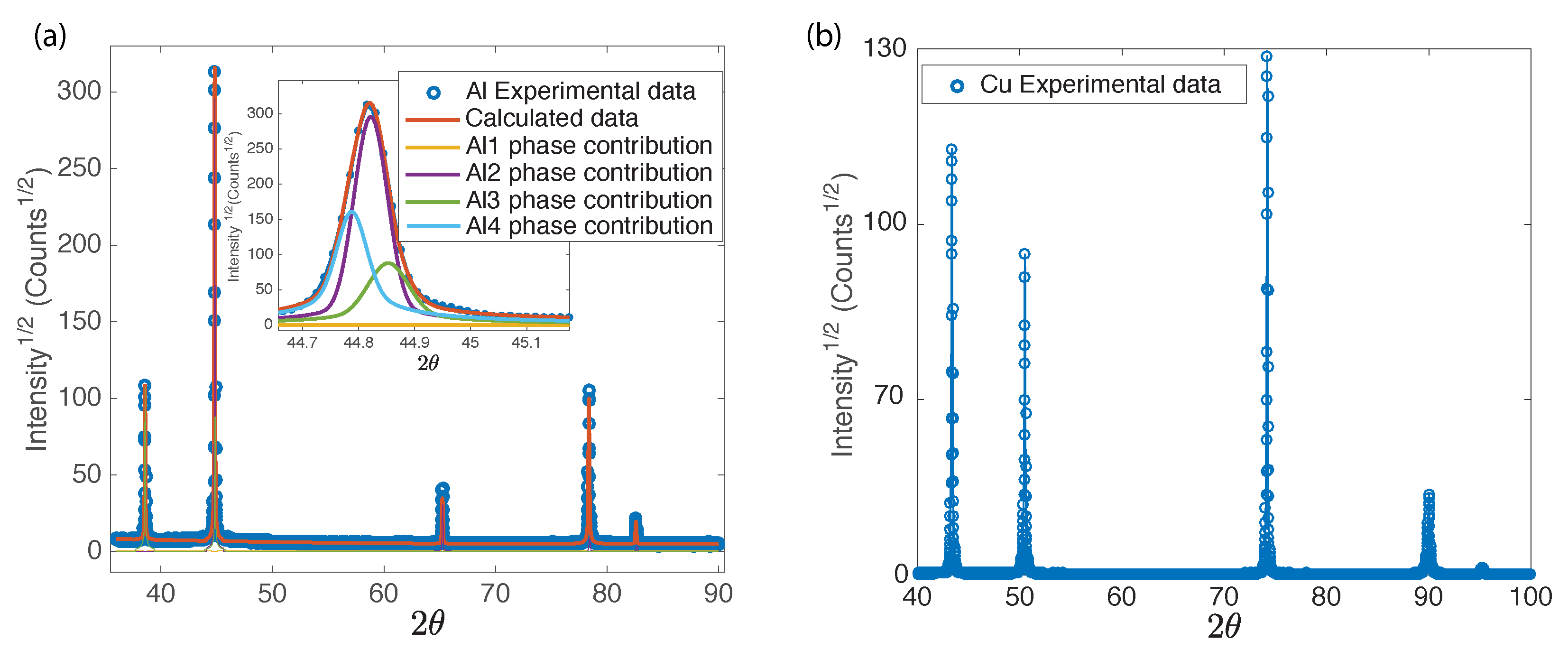
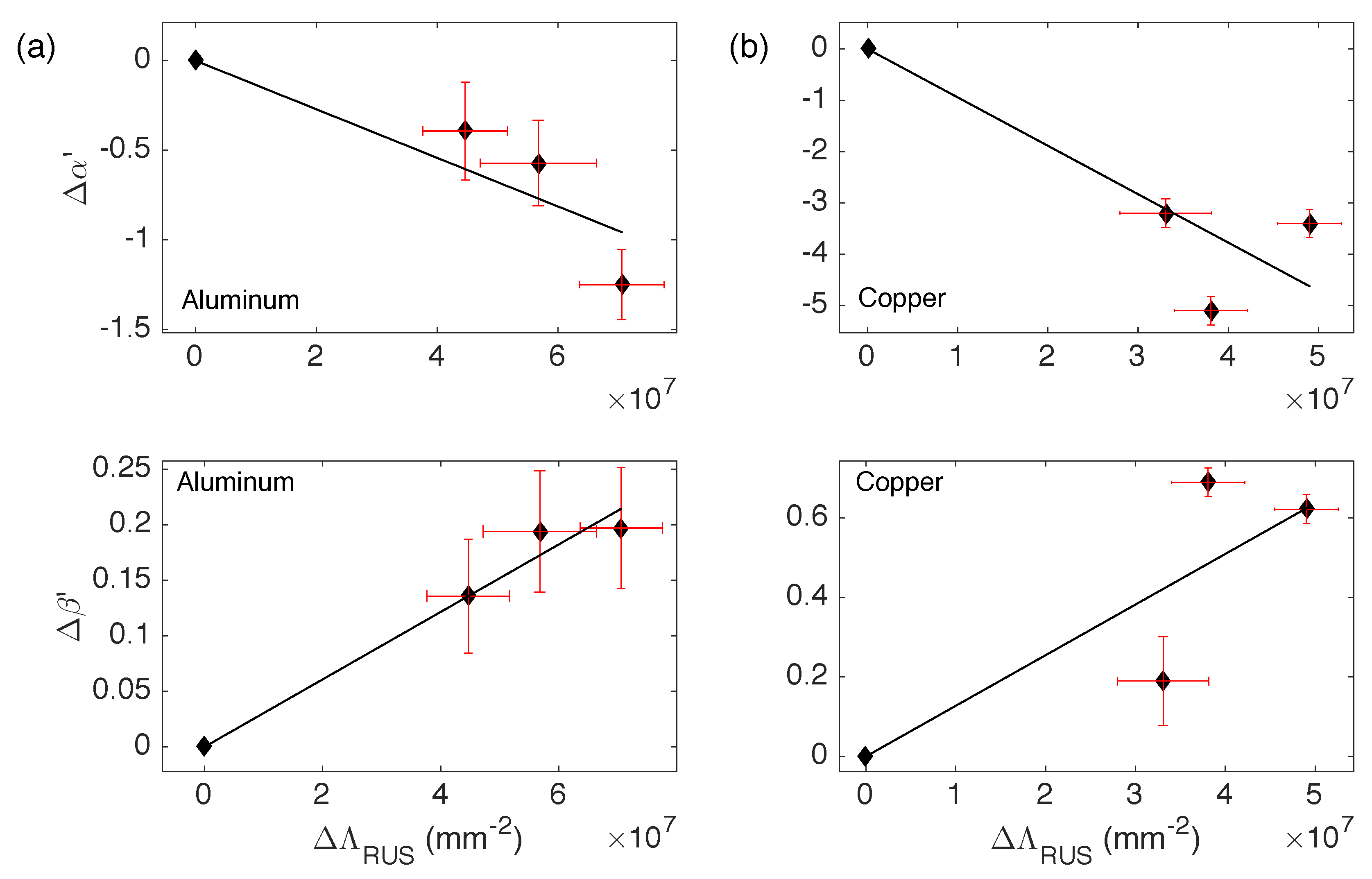
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RUS | Resonant ultrasound spectroscopy |
| TEM | Transmission electron microscopy |
| XRD | X-ray diffraction |
| SHG | Second harmonic generation |
| NRUS | Nonlinear resonant ultrasound spectroscopy |
References
- Oh, S.H.; Legros, M.; Kiener, D.; Dehm, G. In situ observation of dislocation nucleation and escape in a submicrometre aluminium single crystal. Nat. Mater. 2009, 8, 95–100. [Google Scholar] [CrossRef] [PubMed]
- Landau, P.; Schneck, R.Z.; Makov, G.; Venkert, A. In-situ TEM study of dislocation patterning during deformation in single crystal aluminum. J. Phys. Conf. Ser. 2010, 241, 012060. [Google Scholar] [CrossRef]
- Zhang, L.; Sekido, N.; Ohmura, T. real-time correlation between flow stress and dislocation density in steel during deformation. Mater. Sci. Eng. 2014, A611, 188–193. [Google Scholar] [CrossRef]
- Du, J.; Mompiou, F.; Zhang, W.-Z. In-situ TEM study of dislocation emission associated with austenite growth. Scr. Mater. 2018, 145, 62–66. [Google Scholar] [CrossRef]
- McSkimin, H.J. Pulse superposition method for measuring ultrasonic wave velocities in solids. J. Acoust. Soc. Am. 1961, 33, 12–16. [Google Scholar] [CrossRef]
- Chen, C.-H. Ultrasonic and Advanced Methods for Nondestructive Testing and Material Characterization; University of Massachusetts Dartmouth: North Dartmouth, MA, USA, 2007; ISBN 978-981-270-409-2. [Google Scholar]
- Chanbi, D.; Ogam, E.; Amara, S.E.; Fellah, Z. Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods. Materials 2018, 11, 746. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, K.A.; Raisutis, R. Identification and Characterization of Defects in Glass Fiber Reinforced Plastic by Refining the Guided Lamb Waves. Materials 2018, 11, 1173. [Google Scholar] [CrossRef] [PubMed]
- Payan, C.; Garnier, V.; Moysan, J.; Johnson, P.A. Applying nonlinear resonant ultrasound spectroscopy to improving thermal damage assessment in concrete. J. Acoust. Soc. Am. 2007, 121, EL125–EL130. [Google Scholar] [CrossRef] [PubMed]
- Muller, M.; Sutin, A.; Guyer, R.A.; Talmat, M.; Laugier, P.; Johnson, P.A. Nonlinear resonant ultrasound spectroscopy (NRUS) applied to damage assessment in bone. J. Acoust. Soc. Am. 2005, 118, 3946–3952. [Google Scholar] [CrossRef] [PubMed]
- Payan, C.; Ulrich, T.J.; Le Bas, P.Y.; Saleh, T.; Guimaraes, M. Quantitative linear and nonlinear resonance inspection techniques and analysis for material characterization: Application to concrete thermal damage. J. Acoust. Soc. Am. 2014, 136, 537–546. [Google Scholar] [CrossRef] [PubMed]
- Haupert, S.; Guérard, S.; Mitton, D.; Peyrin, F.; Laugier, P. Quantification of nonlinear elasticity for the evaluation of submillimeter crack length in cortical bone. J. Mech. Behav. Biomed. Mater. 2015, 48, 210–219. [Google Scholar] [CrossRef] [PubMed]
- Maurel, A.; Pagneux, V.; Barra, F.; Lund, F. Ultrasound as a probe of plasticity? The interaction of elastic waves with dislocations. Int. J. Bifurcat. Chaos 2009, 19, 2765–2781. [Google Scholar] [CrossRef]
- Maurel, A.; Pagneux, V.; Barra, F.; Lund, F. Wave propagation through a random array of pinned dislocations: Velocity change and attenuation in a generalized Granato and Lücke theory. Phys. Rev. B Condens. Mater. 2005, 72, 174111. [Google Scholar] [CrossRef]
- Granato, A.; Lücke, K. Theory of Mechanical Damping Due to Dislocations. J. Appl. Phys. 1956, 27, 583. [Google Scholar] [CrossRef]
- Migliori, A. Resonant ultrasound spectroscopy. U.S. Patent 5,062,296, 5 November 1991. [Google Scholar]
- Mujica, N.; Cerda, M.T.; Espinoza, R.; Lisoni, J.; Lund, F. Ultrasound as a probe of dislocation density in aluminum. Acta Mater. 2012, 60, 5828–5837. [Google Scholar] [CrossRef]
- Salinas, V.; Aguilar, C.; Espinoza-González, R.; Lund, F.; Mujica, N. In situ monitoring of dislocation proliferation during plastic deformation using ultrasound. Int. J. Plast. 2017, 97, 178–193. [Google Scholar] [CrossRef]
- Migliori, A.; Maynard, J.D. Implementation of a modern resonant ultrasound spectroscopy system for the measurement of the elastic moduli of small solid specimens. Rev. Sci. Inst. 2018, 76, 121301. [Google Scholar] [CrossRef]
- Ulrich, T.J.; McCall, K.R.; Guyer, R.A. Determination of elastic moduli of rock samples using resonant ultrasound spectroscopy. J. Acoust. Soc. Am. 2002, 111, 1667–1674. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.A.; Guyer, R.A.; Ostrovsky, L.A. Nonlinear mesoscopic elastic class of materials. In Proceedings of the International Symposium on Nonlinear Acoustics, Göttingen, Germany, 1–4 September 1999. [Google Scholar]
- Kinney, J.H.; Gladden, J.R.; Marshall, G.W.; Marshal, S.J.; So, J.H.; Maynard, J.D. Resonant ultrasound spectroscopy measurements of the elastic constants of human dentin. J. Biomech. 2004, 37, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, N.; Ogi, H.; Hirao, M. Resonance ultrasound spectroscopy with laser-Doppler interferometry for studying elastic properties of thin films. Ultrasonics 2004, 42, 491–494. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, J. Assessment of material damage in a nickel-base superalloy using nonlinear Rayleigh surface waves. J. Appl. Phys. 2006, 99, 124913. [Google Scholar] [CrossRef]
- Matlack, K.H.; Kim, J.Y.; Jacobs, L.J.; Qu, J. Review of Second Harmonic Generation Measurement Techniques for Material State Determination in Metals. J. Nondestruct. Eval. 2015, 34, 273. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. Electromagnetic Acoustic Transducers; Springer: Tokyo, Japan, 2017; pp. 209–216. ISBN 978-4-431-56036-4. [Google Scholar]
- Ogi, H.; Sato, K.; Asada, T.; Hirao, M. Complete mode identification for resonance ultrasound spectroscopy. J. Acoust. Soc. Am. 2002, 112, 2553–2557. [Google Scholar] [CrossRef] [PubMed]
- Van Den Abeele, K.; Carmeliet, J.; Ten Cate, J.A.; Johnson, P.A. Nonlinear elastic wave spectroscopy (NEWS) techniques to discern material damage. Part II: Single-mode nonlinear resonance acoustic spectroscopy. Res. Nondestruct. Eval. 2000, 12, 31–42. [Google Scholar] [CrossRef]
- Haupert, S.; Renaud, G.; Riviere, J.; Talmant, M.; Johnson, P.A.; Laugier, P. High-accuracy acoustic detection of nonclassical component of material nonlinearity. J. Acoust. Soc. Am. 2011, 130, 2654–2661. [Google Scholar] [CrossRef] [PubMed]
- Spoor, P.S. Elastic Properties of Novel Materials Using PVDF Film and Resonant Acoustic Spectroscopy. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 1996. [Google Scholar]
- Espinoza, C. Caracterización de Densidad de Dislocaciones Mediante Espectroscopía de Resonancia Ultrasónica No Lineal. Master’s Thesis, Universidad de Chile, Santiago, Chile, 2013. [Google Scholar]
- Spoor, P.S.; Maynard, J.D.; Kortan, A.R. Elastic Isotropy and Anisotropy in Quasicrystalline and Cubic AlCuLi. Phys. Rev. Lett. 1995, 75, 3462. [Google Scholar] [CrossRef] [PubMed]
- Zolotoyabko, E. Fast quantitative analysis of strong uniaxial texture using a March–Dollase approach. J. Appl. Cryst. 2013, 46, 1877–1879. [Google Scholar] [CrossRef]
- Lincoln, R.C.; Koliwad, K.M.; Ghate, P.B. Morse-Potential Evaluation of Second- and Third-Order Elastic Constants of Some Cubic Metals. Phys. Rev. Second Ser. 1967, 157, 463–466. [Google Scholar] [CrossRef]
- Vallin, J.; Mongy, M.; Salama, K.; Beckman, O. Elastic Constants of Aluminum. J. Appl. Phys. 1964, 35, 1825–1826. [Google Scholar] [CrossRef]
- Ledbetter, H.M.; Naimon, E.R. Elastic Properties of Metals and Alloys. II. Copper. J. Phys. Chem. Ref. Data 1974, 3, 897–935. [Google Scholar] [CrossRef]
- Cantrell, J.H. Nonlinear dislocation dynamics at ultrasonic frequencies. J. Appl. Phys. 2009, 105, 043520. [Google Scholar] [CrossRef]
- Suzuki, T.; Hikata, A.; Elbaum, C. Anharmonicity Due to Glide Motion of Dislocations. J. Appl. Phys. 1964, 35, 2761. [Google Scholar] [CrossRef]
- Cash, W.D.; Cai, W. Dislocation contribution to acoustic nonlinearity: The effect of orientation-dependent line energy. J. Appl. Phys. 2011, 109, 014915. [Google Scholar] [CrossRef]
- Zhang, J.; Xuan, F.; Xiang, Y. Dislocation characterization in cold rolled stainless steel using nonlinear ultrasonic techniques: A comprehensive model. Europhys. Lett. 2013, 103, 68003. [Google Scholar] [CrossRef]
- Zhang, J.; Xuan, F. A general model for dislocation contribution to acoustic nonlinearity. Europhys. Lett. 2014, 105, 54005. [Google Scholar] [CrossRef]
- Lubarda, V.A. New estimates of the third-order elastic constants for isotropic aggregates of cubic crystals. J. Mech. Phys. Solids 1997, 45, 471490. [Google Scholar] [CrossRef]
- Chakrapani, S.K.; Barnard, D.J. Determination of acoustic nonlinearity parameter (β) using nonlinear resonance ultrasound spectroscopy: Theory and experiment. J. Acoust. Soc. Am. 2017, 141, 919. [Google Scholar] [CrossRef] [PubMed]

| Aluminum | ||||
| Parameter | Al Roll | Al Roll-A15 | Al Roll-A30 | Al Roll-A60 |
| (cm) | ||||
| (cm) | ||||
| (cm) | ||||
| (g/cm) | ||||
| Treatments | ||||
| Rolled | ||||
| Annealed | - | C min | C min | C min |
| Copper | ||||
| Parameter | Cu Roll 2 | Cu Roll-A15 | Cu Roll-A30 | Cu Roll-A60 |
| (cm) | ||||
| (cm) | ||||
| (cm) | ||||
| (g/cm) | ||||
| Treatments | ||||
| Rolled | ||||
| Annealed | - | C min | C min | C min |
| Aluminum | |||
| Treatment | (m/s) | (V) | (V) |
| Roll A60 | |||
| Roll A30 | |||
| Roll A15 | |||
| Roll | |||
| Copper | |||
| Treatment | (m/s) | (V) | (V) |
| Roll A60 | |||
| Roll A30 | |||
| Roll A15 | |||
| Roll | |||
| Aluminum | ||
| Compared Samples | (mm) | (mm) |
| Roll & Roll A60 | ||
| Roll & Roll A30 | ||
| Roll & Roll A15 | ||
| Copper | ||
| Compared Samples | (mm) | (mm) |
| Roll & Roll A60 | ||
| Roll & Roll A30 | ||
| Roll & Roll A15 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinoza, C.; Feliú, D.; Aguilar, C.; Espinoza-González, R.; Lund, F.; Salinas, V.; Mujica, N. Linear Versus Nonlinear Acoustic Probing of Plasticity in Metals: A Quantitative Assessment. Materials 2018, 11, 2217. https://doi.org/10.3390/ma11112217
Espinoza C, Feliú D, Aguilar C, Espinoza-González R, Lund F, Salinas V, Mujica N. Linear Versus Nonlinear Acoustic Probing of Plasticity in Metals: A Quantitative Assessment. Materials. 2018; 11(11):2217. https://doi.org/10.3390/ma11112217
Chicago/Turabian StyleEspinoza, Carolina, Daniel Feliú, Claudio Aguilar, Rodrigo Espinoza-González, Fernando Lund, Vicente Salinas, and Nicolás Mujica. 2018. "Linear Versus Nonlinear Acoustic Probing of Plasticity in Metals: A Quantitative Assessment" Materials 11, no. 11: 2217. https://doi.org/10.3390/ma11112217
APA StyleEspinoza, C., Feliú, D., Aguilar, C., Espinoza-González, R., Lund, F., Salinas, V., & Mujica, N. (2018). Linear Versus Nonlinear Acoustic Probing of Plasticity in Metals: A Quantitative Assessment. Materials, 11(11), 2217. https://doi.org/10.3390/ma11112217






